Abstract
The effect of the spacing between adjacent building floors on the wind distribution and turbulence intensity was analysed using computational fluid dynamics in this study. Five computational models were created with floor spacing ranging from 0.8 m (benchmark) to 1.6 m. The three-dimensional Reynolds-Averaged Navier–Stokes equations along with the momentum and continuity equations were solved using the FLUENT code for obtaining the velocity and pressure field. Simulating a reference wind speed of 5.5 m/s, the findings from the study quantified that at a floor spacing of 1.6 m, the overall wind speed augmentation was 39 % which was much higher than the benchmark model (floor spacing = 0.8 m) indicating an amplification in wind speed of approximately 27 %. In addition, the results indicated a gradual reduction in turbulence kinetic energy by up to 53 % when the floor spacing was increased from 0.8 to 1.6 m. Although the concept was to integrate wind turbines into the building fabric, this study is limited to the assessment of the airflow inside the spaces of building floors which can be potentially harnessed by a vertical axis wind turbine. The findings of this work have indicated that there is a potential for integration which will lead on to future research in this area.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Building energy framework is part of a multifaceted system that includes transport and urban planning and has major social consequences as well as climate change impacts. The energy mix is also important in determining carbon dioxide emissions. Buildings worldwide account for a surprisingly high 40 % of global energy consumption, and the resulting carbon footprint, significantly exceeding those of all transportation combined [1–3]. Energy consumption of the United Arab Emirates (UAE) is driven largely by residential use, with a major proportion of the electricity being consumed by the building sector.
With the ever-increasing economy of the UAE, the dependency on usage of non-renewable resources of energy is cumulating in direct proportion. Nevertheless, the non-renewable potential of these resources is certainly a leading world-wide issue, and one which has gained substantial international interest over the past decades. Large and attractive opportunities exist to reduce building’s energy use at lower costs and higher returns than other sectors. At the same time, substantial investments will be required to achieve this target. These will require the combination of social, economic and environmental actions, including building energy codes, investment subsidies, labelling and reporting mechanisms, increased and trained workforce capacity, and evolving energy-efficient designs and technologies.
There is a shortage of research on exploiting the potential building integrated wind turbines in achieving a sustainable built environment. Apart from using the height of high-rise buildings to increase energy capture, strategically optimising building geometry and its aerodynamic features itself can enhance wind turbine performance by inducing a higher volume of air than the macro-climate. One such proposal is to integrate wind turbines between floors of high rise structures as conceptually described by the rotating tower sustainable building design model. The arrangement uses the power generated to supply each residential apartment and also to rotate the floors, thus creating a dynamic structure [4].
This study numerically investigates the aerodynamic design of the rotating tower or dynamic architecture proposed for Dubai, UAE [4]. In relation to the existing literature [5–8], the CFD modeling approach is used in this paper out in order to determine the influence of floor spacing on the efficiency of building-integrated wind turbines with the spacing-height ratios varying between 25 and 50 %. Individual parameters including air velocity distribution, pressure profiles and turbulence kinetic energy is analysed to illustrate the variations in relation to increasing floor altitude.
Previous related work
Work related to the implementation of renewable energy as power sources in buildings, in particular wind energy is vast. Following is a concise assessment of prior work related to this investigation. In our previous works [5, 6], we have developed a numerical methodology for simulating the performance of a horizontal axis wind turbine integrated into a high-rise structure.
Chaudhry et al. [5] conducted a numerical study using Computational Fluid Dynamics (CFD) on determining the influence of structural morphology on the performance of wind turbines using Bahrain World Trade Centre as the case-study. The study used square, triangular and circular cross-sections of the building in addition to the benchmark model. The findings determined that the optimum cross-sectional configuration for installing wind turbines in high-rise buildings was the circular orientation as the average wind speed at the wind turbines was accelerated by 0.3 m/s resulting in an overall augmentation of 5 %. The results from this study therefore highlighted that circular building morphology is the most viable building orientation, particularly suited to regions with a dominant prevailing wind direction.
Further work by Chaudhry et al. [6] quantified an estimate power generation of 6.4 kW and a capacity factor of 2.9 % for the benchmark model at a reference wind speed of 6 m/s. In addition, the investigation determined that the wind direction of 180° yielded most favorable results with a maximum power production capacity of 29.3 kW indicating a high capacity factor of 13 %
Chong et al. [7] conducted a study on the design of a wind turbine generator for the purpose of energy consumption in buildings. Two vertical axis wind turbines (VAWTs) in cross-wind orientation which were integrated with an enclosure were installed above a cooling tower in order to harness the discharged wind for electricity generation. The tests were conducted with and without the VAWTs on the performance of the system. From the laboratory testing, it was observed that installing VAWT sat a correct position above the exhaust air system did not indicate any significant negative impacts on the performance of the cooling tower model. The performance of the cooling tower model was improved by the increment of intake air speed and the reduction off an motor power consumption. The rotational speed of the VAWTs were very high (>400 rpm) while the tip speed ratios were in the range of 1.28–1.29, making it preferable for electricity generation.
Sharpe and Proven [9] carried out detailed work on the concept and early development of a building integrated wind turbine in Scotland. The Crossflex proposal used in this investigation is based on the Darrieus turbines approach, consisting of two or more flexible aero foil blades attached to both the top and bottom of a vertical rotating shaft.
Although the development of this technology is still in its early stage, the study has outlined the remaining tasks of its work. The subsequent stages will involve supplementary computer modeling using CFD analysis to model airflow over the cowling to establish the nature of augmentation and flow stability that may occur, and to optimize the design in respect of these. This stage will also investigate materials that may be used for the cowling, in terms of both functional and aesthetic performance and also possible behavior of the frame as a mechanism for inducing passive twist in the blades. It is anticipate that these designs will be evaluated against common building types to test methods of fixing, loads distribution and integration under a variety of built form conditions.
Wang et al. [10] developed a methodology for aerodynamic study on a small domestic wind turbine with scoop to improve energy capture under low ambient wind speeds. The work used advanced CFD modelling incorporating the RNG k-e turbulence model. The findings of this work depicted that having a scoop acts as a diffuser and amplifies the airflow speed by a factor of 1.5 times equivalent to an increase in power output of 2.2 times with the same swept area. In addition, the work concluded that CFD can be used as a robust modelling technique for designing such wind turbine rotor blade systems to function within the proposed wind scoop.
Computational domain
The rotating tower is one of the green projects scheduled to be built in Dubai. Once complete, it will stand at 420 m and will comprise of 78 floors [4, 11], each with the freedom to rotate about its own axis.
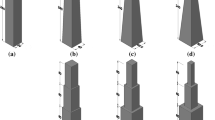
Detailed information about the dimensions of the structure is scarce. One important aspect is the spacing between individual floors which is 20 % of the floor height itself. This spacing is to accommodate for the wind turbine blades integrated inside the building structure. The height of each floor is 5.2 m and hence, the spacing is approximately 0.8 m. The three-dimensional computer-aided design was used for the CFD analysis; with dimensions shown in Fig. 1.
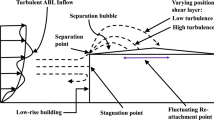
The computational domain comprised of the building geometry, which was designed according to the actual specifications of the high-rise tower and the specific wind turbines. The enclosure was designed to allow for simulating the macro-climate wind profiles over the building as specified in Fig. 2. In order to ensure that the walls of the computational domain will have no or minimal adverse effect on the airflow near the building, the domain was sized appropriately (2.6 H for the side wall and 2.1 H for the top wall). The distancing between the building and inlet or outlet is set based on the AIJ guidelines for simulating urban environments [16].
ANSYS FLUENT 14 commercial software was used to perform The Reynolds-Averaged Navier–Stokes (RANS) computations based on a control volume approach for solving flow equations. The Semi-Implicit Method for Pressure-Linked Equations (SIMPLE) algorithm was used for velocity–pressure coupling. All of the transport equations were discretized using second order upwind scheme. The standard k-e transport model which is frequently used for studying airflows around buildings was used to define the turbulence kinetic energy and flow dissipation rate within the model [12, 13]. The governing equations are the continuity, momentum and energy which are detailed in Eqs. 1–3.
where; \(\vec{v}_{q}\) represents the velocity of phase q and \({\dot{\text{m}}}_{\text{pq}}\) and \(\dot{m}_{qp}\) characterises the mass transfer from the pth to qth phase and vice versa. \(\bar{\bar{\tau }}_{q}\) represents the qth phase stress–strain tensor. h q represents the specific enthalpy of the qth phase and \(\vec{q}_{q}\) represents the heat flux. Q pq represents the intensity of heat exchange between the pth and qth phases and h pq is the interface enthalpy. S q represents the source term.
The use of the standard k-e transport model on building configurations has been found in previous works [11, 14]. The turbulence kinetic energy, k, and its rate of dissipation, e, are obtained from the following transport equations formulated in Eqs. 4 and 5.
where G k represents the generation of turbulence kinetic energy due to the mean velocity gradients, G b represents the generation of turbulence kinetic energy due to buoyancy. Y M represents the contribution of fluctuating dilatation in compressible turbulence to the overall dissipation rate. C 1e , C 2e and C 3e are constants; σ k and σ e are the turbulent Prandtl numbers for k and e.
Mesh generation
The computational volumes were applied with non-uniform mesh due to the complicated shape of the geometry. The meshed model comprised of 2,523,459 nodes and 11,849,200 elements as displayed in Fig. 3. The minimum face angle was 5.67° while the maximum edge length and element volume ratios were 9.9 and 44.6. As observed in Fig. 3, the mesh around the building and spacing between the floors were refined to ensure that the flow field was accurately captured in the simulations.
Grid verification
In order to verify the accuracy of the numerical models, a grid independency test was carried out to determine the variation in results over increasing mesh sizes. Basic concepts associated with mesh refinement deals with the refinement and evaluation of elements where the posterior error indicator is larger than the preset criterion, while mesh enrichment considers running higher order polynomials till the solution is expected to improve with a fixed mesh [13]. Grid verification was carried out using mesh refinements (h-method) in order to optimise the distribution of mesh size h over a finite element.
The area-weighted average value of the static pressure on the building façade was taken as the error indicator (Fig. 4), as the grid was refined from 1,427,500 to 11,849,200 elements. The discretisation error was found to reduce to below 1 % when the cells were increased 11,849,200 and hence the size was used in this investigation. The mesh used for the investigation was based on a grid verification analysis which was performed by conducting additional simulations of the same domain and boundary conditions but with various mesh sizes.
Boundary conditions
Using the benchmark model (floor spacing = 0.8 m), a total of four additional computational models were created with floor spacing variation ranging from 0.8 to 1.6 m in order to determine its impact on the wind velocity and pressure distribution and thus evaluate the potential for integrating wind turbines within the space. Table 1 displays a section of the generated computational models for this investigation.
The applied boundary conditions comprised of a reference velocity (uref) of 5.5 m/s at a height of 420 m (zref) approaching directly perpendicular to the building façade [5, 6]. The geometry was modeled as a solid zone while the enclosure was modeled as a fluid zone for the analyses. The boundary conditions were kept identical throughout the numerical investigation for all analysed models and are displayed in Table 2.
Using the computational domain, a representation of velocity boundary layer profile and turbulence intensity (I) at the windward side of the building is shown in Fig. 5 wherein the wind speed is taken from the direction of the sea. The thickness of boundary layer of the atmosphere varies with wind speed, turbulence level and the type of surface. The power law is an empirical equation expressed in Eq. 1. For neutral stability conditions, α is approximately 1/7, or 0.143, regarded as a reasonable but conservative estimate [15].
where u is the speed at a particular point, uref is the reference speed, z is the height at a particular point and zref is the reference height.
Results and discussion
Figure 6 displays the static pressure gradient at a height of 250 m above ground level on the building model with a spacing of 1.6 m between floors. At an inlet wind speed of 5.5 m/s and wind angle of 0°, the maximum positive pressure of 29 Pa was created on the windward side of the tower. As expected, a negative pressure was created on the leeward side thus highlighting a maximum pressure differential of 102 Pa. Figure 6b shows a more detailed view of the static pressure distribution inside the floor spacing. Similarly, positive pressure was observed on the wind ward side of the internal circular wall and negative pressure on the sides where airflow splits and accelerates.
Air velocity distribution for the building model with spacing of 1.6 m between floors is shown in Fig. 7. The direction of the airflow in the diagram is from left to right. The airflow velocity was reduced up to 2.1 m/s as it approached the wind ward surface of the building. Some of the airflow streamed around the sides of the building with some entering the floor spacing. The airflow inside the spacing accelerates as it moved along the sides of the internal circular wall. Using the inlet speed of 5.5 m/s, the findings showed that the velocity was increased by almost 92 % to 10.6 m/s between the floors of the building. The wind turbine can be designed and positioned inside the spacing to exploit this wind acceleration. A large region of recirculation was observed on the leeward side of the building.
Figure 8 displays the contour levels for the turbulence kinetic energy on the building geometry. The maximum turbulence was observed in the region adjacent between two conforming floors of the building, thus indicating a turbulent exposure of the proposed wind turbines with the incoming flow of air. The maximum turbulence intensity was recorded at 2.5 J/kg while a mean turbulence intensity of 1.1 J/kg was obtained on the windward façade of the geometry.
Figure 9 displays the velocity distribution on the building at increasing altitude ranging from ground level to 450 m. In general, all analysed heights displayed a similar velocity profile with the wind shearing away towards the sides of the tower while creating a region of re-circulation at the leeward end owing to the adverse pressure gradient. However, due to the simulated atmospheric boundary layer flows, a gradual increase in air velocity were observed as the height was gradually increased highlighting a direct proportionality between the two parameters. This phenomenon must be taken into account during the design stage as surrounding structures can have an impact on the airflow distribution particularly, the wind turbines that will be located on the lower floors.
Table 3 displays the summary of area-weighted results for mean velocity, turbulence intensity and pressure variables for the rotating tower building model with floor spacing ranging from 0.8 to 1.6 m. A linear proportionality between floor spacing and air velocity was observed with the speed increasing by 9 % from 8.9 to 9.9 m/s at a floor spacing of 1.6 m respectively. The turbulence intensity was found to decrease from 52 to 34 % signifying the positive influence of varying floor spacing on turbulence characteristics. A detailed demonstration of the floor spacing on the induced wind velocity and turbulence is highlighted in Fig. 10.
The graphical representation of the effect of floor spacing on the wind distribution is shown in Fig. 11. In order to quantify the findings, three individual points were created on the building geometry and the results of air velocity were recorded for each computational model. As observed, all the three points indicated an increase in air velocity as the floor spacing was increased from 0.8 to 1.6 m with a maximum speed of 9.1 m/s. At a floor spacing of 1.6 m, the overall wind speed augmentation was calculated at 39 % which was much higher than the benchmark model (floor spacing = 0.8 m) which indicated an amplification in wind speed of approximately 27 % from the inlet velocity of 5.5 m/s. The investigation depicted that the morphology of the building plays a key role in the overall character of air circulation over the structure and also the spacing between the floors.
The effect of floor spacing on the overall turbulence kinetic energy and pressure variables are quantified in Figs. 12 and 13. An inverse proportionality trend was obtained for parameters as the turbulence kinetic energy across point 1 was found to decrease from 0.36 to 0.17 J/kg as the floor spacing was increased from 0.8 to 1.6 m. The highest variation in turbulence kinetic energy was noted across point 3 which was located directly perpendicular to the incoming wind. On average, the turbulence kinetic energy decreased by 53 % across the points on the sides (Point 1 and 2) when the floor spacing was increased from 0.8 to 1.6 m, thus underlining a considerable improvement in air distribution.
A comparison between the overall floor height of the building and the corresponding wind velocity is displayed in Fig. 14. As expected, the two quantities were found to be in direct proportion to each other. Using the inlet wind speed of 5.5 m/s, an increase of 19 % was obtained at a height of 100 m above ground level. The air velocity was further found to accelerate by 25 % at a height of 450 m. This phenomenon was predominantly because of the boundary layer which is formed due to the spatially integrated heat and moisture exchanges between the urban environment and its overlying air.
Increasing the energy efficiency of high-rise buildings by utilising renewable energy is a major factor in improving the sustainability of the built environment As depicted from the results, structural morphology plays a very important role on the efficiency of building-integrated wind turbines by regulating the induced air stream. For the rotating tower model, the aerodynamic façade assists in an unfluctuating distribution of wind across the building as noted from the velocity gradient represented by discrete point measurements taken in Fig. 11. The airstream was shown to accelerate by 12 % when the floor spacing was increased from 0.8 to 1.6 m. In addition, having an aerodynamic façade with a floor spacing of 1.6 m reduces the overall turbulence kinetic energy over the structure by up to 53 %.
Conclusion
Dynamic architecture is a term devised for a new generation of off-grid high rise structures that rotate. In this paper, the influence of building morphology on wind distribution is presented by investigating the spacing between adjacent building floors of dynamic architecture. Five computational models were created with floor spacing ranging from 0.8 m (benchmark) to 1.6 m. The three-dimensional Reynolds-Averaged Navier–Stokes (RANS) equations along with the momentum and continuity equations were solved for obtaining the velocity and pressure field. Simulating a reference wind speed of 5.5 m/s, the findings from the study quantified that at a floor spacing of 1.6 m, the overall wind speed augmentation was 39 % which was much higher than the benchmark model (floor spacing = 0.8 m) indicating an amplification in wind speed of approximately 27 %. In addition, the study indicated a decrease in turbulence kinetic energy by 53 % when the floor spacing was increased from 0.8 to 1.6 m, thus underlining a considerable improvement in air distribution. The findings from this study depicted that the vertical morphology and aerodynamic features of a building plays a key role in the overall character of air distribution over the structural façade. The results from this study can be used for the design and integration of wind generation technologies into high rise buildings.
References
Key World Energy Statistics, International Energy Agency, Head of Communication and Information Office, 75739 Paris Cedex 15, France
Müller G, Mark F, Jentsch ES (2009) Vertical axis resistance type wind turbines for use in buildings. Renew Energy 34:1407–1412
Killa S, Smith RF (2008) Harnessing energy in tall buildings: Bahrain World Trade Center and Beyond, Council of Tall Buildings and Urban Habitat (CTBUH) 8th World Congress, Dubai, United Arab Emirates, March 3–5
Fisher DH (2008) Rotating tower Dubai, Rotating Tower Technology International Limited (UK)
Chaudhry HN, Calautit JK, Hughes BR (2014) The influence of structural morphology on the efficiency of Building Integrated Wind Turbines (BIWT). Aims Energy 2:219–236
Chaudhry HN, Calautit JK, Hughes BR (2015) Computational analysis to factor wind into the design of an architectural environment. Model Simul Eng Article ID 234601
Chong WT, Yip SY, Fazlizan A, Poh SC, Hew WP, Tan EP, Lim TS (2013) Design of an exhaust air energy recovery wind turbine generator for energy conservation in commercial buildings. Renew Energy 67:252–256
Lu L, Sun K (2014) Wind power evaluation and utilization over a reference high-rise building in urban area. Energy Build 68:339–350
Sharpe T, Proven G (2010) Crossflex: concept and early development of a true building integrated wind turbine. Energy Build 42:2365–2375
Wang F, Bai L, Fletcher J, Whiteford J, Cullen D (2008) The methodology for aerodynamic study on a small domestic wind turbine with scoop. J Wind Eng Ind Aerodyn 96:1–24
Chaudhry HN, Hughes BR (2010) Computational analysis of dynamic architecture. IMechE – J. Power Energy IMechE Part A: Vol 225, Number 1/2010
Launder BE, Spalding DB (1972) Lectures in mathematical models of turbulence. Academic Press, London
Chung TJ (2002) Computational fluid dynamics. Cambridge University Press; illustrated edition, ISBN-0521594162
Calautit JK, Hughes BR, Ghani SA (2013) Numerical investigation of the integration of heat transfer devices into wind towers. Chem Eng Trans 34:43–48
Kubik ML, Coker PJ, Hunt C. (2011) Using meteorological wind data to estimate turbine generation output: a sensitivity analysis. World Renewable Energy Congress; Linkoping, Sweden
Tominaga Y, Mochida A, Yoshie R, Kataoka H, Nozu T, Yoshikawa M, Shirasawa T (2008) AIJ guidelines for practical applications of CFD to pedestrian wind environment around buildings. J Wind Eng Ind Aerodyn 96:1749–1761
Acknowledgments
The authors would like to acknowledge Heriot-Watt University and the University of Sheffield for the use of the research facilities.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
I hereby confirm, on behalf of the authors that none of the authors have any competing interests in the manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Chaudhry, H.N., Calautit, J.K. & Hughes, B.R. Design and aerodynamic investigation of dynamic architecture. Innov. Infrastruct. Solut. 1, 7 (2016). https://doi.org/10.1007/s41062-016-0002-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s41062-016-0002-2