1 Introduction

A key prerequisite to develop reliable and trustworthy Artificial Intelligence (AI) methods is the capability to measure their risks. When applied to high impact and regulated industries, such as energy, finance and health, AI methods need to be validated by national regulators, possibly according to international standards, such as ISO/IEC CD 23894. Most AI methods rely on the application of highly complex machine learning models which, while reaching high predictive performance, lack explainability and robustness. This is a problem in regulated industries, as authorities aimed at monitoring the risks arising from the application of AI methods may not validate them (see, for example, [8]). In line with these issues, [13] further highlights that the interpretation of the outcomes provided by the most powerful methods is difficult due to the lack of knowledge about the underlying processes generating them. As a consequence, these methods suffer from being sensitive to data changes, which in turn can give rise to non-stable results.

It follows that, in all the fields where the use of AI systems may affect human life (health and finance among others), comprehensible results need to be obtained to allow organisations to detect risks, especially in terms of the factors which can cause them. This objective is more evident when dealing with AI systems.

Indeed, AI methods have an intrinsic black-box nature, resulting in automated decision making that can, for example, classify a person into a class associated with the prediction of its individual behaviour, without explaining the underlying rationale. To avoid that wrong actions are taken as a consequence of “automatic” choices, AI methods need to explain the reasons of their classifications and predictions.

The notion of “explainable” AI has become very important in the recent years, following the increasing application of AI methods that impact the daily life of individuals and societies. At the institutional level, explanations can answer different kinds of questions about a model’s operations depending on the stakeholder they are addressed to (see, for example, [4]): developers, managers, model checkers, regulators. In general, to be explainable, AI methods have to provide details or reasons clarifying their functioning.

We remark that our notion of explainability is akin to the notion of transparency (or mechanistic interpretability), which is intended as the reason an algorithm produces a specific output and which is only one type of explainability: see, for example, [6] for a review of other notions of explainability.

From a mathematical view point, the explainability requirement can be fulfilled using linear machine learning models such as, for example, logistic and linear regression models. However, it is worth noting that although in the medical domain no evidence of superior performance of machine learning models over linear machine learning models was actually found (see, for example, [7]), in the presence of complex or large databases, linear models may be less accurate than nonlinear machine learning models, such as neural networks and random forests, which are, however, not explainable and may also be less robust.

This trade-off can be solved empowering accurate machine learning models with innovative methodologies able to explain their classification and prediction output. A recent attempt in this direction can be found in [12], who proposed a SAFE AI approach, based on Lorenz Zonoids, to jointly measure Sustainability, Accuracy, Fairness and Explainability of a machine learning model, extending what proposed by [4] and [5], combining Shapley values (see, for example, [18] and [16]) with Lorenz Zonoids, the multivariate extension of the Gini coefficient (see, for example, [15]).

Shapley values have the advantage of being agnostic: independent on the underlying model with which classifications and predictions are computed, but have the disadvantage of not being normalised and, therefore, difficult to be used in comparisons outside the specific application.

The joint employment of Shapley values and Lorenz Zonoids proposed in [12] provides a unifying tool to measure predictive accuracy, explainability, fairness and sustainability of a machine learning model, leading to a combined SAFEty score, and is particularly useful to compare alternative models.

Although intuitive and transparent, the SAFE approach has the disadvantage of computational complexity, common to all post-processing explainability models based on Shapley values.

In this paper, we aim to solve the issue by means of a pre-processing approach which allows to select a parsimonious set of variable features which not only maintain predictive accuracy (with respect to a more complex full model), but are also explainable and robust.

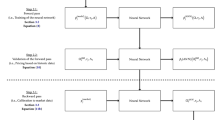
To this aim, we propose to extend the Forward Search approach (FS), employed in assessing the robustness of statistical learning models, to machine learning models.

Our proposal will be tested on a financial forecast problem that concerns the prediction of the price of Bitcoins, by means of five well known “classic” financial variables: the price of Oil, Gold, the Standard and Poor’s index and the exchange rate of the Dollar with Euro and Yuan.

The paper is organised as follows: we first illustrate the proposed methodology; we then describe the data on which we apply the methodology, and discuss the obtained empirical findings. We conclude with a discussion.

2 Methodology

Given that the linear regression model is the workhorse of applied statistics, that is, the most used and useful set of procedures for the analysis of data, we start recalling it, in order to set the notation and explain our procedure.

The linear regression model in matrix form is written as E\((Y) = X\beta \), where there are n observations on a continuous response and X is an \(n \times p\) matrix of the constant term and the values of the \(p-1\) explanatory variables. The elements of X are known constants. The model for the ith of the n observations can be written in several ways as, for example,

$$\begin{aligned} y_i = \eta (x_i,\beta ) + \epsilon _i = x_i^T\beta + \epsilon _i = \beta _0 + \sum _{j=1}^{p-1}\beta _jx_{ij} + \epsilon _i. \end{aligned}$$
(1)

The “second-order” assumptions are that the errors \(\epsilon _i\) have zero mean, constant variance \(\sigma ^2\) and are uncorrelated. In non-robust inference, it is standard to assume that, in addition, the errors are normally distributed. Under the second-order assumptions and normality, the least squares estimates \(\hat{\beta }\) of the parameters \(\beta \) are the maximum likelihood estimators. They minimise the sum of squares \(S(\beta ) = (y - X\beta )^T(y - X\beta )\) and so are solutions of the estimating equation

$$\begin{aligned} X^T(y - X\hat{\beta }) = 0, \end{aligned}$$
(2)

with the solution \(\hat{\beta } = (X^TX)^{-1}X^Ty\). The vector of n predictions from the fitted model is \(\hat{y} = X\hat{\beta } = X(X^TX)^{-1}X^Ty = Hy\), where the projection matrix H is called the hat matrix because it “puts the hats on y”. The vector of least squares residuals is

$$\begin{aligned} e = y - \hat{y} = y - X\hat{\beta } = (I - H)y \end{aligned}$$
(3)

and the residual sum of squares is

$$\begin{aligned} S(\hat{\beta }) = \sum _{i=1}^n e_i^2 = y^T(I - H)y. \end{aligned}$$
(4)

To test the terms of the model we use F tests or, equivalently, t tests if interest is in a single parameter. Calculation of the t tests requires the variances of the elements of \(\hat{\beta }\). Since \(\hat{\beta }\) is a linear function of the observations, \(\text{ var } (\hat{\beta }) = \sigma ^2 (X^TX)^{-1}.\) Let the kth diagonal element of \((X^TX)^{-1}\) be \(v_k\), when the t test for testing that \(\beta _k =0\) is

$$\begin{aligned} t_k = \hat{\beta }_k/(s^2_{\nu }v_k)^{0.5}, \qquad k=1, \ldots , p, \end{aligned}$$
(5)

where \(s^2_{\nu } = S(\hat{\beta })/(n-p)\) is an estimate of \(\sigma ^2\) on \( \nu = n-p\) degrees of freedom. If \(\beta _k = 0,\;t_k\) has a t distribution on \(\nu \) degrees of freedom.

A large value of the t statistic, while encouraging, says nothing about the contribution of particular groups of observations to various aspects of the fit, such as their importance, if any, in the evaluation of its significance. The focus of this paper is the choice of the predictors that constitute X in such a way that the importance of subsets of units is clearly revealed. In order to appraise the effect that each unit, outlier or not, exerts on the fitted model and more in general to order the units from those most in agreement with a particular model to those least in agreement with it, we use the Forward Search [1]. This method starts from a small, robustly chosen, subset of the data that excludes outliers. We then move forward through the data, adding observations to the subset used for parameter estimation and removing any that have become outlying due to the changing content of the subset. As we move forward, we monitor statistical quantities, such as parameter estimates, residuals and test statistics. Since the search orders the observations by the magnitude of their residuals from the fitted subsets, the value of \(s^2_{\nu }\) increases during the search, although not necessarily monotonically. As a consequence, even in the absence of outliers and model inadequacies, the values of the t statistics for the parameters in the model decrease during the search and are hard to interpret. In order to obtain useful and interpretable forward plots of t tests, we fit a model including all variables except the one of interest, the “added” variable w, so that the regression model becomes

$$\begin{aligned} \text {E}(Y) = X\beta + w\gamma , \end{aligned}$$
(6)

where \(\gamma \) is a scalar. The least squares estimate \(\hat{\gamma }\) can be found explicitly from the normal equations for this partitioned model. If the model without \(\gamma \) can be fitted, \((X^TX)^{-1}\) exists and

$$\begin{aligned} \hat{\gamma } = {w^T(I-H)y}/{w^T(I-H)w} = {w^TAy}/{w^TAw}. \end{aligned}$$
(7)

We now write (7) in terms of residuals. Since \(A = (I- H)\) is idempotent, \(\hat{\gamma }\) can be expressed in terms of the two sets of residuals \(e = \tilde{y} = (I-H)y = Ay\) and the residuals of the added variables \( \tilde{w} = (I-H)w = Aw\). Then

$$\begin{aligned} \hat{\gamma }= & {} {w^T(I-H)y}/{w^T(I-H)w} = {w^TAy}/{w^TAw} \nonumber \\= & {} \tilde{w}^Te/ (\tilde{w}^T\tilde{w}). \end{aligned}$$
(8)

Thus, \(\hat{\gamma }\) is the coefficient of linear regression through the origin of the residuals e on the residuals \(\tilde{w}\) of the new variable w, both sets of residuals coming from regression on the variables in X.

The computation of the t statistic requires the variance of \(\hat{\gamma }\). Since, like any least squares estimate in a linear model, \(\hat{\gamma }\) is a linear combination of the observations, it follows from (7) that

$$\begin{aligned} \text{ var } (\hat{\gamma })= & {} \sigma ^2 {w^TA^TAw}/{(w^TAw)^2} = {\sigma ^2} /(w^TAw) \nonumber \\= & {} \sigma ^2 / ( \tilde{w}^T\tilde{w}). \end{aligned}$$
(9)

Calculation of the test statistic also requires \(s^2_w\), the residual mean square estimate of \(\sigma ^2\) from regression on X and w, given by

$$\begin{aligned} (n - p -1)s^2_w= & {} y^Ty - \hat{\beta }^TX^Ty -\hat{\gamma }w^Ty \nonumber \\= & {} y^TAy - (y^TAw)^2/ (w^TAw). \end{aligned}$$
(10)

The t statistic for testing that \(\gamma = 0\) (known as deletion t statistics [2]) is then

$$\begin{aligned} t_w = {\hat{\gamma }}/(s^2_w/ w^TAw)^{0.5}. \end{aligned}$$
(11)

If w is the explanatory variable \(x_k\), (11) is an alternative way of writing the usual t test (5). In Sect. 4, we use the added variable method, combined with the FS, to provide an informative method of monitoring the evolution of t tests for the individual parameters in the model. Instead of using all the observations, we start with a subset of size \(m=p+1\) robustly chosen. Specifically, we search over subsets of p observations to find the subset that yields the LMS (Least Median of Squares) or LTS (Least Trimmed Squares) estimate of \(\beta \). In other words, for each subset of size p we take the squared residuals for all the observations and store the value of the median or the trimmed sum of squared residuals. The subset with the smallest median of squared residuals (based on all the observations) gives the LMS estimator of \(\beta \) (see [17]). Similarly, the subset with the smallest trimmed sum of squared residuals (based on all the observations) gives the LTS estimator of \(\beta \). It is worth noting that this initial subset serves just to initialise the Forward Search procedure. We move forward to a larger subset by ordering the n squared residuals from the least squares fit to the subset of m observations and using the \(m+1\) observations with the smallest squared residuals as our new larger subset. Usually, one observation is added to the subset at each step, but sometimes two or more are added as one or more leave, which is often an indication of the introduction of some of a cluster of outliers. In this way, we obtain a series of parameter estimates for \(p+1 \le m \le n\), which progresses from very robust at the beginning of the search to least squares at the end. The inclusion in each step of additional unit (the one most in agreement with the subset based on size m, given that every time we select the units with the smallest \(m+1\) squared residuals given the estimate of \(\beta \) based on a subset of size m) enables us to understand how the t statistic changes due to the introduction of this additional unit and therefore to interpret the contribution of each observation or subsets of observations in understanding the significance of each predictor.

We remark that, as in each step an observation may leave the subset, it is not important the choice of the initial subset because the outlying observations enter it in the final stages of the procedure. As discussed above, when moving forward, we monitor statistical quantities, such as parameter estimates, residuals and test statistics. One importance of this approach is that sequential testing for outliers can be used to determine the proportion of outliers in the data and so to provide an empirical estimate of how many observations should be deleted in the robust estimation of the parameters. We notice that the idea of monitoring the performance of a range of robust estimators is not limited to the forward search, but it extends to any robust estimator. This is in stark contrast with the typical robust approach which works with a pre-specified value of robustness or efficiency.

One of the contributions of this paper is that we check the stability of the results varying the value of robustness or efficiency. This paves the way to a new approach of data analysis in which it is possible to understand the effect that each unit or subgroups of units exert on the model and therefore to a sort of explainable robustness.

The application of the FS for standard linear and transformations is described for example in [3]. Note that the procedure described above for the linear regression model can be applied to any other complex model, like for example neural network with any kind of complexity based on any number of hidden layers. The basic ingredients of the FS (fitting of model based on a subset of units robustly chosen with a breakdown point in a such a way that the subset is not affected by outliers; the prediction for all the units based on the model parameters based on the subset; the choice of the next subset using the smallest \(m+1\) squared residuals) can, in principle, be applied to any model. Finally, also the monitoring approach, which is based on the analysis of the evolution of particular statistics of interest (in our case the t statistic), can be applied to any model.

In Sect. 4, we show the monitoring of the t statistics based on a neural network regression model. The comparison of the monitoring of a simple model like linear multiple regression with that coming from a more sophisticated specification can lead us to better interpret which is the subset of units which mostly benefits from the application of the more complex model. In presence of time series data, as we see in Sect. 4, this allows us to interpret the sub-periods of time which require a nonlinear specification.

The contribution of this paper is to extend, for the first time in the literature, the FS tools to the field of modern neural networks and to show the gain of interpretability that the monitoring approach can have in the nonlinear world. Moreover, the proposed extension seems in parallel with the ongoing research direction in machine learning literature, addressed to the detection of instances that may be seen as outliers and hence overly impacting on the training procedure (for more details, see [19] and [20]).

3 Data

To give an illustrative example of how to apply our proposal and to better appreciate its benefits, we consider the data analysed in [10], which report information on the daily Bitcoin prices in eight different crypto exchanges, recorded from a time period between May 18, 2016, and April 30, 2018.

We remark that the same data were considered by also [11], to explain the Bitcoin price variations as a function of the available financial explanatory variables. The authors selected, as the set of the explanatory variables, the time series observations for the SP500 index together with the Oil and Gold prices.

Fig. 1
figure 1

Evolution of: a Bitcoin prices, b SP500 index, c Gold and d Oil prices, e USD/Eur and f USD/Yuan exchange rates in the time period between May 18, 2016, and April 30, 2018

Full size image

A further investigation of these data was further provided in a recent work by [12], who introduced a SAFE Artificial Intelligence approach aimed at formalising a new global normalised measure for the assessment of the contribution of each additional explanatory variable to the explanation of the Bitcoin prices.

For the sake of coherence with the cited applications based on the considered data, here we choose the time series observations on the Bitcoin prices in the Coinbase exchange as the response variable to be predicted. As suggested by [10] and [11], the time series for Oil, Gold and SP500 prices are taken into account as candidate financial explanatory variables. The choice of such predictors is motivated by their economic importance. Moreover, it is worth noting that, in line with [9], the exchange rates USD/Yuan and USD/Eur are also included as additional explanatory variables.

Our aim is to exploit the Forward Search procedure framework and extend it to jointly assess accuracy, explainability and robustness. The Forward Search procedure appears as a powerful method to detect in advance which are the most explainable variables for different groups of observations and, in particular, for the more central and the more extreme.

Before discussing the findings derived from the implementation of our proposal, a descriptive analysis of the data is required to provide an exhaustive picture of the involved variable features.

We start by plotting the time evolution of the Bitcoin prices, together with that related to the classical asset prices, the SP500 index and the exchange rates, in the considered time period. The trend is displayed in Fig. 1. Specifically, from Fig. 1a it arises that the Bitcoin prices appear quite stable until the beginning of the 2017 year. But, since the first six months of the 2017 year, the Bitcoin prices begin to progressively increase reaching the maximum at the end of the same year. This dynamics is followed by a downtrend, which starts from January 2018.

While the trend of the SP500 increases overtime, as shown in Fig. 1b, the prices of Gold and Oil are characterised by uptrend and downtrend. The former is more evident at the end of the 2016 year for Gold (Fig. 1c), while for Oil it occurs some months before the end of the 2016 year (Fig. 1d).

Finally, the behaviour of the exchange rates USD/Eur and USD/Yuan is quite similar overtime (Fig. 1e, f).

To better understand the dynamics reported in Fig. 1, some summary statistics on the considered data are provided in Table 1.

Table 1 Summary statistics for Coinbase Bitcoin prices, classic asset prices, SP500 index and exchange rates (mean, standard deviations (sd), coefficient of variation (cv), minimum and maximum values)
Full size table

Results in Table 1 highlight that both the mean values, the standard deviations and the minimum and maximum values are largely different with respect to those of the classical assets, such as Gold and Oil, the SP500 index and the exchange rates. To better appreciate the volatility magnitude of the prices, the coefficient of variation (cv) is computed and reported in Table 1. The findings show that the exchange rates are much less volatile than the Bitcoin and classical asset prices. Indeed, for USD/Eur and USD/Yuan the standard deviations are only \(5\%\) and \(3\%\) the size of the mean, respectively. A similar result in terms of volatility is achieved by Gold, whose standard deviation corresponds to \(4\%\) the size of the mean, while for Oil and SP500 the standard deviations slightly increase reaching values which are less than \(10\%\) of the mean.

4 Empirical findings

In this section, we present the results from the application of our proposal to the Bitcoin data (Sect. 4.3). Before implementing our approach, a preliminary analysis is needed to evaluate the relationship between the Coinbase Bitcoin prices and the classical asset prices, together with the SP500 index and the exchange rates (Sect. 4.1).

Specifically, in Sect. 4.2, we apply both a linear regression model, which is explainable by design, and a neural network model, which belongs to the class of black-box models. When resorting to the linear regression model, we provide a snap-shot of the explainable variables by evaluating the significance of the corresponding generated effects on the Coinbase Bitcoin prices. In addition, a neural network model is also built for the same data.

The analysis based on both the linear regression and neural network models is then replicated through the implementation of the Forward Search procedure, which is addressed to give a moving picture of the variable explainability with respect to both different groups of observations and the more central or extreme ones.

4.1 Exploratory analysis

With the purpose of detecting the strength of the relationship between the Coinbase Bitcoin prices and the prices of the classical assets, the SP500 index and the exchange rates, we present in Fig. 2, the relating pairwise correlations.

Fig. 2
figure 2

Correlation matrix between the considered asset prices

Full size image

Figure 2 shows that the correlations between the Coinbase Bitcoin prices with classical assets, like Gold and Oil, are low. This finding is confirmed also by the recent literature that classify Bitcoins as speculative assets to be used for the construction of diversified portfolios.

Note that, differently, the correlation between the Coinbase Bitcoin prices and the SP500 index, as well as the exchange rates, is high: in the former case a direct relationship occurs, while in the latter case a negative relationship arises.

By looking at the correlation magnitude, the main factors impacting the Coinbase Bitcoin prices are the SP500 index and the exchange rates.

4.2 Linear regression

The first step is to build a linear regression model for predicting the Coinbase Bitcoin prices by means of the classical asset prices, the SP500 index and the exchange rates as predictors.

Before fitting the model, we put data on the same scale through the standardisation. Indeed, as noted from Table 1, the involved variables are expressed according to non-comparable scales. We then need to rescale the original variables to have a mean of zero and standard deviation of one.

Table 2 presents the estimates of the regression coefficients associated with each predictor, together with the related t statistics and p-values.

Table 2 Estimated regression coefficients
Full size table

The findings included in Table 2 allow to confirm the considerations derived from the correlation analysis. The most significant variable to the explanation of the Coinbase Bitcoin prices is the SP500 index which presents a high value of the t statistic. It is worth noting that, although the remaining predictors play a relevant role in explaining the Coinbase Bitcoin prices, the significance of the variables may be affected by the presence of observations that are extreme or whatever rather far from the mean value. This motivates the need of adopting a more sophisticated technique, such as the Forward Search procedure, for detecting anomalous values and making the explainability assessment more robust.

The analysis is then led by also applying a neural network with a hidden layer, as an example of a non-explainable by design model.

4.3 Robust and explainable analysis

We first apply our proposed methodology to the fitted values obtained from the linear regression model. Figure 3 reports the obtained values of the deletion t statistics, which tests whether each variable can be removed from the full model, for an increasing number of observations (ordered in terms of “distance” from the mean).

Fig. 3
figure 3

Evolution of the deletion t statistics for linear regression model

Full size image

Figure 3 shows that the SP500 variable explains most of the explained sum of squares, with values of the deletion t statistic always indicating a significant effect. Differently, both exchange rate variables become significant only when more extreme, farther from the mean, observations are considered. And, finally, neither Gold nor Oil are significant, regardless of the considered sample.

Figure 4 reports the obtained values of the deletion t statistics, for the neural network model, testing whether each variable can be removed from the full model, for an increasing number of observations (ordered in terms of “distance” from the mean).

Fig. 4
figure 4

Evolution of the deletion t statistics for the neural network model

Full size image

Figure 4 shows that the SP500 variable explains most of the explained sum of squares also for the neural network model, and consistently as we move away from the most central observations. Both exchange rates become relevant for more extreme observations. An important difference with respect to the findings obtained in Fig. 3 for the linear model is that both coefficients appear to be large only with a negative sign, consistently with the findings in the extant literature.

Finally, both Gold and Oil have a limited impact, throughout the data sample.

5 Conclusions

Machine learning models are boosting Artificial Intelligence applications in many domains. This is mainly due to their advantage, in terms of predictive accuracy, with respect to “classic” linear statistical learning models. However, although machine learning models could reach high predictive performance, they are “black-box”, not explainable, and may not be robust under data variations. The methods available in the literature to measure accuracy, explainability and robustness are based on post-processing approaches, such as Shapley values, which are computationally intensive.

In the paper, we have proposed an alternative method to jointly measure accuracy, explainability and robustness, based on the Forward Search methodology. The method allows: a) to obtain a parsimonious set of predictors, improving robustness while maintaining accuracy; b) to obtain a measurement of the importance of each predictor, measuring its impact when removed from the model containing all predictors.

Our proposal has been exemplified in the context of Bitcoin price predictions. The obtained empirical findings have shown the validity of the proposed method, consistent across different models, and in line with the extant literature findings.

More research is needed to develop statistical methods that can assess the trustworthiness of machine learning models, in different fields of application. This will allow policy makers and regulators, but also developers and users, to check the compliance of Artificial Intelligence applications to the regulatory requirements that are being proposed, such as the European AI act.

More research is also necessary on the related concept of controllable AI (see e.g. [14]), which is emerging in the light of the evolution of the regulatory developments which has followed the diffusion of large language models. Controllable AI is related to the discussion around the assignment of risk levels to different technologies, in connection with the need to protect AI against potential adversaries and to protect individuals from AI decisions that could harm their well-being.