1 Introduction

Advances in technology are providing data scientists with an unprecedented amount of high-dimensional data. Electrocardiogram signals, fMRI images or Mortality curves are relevant examples of what is nowadays called Functional Data [1]. In Functional Data Analysis (FDA), each observation is a function that constitutes an infinite dimensional object. Analysing functional outliers is critical in several contexts, including functional regression [2], robust functional principal component analysis [3], functional outlier visualisation [4], robust functional data clustering [5]; and also in several applied context where FD is involved [6].

Functional outliers are commonly classified into two categories: magnitude outliers and shape outliers [7, 8]. The contribution of this paper, is to propose a novel depth measure for functional data to handle both type of functional outliers simultaneously. To achieve this goal, we introduce a density kernel depth that relies on a finite dimensional and stable representation of functions. The kernel depth measure satisfies desirable properties, as we formally discuss in Sect. 3.1, and induces a centre—outward ordering on functions. We also propose suitable estimation methods that are based on a One-Class-Neighbour-Machine, a non parametric estimator of density level sets. Furthermore, we discuss a statistically sound bootstrap approach to infer functional outliers in data.

The remainder of the paper is organised as follows: Sect. 2 propose a suitable representation model for functional data. In Sect. 3 we introduce a density kernel depth measure, and also discuss its properties and suitable estimation methods. In Sect. 4 we provide an algorithm for functional outlier detection based on bootstrap procedure. In Sect. 5, we present a Monte Carlo simulation study and a real data application to mortality curves. Finally, in Sect. 6 we conclude the paper.

2 An RKHS framework for functional data

In what follows we consider a square integrable stochastic processes \(\mathcal {X}(t)\in \mathcal {H}\) in a separable Hilbert space of functions \(\mathcal {H} \subset L_2(T)\), where \(T\subset \mathbb {R}\) is a compact and convex set. As usual in practice, we also assume that curves are sampled over a discrete grid of points \({\textbf {t}}=\{t_1,\dots ,t_p\}\), being \(p\gg 0\), in a signal plus noise fashion as follows:

$$\begin{aligned} \textbf{x} = {x}({\textbf {t}}) + \textbf{e}, \end{aligned}$$
(1)

where \(\textbf{x} = \{{x}(t_1) + e_1,\dots ,{x}(t_p)+e_p\}\) is the vector with the observed data and \(\textbf{e}=(e_1,\dots ,e_p)\) is an independent and zero-mean residual term.

Most functional data analysis approaches for preprocessing raw data as in Eq. (1) suggest to proceed as follows: Choose an orthogonal basis of functions \(B = \{\phi _i\}_{i\ge 1}\), where each \(\phi _i\in \mathcal {H}\), and then represent each functional datum by means of a linear combination in the \({\text {Span}}(B)\) [9, 10]. A usual choice is to consider \(\mathcal {H}\) as a Reproducing Kernel Hilbert Space (RKHS) of functions [11]. In this case, the elements in the spanning set B are the eigenfunctions associated to the positive-definite and symmetric kernel \(K: T \times T\rightarrow \mathbb {R}\) that span \(\mathcal {H}\). In our setting, the functional representation problem can be framed as follows: We observe each curve on p sample points and the corresponding functional data estimator is obtained solving the following regularization problem:

$$\begin{aligned} \widehat{x}(t) := {\text {arg}} \min _{h\in \mathcal {H}} \sum ^{p}_{j=1}L(x(t_j),h(t_j))^2 + \gamma \Omega (h), \end{aligned}$$
(2)

where L is a strictly convex functional with respect to the second argument, \(\gamma > 0\) is a regularization parameter (chosen by cross–validation), and \(\Omega (h)\) is a regularization term. By the Representer Theorem [12], Th. 5.2,p. 91] [13], Pr. 8,p. 51] the solution of the problem stated in Eq. (2) exists, is unique, and admits a representation of the form:

$$\begin{aligned} \widehat{x}(t) = \sum ^p_{j=1} \alpha _{j}K(t,t_j). \end{aligned}$$
(3)

In the particular case of a squared loss function \(L(w,z)=(w-z)^2\) and considering \(\Omega (h) = \int _T h^2(t) \,\texttt {d}t\), the coefficients of the linear combination in Eq. (3) are obtained solving the following linear system:

$$\begin{aligned} (\gamma p \textbf{I} + \textbf{K}) \varvec{\alpha }= \textbf{x}, \end{aligned}$$
(4)

where \(\varvec{\alpha }= (\alpha _{1},\dots ,\alpha _{p})^{T}\), \(\textbf{I}\) is the identity matrix of order p, and \(\textbf{K}\) the is the \(p\times p\) Gram matrix with the kernel evaluations, \([\textbf{K}]_{k,l} = K(t_k,t_l)\), for \(k = 1, \ldots , p\) and \(l = 1, \ldots , p\). A main drawback on the estimation entitled in Eq. (3) is the instability of \(\varvec{\alpha }\), which change substantially under small perturbations in data. To avoid such problem, we resort on Mercer theorem [11] and consider an alternative functional estimator based on the projection of \(\widehat{x}(t)\) onto the functional space generated by the first \(d\ll p\) eigenfunctions of K:

$$\begin{aligned} \widehat{x}(t) \approx \tilde{x}(t)= \sum _{j=1}^d \lambda _j \phi _j(t)=\varvec{\lambda }^T \varvec{\Phi }(t), \end{aligned}$$
(5)

where \(\varvec{\lambda }= (\lambda _1,\dots ,\lambda _d)\) are the projection coefficients onto the functional space generated by the first d eigenfunctions of K (i.e. \(\lambda _j \equiv l_j (\varvec{\alpha }^T {\textbf {v}}_j)/\sqrt{p}\), where \((l_j,{\textbf {v}}_j)\) is the \(j^{\text {th}}\) eigen pair of Gram matrix \({\textbf {K}}\)), \(\varvec{\Phi }(t)=(\phi _1(t),\dots ,\phi _d(t))\) is a vector function with the first d eigenfunctions associated to K, and \(d\ll p\) is a resolution parameter such that for a small \(\varepsilon _d\) it holds that \(\sup _{t \in T} \mid \widehat{x}(t) - \tilde{x}(t) \mid \le \varepsilon _d\), see [14] for further details. The proposed depth measures for functional data relies on the computation of \(\varvec{\lambda }\), as we discuss in next Section.

3 Depth measures for functional data

There are several notions of depth measures in Statistics, all of them involve the computation of a quantity that represent the centrality of a given point \({\textbf {z}} \in \mathbb {R}^d\) with respect to a probability distribution f. In this way, depth measures induce an order in data, and are a natural tool to identify outliers.

Some remarkable examples of depth measures for functional data are in order. In Fraiman and Muniz [15], the authors propose the Integrated Depth that resort on a trimmed functional mean estimator to ranks the functions. The Random Tuckey Depth [16] and the Random Projection Depth [17], rely on random projections of the functional data and the computation of the deepest function using univariate statistics. Another well known example is the case of the h-Mode Depth [17], that considers the expected kernel distances for each curve using the \(L_2\) norm, see Example 1.

Example 1

h-Mode depth.

$$\begin{aligned} \text {h-MD}(x(t))=E(K_h(\Vert x(t)-\mathcal {X}(t)\Vert _{L_2}), \end{aligned}$$

where K is a kernel function and h is the bandwidth parameter.

In FDA, the graphical analysis is always a complementary approach in terms of visualisation and interpretation of outliers. In this sense, the Band Depth and Modified Band depth introduced in López-Pintado and Romo [18] are suitable methods. An interesting review on topological functional depth measures can be found in [19] and [20]. We introduce next our depth measure that rely on density kernels.

3.1 Depth induced by density kernels

Let \(Z \in \mathbb {R}^d\) be a random vector with density function f, the function \(g: \mathbb {R}^d \rightarrow \mathbb {R}\) is f-monotone if satisfies the following condition:

$$\begin{aligned} f(\textbf{z})\ge f(\textbf{y}) \Rightarrow g(\textbf{z}, f)\ge g(\textbf{y}, f). \end{aligned}$$
(6)

As an example, consider the parametric model \(Z\sim N(\mu ,\sigma ^2)\); then \(g(x,(\mu ,\sigma ^2))=-(x-\mu )^2/\sigma ^2\) is f-monotone. A density kernel \(K_f: \mathbb {R}^d \times \mathbb {R}^d \rightarrow \mathbb {R}\) is defined as the product of two f-monotone functions as follows:

$$\begin{aligned} K_f(\textbf{z},\textbf{y})= g(\textbf{z}, f)g(\textbf{y}, f). \end{aligned}$$
(7)

Notice that \(K_f\) depends on the density function f that is unknown or intractable in practice. We address the estimation of \(K_f\) using asymptotically f-monotone functions as discussed in next subsection. The density kernel depth measure is then obtained by combining a density kernel with a deepest (central) curve. To define the later, consider a statistical model f (a bounded density function) for the projection coefficients (i.e. \(\varvec{\lambda }\sim f\)), the deepest curve \(\tilde{x}_{\text {mo}}(t)=\sum _{j=1}^d m_j \phi _j(t)\) is in correspondence to the parameter \({\textbf {m}}\equiv (m_1,\dots ,m_d) =\displaystyle {\text {argmax}}_{\mathbf {\varvec{\lambda }} \in \mathbb {R}^d }f(\varvec{\lambda })\) (i.e. \({\textbf {m}}\) is the mode of f). Finally, the density kernel depth (DKD) is defined as follows:

Definition 1

Density Kernel Depth. Let f be the density of the projection coefficients \(\varvec{\lambda }\), and let \(\tilde{x}_{\text {mo}}(t)=\sum _{j=1}^d m_j \phi _j(t)\) be the deepest curve where \({\textbf {m}}\equiv (m_1,\dots ,m_d)\) represent the mode of f, the DKD of the curve \(\tilde{x}(t)= \varvec{\lambda }^T \varvec{\Phi }(t)\) is defined as follows:

$$\begin{aligned} \text {DKD}(\tilde{x}(t),f,K_f) \equiv g(\varvec{\lambda },f)g(\textbf{m}, f), \end{aligned}$$
(8)

Proposition 1

The DKD satisfies the following desirable properties [21] for depth measures:

  1. P1.

    Maximality at center: The DKD take the largest value evaluated at the deepest curve, i.e. \(\sup _{x(t) \in \mathcal {H}} \text { DKD}(x(t),f,K_f) =\text { DKD}(\tilde{x}_{\text {mo}}(t),f,K_f)\).

  2. P2.

    Monotonicity relative to the deepest function: For two curves \(\tilde{x}_1(t)\) and \(\tilde{x}_2(t)\) such that \(f(\varvec{\lambda }_1)\le f(\varvec{\lambda }_2)\) (i.e. \(\tilde{x}_1(t)\) is further apart from the central curve \(\tilde{x}_{\text {mo}}(t)\) than \(\tilde{x}_2(t)\)), it holds that \(\text { DKD}(\tilde{x}_1(t),f,K_f) \le \text { DKD}(\tilde{x}_2(t),f,K_f).\)

  3. P3.

    Vanishes at infinity: \(\text { DKD}(\tilde{x}(t),f,K_f)\rightarrow 0\) as \(\Vert \varvec{\lambda }\Vert \rightarrow \infty .\)

  4. P4.

    Invariant under affine transformations: Let \(\mathcal {T}\) be the class of affine transformations in \(\mathcal {H}\) and let \(\tau \in \mathcal {T}\) be an affine map, then \(\text { DKD}(\tilde{x}(t),f,K_f) = \text { DKD}(\tau \circ \tilde{x}(t),f,K_f).\)

In addition to properties P1–P4, the order induced by the DKD is also invariant under changes in the basis function \(B=\{\phi _1(t),\dots ,\phi _d(t)\}\) that span the linear subspace in \(\mathcal {H}\) where we project the curves. We give more details and a formal proof in the supplementary material. In the following subsection we address the details involved in the estimation of DKD from data.

3.2 Estimating the density kernel depth

Notice that \(g(\cdot ,f)\) depends on the density function f that is unknown or intractable in practice; this leads to the following related concept: Given a random sample \(S_n = \{Z_1, \dots ,Z_n\}{\mathop {\sim }\limits ^{iid}}f\), then \(g(\textbf{z},S_n)\) is asymptotically f-monotone if the following relation holds: \(\displaystyle f(\textbf{z})\ge f(\textbf{y}) \Rightarrow \lim _{n\rightarrow \infty } P(g(\textbf{z}, S_n)\ge g(\textbf{y}, S_n))=1\). As an example of asymptotic monotone function consider \(g(\textbf{z}, S_n)=1/d_k(\textbf{z},S_n)\); where \(d_k(\textbf{z},S_n)\) is the distance from \(\textbf{z}\) to its (random) k–nearest neighbour in \(S_n\) (for \(1\le k<n\)). Therefore, a suitable estimator for \(K_f\) is given by the product of two asymptotically f-monotone functions.

The estimation of the DKD is based on an asymptotically f-monotone function \(g(\cdot ,S_n)\) which is proportional to a non–parametric consistent estimator of f –the density function that corresponds to the projection coefficients. Our density estimation method is based on the One–Class Neighbor Machine (OCNM), a well known nonparametric density level set estimator [22, 23]. The \(\nu \)-level set of f is defined as \(V_{\nu }(f) = \{\varvec{\lambda }\in \mathbb {R}^d:\, f(\varvec{\lambda })\ge \alpha _\nu \}\), such that \(P(V_{\nu }(f))=1-\nu \) for \(0<\nu <1\). Some comments about the density estimation method are in order. The OCNM is a consistent estimator of \(\nu \)-level sets under mild conditions on f. In addition, the OCNM relies on a linear–convex optimization problem, entailing important computational advantages in comparison to other standard nonparametric density estimation approaches such as kernel method. For more details about the OCNM we refer to [23].

The estimation of DKD via the OCNM is straightforward. Given a sample of n discretised curves as in Eq. (1), \(\mathcal {D}_n = \{{\textbf {x}}_1,\dots ,{\textbf {x}}_n\}\) and its corresponding projection coefficients \(\{\varvec{\lambda }_1,\dots ,\varvec{\lambda }_n\}\) according to Eq. (5); we use the OCNM to estimate density contour clusters \(\widehat{V}_\nu \) around the estimated mode \(\widehat{{\textbf {m}}}\) for an increasing sequence \(\varvec{\nu }\equiv \{\nu _1,\dots ,\nu _m\}\), such that \(0\le \nu _1<\dots <\nu _m\le 1\). Notice that \(\widehat{{\textbf {m}}}\in \{\varvec{\lambda }_1,\dots ,\varvec{\lambda }_n\}\) corresponds to the sample curve which belongs to the highest \(\nu \)–density level set. We consider the following asymptotic f–monotone function: \(g(\varvec{\lambda },\mathcal {D}_n)=\sum _{i=1}^mi\mathbb {I}_{\widehat{V}_i}(\varvec{\lambda })\), where \(\mathbb {I}_{\widehat{V}_i}(\varvec{\lambda })\) is the indicator function that take value 1 if \(\varvec{\lambda }\in \widehat{V}_{\nu _i}\) and 0 otherwise. In this sense, the estimated \(\text {DKD}(\tilde{x}(t),\mathcal {D}_n,K_f)\equiv g(\varvec{\lambda },\mathcal {D}_n)g(\widehat{{\textbf {m}}} ,\mathcal {D}_n)\) order the sampled curves around the estimated center \(\widehat{x}_{\text {mo}}(t)=\widehat{{\textbf {m}}}^T\varvec{\Phi }(t)\); i.e. high values of DKD corresponds to estimated central curves and vice-verse.

4 Functional outlier detection

Depth measures induces a centre-outward ordering, and constitute a natural tool to assess the presence of outlying curves in the sample. From an statistical perspective, the analysis of atypical curves relies on the distribution of \(\text {DKD}(\widetilde{X}(t),f,K_f)\). Nevertheless, nither the exact nor the asymptotic distribution of \(\text {DKD}\) is known. For this reason, we employ bootstrap methods to approximate such distribution and determine which curves in the sample are more likely to be outliers. In Algorithm 1, we present our bootstrap method that resembles the procedure given in [24]. For the analysis of outlier functional data, a suitable threshold \(q\in (0,1)\) (q is intended to be the type I error on the identification method) needs to be specified in advance. In the case of Australian mortality curves discussed in Sect. 5, we choose \(q=0.01\); nevertheless in practice we recommend to conduct a sensitivity analysis regarding the value given to this sensible parameter.

Algorithm 1
figure a

Bootstrap based outlier identification method.

Full size image

Some comments on Algorithm 1 are in order. Step 1 and 2 entails standard statistical procedures. Step 3 involves some parametric perturbation on data in order to produce a robust estimation of the true DKD quantile.

5 Experiments

In this section we develop numerical experiments to assess the performance of the proposed depth measure in the task of functional outlier detection. The implementation of DKD is available in the ‘bigdatadist’ R-package, and the R code to reproduce the experiments are provided as supplementary material.

Hereafter, for the functional data representation, we consider a Gaussian kernel function \(K(t,s)=\exp ({-\sigma \Vert t-s\Vert ^2})\). The bandwidth parameter \(\sigma \) and the dimension of the basis function system d given in Eq. (5) where cross-validated through grid search. To compare our method we consider several functional depth methods: the modified band depth (MBD) [18] already implemented in the R-package ‘depthTools’ [25], the random Tukey depth (RTD) and the h-mode depth (HMD), see [16, 17], implemented in the R-package ‘fda-usc’ [26], and the functional spatial depth (FSD), see [27].

5.1 Monte Carlo simulation study

Simulation setting We simulated a sample of \(n = 400\) curves, where a small proportion \(q \in [0,1]\), known a priori, presents an atypical pattern. The remaining \(n(1-q)\) curves are considered the main data. We study the performance of DKD over three data configurations (scenarios a, b and c) and for three different values of the contamination parameter \(q\in \{1\%, 5\%,10\% \}\). Specifically, we consider the following generating processes:

$$\begin{aligned} X_l(t)= & {} \sum _{j=1}^4 \xi _j \sin (j\pi t)+ \varepsilon _l(t), \text { for } l=1,\dots ,(1-q)n,\\ Y_l(t)= & {} \sum _{j=1}^4 \zeta _j \sin (j\pi t)+\varepsilon _l(t), \text { for } l=1,\dots ,q n/2,\\ Z_l(t)= & {} \sum _{j=1}^4 \eta _j \sin (j\pi t)+ \varepsilon _l(t), \text { for } l=1,\dots ,q n/2, \end{aligned}$$

where \(t\in T\equiv [0,1]\) and \(\varepsilon _\cdot (t)\) are independent and zero mean random error functions.

  1. (a)

    Symmetric scenario \((\xi _1,\dots ,\xi _4)\) follows a multivariate normal distribution (MND) with mean \(\varvec{\mu }_{\xi } = (4,2,4,1)\) and diagonal co-variance matrix \(\varvec{\Sigma }_{\xi } = {\text {diag}}(5, 2, 2, 1)\). To generate magnitude outliers, we consider \((\zeta _1,\zeta _2,\zeta _3,\zeta _4)\) following a MND with parameters \(\varvec{\mu }_{\zeta } = 2.5\varvec{\mu }_{\xi }\) and \(\varvec{\Sigma }_{\zeta } = (2.5)^2\varvec{\Sigma }_{\xi }\). To generate shape outliers, we specify \((\eta _1,\eta _2,\eta _3,\eta _4)\) as MND with parameters \(\varvec{\mu }_{\eta } = (4,-2,1,3)\) and \(\varvec{\Sigma }_{\eta } = \varvec{\Sigma }_{\xi }\).

  2. (b)

    Asymmetric scenario In this case, \(\{\xi _1,\dots ,\xi _4\}\) are independent Chi-square distributed random variables (ICrv) with 16, 16, 12, 12 degrees of freedom respectively; while \(\{\zeta _1,\zeta _2,\zeta _3,\zeta _4\}\) are ICrv with 40, 40, 30, 30 degrees of freedom respectively; and \((\eta _1,\eta _2,\eta _3,\eta _4)\) follows a MND with mean \(\varvec{\mu }_{\eta } = (18,16,8,-10)\) and variance \(\varvec{\Sigma }_{\eta } = {\text {diag}}(15,12,12,15)\).

  3. (c)

    Bi-modal scenario: \(\varvec{\xi }\) follows a mixture of two MND as follows: \((\xi _1,\dots ,\xi _4)\sim 0.5N_4(\varvec{\mu }_{\xi ,1},\varvec{\Sigma }_{\xi }) + 0.5N_4(\varvec{\mu }_{\xi ,2},\varvec{\Sigma }_{\xi })\), where \(\varvec{\mu }_{\xi ,1} = (1,1,1,1)\), \(\varvec{\mu }_{\xi ,2}=(9,9,9,9)\), and \(\varvec{\Sigma }_{\xi } = {\text {diag}}(5,2,2,1)\) is a diagonal covariance matrix. Outliers are generated as follows: \((\zeta _1,\zeta _2,\zeta _3,\zeta _4)\sim N_4(\varvec{\mu }_{\zeta },\varvec{\Sigma }_{\zeta })\), where \(\varvec{\mu }_{\zeta } = (8,4,8,2)\) and \(\varvec{\Sigma }_{\zeta } = 4\varvec{\Sigma }_{\xi }\); and \((\eta _1,\eta _2,\eta _3,\eta _4)\sim \ 0.5N_4(\varvec{\mu }_{\eta ,1},\varvec{\Sigma }_{\eta }) + 0.5N_4(\varvec{\mu }_{\eta ,2},\varvec{\Sigma }_{\eta })\) with parameters \(\varvec{\mu }_{\eta ,1} = (-4,4,-1,-3)\), \(\varvec{\mu }_{\eta ,2}=(5,5,5,5)\) and \(\varvec{\Sigma }_{\eta } = 0.5{\text {diag}}(1,1,1,1)\).

To illustrate the generating process, in Fig. 1, we show one instance of the simulated curves in the scenarios (a) to (c) for \(q=10\%\).

Fig. 1
figure 1

Functional data: 400 curves corresponding to \(q=10\%\) In grey (), we represent instances of regular curves X(t), abnormal curves Y(t) depicted in amber (), and Z(t) in light-blue (). (color figure online)

Full size image

Results

To evaluate the outlier detection performance of the DKD we develop a Monte Carlo simulation study. To this end, for each scenario and contamination level, we generate \(M = 1000\) data replications and report the following average metrics: True Positive Rate \(\text {TPR}=\frac{\text {TP}}{q\times n}\) (sensitivity); True Negative Rate \(\text {TNR}=\frac{\text {TN}}{(1-q)\times n}\) (specificity), and the area under the ROC curve aROC.

The Monte Carlo simulation results are presented in Table 1. The DKD resents a remarkable performance among other functional depths measures in the three scenarios considered for different levels of contamination \(q\in \{1\%,5\%,10\%\}\). However in the case where \(q = 1\%\) the difference with respect to other depth measures is not statistically significant. Among the three different scenarios the performance of the DKD increases with respect to the rest of the competitors in scenario (b) and (c), where me move away from the Gaussian setting.

Table 1 Scenarios and contamination percentages q in columns
Full size table

5.2 Detecting outlying curves in the Australian mortality database

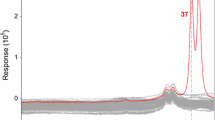
For this experiment we consider age-specific log-mortality rates of Australian males. The data is publicly available in the R-package ‘fds’Footnote 1 [28]. The data set consists of 103 curves that are registered over a range of 0-100 age cohorts, with each curve corresponding to one year between 1901 and 2003. As shown in Fig. 2, for low-age cohorts (until 12 years approximately), the mortality rates present a decreasing trend and then start to grow until late ages, where all cohorts achieve a 100% mortality rate.

Fig. 2
figure 2

Australian Mortality data: regular curves in gray (), deepest curve black-dashed () and outliers detected by the DKD in red () (color figure online)

Full size image

Results Outlier detection is an unsupervised learning problem. Therefore, we do not know a-priori if there are any outlying curves (years) in this data set. Following the procedure detailed in Algorithm 1, we estimate the cut-off point q such that mislabelling of correct observations as outliers is about 1%. The results are presented in Table 2 and Fig. 2. The outliers detected by the DKD are years: 1919, 1943-1945. The year 1919 corresponds to the influenza pandemic episode that caused around 15, 000 casualties, as the virus spread through Australia. Given the pattern in the curve corresponding to year 1919, this curve can be visually identified and labelled as a magnitude outlier. In a related study that rely on the same data [29], the authors identified 1919 as an anomalous observation as well.

Moreover, these curves exhibit a distinctive shape compared to the others, lacking any prominent points (age-cohorts) that would indicate their dissimilarity. As a result, visually detecting them is exceedingly difficult. Specifically, for the age-cohorts between 15 to 40, one can observe a discrepancy in the curve patterns, so they can be considered as shape outliers. It is particularly relevant to identify outliers in this dataset to achieve reliable predictions of mortality curves. With the onset of the COVID-19 pandemic, improved predictions can aid governments in making better-informed decisions.

The DKD handle both type of functional outliers, as follows from the simulations in the previous section. In Table 2 we compare our findings against other standard benchmarks introduced in the Monte Carlo simulation study as well as the Outliergram -particularly devised to capture shape outliers- [7] and the Functional Boxplot [8] (see Supplementary Material). Both devices are already implemented in the R-packages ’roahd’ and ’fda’ respectively. The Outliergram identifies the year ’1914’ as an outlier, while the Functional Boxplot has not pinpointed any anomalous observation. These tools are based on the Modified Band Depth measure. This approach is very efficient identifying magnitude outliers or shape outliers that present a sharp difference with respect to the rest of the sample. In this case the shape outliers are hidden within the rest of the data and this could explain the poor performance of the method. Finally, is also interesting to notice that the mortality curve corresponding to year 2003 is identified as an outlier for all the competitors. Since year 2003 is located on the outwards of the data with respect to the deepest curve, we tend to see these find as a type-II-error in the analysis.

Table 2 Outliers curves detected by the different methods (\(q = 1\%\)).
Full size table

6 Conclusions

In this work, we propose a density kernel depth (DKD) measure as a tool for detecting outliers in functional data. The DKD method relies on a stable low-dimensional representation of curves in a linear subspace of a Reproducing Kernel Hilbert Space. We discuss interesting properties associated with the DKD and address the subtleties involved in its estimation. We showcase the performance of our method through a Monte Carlo simulation study using three different scenarios: symmetric, asymmetric, and bi-modal models for functional data. The DKD is able to identify the presence of shape and magnitude outliers not only in simulated data but also in the analysis of Australian male mortality rate curves. Although the DKD has a remarkable performance in identifying outliers that are hidden within the rest of the curves and are extremely difficult to spot visually, we suggest combining DKD analysis with the outliergram [7] and functional boxplot methods [8] to achieve more robust results.