Personalized market response analysis for a wide variety of products from sparse transaction data

Abstract

Advanced database marketing is designed to ascertain individual customers’ market responses with a discount or display of widely various products from transaction data. However, transaction data recorded in a supermarket or electric commerce are fundamentally sparse because most customers purchase only a few products from all products in shops. Existing methods are not applicable to elucidate the personalized response because of a lack of sample size of purchased data. This paper proposes a personalized market response estimation method for a wide set of customers and products from these sparse data. The method compresses a sparse transaction data with information related to response to marketing variables into a reduced-dimensional space for feasible parameter estimation. Then, they are decompressed into original space using augmented latent variables to obtain individual response parameters. Results show that the method can find suitable marketing promotions for individual customers to every analyzed product.

1 Introduction

Personalized marketing is a key strategy of modern database marketing that supports targeting recommendations, promotions and direct-mail campaigns in various business fields. The analysis of personalized marketing responses from retailer transaction data is challenging because of the fundamental sparsity of observed purchases. In truth, very few customers purchase most products on most of their shopping trips. When a purchase is recorded in one category, it is frequently for just one offering. The actual sample of transactional data is much smaller than the data space reflected by a data cube with dimensions corresponding to the number of customers, number of products and occasions. Under such circumstances, standard marketing models for choice break down because of the high frequency of nonpurchase for almost every product.

Additionally, increasing the number of products in a traditional marketing model is problematic because of potential complexities in the structure of demand based on an orthodox economics model and the accompanying increase in the required number of model parameters. Existing models of choice and demand, for example, are typically limited to fewer than twenty or so product alternatives that are tracked across possibly hundreds of customers [9, 30]. Unfortunately, that goal is often at odds with the goals of practitioners who want to optimize a marketing promotion for a wide set of customers and products in their shops.

As described in this paper, we propose a method of personalized market response analysis that can treat widely diverse products. The method identifies effective marketing promotions of individual products to individual customers using sparse transaction data. To resolve the difficulty of data sparsity, we first compress the data space comprising customers and products to a reduced-dimensional latent class. For the dimension reduction of customers and products, we propose a model that includes a latent variable model and a marketing model with response parameters to marketing variables such as discounts or marketing promotions. Response parameters are introduced into the latent class by connecting each choice to its own marketing variable. Consequently, it is possible to estimate the parameters stably because a sufficiently large sample size can be used. Then, we decompress the extracted associations back to individual customers using estimated parameters of customers and products for personalization.

Our model identifies the latent class for each customer at each point in time, providing information related to the array of products that a customer is likely to purchase. It is a key variable for construction of personalized information. We do not make a priori assumptions about substitute and complementary goods in the spirit of market basket analysis in data mining. Our model takes an exploratory approach to analysis. It does not test assumptions of the form of the utility function across hundreds of offerings. However, our model does include marketing variables so that their effects on choice can be measured and used for prediction.

The contributions of this paper are the following:

• Proposition of an individual market response estimation method for widely diverse products.

• Development of a marketing model with a latent variable model.

• Findings of personalized effective marketing variables for widely diverse products from sparse transaction data in a supermarket.

Sections 2 and 3 describe a review of related work and preliminary research related to our method. We present the proposed method for personalized marketing for widely diverse products in Sect. 4. Section 5 presents a description of an empirical study using real transaction data. Conclusions are offered in Sect. 6.

2 Related works

2.1 Marketing model for personalization

The marketing model of customer heterogeneity [1, 23] for choice behavior commonly studied in the marketing field uses the framework of hierarchical Bayes modeling [30]. Details are described in Sect. 3.1. Heterogeneity models can measure the effects of marketing promotion for individual customers explicitly as market response coefficients. The main purpose is to elucidate the richness of the competitive environment within a product category or brand. The models are constructed by some marketing variables, parameters and structures with economics concepts such as a budget constraint, presence of substitutes and complements and/or utility functions. However, most advanced models entail a high computational cost to estimate parameters because the model structure that expresses a process of customer purchase behavior in the style of economics tends to be complicated. Therefore, existing models of choice and demand, for example, are typically limited to fewer than twenty or so product alternatives.

Our model is similar to adaptive personalization systems proposed by [3, 8, 10, 31]. However, it differs in that our model structure facilitates analysis of widely various product categories.

2.2 Dimension reduction method

Many statistical and data-mining methods for dimension reduction have been assessed for transaction data analysis: traditional latent class analysis [13], correspondence analysis [14], self-organization maps [38] and joint segmentation [29]. The benefits of such methods are that they can treat a large set of customer and product data to seek hidden patterns in reduced-dimensional space. Tensor factorization [25, 39] can decompose a data cube of a large set of customers, products and time periods to a scalable low-rank matrix to find hidden patterns related to customer behavior. However, such studies cannot address a marketing variable structure explicitly like marketing models. Our method is designed to extract information related to individual customers’ responses to changing marketing variables directly.

2.3 Topic modeling and latent variables model

The topic model, a kind of latent variable model, is a generalization of a finite mixture model in which each data point is associated with a draw from a mixing distribution [35]. Models of voting blocs [12, 32] track the votes of legislators (aye or nay) across multiple bills, with each bill associated with a potentially different concern or issue. Similarly, the latent Dirichlet allocation (LDA) model [6] allocates words within documents to a few latent topics with patterns that are meaningful and interpretable. Each vote and each word are associated with a potentially different issue or topic. Therefore, the mixing distribution is applied to the individual vector of observations and not to the entire set of observations (e.g., series of votes a legislator or set of words by an author) of the panelist. In our analysis of household purchases, we allow the vector of observed purchases across all product categories on an occasion to be related to a different latent context (topic or issue). This allowance enables us to view a customer’s purchases as responding to different needs or occasions (e.g., family dinner, snacks) and enables us to identify the ensemble of goods that collectively define latent purchase segments across numerous products.

In the analysis of purchase behavior using topic models for transaction data [18], dynamic patterns between purchased products and customer interests are extracted. [17] fused heterogeneous transaction data and customer lifestyle questionnaire data, whereas [19] identified customer purchase patterns using a topic model with price information related to the purchased products. These approaches identify patterns among customers and products. Topic models typified by the labeled LDA [28] and the supervised LDA [7] that extend LDA by incorporating additional data in the analysis have been proposed. Various latent variable models typified by the infinite relational model [22], the ideal point topic model [12], the stochastic block model [27] and the infinite latent feature model [15] have also been proposed for knowledge discovery of binary relations from multiple variables. However, none of these approaches is suitable for relating marketing variables to individual customer choices as explanatory variables.

3 Preliminary

3.1 Hierarchical Bayes probit model

The binary probit model is a popular marketing model for choice, i.e., purchase or not purchase. Let $y_{cit}$ denote customer c’s purchase record of product i at time t, assigning $y_{cit}=1$ if customer c purchased the product, and $y_{cit}=0$ otherwise. We assume the dataset includes C customers and I products through T periods. Denote $u_{cit}$ as the utility of customer c’s purchase record of product i at time t. We assume a binary probit model with $u_{cit}>0$ if $y_{cit}=1$, and $u_{cit} \le 0$ if $y_{cit}=0$. The marketing variables of products i at time t are expressed as a vector ${{\varvec{x}}}_{it} = [x_{it1}, \ldots , x_{tiM}]^{T}$, where M is the number of marketing variables. ${{\varvec{x}}}_{it}$ includes information related to the price or promotion of products.

Here, we consider an analysis of product i only. The binary probit model expresses $u_{cit}$ by a linear regression model as

$$\begin{aligned} u_{cit} = {{\varvec{x}}}^{T}_{it} {\varvec{\beta }} + \epsilon _{cit}, \end{aligned}$$

(1)

where ${\varvec{\beta }} = [\beta _{1}, \ldots , \beta _{M}]^{T}$ is a regression coefficient vector with respect to product i and $\epsilon _{uit}$ is a Gaussian error with mean 0 and variance 1. Next, we consider a probability of $u_{cit} > 0$. The probability naturally is coincident with the probability of $y_{cit}=1$. The probability $p(u_{cit} > 0)$ can be determined as

$$\begin{aligned} p(u_{cit}> 0)= & {} p\left( {{\varvec{x}}}^{T}_{it} {\varvec{\beta }} + \epsilon _{cit}>0\right) \nonumber \\= & {} F({{\varvec{x}}}^{T}_{it} {\varvec{\beta }}), \end{aligned}$$

(2)

where F is a cumulative distribution function of the Gaussian distribution. These model structures and assumptions are a natural and reasonable assumption for customer choice. Many works use the model in marketing, economics and urban engineering [36].

If we extend the probit model to treat personalized parameter ${\varvec{\beta }}_{c} = [\beta _{c1}, \ldots , \beta _{cM}]^{T}$ $(c=1, \ldots , C)$ for individual customers simply, then the model is not able to estimate the coefficients because of a lack of data sampling for the reason that most customers do not purchase most products.

The hierarchical Bayes probit model [1] can estimate ${\varvec{\beta }}_{c}$ using the assumption of prior distribution of ${\varvec{\beta }}_{c}$. Multivariate normal distribution is used as a prior distribution of ${\varvec{\beta }}_{c}$ because it is a conjugate distribution of likelihood function of the probit model. The assumption of prior distribution is convenient for parameter estimation and is used in many existing works [30]. However, the models do not treat widely diverse products and are typically limited to fewer than twenty or so products [9, 30] because of high computational costs.

3.2 Dimension reduction by LDA

Here we briefly introduce the idea of topic models in the context of customer purchases. We seek the probability p(i|c) that customer c purchases product i. However, the probabilities cannot be calculated accurately because of data sparseness. The topic model calculates p(i|c) by introducing a latent class $z \in \{1 \dots Z\}$ whose dimension is markedly smaller than the numbers of customers and products.

The latent variable is used to represent the sparse data matrix as a finite mixture of vectors commonly found in topic models.

$$\begin{aligned}&\left[ \begin{matrix} p\left( i=1|c=1 \right) &{} \cdots &{} p\left( i=1|c=C \right) \\ \vdots &{} \ddots &{} \vdots \\ p\left( i=I|c=1 \right) &{} \cdots &{} p\left( i=I|c=C \right) \\ \end{matrix} \right] \nonumber \\&=\sum \limits _{z=1}^{Z}{\left[ \begin{matrix} p\left( 1|z \right) \\ \vdots \\ p\left( I|z \right) \\ \end{matrix} \right] }\left[ \begin{matrix} p\left( z|1 \right) &{} \cdots &{} p\left( z|C \right) \\ \end{matrix} \right] . \end{aligned}$$

(3)

More specifically, we decompose a large probability matrix of size $I \times C$ to two small probability matrices of sizes $I \times Z$ and $Z \times C$ based on the property of conditional independence. Hereinafter, we denote the probability that customer c belongs to the latent class z as p(z|c) and designates it as the membership probability. Also, for simplification, the probability that customers belonging to latent class z purchase the product i is p(i|z).

Parameter $\theta _{cz}$ of categorical distribution is used for probability p(z|c). The categorical distribution is multinomial with parameters $\varvec{\theta }_c$ = $\left[ {{\theta }_{c1}}\cdots {{\theta }_{cZ}} \right]$. The $\varvec{\theta }_c$ is specified so that the selection probability of customer c with respect to product i is conditionally independent if the latent class z is given: all information about customer heterogeneity of purchases is conveyed through the latent classes. The prior distribution for $\varvec{\theta }_c$ is assumed the Dirichlet distribution as the natural conjugate prior distribution of categorical distribution:

$$\begin{aligned} {\varvec{\theta }_{c}}\sim \text {Dirichlet}\left( \varvec{\tilde{\gamma }} \right) , \end{aligned}$$

(4)

where $\varvec{\tilde{\gamma }}$ is a hyperparameter of Dirichlet distribution.

The main difference between voting blocs model and LDA is assumed distributions for probabilities p(i|z) in the $I \times Z$ matrix. The voting blocs model presumes a Bernoulli distribution for the probability p(i|z). LDA assumes a categorical (i.e., multinomial) distribution for the probability matrix.

3.3 Problem settings

Here, we suppose the following three situations. (1) Given that dataset $\{ y_{cit} \}$ is sparse, that is, most $y_{cit}$ is zero, and (2) that the number of target products I is greater than several hundred, then (3) we assume the following marketing model for the customer’s purchase behavior as

$$\begin{aligned} u_{cit} = {{\varvec{x}}}^{T}_{it} {\varvec{\alpha }}_{ci} + \epsilon _{cit}, \end{aligned}$$

(5)

where ${\varvec{\alpha }}_{ci} = [\alpha _{ci1}, \ldots , \alpha _{ciM}]^{T}$ is a regression coefficient vector of customer c with respect to product i. For the situation described above, we consider a method to ascertain personalized market response coefficients $\{ {\varvec{\alpha }}_{ci} \}$.

4 Proposed method

4.1 Model development

Under circumstances of sparse data, it is not possible to estimate the parameters ${\varvec{\alpha }}_{ci}$ directly in existing methods such as maximum likelihood estimation because of a lack of sample size of purchase data. To resolve that difficulty, we reduce the dimension of customers and products to latent classes in which similar customers in terms of purchase behavior with marketing variables are summarized. We estimate the parameters associated with a latent class in the dimension reduced space using a purchased dataset of customers that belong to the same latent class. In that situation, it is possible to estimate the parameters stably because we can use a sufficiently large sample size. We recover information of ${\varvec{\alpha }}_{ci}$ using the estimated parameters in latent class ${\varvec{\beta }}_{zi}$ and latent class membership at each observation $z_{cit}$. Definitions of ${\varvec{\beta }}_{zi}$ and $z_{cit}$ are described later.

Here, we couple the binary choice probability with a voting bloc model to reduce a space dimension of customers and products.

$$\begin{aligned} p\left( {{u}_{cit}}>0 \right) =\sum \limits _{z=1}^{Z}{p\left( {{u}_{it}}>0|z \right) p\left( z|c \right) } \end{aligned}$$

(6)

We denote the utility associated with the latent class z as $u_{it}^{(z)}$; then, the choice probability can be represented as $p(u_{it}>0|z) = p(u_{it}^{(z)}>0)$. Assuming a linear Gaussian structure on the utility $u_{it}^{(z)}$ for marketing variables, the right-hand side of (3) can be represented as

$$\begin{aligned} \sum \limits _{z=1}^{Z}{\left[ \begin{matrix} F\left( {\varvec{x}_{it}^{T}}{\varvec{\beta }_{z1}} \right) \\ \vdots \\ F\left( {\varvec{x}_{It}^{T}}{\varvec{\beta }_{zI}} \right) \\ \end{matrix} \right] }\left[ {{\theta }_{1z}}\cdots {{\theta }_{Cz}} \right] \end{aligned}$$

(7)

where $\varvec{\beta }_{zi}= [\beta _{zi1}, \dots , \beta _{ziM}]^T$ is a response coefficient vector of latent class z with respect to product i. The heterogeneity of latent class is introduced through a hierarchical model with a random effect for response coefficient $\varvec{\beta }_{zi}$,

$$\begin{aligned} \varvec{\beta }_{zi} \sim N_M(\varvec{\mu }_i,V_i), \end{aligned}$$

(8)

where the prior distributions for $\varvec{\mu }_i$ and $V_i$ follow an M-dimensional multivariable normal distribution $N_M(\tilde{\varvec{\mu }}$, $\tilde{\sigma }^2 V_i)$ and an inverse Wishart distribution $IW(\tilde{W}$,$\tilde{w})$, where $\tilde{\varvec{\mu }}$, $\tilde{\sigma }^2$, $\tilde{W}$ and $\tilde{w}$ are hyperparameters specified by the analyst. We assume that the M-dimensional coefficient vector $\varvec{\beta }_{zi}$ for each segment, z, is a draw from a distribution with mean and covariance that is product-specific.

The likelihood is given as

$$\begin{aligned}&\ell \left( \left\{ {{y}_{cit}} \right\} |\left\{ {\varvec{\theta }_{c}} \right\} ,\left\{ {\varvec{\beta }_{zi}} \right\} ,\left\{ {\varvec{x}_{it}} \right\} \right) \nonumber \\&=\prod \limits _{c=1}^{C}{\prod \limits _{i\in {{I}_{c}}}^{{}}{\prod \limits _{t\in {{T}_{c}}}^{{}}{\sum \limits _{z=1}^{Z}{\left[ {{\theta }_{cz}}p\left( {{y}_{cit}}|{\varvec{x}_{it}},{\varvec{\beta }_{zi}},z \right) \right] }}}} \end{aligned}$$

(9)

where $p(y_{cit}|x_{it},\beta _{zi},z)$ denotes the kernel of the binary probit model conditional on z and where $T_c$ denotes a subset of t in which customer c purchased any product in a store. Also, $I_c$ is a subset of products i purchased by customer c at least once during the period $t=1, \dots , T$, i.e., ${{T}_{c}}\in \left\{ t|\sum \nolimits _{i=1}^{I}{{{y}_{cit}}>0} \right\}$ and ${{I}_{c}}\in \left\{ i|\sum \nolimits _{t=1}^{T}{{{y}_{cit}}>0} \right\}$.

Equation (8) is difficult to use directly because the likelihood includes summations over latent class z. Instead, we use a data augmentation approach [34] with respect to latent variable z. We introduce variables $z_{cit} \in \{1, \ldots , z \dots , Z\}$ denoting the label of the latent class for each customer c, each purchased product i and each purchasing event t. Conditioning on the $z_{cit}$ for each purchasing transaction, as in the LDA [6], the likelihood in (7) simplifies to

$$\begin{aligned}&\ell \left( \left\{ {{y}_{cit}} \right\} | \left\{ {\varvec{\theta }_{c}} \right\} ,\left\{ {{z}_{cit}} \right\} ,\left\{ {\varvec{\beta }_{zi}} \right\} ,\left\{ {\varvec{x}_{it}} \right\} \right) \nonumber \\&= \prod \limits _{c=1}^{C}{\prod \limits _{i\in {{I}_{c}}}^{{}}{\prod \limits _{t\in {{T}_{c}}}^{{}}{p\left( {{z}_{cit}}=z|{\varvec{\theta }_{c}} \right) p\left( {{y}_{cit}}|{\varvec{x}_{it}},{\varvec{\beta }_{zi}},{{z}_{cit}=z} \right) }}} \end{aligned}$$

(10)

where $p(z_{cit}=z|\varvec{\theta }_c)$ denotes a categorical distribution when $\varvec{\theta }_c$ is given. Hereinafter, $( z_{cit}=z )$ is denoted as $z_{cit}$ to simplify notation.

The posterior distribution of parameters including latent variables of states $\{z_{cit}\}$ and augmented utilities $\{u_{cit}^{(z)}\}$ of proposed model is then given as

$$\begin{aligned}&p\left( {\{\varvec{\theta }_c \},\{z_{cit} \}, \left\{ u_{cit}^{(z)} \right\} , \{\varvec{\beta }_{zi} \},\{\varvec{\mu }_i \},\{V_i \}\mid \{\varvec{x}_{it} \},\{y_{cit} \}} \right) \nonumber \\&= p\left( {\left\{ {\varvec{\theta }_c } \right\} \mid \{z_{cit} \}} \right) \nonumber \\&\quad \times p\left( {\left\{ {z_{cit} } \right\} \mid \left\{ {\varvec{\theta }_c, \varvec{\beta }_{zi}, \varvec{x}_{it}, y_{cit} } \right\} } \right) \nonumber \\&\quad \times p\left( {\left\{ {u_{cit}^{(z)} } \right\} \mid \left\{ {\varvec{\beta }_{zi}, z_{cit}, \varvec{x}_{it}, y_{cit} } \right\} } \right) \nonumber \\&\quad \times p\left( {\left\{ {\varvec{\mu }_i, V_i } \right\} \mid \{\varvec{\beta }_{zi} \}} \right) \nonumber \\&\quad \times p\left( {\left\{ {\varvec{\beta }_{zi} } \right\} \mid \left\{ {u_{cit}^{(z)}, \varvec{\mu }_i, V_i, \varvec{x}_{it} } \right\} } \right) \nonumber \\&\propto p\left( { \{\varvec{\theta }_c \},\{z_{cit} \}, \left\{ u_{cit}^{(z)} \right\} , \{\varvec{\beta }_{zi} \},\{\varvec{\mu }_i \}, \{V_i \},\{\varvec{x}_{it} \},\{y_{cit} \} } \right) \nonumber \\&= \left[ {\prod \limits _{c = 1}^C {p\left( {\varvec{\theta }_c } \right) } } \right] \left[ {\prod \limits _{i = 1}^I {p\left( {\varvec{\mu }_i, V_i } \right) } \prod \limits _{z = 1}^Z {p\left( {\varvec{\beta }_{zi} \mid \varvec{\mu }_i, V_i } \right) } } \right] \nonumber \\&\quad \, \Biggl [ \prod \limits _{c = 1}^C \prod \limits _{i \in I_c} \prod \limits _{t \in T_c} p\left( {z_{cit} \mid \varvec{\theta }_c } \right) p\left( {u_{cit}^{(z)} \mid \varvec{\beta }_{zi}, z_{cit}, \varvec{x}_{it}, y_{cit} } \right) \nonumber \\&\quad \, p\left( {y_{cit} \mid \varvec{\beta }_{zi}, z_{cit}, \varvec{x}_{it} } \right) \Biggl ]. \end{aligned}$$

(11)

4.2 Characteristics of the proposed model

Figure 1 presents a graphical representation of the proposed model. Here, it is noteworthy that $\{\varvec{\beta }_{zi}\}$ differs from smoothing parameters in the literature of LDA [6]. The $\{\varvec{\beta }_{zi}\}$ in our model, which are regression coefficient vectors for marketing activities, play a key role in our analysis because latent segments and augmented utilities are characterized by the estimated $\{\varvec{\beta }_{zi}\}$.

Fig. 1

Graphical representation of the proposed model

The latent classes z serve to define types of purchase baskets across the I products. The first term of (7) defines a vector of choice probabilities for each product under study, assuming that the purchase occasion is of type z. Products with high probability are likely to be jointly present in the basket. Therefore, our model identifies likely bundles of goods purchased for shopping trips of different types. The second term is the probability that a customer’s purchases are of type z. Our model does not model heterogeneity in a traditional manner of marketing models, where there is a common set of customer’s parameters for all purchases of an individual. We instead assume that each purchase belongs to one of Z types, and that customers can also be characterized in terms of the probability their purchases are of these types.

Our model differs from related standard models in two respects. First, the likelihood is defined over products and time periods in which purchases are observed to take place at least once, as indicated by variables $T_c$ and $I_c$. It is composed not only of purchase but also of nonpurchase occasions for identifying market response parameters. In this sense, our model differs from topic models used in text analysis where the likelihood is formed using the words present in a corpus, not the words that are not present. Second, heterogeneity is introduced at the observation, allowing the different transactions of a customer to reflect different latent states, z at every (c, i, t), as denoted by $z_{cit}$. It provides us with useful information for characterizing customers and products and for predicting their purchases. This information differs from the traditional latent class model [21], where the likelihood of all customer purchases contributes to inferences about a customer’s latent class membership (z) and parameters ($\beta$).

4.3 Estimation of personalized market response coefficients

The estimated posterior mean $\hat{\varvec{\beta }}_{zi}$, $\hat{u}_{cit}^{(z)}$ and $\hat{z}_{cit}^{(z)}$ can be transformed into statistics that are relevant for personalization. Here, $\hat{z}_{cit}^{(z)} \equiv \varvec{E}[p(z_{cit}=z)], z=,1...,Z$ at each point of data cube (c, i, t). Given the estimates $\hat{\varLambda }=\{\hat{\varvec{\beta }}_{zi}, \hat{u}_{cit}^{(z)}, \hat{z}_{cit}^{(z)} \}$, we can construct market response estimates for each customer and each product from $\hat{\varLambda }=\{\hat{\varvec{\beta }}_{zi}, \hat{u}_{cit}^{(z)}, \hat{z}_{cit}^{(z)}\}$ by projecting the estimates of latent utility on marketing variables. The estimates are obtained from an auxiliary regression of latent utility $\hat{U}_{ci}^{(k)}$ stacked by $\hat{u}_{cit}^{(k)}$ with the state $k= \text {argmax} \; \hat{z}_{cit}^{(z)}$ changing over time on the corresponding marketing variables $X_{ci}$ constituted by $\varvec{x}_{it}$ $(t \in T_c)$.

$$\begin{aligned} \hat{\varvec{\alpha }}_{ci}=\left( {X_{ci}}^{T}X_{ci}\right) ^{-1}{X_{ci}}^{T}\hat{U}_{ci}^{(k)}. \end{aligned}$$

(12)

The estimates presented above provide a bridge between the granularity of the model, where heterogeneity is introduced at each point in the data cube, and managerial inferences and decisions that are made across products (e.g., which customers to reward), across customers (e.g., which products to promote) and over time. In addition, the standard t test in the standard linear regression models is useful for testing the significance of estimates.

4.4 Parameter estimation

We use variational Bayes (VB) inference [5, 20], instead of the standard Markov chain Monte Carlo (MCMC) inference. MCMC methods can incur large computational cost in large-scale problems. VB inference approximates a posterior distribution of target by variational optimization in a computationally efficient manner. This approximation is necessary for our analysis. VB has another advantage over MCMC in that it is not prone to the label-switching problem encountered in MCMC estimation [24]. The VB inference, the update equation and the derivations for our model are detailed in Appendices A and B. The precision and computation time of parameter estimation of our model by the VB and MCMC in some situations are shown in Appendices E and F, respectively.

5 Application

5.1 Data description and settings

A customer database from a general merchandise store, recorded from April 1 to June 30 in 2002, is used in our analysis. A customer identifier, price, display and feature variables were recorded for each purchase occasion. The dataset includes 94,297 transactions involving 1650 customers and 500 products. The products were chosen by being displayed and featured at least once in the data period. The marketing variables are price $(P_{it})$, display $(D_{it})$ and feature $(F_{it})$; that is, $\varvec{x}_{it}=[1 \,\, P_{it} \,\, D_{it} \,\, F_{it}]^T$. Also, $P_{it}$ is the price relative to the maximum price of product i in the observational period. The display and feature are binary entries, equal to one if the product i is displayed or featured at time t, and zero otherwise.

In VB estimation, the iterations are terminated when the variational lower bound improves by less than $10^{-3} \%$ of the current value in two consecutive iterations. (The variational lower bound is described in Appendix C.) The hyperparameters and initial values are set as explained in Appendix A. These settings for the hyperparameters and the stopping rule of the VB iterations are adopted hereinafter for all empirical studies.

Table 1 RMSEs of predictions of the four methods

5.2 Prediction performance

Table 1 presents the root-mean-square error (RMSE) of the four methods with respect to the number of Z. The RMSE represents the difference between purchased behavior $y_{cit}=1$ and $p(y_{cit}=1)$ in the data cube and is calculated using hold-out samples recorded during July 1–31 in 2002. We measure the prediction performance of the four methods to unknown samples. The table includes results of the probit model, the logit model, the latent class logit model [21] and the proposed method. The RMSEs of probit model and logit model are calculated on the presumption that the data are generated by only one consumer’s behavior for each product. The latent class logit model assumes latent class of customer only. The RMSEs of the three models are calculated independently for each product. The calculation of RMSEs of the latent class logit model with respect to $Z=10,15$ and 20 does not converge. We used R function glm for probit and logit model. Then we used R package FlexMix for latent class logit model. Results show that the proposed method has a higher prediction performance than other methods.

Additionally, we find the decrease of RMSE of proposed method to be smooth around $Z=10$ from the table. We illustrate the following analysis using a $Z=10$ solution. Conditioning on the number of segments using variational lower bound is common practice in mixture model [5, 11]. We tried, but were unsuccessful in estimating an optimal Z because variances of estimated values of variational lower bound in multiple trials for each Z were too large to ascertain an optimal Z. Therefore, we leave this as an area for future research.

5.3 Insight to personalized marketing

5.3.1 Heterogeneity analysis

The management of pricing, displays and feature activity within a store involves decisions that cut across time and customers, and which require knowledge of which product categories are most sensitive to these actions. More recently, targeted coupon delivery systems have allowed for the individual-level customization of prices. Managing these decisions requires a view of the sensitivity of customers and product categories to these actions.

Individual-level estimates of market response are obtained using Eq. (12), and two-sided significance test on each estimate with the level of 5% is conducted by t test for deciding effectiveness of marketing variables in empirical analysis. In fact, customers will display variation in their sensitivity to variables such as price across product categories because of varying aspects of the product categories (e.g., necessary versus luxury goods, amount of product differentiation, price expectations) and different purposes of the shopping visit over time (e.g., shopping for oneself or others, large versus small shopping trip).

We can marginalize $\hat{\varvec{\alpha }}_{ci}$ by either of its arguments, c and i, to obtain characterizations of customers and products useful for analysis. The empirical marginal distribution of customer parameter estimates is obtained by averaging across the 500 products in our analysis, i.e., $\left\{ {\sum \nolimits _{c=1}^{C}{{{\hat{\varvec{\alpha }} }_{ci}}}}/{C}\; \right\}$. A histogram of 500 products for each marketing variable is displayed on the left side of Fig. 2, providing information related to the general distribution of heterogeneity faced by the firm for actions such as price customization. We find the individual estimates to be plausible in that the price coefficients are negative and the display and feature coefficients are estimated as positive.

Fig. 2

Marginal distribution of parameter estimates of individual customers

Fig. 3

Marginal distribution of parameter estimates of individual products

Fig. 4

Personalized effective marketing variables for individual customers and products: 100 customers and 100 products

We can also summarize heterogeneity across customers and examine the distribution of marketing variables for the 500 products in our analyses. The empirical marginal distributions of individual products, averaging over 1650 customers, i.e., of $\left\{ {\sum \nolimits _{i=1}^{I}{{{\hat{\varvec{\alpha }} }_{ci}}}}/{I}\; \right\}$, are depicted in Fig. 2. The products that were never displayed and featured in the data period have been omitted from the histograms in Fig. 3. These estimates are useful for ascertaining which product categories should receive merchandising support in the form of in-store displays and feature advertising. Results show that the estimates are plausible in most product categories with negative price coefficients, and positive display and feature coefficients, but there exists fairly wide variation in the effectiveness of these variables across products. Many product categories appear to be unresponsive to merchandising efforts.

5.3.2 Personalized effective marketing promotions

Figure 4 provides a two-dimensional summary of the data and coefficient estimates for top 100 products and customers. Figure 4a is a scatter plot of two-dimensional data cube with respect to customers (c) and products (i), aggregated along the time (t) dimension. If a customer has never purchased a specific product in the dataset, then the coordinate (i, c) is colored “white.” It is “black" if they have purchased the product at least once. We observe that customer-product space is still very sparse.

Figures 4b–d shows the results of testing with a 5% level of significance level for nonzero individual response coefficients. In Fig. 4b, the coordinates with a significant price coefficient indicated as “black" and “white" show that the estimate is not significant. The effectiveness of displays and feature promotions is defined similarly. We find that our model produces many significant price, display and feature coefficients.

An interesting aspect of our analysis is that because of the imputation present in the latent variable model for nonpurchases, significant coefficients can arise even when a customer has never purchased a product. The latent variable model greatly reduces the dimensionality of the data cube and produces individual estimates in a sparse data environment. Our analyses yield coefficient estimates at the individual customers and products by way of the latent topics that transcend the product categories. Our model enables marketers to develop effective pricing and promotional strategies by recognizing the presence of latent topics, or shopping baskets, present at each point in time in the data cube.

6 Conclusion

We proposed a descriptive model of demand based on the idea of latent variables where products purchased by customers. We allow for a product’s purchase probability to be affected by price, display and feature advertising variables, but do not treat purchases as arising from a process of constrained utility maximization. An important benefit of this approach is that it enables us to side-step complications associated with competitive effects and model a much larger set of products than that possible with existing economic models. By retaining prices and other marketing variables in our model, we can predict the effects of these variables on own sales. This trade-off is unavoidable in the analysis of transaction databases where purchases are tracked across thousands of products. The proposed model is applicable to personalized marketing across numerous and diverse products. We show how the model is useful to produce information useful for personalized marketing for both specific customers and specific products, and how it effectively accommodates data sparseness caused by infrequent customer purchases.

Future research will combine marketing models and other latent variable models or tensor factorization methods and compare the prediction performance with that of the proposed model. We would like to apply the method to other market datasets to verify the prediction performance. Additionally, our model includes the assumption that the stability of the topic structure is over time. However, it is possible that customers’ market response and purchase patterns change over time because of factors such as new trends, state dependence and the arrival of new purchase and delivery technologies. We believe that the development of a dynamic topic model for purchase is an interesting extension of our work, and leave this point for future research.

Appendices

Appendix A: Variational Bayes inference for the proposed model

This appendix details the variational inference of proposed model. The target and approximate distributions are denoted, respectively, as p and q. The latter is called the variational distribution. Distributions p and q share a parameter set $\varvec{\varTheta }$. In general, when the data $\varvec{D}$ are given, the log marginal likelihood $\log p(\varvec{D})$ of the target distribution is decomposed into two components as

$$\begin{aligned} \log p\left( \varvec{D} \right)&=L\left( q \right) +KL\left( q\left\| p \right. \right) \end{aligned}$$

(A1)

$$\begin{aligned} L\left( q \right)&=\int {q\left( \varvec{\varTheta }\right) }\log \left\{ p\left( \varvec{D},\varvec{\varTheta }\right) q{{\left( \varvec{\varTheta }\right) }^{-1}} \right\} dZ \end{aligned}$$

(A2)

$$\begin{aligned} KL\left( q\left\| p \right. \right)&=-\int {q\left( \varvec{\varTheta }\right) \log \left\{ p\left( \varvec{\varTheta }| \varvec{D} \right) q{{\left( \varvec{\varTheta }\right) }^{-1}} \right\} }dZ, \end{aligned}$$

(A3)

where L(q) is the variational lower bound in VB inference, and $KL\left( q\left\| p \right. \right)$ is the Kullback–Leibler divergence of the target and variational distributions. Actually, $KL\left( q\left\| p \right. \right)$ is well known to be zero if p and q are the same distribution. Therefore, a reasonable solution to estimating the posterior distribution p is the variational distribution q for which $KL\left( q\left\| p \right. \right)$ is minimized. However, it is difficult to evaluate the value of $KL\left( q\left\| p \right. \right)$ because the expression involves a posterior distribution of $p( \varvec{\varTheta }| \varvec{D})$.

In contrast, L(q) involves a joint distribution $p( \varvec{D}, \varvec{\varTheta })$ that is easily evaluated in many cases because it is obtained as the product of the prior and the likelihood in Bayesian models. In fact, maximizing L(q) is equivalent to minimizing $KL\left( q\left\| p \right. \right)$ because the log marginal likelihood of the target distribution is constant for a given dataset. Under these circumstances, assuming that the distribution q and parameter set $\varvec{\varTheta }$ are decomposable for some groups, the parameters are called variational parameters $q\left( \varvec{\varTheta }\right) =\prod \limits _{j=1}^{J}{{{q}_{j}}\left( {{\varvec{\varTheta }}^{\left( j \right) ^*}} \right) }$ and can be maximized by the following updating algorithm [20]:

$$\begin{aligned} \varvec{\varTheta }^{(j)*\{new\}}&\leftarrow \mathop {\arg \max }\limits _{\varvec{\varTheta }^{(j)*}} L \left( { \prod \nolimits _j^J q_j \left( {\varvec{\varTheta }^{(j)*}} \right) } \right) \nonumber \\&\propto \exp \left( {\varvec{E}_{k \ne j} \left[ {\log p\left( {\varvec{D},\varvec{\varTheta }} \right) } \right] } \right) . \end{aligned}$$

(A4)

The variational parameters are updated for each variational parameter set $\varvec{\varTheta }^{(j)^*}$ until convergence of the algorithm. The initial variational parameters are proper random values. The VB is guaranteed to converge after several iterations because L(q) is convex with respect to each $q_j (\varvec{\varTheta }^{(j)^*})$ [5]. The variational lower bound increases monotonically as the iteration proceeds. Therefore, convergence can be confirmed by checking the value of L(q) at each iteration.

We introduce the variational distributions and parameters for the proposed model. The parameters and variational parameters are denoted as

$\varvec{\varTheta } =$ $\left\{ { \{\varvec{\theta }_c \}, \{z_{cit} \}, \left\{ u_{cit}^{(z)} \right\} , \{\varvec{\beta }_{zi} \}, \{\varvec{\mu }_i \}, \{V_i \}} \right\}$ and

$\varvec{\varTheta }^*=$ $\bigl \{$ $\left\{ {\varvec{\gamma }_{c}^*} \right\} ,$ $\left\{ {\varvec{\theta }_{cit}^*} \right\} ,$ $\left\{ {\varvec{\beta }_{zi}^*} \right\} ,$ $\left\{ {V_{iz}^{\beta *} } \right\} ,$ $\left\{ {\varvec{\mu }_i^{*} } \right\} ,$ $\left\{ {\sigma _i^{\mu *} } \right\} ,$ $\left\{ {w_i^*} \right\} ,$ $\left\{ {W_i^*} \right\}$ $\bigl \}$, respectively, while the variational distributions are configured as

$$\begin{aligned}&q\left( {\varvec{\varTheta } \mid \varvec{\varTheta }^*, \{\varvec{x}_{it} \},\{y_{cit} \}} \right) \nonumber \\&\quad = \left[ { \prod \limits _{c = 1}^C q_c \left( {\varvec{\theta }_c \mid \varvec{\gamma }_{c}^*} \right) } \right] \left[ { \prod \limits _{c = 1}^C \prod \limits _{i \in I_c} \prod \limits _{t \in T_c} q_z \left( {z_{cit} \mid \varvec{\theta }_{cit}^*} \right) } \right] \nonumber \\&\quad \left[ { \prod \limits _{c = 1}^C \prod \limits _{i \in I_c } \prod \limits _{t \in T_c } q_u \left( {u_{cit}^{(z)} \mid \varvec{\theta }_{cit}^*, \varvec{\beta }_{zi}^*}, \varvec{x}_{it}, y_{cit} \right) } \right] \nonumber \\&\quad \, \left[ { \prod \limits _{i = 1}^I \prod \limits _{z = 1}^Z q_\beta \left( {\varvec{\beta }_{zi} \mid \varvec{\beta }_{zi}^*, V_{zi}^{\beta *} } \right) } \right] \nonumber \\&\quad \left[ { \prod \limits _{i = 1}^I q_{\mu , V} \left( { \varvec{\mu }_i, V_i \mid \varvec{\mu }_i^{*}, \sigma _i^{\mu *}, w_i^*, W_i^*} \right) } \right] \end{aligned}$$

(A5)

where $q_c$ is a Dirichlet distribution with variational parameter $\varvec{\gamma }_{c}^*$. Also, $q_z$ represents a categorical distribution with variational parameter $\varvec{\theta }_{cit}^*$, $q_u$ denotes a truncated normal distribution, $q_\beta$ stands for an M-dimensional multivariable normal distribution with two variational parameters (mean vector $\varvec{\beta }_{zi}^*$ and covariance matrix $V_{zi}^{\beta *} )$, and $q_{\mu , V}$ signifies a multivariable normal–inverse Wishart distribution with variational parameters $\varvec{\mu }_i^{*}$, $\sigma _i^{\mu *}$, $w_i^*$, $W_i^*$.

We set hyperparameters as $\tilde{\varvec{\gamma }} = [0.01, \ldots , 0.01]^{T}$, $\tilde{\varvec{\mu }} = [0, \ldots , 0]^{T}$, $\tilde{{\sigma }}^{2} = 1$, $\tilde{{W}} = \varvec{I}_{M}$ and $\tilde{{w}} = 10$ and initial values as $\{ \varvec{\theta }_{cit}^{(0)*} \} \sim Dirichlet ( \varvec{\tilde{\gamma }})$, $\{ {\varvec{\beta }}^{(0) *}_{zi}, \varvec{\mu }_i^{(0)*} \} \sim N_{M}([-1,0,0,0]^{T},0.1 \times \varvec{I}_{M})$, $\{ {\sigma _i^{\mu (0) *} } \}=(\tilde{\sigma }^{-2}+Z)^{-1}$, $\{ {w_i^{(0)*} } \} = \tilde{{w}} +Z$ and $\{ {V_{iz}^{\beta (0)*} }, {W_i^{(0)*} } \} = \varvec{I}_{M}$. These settings are adopted in all empirical studies. $\{ { \varvec{\gamma }_{c}^{(0)*} } \}$ are given by other initial parameters in VB procedure.

Appendix B: Derivation of VB algorithm for proposed model

The update procedure derives from the analytical calculation of Equation (13). The update equation for each variational parameter is obtained from the following expectation values

$$\begin{aligned}&\varvec{E}_{ \ne q_j } \left[ {\log p\left( {\varvec{D},\varvec{\varTheta }} \right) } \right] \nonumber \\&\quad \equiv \varvec{E}_{k \ne j} \left[ {\log p\left( {\varvec{D},\varvec{\varTheta }} \right) } \right] \nonumber \\&\quad = \int \log p\left( {\varvec{D},\varvec{\varTheta }} \right) \prod \limits _{k \ne j} q_i \left( {\varvec{\varTheta }^{(i)*} } \right) d\varvec{\varTheta }^{(i)*}, \end{aligned}$$

(B1)

where $\varvec{D} = \left\{ {\left\{ {\varvec{x}_{it} } \right\} ,\,\left\{ {y_{cit} } \right\} } \right\}$.

The update procedures of variational parameters $\varvec{\gamma }_{c}^*$, $\varvec{\theta }_{cit}^*$, $\varvec{\beta }_{iz}^*$, $V_{iz}^{\beta *}$, $\varvec{\mu }_i^{*}$, $\sigma _i^{\mu *}$, $w_i^*$ and $W_i^*$ are presented below.

1.1 Optimization of $\varvec{\gamma }_{c}^*$

The Dirichlet and categorical distributions are of the following forms.

$$\begin{aligned}&\displaystyle \text {Dirichlet}\left( {\varvec{\theta }_c \mid \tilde{\varvec{\gamma }}} \right) = \frac{\prod \nolimits _{z = 1}^Z {\varGamma \left( {\tilde{\gamma }_z } \right) } }{\varGamma \left( {\sum \nolimits _{z = 1}^Z {\tilde{\gamma }_z } } \right) }\prod \limits _{z = 1}^Z {\theta _{cz}^{\tilde{\gamma }_z - 1} } \nonumber \\{}&\displaystyle \text {Categorical}\left( {z_{cit} \mid \varvec{\theta }_c } \right) = \prod \limits _{z = 1}^Z {\theta _{cz}^{\delta \left( {z_{cit} = z} \right) } } \end{aligned}$$

(B2)

Therein, $\varGamma \left( \cdot \right)$ is the gamma function. Also, $\delta ( z_{cit}=z )$ is the Dirac delta function defined as $\delta ( z_{cit}=z ) = 1$ if $z_{cit}=z$ and $\delta ( z_{cit}=z ) = 0$. The expectation value $\varvec{E}_{ \ne q_\theta } \left[ {\log p\left( {\varvec{D},\varvec{\varTheta }} \right) } \right]$ is then calculated for each c as

$$\begin{aligned}&\varvec{E}_{ \ne q_\theta } \left[ {\log p\left( {\varvec{D},\varvec{\varTheta }} \right) } \right] = \log p\left( {\varvec{\theta }_c } \right) + \varvec{E}_{q_z } \left[ {\log p\left( {\left\{ {z_{cit} } \right\} \mid \varvec{\theta }_c } \right) } \right] \nonumber \\&\quad + \text {const.} \nonumber \\&= \log \varGamma \left( {\sum \nolimits _{z - 1}^Z {\tilde{\gamma }_z } } \right) - \sum \limits _{z = 1}^Z {\log } \varGamma \left( {\tilde{\gamma }_z } \right) \nonumber \\&\quad + \sum \limits _{z = 1}^Z \left[ {\left( {\tilde{\gamma }_z + \sum \limits _{i \in I_c } \sum \limits _{t \in T_c } \theta _{citz}^*- 1} \right) } \right] \log \theta _{cz} + \text {const,}\nonumber \\ \end{aligned}$$

(B3)

where $\theta _{citz}^*$ is an element of $\varvec{\theta }_{cit}^*$. Here and hereinafter, const. denotes any term not included in the relevant parameters. The second line of the above equations describes a log-Dirichlet function with parameter $\tilde{\gamma }_z + \sum \limits _{i \in I_c}\sum \limits _{t \in T_c} \theta _{citz}^*$. Therefore, we obtain the following.

$$\begin{aligned} \varvec{\gamma }_{c}^*\leftarrow \tilde{\varvec{\gamma }} + \sum \limits _{i \in I_c } \sum \limits _{t \in T_c } \varvec{\theta }_{cit}^*\end{aligned}$$

(B4)

1.2 Optimization of $\varvec{\theta }_{cit}^*$

Here we designate a digamma function as $\varPsi \left( \cdot \right)$, which will be useful for later discussion, and summarize the property of truncated normal distribution in the probit model. $u_{cit}^{(z)}$ follows a normal distribution with mean $\varvec{x}_{it}^T \varvec{\beta }_{zi}$ and variance 1. Moreover, $u_{cit}^{(z)}$ must satisfy $y_{cit} = 1$ if $u_{cit} > 0$ and $y_{cit} = 0$ if $u_{cit} \le 0$. Therefore, $u_{cit}^{(z)}$ is generated from a truncated normal distribution as

$$\begin{aligned} u_{cit}^{(z)} \sim \left\{ \begin{array}{ll} TN_{(0,\infty )} \left( {\varvec{x}_{it}^T \varvec{\beta }_{zi}, 1} \right) &{}\quad \text {if }y_{cit} = 1\\ TN_{( - \infty , 0)} \left( {\varvec{x}_{it}^T \varvec{\beta }_{zi}, 1} \right) &{}\quad \text {if }y_{cit} = 0\\ \end{array} \right. \;. \end{aligned}$$

(B5)

Therein, $TN_{(n_1, n_2 )} \left( { \cdot , \cdot } \right)$ denotes a normal distribution truncated from $n_1$ to $n_2$. The distribution of $u_{cit}^{(z)}$ is therefore expressed as

$$\begin{aligned}&p\left( {u_{cit}^{(z)} \mid \varvec{\beta }_{zi}, z_{cit} ,\varvec{x}_{it}, y_{cit} } \right) \nonumber \\&\quad = \frac{1}{\varOmega _{cit}^{(z)} }\frac{1}{\sqrt{2\pi } }\exp \left\{ { - \frac{1}{2}\left( {u_{cit}^{(z)} - \varvec{x}_{it}^T \varvec{\beta }_{zi} } \right) ^2} \right\} , \end{aligned}$$

(B6)

with $\varOmega _{cit}^{(z)} \equiv \left\{ {F\left( { \varvec{x}_{it}^T \varvec{\beta }_{zi} } \right) } \right\} ^{y_{cit}}\left\{ {1-F\left( { \varvec{x}_{it}^T \varvec{\beta }_{zi} } \right) } \right\} ^{\left( {1-y_{cit}} \right) }$. In addition, the expectation value and variance are expressed as

$$\begin{aligned} \varvec{E}\left[ {u_{cit}^{(z)} } \right]&= \varvec{x}_{it}^T \varvec{\varvec{\beta }}_{zi}^*+ \varphi _{cit}^{(z)} \end{aligned}$$

(B7)

$$\begin{aligned} \varvec{V}\left[ {u_{cit}^{(z)} } \right]&= 1 - \varvec{x}_{it}^T \varvec{\beta }_{zi}^*\varphi _{cit}^{(z)} - \left( {\varphi _{cit}^{(z)} } \right) ^2, \end{aligned}$$

(B8)

where $\varphi _{cit}^{(z)} \equiv (-1)^{(1-y_{cit})} f\left( { \varvec{x}_{it}^T \varvec{\beta }_{zi}^*} \right) / \varOmega _{cit}^{(z)*}$ and $\varOmega _{cit}^{(z) *} \equiv \left\{ {F\left( { \varvec{x}_{it}^T \varvec{\beta }_{zi}^{*} } \right) } \right\} ^{y_{cit}}\left\{ {1-F\left( { \varvec{x}_{it}^T \varvec{\beta }_{zi}^{*} } \right) } \right\} ^{\left( {1-y_{cit}} \right) }$. Consequently, the expected value $\varvec{E}_{\ne q_z } \left[ {\log p\left( {\varvec{D},\varvec{\varTheta }} \right) } \right]$ is given as

$$\begin{aligned}&\varvec{E}_{ \ne q_z } \left[ {\log p\left( {\varvec{D},\varvec{\varTheta }} \right) } \right] = \varvec{E}_{q_c } \left[ {\log p\left( {z_{cit} \mid \varvec{\theta }_c } \right) } \right] \nonumber \\&\quad + \varvec{E}_{q_u, q_\beta } \left[ {\log p\left( {u_{cit}^{(z)} \mid \varvec{\beta }_{zi}, z_{cit}, \varvec{x}_{it}, y_{cit} } \right) } \right] + \text {const.} \end{aligned}$$

(B9)

The first term in the right-hand side of Eq. (B9) is obtained as $\varPsi \left( {\gamma _{cz}^*} \right) - \varPsi \left( {\sum \nolimits _{z - 1}^Z {\gamma _{cz}^*} } \right)$ [6], whereas the second term is evaluated as

$$\begin{aligned}&\varvec{E}_{q_u, q_\beta } \left[ { \log p \left( { u_{cit}^{(z)} \mid \varvec{\beta }_{zi}, z_{cit}, \varvec{x}_{it}, y_{cit} } \right) } \right] \nonumber \\&= \varvec{E}_{q_u, q_\beta } \left[ { - \log \sqrt{2\pi } \varOmega _{cit}^{(z)} - \frac{1}{2} \left( { u_{cit}^{(z)} - \varvec{x}_{it}^T \varvec{\beta }_{zi} } \right) ^2 } \right] \nonumber \\&= -\, \varvec{E}_{q_\beta } \left[ {\log \varOmega _{cit}^{(z)} } \right] - \frac{1}{2}\varvec{E}_{q_u} \left[ {\left( {u_{cit}^{(z)} } \right) ^2} \right] \nonumber \\&\quad + \varvec{E}_{q_u, q_\beta } \left[ {u_{cit}^{(z)} \varvec{x}_{it}^T \varvec{\beta }_{zi} } \right] - \frac{1}{2}\varvec{E}_{q_\beta } \left[ {\left( {\varvec{x}_{it}^T \varvec{\beta }_{zi} } \right) ^2} \right] + \text {const.} \end{aligned}$$

(B10)

To solve Eq. (B9) for $\theta _{citz}^*$, we must evaluate the four terms of Eq. (B10). The first term includes a CDF from which the expectation value is difficult to obtain analytically. Therefore, we expand the term as a zeroth-order Taylor expansion in terms of the CDF of normal distribution and the logarithm function. Such bold approximation is standard strategies for adapting topic models with VB to practical computation (e.g., zeroth-order Taylor approximation by [4, 33], and zeroth- and first-order delta approximation by [8]). The four expectation values in Eq. (B10) are then written as

$$\begin{aligned} \varvec{E}_{q_\beta } \left[ {\log \varOmega _{cit}^{(z)} } \right]\approx & {} \text {const}, \nonumber \\ \varvec{E}_{q_u} \left[ {\left( {u_{cit}^{(z)} } \right) ^2} \right]= & {} \varvec{V} \left[ {u_{cit}^{(z)} } \right] + \left( {\varvec{x}_{it}^T \varvec{\beta }_{zi}^{*} + \varphi _{cit}^{(z)} } \right) ^2,\nonumber \\ \varvec{E}_{q_u, q_\beta } \left[ {u_{cit}^{(z)} \varvec{x}_{it}^T \varvec{\beta }_{zi} } \right]= & {} \left( {\varvec{x}_{it}^T \varvec{\beta }_{zi}^{*} + \varphi _{cit}^{(z)} } \right) {\varvec{x}_{it}^T \varvec{\beta }_{zi}^*} + \varvec{x}_{it}^T V_{zi}^{\beta *} \varvec{x}_{it}, \nonumber \\ E_{q_\beta } \left[ {\left( {\varvec{x}_{it}^T \varvec{\beta }_{zi} } \right) ^2} \right]= & {} \varvec{x}_{it}^T V_{zi}^{\beta *} \varvec{x}_{it} + \left( {\varvec{x}_{it}^T \varvec{\beta }_{zi}^*} \right) ^2. \end{aligned}$$

(B11)

Finally, $\theta _{citz}^*$ is updated as

$$\begin{aligned} \theta _{citz}^*\leftarrow \frac{\exp \left( {\rho _{citz} } \right) }{\sum \limits _{j = 1}^Z {\exp \left( {\rho _{citj} } \right) } }, \end{aligned}$$

(B12)

where

$$\begin{aligned} \rho _{citz} =&\, \varPsi \left( {\gamma _{cz}^*} \right) - \varPsi \left( {\sum \nolimits _{z-1}^Z \gamma _{cz}^*} \right) + \frac{1}{2} \varvec{x}_{it}^T \varvec{\beta }_{zi}^*\varphi _{cit}^{(z)} \nonumber \\&+ \frac{1}{2} \varvec{x}_{it}^T V_{zi}^{\beta *} \varvec{x}_{it} . \end{aligned}$$

(B13)

1.3 Optimization of $\varvec{\beta }_{zi}^*$ and $V_{zi}^{\beta *}$

First, we derive an inverse Wishart distribution function and adopt some well-known properties of multivariable normal and inverse Wishart distributions [2, 5].

$$\begin{aligned}&\text {IW}\left( {\tilde{W},\tilde{w}} \right) = \frac{\left| \tilde{W} \right| ^{\tilde{w}/2}}{2^{\tilde{w}M}\varGamma (\tilde{w} / 2)} \left| {V_i } \right| ^{-\frac{\tilde{w} + M + 1}{2}} \exp \left\{ { - \frac{1}{2}tr\left( {\tilde{W}V_i^{-1} } \right) } \right\} , \nonumber \\&\varvec{E}_{q_V } \left[ {\log \left| {V_i } \right| } \right] = \sum \limits _{m = 1}^M {\varPsi \left( {\frac{w_i^*+ 1 - m}{2}} \right) } + M\log 2 + \log \left| {W_i^{*- 1} } \right| , \nonumber \\&\varvec{E}_{q_V } \left[ {V_i^{-1} } \right] = w_i^*W_i^{*- 1}, \nonumber \\&E_{q_\mu , q_V } \left[ {\left( {\varvec{\beta }_{zi} - \varvec{\mu }_i } \right) ^T V_i^{-1} \left( {\varvec{\beta }_{zi} - \varvec{\mu }_i } \right) } \right] \nonumber \\&\quad = \left( {\varvec{\beta }_{zi} - \varvec{\mu }_i^{*} } \right) ^Tw_i^*W_i^{*- 1} \left( {\varvec{\beta }_{zi} - \varvec{\mu }_i^{*} } \right) + \sigma _i^{\mu *}\;. \end{aligned}$$

(B14)

We obtain the optimization procedures of $\varvec{\beta }_{zi}^*$ and $V_{iz}^{\beta *}$ by the following expected value:

$$\begin{aligned}&\varvec{E}_{\ne q_\beta } \left[ {\log p\left( {\varvec{D},\varvec{\varTheta }} \right) } \right] = \varvec{E}_{q_\mu ,q_V } \left[ { \log p\left( {\varvec{\beta }_{zi} \mid \varvec{\mu }_i, V_i } \right) } \right] \nonumber \\&\quad + \varvec{E}_{q_u, q_z} \left[ {\log p\left( { \left\{ {u_{cit}^{(z)} } \right\} \mid \varvec{\beta }_{zi}, \left\{ {z_{cit}, \varvec{x}_{it}, y_{cit} } \right\} } \right) } \right] + \text {const.} \nonumber \\&\qquad = -\, \frac{1}{2}\varvec{E}_{q_\mu , q_V} \left[ {\left( {\varvec{\beta }_{zi} - \varvec{\mu }_i } \right) ^TV_i^{-1} \left( {\varvec{\beta }_{zi} - \varvec{\mu }_i } \right) } \right] \nonumber \\&\quad \qquad - \frac{1}{2}\sum \limits _{c = 1}^C {\sum \limits _{t \in T_c } {\varvec{E}_{q_u, q_z } \left[ {\left( {u_{cit}^{(z)} - \varvec{x}_{it}^T \varvec{\beta }_{zi} } \right) ^2} \right] } } + \text {const.} \end{aligned}$$

(B15)

The first and second terms of the second line are given by the last and third lines of Eq. (B11), whereas the third and fourth terms are given, respectively, by Eqs. (B2) and (B3), derived in a manner similar to Equation (B10). $\varvec{\beta }_{zi}^*$ and $V_{zi}^{\beta *}$ are then updated arithmetically as

$$\begin{aligned} \begin{array}{@{}l} \displaystyle \varvec{\beta }_{zi}^*\leftarrow \left\{ {w_i^*W_i^{*- 1} + X_{zi} X_i^T } \right\} ^{-1} \left\{ {w_i^*W_i^{*- 1} \varvec{\mu }_i^{*} + X_{zi} \bar{\varvec{u}}_{zi} } \right\} \\ {} \displaystyle V_{zi}^{\beta *} \leftarrow \left\{ {w_i^*W_i^{*- 1} + X_{zi} X_i^T } \right\} ^{-1} \end{array} \end{aligned}$$

(B16)

where $\bar{\varvec{u}}_{zi} \equiv \left[ { \left\{ \varvec{E}\left[ {u_{cit}^{(z)} } \right] \right\} _{c = 1, \ldots , C,t \in T_c } } \right] ^T$,

$$\begin{aligned}&X_i \equiv \left[ { \left\{ {\varvec{x}_{it} } \right\} _{c = 1, \ldots , C,t \in T_c } } \right] , \\&\text {and } X_{zi} \equiv \left[ { \left\{ {\theta _{citz}^*\varvec{x}_{it} } \right\} _{c = 1, \ldots , C,t \in T_c } } \right] . \end{aligned}$$

The $\bar{\varvec{u}}_{zi}$ is a vector, and $X_i$ and $X_{zi}$ are matrices. The numbers of elements in $\bar{\varvec{u}}_i$, $X_i$ and $X_{zi}$ are decided by the size of the customer base and by $T_c$.

1.4 Optimization of $\varvec{\mu }_i^{*}$, $\sigma _i^{\mu *}$, $w_i^*$ and $W_i^*$

Here we consider a joint distribution of a multivariable normal distribution of $\varvec{\mu }_i$ and an inverse Wishart distribution of $V_i$ and derive the update equations for variational parameters of four types from this joint distribution. To this end, we require the following expectation value from the joint distribution function.

$$\begin{aligned}&\varvec{E}_{ \ne q_\mu , q_V } \left[ {\log p\left( {\varvec{D},\varvec{\varTheta }} \right) } \right] = \log p\left( {\varvec{\mu }_i, V_i } \right) \nonumber \\&\quad + E_{q_\beta } \left[ {\log p \left( { \left\{ {\varvec{\beta }_{zi} } \right\} \mid \varvec{\mu }_i, V_i } \right) } \right] + \text {const.} \nonumber \\&\qquad = - \frac{1}{2}\log \left| {V_i } \right| - \frac{1}{2}\tilde{\sigma }_\mu ^{-1} \left( {\varvec{\mu }_i - \tilde{\varvec{\mu }}^\mu } \right) ^TV_i^{-1} \left( {\varvec{\mu }_i - \tilde{\varvec{\mu }}^\mu } \right) \nonumber \\&\quad \qquad - \frac{\tilde{w} + M + 1}{2}\log \left| {V_i } \right| - \frac{1}{2}tr\left\{ {\tilde{W}V_i^{-1} } \right\} \nonumber \\&\qquad - \frac{1}{2}Z \cdot E_{q_\beta } \left[ {\log \left| {V_i } \right| } \right] - \frac{1}{2}\sum \limits _{z = 1}^Z E_{q_\beta } \nonumber \\&\quad \qquad \times \left[ { \left( {\varvec{\mu }_i - \varvec{\beta }_{zi} } \right) ^TV_i^{-1} \left( {\varvec{\mu }_i - \varvec{\beta }_{zi} } \right) } \right] + \text {const.} \end{aligned}$$

(B17)

First, we extract from this expectation value all terms linked to multivariable variational parameters $\varvec{\mu }_i^{\mu *}$ and $\sigma _i^{\mu *}$. That is

$$\begin{aligned} \varvec{E}_{\ne q_\mu }&\left[ {\log p\left( {\varvec{D},\varvec{\varTheta }} \right) } \right] = - \frac{1}{2}\tilde{\sigma }_\mu ^{-1} \left( {\varvec{\mu }_i - \tilde{\varvec{\mu }}^\mu } \right) ^TV_i^{-1} \left( {\varvec{\mu }_i - \tilde{\varvec{\mu }}^\mu } \right) \nonumber \\&\quad - \frac{1}{2}\sum \limits _{z = 1}^Z {E_{q_\beta } \left[ { \left( {\varvec{\mu }_i - \varvec{\beta }_{zi} } \right) ^TV_i^{-1} \left( {\varvec{\mu }_i - \varvec{\beta }_{zi} } \right) } \right] } + \text {const.} \end{aligned}$$

(B18)

The second term in the equation above is obtained in the same manner as Eq. (B14). The multivariable normal distribution function is then constructed in a straightforward manner as shown below:

$$\begin{aligned}&\varvec{\mu }_i^{*} \leftarrow \left( {\tilde{\sigma }_\mu ^{-1} + Z} \right) ^{-1} \left( {\tilde{\sigma }_\mu ^{-1} \tilde{\varvec{\mu }}^\mu + \sum \limits _{z = 1}^Z {\varvec{\beta }_{zi}^*} } \right) , \nonumber \\&\sigma _i^{\mu *} \leftarrow \left( {\tilde{\sigma }_\mu ^{-1} + Z} \right) ^{-1}. \end{aligned}$$

(B19)

Next, we optimize $w_i^*\text { }$ and $W_i^*$ using Eq. (B14) and the relation $\log q\left( {V_i } \right) = \log q\left( {\varvec{\mu }_i, V_i } \right) - \log q\left( {\varvec{\mu }_i \mid V_i } \right)$.

$$\begin{aligned}&\varvec{E}_{\ne q_V} \left[ {\log p\left( {\varvec{D},\varvec{\varTheta }} \right) } \right] \nonumber \\&\quad = \varvec{E}_{\ne q_\mu , q_V} \left[ {\log p\left( {\varvec{D},\varvec{\varTheta }} \right) } \right] - \varvec{E}_{ \ne q_\mu } \left[ {\log p\left( {\varvec{D},\varvec{\varTheta }} \right) } \right] \end{aligned}$$

(B20)

The expectation value $\varvec{E}_{\ne q_V} \left[ {\log p\left( {\varvec{D},\varvec{\varTheta }} \right) } \right]$ is calculated in a straightforward manner using Eqs. (B15) and (B16). Finally, we obtain the update equations for $w_i^*$ and $W_i^*$ as

$$\begin{aligned} W_i^*\leftarrow&\tilde{W} + \sum \limits _{z = 1}^Z {V_{zi}^{\beta *} } + \tilde{\sigma }_\mu ^{-1} \tilde{\varvec{\mu }} \tilde{\varvec{\mu }} \nonumber \\&+ \sum \limits _{z = 1}^Z {\varvec{\beta }_{zi}^*\varvec{\beta }_{zi}^{*T}} - \left( {\tilde{\sigma }_\mu ^{-1} + Z} \right) \varvec{\mu }_i^{*} \varvec{\mu }_i^{*T}, \nonumber \\ w_i^*\leftarrow&\tilde{w} + Z. \end{aligned}$$

(B21)

It is noteworthy that $\sigma _i^{\mu *}$ and $w_i^*$ are constant if the hyperparameters and the number latent class are given.

1.5 Posterior mean $\hat{\varvec{\beta }}_{zi}$, $\hat{u}_{cit}^{(z)}$ and $\hat{z}_{cit}^{(z)}$

The estimated posterior means $\hat{\varvec{\beta }}_{zi}$, $\hat{u}_{cit}^{(z)}$ and $\hat{z}_{cit}^{(z)}$ used in Sect. 4 in order to construct statistics for joint segmentation and personalization are calculated as $\hat{\varvec{\beta }}_{zi} \equiv \varvec{E}[\varvec{\beta }_{zi}] = \varvec{\beta }_{zi}^{*}$, $\hat{u}_{cit}^{(z)} \equiv \varvec{E}[{u}_{cit}^{(z)}] = \varvec{x}_{it}^T \varvec{\varvec{\beta }}_{zi}^*+ \varphi _{cit}^{(z)}$ and $\hat{z}_{cit}^{(z)} \equiv \varvec{E}[p(z_{cit}=z)] =\theta _{citz}^*$ using VB estimates after the iterative procedure converges.

Appendix C: Variational lower bound of proposed model

The variational lower bound $L\left( {\varvec{\varTheta }^*} \right)$ is given as

$$\begin{aligned} L\left( {\varvec{\varTheta }^*} \right) =&\,\int {\left[ {q\left( {\varvec{\varTheta }\vert \varvec{\varTheta }^*} \right) \log \frac{p\left( {\varvec{\varTheta }, \left\{ {\varvec{x}_{it} } \right\} , \left\{ {y_{cit} } \right\} } \right) }{q\left( {\varvec{\varTheta }\vert \varvec{\varTheta }^*} \right) }} \right] } d\varvec{\varTheta } \nonumber \\ =&\, \varvec{E}_{q_{\varvec{\varTheta }_\beta } } \left[ { \log \frac{p\left( {\varvec{\varTheta }, \left\{ {\varvec{x}_{it} } \right\} , \left\{ {y_{cit} } \right\} } \right) }{q\left( {\varvec{\varTheta }\vert \varvec{\varTheta }^*} \right) }} \right] \nonumber \\ =&\, L_\theta ^{(p)} + L_z^{(p)} + L_u^{(p)} + L_\beta ^{(p)} + L_{\mu ,V}^{(p)} \nonumber \\&- \,L_\theta ^{(q)} - L_z^{(q)} - L_u^{(q)} - L_\beta ^{(q)} - L_{\mu ,V}^{(q)}, \end{aligned}$$

(C1)

where each component of $L\left( {\varvec{\varTheta }^*} \right)$ represents the expectation of variables of the proposed model. The expectations except $L_u^{(p)}$ and $L_u^{(q)}$ are the following:

$$\begin{aligned} L_\theta ^{(p)} =\,&\varvec{E}_{q_c} \left[ {\log p \left( { \left\{ {\varvec{\theta }_c } \right\} } \right) } \right] \nonumber \\ =&\sum \limits _{c = 1}^C \biggl [ \log \varGamma \left( {\sum \nolimits _{z = 1}^Z {\tilde{\gamma }_z } } \right) - \sum \limits _{z = 1}^Z {\log } \varGamma \left( {\tilde{\gamma }_z } \right) \nonumber \\&+\, \sum \limits _{z = 1}^Z {\left( {\tilde{\gamma }_z - 1} \right) \left\{ {\varPsi \left( {\gamma _{cz}^*} \right) - \varPsi \left( {\sum \nolimits _{z = 1}^Z {\gamma _{cz}^*} } \right) } \right\} } \bigg ], \end{aligned}$$

(C2)

$$\begin{aligned} L_z^{(p)} =\,&\varvec{E}_{q_z,q_c } \left[ { \log p\left( { \left\{ {z_{cit} } \right\} \vert \left\{ {\varvec{\theta }_c } \right\} } \right) } \right] \nonumber \\&= \sum \limits _{c = 1}^C {\sum \limits _{i \in I_c } {\sum \limits _{t \in T_c } {\sum \limits _{z = 1}^Z {\theta _{citz}^*\left\{ {\varPsi \left( {\gamma _{cz}^*} \right) - \varPsi \left( {\sum \nolimits _{z = 1}^Z {\gamma _{cz}^*} } \right) } \right\} } } } }, \end{aligned}$$

(C3)

$$\begin{aligned} L_\beta ^{(p)} =\,&\varvec{E}_{q_\beta ,q_\mu ,q_{V^\beta } } \left[ {\log p \left( { \left\{ {\varvec{\beta }_{zi} } \right\} \vert \left\{ {\varvec{\mu }_i ,V_i } \right\} } \right) } \right] \nonumber \\ =&- \,\frac{1}{2}\sum \limits _{i = 1}^I \sum \limits _{z = 1}^Z \biggl [ M\log 2\pi + \sum \limits _{m = 1}^M {\varPsi \left( {\frac{w_i^*+ 1 - m}{2}} \right) } \nonumber \\&+ \,M\log 2 + \log \left| {W_i^{*- 1} } \right| + \left( {\varvec{\mu }_{zi}^*- \varvec{\mu }_i^{\mu *} } \right) ^Tw_i^*\left( {W_i^*} \right) ^{-1} \nonumber \\&\quad \left( {\varvec{\mu }_{zi}^*- \varvec{\mu }_i^{\mu *} } \right) + tr\left\{ {w_i^*\left( {W_i^*} \right) ^{-1}V_{zi}^{\beta *} } \right\} + \sigma _i^{\mu *} \biggl ], \end{aligned}$$

(C4)

$$\begin{aligned} L_{\mu ,V}^{(p)} =\,&\varvec{E}_{q_\mu ,q_{V^\beta } } \left[ {\log p \left( { \left\{ {\varvec{\mu }_i ,V_i } \right\} } \right) } \right] \nonumber \\ =&- \frac{1}{2} \sum \limits _{i = 1}^I \left[ M \log 2\pi + \tilde{\sigma }_\mu ^{-1} \bigl [ \left( {\varvec{\mu }_i^{\mu *} - \varvec{\tilde{\mu }}^\mu } \right) ^Tw_i^*{W_i^*}^{-1}\right. \nonumber \\&\quad \left( {\varvec{\mu }_i^{\mu *} - \varvec{\tilde{\mu }}^\mu } \right) + \sigma _i^{\mu *} \bigl ] - \tilde{w} \log \left| \tilde{W} \right| +\log 2 +2 \log \varGamma \left( {\frac{\tilde{w}}{2}} \right) \nonumber \\&+ \,tr\left\{ {\tilde{W}{W_i^*}^{-1}} \right\} + (\tilde{w} + M + 2) \nonumber \\&\quad \left. \left\{ {\sum \limits _{m = 1}^M {\varPsi \left( {\frac{w_i^*+ 1 - m}{2}} \right) } + M\log 2 + \log \left| { {W_i^*}^{-1}} \right| } \right\} \right] , \end{aligned}$$

(C5)

$$\begin{aligned} L_\theta ^{(q)} = \,&\varvec{E}_{q_c } \left[ {\log q_c \left( { \left\{ {\varvec{\theta }_c } \right\} \vert \left\{ {\varvec{\gamma }_c^*} \right\} } \right) } \right] \nonumber \\ =&\sum \limits _{c = 1}^C \Biggl [ \log \varGamma \left( {\sum \nolimits _{z - 1}^Z {\gamma _{cz}^*} } \right) - \sum \limits _{z = 1}^Z {\log } \varGamma \left( {\gamma _{cz}^*} \right) \nonumber \\&+ \,\sum \limits _{z = 1}^Z {\left( {\gamma _{cz}^*- 1} \right) \left\{ {\varPsi \left( {\gamma _{cz}^*} \right) - \varPsi \left( {\sum \nolimits _{z - 1}^Z {\gamma _{cz}^*} } \right) } \right\} } \Biggl ], \end{aligned}$$

(C6)

$$\begin{aligned} L_z^{(q)}&=\, \varvec{E}_{q_z } \left[ {\log q_z \left( {\left\{ {z_{cit} } \right\} \vert \left\{ {\varvec{\theta }_{cit}^*} \right\} }\right) } \right] \nonumber \\&= \sum \limits _{c = 1}^C {\sum \limits _{i \in I_c } {\sum \limits _{t \in T_c } {\sum \limits _{z = 1}^Z {\theta _{citz}^*\log \theta _{citz}^*} } } } , \end{aligned}$$

(C7)

$$\begin{aligned} L_\beta ^{(q)}&= \varvec{E}_{q_\beta } \left[ {\log q_\beta \left( { \left\{ {\varvec{\beta }_{zi} } \right\} \vert \left\{ {\varvec{\mu }_{zi}^*,V_{zi}^{\beta *} } \right\} } \right) } \right] \ \nonumber \\&= - \frac{1}{2}\sum \limits _{i = 1}^I {\sum \limits _{z = 1}^Z {\left\{ {M\log \left( {2\pi e} \right) + \log \left| {V_{zi}^*} \right| } \right\} } } \end{aligned}$$

(C8)

and

$$\begin{aligned} L_{\mu ,V}^{(q)} =&\, \varvec{E}_{q_\mu ,q_{V^\beta } } \left[ {\log q_{\mu ,V^\beta } \left( { \left\{ {\varvec{\mu }_i ,V_i } \right\} \vert \left\{ {\varvec{\mu }_i^{\mu *} ,\sigma _i^{\mu *} ,w_i^*,W_i^*} \right\} } \right) } \right] \nonumber \\ =&\,-\, \frac{1}{2}\sum \limits _{i = 1}^I \left[ M\log 2\pi + \log \left| {\sigma _i^{\mu *} } \right| - w_i^*\log \left| {W_i^*} \right| \right. \nonumber \\&+ \,w_i^*M\log 2 + \frac{1}{2}\log \varGamma \left( {\frac{w_i^*}{2}} \right) + \left( {w_i^*+ M + 2} \right) \nonumber \\&\quad \left\{ {\sum \limits _{m = 1}^M {\varPsi \left( {\frac{w_i^*+ 1 - m}{2}} \right) } + M\log 2 + \log \left| { {W_i^*} ^{-1}} \right| } \right\} \nonumber \\&\left. + \,w_i^*+ 1 \right] . \end{aligned}$$

(C9)

1.1 Derivation of $\varvec{L_u^{(p)} - L_u^{(q)} }$

The entropy of $u^{(z)}_{cit}$ is given as

$$\begin{aligned} \varepsilon =&- \frac{1}{2}\left\{ {\varvec{E}\left[ {\xi ^2} \right] - 2\varvec{x}_{it}^T \varvec{\mu }_{zi}^*\varvec{E}\left[ \xi \right] \!+\! \left( {\varvec{x}_{it}^T \varvec{\mu }_{zi}^*} \right) ^2 + \log (2\pi )} \right\} \\&- \,\log \varOmega _{cit}^{(z) *} , \end{aligned}$$

where $\xi$ is a random variable of the distribution [16]. Therefore,

$$\begin{aligned}&L_u^{(p)} - L_u^{(q)} = \varvec{E}_{q_u ,q_\beta ,q_z } \left[ {\log p \left( { \left\{ {u_{cit}^{(z)} } \right\} \big \vert \left\{ {\varvec{\beta }_{zi},z_{cit} ,\varvec{x}_{it} ,y_{cit} } \right\} } \right) } \right] \nonumber \\&- \,\varvec{E}_{q_u } \left[ {\log q_u \left( { \left\{ {u_{cit}^{(z)} } \right\} \big \vert \left\{ { \varvec{\theta }_{cit}^*, \varvec{\beta }_{zi}^*, \varvec{x}_{it} ,y_{cit} } \right\} } \right) } \right] \nonumber \\ =&- \frac{1}{2}\sum \limits _{i = 1}^I \sum _{z=1}^{Z} {\left[ {Tr \left\{ {X_i X_i \left( {\varvec{\mu }_{zi}^*\varvec{\mu }_{zi}^{*T} + V_{zi}^{\beta *} } \right) } \right\} } \right] }\nonumber \\&+ \,\sum \limits _{c = 1}^C {\sum \limits _{i \in I_c } {\sum \limits _{t \in T_c } \sum _{z=1}^{Z} {\left\{ {\frac{1}{2}\theta _{citz}^*\left( {\varvec{x}_{it}^T \varvec{\mu }_{zi}^*} \right) ^2 + \theta _{citz}^*\log \varOmega _{cit}^{(z) *} } \right\} } } } . \end{aligned}$$

(C10)

The value of $L\left( {\varvec{\varTheta }^*} \right)$ is calculated using summation of the 10 expectations from (C1)–(C10) above.

Appendix D: Gibbs sampler

The joint posterior distribution, assuming conditional independence between variables, provides the full conditional posterior distributions:

$$\begin{aligned} \begin{array}{@{}l} \varvec{\theta }_c \mid - \sim p\left( {\varvec{\theta }_c \mid z_{cit} } \right) \\ {} z_{cit} \mid - \sim p\left( {z_{cit} \mid \varvec{\theta }_c, \{\varvec{\beta }_{zi} \},\{\varvec{x}_{it} \},\{y_{cit} \}} \right) \\ {} u_{cit}^{(z)} \mid - \sim p\left( {u_{cit}^{(z)} \mid z_{cit}, \varvec{\beta }_{zi}, \varvec{x}_{it}, y_{cit} } \right) \\ {} \varvec{\beta }_{zi} \mid - \sim p\left( {\varvec{\beta }_{zi} \mid \{u_{cit}^{(z)} \},\varvec{\mu }_i, V_i, \left\{ {\varvec{x}_{it} } \right\} } \right) \\ {} \varvec{\mu }_i \mid - \sim p\left( {\varvec{\mu }_i \mid \{\varvec{\beta }_{zi} \},V_i } \right) \\ {} V_i \mid - \sim p\left( {V_i \mid \{\varvec{\beta }_{zi} \},\varvec{\mu }_i } \right) \end{array} \end{aligned}$$

(D1)

1.1 Sampling of $\varvec{\theta }_c$

The $\varvec{\theta }_c$ is generated by a Dirichlet categorical relation. The Dirichlet distribution is a conjugate prior of a categorical distribution. For each customer c, $\varvec{n}_c = \left[ {n_{c1}, \ldots , n_{cZ}} \right] ^T$ denotes the number of generated latent classes $z_{cit}$ by categorical distribution of parameter $\varvec{\theta }_c$ in each MCMC step. A Dirichlet categorical relation gives the posterior distribution with respect to $\varvec{\theta }_c$ as

$$\begin{aligned} p\left( {\varvec{\theta }_c \mid - } \right) = p\left( {\varvec{\theta }_c } \right) p\left( {z_{cit} \mid \varvec{\theta }_c } \right) = \text {Dirichlet}\left( {\varvec{n}_c + \tilde{\gamma }} \right) . \end{aligned}$$

(D2)

1.2 Sampling of $z_{cit}$

The posterior probability of $(z_{cit} = z)$ is given as shown below.

$$\begin{aligned} \Pr \left\{ {z_{cit} = z\mid \varvec{\theta }_c, \left\{ {\varvec{x}_{it} } \right\} ,\left\{ {\varvec{\beta }_{zi} } \right\} , \left\{ {y_{cit} } \right\} } \right\} = \frac{\theta _{cz} \varOmega _{cit}^{ \left( z \right) } }{\sum \nolimits _{j = 1}^Z {\theta _{cz} \varOmega _{cit}^{\left( j \right) } } } \end{aligned}$$

(D3)

1.3 Sampling of $u_{cit}^{(z)}$

The distribution of $u_{cit}^{(z)}$ is described in Appendix B.2. $u_{cit}^{(z)}$ is sampled from a truncated normal distribution in Eq. (B5). This well-known sampling approach is called data augmentation [34].

1.4 Sampling of $\varvec{\beta }_{zi}$, $\varvec{\mu }_i$ and $V_i$

The full conditional posterior distribution of $\varvec{\beta }_{iz}$, $\varvec{\mu }_i$ and $V_i$ is derived from a hierarchical linear regression model. In our case, $\varvec{\beta }_{zi}$ for each i and each z is sampled from

$$\begin{aligned} \varvec{\beta }_{iz} \sim N_M \left( {R^{-1} \left\{ { \left( {\bar{X}_{zi}^T \varvec{u}_{zi}^{(z)} } \right) + V_i^{-1} \varvec{\mu }_i } \right\} , R^{-1} } \right) , \end{aligned}$$

(D4)

where $R \equiv \bar{X}_{zi}^T \bar{X}_{zi} + V_i^{-1}$, $\varvec{u}_{zi}^{(z)} \equiv \left[ {\left\{ {u_{cit}^{(z)} } \right\} _{c \in z_c = z,\ t \in T_c} } \right] ^T$ and $\bar{X}_{zi} \equiv \left[ {\left\{ {\varvec{x}_{it} } \right\} _{c \in z_c = z,t \in T_c } } \right] ^T$.

$\varvec{\mu }_i$ is sampled from

$$\begin{aligned} \varvec{\mu }_i \sim N_M \left( {\left( {Z + \tilde{\sigma }_\mu } \right) ^{-1} \sum \limits _{z = 1}^Z {\varvec{\beta }_{zi} }, V_i + \left( {Z + \tilde{\sigma }_\mu } \right) ^{-1}\varvec{I}_M } \right) , \end{aligned}$$

(D5)

for each i. Here, the hyperparameters are set to $\tilde{\varvec{\mu }} = \left[ \begin{array}{cccc} 0 &{} 0 &{} 0 &{} 0 \\ \end{array} \right] ^T$.

Finally, $V_i$ for each i is sampled from

$$\begin{aligned} V_i \sim IW\left( {\tilde{w} + Z, \tilde{W} + B^TB} \right) , \end{aligned}$$

(D6)

where $B \equiv \sum \nolimits _{z = 1}^Z \left( {\varvec{\beta }_{zi} - Z^{-1}\sum \limits _{z = 1}^Z {\varvec{\beta }_{zi} } } \right)$.

Appendix E: Simulation study

In this simulation study, purchase records are generated by simulation using marketing variables. The marketing variables are extracted from a real customer database of a general merchandise store. The marketing variables vector comprises discount $(\bar{D}_{it})$, display $(D_{it})$ and feature $(F_{it})$, that is, $\varvec{x}_{it}=[1 \,\, \bar{D_{it}} \,\, D_{it} \,\, F_{it}]^T$. Discount, display and feature are binary entries, equal to one if the product i is discounted, displayed or featured at time t, and zero otherwise.

We assume that any customer belongs to one of three segments characterized by response coefficients for marketing variables. First segment (Segment 1) has a response coefficient $\bar{\varvec{\beta }}_{1} = [-\,0.5, 1, 0, 0]^{T}$, i.e., customers in the segment sensitively respond to discount of products and are unaffected from display or feature. Similarly, we use $\bar{\varvec{\beta }}_{2} = [-\,0.5, 0, 1, 0]^{T}$ and $\bar{\varvec{\beta }}_{3} = [-\,0.5, 0, 0, 1]^{T}$ as response coefficient vectors for second (Segment 2) and third segments (Segment 3) that are influenced, respectively, from display and feature promotion only. The three vectors are set as true values of the response parameter. This setting means that all products have the same properties on the response to marketing promotions for a simplification of analysis. The verification or check of parameter estimation will be too complicated if we use a different coefficient vector for each product.

Next, we make coefficient vectors of individual customers. Here, we presume that each segment consisting of 100 customers and 50 products is in a store. The individual coefficient vectors $\bar{\varvec{\alpha }}_{ci}$ are generated by the following: $\bar{\varvec{\alpha }}_{ci} \sim N_{M}(\bar{\varvec{\beta }}_{1},\sigma \varvec{I}_{M}) \; (c=1, \ldots , 100)$, $\bar{\varvec{\alpha }}_{ci} \sim N_{M}(\bar{\varvec{\beta }}_{2},\sigma \varvec{I}_{M}) \; (c=101, \ldots , 200)$ and $\bar{\varvec{\alpha }}_{ci} \sim N_{M}(\bar{\varvec{\beta }}_{3},\sigma \varvec{I}_{M}) \; (c=201, \ldots , 300)$, and $\sigma$ is set as 0.1. $\varvec{I}_{M}$ is the identity matrix of size M. Then, the utilities for 30 days are simulated by $\bar{u}_{cit} = \varvec{x}_{it}^{T} \bar{\varvec{\alpha }}_{ci} + \bar{\epsilon }_{cit} \; (\bar{\epsilon }_{cit} \sim N(0,1) )$. The purchased records $\{ \bar{y}_{cit} \}$ are generated as $\bar{y}_{cit} = 1$ if $\bar{u}_{cit} > 0$ and $\bar{y}_{cit} = 0$ otherwise.

Here, we generate 10 simulation datasets using the procedures explained above. Table 2 presents the means and standard deviations of estimates with 200 iteration using the ten simulation dataset. The numbers in Table 2 are calculated as $50^{-1} \sum ^{I}_{i=1} {\hat{\varvec{\beta }}_{zi}}$. ($\hat{\varvec{\beta }}_{zi}$ represents a estimated posterior mean of $\varvec{\beta }_{zi}$.) Results indicate that the VB estimates are close to true values for all parameters in every segment.

Table 2 Estimates of simulation data

Appendix F: Computation time

The computation time is investigated for $C = \{1000, 5000,$ $10000\}$, $I = \{100, 500, 1000\}$, $T = 30$ and $Z = \{5, 10, 20\}$ in the same situation of simulation study in Appendix E. Consequently, 27 scenarios were explored in the study. The MCMC estimator is described in Appendix D. Then, we forecast the simulation times for 6000 MCMC samples from 10 samples for computational feasibility. In fact, the selection of 6000 MCMC samples is consistent with the simulation study of [8]. The simulated data are the same as those used above. The results reported below were calculated in identical computational environment (64-bit version of Python 2.7.5 with NumPy, implemented on a 3.5-GHz processor (Quad-Core Xeon; Intel Corp.) with 256-GB memory).

Table 3 reports the computation time in hours for the VB and MCMC estimators. For both algorithms, the computational cost increases linearly with the size of the dataset specified in terms of the numbers of customers, products and latent classes. In all scenarios, the times of MCMC computations exceed those of VB. The VB algorithm is approximately 20–50 times more efficient than MCMC, depending on the scenario. The time of computation using large-scale data ($C = 10000, \;\;I = 1000$) by MCMC is estimated as over 450 h. MCMC becomes increasingly prohibitive as the numbers of customers and choice alternatives increase.

Table 3 Simulation time by VB and MCMC

Table 4 Characteristics of latent classes

Appendix G: Interpretation of latent classes

We obtain the probability of customer segment membership by aggregating over products (i) and time (t):

$$\begin{aligned} p\left( c \in z| \hat{\varLambda } \right) =\frac{\sum _{i \in I}\sum _{t \in T_c} \hat{z}_{{cit}}^{(z)}\times I(y_{cit}=1)}{\sum _{z_k=1}^{Z}\sum _{i \in I}\sum _{t \in T_c} \hat{z}_{{cit}}^{(z)}\times I(y_{cit}=1)} \end{aligned}$$

(C1)

and aggregating over customers (c) and time (t) yields the probability of product segment membership.

$$\begin{aligned} p\left( i \in z| \hat{\varLambda } \right) =\frac{\sum _{c=1}^{C}\sum _{t \in T_c} \hat{z}_{{cit}}^{(z)}\times I(y_{cit}=1)}{\sum _{z_k=1}^{Z}\sum _{c}^{C}\sum _{t \in T_c} \hat{z}_{{cit}}^{(z)}\times I(y_{cit}=1)} \end{aligned}$$

(C2)

Therein, $I(\cdot )$ is the indicator function equal to one if the augment holds and zero otherwise. We take the sums over the instances of purchase because we believe that nonpurchase can occur for many reasons other than nonmembership (e.g., having large household inventory of the product). Our estimates of customer and product latent membership are driven by customer actions and not their inactions.

Our model of purchase behavior allows for heterogeneity at each observation that acknowledges that each purchase occasion can be viewed as the building block for analysis. Some occasions are associated with trips to the store, whereas other occasions might have been more focused on a specific set of offerings. Moreover, customers might exhibit behavior consistent with multiple occasions, or topics, over time. Although it might be desirable for firms to classify goods and respondents to segments for understanding customers and goods of different types, our model can be applied to analysis at a more disaggregate level. Alternatively, our model is useful to associate both offerings and customers to latent topics, or segments, for understanding and managing market basket purchases.

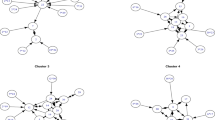
Table 4 displays the results of the joint segmentation of products and customers using Eqs. (C1) and (C2). The five products with the highest probability and their average levels of marketing activity are shown for the respective segments. The first column reports the brand name. The second column reports the product category associated with the offering. The remaining columns display the average level of marketing activity, i.e., the average price rate, average display rate and average feature rate. The title of each segment includes the numbers of products and customers who are jointly classified into the same segment. The segments are interpreted as follows.

The first segment has 31 customers and 9 products assigned to it. This segment includes beverages across different categories with small discount rates and low rates of feature advertising. The second segment is characterized as being composed of the identical brands in the dessert category. The products are infrequently discounted and have a higher rate of display than the first segment. Segments 3 through 7 have fewer customers and products. They exhibit greater variation in the level of marketing activity. Particularly, Segment 5 contains two offerings in both the ice cream and dressing categories with the same brand names, both with high rates of display and feature activity. Segment 6 includes mainly products from the drink category. It is similar in marketing activity with segment 5. Segment 7 also comprises drink products with higher marketing levels as well as other products with lower levels of activities. Products in segment 8 comprise a variety of product categories with higher level of display. Segment 9, the largest cluster with 946 customers and 332 products, is characterized as having the highest level of display activity. Segments 8 and 10 include less discounting and more displayed products. The former is double-sized and triple-sized in terms of customers and products.

The potential use of this information is in managing cross-category behavior. Knowing the products typically purchased for shopping trips of different types is useful to ascertain the range of impact of price promotions and merchandising activity. If customers have a budget for a particular shopping occasion, rather than for a particular product category, then the influence of a price reduction will have a broader effect in traditional models of demand. Our model allows for the identification of the boundary of effects as part of the topic, or latent segment, characterization.