1 Introduction

Internal migration can be an important component for adjusting asymmetric regional labour market shocks. For a fast-developing economy like India, which is also experiencing rapid population growth, efficient internal migration of labour may be even more important (Lagakos 2020). Still, in a large country such as India with different language groups, internal migration may also face political and administrative barriers as documented in Aggarwal et al. (2020), Bhagat (2012), Borhade (2012) and Kone et al. (2018).

In this paper, we estimate how net migration, proxied by regression-controlled population change in a region, reacts to regional labour market shocks in India. We measure asymmetric regional labour market shocks by changes in the ratio of the regional non-employment rate to the average non-employment rate of all Indian regions as well as by changes in the ratio of the average full-time wage in a region to the average wage of all Indian regions. We use both states/union territories and districts as regional units.Footnote 1 Based on regressions using regional and year fixed effects, we find that Indian workers respond to asymmetric regional labour market conditions. Indeed, when comparing our results to those obtained for the United States (US) and the European Union (EU) applying the same methodology as in Jauer et al. (2019), we find that regional adjustment in India occurs primarily at the district level but not at the state level, whereas it occurs at both of these levels in the US and in Europe. This finding is not inconsistent with concerns raised in the literature on barriers to mobility: maybe the dynamics of the Indian economy requires much more labour mobility for India to unleash its economic potential.

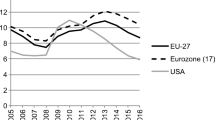
During the last two decades, India has seen significant macroeconomic and labour market changes: India has seen larger population growth since the year 2000 than the US, the EU, or China, but its GDP growth has been below the one of China since the late 2000s (see Figs. 1 and 2). This raises the question whether India is making full use of its labour market potential. Indeed, the employment to population ratio for people older than 15 years of age has been decreasing for the last two decades in India and is now below the one of the US, the EU, and China (Fig. 3), see also Verick (2014). The unemployment rate has increased recently (Fig. 4), although—given the lack of a European or the US style unemployment benefit system—we have doubts whether it is as meaningful as a statistic here as the non-employment rate, which will be our preferred statistic to measure (the inverse of) labour market tightness. For the employed, there have been significant structural shifts: India has experienced a decrease in the (still high) share of agricultural employment. This is not only reflected in an increase in the share of service employment: in striking contrast to the US and the EU, India and China have experienced industrialisation of their workforces in the first decade of the 21st century and slightly beyond (Figs. 5, 6 and 7). India may thus experience a form of development similar to the Lewis (1954) model, for which internal migration is a crucial component.

Fig. 1
figure 1

Population by country. Data Source: https://data.worldbank.org

Full size image
Fig. 2
figure 2

GDP by country. Data Source: https://data.worldbank.org

Full size image
Fig. 3
figure 3

Employment to population ratio by country. Data Source: https://data.worldbank.org

Full size image
Fig. 4
figure 4

Unemployment rates by country. Data Source: https://data.worldbank.org

Full size image
Fig. 5
figure 5

Employment share agriculture by country. Data Source: https://data.worldbank.org

Full size image
Fig. 6
figure 6

Employment share industry by country. Data Source: https://data.worldbank.org

Full size image
Fig. 7
figure 7

Employment share services by country. Data Source: https://data.worldbank.org

Full size image

The paper is structured as follows. Section 2 describes our data set and presents descriptive statistics in the form of graphs. Section 3 presents the regression results. Section 4 concludes.

2 Data and Descriptive Statistics

We use individual-level survey data from the Employment and Unemployment Survey (EUS) by the National Sample Survey Office (NSSO) of India, rounds 60 (collected from January 2004 to June 2004), 62 (collected from July 2005 to June 2006), 64 (collected from July 2007 to June 2008), 66 (collected from July 2009 to June 2010), and 68 (latest available, collected from July 2011 to June 2012). Because round 60 was only collected during 6 instead of 12 months, we will check the sensitivity of our results with respect to exclusion or inclusion of round 60. Round 61 is excluded because our estimating equation will contain a lag structure and we want to maintain a similar (2-year) lag throughout the sample.

Using sampling weights, we build regional-level data (at the state/union territory or district level) for the population growth factor, the non-employment rate (1 minus the employment-population ratio), and the unemployment rate. In doing that, we only consider people of working age (15–64 years). Using sampling weights, we also generate the average wage per region as a proxy for earnings potential. Because we do not have information on hours of work, we only use full-time workers who usually work at least 5 days per week full-time.

We exclude the following small union territories: Andaman and Nicobar Islands, Lakshadweep (both islands), and Puducherry (set of geographically disconnected territories). Because of changes to districts and inconsistencies in the data, Delhi and Goa are treated as a single entity in the district data. The following districts are excluded due to lack of wage information: Lakhisarai (Bihar), Upper Siang (Arunachal Pradesh), and Tamenglong (Manipur). We also excluded Leh Ladakh, Kargil, and Punch (all in Jammu and Kashmir), because data for these districts are only available in round 68 (collected from July 2011 to June 2012) of the EUS survey. This leaves us with 32 states/union territories and 570 districts, which we observe bi-annually in 5 different years over a time period of about 8 years.Footnote 2

The size of the population is heterogeneous across states and districts as exhibited in Figs. 8 and 9. Average wages increased in virtually all states after 2008 (Fig. 10). However, the increase in wages was also accompanied by regional diversion from 2008 to 2012, whereas there seems to have been regional wage conversion between 2004 and 2008, see the corresponding coefficients of variation in Fig. 11. When considering wages by district, there also seems to be increasing diversion together with wage increases after 2008 (even when ignoring the outlier, see Fig. 12 and the corresponding coefficients of variation in Fig. 13). Himanshu (2017) also reports a “rapid acceleration” of wages “during 2008–2013” (p. 309).

Fig. 8
figure 8

Population by state. Data Source: EUS by NSSO, Rounds 60 and 62–68

Full size image
Fig. 9
figure 9

Population by district. Data Source: EUS by NSSO, Rounds 60 and 62–68

Full size image
Fig. 10
figure 10

Average wage by state. Data Source: EUS by NSSO, Rounds 60 and 62–68

Full size image
Fig. 11
figure 11

Average wage and coefficient of variation of the average wage over states. Data Source: EUS by NSSO, Rounds 60 and 62–68

Full size image
Fig. 12
figure 12

Average wage by district. Data Source: EUS by NSSO, rounds 60 and 62–68

Full size image
Fig. 13
figure 13

Average wage and coefficient of variation of the average wage over districts. Data Source: EUS by NSSO, Rounds 60 and 62–68

Full size image

On the other hand, there seems to be a convergence in the non-employment rates by both states and districts, despite of rising non-employment rates (Figs. 14 and 15, for the corresponding coefficients of variation, see Figs. 16 and 17). The dispersion of the regional unemployment rate seems to move more erratically over time, especially when plotted by district (Figs. 18 and 19). There appears to be an increase in the dispersion when plotted by state (Fig. 18), but we consider the non-employment statistic to be more reliable than the unemployment statistic. Indeed, as Figs. 20 and 21 show, there is a clear increase in the non-employment rate over time (when averaged over states and districts), whereas there is no such clear trend for the unemployment rate.

Fig. 14
figure 14

Non-employment rate by state. Data Source: EUS by NSSO, Rounds 60 and 62–68

Full size image
Fig. 15
figure 15

Non-employment rate by district. Data Source: EUS by NSSO, Rounds 60 and 62–68

Full size image
Fig. 16
figure 16

Coefficient of variation of the non-employment and unemployment rates by states. Data Source: EUS by NSSO, Rounds 60 and 62–68

Full size image
Fig. 17
figure 17

Coefficient of variation of the non-employment and unemployment rates by districts. Data Source: EUS by NSSO, Rounds 60 and 62–68

Full size image
Fig. 18
figure 18

Unemployment rate by state. Data Source: EUS by NSSO, Rounds 60 and 62–68

Full size image
Fig. 19
figure 19

Unemployment rate by district. Data Source: EUS by NSSO, Rounds 60 and 62–68

Full size image
Fig. 20
figure 20

Unemployment rate and non-employment rate averaged over states. Data Source: EUS by NSSO, Rounds 60 and 62–68

Full size image
Fig. 21
figure 21

Unemployment rate and non-employment rate averaged over districts. Data Source: EUS by NSSO, Rounds 60 and 62–68

Full size image

3 Methodology and Results

Following Jauer et al. (2019), we estimate the following regression with the regional population growth factor on the left hand side and the region’s ratio of its unemployment/non-employment rate (ur) to the national average as well as the ratio of the region’s wage rate (y) to the national average on the right hand side. The estimating equation is:

$$\begin{aligned} \ln \left( \frac{\hbox{pop}_{\textrm{it}}}{\hbox{pop}_{\textrm{it}-2}}\right) =\alpha _0 + \alpha _1 \ln \left( \frac{\hbox{ur}_{\textrm{it}-2}}{\hbox{ur}_{\textrm{nt}-2}}\right) + \ln \left( \frac{y_{\textrm{it}-2}}{y_{\textrm{nt}-2}}\right) + \eta _t + \mu _i + \varepsilon _{\textrm{it}} \end{aligned}$$
(1)

Because we have bi-annual regional panel data, we include both region and time fixed effects (FE), \(\mu _i\) and \(\eta _t\), respectively. Because the national averages in the denominators on the right hand side are constant between regions, they are taken account of by the year fixed effects. If the region and time fixed effects take account of natural population growth, using the population growth factor on the left hand side—regression-adjusted by region and time effects—will effectively measure population change due to net migration.Footnote 3

$$\begin{aligned}& \hbox{ln}\left(\frac{\hbox{pop}_{\textrm{it}}}{\hbox{pop}_{\textrm{it}-2}}\right)- \eta _t - \mu _i = \hbox{ln}\left( \frac{\Delta ^t_{t-2}\hbox{pop}_{\textrm{it}}+\hbox{pop}_{\textrm{it}-2}}{\hbox{pop}_{\textrm{it}-2}}\right)- \eta _t - \mu _i \\ & \quad \approx\hbox{ln}\left(\frac{\hbox{mig}_{\textrm{it},t-2} +\hbox{pop}_{\textrm{it}-2}}{\hbox{pop}_{\textrm{it}-2}}\right)\end{aligned}$$
(2)

Under these assumptions, we follow Jauer et al. (2019) and interpret the coefficients on the unemployment/non-employment rate and on the wage as the reactions of net migration to regional labour market shocks. Because of the log–log specification, the coefficient on the wage can be interpreted as an elasticity. Similarly, the coefficient on the unemployment/non-employment rate is an elasticity, but here we are more interested in how much of an increase in non-employment in a region can possibly be adjusted by net migration (discussed below).

Table 1 shows ordinary least squares (OLS, first two columns, the latter restricted to the population up to age 50) and fixed-effects (FE, last two columns, the latter restricted to the population up to age 50) regression results at the state level. The upper panel of the table presents the specifications with lagged relative unemployment and the lower panel the specifications with lagged relative non-employment as measure of labour market tightness. Within these panels the upper (lower) block refers to rounds 62 (60) to 68 of the EUS, hence years 2005 (2004) to 2012. In the OLS results without region fixed effects, which exploit both within- and between-state variation in the impact variables, none of the unemployment, non-employment nor wage variables are statistically significant. Still, the coefficients have the expected signs.

Table 1 Regressions at the state level
Full size table

In the fixed-effects regressions, the coefficients for state unemployment and non-employment are still statistically insignificant, but the wage rate is statistically significant. The interpretation for the FE coefficients in the third column of Table 1 is that a 1.0% increase in the wage of a region increases the population growth factor by approximately 0.45% (coefficients are rather similar across the panels in the third column). This estimate is larger than the estimates reported by Jauer et al. (2019) for the USW and the EU, which are statistically insignificant in many cases. However, these authors have a 1-year time lag. Hence, in order to produce comparable results for the US and the EU, in Appendix Table 7 we use the data of Jauer et al. (2019) and re-estimate their main models with a 2-year lag. Still, the wage effect estimates for the US and the EU remain smaller than the ones for India. When we add round 62 and the lagged variables from round 60 to the sample as a robustness check (the second blocks in the panels of Table 1), we mostly obtain similar results for both OLS and FE estimates.

Using Indian districts instead of states as units of analysis (Table 2), the coefficient of the non-employment rate becomes statistically significant, although the coefficient of the unemployment rate is still statistically insignificant with a point estimate close to zero. Again, results are qualitatively robust to the inclusion of round 62 and the lagged variables from round 60.

Table 2 Regressions at the district level
Full size table

Results in general are also qualitatively and quantitatively similar when restricting the sample to the population up to age 50 (Table 1, columns 2 and 4 at the state level and Table 2 columns 2 and 4 at the district level), which might be more mobile. The coefficients are only a bit larger in most cases. This might be explained by India being a young country, so that the cohorts above age 50 are comparatively small, which lessens their influence on the estimates for the total working age population.Footnote 4

How can we interpret the size of the estimate for the unemployment or non-employment rate? In order to simulate how much of an increase in non-employment in a region can possibly be adjusted by net migration, Tables 3 and 4 show what a one per cent increase in unemployment or non-employment amounts to in absolute numbers and set this in relation to the migration-induced population change of \(\alpha _1\) per cent. The inverse ratio between these two is the fraction of the unemployment or non-employment change that can at most be adjusted by migration (population change). This upper bound would only be reached if all migration (population change) were labour market related and actually offset the asymmetric shock. Tables 5 and 6 present the corresponding results for the US and the EU based on the data used in Jauer et al. (2019), but with a 2-year lag structure, as we have in the data for India. The regression results on which these simulations are based are reported in Table 7.

Table 3 Simulated unemployment/non-employment adjustment due to migration at the state level (based on fixed-effect estimates)
Full size table
Table 4 Simulated unemployment/non-employment adjustment due to migration at the district level (based on fixed-effect estimates)
Full size table
Table 5 Simulated unemployment/non-employment adjustment due to migration at the district level (based on fixed-effect estimates), EU-27, Eurozone, and USA, larger regions 2006–2016
Full size table
Table 6 Simulated unemployment/non-employment adjustment due to migration at the district level (based on fixed-effect estimates), EU-27, Eurozone, and USA, smaller regions 2006–2016
Full size table

In Table 3, which reports simulations at the state level, none of the coefficients underlying the simulations is statistically significant and the simulated per cent of the shock adjusted due to migration changes sign. However, when considering the district level, the simulated adjustments based on the statistically significant coefficients, which are exclusively the coefficients of non-employment, are consistently between 28 per cent and 37 per cent. When comparing the results for India with those for the US and the EU in Tables 5 and 6, we make two key observations. First, whereas none of the estimates at the state level are statistically significant for India, for the US and Europe, all the estimates both at the state/NUTS-1 and the district level are statistically significant and the adjustments are of similar size, even larger at the state than at the district level. This is consistent with limited adjustment to non-employment disparities across state boundaries in India when compared to the US and the EU. Second, whereas we only observe an adjustment to non-employment, but not to unemployment disparities in India, in the US and in Europe, the adjustment is larger with respect to unemployment than with respect to non-employment.

4 Conclusion

In this paper, we have used the EUS-NSSO data to create regional panel data sets for both Indian states and districts. Based on this panel, we have estimated how the population in these regions adjusts to asymmetric labour market shocks within a 2-year time period. These asymmetric labour market shocks have been proxied from the same data source using the average wage and unemployment or non-employment rate in the state or district, lagged by 2 years.

Based on fixed-effects models, we find that Indian workers migrate (proxied by regression-adjusted population change) in response to wage and non-employment shocks. However, the unemployment rate does not seem to be a very reliable statistic in this context. When compared with results applying the same methodology using data for the US and the EU for a similar time period (Jauer et al. 2019), we find no significant response of Indian workers to non-employment disparities across Indian states, but only to Indian districts, whereas the response to disparities is similar across states/NUTS-1 regions and districts in the US and in Europe.