ripple2vec: Node Embedding with Ripple Distance of Structures

Abstract

Graph is a generic model of various networks in real-world applications. And, graph embedding aims to represent nodes (edges or graphs) as low-dimensional vectors which can be fed into machine learning algorithms for downstream graph analysis tasks. However, existing random walk-based node embedding methods often map some nodes with (dis)similar local structures to (near) far vectors. To overcome this issue, this paper proposes to implement node embedding by constructing a context graph via a new defined ripple distance over ripple vectors, whose components are the hitting times of fully condensed neighborhoods and thus characterize their structures as pure quantities. The distance is able to capture the (dis)similarities of nodes’ local neighborhood structures and satisfies the triangular inequality. The neighbors of each node in the context graph are defined via the ripple distance, which makes the short random walks from a given node over the context graph only visit its similar nodes in the original graph. This property guarantees that the proposed method, named as $\mathsf {ripple2vec}$, is able to map (dis)similar nodes to (far) near vectors. Experimental results on real datasets, where labels are mainly related to nodes’ local structures, show that the results of $\mathsf {ripple2vec}$ behave better than those of state-of-the-art methods, in node clustering and node classification, and are competitive to other methods in link prediction.

1 Introduction

Graph is a generic model of various networks in real-world applications, e.g., social network analysis [22], knowledge representation and inference [18], chemoinformatics and computational biology [24]. Effective graph analyses, often time- and space-consuming tasks due to the nature of graph data, help users better understand the structure of societies [22], languages [28], molecules and many others, which benefits lots of meaningful operations such as node classification [30], item recommendation [21], information propagation [29] and performance prediction [2]. Many approaches have been proposed to perform such analyses [20,21,22, 25]. At the same time, recent years have witnessed a surge of successes in processing data with machine learning (ML) algorithms, which operate on structured data and often require to represent symbolic data as numerical vectors. In order to analyze graph data with ML algorithms, people turn to graph embedding, i.e., representing nodes [4,5,6,7, 9] (edges [12] and graphs [11], resp.) in low-dimensional vector spaces such that the vectors of similar structures have small distances. This paper focuses on node embedding with direct embedding methods.

The goal of node embedding, given a graph G(V, E) and an integer $d\in N$, is to find a mapping $f: V\rightarrow R^d$ such that $dis_G(u,v)\approx \ \parallel f(u)-f(v)\parallel _2$, where $dis_G(u,v)$ is the similarity between u and v. Usually, it is difficult to define $dis_G$ to quantify precisely the semantic relationships and similarities between nodes in G(V, E) [26]. For example, general $dis_G$s are adopted in traditional algorithms such as multi-dimensional scaling (MDS) [33], IsoMap [32], Laplacian eigenmap [31], and local linear embedding (LLE) [34], which suffer from high space and time cost. And, new ideas are developed in recent algorithms [4,5,6,7,8,9, 13, 15, 16].

Some algorithms follow the framework of random walk [4, 6] or its variants [13, 14, 17] to measure the proximities between nodes with their co-occurrence on short random walks over the graph. However, such co-occurrences are based on the adjacency relationships instead of the similarity, which makes it hard to map nodes with similar local structures to vectors with small distances.

Instead, people sample random walks from context graphs, which are constructed via different similarity measures of local structures. For example, $\mathsf {HONE}$ [8] and $\mathsf {RUM}$ [23] construct weighted motif adjacency graphs by counting the occurrences of a set of network motifs. Such methods require user to provide suitable network motifs, which is usually a nontrivial task. Also, $\mathsf {HARP}$ [16] constructs a hierarchy of coarsened graphs by collapsing related nodes into “supernodes.” It still depends on the adjacency relationships of the original graph, while $\mathsf {struc2vec}$ [7] applies DTW algorithm on degree sequences to measure the similarity of local structures. Notice that DTW algorithm ignores partially the effects of connection patterns within neighborhoods. As a result, nodes with similar local structures may be mapped to far vectors.

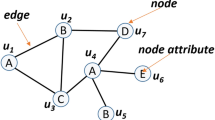
Therefore, there is still much space to improve the way to capture the similarity of local neighborhoods. For example, consider the first (second resp.)-order neighborhoods $N_1(u)$, $N_1(v)$ ($N_2(u)$, $N_2(v)$ resp.) of nodes u, v in Fig. 1. Obviously, there are edges in both $N_1(v)$ and $N_2(v)$, but no edges in neither $N_1(u)$ nor $N_2(u)$. That is, $N_i(u)$ and $N_i(v)$ ($i=1,2$) have different local structures, which cannot be captured by applying DTW algorithm on degree sequences (like in [7]) because $N_i(u)$ and $N_i(v)$ have a same sequence. Besides, such differences cannot be easily captured explicitly by neither predefined graphlets (like in [8]) nor other existing methods, to the best of our knowledge.

Fig. 1

Local structures caught by ripple vectors

Based on this observation and several wonderful existing ideas [1, 4, 7, 16], this paper proposes a metric (named as $\mathsf {ripple}$ $\mathsf {distance}$) to capture above differences and leverages it to build a context graph (for node embedding), which helps map nodes with (dis)similar local structure to (far) near vectors.

Specifically, we first describe the local neighborhood structures of each node u as a ripple vector r(u), where each component $r_i(u)$ quantifies approximately the structure of the ith-order neighborhood $N_i(u)$ as the expected hitting time of a random walk in the Fully Condensed Abstract Neighborhood Graph $F_i(u)$. The intuitive meaning of $r_i(u)$ is the average steps of the random walk, which is determined inherently by the structure of $N_i(u)$, to escape $N_i(u)$ from $N_0(u)\cup \cdots \cup N_{i-1}(u)$. For instance, Fig. 2 illustrates the FCANGs of $N_1(u),N_1(v),N_2(u)$ and $N_2(v)$ of node u, v in Fig. 1. Furthermore, $r(u)=\langle 3, 2.67, 7.2\rangle$ and $r(v)=\langle 3, 4.0, 4.62\rangle$ (See Sect. 4.2 for their computation). As a whole, ripple vector catches the structure of the nested local neighborhoods of each node, just like the shapes of water waves in diffusion sense the positions of the obstacles on the surface of the water.

Then, we propose to use $\mathsf {ripple}$ $\mathsf {distance}$ r(u, v), which is defined as $\sum _{0}^{k} w_i(1-\frac{\min (r_i(u),r_i(v))}{\max (r_i(u),r_i(v))})$, to measure the (dis)similarity of modes’ local structures. The configurability of weights brings a flexibility of our method to different applications. And ripple distance satisfies the triangular inequality, no matter how the weights are chosen. This lays a solid foundation for $\mathsf {ripple2vec}$ to map (dis)similar nodes to (far) near vectors.

Finally, with the help of the ripple distance, we construct a multilayer context graph $G_c$ to implement node embedding by sampling short random walks from it. Node u in each i-th layer of $G_c$ has $\log |V|$ neighbors corresponding to $\log |V|$ similar nodes (measured with the i-th-order ripple distance) of u in the original graph, which makes the co-occurring nodes in short random walks have high similarity. Efficient algorithm to compute the context graph is designed to guarantee its scalability.

Our main contributions include:

• We quantify the local structures of nodes in (un)weighted graphs as ripple vectors and define the ripple distance over them to measure the (dis)similarity between nodes.

• We implement a node embedding (named as $\mathsf {ripple2vec}$) in the framework of $\mathsf {struc2vec}$ by adapting ripple distance to define the context graphs. It helps map (dis)similar nodes to (far) near vectors.

• Extensive experiments are conducted on real datasets to show the superiority of the $\mathsf {ripple2vec}$, i.e., it is stronger to capture explicitly the similarity of local structures, scales well and benefits downstream applications well.

Notations used in this paper are summarized in Table 1.

The remainder is organized as below. Section 2 summarizes related work. Section 3 formalizes the problem and presents explain our motivation further. Our solution is given in Sect. 4. And, Sect. 5 reports the experimental results, followed by the conclusion in Sect. 6.

Table 1 Convention of notations

2 Related Work

There are different types of node embedding algorithms (see [3, 26] for surveys and classification). Our method belongs to direct encoding algorithms.

2.1 Traditional Methods

Traditional dimension reduction algorithms, such as $\mathsf {EigenMap}$ [31], $\mathsf {MDS}$ [33], $\mathsf {LLE}$ [34] and IsoMap [32], can be used as node embedding algorithms. All these algorithms can be adapted to work coordinately with our ripple distance. For example, $\mathsf {EigenMap}$ and $\mathsf {MDS}$ can be applied directly on graph $G_(V,E^\prime )$, where $E^\prime$ consists of all node pairs with their ripple distances as weights. And, $\mathsf {LLE}$ and $\mathsf {IsoMap}$ can be applied on graph $G_(V,E^{\prime \prime })$, where $E^{\prime \prime } \subset E^\prime$ only contains edges between each node with its k-nearest neighbors under the ripple distance. However, such adaptions suffer from high time cost of $\varOmega (|V|^2)$ and are not affordable.

2.2 Random Walk-Based Methods

Many recent successful direct embedding algorithms take advantage of the framework of random walk (or its variants), which was first proposed in $\mathsf {DeepWalk}$ [4]. Its innovation is to stochastically measure the proximity between nodes with their co-occurrence on short random walks over a graph. $\mathsf {DeepWalk}$ generated random walks in a DFS manner, while $\mathsf {node2vec}$ [6] in a BFS manner.

Instead of sampling random walks over the original graph, $\mathsf {HONE}$ [8] seizes the similarities of local structures by counting the occurrences of a set of network motifs (i.e., graphlets or orbits) to form a weighted motif adjacency graph and then applies random walk approaches (e.g., $\mathsf {DeepWalk}$ and $\mathsf {node2vec}$) on it. Also, $\mathsf {HARP}$ [16] realizes a node embedding by generating iteratively a hierarchy of coarsened graphs (by collapsing related nodes into “supernodes”) and then applying random walk approaches (e.g., $\mathsf {DeepWalk}$ and $\mathsf {node2vec}$) on these coarsened graphs in an inverse order. Notice that the idea of using coarsened supernode to characterize local structures is explored in the definition of the ripple vector. Likewise, $\mathsf {struc2vec}$ [7] defines a multilayer graph with a recursively defined distance to formalize the similarities between local structures of nodes in the original graph and then applies on the multilayer graph the idea of random walk such that it has more opportunities to visit nodes with similar local structures. $\mathsf {struc2vec}$ utilizes DTW distance on ordered degree sequences of $N_k(u), N_k(v)$ to define the similarity of local structures of u, v, while ripple distance uses the difference between particular hitting times of the coarsened neighborhoods. This integration of collapsing neighborhood and random walking makes ripple distance more powerful in capturing the similarity of local structures. Moreover, the similar expressions of the distances in $\mathsf {ripple2vec}$ and $\mathsf {struc2vec}$ make it possible to adapt the framework of $\mathsf {struc2vec}$ to the ripple distance directly.

There are some other extensions of the random walk idea. For example, $\mathsf {HOPE}$ [13] extends $\mathsf {DeepWalk}$ to learn embeddings by using random walks that “skip” or “hop” over multiple nodes at each step, resulting in a proximity measure similar to $\mathsf {GraRep}$ [14], while Chamberlan et al. [17] modify the inner product of node2vec to use a hyperbolic distance measure (rather than Euclidean distance). Our $\mathsf {ripple2vec}$ aims to leverage the local structures caught precisely by the ripple distances and thus is perpendicular to these methods.

2.3 Other Methods

$\mathsf {LINE}$ [5] expresses the likelihood of the first and second proximity with the sigmoid function of the inner products of target vectors directly and then learns the target vectors by optimizing a loss function derived from the KL divergence metric between the empirical distribution. However, its strong assumption of conditional independence (i.e., $Pr[N(u)|u] = \varPi _{v_i\in N(u)}Pr[v_i]$) makes it hard to catch the dissimilarities between nodes of the same neighborhood with different structures, as ripple distance does.

$\mathsf {SDNE}$ [9] and $\mathsf {DNGR}$ [10] are representatives of deep learning methods (see [3, 26] for surveys). They associate each node with a neighborhood vector which contains the proximities between this node and other nodes and learn node embedding with deep neural networks. DNGR defines the vector according to the pointwise mutual information of two nodes co-occurring on random walks, similar to $\mathsf {DeepWalk}$ [4] and $\mathsf {node2vec}$ [6]. $\mathsf {SDNE}$ simply chooses the node’s adjacency vector as the vector. Both vectors may be replaced with the ripple distance vector (left as our future work).

Graph convolutional neural networks (GCNs) [30, 36] obtain node embedding by aggregating the features of neighbor nodes either in spectral domain or vertex domain. They leverage the local structures implicitly in downstream applications (e.g., [30]), while $\mathsf {ripple2vec}$ aims to exploit local structures explicitly. Graph kernel methods (see [19] for a recent survey) usually map graph to vectors by counting the appearance of substructures such as paths and trees, which is perpendicular to $\mathsf {ripple2vec}$.

3 Problem Statement and Motivation

Node embedding aims to represent nodes of a graph in a low-dimensional Euclidean vector space. Formally, given a graph G(V, E) with node set V and edge set E, the goal of node embedding is to learn a mapping function $f: V\rightarrow R^d$ ($d\ll |V|$) such that the distance $\parallel f(u)-f(v)\parallel _2$ explicitly preserves the similarity between the local structures of arbitrary $u,v\in V$.

The key point of node embedding is that the similarity between local neighborhood structures of nodes must be preserved essentially. However, different understandings of the size and the structure of the local neighborhood result in different definitions of the similarity, which further have great impacts on the quality of node embedding. For example, $\mathsf {HONE}$ [8] counts the occurrences of predefined graphlets to measure the similarity. $\mathsf {DeepWalk}$ [4] and $\mathsf {node2vec}$ [6] leverage the co-occurrences of nodes in short random walks to measure the similarity. $\mathsf {SDNE}$ [9] uses the first- and the second-order proximity to measure the similarity. $\mathsf {struc2vec}$ [7] aligns the sorted degree sequences to measure the similarity, and so on. These popular methods have two main disadvantages: (1) The similarity measures do not satisfy the triangular inequality in any way; (2) dissimilar nodes are often mapped to near vectors.

These issues motivate us to seek a new metric to capture the local neighborhood similarities such that (1) The dissimilarities (like in Fig. 1) not caught by existing methods can be easily captured by the new method; (2) it helps us realize a node embedding who maps similar nodes to near vectors and dissimilar nodes to far vectors with acceptable computation cost. This can be accomplished by requiring the new metric satisfies the triangular inequality. That is, nodes with more similar local structures have smaller distance, while nodes with more dissimilar local structures have larger distances. Since node embedding preserves similarities, a node embedding implemented with the new metric naturally maps (dis)similar nodes to (far) near vectors. To obtain such an embedding, we construct a multilayer context graph such that each node is adjacent to its most similar nodes. Therefore, the pioneering random walk framework over the context graph generates the context for each node (consisting of its most similar nodes) and results in an expected node embedding.

In summary, we devote to solve the following problem:

Input A weighted or unweighted graph G(V, E), integer $d>0$.

Output A learned mapping function: $f: V\rightarrow R^d$ such that nodes with (dis)similar local neighborhood structures are mapped to (far) near vectors.

Method Adapting the popular random walk framework to a context graph $G_c(V_c, E_c)$ derived from new similarity measure satisfying triangular inequality in some way.

4 The Proposed Model

This section presents our solution of the node embedding problem. The framework is presented in Subsection 4.1, and the key steps will be expanded in Subsections 4.2 and 4.3.

4.1 Framework of $\mathsf {ripple2vec}$

The framework of $\mathsf {ripple2vec}$ (See Alg. 1) follows the generic framework of $\mathsf {struc2vec}$ [7] and runs in $O(d_{max}^K|V|+ K^2|V|\log ^2|V|)$ time.

It first computes, by invoking $\mathsf {rippleVector}$ (See Subsection 4.2), a K+1-dimensional vectors for all nodes to depict their Kth-order local neighborhood structures (Line 1). Usually, $K=4$ is enough (See Sect. 5), because ripple vectors catch approximately the local neighborhood structures well, and higher order of local structures is often meaningless as shown in [6].

Then, it invokes $\mathsf {contextGraph}$ (see Sect. 4.3) to construct a weighted multilayer context graph $G_c(V_c, E_c)$ (Line 2), in which all nodes in V appear in each layer. In each i-th layer, u has exactly $\log |V|$ neighbors, which are the nearest neighbors in the i-th-order ripple distance. Edge weights among every node pair within each layer are defined in a same way as $\mathsf {struc2vec}$.

After that, it generates context for each node by sampling p random walks with length at most l (Line 3, Line 4). Notice that each random walk from u contains only u’s similar nodes from G.

Finally, it accomplishes the mapping with the well-known learning algorithm $\mathsf {word2vec}$ [28] (Line 5).

4.2 Ripple Vectors and Ripple Distance

This subsection develops a metric, which is integrated into $\mathsf {ripple2vec}$ in next subsection, to measure the similarity of the structures of the local neighborhoods of any pair of nodes. Our statement focuses on unweighted graphs, although it can be directly extended to weighted graphs. Subsection 4.2.1 introduces the ripple vectors. And, Subsection 4.2.2 discusses the ripple distance.

4.2.1 Ripple Vector

Given a graph G(V, E), let diam(G) be the diameter of G, i.e., the maximum length of the shortest paths between two nodes of G. For $\forall u\in V$ and $0\le k\le diam(G)$, the collection of vertices exactly k-hop away from u in G is called as the k-th-order neighborhood of u and denoted as $N_k(u)$. For example, consider the graph in Fig. 1. We have $N_0(u) = \{u\}$, $N_1(u) = \{u_{11},u_{12},u_{13}\}$, and $N_2(u) = \{u_{21},u_{22},u_{23},u_{24},u_{25}\}$.

Intuitively, we intend to quantify the structure of $N_k(u)$ as a single value $T_k(u)$. And, all $T_k(u)$s, together with $d_u(G)$, consist of the ripple vector r(u) of u. Therefore, if $N_k(u)$ is viewed as a ripple k-hop away from u and $T_k(u)$ quantifies the structure of $N_k(u)$, then the ripple vector r(u) characterizes the whole structure of $N_0(u)\cup \cdots \cup N_{diam(G)}(u)$, just like water waves in diffusions on the surface of the water area.

The structure of each $N_k(u)$ ($0<k<diam(G)$) is determined by three kinds of edges, i.e., the edges between $N_{k-1}(u)$ and $N_k(u)$, the edges between $N_{k}(u)$ and $N_{k+1}(u)$, and edges within $N_k(u)$. In what follows, we first represent this structure approximately by constructing a 5-node weighted undirected graph $F_k(u)$, which is called as Fully Condensed Abstract Neighborhood Graph (or FCANG in short), and then quantify it as a single value.

$F_k(u)$ has 5 nodes $u_0,u_1,u_2,u_3,u_4$. Each $u_i$ is a subset of V.

• $u_0 = N_0(u)\cup \cdots \cup N_{k-1}(u)$;

• $u_4 = N_{k+1}(u)$;

• $u_3= \{v\in N_k(u)| (v,x) \in E$ for some $x\in u_4\}$;

• $u_2=\{v\in N_k(u)-u_3| (v,v^\prime ) \in E$ for some $v^\prime \in u_3\}$;

• $u_1 = N_{k}(u)-u_3-u_2$;

Edges in $F_k(u)$ can be added as below. If $u_i\ne \emptyset$ ($i=1,2,3$), then there is an edge $(u_0, u_i)$. If there is an edge in G(V, E) with both endpoints from $u_i$, then there is a self-circle at $u_i$. Moreover, if $u_2\ne \emptyset$ ($u_3\ne \emptyset$ resp.), then edge $(u_2, u_3)$ ($(u_3,u_4)$ resp.) exits. Actually, each edge $(u_i,u_j)$ in $F_k(u)$ represents a type of connections near $N_k(u)$. Therefore, it can be weighted as the number $n_{ij}$ of edges in G(V, E) with one endpoint from $u_i$ and the other from $u_j$.

Example 1

Figure 2 illustrates the first- and the second-order FCANGs of nodes u, v, z in Fig. 1, where the weights are not given explicitly. Particularly, in $F_2(z)$, $z_1=\{ z_{21}\}$, $z_2 = \{ z_{25}\}$ and $z_3 =\{ z_{22},z_{23},z_{24}\}$. Since $z_i\ne \emptyset$ and there is no edge in G(V, E) with both endpoints from $z_i$ ($i=1,2,3$), the edge set of $F_2(z)$ is $\{(z_0, z_1), (z_0, z_2), (z_0, z_3), (z_2, z_3), (z_3, z_4)\}$. In contrast, in $F_1(z)$, $z_1=\emptyset$, $z_2 = \emptyset$ and $z_3 =N_1(z)$. Since edge $(z_{12},z_{13})$ of G(V, E) has both endpoints from $z_3$, the edge set of $F_2(z)$ is $\{(z_0, z_3), (z_3, z_3), (z_3, z_4)\}$.

Fig. 2

The FCANGs of nodes u, v, z in Fig. 1

The structure of the FCANG $F_k(u)$ can be quantified in the mass as the expected hitting time of random walk in $F_k(u)$ from $u_0$ to $u_4$, which intuitively is the average random walk steps to escape from $N_k(u)$. It is well known that the hitting time is inherently affected by the structure of $F_k(u)$.

Definition 1

In graph G(V, E), for $\forall u\in V$ and $1\le k\le diam(G)$, the k-th-order escaping time of u, denoted as $T_k(u)$, is defined as the expected hitting time of random walk from $u_0$ to $u_4$ in $F_k(u)$.

Definition 2

In graph G(V, E), for $\forall u\in V$ and $1\le k\le diam(G)$, the k-th-order ripple vector of u, denoted as $r_k(u)$, is defined as the vector $\langle d_G(u),$ $T_1(u),\cdots ,$ $T_k(u)\rangle$.

$T_k(u)$ ($k>0$) can be computed with the closed formula derived in [1]. This can be done by first filling the state transition probability matrix $B_k(u)$ such that $B_k(u)(a,b) =\frac{w(a,b)}{\sum _{(a,b^\prime )\in E^{(u)}_k} w(a,b^\prime )}$ and then taking $T_k(u)$ as the sum of u’s row of matrix $(I-B_k(u))^{-1}$, which can be computed in O(1) time. Specifically, given edge weights $n_{01},n_{02},n_{03},n_{11},n_{22},n_{32},n_{33},n_{43}$ in $F_k(u)$, the matrix $B_k(u)_{4\times 4}$ can be constructed by updating 0 matrix as below. For the first row, $B_k(u)(0,a) = \frac{n_{0a}}{n_{01}+n_{02}+n_{03}}$ for $a=1,2,3$. For the second row, if $n_{01}>0,$ then $B_k(u)(1,0) = \frac{n_{01}}{n_{01}+2n_{11}}$ and $B_k(u)(1,1) = \frac{2n_{11}}{n_{01}+2 n_{11}}$. For the third row, if $n_{02}>0,$ then $B_k(u)(2,a) = \frac{n_{a2}}{n_{02}+2n_{22}+n_{32}}$ for $a=0,3$ and $B_k(u)(2,2) = \frac{2n_{22}}{n_{02}+2n_{22}+n_{32}}$. For the last row, $B_k(u)(3,a) = \frac{n_{a3}}{n_{03}+n_{23}+2n_{33}+n_{43}}$ for $a=0,2$, and $B_k(u)(3,3) = \frac{2n_{33}}{n_{03}+n_{23}+2n_{33}+n_{43}}$.

Example 2

Consider the FCANG $F_2(z)$ in Fig. 2. We count the edges in Fig. 1 and obtain $n_{01}=3$, $n_{02}=1$,$n_{03}=3$, $n_{11}=0$, $n_{22}=0$, $n_{32}=2$, $n_{33}=0$ and $n_{43}=4$. Therefore, we have

as shown in Fig. 2. Thus, $T_2(z)=((I-B_2(z))^{-1}(1,1,1,1)^T)_1=8.5$. Similarly, we have $T_1(z)=3.14$. Therefore, the second-order ripple vector of z is $r_2(z)=\langle 3, 3.14 , 8.5\rangle$. Likewise, $r_2(u)=\langle 3, 2.67, 7.2\rangle$, and $r_2(v)=\langle 3, 4.0 , 4.62\rangle$. According to these vectors, u, v, z in Fig. 1 can be distinguished from each other easily.

Algorithm 2 computes the Kth-order ripple vectors for all nodes by extending the procedure above directly. It is noticeable that $n_{ii}$ is increased when each endpoint of an edge is considered. Therefore, factor 2 disappears in the formula to update $B_i(u)$. Now notice that the inverse of $B_i(u)$ can be computed in O(1), each $T_i(u)$ is obtained in $O(|N_i(u)|)$ time. Since $|N_i(u)|\le d^i_{max}$ where $d_{max}$ is the maximum degree in G(V, E), Alg. 2 runs in $O(d^K_{max}|V|)$ time. For example, when $K=2$, it runs in $O(d^2_{max}|V|)$ time.

Remark

Ripple vector can also be defined without splitting $N_k(u)$ into $u_1,u_2$ and $u_3$, which makes matrix $B_k(u)$ have rank $|N_k(u)|,$ and Alg. 2 have prohibitively high cost to apply.

4.2.2 Ripple Distance

We first define the distance and then prove it satisfies the triangular inequality and present some implications.

The ripple vector quantifies node’s hierarchical local structures as its components. Therefore, the difference between ripple vectors, which is a weighted sum of the difference of each component, measures the similarity of local structures of nodes. To obtain 0 distance for identical vectors, the difference of the corresponding component of two ripple vectors considers the ratio of the minimal value to the maximal value.

Definition 3

In graph G(V, E), for $\forall u,v\in V$ and $0\le k\le diam(G)$, the k-th-order ripple distance between u and v w.r.t weights $\mathbf{w} = \langle w_1,\cdots , w_k\rangle$ ($w_i>0$), denoted as $r^{(w)}_k(u,v)$ or $r_k(u,v)$ in short when $\mathbf {w}$ is clear, is defined as $\sum _{i=0}^{k}w_{i}\cdot [1- \frac{min(r_i(u),r_i(v))}{max(r_i(u),r_i(v))}]$.

The ripple distance can focus on the differences in one or several decomposed neighborhoods by adjusting the aggregation weights, which results in a great flexibility of its applications. We do not discussed how to set the weights and take $\mathbf{w} =\langle \frac{100}{k+1},\frac{100}{k+1},\cdots , \frac{100}{k+1}\rangle$ for $r_k(u,v)$ in all experiments. No matter what $\mathbf{w}$ is, the distances satisfy the triangular inequality.

Theorem 1

If $T_k(u)>0$ for $\forall u\in V$ in graph G(V, E), then the ripple distance is really a distance of the vector set $\{r_k(u)|r_k(u)=\langle T_0(u)=d_G(u),T_1(u)\cdots ,T_k(u)\rangle ,u\in V\}$.

Proof

Obviously, we have (1) $r_k(u,v)\ge 0$; (2)$r_k(u,v)=r_k(v,u)$; (3) $r_k(u,v)=0$ if and only if $r_k(u)=r_k(v)$. We only need to verify the triangular inequality.

First of all, notice that $1-\frac{min(a,b)}{max(a,b)}-\frac{min(b,c)}{max(b,c)}+\frac{min(a,c)}{max(a,c)}\ge 0$ for $\forall a,b,c>0$. In fact, assume $a\le b\le c$ without loss of generality, we have $1-\frac{min(a,b)}{max(a,b)}-\frac{min(b,c)}{max(b,c)}+\frac{min(a,c)}{max(a,c)}=1-\frac{a}{b}-\frac{b}{c}+\frac{a}{c}=(1-\frac{a}{b})(1-\frac{b}{c})\ge 0$.

For $\forall x,y,z\in V$, we have $r_{k} (x,y) + r_{k} (y,z) - r_{k} (x,z) = \sum\nolimits_{{i = 0}}^{k} {w_{i} } \cdot \left[ {1 - \frac{{min(T_{i} (x),T_{i} (y))}}{{max(T_{i} (x),T_{i} (y))}} - \frac{{min(T_{i} (y),T_{i} (z))}}{{max(T_{i} (y),T_{i} (z))}} + \frac{{min(T_{i} (x),T_{i} (z))}}{{max(T_{i} (x),T_{i} (z))}}} \right] \ge 0$.

Remark

(1) With the ripple distance rather than the Euclidean distance, ripple vectors generated by Alg. 2 realize a node embedding. (2) Ripple distances between $\forall u,v\in V$ form a similarity matrix, on which the traditional dimension reduction algorithms can be applied to implement a node embedding in $O(|V|^2)$ time.

4.3 Multi-layer Context Graph

This subsection presents the algorithm $\mathsf {contextGraph}$, which constructs for $\mathsf {ripple2vec}$ (see Subsection 4.1) a multilayer context graph $G_c(V_c, E_c)$ such that (1) the number of layers is the same as the dimension of the ripple vectors (see Subsection 4.2); (2) each node u in G(V, E) has a counterpart node in each i-th layer with $\log |V|$ nodes of smallest ripple distances $r_i(u,\cdot )$ as its neighbors; and (3) counterpart nodes of the same $u\in V$ in different layers are connected as in the context graph of $\mathsf {struc2vec}$ [7]. So, the key of $\mathsf {contextGraph}$ is to find the neighborhood $N^{(i)}(u)$ of each $u\in V$ in each i-th layer.

A straightforward way to complete this task is to compute, for each i, $r_i(u,v)$ for all vs and take $\log |V|$ nearest nodes among them as u’s neighbors in the i-th layer. However, this method takes a prohibitively high cost of $O(|V|^2)$.

Fortunately, the ripple distance is a “monotone” function in the sense that the more similar the local structures are, the smaller the distance between them is, which is implied by the triangular inequality. And, this monotonicity can be utilized to speed up the computation with the help of the threshold algorithm [35], which aims to find t largest aggregation results from a list of sorted arrays by scanning them parallelly until a stop condition is satisfied. During parallel scanning, aggregated results of all seen objects are obtained via random access of data. These results are stored, and the highest ones are managed with a max-heap of a fixed size t. Once there are t seen objects whose scores in each array are higher than the current lowest thresholds of the same arrays, the scan terminates and objects in the heap are the final results. We refer the readers to [35] to learn more details. We adapt the threshold algorithm to compute $G_c(V_c, E_c)$ by reorganizing each component of all ripple vectors as a sorted array and scanning all arrays parallelly and bidirectionally.

Precisely, let $R_{|V|\times (K+1)}$ be the ripple vectors and $L_i$ be the sorted array storing $\{\langle R_{u,i}, u\rangle | u\in V\}$ for $0\le i\le K$. Additionally, $L_i$ has some attributes to memorize information. For instance, $L_i.tVal$ is the value which defines the starting position of the parallel scan in $L_i$. $L_i.up$ ($L_i.down$ resp.) is the position of the parallel scan in upward (downward resp.) direction. $L_i.uRatio$ and $L_i.dRatio$ are the corresponding ratio at position $L_i.up$ and $L_i.down$. L.th memorizes the current lowest threshold of the scan in L. Each array can use $\mathsf {scanInit()}$ to initialize the scan with a given value and $\mathsf {next()}$ to get next tuple of the scan. These two procedures are as below.

• Procedure $\mathsf {L.scanInit}$ (tVal)

• 1. $p\leftarrow$ index of tVal in L;

• 2.$L.dRatio\leftarrow$ ($p>1$)? $\frac{L[p-1].ripple}{tVal}$ : 0;

• 3.$L.uRatio\leftarrow$ ($p<|V|$)? $\frac{tVal}{L[p+1].ripple}$ : 0;

• 4.$L.up\leftarrow p+1$; $L.down\leftarrow p-1$;

• 5.$L.th \leftarrow \max (L.uRatio, L.dRatio)$; $L.tVal\leftarrow tVal$;

• Procedure $\mathsf {L.next}$ ()

• 1.if $L.uRatio \ge L.dRatio$ then

• 2. $L.up \leftarrow L.up+1$; $p \leftarrow L.up$;

• 3. $L.uRatio \leftarrow$ ($L.up\le |V|$)? $\frac{L.tVal}{L[L.up].ripple} : 0$

• 4.Else

• 5. $L.down \leftarrow L.down-1$; $p \leftarrow L.down$;

• 6. $L.dRatio \leftarrow$ ($L.down\ge 1$)? $\frac{L[L.down].ripple}{L.tVal} : 0$

• 7.$L.th\leftarrow \max (L.dRatio, L.uRatio)$;

• 8.return L[p].node;

Algorithm $\mathsf {contextGraph}$ is sketched in Alg. 3. It first transcripts ripple vectors $R_{|V|\times (K+1)}$ into sorted arrays $L_0,\cdots , L_K$ (Line 1-Line 2). Then, it computes the neighborhood $N^{(i)}(u)$ in each $layer_i$ for each $u \in V$ (Line 3-Line 26). To do so, it initializes D to record the seen neighbors and Rounds to account the rounds of the parallel scan (Line 4). After that, it computes $\log |V|$ nearest neighbors with $r_i(\cdot ,\cdot )$ for $i=0,1,\cdots , K$ sequentially (Line 6-Line 25) and takes $\log _2|V|$ nodes with smallest distance with u as u’s neighbors in $layer_i$ (Line 26). Finally, it adds edges between different layers in a same way as in $\mathsf {struc2vec}$.

When computing $N^{(i)}(u)$, it first scans Rounds nodes in $L_i$ (Line 7-Line 9), which guarantees that a same number of nodes in each of $L_0,\cdots , L_i$ have been scanned. The new met nodes are recorded in new. Then, it updates each $i-1$-th-order ripple distance in D to the i-th-order distances and rechecks the condition: $\frac{\min (R_{v,j},R_{u,j})}{\max (R_{v,j},R_{u,j})}\ge L_j.th$ holds for each $j\le i$ and counts the number of seen nodes v which satisfy this condition (Line 10-Line 13). After that, it computes the i-th-order distances for all nodes in new, appends them to D and counts the number of nodes satisfying the same condition (Line 14-Line17). If $count\ge \log |V|$, i.e., at least $\log |V|$ seen nodes satisfy the condition, then $N^{(i)}(u)$ has been obtained. Else, the algorithm scans parallelly all arrays $L_0,\cdots L_i$ until $count\ge \log |V|$ (Line 18-Line 25). For each new met node v, it appends $\langle r_i(u,v), v, N\rangle$ to D (Line 19-Line 21). After each round of parallel scan, it checks for each unlabeled node in D whether it satisfies the condition and increases count if necessary (Line 22-Line 24).

Notice that the condition $|D|<(i+1)\times \log _2|V|$ in Line 18 limits the rounds executed in parallel scans. Therefore, the algorithm only finds for each node $\log |V|$ near neighbors rather than exact $\log |V|$ nearest neighbors, which guarantees its scalability (see Sect. 5).

Fig. 3

Illustration of the running of Alg. 3

Example 3

Ignore the second condition in Line 18, Fig. 3 illustrates the computation of the 2-nearest neighbors of node 2, whose ripple vector and positions are all marked with red color, in $layer_0$ and $layer_1$ with Alg. 3 and the given data. The i-th components of all ripple vectors are sorted in array $L_i$ ($i=0,1$).

The computation of $N^{(0)}(2)$ scans $L_0$ only. After two nodes are scanned (as the yellow shaded cells in $L_0$), both H and D record $\{\langle 3, 0.1 \rangle , \langle 4, 0.33 \rangle \}$. And, $L_0.th = th_{11}=0.53$. Since $\frac{\min (R_{v,0},R_{2,0})}{\max (R_{v,0},R_{2,0})}\ge 0.53$ holds for both $v=3$ and $v=4$, we know $N^{(0)}(2)=\{3,4\}$.

The computation of $N^{(1)}(2)$ scans both $L_0$ and $L_1$. Since two nodes in $L_0$ have been scanned when $N^{(0)}(2)$ is computed, we first scan two nodes in $L_1$ (shown as the yellow shaded cells in $L_1$). And, two new nodes are met, i.e., $new=\{6, 7\}$. After we update distances in D and append nodes 6, 7 to D, we get $D=\{\langle 3, 0.33 \rangle , \langle 4, 0.48 \rangle , \langle 6, 0.69 \rangle ,\langle 7, 0.69 \rangle \}$, and $H=\{\langle 3, 0.33 \rangle , \langle 4, 0.48 \rangle \}$. At this time, $L_1.th = th_{21}= 0.85$. Since $\frac{\min (R_{v,0},R_{2,0})}{\max (R_{v,0},R_{2,0})}< 0.53$ for $v=6, 7$ and $\frac{\min (R_{v,1},R_{2,1})}{\max (R_{v,1},R_{2,1})}< 0.85$ for $v=3, 4$, the algorithm has to scan $L_0$ and $L_1$ parallelly further. After two rounds of parallel scan, we get the results shown as the green shaded cells in $L_0$ and $L_1$. $L_0.th = th_{12}=0.44$ and $L_1.th = th_{22}=0.61$, H does not change, and D becomes $\{\langle 3, 0.33 \rangle , \langle 4, 0.48 \rangle , \langle 6, 0.69 \rangle ,$ $\langle 7, 0.69 \rangle ,$ $\langle 1, 0.86 \rangle ,$ $\langle 9, 1.09 \rangle \}$. Now, since both $\frac{\min (R_{v,0},R_{2,0})}{\max (R_{v,0},R_{2,0})}\ge 0.44$ and $\frac{\min (R_{v,1},R_{2,1})}{\max (R_{v,1},R_{2,1})}\ge 0.61$ hold for $v=3, 4$, we get $N^{(1)}(2)=\{3,4\}$.

Algorithm 3 runs in $O(K^3|V|\log ^2|V|)$ time, where K is the dimension of ripple vectors. In fact, there are K layers in $G_c$. Each node in a layer has $\log |V|$ neighbors in that layer. Computation of these $\log |V|$ neighbors for counterpart nodes in different layers is shared according to the definition of the ripple distance (see Line 5-Line 25), where at most $K\log |V|$ Kth-order ripple distances are computed, each of which needs $O(K\log |V|)$ operations ($|D|<(K+1)\log |V|$). Totally, Line 1-Line 26 spend $O(K^2|V|\log ^2|V|)$ time. Line 27 adds edges across successive layers. Since there are totally 2K|V| such edges (see [7]) and the weight of each edge is determined in $\log |V|$ time, Line 27 needs a total time of $O(K|V|\log |V|)$.

5 Experiments

This section evaluates $\mathsf {ripple2vec}$ ’s performance on various settings. Subsection 5.1 evaluates the capability to capture the (dis)similarities of local structures. Subsection 5.2 evaluates performance in classical tasks. Subsection 5.3 evaluates performance in network alignment. Subsection 5.4 shows the effects of the dimension K of ripple vectors and the method of setting weights. Subsection 5.5 evaluates its scalability.

We compare $\mathsf {ripple2vec}$ with 7 algorithms, i.e., $\mathsf {DeepWalk}$ [4], $\mathsf {node2vec}$ [6], $\mathsf {LINE}$ [5], $\mathsf {SDNE}$ [9], $\mathsf {struc2vec}$ [7], GCN[36] and $\mathsf {GAlign}$ [37]. To evaluate the roles of Alg. 3, we adapt the ripple distance to $\mathsf {struc2vec}$ without any other changes (labeled as $\mathsf {ripple+struc2vec}$). Additionally, $\mathsf {ripple2vec}$ with the second condition in Line 17 of Alg. 3 canceled (labeled as $\mathsf {ripple+unlimited}$) is also considered.

All algorithms are implemented in Python 3 and run with five threads on an Inspur Server with Intel Xecon 128x2.3GHz CPU and 3Tb RAM running CentOS7 Linux as its operating system.

5.1 Capability to Capture Similarities

We conduct experiments on bcspwr01¹ in Fig. 4(a) to evaluate $\mathsf {ripple2vec}$ ’s capability to capture (dis)similarities of the local neighborhood structures. Bcspwr01 depicts the skeleton of a fish with 39 vertices and 46 edges (see Fig. 4(a)). Since all these vertices play different roles on the body of the fish, most of them have different local neighborhood structures. We expect that nodes with similar neighborhood structures (e.g., 34 and 35) are mapped to near points in the plain, while dissimilar nodes are mapped to distinguishable points. Experimental results are shown in Fig. 4, from which we have following two observations.

Fig. 4

2D embeddings of bcspwr01 obtained by different algorithms

Firstly, $\mathsf {ripple2vec}$ performs better than these state-of-the-art methods. In fact, for each of the existing methods, it maps some nodes with similar local neighborhood structures to further vectors and some dissimilar nodes to nearer vectors. For instance, nodes 38 and 39 have the same decomposed neighborhoods, which are different from those of nodes 16, 31 and 34 (see Fig. 4a). However, in the node embedding f generated by $\mathsf {DeepWalk}$, f(38) is closer to f(16), f(31), f(34) than to f(39) (see Fig. 4b). Similar phenomenon can also be observed for $\mathsf {SDNE}$ (see Fig. 4e). For $\mathsf {node2vec}$, f(38) and f(39) are almost the farthest vectors (see Fig. 4(c)). Similarly, nodes 34 and 35 with a same local structure are mapped to further vectors by $\mathsf {LINE}$ (see Fig. 4(d)). Their weaker abilities stem from the fact that they are designed to draw the context of nodes without explicit consideration of structural similarity. On the contrary, $\mathsf {struc2vec}$ applies DTW algorithm on the sorted degree sequences of the decomposed neighborhoods to catch the (dis)similarity of local structures. Thus, it scatters all nodes better than the previous methods (see Fig. 4f). However, some dissimilar nodes (such as 18 and 33) are mapped to nearer vectors, while some similar nodes (such 38 and 39) are mapped to further vectors. In contrast, $\mathsf {ripple2vec}$ uses ripple distance over ripple vectors to capture the (dis)similarity of local structures. It almost always maps similar nodes to near vectors and dissimilar nodes to far vectors, no matter what the value of K is (see Fig. 4h) and 4(i)).

Secondly, we find that if we replace the distance in the framework of $\mathsf {struc2vec}$ with the ripple distance, then the resulting method (i.e., $\mathsf {ripple+{\mathsf {struc2vec}}}$) has a weaker ability to capture similarities of local neighborhood structures (see Fig. 4(g)) than $\mathsf {ripple2vec}$. In this case, some similar nodes (e.g., 3 and 4, 38 and 39) are mapped to further vectors than those in $\mathsf {ripple2vec}$. This indicates that the context graph constructed in Sect. 4.3 is meaningful.

Fig. 5

2D embeddings of barbell obtained by different algorithms

Both observations can be verified on the Barbell-(2,10) and the mirrored karate. Figures 5 and 6 present only partial results. For full results, we refer the readers to our technique report. Barbell-(2,10) [7] is the graph obtained by connecting two 10-cliques with a path of 10 nodes (Fig. 5a). Both $\mathsf {struc2vec}$ and $\mathsf {ripple2vec}$ can distinguish the differences in the local neighborhood structures (5b and 5c). The mirrored karate [7] is the graph obtained by connecting two isomorphic karate networks, where $\mathsf {ripple2vec}$ behaves much better than $\mathsf {struc2vec}$. For example, $\mathsf {ripple2vec}$ almost always maps any pair of mirrored nodes to the same vectors, while $\mathsf {struc2vec}$ does not (e.g., nodes 12 and 67, 30 and 36). Besides, some dissimilar nodes not captured by $\mathsf {struc2vec}$ are caught by $\mathsf {ripple2vec}$ (e.g., nodes 35 and 36, 38 and 39).

Fig. 6

2D embeddings of karate-mirrored obtained by different algorithms

5.2 Performance in Classical Analysis Tasks

The capability of $\mathsf {ripple2vec}$ to map nodes with similar local structures to near vectors can be leveraged for node clustering when the clusters of nodes are more related to their local structures than to other features. To verify this, we conduct experiments on three air-traffic networks: Brazilian air-traffic network², American air-network³ and European air-traffic network⁴, which are unweighted, undirected networks with nodes corresponding to airports, edges indicating the existence of commercial flights and the label on each node marking the airport’s level of activity (measured in fights and people, totally 4 levels are used). Table 2 reports the statistics of each dataset (see [7] and its GitHub link⁵ for more details). We conduct experiments to observe the behaviors of $\mathsf {ripple2vec}$ in node classification and link prediction.

Table 2 Statistics of networks

All algorithms map nodes to 128-dimensional vectors. For $\mathsf {LINE}$ and $\mathsf {SDNE}$, we take default parameters. For $\mathsf {DeepWalk}$, $\mathsf {node2vec}$, $\mathsf {struc2vec}$ and $\mathsf {ripple2vec}$, we take 80 walks with length 40 for each node and 8 as Skip-Gram window in word2vec. Both optimizations in [7] are considered. GCN takes the identity matrix as its input features. We fix $K=4$ (see Subsection 5.4 for changing K). The embedded vectors of each dataset are partitioned into training data and test data in different ways by setting each $i\in [0,10]$ as a random seed correspondingly. Each experiment is repeated 5 times, and the average behaviors are reported.

Table 3 Average adjusted Rand index of k-means algorithm on node embeddings generated by different algorithms

For node clustering, we run k-means algorithm on the embedded vectors to cluster all nodes into 4 classes. The performance is evaluated as the adjusted Rand index (ARI), which ranges in $[-1, 1]$ with larger values indicating stronger consistencies between the clustering results and the actual clusters. Table 3 reports the experimental results. Notice that $\mathsf {ripple2vec}$ outperforms other algorithms remarkably, which verifies the facts that $\mathsf {ripple2vec}$ is stronger to map nodes with similar local structures into near vectors.

Table 4 Performance of node classification with k-NN algorithm on node embeddings generated by different algorithms

For node classification, we take labels in training data as known and classify nodes in test data by finding their k-NN ($k=11$) neighbors in training data. The performance is evaluated as average accuracy and average macro $F_1$ score. Table 4 reports the results. Notice that $\mathsf {ripple2vec}$ is competitive to $\mathsf {struc2vec}$ on all datasets. It is better than GCN on Brazil and competitive to GCN on other datasets. And, it always outperforms all other algorithms. These observations verify further the facts that $\mathsf {ripple2vec}$ is stronger to map nodes with similar local structures into near vectors.

Table 5 Performance of link prediction with logistic regression algorithm on node embeddings generated by different algorithms

For link prediction, we train a logistic regression model with the training datasets and use it to predict the edges in the corresponding test datasets. The performance is evaluated as average accuracy and average area under curve (AUC). Table 5 reports the experimental results. Notice that $\mathsf {ripple2vec}$ is competitive to all other algorithms, although the logistic regression model uses nonlinear activation function to eliminate some advantages of mapping nodes with similar local structures into near vectors.

Moreover, in all three experiments above, we notice that the second condition in Line 17 of Alg. 3 has a little bit of impacts on the performance (comparing the results of $\mathsf {ripple2vec}$ with $\mathsf {ripple+unlimited}$). However, it affects the scalability of the algorithm greatly. On the contrary, adapting directly the ripple distance to the framework of $\mathsf {struc2vec}$ behaves worse than $\mathsf {ripple2vec}$ in both node clustering and node classification (comparing the results of $\mathsf {ripple2vec}$ with $\mathsf {ripple+struct}$). Both observations demonstrate the effectiveness of the design in Sect. 4.3.

5.3 Performance in Network Alignment

In addition to node classification, node cluster and link prediction, ripple vector can also be used in network alignment work. To show this, we use ripple vector to improve the $\mathsf {GAlign}$ [37](the improved algorithm denoted by RAlign). $\mathsf {GAlign}$ is a state-of-the-art method, which is an unsupervised network alignment method, but the accuracy of the network alignment is not worse than the supervised network alignment method. In the RAlign algorithm, we denote the alignment matrix obtained by the $\mathsf {GAlign}$ algorithm through node attribute training as S1 and then use the ripple vector of each node as an additional attribute of each node and use the $\mathsf {GAlign}$ algorithm to train the alignment matrix on the additional attributes, denoted as S2. The weighted summation of S1 and S2 is used to obtain the alignment matrix S, and finally, S is used for network alignment.

We use 4 real datasets: Allmovie-Imdb [37], Douban Online–Offline [41], ppi and blogCatalog. The Allmovie-Imdb dataset is a movie network dataset from the Rotten Tomatoes website and the Imdb website. The nodes represent movies, and the edges represent two movies with at least one co-actor. Douban Online–Offline dataset is a dataset from Chinese social networks. The nodes represent users, and the edges represent friendships. The ppi network is short for protein–protein interaction network. The nodes represent proteins, and the edges represent the interaction between two proteins. And, the blogCatalog dataset is a social relationship network, with nodes representing users and edges representing whether there is a social relationship (such as a friend relationship). Table 6 summarizes the statistics of these datasets.

On all datasets, we generate network alignment datasets for testing by randomly removing 20% of the edges and randomly modify the attributes of 15% of the nodes on a single real network to generate different subnetworks.

Table 6 Datasets used in network alignment

We compare RAlign with 4 algorithms, i.e., $\mathsf {GAlign}$ [37], $\mathsf {IsoRank}$ [38], $\mathsf {FINAL}$ [39], $\mathsf {REGAL}$ [40]. Among them, the IsoRank and FINAL are supervised algorithms. For these two algorithms, we use 20% of the ground truth as the training data. The performance is evaluated as $Acc_1$, $Acc_5$, $Acc_{10}$ and MAP[42], where $Acc_q$ indicates whether the first q candidates have a correct matching and $MAP = mean(\frac{1}{ra})$, where ra is the rank of true anchor target in the sorted list of anchor candidates. The experimental results are reported in Table 7.

Table 7 Network alignment comparison

Table 7 tells us that (1) on the artificial synthetic dataset, the various metrics of network alignment using RAlign are much higher than other algorithms; (2) on two real datasets, the obtained test results also meet our expectations, RAlign only performs worse than other algorithms in three tests, and RAlign ranks second in these three tests. This proves that ripple vector can capture the local structure of the network well, and this ability is also effective in the field of network alignment.

5.4 Effects of the Dimension and the Weights

Next, we will show the effects of the dimension K and the weights to help you understand how to better adjust the parameters.

Effects of K on the performance of $\mathsf {ripple2vec}$. On all datasets in Subsection 5.2 with the same experimental settings, we change the dimension K of the ripple vectors and observe its impacts on the performance of $\mathsf {ripple2vec}$ in these analysis tasks.

Figure 7 reports the average accuracies and the standard deviations. We find that the average accuracies increase a little bit slowly when the dimension changes from 2 to 4 and keep stable when it becomes larger, which is consistent with the fact that the local structures near nodes are more useful than those far from nodes in usual graph analysis tasks.

Effects of weights on the performance of $\mathsf {ripple2vec}$. With the same settings in Subsection 5.2, we use four different groups of weights in the ripple distance and observe their impacts on these classical analysis tasks.

• W0: $w_0=5,w_1=4,w_2=3,w_3=2,w_4=1$;

• W1: $w_0=1,w_1=2,w_2=3,w_3=4,w_4=5$;

• W2: $w_0=20,w_1=20,w_2=20,w_3=20,w_4=20$;

• W3: $w_0=1,w_1=1,w_2=1,w_3=1,w_4=1$;

Figure 8 reports the results. We find that (1) accuracies in former two tasks change more dramatically than in the last one. This is because the sigmoid activation function in the selected algorithm weakens the impacts of distances between embedded vectors. (2) The impacts of the weights are dataset-specific, since any group of weights does not always outperform others both in node clustering and node classification.

Fig. 7

Impacts of the dimension of the ripple vectors on the performance of $\mathsf {ripple2vec}$

Fig. 8

Impacts of the weights of the ripple vectors on the performance of $\mathsf {ripple2vec}$

5.5 Scalability

Fig. 9

Performance in node clustering, node classification, link prediction and scalability

To check the scalability of $\mathsf {ripple2vec}$, we fix $K=4$ and run it on instances of the Erd$\ddot{o}$s–R$\acute{e}$nyi random graph model. We take the number of nodes as $10^2, 10^3, 10^4, 10^5$ and $10^6,$ respectively, and other parameters as in Subsection 5.2. The results are reported in Fig. 9, which indicates that $\mathsf {ripple2vec}$ scales super-linearly under curve of $|V|\log ^2|V|$. This is consistent with our analysis.

6 Conclusion

This paper proposes to improve the node embedding by constructing a context graph with a new defined ripple distance over ripple vectors, whose components are the hitting times of the fully condensed neighborhoods and thus characterize the structures of the neighborhoods as pure quantities. The ripple distance satisfies the triangular inequality and is able to capture the (dis)similarities of the local neighborhood structures. The neighbors of each node in the context graph are optimized to its nearest neighbors under the ripple distance, which guarantees that the short random walks from the node in the context graph only visit its similar nodes in the original graph, which makes $\mathsf {ripple2vec}$ map similar nodes to near vectors and dissimilar nodes to far vectors. Algorithms to compute the ripple vectors and the context graph are carefully designed, which makes $\mathsf {ripple2vec}$ scale well. As a future work, we will integrate structure similarity captured by $\mathsf {ripple2vec}$ with deep neural networks like GCN and graph kernels to improve the performance of downstream graph analysis tasks.