1 Introduction

Community structure generally exists in networks [27], where nodes are more densely connected in the same community. Community detection, which aims to discover the community structure of networks, is a fundamental problem in analyzing complex networks and has attracted much attention recently [5, 8, 22, 37, 46]. Most community detection methods detect all communities in the network. However, for a large-scale network, we may not care about all the communities in the network, but only care some local communities, such as the ones containing a particular node, called seed node. In addition, working on the entire network is time-consuming, especially on large-scale networks. Sometimes it is also hard or impossible to obtain the complete information of the network, such as the World Wide Web.

Local community detection [25, 34], which finds the communities of a given seed node, is proposed to handle the above situations, and it has many applications in the real world. For instance, in collaboration networks [36], we may discover the collaboration group of a particular person through local community detection; in product networks, the platform may need to find the products that customers are interested in by detecting the community of purchased products. Most existing algorithms [2, 38] for local community detection are based on a strict assumption that the seed node only belongs to a single community; however, in real-world networks, quite a number of nodes appear in multiple communities. For example, a person in a collaboration network may belong to several collaboration groups with different topics, or an item in a product network may belong to different categories. It is a more challenging task to detect all local communities related to the seed node; we call this problem multiple local community detection (MLCD). Yang and Leskovec [36] detected multiple hierarchical communities by finding multiple local minima in the local community detection method. He et al. [17] introduced a local spectral subspaces-based algorithm (LOSP) to expand different seed sets to communities, which are generated from the ego-network of the given seed node. Kamuhanda and He [19] proposed a nonnegative matrix factorization algorithm to detected multiple communities and automatically determine the number of detected communities. Hollocou et al. [18] solved the problem by expanding the initial seed to a candidate seed set and applying a local community detection algorithm (e.g., PageRank-Nibble [2]) for seeds in the seed set individually. However, these proposed methods still have the following two problems.

  1. 1.

    Sensitive to the position of the seed node Existing methods select a new community member from nodes around the seed node, for instance, adding surrounding nodes to detected communities one by one until reaching the local optimum of some quality functions (e.g., conductance) [10, 17, 36, 44], or applying matrix factorization methods on the subgraph expanded by the seed node [19]. These methods tend to involve correct nodes and get high-quality (e.g., accuracy) detected communities, if most of the nodes near the seed node belong to the same community as the seed node. Otherwise, they will get low-quality communities. Therefore, the quality of detected communities is sensitive to the position of the seed node in the community.

  2. 2.

    Insensitive to the local structure of the seed node Different nodes in a network have different local structures, resulting in different properties of communities, like degree centrality, closeness centrality, and betweenness centrality. For the MLCD problem, different seed nodes have different numbers of communities that they belong to. However, existing works are insensitive to such characteristics of the seed nodes. The number of detected communities they output is highly related to the input parameters [18, 19] or the characteristics of the entire network [17], and it cannot adaptively change with the number of ground-truth communities of the seed node.

Besides identifying community structure on static networks, community detection on dynamic networks has recently drawn increasing attention [1, 4, 7, 31, 33, 42]. In many applications, data are continuously generated; nodes and edges could be inserted into a network or removed from it. The dynamic network does not usually change significantly among snapshots and repeatedly applying the static algorithm on each snapshot would be time-consuming and computationally prohibitive. Some dynamic local community detection methods were introduced [13, 26, 41], but as far as we know, no Dynamic Multiple Local Community Detection algorithm (DMLCD) algorithm has been studied at present.

In this paper, we introduce a novel approach, called High-quality seed based Multiple Local Community Detection (HqsMLCD), for the multiple local community detection task to address the above problems on static networks. HqsMLCD follows the general framework introduced by MULTICOM [18] and improves the accuracy of detected communities via identifying high-quality seed nodes. HqsMLCD finds high-quality seeds based on network embedding methods, which mitigates the impact of the seed node position. Furthermore, it uses local clustering methods to recognize the local structures of the seed node and determines the number of high-quality seeds adaptively. Finally, HqsMLCD expands each high-quality seed to find accurate local communities via existing local community detection methods. For the task of DMLCD, we also introduce a method, called High-quality seed based Dynamic Multiple Local Community Detection (HqsDMLCD), on top of HqsMLCD. HqsDMLCD outputs local communities incrementally for each snapshot. Based on HqsMLCD, HqsDMLCD dynamically generates random walk in network embedding process and incrementally expands high-quality seeds to multiple communities.

We conducted extensive empirical studies for the static algorithm HqsMLCD and the dynamic algorithm HqsDMLCD on five real-world networks. The results demonstrate that HqsMLCD achieves the best accuracy of MLCD compared with the state-of-the-art methods. HqsDMLCD generates high-quality local communities that are similar to those detected by our static algorithm HqsMLCD. We summarize our contributions as follows:

  • We introduce the concept of high-quality seeds and develop an effective method to discover the high-quality seeds.

  • We introduce two algorithms HqsMLCD and HqsDMLCD based on high-quality seeds for the static and dynamic multiple local community detection task, respectively.

  • We conduct extensive experiments for both HqsMLCD and HqsDMLCD to demonstrate their effectiveness.

This paper extends our preliminary work [24] as follows: First, we extend the network embedding to dynamic network embedding which can incrementally generate random walks. Second, we implement a dynamic local community detection method through approximate Personalized PageRank value incrementally. Third, we conduct extensive experiments to verify the effectiveness of our method on dynamic networks.

The rest of the paper is organized as follows: we present the background and related work in Sect. 2, and we introduce the concept of high-quality seeds in Sect. 3. In Sects. 4 and 5, we elaborate our static algorithm HqsMLCD and dynamic algorithm HqsDMLCD, respectively. In Sect. 6, we provide experimental results, and we draw conclusions in Sect. 7.

2 Background and Related Work

Before introducing our algorithm, we present the notations that we use throughout the paper, the problem definition and the general framework of multiple local community detection, and some closely related work.

2.1 Notations

We go over several key concepts, and the frequently used notations in this paper are summarized in Table 1.

  • Network Let \(G=(V,E)\) be an undirected, unweighted network, where \(V=\left\{ v_1,v_2,\ldots ,v_n \right\} \) is the set of n nodes in G, and E is the edge set of G.

  • Communities For a seed node \(v_s\), let \(C_s\) be the set of ground-truth communities that contain \(v_s\), each community \(c_i \in C_s\) is the set of nodes belonging to \(c_i\). Similarly, \(C_d\) is the set of communities detected by community detection methods.

  • Network Embedding For a network G, its network embedding \(Y_G \in {\mathbb {R}}^{n \times d}\) is a matrix of vertex latent representation, where d is the dimension of embedding, and \(Y_G(v)\) denotes the embedding vector of node v.

  • Snapshots A dynamic network \({\widetilde{G}}\) could be presented as a sequence of snapshots, i.e., \({\widetilde{G}}=\left\{ G^{(1)}, G^{(2)}, \ldots G^{(t)} \right\} \). Each snapshot \(G^{(t)}=(V^{(t)},E^{(t)})\) represents the network structure of the dynamic network \({\widetilde{G}}\) at time t.

Table 1 Frequently Used Notations
Full size table

2.2 Problem Definition

Multiple Local Community Detection (MLCD)

Given a network G and a seed node \(v_s\). Multiple local community detection algorithms return a set of detected communities \(C_d\).For each community \(c_i \in C_s\),we consider the most similar community \(c_j \in C_d\) as the corresponding detected community of \(c_i\).The algorithm aims to return communities that are as similar as possible to the ground-truth

$$\begin{aligned} \frac{{{\mathop { \sum }\nolimits _{{c_i \in C_s}}{max \left\{ sim \left( c_i,c_j \right) | c_j \in C_d \right\} }}}}{{ \left| C_s \right| }}, \end{aligned}$$
(1)

where \(sim(c_i, c_j)\) is a metric that measures the similarity between \(c_i\) and \(c_j\), generally using \(F_1\) score.

Dynamic Multiple Local Community Detection (DMLCD)

Given a dynamic network \({\widetilde{G}}\) and a seed node \(v_s\). Dynamic multiple local community detection algorithms return a sequence of the set of detected communities \(\widetilde{C_d}= \left\{ C_d^{(1)},C_d^{(2)},\ldots ,C_d^{(t)} \right\} \), where \(C_d^{(t)}\) represents the set of detected communities on \(G^{(t)}.\) Let \(C_s^{(t)}\)denotes the set of detected communities by the static algorithm, for each community \(c_i^{(t)} \in C_s^{(t)}\),we consider the most similar community \(c_j^{(t)} \in C_d^{(t)}\) as the corresponding detected community of \(c_i\).The algorithm aims to return communities that are as similar as possible to the outputs of static algorithm, i.e., maximizing

$$\begin{aligned} \frac{\sum \limits _{t=1}^T \frac{{{\mathop { \sum }\nolimits _{{c_i^{(t)} \in C_s^{(t)}}}{max \left\{ sim \left( c_i^{(t)},c_j^{(t)} \right) | c_j^{(t)} \in C_d^{(t)} \right\} }}}}{{ \left| C_s^{(t)} \right| }}}{T}, \end{aligned}$$
(2)

where T is the last timestamp.

Score

\(\varvec{F_1}\) Given a ground-truth community \(c_i\) and a detected community \(c_j\), \(F_1\) score is defined as

$$\begin{aligned} F_1(c_i,c_j)=\frac{2precision(c_i,c_j) \times recall(c_i,c_j)}{precision(c_i,c_j)+recall(c_i,c_j)}, \end{aligned}$$
(3)

where \(precision(c_i,c_j)=\frac{|c_i \cap c_j|}{|c_j|}\), \(recall(c_i,c_j)=\frac{|c_i \cap c_j|}{|c_i|}\).

2.3 General Framework of MLCD

Existing works on multiple local community detection follow a general framework [18, 28], which separates into two steps: 1) finding new seeds on the basis of the initial seed node; 2) and then applying local community detection methods to new seeds to obtain multiple detected communities. Figure 1 illustrates the overview of the general framework.

Fig. 1
figure 1

General framework

Full size image

2.4 Related Work

2.4.1 Multiple Local Community Detection

Most of the existing local community detection methods are based on seed set expansion. Specifically, they first take the given seed node as an initial community, then apply a greedy strategy to add nodes to the community until reaching the local or global minimum of some quality functions (e.g., local modularity). Many works improve this method by generating reasonable order of nodes to add to the detected community, such as using random walk [2, 3], combining higher-order structure [38], and applying spectral clustering methods [16, 17].

The above local community detection methods focus on detecting a single community of the seed node, ignoring the fact that the given seed node may belong to other overlapping communities in the real-word network. To address this issue, few methods have been introduced. Yang and Leskovec [36] proposed a method that only detects multiple communities by finding multiple local minima of the quality function (e.g., conductance) used in the greedy strategy, which causes that the latter detected community completely contains the former one. LOSP [17] generates several seed sets from the ego-network of the initial seed node, then expands these seed sets based on their local spectral subspace. Hollocou et al. [18] first found new seeds by clustering the network which is embedded in a low-dimensional vector space by a score function of seed set, like Personalized PageRank, then expanded them to multiple communities; however, new seeds are always far away from the initial seed, cause the communities expanded by new seeds including a lot of nodes that beyond the ground-truth communities and may not contain the initial seed, which is inconsistent with the goal of recovering all the communities of the seed node. Kamuhanda and He [19] applied nonnegative matrix factorization on the subgraph extracted by using Breadth-First Search (BFS) on the initial seed node to solve this problem; it is a novel idea, but the members of detected communities are limited in the range of the subgraph, which ignores the structure of the network, and the number of communities decided by the algorithm is highly related to the size of the subgraph, which is inflexible and illogical. Inspired by MULTICOM [18], Ni et al. [28] proposed a method LOCD following the framework introduced in Sect. 2.3 recently. The difference between LOCD and our work includes two main following points. First, we proved the existence of high-quality seeds (Sect. 3.1) and clearly defined quality score and high-quality seeds with network representation learning. Second, we improved the accuracy of high-quality seeds through clustering methods and examined the effectiveness through ablation study. Besides, we used more evaluations and baselines in experiments and tested on more real-world datasets. According to the \(F_1\) score on Amazon in their paper, our work (0.895) outperforms LOCD (0.7863). Another similar problem to MLCD is the overlapping community search problem. Cui et al. [9] and Yuan et al. [40] proposed methods to find overlapping local communities based on k-clique percolation community [29]; however, communities detected by this kind of methods must be consistent to their definition of structure; it might be not flexible. Besides, the parameter k of k-clique is difficult to decide in practice and different k results in very different communities.

2.4.2 Dynamic Local Community Detection

Detecting the evolving local community structure of dynamic networks has recently drawn increasing attention. Zakrzewska and Bader [41] introduced a dynamic seed set expansion algorithm which incrementally updates the fitness score (e.g., conductance) of each snapshot and ensures the sequence of fitness scores remains monotonically increasing, then restarts the static algorithm. Nathan et al. [26] first updated the personalized centrality vector every time the network changes, then obtained the new local community from the updated centrality vector. Fu et al. [13] proposed a method L-MEGA based on motif-aware clustering. They first approximated multi-linear PageRank vector through edge filtering and motif push operation, then applied incremental sweep cut to get the local community.

Existing dynamic local community detection methods only detect a single community for the seed node for each snapshot; however, as mentioned above, the seed node may belong to multiple communities. In this paper, we extend our static algorithm to the dynamic network to address this issue. The details of the dynamic algorithm HqsDMLCD will be introduced in Sect. 5.

3 High-Quality Seeds

According to the general framework of MLCD, we find local communities by expanding seed nodes; different seed nodes result in different detected communities. We call seed nodes that can generate communities close to the ground-truth communities as high-quality seeds. In this section, we first empirically verify the existence of high-quality seeds and then qualitatively analyze how to find them.

3.1 The Existence of High-Quality Seeds

We assume that for all nodes in a ground-truth community, the high-quality ones can generate communities that are more similar to the ground-truth community than other nodes through a certain local community detection method (e.g., PageRank-Nibble [2]). In order to demonstrate the existence of high-quality seeds, we conduct an empirical study.

Three real-world networks Amazon, DBLP, and Youtube are used. For each network G, we randomly pick 30 nodes as seed nodes \(v_s\). For a seed node \(v_s\), we choose a ground-truth community \(c_s\) that \(v_s\) belongs to, then use PageRank-Nibble for \(v_s\) and all other nodes belong to \(c_s\) to detect their local communities, finally compute the \(F_1\) score. Figure 2a illustrates the average \(F_1\) score of communities detected by the 30 seed nodes and the best communities detected by nodes from the ground-truth community that the seed nodes belong to.

Fig. 2
figure 2

Experimental results of high-quality seeds

Full size image

We can see that, in the community to which the randomly picked seed node belongs, there exist nodes that can generate a better community than the seed node through a local community detection method, and we call such nodes high-quality seeds.

3.2 High-Quality Seed Identification with Network Representation Learning

Since most existing local community detection methods are based on seed set expansion, which tends to include the neighbors of the seed node into the detected community, high-quality seeds should have high similarity with their neighbors in the same community. Furthermore, the detected community should contain the initial seed node; therefore, high-quality seeds are expected to have high similarity with the initial seed node.

To find high-quality seeds with the above characteristics, we need a similarity measure that can imply whether nodes belong to the same community. Nowadays, network representation learning (aka., network embedding) is a popular approach to learn low-dimensional representations of nodes and effectively preserve the network structure, like the community structure. Thus intuitively, the similarity between node embeddings could be approximated as the probability of belonging to the same community, so we use node embeddings to select high-quality seeds.

We also conduct an experiment to verify our intuition. First, we randomly pick 100 seed nodes in each of the networks Amazon, DBLP, and Youtube, then sample a subgraph around each seed node with BFS and learn the embeddings of these subgraphs. From each subgraph, we select 50 “same-com-pairs” which refers to node pairs composed of two nodes from the same community and 50 “diff-com-pairs” which refers to node pairs composed of two nodes from different communities. After that, for each subgraph, we compute the difference between average cosine similarity of “same-com-pairs” and “diff-com-pairs”, if the difference is greater than 0, the similarities between node embeddings are considered capable of detecting community relations, and the results as shown in Fig. 2b.

It shows that most similarities between embeddings of nodes from the same community are greater than those from different communities, which means the similarities could partially reflect the probability of whether belonging to the same community. Thus, network representation learning can be used to find high-quality seeds; the specific quantitive method is introduced in Sect. 4.

4 Multiple Local Community Detection with High-Quality Seeds

In this section, we present our proposed method, multiple local community detection with high-quality seeds (HqsMLCD for short). Our optimizations focus on the selection of new seeds in the general framework described in Sect. 2.3, and we use the new high-quality seeds as the input of local community detection methods to detect multiple communities.

Fig. 3
figure 3

Framework of HqsMLCD

Full size image

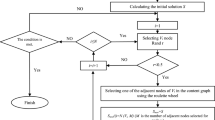
Figure 3 shows the overall framework of HqsMLCD. We first use BFS to sample a subgraph around the given seed node to find all candidates of high-quality seeds, then apply network representation learning methods on the subgraph to obtain embeddings of candidate nodes (Sect. 4.1). On top of the embeddings, we further cluster the candidate nodes into several clusters (Sect. 4.2). After that, we calculate the Quality Score of all candidates in clusters, and nodes with the highest quality score in each cluster are considered as high-quality seeds (Sect. 4.3), which are expanded to detected communities finally by the local community detection method (Sect. 4.4).

figure a

Algorithm 1 illustrates the pseudo-code. From line 2 to line 3, we sample a subgraph and learn its embedding. At line 4, we cluster the nodes in the subgraph into several clusters. Then, we get high-quality seeds from these clusters (Line 5–11). At last, we expand high-quality seeds to multiple detected communities (Line 12–15).

4.1 Sampling and Embedding Candidate Subgraph

For a network G and the seed node \(v_s\), to find high-quality seeds, we first sample a subgraph \(G_s\) where high-quality seeds are selected in, named candidate subgraph. The sampling method we used is breadth-first search (BFS) since it can uniformly include nodes around the seed node. The number of steps of BFS is determined through parameter tuning, and the details are described in Sect. 6.3.1. Then we get embedding \(Y_{G_s}\) of the candidate subgraph with the network representation learning method. We choose the unsupervised method DeepWalk [30] in the implementation since we don’t have any labeled data in advance. DeepWalk feeds random walk paths as sentences to the Skip-gram model, and Skip-gram tries to predict “context” of “word” in “sentence”, i.e., predict nearby nodes of the node on a random walk path.

4.2 Clustering Candidate Subgraph

We then cluster the embedded candidate subgraph into several clusters. As illustrated in Fig. 3, candidate nodes in \(G_s\) may come from several different ground-truth communities, we want to select one single node as the high-quality seed in each ground-truth community so that we could recover the correct number of communities and avoid missing some ground-truth communities. We choose density-based spatial clustering of applications with noise (DBSCAN) method [12] in this step, as DBSCAN could automatically decide the number of clusters, i.e., number of detected communities in our algorithm. We use the similarity between node embeddings as the metric of DBSCAN, so we could partition the nodes of different communities flexibly, as we demonstrate in Sect. 3.2.

Fig. 4
figure 4

Example of clustering and non-clustering candidate subgraph

Full size image

For instance, given a seed node \(v_s\) and its candidate subgraph as in Fig. 4, without clustering, we may generate high-quality seeds that are close to each other and would lead to the neglect of the nodes in some ground-truth communities as their quality score may less than nodes in other clusters. Besides, without clustering, the number of high-quality seeds should be given as a parameter, which is hard to know in advance in practice.

4.3 Quality Score and High-Quality Seed Identification

After getting several clusters of candidate nodes, we compute the quality score of every node in all clusters, and select nodes with the highest quality score in each cluster as high-quality seeds. As we mentioned in Sect. 3.2, high-quality seeds have a high possibility of belonging to the same community as their neighbors and the initial seed node \(v_s\). Using cosine similarity between node embeddings approximated as the probability of belonging to the same community, we define the quality score QS of node v as

$$\begin{aligned} QS(v)=\frac{{{\mathop { \sum }\limits _{{u \in N \left( v \right) }}{Sim \left( Y_{G_s}(u),Y_{G_s}(v) \right) }}}}{{|N \left( v \right) | }}+Sim \left( Y_{G_s}(v),Y_{G_s}(v_s) \right) , \end{aligned}$$
(4)

where N(v) is the set of neighbors of v. The similarity between the node and its neighbors makes better performance while applying the local community detection method on it, and similarity between the node and the seed node \(v_s\) ensures \(v_s\) be involved in detected communities, which is one of the main goals of MLCD.

4.4 Expand to Detected Communities

In this step, each high-quality seed is expanded to a detected community by a local community detection algorithm based on seed set expansion. We use PageRank-Nibble method [2] which is widely used in local community detection. Further, we also make the following two changes to PageRank-Nibble: (1) if the current detected community is identical with some community detected before, we find the next local minima of the sweep procedure to generate a larger community, so we could find not only communities with different structures but also hierarchical communities, which both exist in real-world networks. (2) Inspired by Kamuhanda and He [19] who added the neighbors of initial community members to refine the final community, we also introduce a refinement step which adds the given seed node to the detected community when the detected community doesn’t contain it and at least one of its neighbors is involved in the detected community. Finally, we obtain multiple communities as the results. PageRank-Nibble uses conductance as the stop criteria, makes sure the detected communities with low conductance, and combining our selection of seed nodes, the detected communities can achieve higher similarity with the ground-truth community.

4.5 Time Complexity

Here we analyze the time complexity of each step of HqsMLCD. The time complexity of BFS is \(O(n+m)\), where n is the number of nodes, and m is the number of edges in the subgraph. The complexity of both DeepWalk and DBSCAN is O(nlogn). High-quality seeds can be identified with O(n). Pagerank-Nibble costs \(O(vol(Supp(p))+n_plogn_p)\), where p is the PageRank vector, Supp(p) is the support of p, vol(S) denotes the volume of subset S, and \(n_p=|Supp(p)|\).

5 Dynamic Multiple Local Community Detection

In this section, we introduce our proposed dynamic method, dynamic multiple local community detection with high-quality seeds (HqsDMLCD for short). HqsDMLCD follows the framework of the static algorithm HqsMLCD. We modify two key steps: embedding candidate subgraph (Sect. 5.1) and expand high-quality seeds (Sect. 5.2) to adapt the dynamic networks. The modified steps could incrementally calculate network embedding and expand the detected communities, reducing time consumption caused by repeated calculations.

figure b

Algorithm 2 illustrates the pseudo-code. For each snapshot (Line 2), we sample a subgraph with BFS (Line 4), then dynamically learn the embedding of the subgraph (Line 5). At line 6, we cluster the candidate nodes into several clusters. From line 7 to line 13, we calculate the quality score of nodes in each cluster to get high-quality seeds. At last, we expand high-quality seeds incrementally to detect communities for the current snapshot. Note that we record high-quality seeds for the calculation of the next snapshot (Line 18).

5.1 Dynamic Embedding Candidate Subgraph

Dynamic network embedding has been studied extensively, and many methods have been proposed [35], including matrix factorization based [21, 47], Skip-Gram based [11, 23, 48], auto-encoder based [14, 39] and neural networks based [32, 45] methods. In this step, we do not directly use an existing method; there are two main reasons: first, the network representation method DeepWalk, which we used in the static algorithm, plays an important role in the entire algorithm process and has a very good effect; we would like to keep the dynamic embedding methods as similar as possible to DeepWalk to get similar network embedding and maintain the accuracy of the algorithm; second, some existing methods entail much more time than DeepWalk, one of the biggest goals of DMLCD algorithms is to reduce running time by avoiding repeated calculations.

In this step, we borrow the idea from NetWalk [39] and extend DeepWalk to be a dynamic network embedding method. NetWalk dynamically updates the random walks with vertex reservoir. Vertex reservoir S(v) of node v stores several repeatable neighbor nodes of v with equal probability, when edges are added or deleted, NetWalk updates the corresponding vertex reservoir, then updates random walks through the vertex reservoir to ensure the randomness and correctness of random walks.

We first generate random walks incrementally, which follows the steps proposed by NetWalk. Then we feed random walks of the current snapshot to the Skip-gram model to get the temporal network embedding. Doing so could preserve the embedding results of DeepWalk effectively and reduce the time consumption.

5.2 Dynamic Expanding High-Quality Seeds

The expanding process of the static algorithm is based on Pagerank-Nibble, which consists of two key steps: approximate Personalized PageRank (PPR) value and the sweep procedure. Through our empirical studies, approximating PPR value costs nearly half of the time, thus incrementally approximating PPR values would greatly improve the efficiency of the algorithm on dynamic networks.

In this step, we refer to the approximating PPR method proposed by Zhang et al. [43] and extend Pagerank-Nibble to dynamic networks. On each snapshot, for each of the same high-quality seeds as in the previous snapshot, we first update the approximated PPR value based on the value of the last snapshot. For each added edge (u, v), we need to update the residual value R(u) and R(v):

$$\begin{aligned} R(u)+&=\frac{(1-\alpha )\times P(v)-P(u)-\alpha \times R(u) + \alpha \times \varvec{1}_u}{\alpha \times d(u)} \end{aligned}$$
(5)
$$\begin{aligned} R(v)+&=\frac{(1-\alpha )\times P(u)-P(v)-\alpha \times R(v) + \alpha \times \varvec{1}_v}{\alpha \times d(v)} \end{aligned}$$
(6)

where \(\alpha \) is the teleport probability, P(v) is the estimate PPR value of node v, R(v) is the residual value of node v, and d(v) is the degree of node v. For each deleted edge (u, v), we subtract the corresponding value from R(u) and R(v). Then we continue to approximate the PPR value until each value of the residual vector R less than the threshold \(\epsilon \). Since we focus on the local communities of the seed node, we do not need the accurate PPR vector of the entire network, we only calculate the PPR value of nodes in the candidate subgraph, i.e., we neglect the nodes beyond to the candidate subgraph even the residual values might be greater than the threshold. This action reduces a lot of time for approximating PPR and does not affect the accuracy much through the experimental results in Sect. 6.4.1. For those high-quality seeds that are different from the previous snapshot, we approximate their PPR value with the static method Pagerank-Nibble. After approximating PPR vector incrementally, we perform sweep procedure with it, and finally get multiple local communities of the initial seed node at this snapshot.

6 Experiments

In this section, we evaluate HqsMLCD and HqsDMLCD on real-world networks. We first introduce the evaluation criteria of our experiments, then we present the basic information of datasets, the comparison methods, and the state-of-the-art baselines. After that, we present the results on parameter tuning and the results of comparing with existing methods for HqsMLCD. Finally, we present the experimental results of our dynamic method HqsDMLCD.

6.1 Evaluation Criteria

  • \(F_1\) Score Defined in Eq. 3

  • Conductance The conductance of a set \(S \subset V\) is

    $$\begin{aligned} \Phi (S) = \frac{cut(S)}{min(vol(S),vol(V \backslash S))}, \end{aligned}$$
    (7)

    where cut(S) is the number of edges with one endpoint in S, and another one not; vol(S) is the sum of the degree of nodes in S.

  • The number of detected communities \(C_d\) denotes the set of detected communities, and the number of detected communities is \(|C_d|\).

  • The seed node coverage We expect to find multiple communities that contain the initial seed node \(v_s\), so the coverage of \(v_s\) is a key criterion, which is defined as

    $$\begin{aligned} cov(v_s, C_d)=\frac{| \left\{ c_i|v_s \in c_i, c_i \in C_d \right\} |}{|C_d|}. \end{aligned}$$
    (8)

6.2 Datasets, Comparison Protocols and State-of-the-Art Methods

6.2.1 Datasets

For the static algorithm HqsMLCD, in order to quantify the comparison of algorithm results with the actual situation. We use three real-world static networks with ground-truth communities provided by SNAP [20, 36]: the product network Amazon, the collaboration network DBLP, and the online social network LiveJournal. All three networks are unweighted and undirected and are widely used in academic literature. Tables 2 and 3 show the statistics of them and their ground-truth communities.

Table 2 Statistics of read-world datasets
Full size table
Table 3 Statistics of communities in read-world datasets
Full size table

For the dynamic method HqsDMLCD, we test it on five real-world networks. Three of them are static networks: Amazon, DBLP, and LiveJournal, same as we used in the static experiment; the other two of them are dynamic social networks, Digg [6] and Slashdot [15], these two datasets contain the timestamp of each edge and are also widely used in academic literature. Table 2 also shows the statistics of these two dynamic networks.

6.2.2 Comparison Protocols for HqsMLCD.

We use the top 5000 communities provided by SNAP as the ground-truth communities in our experiments. The number of ground-truth communities after removing the duplicate shows in Table 3. Then we group the nodes in ground-truth communities according to the number of communities they belong to (i.e., overlapping memberships or om for short [17, 19], node with \(om=2\) means it belongs to 2 communities at the same time). The number of nodes with different om of three datasets shows in Table 4. Note that there are too few nodes belonging to more than five communities to achieve meaningful experimental results.

Table 4 The number of nodes with different om
Full size table

In the following experiments, for each om group, we randomly pick 500 nodes as the initial seed node if there are more than 500 nodes in the group, otherwise, pick all nodes in the group. Besides, we only pick seed nodes whose communities sizes are between 10 and 100. (The range of DBLP is 0 to 200, because of its larger community structure.)

6.2.3 Baselines for HqsMLCD

We compare our algorithm with several state-of-the-art multiple local community detection methods. He et al. [17] generated several seed sets from the ego-network of the initial seed node, then applied LOSP to obtain multiple detected communities. MULTICOM [18] finds new seeds based on the Personalized PageRank score of seed set, then expands new seeds by PageRank-Nibble. MLC [19] uses nonnegative matrix factorization on the subgraph around the initial seed node to get multiple communities. In addition, to verify the effectiveness of clustering proposed in Sect. 4.2, we also consider HqsMLCD-nc as a baseline, which is HqsMLCD without clustering phase.

6.2.4 Comparison Protocols for HqsDMLCD

We select the first \(50\%\) edges according to the timestamp as the initial network and then divide the remaining edges into 100 snapshots evenly. For static networks, we first randomly shuffle the order of edges, then do the same operations as dynamic networks. Since there are no ground truth communities on these snapshots, and our static algorithm HqsMLCD performs well, we compare our dynamic algorithm HqsDMLCD with the static one to evaluate the effectiveness of HqsDMLCD. Furthermore, the parameters (e.g., BFS steps) of the dynamic algorithm are inherent from the ones of the static algorithm using the same dataset.

6.3 Evaluations for HqsMLCD

6.3.1 Parameter Tuning of the BFS Steps

One of the main parameters of HqsMLCD is the steps of BFS, so we study the effectiveness of it. Figure 5 shows the average \(F_1\) score on Amazon, DBLP and LiveJournal that use different BFS steps in HqsMLCD. We can see that the \(F_1\) score reaches peak value when the BFS step equals a suitable value (e.g., BFS step equals 3 on Amazon), and the best step of BFS varies on different datasets. The BFS step determines the range of high-quality seed selection. Too small steps may not contain high-quality seed nodes, but too large steps will contain too much noise. Note that for LiveJournal we only set the BFS step to be 1, 2, and 3, because the subgraphs in LiveJournal with steps larger than 3 contain too many noisy nodes, and are too large to be processed efficiently.

Fig. 5
figure 5

The average \(F_1\) score of applying different BFS steps in HqsMLCD

Full size image

6.3.2 Accuracy Comparison

In this section, we use the \(F_1\) score to measure the accuracy of multiple detected communities. Table 5 lists the average \(F_1\) scores grouped by om of five methods on three datasets, and the last column shows the average \(F_1\) scores of using nodes as seed nodes from all om groups.

Table 5 \(F_1\) score results
Full size table

We can see that HqsMLCD achieves the best results on three real-world networks, and most results of HqsMLCD-nc outperform the other three baselines. The advantage of them mainly comes from the high-quality seeds we used to detect local communities. Besides, HqsMLCD is better than HqsMLCD-nc, demonstrating that clustering candidate subgraph is effective.

6.3.3 Conductance Comparison

We also compare the conductance of the detected communities by different MLCD algorithms. Figure 6 shows the average conductance of communities detected by each algorithm. HqsMLCD and HqsMLCD-nc outperform the other three methods on all three datasets. Note that LOSP, MULTICOM, HqsMLCD-nc, and HqsMLCD all use conductance as the measure to generate detected communities, and our methods still outperform LOSP and MULTICOM, which means the high-quality seeds we select can indeed generate better communities. Comparing with MLC, HqsMLCD also achieves lower conductance. This implies with the help of high-quality seeds, the seed expansion-based method can also surpass the nonnegative matrix factorization-based solution.

Fig. 6
figure 6

Conductance results

Full size image

6.3.4 Number of Detected Communities

Here we compare the number of detected communities of different methods to demonstrate the ability to capture the local structures with respect to the given seed node. Figure 7 illustrates the number of detected communities of LOSP, MLC, and HqsMLCD for nodes with different om on Amazon, DBLP, and LiveJournal. Note that MULTICOM and HqsMLCD-nc require the number of detected communities as an input parameter, they have no ability to adaptively determine the number of communities, so we do not visualize them in the figure. The black line represents the number of communities that seed nodes actually belong to, i.e., om. We can see that the trends of MLC and LOSP remain stable when om increases, but the results of HqsMLCD are consistent with the trend of ground-truth. This phenomenon implies that our algorithm can recognize different local structures and utilize them for community detection.

Fig. 7
figure 7

Number of detected communities

Full size image

6.3.5 Seed Node Coverage

Next, we examine the seed node coverage of detected communities. It is an important indicator, as the target of multiple local community detection is to detect multiple communities that the seed node belongs to. We evaluate seed coverage of MULTICOM, MLC, HqsMLCD-nc, and HqsMLCD on Amazon, DBLP, and LiveJournal. Since LOSP includes the seed node in every seed set, we do not compare it here. Figure 8 illustrates the average seed coverage on three datasets grouped by om. It is clear to see that HqsMLCD-nc and HqsMLCD outperform MULTICOM and MLC. Note that our method uses the same framework as MULTICOM, but HqsMLCD identifies the high-quality seeds similar to the given seed node via network representation. However, MULTICOM may find new seeds far away from the initial seed node. Therefore, except the community expanded by the initial seed node, the communities generated by new seeds of MULTICOM hardly contain the initial seed node.

Fig. 8
figure 8

Seed coverage results

Full size image

6.3.6 Running Time

At last, we compare the running time of these algorithms on Amazon, DBLP, and LiveJournal. For each method, we calculate the average time of detecting all communities of a single seed node on different datasets, Table 6 shows the result. We can see that the running time of LOSP increases rapidly as the size of the network increases and cost more than 500 seconds for a single seed node on LiveJournal. Although HqsMLCD doesn’t achieve the best time efficiency, HqsMLCD, MLC, and MULTICOM have a similar time cost. Considering the improvement brought by HqsMLCD for the community detection problem, such a little overhead of the time cost is acceptable.

Table 6 Average running time (s) of detecting all communities of a seed node
Full size table

6.4 Evaluations for HqsDMLCD

The goal of DMLCD is to detect multiple local communities of the given seed node on the dynamic network and maintain accuracy while reducing time consumption compared to static algorithms. We use \(\varvec{F_1}\) Score, Conductance, and Seed Node Coverage for accuracy evaluation, and compare the running time with the static algorithm.

6.4.1 Accuracy Comparison

In this section, we use the \(F_1\) score to measure the accuracy of dynamic multiple detected communities. For each snapshot, we use the results of HqsMLCD as the ground-truth and calculate the \(F_1\) score of multiple local communities detected by HqsDMLCD. We show the average \(F_1\) score of all snapshots on five datasets in Fig. 9.

Fig. 9
figure 9

\(F_1\) score results

Full size image

We can see that the \(F_1\) score of our dynamic algorithm HqsDMLCD is higher than 0.8 on all five datasets and even higher than 0.9 on LiveJournal, which demonstrates HqsDMLCD achieves similar results with our static algorithm. The high \(F_1\) score is mainly due to the appropriate improvement of the static algorithm: dynamic network embedding and dynamic high-quality seeds expanding. We cleverly implement incremental calculation in network embedding phase and expanding the high-quality seeds phase, which preserves the excellent results of the static algorithm and achieves the purpose of dynamic calculation.

6.4.2 Conductance Comparison

We also compare the average conductance of the detected communities by HqsDMLCD and HqsMLCD. Figure 10 shows the results. HqsDMLCD achieves similar conductance with HqsMLCD on all datasets, and even better on some datasets(DBLP, Digg, and Slashdot), which means the communities detected by dynamic algorithm HqsDMLCD have the same high-quality as those detected by the static algorithm. As we can know from experiments of HqsMLCD, the high quality communities mainly benefit from high-quality seeds. The conductance results imply that HqsDMLCD gets seeds of similar quality to the high-quality seeds detected by HqsMLCD, which then expand to similar high-quality communities.

Fig. 10
figure 10

Conductance results

Full size image
Fig. 11
figure 11

Seed Coverage results

Full size image

6.4.3 Seed Node Coverage

Then we compare the seed node coverage of the detected communities by HqsDMLCD and HqsMLCD. As we mentioned before, seed node coverage is an important indicator. We calculate the average seed node coverage of detected communities on five real-world datasets. Figure 11 shows the results. We can see that HqsDMLCD achieves similar results with HqsMLCD on all datasets. The high seed node coverage means that most of the detected communities contain the seed node and indicates HqsDMLCD realizes the target of detecting multiple local communities that contain the seed node in dynamic settings.

6.4.4 Running Time

At last, we compare the running time of HqsDMLCD and HqsMLCD on all datasets. For both algorithms, we calculate the average time of detecting multiple communities for a seed node on a snapshot. The main goal of dynamic multiple local community detection methods is to reduce time consumption. As we can see in Fig. 12, HqsDMLCD greatly reduced running time on dynamic networks, on all datasets, HqsDMLCD reduces the running time by at least \(25\%\) compared to HqsMLCD, and by up to \(88\%\). These results demonstrate that our dynamic algorithm HqsDMLCD effectively reduces the running time on dynamic networks, and without sacrificing accuracy. The advantage mainly comes from two key steps we modified: dynamic embedding candidate subgraph and dynamic expand high-quality seeds, incremental calculation could reduce repeated calculation by the static algorithm on dynamic networks.

Fig. 12
figure 12

Average running time (s)

Full size image

7 Conclusion

In this paper, we proposed a method, HqsMLCD, for recovering all communities to which a seed node belongs. In HqsMLCD, we first embedded and clustered the candidate subgraph which sampled from the whole network, then selected high-quality seeds through the quality scores, at last, expanded each high-quality seed to a detected community. Besides, in order to address the multiple local community detection problem on dynamic networks, we extended the static algorithm to HqsDMLCD. HqsDMLCD detected multiple communities on dynamic networks incrementally through dynamic embedding candidate subgraph and dynamic expanding high-quality seeds. The comprehensive experimental evaluations on various real-world datasets demonstrate the effectiveness of both static and dynamic community detection algorithms.