Abstract
Word embedding has been well accepted as an important feature in the area of natural language processing (NLP). Specifically, the Word2Vec model learns high-quality word embeddings and is widely used in various NLP tasks. The training of Word2Vec is sequential on a CPU due to strong dependencies between word–context pairs. In this paper, we target to scale Word2Vec on a GPU cluster. To do this, one main challenge is reducing dependencies inside a large training batch. We heuristically design a variation of Word2Vec, which ensures that each word–context pair contains a non-dependent word and a uniformly sampled contextual word. During batch training, we “freeze” the context part and update only on the non-dependent part to reduce conflicts. This variation also directly controls the training iterations by fixing the number of samples and treats high-frequency and low-frequency words equally. We conduct extensive experiments over a range of NLP tasks. The results show that our proposed model achieves a 7.5 times acceleration on 16 GPUs without accuracy drop. Moreover, by using high-level Chainer deep learning framework, we can easily implement Word2Vec variations such as CNN-based subword-level models and achieves similar scaling results.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
In recent years, there is a growing interest in word embedding models, where words are embedded into low-dimensional (dense) real-valued vectors. Semantically, similar words tend to be close in this vector space. The trained word embeddings can be directly used for solving intrinsic tasks like word similarity and word analogy [16, 17, 20]. Word embeddings have also become the building blocks for extrinsic tasks, such as part-of-speech tagging, chunking, named entity recognition [11] and text classification [27, 49].
Multiple models of training word embeddings have been proposed in recent years [8, 9, 12, 30, 35, 36, 39, 40, 45, 48]. Probably, one of the most popular models among them is Word2Vec [39]. It achieves state-of-the-art results on a range of linguistic tasks.
The original Word2Vec is implemented using C programming language for a single CPU. Training on this hardware may not be the best choice, specially for word2Vec variations, such as subword-level embedding models [33]. Those variations often need deep neural networks as submodules, which is hard to implement without deep learning frameworks. Moreover, the training and inferencing require a large amount of tensor computations, which is slower compared to implementations on GPU(s).
However, despite the advantages of using GPU(s), directly fitting Word2Vec and its variations on them is not feasible. Scaling often results in low-quality of learned embeddings or suboptimal GPU utilization. The main challenge is batch size. More precisely, when large batch size is applied, the embeddings’ quality drops dramatically. If we reduce the batch size, the training speed drops dramatically. There is always a trade-off between effectiveness and efficiency.
There are also two more issues in Word2Vec. The first is online learning scheme. Original Word2Vec cannot control the number of iterations, since it scans through the corpus and optimizes the cosine distance between word–context pairs. The training time (iteration number) is thus proportional to the size of the corpus. This makes the algorithm hard to train on big corpus.
The second issue is the insensitivity to low-frequency words. For a word, the number of updating times is equal to its frequency. However, the divergence between words’ frequencies is too large (as shown in Table 2) .This causes high loss and variance for low-frequency words. This also limits the use of the large batch size and causes suboptimal GPU utilization.
We propose an alternative training scheme called W2V-CL (Word2Vec with controllable number of iterations and large batch size). W2V-CL model samples word and contextual words from the corpus uniformly. Each word is assigned with an equal number of context samples (context size). In this way, the training time depends only on the vocabulary size and the context size, which solves the online learning scheme issue. During training, W2V-CL model scans through all sampled word–context matrix and optimizes the distance between corresponding embedding. The high-frequency and low-frequency words are updated equally, which solves the low-frequency words issue. This in turn allows us to use a larger batch size (equal to the vocabulary size) and better utilize GPU resources. We also intuitively designed a two-step updating trick which avoids updating conflicts inside a batch.
Experiments show that on a single GPU, our model is around 2 times faster than the baseline without accuracy drop. Due to the large batch size used in our model, W2V-CL can be scaled on multiple compute nodes. Compared to the single GPU result, we achieve 5.5 times speedup using 8 GPUs, and around 8 times speedup using 2 compute nodes with total 16 GPUs.
Since W2V-CL model only requires the pre-assignment of word–context matrix, it can be directly integrated into almost any deep learning frameworks. This paper takes Chainer deep learning framework [51] as an example and demonstrates the flexibility of W2V-CL model by implementing the CNN-based subword-level word embedding model [33] on top of it. Experiments show similar trends of scaling, and faster training speed compared to the original Chainer implementation.
2 Word2Vec
Due to the popularity and state-of-the-art performance, we choose the Skip-Gram model with negative sampling in Word2Vec [39] as our word embedding baseline. For simplicity, we directly refer it as Word2Vec in the rest of this paper.
Given a training corpus C consisting of |C| words \(w_1, w_2, w_3, \ldots , w_{|C|}\), Word2Vec first extracts the word–context pair collection P. Each element \((w, c) \in P\) represents a word and its corresponding contextual word. There are multiple ways of defining the context types and representations [30, 52, 53]. In this work, we use the linear context type and unbound representation [34]: the words that precede and follow the target word within some fixed distance are considered as context. An example of the word–context pair collection P is shown in Table 1.
The objective function of Word2Vec is defined as:
where \({\mathbf {w}}\) is the vector of word w.
As shown in Fig. 1, for implementation, this equation basically scans through the word–context pair collection P. For each pair, it calculates the probability of word vector \({\mathbf {w}}\) predicting contextual word c. More specifically, this probability is defined as:
where \({\mathbf {c}}\) is the vector of contextual word c and \(V_C\) is the vocabulary of all contextual words.
However, this form of definition is difficult to calculate, since \(\sum _{c' \in V_C}e^{{\mathbf {w}}^T {\mathbf {c'}}}\) requires iterating through all contextual words in the vocabulary. The size of vocabulary is often ranging from 10,000 to 50,000. Therefore, as proposed in [38], an alternative likelihood called negative samplingFootnote 1 is used, where the log probability in Eq. 1 can be estimated as:
where K is the negative sampling size, which normally ranging from 5 to 20. \({\mathcal {N}}_{w,c}\) is the negative example that sampled from the vocabulary V, \({\mathbf {w}}\) is the vector for word w and \(\sigma\) is the sigmoid function:
The negatively sampled word \(c_{i}\) is randomly selected on the basis of its unigram distribution:
where \(\#(w)\) is the number of times that word w appears in the corpus and ds is the distribution smoothing hyper-parameter which is empirically defined as 0.75.
2.1 Word2Vec on GPUs
As shown in the previous section, the original Word2Vec implementation on CPU (Word2Vec ToolkitFootnote 2) is implemented using C language. It moves over each word in the corpus and repeats the training steps in an online fashion. In order to take the advantage of GPU, recent deep learning frameworks implement and optimize Word2Vec using mini-batch training.
We choose Chainer deep learning framework [51] in this study. Chainer is a Python-based deep learning framework and supports the use of CUDA/cuDNN for building and training neural networks. For simplicity, we refer to Chainer’s Word2Vec implementation as W2V-Vanilla in the rest of this paper.
Figure 2 illustrates how Chainer frameworkFootnote 3 implements the Word2Vec algorithm. Similar to Word2Vec on CPU, there are mainly 6 steps in the training of W2V-Vanilla model:
-
1.
Extracting word–context pairs collection P
As shown in Table 1, this collection is exactly the same as which in Word2Vec on CPU.
-
2.
Splitting batches
Unlike Word2Vec on CPU, since W2V-Vanilla model trains on the GPU, a batch should be sent to accelerate the training process. A larger batch size can make the model utilizing more GPU resources. We will discuss the batch size settings in Sect. 2.4. Note that if we ignore the hardware, theoretically, Word2Vec on CPU can be regarded as a special case of W2V-Vanilla model where the batch size is set to 1.
-
3.
Negative sampling
W2V-Vanilla model applies negative sampling techniques inside each batches. Each batches are sampled and enlarged \(K+1\) times to form pairs of final batch size |B|, where K is the negative sampling size.
-
4.
Look-up table or convolutional neural network (CNN)
Each words and contextual words in a batch are converted into vectors. Normally, this step is done by searching a “look-up table”, where each word has corresponding vectors stored in a “word vector matrix”. We can also apply some more advanced models based on word’s morphology, such as CNN-based subword-level model [33]. Details of this model will be discussed in Sect. 5.8.
-
5.
Dot production
All the word vectors and context vectors are then sent to GPU for calculation iteratively. Since the calculation is simply row-wise dot product, the GPU is able to perform it in parallel.
-
6.
Loss calculation and back-propagation The dot product results are compared with prediction labels and then back-propagate based on differences.
Compared to Word2Vec on CPU, W2V-Vanilla model is more flexible, since it relies on multiple high-level deep learning primitives. For example, in step 4, one can easily implement CNN-based subword-level word embeddings. On the contrary, it would be hard to implement it using pure C or CUDA, especially for both forward pass and back-propagation. Moreover, the resulting word embeddings can be directly read as input for neural networks on downstream tasks, or even trained jointly with other natural language processing models.
Due to the above reasons, this work focuses on accelerating W2V-Vanilla model instead of Word2Vec on CPU.
2.2 Issues with the Online Learning Scheme
As discussed in the previous section, original Word2Vec is trained in an online fashion. It scans through the corpus to obtain word–context pairs and optimize the distance between them based on the objective function. The training time (iteration number) is directly depend on the corpus size. The larger the corpus is, the longer training time is needed.
This online learning scheme also fixes the order of training word–context pairs. Pairs that appear at the head of the corpus are always optimized first, and vice versa. We argue that it is possible to re-arrange the order of training for similar quality of learned word embeddings, and higher training speed.
2.3 Issues with Low-Frequency Words
Aside from the online training issue, there is also a convergence issue emerging from how Word2Vec treats high-frequency and low-frequency words. The number of times a vector updates depends on the number the corresponding word appears in collection P, which in terms depend on the word’s frequency.
It is reasonable to treat high-frequency words more carefully since they are often also more frequent in downstream tasks. However, intuitively, millions of updates may be too much for learning an embedding for a given word. It may also be problematic that the vectors of low-frequency words update too few times and could not be properly learned.
Table 2 lists the top-10 high-frequent words and top-10 low-frequent words in the Text8 corpus (described in Sect. 5.1). As shown in this table, adjective words like “bored” and “ridiculous” appear only 50 times while determinative word “the” appears 1,061,396 times. This indicates that the vector of word “the” will update 21,228 times more often than the vector of word “bored” and “ridiculous”. However, intuitively, word “bored” and “ridiculous” may be more important since it contains certain semantic information.
If we focus on the word pair frequency, this issue seems more dramatic. As shown in Table 3, all of the top 10 most common word–context pairs are actually the combination of determinative words, preposition words and conjunction words, which do not contain much semantic information. In traditional natural language processing models, those words are usually referred as “stop words”, which are filtered out before or after data processing [47]. As shown later in our experiments (Sect. 5.6), the variance of low-frequency words can be largely reduced by training each word with equal number of times in our proposed model.
2.4 Profiling Training Speed on GPUs
Number of words/second with different batch sizes. Dot product Calculate the dot product of two input matrices directly using CuPy. Loss function Calculate the loss of two input matrices directly using CuPy. Forward pass Calculate the loss of a batch of word pairs using Chainer. All operations Train the full model using Chainer. Note that for forward pass, the scaling results are not linear when batch size is larger than 32,768. This is due to the saturation of GPU utilization
In order to saturate the GPU utilization, sufficient number of threads/operations have to be executed per batch update. Moreover, as each batch needs to be transferred from host memory to GPU, increased computation per batch alleviates communication overhead. Since the dimension of embeddings is fixed, the only way to increase the amount of computation per batch is to have more samples. Finally, having a larger batch size improves the scalability on multiple GPUs, as the amount of data to be sent through the network does not depend on the batch size, but only in the size of the model’s parameters.
In our experiments, we have observed GPU performance to be inferior to what can be estimated for just the dot product of embedding vectors. This can be explained by multiple layers of overhead imposed by the deep learning framework: computation history needs to be recorded for tape-based differentiation etc. Yet for all the operations involved, we observe similar performance dynamics with respect to the batch size.
The bottom line is that larger batch sizes are always beneficial performance wise, as measured empirically and illustrated in Fig. 3. For the simple dot product computation and loss function calculation, the number of words per second increases linearly with the batch size. Note that the loss function calculation is around 25 times slower than the simple dot product. It is reasonable since the loss function calculation requires nonlinear operations. For more advanced forward pass and all operations, the number of words per second increases almost linearly with the batch size. However, when batch size is larger than \(2^{15}=32{,}768\), the improvement rate decreases. This suggests that GPU utilization will be partially saturated when batch size became too large.
2.5 The Challenge with Large Batch Size
It seems promising in the previous section to directly use large batch size in W2V-Vanilla model. However, during profiling, we find there are two issues that limit W2V-Vanilla model use the large batch size, which forms the main challenge of this paper.
The first and most obvious issue with large batch sizes is the memory boundedness of the algorithm. It is especially problematical when training neural networks, as per-neuron gradients have to be stored to perform back-propagation (in deep learning frameworks, this is often referred as computational history).
Illustration of flat and sharp minimum [25]. The Y-axis indicates value of the loss function. The X-axis indicates parameters (reduced to 1 dimension). In sharp minimum, the value of loss function changes rapidly with parameters in a relatively small range. Suppose a set of parameters achieves the lowest loss in training function, the loss on testing function for flat minimum is much lower than that for sharp minimum
As shown in Fig. 4, similar to the results of speed, the memory footprint increases linearly with the batch size. The Tesla K80 GPU used in our experiments has 12 GB memory, and thus, \(2^{16}=65{,}536\) is the maximum number of batch size that used to train the full Word2Vec algorithm. Note that currently the largest single GPU memory is 36 GB (Quadro GV100), which is 3 times larger than the memory of Tesla K80 GPU in our experiment. We believe there will be GPUs with even larger memory released in the future due to the rapid development of the GPU hardware industry.
Another more dramatic issue with large batch size is low quality of learned models, which is word embeddings in our case. This issue has already been observed in the field of computer vision. For examples, the AlexNet [29] achieves more than 80% accuracy on ImageNet with a batch size of 512. However, when batch sizes more than 4096 are used, the accuracy drops to under 60%.
Previous research [21] shows that there can be flat and sharp minimums (as shown in Fig. 5) in training functions. Models with large batch size tend to converge to the sharp minimum and result in bad performance on a range of computer vision tasks [25].
Word embedding models probably suffer more issues with large batch size compared to models in computer vision tasks. For example, in image classification models, each batch contains distinct images or images’ features as inputs. Each image appears once and only once within a batch. However, in W2V-Vanilla, each batch often contains duplicated words which appear in several positions (i.e. word “i” appears in input instances “i-like” and “i-apple” as shown in Table 1). Intuitively, the conflicts in W2V-Vanilla should result in bad quality of learned embeddings and should be eliminated.
It is hard to prove the sharp minimum and conflict issues in theory. However, our empirical experiments demonstrate that word embeddings trained with larger batch size result in worse performances on a range of tasks. The explicit experiment settings and results are shown in Sect. 5.3, and we choose batch size of 1024 to ensure the quality of learned embeddings. The main challenge of scaling Word2Vec is finding a way to increase batch size while preserving the quality of learned embeddings.
3 Word2Vec with Controllable Number of Iterations and Large Batch Size
We propose an alternative to W2V-Vanilla model, which is called W2V-CL (Word2Vec with Controllable Number of Iterations and Large Batch Size). In this section, we first introduce the model’s details and show the advantages of our model by addressing the challenge and issues in W2V-Vanilla. Then we formalize the theoretical computation complexity and introduce the training approach on multiple GPUs and compute nodes.
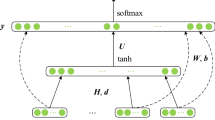
The overall architecture of W2V-CL model is shown in Fig. 6. Given a training corpus C and its vocabulary V, the first step of W2V-CL model is to sample word–context pairs uniformly from C. Each word in the vocabulary is assigned with l context samples. This pre-processing step creates a word–context matrix M with size of (|V|, l), as shown in Table 4. Element \(m_{i,j} \in M\) represents the \(j_{th}\) contextual words of the \(i_{th}\) word in the vocabulary.
More precisely, we scan through the corpus before training and extract the contextual words for all the words in the vocabulary. For high-frequency words that have contextual words more than l, we randomly discard the abundant contextual words. For low-frequency words that have fewer contextual words than l, we randomly duplicate the existing contextual words. After the word–context matrix M is built, we shuffle each row of the matrix to ensure the randomness. Our pilot experiments show that the shuffling operation results in more stable training dynamics.
This pre-processing step is done on CPU using only one single thread. Empirically, it takes around 400 s to process 100 M corpus. Note that this step can be accelerated using parallel computing. Since word–context matrix M can be stored and reused, we consider matrix M as a special form of corpus and do not consider the time complexity of this pre-processing step in the rest of our experiments.
The objective function of W2V-CL model is similar to the original Word2Vec as shown in Eq. (1). However, instead of scanning through the corpus, W2V-CL model scans through the word–context matrix M:
where \(w_i\) is the \(i_{th}\) word in the vocabulary. With negative sampling technique, the final objective function of W2V-CL is defined as:
For each iteration, the batch size is set to |V|. As shown in the right part of Fig. 7, each batch contains 2 word lists. In the left word list, words appear once and only once. The right contextual word list is from either a column in the word–context matrix M or negative sampling, where a word (especially a high-frequency word) may appear several times and still brings conflict.
As discussed in Sect. 2.5, the conflicts may result in low quality of learned embeddings. In order to avoid updating conflicts while preserving efficient updating, we adopt a two-step updating trick inspired by the two-step EM algorithm adopting alternating minimization [42]. In the first step, the left word list looks up the word vector table, and the right word list looks up the context vector table. When updating, only the word vectors (indexed by the left word list without conflicts) are updated. In the second step, we exchange the role of word and context:Footnote 4 the left word list looks up the context vectors, and the right word list looks up the word vectors. When updating, only the context vectors (indexed by the left word list without conflicts) are updated. Thus, we utilize the appear-once-and-only-once nature of words in left list and update their corresponding word vectors and context vectors alternatively. In this way, both word vectors and context vectors are updated without conflicts, and the updating chance for each vector is ensured equivalent.
3.1 Advantages of W2V-CL over W2V-Vanilla
Our W2V-CL model addresses one main challenge (mentioned in Sect. 2.5) and two issues (mentioned in Sects. 2.2, 2.3) of W2V-Vanilla model. For the large batch size challenge, our model tries to avoid conflicts by updating every word in the vocabulary once and only once in each batch. The batch size B is set to the vocabulary size |V|, which is usually ranging from 10,000 to 50,000. This number is much larger than the batch size of 1024 used in W2V-Vanilla model. Note that this solution is based solely on intuition instead of concrete motivation in theory. However, we show our model’s effectiveness and efficiency empirically in the experiments.
For the online learning scheme issue, our W2V-CL model iterates through the word–context matrix M instead of the corpus. The training time is only depend on the size of word–context matrix M, which is directly controlled by users. Since we use a shuffle operation on the matrix, words are processed arbitrarily. In contrast, W2V-Vanilla model always first processes at the head of the corpus.
For the low-frequency words issue, our W2V-CL model learns the embedding of each word using word–context matrix M. In this matrix, each word has equal number of contextual words and updated equally. For examples, in W2V-Vanilla model (Table 2), word “the” is updated for 1,061,396 times while word “bored” and “ridiculous” are updated only for 50 times, while in our model all the words are updated equally for l times (l is set to 65,536 in our experiments).
3.2 Theoretical Computational Complexity
As shown in Eq. 3, outside the brackets, W2V-Vanilla model iterates through the word–context pair collection P. If we ignore the boundary of sentences,Footnote 5 the size of collection |P| is actually equal to \(|C| \cdot 2 \cdot win\), where |C| is the corpus size and win is the window size. Suppose the number of operations inside the brackets is o, the total number of operations for W2V-Vanilla model is \(|C| \cdot 2 \cdot win \cdot o\).
As for W2V-CL model’s objective function in Eq. 7, the item that inside the brackets is:
which is actually similar to the item in W2V-Vanilla model:
where they have the same number of operations o. Overall, the total number of operations for W2V-CL model is \(l \cdot |V| \cdot o.\)
According to Heaps’ law (also referred Herdan’s law) [15], the vocabulary size |V| is a function of corpus size |C| and can be formulated as:
where K and \(\beta\) are hyper-parameters for Heaps’ equation. For a typical English corpus, K is usually between 10 and 100 and \(\beta\) is usually between 0.4 and 0.6.
Powered by this observation, we can rewrite the number of operation in W2V-CL model as \(l \cdot K \cdot |C|^{\beta } \cdot o\). Once we divide the number of operation in W2V-Vanilla model by that in W2V-CL model, we get:
In another words, W2V-Vanilla model theoretically needs ratio times more operations than W2V-CL model. Since win, l, K and \(\beta\) are fixed parameters in the ratio definition, W2V-CL model is even more efficient on large corpus.
Limited by the memory, word embedding models often need to discard words that appear less than a certain criteria. When this trick is applied, the vocabulary size |V| is even smaller.
Instead of purely relying on theory, we also verify Heaps’ law on Text8 corpus for both full vocabulary and vocabulary with discarded words. Figure 8 (blue line/cross vs. red line/cross) shows that by cutting words that appear \(<\,50\) times, the vocabulary size decreases dramatically. We find that the best fitting numbers for parameter K and \(\beta\) are 7.13 and 0.71, respectively. Note that parameter K is slight out of the expected ranges of Heaps’ law. We suspect this is due to the large number of internet language that used in Text8, since this corpus is built based on Wikipedia.
3.3 Scaling W2V-CL Model Using Multiple GPUs and Compute Nodes
We also explore the possibility of using multiple compute nodes and multiple GPUs to scale our W2V-CL model. There are mainly two types of scaling strategies in deep learning: model parallelism and data parallelism. The model parallelism strategy requires parallelable models, such as stacked-CNNs that deployed in parallel. However, the Word2Vec algorithm does not fit into that category, since only dot productions (and a single-layer CNN in the subword-level model) are performed.
We choose data parallelism in this study. The data parallelism strategy requires a large amount of input data. In the case of training word embedding models, the data refers to the corpus, which is normally large enough. With the larger batch size used in our W2V-CL model, the GPU(s) perform more computations before averaging gradients and updating the model weights. In this way, the number of iterations is reduced and thus speeds up the training.
More specifically, as shown in Fig. 9, there are mainly 3 steps of our data parallelism strategy:
-
1.
Splitting the batch into sub-batches
Suppose there are N GPUs (workers), we equally assign each GPU with |B| / N word–context pairs, where |B| is the batch size.
-
2.
Forward passing
This step is the same as Word2Vec on a single GPU, including negative sampling, look-up table or CNN, dot production and loss calculation.
-
3.
Gradient aggregation and back-propagation
Once the loss is calculated, for each iteration, the GPUs communicate to obtain the averaged gradient over gradients of all GPUs. Then, the aggregated gradients are used to improve the model in the back-propagation over the word embeddings.
For fair comparison, we also implement the parallelized W2V-Vanilla model using exactly the same approach.
4 Related Work
In the field of computer vision, scaling models such as AlexNet to solve ImageNet challenge is a hot topic. As discussed in Sect. 2.5, there are issues with large batch sizes [21]. There is work [25] that tries to solve this issue using data augmentation and starting with small batch size, but does not find any working solution. One way to solve this issue is to train with more iterations and results in better accuracy [22]. However, more iterations require multiplied training time. Recently, there are works [54, 55] use carefully designed learning hyper-parameters and are able to train with a batch size of 32,768 without accuracy loss. But these works are over-specified and do not directly adapt to other models. For example, they are based on layer-wise adaption, while original Word2Vec algorithm only has one layer.
For Word2Vec algorithm in our case, due to the flexibility, we take the Chainer framework as an example of scaling. There are also several other deep learning frameworks that have implemented this algorithm on GPU(s), such as Gensim with KerasFootnote 6 and Theano.Footnote 7 However, those frameworks share the same issues with W2V-Vanilla on Chainer and perform worse than original Word2Vec in terms of speed [18]. TensorFlowFootnote 8 implements Word2Vec on CPU and calls C++ functions, which achieved comparable speed as the original Word2Vec.
Another promising direction for accelerating Word2Vec is directly parallelizing it on clusters regardless of the conflicts. In fact, the original Word2Vec implementation originally utilizes multiple threads for acceleration. So it seems promising to extend the same model with greater number of threads on multiple computing nodes. However, as shown in Spark MLLib [37] and Deeplearning4j [50], the accuracy drops significantly when more compute nodes are employed. To the best of our knowledge, the most promising work on CPU(s) is to convert the dot product to matrix multiplication by carefully aligning the order of word–context pairs. It speeds up the original Word2Vec 2–3 times on Intel BDW and Intel KNL [24] without accuracy drop.
There are also works that tries to accelerate Word2Vec on GPUs using CUDA [4, 18]. These two methods assign each CUDA block with a whole sentence instead of word pairs. This ensures the good quality of learned word embeddings. Using 2 GPUs, 21.3 times speedup over 1-threaded CPU is achieved in [4]. Similarly, using 8 GPUs, around 9x speedup over an 8-threaded CPU is achieved in [18]. However, being written in a low-level CUDA, these models are hard to extend if the users want to combine them with, for instance, deep neural layers. On the contrary, our work is more flexible focusing on high-level implementations, so that users can easily implement Word2Vec variations. As an example, we show how to implement a CNN-based subword-level model in Sect. 5.8. To the best of knowledge, our work is the first that accelerates subword-level model and scale it with multiple GPUs.
5 Experiments
5.1 Implementation Details
We implement W2V-CL model using Chainer deep learning framework [51]. For scaling to multiple computing nodes equipped with GPUs, we use the ChainerMN framework [2], which is an additional package for Chainer. We choose Text8Footnote 9 corpus as the training data. The word embedding size N is set to 500. The negative sampling size is set to 5, and the window size is set to 2. Following Chainer’s original Word2Vec implementation, we use Adam [28] as the optimization function, which performs much better than SGD [26] in our pilot experiments. Words which appear fewer than 50 times are directly discarded, which results in a vocabulary size of 18498. All models are trained for 1 epoch on the Nvidia Tesla K80 GPU(s).
5.2 Datasets
In order to measure the quality of learned word embeddings, we choose word similarity, word analogy, concept categorization, and text classification tasks as benchmarks.
5.2.1 Word Similarity
Word similarity task aims at producing semantic similarity scores of word pairs, which are compared with the human scores using Spearman’s correlation. The cosine distance is used for generating similarity scores between two word vectors. For example, as shown in Fig. 10, given two word pairs “apple-orange” and “apple-train”. The word “apple” and “orange” should be closer to each other since they are both fruits. Consequently, the cosine distance between word “apple” and “orange” should be smaller than that between “apple” and “train”.
There are several datasets proposed for evaluating word similarity. Probably, the most widely used one is WordSim353 (WS) [16] dataset. It consists of 353 pairs of words (divided into similarity (sem.) and relatedness (rel.) categories [1, 56]). The ground truth similarity is the averaged score from 13 to 16 human annotators. Sim 999 (Sim) dataset [20] tries to improve WordSim353 dataset by selecting more balanced words and excludes relatedness from similarity (i.e. related word pairs like “forest” and “tiger” are not judged similar in Sim 999 dataset). MEN dataset [10] contains 3000 pairs of randomly selected words that occur as ESP-Game dataset.Footnote 10 Mech Turk (MT) dataset [46] contains 287 word pairs are selected by a machine algorithm from New York Times corpus and similarity scores of them are obtained via crowd-sourcing. Rare Words (RW) dataset [35] consists of 2034 word pairs regarding rare words. We use all the datasets mentioned above in our experiments.
5.2.2 Word Analogy
The word analogy task aims at answering questions generalized as “a is to a’ as b is to \(\_\_\) ?”, such as “man is to woman as uncle is to \(\_\_\) ?”. As shown in Fig. 10, the answer should be “aunt”, and this question is about gender transformation of words. Similarly, for the question “king is to kings as queue is to \(\_\_\) ?”, the answer should be “queues” since this question is about plural transformation (Fig. 11).
For datasets, we use Google analogy dataset along with BATS analogy dataset [17]. Google analogy dataset includes 9 morphological and 5 semantic categories (i.e. the famous country:capital category), with 20–70 unique word pairs per category: 8869 semantic and 10,675 syntactic questions in total [39]. Relatively, BATS is bigger, more balanced and more representative, consisting of 4 subdatasets: inflectional morphology, derivational morphology, lexicographic semantics and encyclopaedic semantics. Each subdataset then consists of 10 kinds of pair-wise relationships (i.e. for relationship kind member under subdataset lexicography, player:team is an instance), and each kind contains 50 unique word pairs, amounting to 99,200 in total. Accuracy is used as merit for this task. For evaluation, we use the LRCos method [14] for solving word analogies, which significantly improves on the traditional vector offset method [39].
5.2.3 Concept Categorization
Given a set of words, concept categorization task (also often referred as word categorization or word clustering) assigns words with different categories. For example, as shown in Fig. 12, given words “cat”, “dog”, “swan” and “eagle”, the first two words should form a cluster since they are animals while the last two words should form another cluster since they are birds. Note that a model do not need to provide the clusters’ names, and the number of clusters is pre-defined.
We choose Battig and Montague (BM) [7], Almuhareb and Poesio (AP) [3], Baroni and Lenci Evaluation of Semantic Spaces (BLESS) [23], and ESSLLI [6] as datasets. Detailed summary of these datasets is listed in Table 5. Following previous work [5], purity is used as the evaluation criteria. We consider concept categorization as a clustering task
and choose K-means clustering algorithm for evaluation.Footnote 11
5.2.4 Text Classification
Text classification task is one of the most fundamental tasks in natural language processing. It aims at assigning a text with a pre-defined category. We choose the Stanford sentiment treebank (stsa) [49], customer product reviews (custrev) [41], MPQA opinion corpus (mpqa) [13] and movie review sentiment (rt) [44] datasets for text classification. These datasets are all sentiment-related classification. We also choose subj [43] dataset for subjectivity/objectivity classification. Detailed summary of these datasets is listed in Table 6. We use convolutional neural network (CNN) for evaluationFootnote 12 and accuracy as merit.
5.3 Impact of the Batch Size
We illustrate the problem of sharp minimum in large batch training process in Sect. 2.5. In this section, we demonstrate how large batch sizes impact embedding qualities negatively on W2V-Vanilla model. Furthermore, we use our observation to guide batch size setting of the W2V-Vanilla model.
Empirically, we measure how word embedding qualities change through the scores of word similarity and word analogy tasks. As shown in Fig. 13, we generate 9 word embeddings via different batch sizes and test them on word similarity and word analogy tasks (13 datasets in total). Probably due to the same sharp minimum issue in computer vision, the scores drop uniformly when we increase the batch size. Distinctly, when the batch size is over \(2^{10}= 1024\), the qualities turn down much quickly. Hence, in the rest of this paper, all the experiments on W2V-Vanilla set batch size to 1024. This is also similar to the default setting used in Chainer’s implementation, where a batch size of 1000 is used.
5.4 Impact of the Context Size l
The most important hyper-parameter in our W2V-CL model is the context size l. Since the vocabulary size is fixed for a given corpus, the context size l directly defines how big the word–context matrix M is. Consequently, it affects the quality of learned embeddings, as well as the training speed.
As shown in Fig. 14, we test the effect of different context size on word similarity and word analogy tasks. It is clear that larger context size yields higher scores. However, the scores stop growing when the context size reaches around \(2^{16}=65{,}536\). We thus set context size to this number in the following experiments.
For context size 65,536, the word–context matrix M has \(|V| \cdot l= 18{,}498 \cdot 65{,}536 = 12\) billion elements. This indicates that we have to do 12 billion dot product operations in total in one epoch of training. In the case of W2V-Vanilla model, the number of dot product operations directly depends on the corpus size. There are 0.17 billion words in total in the vocabulary. For each word, we have to calculate 4 contextual words and 5 negative samples. The total number of operations is \(0.17 \times 4 = 0.68\) billion in W2V-Vanilla model, which is around 17.6 times less than W2V-CL model.
If we ignore the training speed boost with large batch size, this observation suggests that compared to W2V-Vanilla model, our W2V-CL model theoretically has larger number of operations. Nonetheless, due to the large batch size used in W2V-CL model, it is still faster than W2V-Vanilla model as shown in Sect. 5.6. Moreover, as shown in Eq. 11, W2V-CL model does not depend on the corpus size. The larger the corpus size, the more efficient W2V-CL model is.
5.5 The Quality of Learned Word Embeddings
In this section, we evaluate the quality of learned word embeddings. As shown in Fig. 15, W2V-Vanilla and W2V-CL models perform comparably on word similarity, word analogy, concept categorization and text classification tasks. More precisely, W2V-CL model performs better than W2V-Vanilla model on 12 out of 20 datasets. It is safe to conclude that our W2V-CL model is not worse than W2V-Vanilla model in terms of the quality.
The results may first look counter-intuitive since these two models have different training strategies and objective functions. However, all these models are actually based on the distributional hypothesis [19]. No matter how they are trained, the goal is still to make “words that occur in similar contexts to have similar embeddings”. As also shown in previous works [31, 32], when the hyper-parameters are set to the same values, it is hard to find a consistent advantage of one model over another.
5.6 Analysing the Loss of Individual Words
In this section, we analyse the loss of high-frequency words and low-frequency words. In every iteration, we save the losses for each individual words and draw the loss curve in Figs. 16 and 17. The total training time is similar in all the subfigures. Note that the W2V-Vanilla model uses the batch size of 1024, and W2V-CL model uses the batch size of 65,536. On a single GPU, W2V-Vanilla model takes 1769 s to train for 9000 iterations. W2V-CL model takes 1867 seconds to train for 1200 iterations.
For both models, the losses of high-frequency words show the same trends (Fig. 16). They all gradually decrease as the number of iterations increases. W2V-Vanilla model even achieves lower loss. This is mainly due to the massive updating times for high-frequency words.
However, for the low-frequency words (Fig. 17), the losses actually increase or stay high in W2V-Vanilla model. The updating times of low-frequency words in W2V-Vanilla model are low. As we discussed in Sect. 2.3, it is hard to learn meaningful word embeddings with few updates.
It is obvious that for low-frequency words in Fig. 17, W2V-Vanilla model has much higher variance compared to the W2V-CL model. Intuitively, embeddings with lower variances perform more consistently in downstream tasks.
Note that for W2V-CL model, in the last iteration, the average loss of high-frequency words is much higher than the low-frequency words (1.5 vs. 0.7). The high-frequency words are related to much more contextual words than low-frequency words and are harder to optimize.
5.7 Scaling with Multiple Compute Nodes
Figure 18 shows the scaling results with multiple computing nodes equipped with GPUs. The GPU is Tesla K80, the same as previous sections. We use 2 compute nodes connected inside a 1 GMbs bandwidth network, and each compute node has 8 GPUs. For scaling results with no more than 8 GPUs, only 1 compute node is used. For results with more than 8 GPUs, we use 2 compute nodes simultaneously.
The results on single GPU are comparable to the profiling results in Sect. 2.4. In Fig. 3, when all operations are performed and batch size set to 65, 536, the number of word per second is around 122,780. In our experiments, the batch size is equal to the vocabulary size: 71,290. When only one GPU is used, the number of word per second is around 99,237, which is slightly lower due to the process of reading of word–context matrix M.
Our W2V-CL model scales almost linearly with the number of GPUs. Using 2 GPUs on a single compute nodes, our model achieves around 193,193 words per second, which is 1.9 times faster than single GPU implementation. When more GPUs are used, the time needed to distribute and gathering data is increasing. Using 8 GPUs on a single compute nodes, our model achieves around 11 million words per second, which is 5.5 times faster than single GPU implementation. It also achieves 7.5 times speedup using 2 compute nodes with total 16 GPUs.
Note that W2V-Vanilla model actually gets lower speed when using multiple GPUs. This is mainly due to the small batch size. As shown in Fig. 13, since the accuracy drops when batch size becomes large, we fix the size to 1024. When multiple GPUs are used, the batch size distributed into each GPUs is only proportion to 1024, and the time is mostly wasted on distributing and gathering dating after each computation.
For multiple GPUs, the learned word embeddings is theoretically the same as single GPU results. However, empirically, in our pilot experiments, due to the randomness in Chainer framework, the performances on word similarity and word analogy tasks are slightly different in Figs. 15, 20.
5.8 Training CNN-Based Subword-Level Word Embeddings
Since our W2V-CL model is implemented using Chainer framework, it is easy to modify and extend it to different variations, especially deep neural networks. We explore this flexibility by implementing the CNN-based subword-level word embeddings model [33] on top of W2V-CL model.
As shown in Fig. 19, the only difference between training word-level word embeddings and CNN-based subword-level word embeddings is the way of obtaining word vectors. For word-level word embeddings, each word is directly assigned with a vector. As for CNN-based subword-level word embeddings, word is not treated as the smallest unit, and the character information is taken into consideration. The vector of a word is composed from its character or character n-grams vectors. More precisely, the objective function of CNN-based subword-level word embeddings model is defined as:
where \(\mathbf {CNN(w_i)}\) is the composed vector through a convolutional neural network.
\(\mathbf {CNN( \cdot )}\) first extracts the characters in the word and assigns vectors for those characters. All those character vectors are then fed into a convolutional neural network (CNN). Finally, the convolution results are flattened, and fed into a fully connected layer to form the word vector. This vector is trained using the same strategy as traditional word-level models.
As a natural language processing researcher, implementing a CNN module from scratch is not easy, especially for both inference and training. However, since our W2V-CL model is implemented using Chainer deep learning framework, we can directly call Chainer’s CNN functions with a few lines of code. The simplicity and flexibility are the main reasons that we choose to use this deep learning framework instead of CUDA. To the best of knowledge, our work is the first to accelerate subword-level word embeddings.
Figure 20 shows W2V-Vanilla and W2V-CL models’ performance on a range of NLP tasks. Similar to the findings of word-level models in Fig. 15, W2V-Vanilla model and W2V-CL model perform comparable. It is hard to conclude one model better than another in terms of the quality.
However, the training speed of these models is quite different. Figure 21 shows the scaling results of CNN-based subword-level word embedding models for both vanilla setting and ours. The trends of CNN-based subword-level word embeddings are similar to that on word-level word embeddings. On single GPU, our W2V-CL model is around 2 times faster than W2V-Vanilla model. Compared to single GPU performances, we are able to speed up the training around 9 times with 16 GPUs. These scaling results are actually better than word-level word embedding models, where only 7.5 times speedup with 16 GPUs. This is due to the large number of matrix multiplication operation used in CNNs, which is more suitable for the GPU than dot product operation.
Compared to the training speed of word-level models in Fig. 18, the speed of CNN-based subword-level W2V-CL model is around 2 times slower. This is reasonable since CNN module in the subword-level model requires additional computation.
6 Conclusion
We propose W2V-CL model, an algorithm for training word embeddings with controllable number of iterations and large batch size. W2V-CL model has the following advantages compared to the reference approach:
-
W2V-CL model is able to train with larger batch size without accuracy loss. The larger batch size in turn enables better GPU utilization, and as a result, the model trains roughly 2 times faster the baseline model.
-
By extracting word–context matrix M at the pre-processing step, W2V-CL model eliminates the need to train on an entire large corpus, which makes the training process more controllable.
-
W2V-CL model samples low-frequency and high-frequency (in terms of occurrences in the corpus) words uniformly to get enough coverage for rare tokens. This results in smaller variance for low-frequency words.
Due to above advantages, the proposed model is able to efficiently scale to multiple compute nodes and GPUs. Compared to the single GPU results, our implementation showed 5.5 times speedup using 8 GPUs and 7.5 times speedup using 2 compute nodes with 16 GPUs in total.
W2V-CL model is also flexible, especially in comparison with the low-level CUDA implementations. We demonstrate the advantage by implementing a CNN-based subword-level word embedding model on top of W2V-CL with little effort. Our subword-level implementation is around 2 times faster than the reference implementation and also scales well on multiple GPUs and computes nodes.
Availability of Data and Materials
The datasets used and/or analysed during the current study are available from the corresponding author on reasonable request.
Notes
There are also other methods to reduce the computation complexity, such as Hierarchical Softmax [38].
In Word2Vec algorithm, most of the target words have \(2 \cdot win\) contextual words. However, if a word appears in the head of a corpus, it may have contextual words less than \(2 \cdot win\). For example, in Table 1, word “i” only has 2 contextual words instead of \(2*2=4\).
We use scikit-learn’s clustering API to implement this evaluation.
We modify the official text classification examples in Chainer framework to support pre-trained word embeddings as inputs.
References
Agirre E, Alfonseca E, Hall K, Kravalova J, Paşca M, Soroa A (2009) A study on similarity and relatedness using distributional and wordnet-based approaches. In: NAACL. Association for Computational Linguistics, pp 19–27
Akiba T, Fukuda K, Suzuki S (2017) ChainerMN: scalable distributed deep learning framework. In: Proceedings of workshop on ML systems in the thirty-first annual conference on neural information processing systems (NIPS)
Almuhareb A (2006) Attributes in lexical acquisition. Doctoral dissertation, University of Essex
Bae S, Yi Y (2016) Acceleration of word2vec using GPUs. In: International conference on neural information processing. Springer, pp 269–279
Baroni M, Dinu G, Kruszewski G (2014) Don’t count, predict! a systematic comparison of context-counting vs. context-predicting semantic vectors. In: Proceedings of the 52nd annual meeting of the association for computational linguistics (Volume 1: Long Papers), vol 1, pp 238–247
Baroni M, Evert S, Lenci A (2008) Esslli 2008 workshop on distributional lexical semantics. Association for Logic, Language and Information, Hamburg, Germany
Baroni M, Murphy B, Barbu E, Poesio M (2010) Strudel: a corpus-based semantic model based on properties and types. Cognit Sci 34(2):222–254
Bengio Y, Ducharme R, Vincent P, Janvin C (2003) A neural probabilistic language model. J Mach Learn Res 3:1137–1155
Bojanowski P, Grave E, Joulin A, Mikolov T (2017) Enriching word vectors with subword information. Trans Assoc Comput Linguist 5:135–146
Bruni E, Boleda G, Baroni M, Tran NK (2012) Distributional semantics in technicolor. In: ACL. Association for Computational Linguistics, pp 136–145
Collobert R, Weston J (2008) A unified architecture for natural language processing: deep neural networks with multitask learning. In: ICML. ACM, pp 160–167
Collobert R, Weston J, Bottou L, Karlen M, Kavukcuoglu K, Kuksa P (2011) Natural language processing (almost) from scratch. J Mach Learn Res 12:2493–2537
Deng L, Wiebe J (2015) Mpqa 3.0: an entity/event-level sentiment corpus. In: Proceedings of the 2015 conference of the North American chapter of the association for computational linguistics: human language technologies, pp 1323–1328
Drozd A, Gladkova A, Matsuoka S (2016) Word embeddings, analogies, and machine learning: beyond king - man + woman = queen. In: COLING
Egghe L (2007) Untangling Herdan’s law and Heaps’ law: mathematical and informetric arguments. J Am Soc Inf Sci Technol 58(5):702–709
Finkelstein L, Gabrilovich E, Matias Y, Rivlin E, Solan Z, Wolfman G, Ruppin E (2001) Placing search in context: the concept revisited. In: WWW. ACM, pp 406–414
Gladkova A, Drozd A, Matsuoka S (2016) Analogy-based detection of morphological and semantic relations with word embeddings: what works and what doesn’t. In: NAACL-HLT, pp 8–15
Gupta S, Khare V (2017) Blazingtext: scaling and accelerating word2vec using multiple GPUs. In: Proceedings of the machine learning on HPC environments. ACM, p 6
Harris Z (1954) Distributional structure. Word 10(23):146–162
Hill F, Reichart R, Korhonen A (2016) Simlex-999: evaluating semantic models with (genuine) similarity estimation. Comput Linguist 41:665–695
Hochreiter S, Schmidhuber J (1997) Flat minima. Neural Comput 9(1):1–42
Hoffer E, Hubara I, Soudry D (2017) Train longer, generalize better: closing the generalization gap in large batch training of neural networks. In: Advances in neural information processing systems, pp 1731–1741
Jastrzebski S, Leśniak D, Czarnecki WM (2017) How to evaluate word embeddings? on importance of data efficiency and simple supervised tasks. arXiv preprint arXiv:1702.02170
Ji S, Satish N, Li S, Dubey P (2016) Parallelizing word2vec in multi-core and many-core architectures. arXiv preprint arXiv:1611.06172
Keskar NS, Mudigere D, Nocedal J, Smelyanskiy M, Tang PTP (2016) On large-batch training for deep learning: generalization gap and sharp minima. arXiv preprint arXiv:1609.04836
Kiefer J, Wolfowitz J (1952) Stochastic estimation of the maximum of a regression function. Ann Math Stat 23:462–466
Kim Y (2014) Convolutional neural networks for sentence classification. In: EMNLP, pp 1746–1751
Kingma DP, Ba J (2014) Adam: a method for stochastic optimization. arXiv preprint arXiv:1412.6980
Krizhevsky A, Sutskever I, Hinton GE (2012) Imagenet classification with deep convolutional neural networks. In: Advances in neural information processing systems, pp 1097–1105
Levy O, Goldberg Y (2014) Dependency-based word embeddings. In: ACL, pp 302–308
Levy O, Goldberg Y (2014) Neural word embedding as implicit matrix factorization. In: NIPS, pp 2177–2185
Levy O, Goldberg Y, Dagan I (2015) Improving distributional similarity with lessons learned from word embeddings. TACL 3:211–225
Li B, Drozd A, Liu T, Du X (2018) Subword-level composition functions for learning word embeddings. In: Proceedings of the second workshop on subword/character level models, pp 38–48
Li B, Liu T, Zhao Z, Tang B, Drozd A, Rogers A, Du X (2017) Investigating different syntactic context types and context representations for learning word embeddings. In: EMNLP, pp 2411–2421
Luong T, Socher R, Manning C (2013) Better word representations with recursive neural networks for morphology. In: Proceedings of the seventeenth conference on computational natural language learning, pp 104–113
Melamud O, Goldberger J, Dagan I (2016) context2vec: learning generic context embedding with bidirectional lstm. In: Proceedings of the 20th SIGNLL conference on computational natural language learning, pp 51–61
Meng X, Bradley J, Yavuz B, Sparks E, Venkataraman S, Liu D, Freeman J, Tsai D, Amde M, Owen S et al (2016) Mllib: machine learning in apache spark. J Mach Learn Res 17(1):1235–1241
Mikolov T, Chen K, Corrado GS, Dean J (2013) Efficient estimation of word representations in vector space. CoRR arXiv:abs/1301.3781
Mikolov T, Sutskever I, Chen K, Corrado GS, Dean J (2013) Distributed representations of words and phrases and their compositionality. In: NIPS, pp 3111–3119
Mikolov T, Wt Yih, Zweig G (2013) Linguistic regularities in continuous space word representations. In: HLT-NAACL, vol 13, pp 746–751
Nakagawa T, Inui K, Kurohashi S (2010) Dependency tree-based sentiment classification using crfs with hidden variables. In: NAACL. Association for Computational Linguistics, pp 786–794
O’Sullivan JA (1998) Alternating minimization algorithms: from Blahut–Arimoto to expectation-maximization. In: Vardy A (ed) Codes, curves, and signals, vol 485. Springer, Boston, pp 173–192
Pang B, Lee L (2004) A sentimental education: sentiment analysis using subjectivity summarization based on minimum cuts. In: ACL. Association for Computational Linguistics, pp 271–278
Pang B, Lee L (2005) Seeing stars: exploiting class relationships for sentiment categorization with respect to rating scales. In: ACL. Association for Computational Linguistics, pp 115–124
Pennington J, Socher R, Manning CD (2014) Glove: global vectors for word representation. In: EMNLP, pp 1532–1543
Radinsky K, Agichtein E, Gabrilovich E, Markovitch S (2011) A word at a time: computing word relatedness using temporal semantic analysis. In: WWW. ACM, pp 337–346
Rajaraman A, Ullman JD (2011) Mining of massive datasets. Cambridge University Press, Cambridge
Salle A, Idiart M, Villavicencio A (2016) Matrix factorization using window sampling and negative sampling for improved word representations. In: The 54th annual meeting of the association for computational linguistics, p 419
Socher R, Perelygin A, Wu JY, Chuang J, Manning CD, Ng AY, Potts C (2013) Recursive deep models for semantic compositionality over a sentiment treebank. In: EMNLP, vol 1631. Citeseer, p 1642
Team D (2016) Deeplearning4j: Open-source distributed deep learning for the JVM. Apache Software Foundation License 2
Tokui S, Oono K, Hido S, Clayton J (2015) Chainer: a next-generation open source framework for deep learning. In: Proceedings of workshop on machine learning systems (LearningSys) in the twenty-ninth annual conference on neural information processing systems (NIPS), vol 5
Vulic I, Korhonen A (2016) Is “universal syntax” universally useful for learning distributed word representations? In: ACL, p 518
Yatbaz MA, Sert E, Yuret D (2012) Learning syntactic categories using paradigmatic representations of word context. In: EMNLP-CoNLL, pp 940–951
Ying C, Kumar S, Chen D, Wang T, Cheng Y (2018) Image classification at supercomputer scale. arXiv preprint arXiv:1811.06992
You Y, Gitman I, Ginsburg B (2017) Scaling sgd batch size to 32k for imagenet training. arXiv preprint arXiv:1708.03888
Zesch T, Müller C, Gurevych I (2008) Using wiktionary for computing semantic relatedness. In: AAAI, vol 8, pp 861–866
Acknowledgements
This work was partially supported by National Natural Science Foundation of China Grant Nos. U1711262 and 61472428. This work was also partially supported by Japan Society for the Promotion of Science Grant Nos. JP17K12739 and JPMJCR1687.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Li, B., Drozd, A., Guo, Y. et al. Scaling Word2Vec on Big Corpus. Data Sci. Eng. 4, 157–175 (2019). https://doi.org/10.1007/s41019-019-0096-6
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s41019-019-0096-6