1 Introduction

Timber offers many advantages such as lightness, aesthetic, and a high strength-to-weight ratio. In addition, it fulfils the evolving requirements of decarbonising the environment, and reducing energy consumption, which justifies its use in green buildings. This renewed interest has sparked a need for a high level of knowledge of its structural behaviour [1,2,3,4,5,6,7]. However, its mechanical behaviour is not well known at elevated temperatures. This is particularly true for engineered massive timber, which comes in the forms of LVL (Laminated Veneer Lumber), Glulam timber, and more recently CLT (Cross Laminated Timber). It is more difficult to determine its strength under these conditions [8, 9]. In most cases, the failure of these structures is related to the combustion of the wood material [10,11,12,13,14,15,16,17]. Indeed, the combustibility of timber distinguishes it from other building materials and poses a serious threat to the fire safety of timber structures [18]. It is not surprising therefore that many regulatory authorities are concerned about the fire resistance of timber structures [19]. Yet, modern codes of practice are not biased against any material. Their aim is to ensure that structures remain stable for a given time of exposure to fire to facilitate the intervention of the fire brigade to minimize human and property losses and to prevent the rapid spread of fire to neighbouring buildings.

Even though wood is a combustible material, timber structures are remarkably resistant to fire because timber chars. The charred layer acts as an insulator and protects the residual cross section from high temperatures. Moreover, it stops the supply of oxygen. However, from a mechanical point of view, the charred layer has no strength. A major hurdle to the widespread use of timber in construction, therefore, is its combustibility, which raises questions about its fire resistance.

Timber is the only building material for which data relating to its physico-thermal properties are the least available. Moreover, the knowledge available in this field of research is for the most part empirical. Most of the data were obtained in laboratory furnaces on small samples [19, 20]. Data from a real fire test on a building are rarely available in the literature [21] because of the inherent difficulties in carrying out such tests. Real scale fire tests are not only expensive to carry out, but they require the presence of firefighters and the installation of protective measures to prevent the spread of fire to the surrounding environment. This lack of data makes the development of advanced methods of analysis, necessary for performance-based design, difficult [18, 22,23,24].

Accordingly, the existing approaches for design are prescriptive. Eurocode 5 [1] recommends the fire resistance of a section to be determined by deducting from the initial section the thickness of the charred layer on each facet exposed to fire. The thermal degradation of the mechanical properties is accounted for by increasing the thickness of the layer.

The development of advanced models requires therefore a research effort that not only exploits the results of all the available fire tests, be it large or small, but also uses numerical simulation requiring a good control of the input parameters. A notable effort in this area was made by Quiquero et al. [23]. To increase the opportunities for the use of new products made from post-tensioned timber in construction, they used the finite element code Abaqus [25] to assess the fire behaviour of post-tensioned timber beams under normal (ambient temperature) and extreme (fire) conditions. The results of the simulations were validated with experimental results. Following the same approach, a numerical procedure to predict the thermo-mechanical behaviour of laminated timber structures exposed to elevated temperatures is presented herein. However, rather than using the material models available in Abaqus, the thermal and numerical constitutive laws are developed separately and implemented as user subroutines in the Abaqus code via the routines Umatht and Umat respectively. The chosen constitutive laws are formulated from simple engineering approaches [1,2,3,4]. They have the advantage of being easy to integrate into commercial codes. The proposed methodology also applies the EC5 [1] regulatory approach and consists of a heat transfer analysis sequentially coupled with a structural response. The stress analysis is modelled with an elasto-plastic model with nonlinear isotropic hardening [26,27,28,29,30].

2 Theoretical Aspects of the Thermomechanical Model

2.1 Heat Transfer

The differential equation of heat conduction in a medium is described by Fourier’s law

$${\rho C}_{\text{p}} \frac{{\partial {\text{T}}}}{{\partial {\text{t}}}} = \frac{\partial }{{\partial {\text{x}}}}\left[ {{\uplambda }_x \frac{{\partial {\text{T}}}}{{\partial {\text{x}}}}} \right] + \frac{\partial }{{\partial {\text{y}}}}\left[ {{\uplambda }_y \frac{{\partial {\text{T}}}}{{\partial {\text{y}}}}} \right] + \frac{\partial }{\partial z}\left[ {{\uplambda }_z \frac{{\partial {\text{T}}}}{\partial z}} \right] + {\text{Q}}_{\text{r}}^{\prime\prime}$$
(1)

where T (K) is the temperature; \({\lambda }_{x}\), \({\lambda }_{y}\),\({\lambda }_{z}\) [W/m.K] are the thermal conductivities in the directions x, y and z; ρ [kg/m3] is the density; Cp [J/(kg K)] is the specific heat; t (s) the time; and \({Q}_{r}^{{\prime}{\prime}}\) [W/m3] a source of heat generation.

In EC5 [1], the term \({Q}_{r}^{{\prime}{\prime}}\), referring to the heat generated during the complex reactions accompanying the combustion of timber, is not taken explicitly in Eq. (1) but rather implicitly through the variation with temperature of the thermo-physical properties \(\lambda\), ρ, and Cp. In theory the thermal conductivity should stabilise from 300 °C onwards, which corresponds to the formation of the charred layer that acts as an insulator, then should continue to decrease slowly but gradually. Indeed, the variation in the relative density ρ as a function of temperature indicates that solid wood turns into charcoal at a rate of about 25% of the initial mass between 400 and 800 °C. Beyond this limit, the charcoal is transformed into volatiles (combustion stage). As the mass decreases (which makes sense because wood burns, EC5 [1] suggests correcting the standard heat equation by considering the decrease in the mass ρ. Furthermore, EC5 [1] considers the evolution of \(\rho {c}_{p}\) to deduce the evolution of \(\lambda\) as a function of the temperature. For this reason, the values of the thermal conductivity \(\lambda\) and the specific heat \({c}_{p}\) continue to increase from 400 °C, which is not fully justified as reported in the literature [9]. Nonetheless, this approach has been adopted by many authors [27, 28]. Figure 1 shows the evolution with temperature of these properties.

Fig. 1
figure 1

Thermo-physical properties of softwood as a function of temperature EC5 [1]

Full size image

The thermal conductivity λ of a timber sample depends on its orientation with respect to the directions of orthotropy shown in Fig. 2. Experimental data show that the conductivities in the radial (R) and transverse (T) directions are very close. On the other hand, the value of the conductivity in the longitudinal direction, coincident with the direction of the fibers, is much higher (1.5–2.8 times greater) than in the transverse direction [29]. At an ambient temperature of about 20 °C, timber has a conductivity ranging from 0.12 to 0.25 W/(m K).

Fig. 2
figure 2

Orthotropic directions in timber

Full size image

The specific heat is very sensitive to the vaporisation of the free water. It records a jump from 1700 J/(kg K) at 96 °C to 13,695 J/(kg K) at 100 °C in the drying phase as a result of the latent heat of water. The value of Cp then drops to 2173 J/(kg K) at 120 °C when the water is supposed to have completely evaporated. Beyond this value, Cp continues to drop slowly up to a value of 719 J/(kg K) at a temperature of 300 °C, which corresponds to the formation of the charred layer. The presence of the charred layer slowly increases the value of Cp.

The relative density ρ/ρ0 is equal to unity between 100 and 200 °C. The formation of the charred layer at 300 °C causes the relative density to drop by about 50%. It continues to drop with increasing temperatures. Timber has lost 73% of its initial mass by the time its temperature reaches 600 °C.

2.2 Mechanical response

The state variables used in the mechanical model are summarised in Table 1.

Table 1 State variables
Full size table

In the phenomenological approach, the hypothesis of small deformations allows the decomposition of the strain tensor into two additive components: elastic, \(\underline {\upvarepsilon }^{\text{e}}\), and plastic, \(\underline {\upvarepsilon }^{\text{p}}\); that is:

$$\underline {\upvarepsilon } = \underline {\upvarepsilon }^{\text{e}} + \underline {\upvarepsilon }^{\text{p}}$$
(2)

For an orthotropic material, the elastic strain is reversible and is related to the Cauchy stress through Hooke’s law:

$$\underline {\upsigma } = \underline{\underline \Lambda } {:}\underline {\upvarepsilon }^{\text{e}}$$
(3)

The fourth order tensor \(\underline{\underline \Lambda }\) is given in a matrix form as

$$\underline{\underline{\Lambda } } = \left[ {\begin{array}{*{20}c} {C_{11} } & {C_{12} } & {C_{13} } & 0 & 0 & 0 \\ {C_{12} } & {C_{22} } & {C_{23} } & 0 & 0 & 0 \\ {C_{13} } & {C_{23} } & {C_{33} } & 0 & 0 & 0 \\ 0 & 0 & 0 & {C_{44} } & 0 & 0 \\ 0 & 0 & 0 & 0 & {C_{55} } & 0 \\ 0 & 0 & 0 & 0 & 0 & {C_{66} } \\ \end{array} } \right]$$
(4)

with

$$C_{11} = \frac{{1 - \nu_{23} \nu_{32} }}{{\Delta {\text{E}}_{2} {\text{E}}_{3} }};\quad C_{22} = \frac{{1 - \nu_{13} \nu_{31} }}{{\Delta {\text{E}}_1 {\text{E}}_{3} }};\quad C_{33} = \frac{{1 - \nu_{12} \nu_{21} }}{{\Delta {\text{E}}_1 {\text{E}}_2 }}$$
$$C_{12} = \frac{{\nu_{21} + \nu_{31} \nu_{23} }}{{\Delta {\text{E}}_{2} {\text{E}}_{3} }};\quad C_{13} = \frac{{\nu_{31} + \nu_{21} \nu_{32} }}{{\Delta {\text{E}}_2 {\text{E}}_{3} }};\quad C_{23} = \frac{{\nu_{32} + \nu_{12} \nu_{31} }}{{\Delta {\text{E}}_1 {\text{E}}_{3} }}$$
(5)
$${\text{C}}_{44} {\text{ = 2G}}_{{12}} {;}\quad {\text{C}}_{55} {\text{ = 2G}}_{{23}} {;}\quad {\text{C}}_{66} {\text{ = 2G}}_{{13}}$$
$$\Delta = \frac{{1 - \nu_{12} \nu_{21} - \nu_{23} \nu_{32} - \nu_{13} \nu_{31} - 2\nu_{21} \nu_{32} \nu_{13} }}{{{\text{E}}_1 {\text{E}}_{2} {\text{E}}_{3} }}$$

where Ei is the elastic modulus in the direction i; νij et Gij are respectively the Poisson’s ration and shear modulus in the plan (i–j). The orthotropic directions are shown in Fig. 2.

Under isothermal conditions, the dissipative plastic potential and the plastic criterion are respectively written as:

$${\text{F}}_{\text{p}} = {\text{f}}_{\text{p}} + \frac{{1}}{{2}}\frac{{\text{b}}}{{\text{Q}}}{\text{R}}^{2} ;\quad {\text{R}} = {\text{Qr}}$$
(6)
$${\text{f}}_{\text{p}} =\sqrt {{\underline {\upsigma } {:}\underline{\underline {\text{H}}} {:}\underline {\upsigma } }} -{\text{R}}- \upsigma_{\text{e}}$$
(7)

with:

$$\underline{\underline{H} } = \left[ {\begin{array}{*{20}c} {G + H} & { - H} & { - G} & 0 & 0 & 0 \\ { - H} & {H + F} & { - F} & 0 & 0 & 0 \\ { - G} & { - F} & {F + G} & 0 & 0 & 0 \\ {\,} & {\,} & {\,} & {2N} & 0 & 0 \\ {\,} & {\,} & {\,} & {\,} & {2M} & 0 \\ {\,} & {\,} & {\,} & {\,} & {\,} & {2L} \\ \end{array} } \right]$$
(8)

\(\underline{\underline {\text{H}}}\) is the Hill fourth order tensor defined in [31]. It is a function of six constants (F, G, H, L, M and N); \({\upsigma }_{\text{e}}\) is the elasticity limit; Q and b are the isotropic hardening parameters.

Using the normality rule, the complementary relations are derived as follows [26]:

$$\underline {{\dot{\varepsilon }}}^{\text{p}} = {\dot{\lambda }}\frac{{\partial {\text{F}}_{\text{p}} }}{{\partial \underline {\upsigma } }} = {\dot{\lambda }}\frac{{\partial {\text{f}}_{\text{p}} }}{{\partial \underline {\upsigma } }} = {\dot{\lambda }}\frac{{\underline{\underline {\text{H}}} {:}\underline {\upsigma } }}{{\left\| {\underline {\upsigma } } \right\|}} = {\dot{\lambda }}\underline {\text{n}}$$
(9)
$${\dot{\text{r}}} = - {\dot{\lambda }}\frac{{\partial {\text{F}}_{\text{p}} }}{{\partial {\text{R}}}} = {\dot{\lambda }}\left[ {{1} - {\text{br}}} \right]$$
(10)

where \(\underline {\text{n}}\) is the normal to the loading surface; \({\dot{\lambda }} > {0}\) is the plastic multiplier determined using the consistency condition:

$${\text{f}}_{\text{p}}= \dot {\text{ {f}}}_{\text{p}} = 0$$
(11)

The Hill constants defined in Eq. (8) for a structural timber can be obtained with the following relations [27, 32]:

$$F = \sigma_e^2 \left( {\frac{1}{{f_{c,90} .f_{t,90} }} - \frac{1}{{2.f_{c,0} .f_{t,0} }}} \right);\quad G = H = \frac{\sigma_e^2 }{{2f_{c,0} .f_{t,0} }}$$
(12)
$$N = M = L = \frac{\sigma_e^2 }{{3f_{v,12}^2 }}$$
(13)

where: fc,i and ft,i are respectively the compressive and tension strengths in the direction (i); and fv,ij is the shear strength in the plan (i–j).

2.3 Thermomechanical Coupling Between the Material Properties

When wood is exposed to fire, it undergoes chars. The charred layer experiences a complete loss of strength and stiffness, leading to a reduced section. The structural performance of the wood beneath this layer is essentially equivalent to wood at ambient temperatures. However, this reduction in section must be considered in structural modelling. To address this, EC5 [1] recommends considering the compressive strength, tensile strength, and modulus of elasticity (in tension and compression) at elevated temperatures parallel to the grain. These properties are functions of temperature-related variables, necessitating the use of reduction factors. Consequently, this results in the modification of material properties, as depicted in Figs. 3, 4 and 5.

Fig. 3
figure 3

Reduction of the elastic modulus in the longitudinal direction EL

Full size image
Fig. 4
figure 4

Reduction factor Kθ for the strength parallel to the grain

Full size image
Fig. 5
figure 5

Evolution of the elastic modulus with temperature

Full size image

The determination of the fire resistance of timber structures requires:

  1. 1.

    the local values of the elastic modulus, the mechanical strength in tension and compression for softwood to be multiplied by temperature-dependent reduction factors Kθ given in Figs. 3 and 4.

  2. 2.

    The same reduction in strength, illustrated in Fig. 4 for compression parallel to the grain, can be applied for compression perpendicular to the grain.

  3. 3.

    The same reduction in strength can be also applied for the case of shear where the two stress components are perpendicular to the grain.

In the present study, a trilinear approximation as shown in Fig. 5 for the reduction of the Young modulus for a softwood timber [1, 27]. The elastic modulus looses 60% of its initial value at the drying temperature of 100 °C, and becomes equal to zero at 300 °C, when charring starts to occur. In other words, the charring layer does not have any stiffness and/or strength.

The elastic modulus Ei is therefore expressed as:

$${\text{E}}_{\text{i}} ={\text{ E}}_{{\text{0i}}} \times{\text{ f}}_{{\text{th}}} {\text{(T)}}$$
(14)

with:

$$\left\{ \begin{array}{l} {\text{T}} < 20\;^{\circ}{\text{C}}\;\quad \quad \quad \quad {:}\;{\text{f}}_{{\text{th}}} {\text{(T) = 1}}{.} \hfill \\ 20\;^{\circ}{\text{C}} \le {\text{T}} < 100\;^{\circ}{\text{C}}\;\;\,{:}\;{\text{f}}_{{\text{th}}} {\text{(T)}} = - 7.5\times 10^{ - 3} {\text{T}} + {1.15} \hfill \\ 100\;^{\circ}{\text{C}} \le {\text{T}} \le 300\;^{\circ}{\text{C}}\;{:}\;{\text{f}}_{{\text{th}}} {\text{(T)}} = - 2 \times 10^{ - 3} {\text{T}} + {0.6} \hfill \\ \end{array} \right.$$
(15)

E0i being the initial value in the direction (i), measured at an ambient temperature of 20 °C.

The generalised thermoelastic law is written as:

$$\underline \sigma = \underline{\underline{\Lambda } } (T):\underline \varepsilon^e$$
(16)

with:

$${\text{E}}_1 = {\text{ E}}_{{01}} \times {\text{ f}}_{{\text{th}}} {\text{(T);}}\quad {\text{E}}_2 = {\text{ E}}_{{02}}\times {\text{ f}}_{{\text{th}}} {\text{(T);}}\quad {\text{E}}_3 ={\text{ E}}_{{03}} \times{\text{ f}}_{{\text{th}}} {\text{(T)}}$$
(17)

The reduction factor Kθ applied to the mechanical strengths is approximated with the curve corresponding to shear as shown in Fig. 5. It is written as:

$${\text{K}}_{\uptheta } {\text{ = f}}_{{\text{th}}} {\text{(T)}}$$
(18)

The sequential coupling between the thermal analysis and the mechanical response is achieved Eqs. (16) to (18).

3 Finite Element Modelling

3.1 Heat Transfer

Given a continuous virtual temperature field \({\updelta}{\text{T}}\) such that \({\updelta}{\text{T}} = 0\) on \(\partial \Omega_T\). The weak form of the heat transfer Eq. (1) can be obtained as:

$$\int_\Omega {\updelta{\text{T}}\, {\dot{\text{U}}}\,{\text{d}}\Omega} = - \int_\Omega {\updelta {\text{T}}\,\nabla {\text{q}}\,d\Omega } + \int_\Omega {\updelta {\text{T}}\,Q \, d\Omega }$$
(19)

with

$$\rho C_p \dot{T} = \dot{U}$$
(20)

where U is the thermal energy in the volume \(\Omega\).

When discretised with a finite element with shape functions N, Eq. (20) becomes

$$\left[ K \right]_e \left\{ {T_{n + 1} } \right\} = \left\{ {f_{n + 1}^{ext} } \right\}$$
(21)

with:

$$\left[ K \right]_e = \frac{1}{\Delta t}\int_\Omega {\rho C_p } (N \otimes N)d\Omega - \lambda \int_\Omega {(\nabla N \otimes \nabla N)} \, d\Omega$$
(22)
$$\left\{ {f_{n + 1}^{ext} } \right\} = \int_{\partial \Omega_q } {N\overline{q} \, dS} + \int_\Omega {NQ \, d\Omega } + \frac{1}{\Delta t}\int_\Omega {N\rho C_p T_n \, d\Omega }$$
(23)

where \(\left\{ {T_{n + 1} } \right\}\) represents the vector of nodal temperatures; \(\left\{ {f_{n + 1}^{ext} } \right\}\) the vector of thermal forces, and \(\left[ K \right]_e\) the thermal matrix.

Assembling the global thermal matrix and the global vector of external forces yields:

$$\left\{ {f_{n + 1}^{ext} } \right\} = \left[ K \right]_g \left\{ {T_{n + 1} } \right\};\quad \left[ K \right]_g = \sum {\left[ K \right]_e }$$
(24)

where \(\left[ K \right]_g\) is the global thermal matrix, \(\left\{ {T_{n + 1} } \right\}\) the global vector of the unknown temperatures; \(\left\{ {f_{n + 1}^{ext} } \right\}\) the vector of external thermal forces.

An implicit solution of the previous equation yields:

$$\left\{ {R_{n + 1} } \right\} = \left\{ {f_{n + 1}^{int} } \right\} - \left\{ {f_{n + 1}^{ext} } \right\};\quad \left\{ {f_{n + 1}^{int} } \right\} = \left[ K \right]_g \left\{ {T_{n + 1} } \right\}$$
(25)

where \(\left\{ {f_{n + 1}^{int} } \right\}\) is the vector of internal forces; and \(\left\{ {R_{n + 1} } \right\}\) the residual vector at the instant tn+1.

The Newton–Raphson iterative method is used to solve the system of equations within Abaqus/Standard. Equation (25) is linearised using the first term of the Taylor series; that is:

$$\left\{ {R_{n + 1} } \right\}^{(i + 1)} = \left\{ {R_{n + 1} } \right\}^{(i)} + \left[ {\frac{{\partial \left\{ {R_n } \right\}}}{{\partial \left\{ {T_n } \right\}}}} \right]^{(i)} \delta \left\{ {T_n } \right\} = 0$$
(26)

where \(\delta \left\{ {T_n } \right\} = \left\{ {T_n } \right\}^{(i + 1)} - \left\{ {T_n } \right\}^{(i)}\) is the increment in temperature between two successive iterations (i + 1) et (i). To ensure convergence of the iterative system, it is continued until the residual reaches a value close to zero within a certain tolerance [25, 26].

An external user subroutine UMATHT is used to define the thermal behaviour. It is called at every iteration. The subroutine requires the definition of the following variables:

  • The total thermal energy U;

  • The variation in U with respect to temperature \(\frac{\partial U}{{\partial T}}\);

  • The variation in U with respect to the temperature gradients \(\frac{\partial U}{{\partial \left( {\partial T/\partial x_i } \right)}}{\text{ (i = 1, 2, 3)}}.\)

  • The flux vector \(\overline{q} = - q \cdot \underline{n}\),

  • The variation in q with respect to temperature \(\frac{\partial q}{{\partial T}}\);

  • The variation in q with respect to the temperature gradients \(\frac{\partial q}{{\partial \left( {\partial T/\partial x_i } \right)}}{\text{ (i = 1, 2, 3)}}{.}\)

These quantities allow the definition of the Jacobian matrix in the newton Raphson algorithm.

3.2 Mechanical Model

The numerical integration of the constitutive Eqs. (9) and (10) at the instant tn+1 yields to:

$$\underline {\upvarepsilon }_{\text{n}} + 1^{\text{p}} = \underline {\upvarepsilon }_{\text{n}}^{\text{p}} + {{ \Delta \uplambda }}\underline {\text{n}}_{\text{n + 1}}$$
(27)
$${\text{r}}_{\text{n}} + 1 = {\text{ r}}_{\text{n}} {\text{e}}^{- {\text{b}}{{\Delta\uplambda}}} + \frac{{(1 -{\text{ e}}^{ - {\text{b}}\Delta\uplambda} )}}{{\text{b}}}$$
(28)

The plasticity criterion fn+1 must also satisfy the consistency condition:

$${\text{f}}_{{\text{n}} + {1}} = \sqrt {{\underline {\upsigma }_{{\text{n}} + {1}} {:}\underline{\underline {\text{H}}} {:}\underline {\upsigma }_{{\text{n}} + {1}} }} - {\text{R}}_{{\text{n}} + {1}} - {\upsigma }_{\text{e}} = {0}$$
(29)

The local integration algorithm consists of the following steps.

Knowing the total increment of strain \({\Delta }\underline {\upvarepsilon }\) at the instant tn+1, the quantities \(\underline {\upsigma }_{{\text{n}} + {1}}\) and \({\text{R}}_{{\text{n}} + {1}}\) are then obtained.

3.2.1 Elastic Prediction

At the instant tn+1 the response is considered elastic, and the resulting stress is obtained as:

$$\underline {\upsigma }_{{\text{n}} + {1}}^{*} = \underline {\upsigma }_{\text{n}} + \underline{\underline {\Lambda }} {{:\Delta }}\underline {\upvarepsilon }$$
(30)
$${\text{f}}_{{\text{n}} + {1}}^{*} = \sqrt {{\underline {\upsigma }_{{\text{n}} + {1}}^{*} {:}\underline{\underline {\text{H}}} {:}\underline {\upsigma }_{{\text{n}} + {1}}^{*} }} - {\text{R}}_{\text{n}} - {\upsigma }_{\text{e}}$$
(31)

If \({\text{f}}_{{\text{n}} + {1}}^{*} < {0}\), the solution is purely elastic, the stress and the residual at the instant tn+1 are obtained as:

$$\underline {\upsigma }_{{\text{n}} + {1}} = \underline {\upsigma }_{{\text{n}} + {1}}^{*} \;{\text{et}}\;{\text{R}}_{{\text{n}} + {1}} = {\text{R}}_{\text{n}} = 0$$
(32)

3.2.2 Plastic Solution

Otherwise, if \({\text{f}}_{{\text{n}} + {1}}^{*} \ge {0}\), the material has yielded and a plastic correction is necessary such that:

$${\text{f}}_{{\text{n}} + {1}} = \sqrt {{\underline {\upsigma }_{{\text{n}} + {1}} {:}\underline{\underline {\text{H}}} {:}\underline {\upsigma }_{{\text{n}} + {1}} }} - {\text{R}}_{{\text{n}} + {1}} - {\upsigma }_{\text{e}} = 0$$
(33)

It follows that:

$$\underline {\upsigma }_{{\text{n}} + {1}} = \underline {\upsigma }_{{\text{n}} + {1}}^{*} - \underline{\underline {\Lambda }} {{:\Delta }}\underline {\upvarepsilon }^{\text{p}}$$
(34)
$${\text{or}}\;{\Delta }\underline {\upvarepsilon }^{\text{p}} = \Delta{\uplambda}\underline {\text{n}}_{{\text{n}} + {1}}$$
(35)

Substituting in the previous equation yields:

$$\underline {\upsigma }_{{\text{n}} + {1}} = \underline {\upsigma }_{{\text{n}} + {1}}^{*} - \Delta {\uplambda }\underline{\underline {\Lambda }} \,{:}\,\underline {\text{n}}_{{\text{n}} + {1}}$$
(36)

The residual is obtained as

$${\text{R}}_{{\text{n}} + {1}} = {\text{Q r}}_{{\text{n}} + {1}} = {\text{Q}}\left( {{\text{r}}_{\text{n}} {\text{e}}^{ - {\text{b}}\Delta \uplambda} + \frac{{{(1} - {\text{e}}^{ - {\text{b}}\Delta \uplambda} {)}}}{{\text{b}}}} \right)$$
(37)

The unknowns are the plastic multiplier \(\Delta {\uplambda }\) and the normal to the loading surface \(\underline {\text{n}}_{{\text{n}} + {1}}\). The nonlinear system of equations reduces to:

$$\left\{ \begin{array}{l} {\text{f}}_{{\text{n}} + {1}} (\Delta{ \uplambda ,}\,\underline {\text{n}}_{{\text{n}} + {1}} ) = \sqrt {{\underline {\upsigma }_{{\text{n}} + {1}} {:}\underline{\underline {\text{H}}} {:}\underline {\upsigma }_{{\text{n}} + {1}} }} - {\text{R}}_{{\text{n}} + {1}} - {\upsigma }_{\text{e}} = {0} \hfill \\ \underline {\text{h}}_{{\text{n}} + {1}} (\Delta {\lambda ,}\,\underline {\text{n}}_{{\text{n}} + {1}} ) = \underline{\underline {\text{H}}} {:}\underline \sigma_{{\text{n}} + {1}} - \sqrt {{\underline {\upsigma }_{{\text{n}} + {1}} {:}\underline{\underline {\text{H}}} {:}\underline {\upsigma }_{{\text{n}} + {1}} }} \underline {\text{n}}_{{\text{n}} + {1}} = {0}\, \hfill \\ \end{array} \right.$$
(38)

The solution is obtained with the Newton Raphson method.

Once the iterative scheme has converged, the following quantities are updated:

$$\Delta{ \uplambda } = \Delta{ \uplambda } + {{\updelta \Delta \uplambda }}_{{\text{n}} + {1}} \;{\text{and}}\;\underline {\text{n}}_{{\text{n}} + {1}} = \underline {\text{n}}_{\text{n}} + {\updelta }\underline {\text{n}}_{{\text{n}} + {1}}$$
(39)
$$\underline {\upsigma }_{{\text{n}} + {1}} = \underline {\upsigma }_{{\text{n}} + {1}} + \Delta \underline {\upsigma } \;{\text{and}}\;{\text{R}}_{{\text{n}} + {1}} = {\text{R}}_{{\text{n}} + {1}} + \Delta {\text{R}}$$
(40)

3.3 Thermomechanical Coupling

In the present case, the stress does not affect the temperature field, hence a sequentially coupled heat transfer/stress analysis is conducted. The heat transfer analysis is performed first, and then followed by the stress/deformation analysis.

4 Results and Discussion

4.1 Tensile Test

A Laminated Veneer Lumber (LVL) sample having for dimensions 146 × 60 × 900 mm is subjected to a tensile test [20]. The four lateral surfaces are exposed to a standard fire ISO 834-1 [33]. The geometric details and the thermo-mechanical loadings are shown in Fig. 6.

Fig. 6
figure 6

LVL sample subject to a tensile test under a standard fire

Full size image

For reasons of symmetry in both geometry and loading, a quarter of the tensile test specimen is analysed. A mesh sensitivity analysis was carried with different meshes 2150, 3150, 4340, 5830, 6566, 8456 and 9450 elements (including the LVL beam, the plate, and the connecting rods). The finite element solution stabilises from 5830 elements. Hence, a mesh of 6566 elements (4930 for the LVL, 960 for the metallic plates, and 676 for the rods) is used in all the simulations.

The thermomechanical properties of the LVL are given in Table 2. The friction coefficients between the metallic parts and the timber is taken as µ = 0.3. Cinematic continuity is assumed between the laminates.

Table 2 Mechanical properties of the LVL
Full size table

The thermo-physical properties (λ, Cp and ρ) are defined in Fig. 1. The other parameters, such as the coefficient of thermal convection, the emissivity, the average initial density, and the moisture content, are respectively taken equal to hc = 25W/(m2.K), ε = 0.7, ρ0 = 570 kg/m3 and ω = 12%. On the unexposed side of the beam, the coefficient of thermal convection is taken equal to hc = 9W/(m2.K).

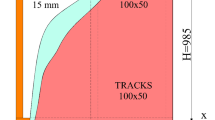
In this study, the focus is on the evolution of the temperature profiles in the useful distance of the specimen of 500 mm (Fig. 6). The temperature profiles at different times of exposure to fire are illustrated in Fig. 7. The charred layer forms around the useful length of the sample. Its thickness increases with time. The residual cross section of the element is rectangular at the beginning t < 5 min (Fig. 7a). Then it becomes non-rectangular because of the combination of bilateral loadings at the corners of the element.

Fig. 7
figure 7

Temperature profiles T [K]

Full size image

Figure 8 shows the evolution of the longitudinal stress σL in the sample at different times of exposure as well as the thickness of the charred layer with zero stress. The residual section has already started to reduce at a time of 5 min, Fig. 8a, and the longitudinal stress is about 14.1 MPa. At a time of t = 15 min, the residual section reduces further, and the longitudinal stress increases to 24.5 MPa. At a time of t = 24.7 min, the value of σL decreases to 17.2 MPa, which corresponds to the failure of the sample.

Fig. 8
figure 8

Evolution of the longitudinal stress σL

Full size image

Figure 9 shows a comparison between the measured [20] and the predicted temperatures for an applied force of 40 kN. The tests temperatures were recorded with two thermocouples at two different depths (T1 = 10 mm and T2 = 20 mm) from the exposed surface. The temperature remains stable, about 20 °C, for a very short time of less than three minutes. Beyond this time, the temperatures start to increase progressively. It can be seen that the predicted temperatures agree quite well with the experimental ones.

Fig. 9
figure 9

Predicted and measured temperatures [20]

Full size image

Figure 10 shows the predicted and measured displacements for two tests with different forces: 40 and 75 kN. It is interesting to note that the displacements follow the same pattern. The rate of increase is at first slow before becoming important. For the test with the 75 kN force, the change in the rate of the displacements takes place at about a time of 12 min. For the test with a force of 40 kN, this change takes place at about 17 min of exposure. It is also interesting to note that the simulated results follow the same pattern, and they agree quite well with the experimental ones.

Fig. 10
figure 10

Predicted and measured longitudinal displacements

Full size image

4.2 Bending Test

A beam made of CLT (Cross Laminated timber) and tested by Fragiacomo et al. [20] is simulated with the developed thermos-mechanical model. The geometrical details, the loading and the boundary conditions are shown in Fig. 11. The fire test was carried out according to [33]. The mechanical properties of the timber are given in Table 3. The average initial density, ρ0, the moisture content, ω, the coefficient of convection, hc, and the emissivity, ε, are respectively equal to 450 kg/m3, 12%, 25W/(m2 K) and 0.8. The beam is meshed with 8400 C3D8T solid elements.

Fig. 11
figure 11

CLT beam in flexure in a fire environment [19]

Full size image
Table 3 Mechanical properties of the CLT
Full size table

The temperature distribution across the cross section at different times of exposure is shown on Fig. 12. The formation of the charred layer starts to at temperatures above 300 °C. The temperature profile chows clearly that the charred layer is uniform across the section. The residual cross section reduces with time of exposure. The beam fails in a catastrophic manner when the thickness of the residual section is not sufficient to resist the applied moment. This takes place at a time of 102 min.

Fig. 12
figure 12

Temperature profiles T [K] across the cross section at different times of exposure

Full size image

Figure 13 shows the evolution of the longitudinal stress σL as a function of time of exposure. As expected, the stress contours show the top fibres in compression and the bottom fibres in tension. With the formation of the charred layer, which does not have any load bearing capacity, the neutral axis moves upward.

Fig. 13
figure 13

Contours of the longitudinal stress σL as a function of time of exposure

Full size image

Figure 14 shows the predicted temperatures at the positions of the thermocouples. They are in good agreement with the measured ones for the whole duration of the test. However, at higher temperatures, there is a discrepancy as shown in Fig. 14b. It is believed that this is due to the pyrolysis phenomenon. Indeed, the engineer's models proposed in EC5 do not account for the phenomena of pyrolysis and combustion. In our opinion, only kinetic models can consider the kinetics of thermal degradation of the wood material during the pyrolysis and combustion phases. However, that is beyond the scope of the present study.

Fig. 14
figure 14

Predicted and measured temperatures at different times of exposure

Full size image

Figure 15 shows the evolution with time of exposure of the deflection at mid-span. The test was stopped after 102 min. The predicted deflection agrees quite well with the measured one. Three stages can be noticed. At ambient temperatures, the response is purely mechanical. Then, the deflection starts to increase progressively after an exposure of 7 min. At this stage the beams have enough load carrying ability to resist the applied moment. After 75 min of exposure, the deflection increases rapidly, which heralds the failure of the beam.

Fig. 15
figure 15

Predicted and measured mid-span deflection

Full size image

5 Conclusion

The main objective of this work is to contribute to the development of analytical tools to understand and predict the fire behavior of laminated timber structures. A thermo-mechanical model consisting of heat transfer analysis sequentially coupled with a structural response was developed. The stress analysis is modelled with an elasto-plastic model with nonlinear isotropic hardening. The model was formulated within the framework of the thermodynamics of irreversible processes with internal variables. The three-dimensional thermomechanical model is implemented within the Abaqus suite of finite element software using external subroutines. It uses the reduction factors for the strength of softwood timber suggested in EC5 [1].

The model was used to simulate two real tests for which experimental results already exist. The first is a Laminated Veneer Lumber sample subject to a tensile force, and the second a Cross Laminated Timber beam tested under bending, both subject to a standard fire. The predictions of the model corroborate the experiments in both the thermal and structural responses. The model predicts the temperature profiles and the displacements accurately for both tests. It can also predict the depth of the charred layer, which starts to form at temperatures above 300 °C. For a rectangular section, it was found that the residual section is not rectangular if all the faces are exposed to fire. Furthermore, the charred layer has no mechanical resistance, which affects and reduces the mechanical resistance of the initial cross section of the element exposed to fire. It was also found that the adoption of the curves suggested by EC5 [1] for the variation of the thermal properties with temperature yields acceptable results when predicting the fire resistance of softwood timber structures.

To improve the accuracy of these numerical models and to better model the thermal degradation of the wood material, it is necessary to apply the kinetic models of pyrolysis based on a multi-scale approach and formulated from Arrhenius laws. These models are widely used to study the behaviour of biomass under high temperatures for energy recovery. However, they are very scarce and rarely used in the literature to analyse the fire behaviour of timber structures. The present study is a right step in this direction.