1 Introduction

Circular Concrete Filled Tubes (CCFT) and Rectangular Concrete Filled Tubes (RCFT) are composite columns made with a circular or rectangular external steel jacket, respectively. These types of columns are commonly used for structural systems, combining the versatility of the metallic structure during the provisional phase and the performance characteristics of the composite structure during its lifetime. Columns of this type can be connected to beams in two different ways: (1) if the frame is metallic, the column usually features lateral flanges or plates that are connected to the steel beams by means of bolts and (2) if the frame is made of concrete or a composite structure, the column can be produced with openings in the jacket that allow a reinforced concrete connection to be obtained. Regions of geometric discontinuity, such as connection points, are critical in CFST [1]: a transfer of longitudinal shear (bond) stress between the concrete infill and the surrounding tube is required to achieve the composite action. Stress transfer takes place within a zone which, in this paper, will be called transferring length and is accompanied by a slippage between the concrete core and the surrounding steel tube.

This article proposes an analytical method which can estimate the evolution of bond stress between steel and concrete near the connection frame, also providing a length value within which this bond develops, thus incrementing the ultimate load that causes the collapse of the column.

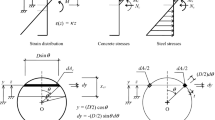
A common method to evaluate the CFST bond–slip behavior is the push-out test (Fig. 1). In this test, the load applied on the concrete is transferred to the steel jacket by means of tangential stress τ, within the length of the steel–concrete interface, l.

Fig. 1
figure 1

Push-out test setup

Full size image

From this test the maximum value of the applied load, \({N}_{\mathrm{u}}\), is obtained, and consequently the ultimate average bond strength \({\tau }_{\mathrm{u},\mathrm{avg}}\) is

$$\tau_{{\text{u,avg}}} = N_{{\text{u}}} /pl$$
(1)

where \(p\) is the internal perimeter of the steel jacket.

Push-out tests have been used over the years with the main purpose of examining which parameter influences the ultimate bond strength in CFST. The first research on bond strength in CCFT was conducted in Ref. [2], where experimental push-out tests were performed and the dispersion of test results was relatively large: the trend of the interfacial bond strength was not clear with regard to the variation in the diameter-to-thickness ratios of the tubes. Moreover, the core concrete strength did not clearly influence the bond strength of CCFT. Some authors [3, 4] highlight that CCFT manifest higher bond strength compared to RCFT and that the bond strength decreases as concrete strength increases due to the negative effect of shrinkage. Moreover, Ref. [5] states that the more effective confinement pressure exerted by the steel jacket on the concrete core in CCFT, compared to RCFT, is the cause of an enhancement in bond strength. An important contribution to understanding the bond transfer mechanism between the steel tube and the concrete infill is given in Ref. [1], which considers the radial displacement of the concrete infill and indicates that it can be divided into two components: a first component, due to Poisson effect and proportional to the \(d/{t}^{2}\), and a second component, due to shrinkage and proportional to \(d\), where \(t\) is the tube thickness and \(d\) is the external dimension. The algebraic sum of these two components with opposite signs greatly influences the bond transfer mechanism, to the extent that, for the first time, an empirical formula has been proposed with the aim of evaluating the bond strength in function of d/t, definitely making it clear that bond strength decreases when d/t increases.

It is also important to underline that parameters such as interface roughness [6], concrete compaction [2, 7] and concrete age [2, 7, 8] affect bond strength in CFST, but these will not be considered in this study. In technical literature, different experimental formulas of \({\tau }_{\mathrm{u},\mathrm{avg}}\) as a function of the \(d/t\) or \(t/{d}^{2}\) parameter for CCFTs and \(h/t\) or \(t/{h}^{2}\) for RCFT (where \(h\) is the rectangular external dimension), have been proposed over the years, with the purpose of considering the Poisson effect and shrinkage, as suggested by Ref. [1]. This paper refers to experimental formulas presented in Refs. [9] and [10] for CCFT and Refs. [9] and [11] for RCFT. In addition to studies of ultimate bond strength, the mechanisms contributing to it have also been assessed by push-out tests. For both CCFT Refs. [2, 10] and RCFT [5, 10,11,12,13], three distinct components that contribute to bond strength have been identified, i.e., chemical adhesion, microlocking and macrolocking. With reference to the experimental study conducted in Refs. [8] and [14], the stress–slip curve can take on three different shapes: it may display a maximum branch followed by a falling one, a maximum branch followed by a falling one rising again at a high slip, or no maximum branch at all. A typical curve of the first type is reported in Fig. 2 in which three zones related to three different mechanisms of resistance can be distinguished.

Fig. 2
figure 2

Push-out qualitative curve [12]

Full size image

Chemical adhesion and microlocking govern the ascending branch of the curve and mainly contribute to obtaining the maximum bond stress, whereas macrolocking determines the residual bond stress that remains at the later stages of the bond stress slip curve. This paper presents a stress–slip curve with a non-linear elastic first branch, representing the adhesion and microlocking mechanism, and a perfectly plastic second branch representing the macrolocking mechanism. While over the years great effort has been made to examine the CFST bond–slip behavior using push-out bond stress, less attention has been paid to the distribution of bond stress within the so-called transferring length. In fact, it is important to note that, at the steel–concrete interface, the bond stress varies along the direction of load transfer before an overall steel–concrete slip occurs [14,15,16]. This gap is reflected in the most recent Code Standards, such as Refs. [17] and [18] in which an average constant bond stress, \({\tau }_{\mathrm{u},\mathrm{avg}}\), is adopted within a transferring length. Furthermore, in these standards, with the exception of the cross-sectional shape, no other factor affecting average bond strength is considered (\({\tau }_{\mathrm{u},\mathrm{avg}}=0.55\) MPa for CCFT and \({\tau }_{\mathrm{u},\mathrm{avg}}=0.40\) MPa for RCFT) and the transferring length has been taken as a fixed value, equal to twice the diameter of the tube for CCFTs or the larger dimension for RCFT.

Here below is a simplified analytical model that allows estimation of the domain within which bond transfer and slips develop (herein defined as the transferring length \(L\)) as well as the distribution of bond stress τ, slip s, steel and concrete stresses \({\sigma }_{\mathrm{c}}\) and \({\sigma }_{\mathrm{s}}\) and strains \({\varepsilon }_{\mathrm{c}}\) and \({\varepsilon }_{\mathrm{s}}\) within this length, and also the ultimate load applied to CFST. It is important to highlight that the analytical model presents a closed-form solution.

2 Proposed Bond–Slip Relationship

The calculation method proposed here is based on a non-linear elastic perfectly plastic bond–slip relationship between confined concrete and steel jacket:

$$\left\{ {\begin{array}{*{20}l} {\tau \left( x \right) = \tau_{u} \left( {\frac{s\left( x \right)}{{\overline{s}}}} \right)^{\alpha } {\text{for}} s\left( x \right) \le \overline{s} \quad\quad\quad \quad \quad\quad\quad\quad(2) } \\ {\tau \left( x \right) = \tau_{u} s\left( x \right) > \overline{s} \quad \quad\quad\quad\quad\quad\quad\quad \quad\quad\quad\quad\,\,\,\,(3) } \\ \end{array} } \right.$$

where \(\alpha\) is a coefficient, proposed here as equal to 0.5, as suggested in [19].

\({\tau }_{u}\) is the maximum local bond strength and \(\overline{s }\) is the slip value at which there is the transit from the non-linear elastic branch governed by the adhesion and microlocking mechanisms (1), to the perfectly plastic branch governed by the macrolocking mechanism [Eq. (2)].

The first branch relationship, [Eq. (2)], is proposed in Ref. [20] for ribbed steel bars embedded in concrete and is also adopted in Ref. [21] to develop a cracking analytical model on concrete tie reinforced with both ribbed and smooth bars, based on the bond–slip relationship.

The maximum local bond strength, \({\tau }_{\mathrm{u}}\), has been expressed with two different equations, one for CCFT and another for RCFT:

$$\tau_{u} = 1.5 \cdot \left[ {211.64 \cdot \left( {25.4 \cdot \frac{t}{{d^{2} }}} \right)} \right]\quad {\text{for CCFT}}$$
(4)
$$\tau_{{\text{u}}} = 1.5 \cdot \frac{{\left[ {1.9 + 10000 \cdot \left( {25.4 \cdot \frac{t}{{h^{2} }}} \right)} \right]}}{145.05} \quad{\text{for RCFT}}$$
(5)

where \(t\) [mm], \(d\) [mm], \(h\) [mm], \({\tau }_{\mathrm{u},\mathrm{avg}}\) [MPa].

Equations (4) and (5) are obtained from the equations proposed by Refs. [9] and [11], respectively:

$$\tau_{{\text{u,avg}}} = 211.64 \cdot \left( {25.4 \cdot \frac{t}{{d^{2} }}} \right) \quad{\text{for CCFT}}$$
(6)
$$\tau_{{\text{u,avg}}} = \frac{{\left[ {1.9 + 10000 \cdot \left( {25.4 \cdot \frac{t}{{h^{2} }}} \right)} \right]}}{145.05} \quad{\text{ for RCFT}}$$
(7)

where \(t\) [mm], \(d\) [mm], \(h\) [mm], \({\tau }_{\mathrm{u},\mathrm{avg}}\) [MPa].

Equations (6) and (7) represent the average ultimate bond stress in push-out tests, \({\tau }_{\mathrm{u},\mathrm{avg}}\). As in Eqs. (2) and (3), the maximum local bond strength, \({\tau }_{\mathrm{u}}\), is presented; Eqs. (6) and (7) have been amplified here by coefficient 1.5, because, as observed by Ref. [15], the maximum local bond stress in push-out tests has a greater value than the corresponding average ultimate bond stress.

In analogy to what is proposed in Ref. [22], slip value \(\overline{s }\) (Eqs. (2) and (3)) is proposed with the following equation:

$$\overline{s} = \frac{C}{{10^{4} }}\tau_{{\text{u}}}$$
(8)

where C [mm] is the external perimeter of the CFST, \({\tau }_{\mathrm{u}}\) is expressed in [MPa] and \(\overline{s }\) in [mm].

3 Formulation of the Problem

Consider a composite beam to CFST column connection of type \(2\) as stated in the introduction; the sum of beam shear forces at the column interface leads to an increment of axial load (here named \(N\)) applied only on the concrete section and then gradually transferred to the steel jacket within transferring length \(L\) through the development of relative slip \(s(x)\) and longitudinal bond stress \(\tau (x)\) between steel and concrete. Summing up, based on the connection typology considered, the incremental load \(N\) directly acts on the concrete and, considering the problem in terms of incremental forces, the steel jacket is unloaded at the application load point. Note that the following equations are developed on the basis of connection type \(2\), but they can be easily applied to the case of connection type \(1\), as stated in the introduction, by considering the concrete load section unloaded. If reference axis \(x\) presents an opposite positive direction compared to the load transfer direction, then equations of force equilibrium on an infinitesimal CFST element within the transferring length (Fig. 3) are obtained:

$$\Sigma F_{{\text{c}}} = A_{{\text{c}}} \sigma_{{\text{c}}} \left( {x + dx} \right) - A_{{\text{c}}} \sigma_{{\text{c}}} \left( x \right) - p dx \tau \left( x \right) = 0$$
(9)
$$\Sigma F_{{\text{s}}} = A_{{\text{s}}} \sigma_{{\text{s}}} \left( {x + dx} \right) - A_{{\text{s}}} \sigma_{{\text{s}}} \left( x \right) + p dx \tau \left( x \right) = 0$$
(10)
Fig. 3
figure 3

Equilibrium of the infinitesimal column portion

Full size image

where \({A}_{\mathrm{c}}\) and \({A}_{\mathrm{s}}\) are the concrete core and steel jacket cross areas, respectively.

Dividing by dx \(\to\) 0 and denoting with \(\sigma^{\prime}_{{\text{c}}} \left( x \right)\) and \(\sigma^{\prime}_{{\text{s}}} \left( x \right)\) the first derivate of concrete and steel jacket stresses, respectively, the following equations are obtained:

$$\sigma^{\prime}_{{\text{c}}} \left( x \right) = \frac{p}{{A_{{\text{c}}} }}\tau \left( x \right)$$
(11)
$$\sigma^{\prime}_{{\text{s}}} \left( x \right) = - \frac{p}{{A_{{\text{s}}} }}\tau \left( x \right)$$
(12)

Considering an elastic behavior for both steel and concrete (i.e., \({\sigma }_{\mathrm{c}}={E}_{\mathrm{c}}{\varepsilon }_{\mathrm{c}}\) and \({\sigma }_{\mathrm{s}}={E}_{\mathrm{s}}{\varepsilon }_{\mathrm{s}}\)), being \({E}_{\mathrm{c}}\) and \({E}_{\mathrm{s}}\) the elastic concrete and steel moduli of elasticity, respectively, the following differential equations are obtained:

$$\varepsilon^{\prime}_{{\text{c}}} \left( x \right) = \frac{p}{{E_{{\text{c}}} A_{{\text{c}}} }}\tau \left( x \right)$$
(13)
$$\varepsilon^{\prime}_{{\text{s}}} \left( x \right) = - \frac{p}{{E_{{\text{s}}} A_{{\text{s}}} }}\tau \left( x \right)$$
(14)

where \(\varepsilon^{\prime}_{{\text{c}}} \left( x \right)\) and \(\varepsilon^{\prime}_{{\text{s}}} \left( x \right)\) are the first strain derivatives of concrete and steel, respectively. The slip between concrete core and steel jacket is defined as

$$s\left( x \right) = u_{{\text{c}}} \left( x \right) - u_{{\text{s}}} \left( x \right)$$
(15)

where \({u}_{\mathrm{c}}\) and \({u}_{\mathrm{s}}\) are the concrete and steel displacements, respectively.

Then, by deriving Eq. (15) and considering strain definitions \(\varepsilon_{{\text{c}}} (x) = u^{\prime}_{{\text{c}}} \left( x \right)\) and \(\varepsilon_{{\text{s}}} (x) = u^{\prime}_{{\text{s}}} \left( x \right)\):

$$s^{\prime}\left( x \right) = \varepsilon_{{\text{s}}} \left( x \right) - \varepsilon_{{\text{c}}} \left( x \right)$$
(16)

Deriving once again Eq. (16) and considering Eqs. (13) and (14), the following second-order differential equation, governing the slip phenomenon within transferring length \(L\), is obtained:

$$s^{\prime\prime}\left( x \right) = \left( {\frac{p}{{E_{{\text{s}}} A_{{\text{s}}} }} + \frac{p}{{E_{{\text{c}}} A_{{\text{c}}} }}} \right)\tau \left( x \right)$$
(17)

It must be noted that in deriving Eq. (17), Poisson’s ratio effect would lead to a triaxial loading on concrete, and, for this reason, it was discarded. However, its influence is taken into account by defining bond strength \({\tau }_{\mathrm{u}}\) in function of the d/t parameter [Eqs. (4–7)]. This simplification leads to a closed-form solution of the problem, making the proposed analytical model suitable for practical design.

As \(\tau \left(x\right)\) can be differently expressed by Eqs. (2) or (3), depending on the slip value, then Eq. (17), as well as its solution, depend on \(s\). In fact, if the axial load applied on concrete is very low, that is, \(s\left(x\right)\) always remains lower than \(\overline{s }\), Eq. (3) holds and Eq. (14) becomes

$$s^{\prime\prime}\left( x \right) = \frac{{\tau_{{\text{u}}} }}{{\overline{s}^{\alpha } }}\left( {\frac{p}{{E_{{\text{s}}} A_{{\text{s}}} }} + \frac{p}{{E_{{\text{c}}} A_{{\text{c}}} }}} \right)s\left( x \right)^{\alpha }\quad x \in \left[ {0,L} \right]$$
(18)

On the contrary, for a sufficiently high axial load on concrete, domain L of the problem is divided into a first zone of amplitude L1 in which \(s\left(x\right)\le \overline{s }\), and a second zone of amplitude L2 in which \(s\left(x\right)>\overline{s }\), and Eq. (17) is expressed by means of Eqs. (2) and (3), by the following system of equations:

$$\left\{ {\begin{array}{*{20}{l}} \begin{array}{l} s''\left( x \right) = \frac{{{\tau _{\rm{u}}}}}{{{{\bar s}^\alpha }}}\left( {\frac{p}{{{E_{\rm{s}}}{A_{\rm{s}}}}} + \frac{p}{{{E_{\rm{c}}}{A_{\rm{c}}}}}} \right)s{\left( x \right)^\alpha }\\ \quad x \in \left[ {0,{L_1}} \right]~~~~{\rm{where}}\;~s\left( x \right) < \bar s\quad \quad(19)~~ \end{array}\\ \begin{array}{l} s''\left( x \right) = \left( {\frac{p}{{{E_{\rm{s}}}{A_{\rm{s}}}}} + \frac{p}{{{E_{\rm{c}}}{A_{\rm{c}}}}}} \right){\tau _{\rm{u}}}~~\\ \quad x \in \left[ {{L_1},L} \right]~~~~~{\rm{where}}\;~s\left( x \right) \ge \bar s\quad\,\, (20)~~~~ \end{array} \end{array}} \right.$$

where L = L1 + L2. In both cases, the problem presents a closed-form solution:

3.1 Case A: \(s\left( x \right) \le \bar s\;~{\rm{V}}\;~x \in \left[ {0,L} \right]\)

This is the case introduced above, in which the axial load on concrete is so low that \(s\left(x\right)<\overline{s }\) and the differential equation governing the slip phenomenon within transferring length \(L\) is given by Eq. (18), that can be solved by introducing two boundary conditions. The x axis originates in the section, where perfect adherence between steel and concrete is restored, so the differential problem becomes

$$\left\{ {\begin{array}{*{20}l} {s^{\prime\prime}\left( x \right) = \frac{{\tau_{{\text{u}}} }}{{\overline{s}^{\alpha } }}\left( {\frac{p}{{E_{{\text{s}}} A_{{\text{s}}} }} + \frac{p}{{E_{{\text{c}}} A_{{\text{c}}} }}} \right)s\left( x \right)^{\alpha } x \in \left[ {0,L} \right]\quad \quad\quad\,\, (21) } \\ {s\left( 0 \right) = 0 \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad \,\,(22)} \\ {s^{\prime}\left( 0 \right) = 0 \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad \, (23) } \\ \end{array} } \right.$$

The solution is supplied in closed-form by

$$s\left( x \right) = C_{1} x^{{C_{2} }} \quad x \in \left[ {0,L} \right]$$
(24)

where constants \({C}_{1}\) and \({C}_{2}\) are expressed as

$$C_{1} = \left[ {\frac{{C_{3} \left( {1 - \alpha } \right)^{2} }}{{2\left( {1 + \alpha } \right)}}} \right]^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {1 - \alpha }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${1 - \alpha }$}}}}$$
(25)
$$C_{2} = \frac{2}{1 - \alpha }$$
(26)

in which \({C}_{3}\) is given by

$$C_{3} = \frac{{\tau_{{\text{u}}} }}{{\overline{s}^{\alpha } }}\left( {\frac{p}{{E_{{\text{s}}} A_{{\text{s}}} }} + \frac{p}{{E_{{\text{c}}} A_{{\text{c}}} }}} \right)$$
(27)

and L indicates the unknown transferring length.

By substituting Eq. (24) in Eq. (2), the bond stress trend in function of \(x\) is obtained:

$$\tau \left( x \right) = \frac{{\tau_{{\text{u}}} C_{1}^{\alpha } x^{{\alpha C_{2} }} }}{{\overline{s}^{\alpha } }} x \in \left[ {0,L} \right]$$
(28)

Furthermore, the expressions of concrete and steel stresses, \({\sigma }_{\mathrm{c}}(x)\) and \({\sigma }_{\mathrm{s}}(x)\), are obtained by integrating Eqs. (11) and (12) and also considering Eq. (28):

$$\sigma_{{\text{c}}} \left( x \right) = \sigma_{{{\text{c}}0}} + \frac{{p\tau_{{\text{u}}} }}{{A_{{\text{c}}} \left( {\alpha C_{2} + 1} \right)}}\left( {\frac{{C_{1} }}{{\overline{s}}}} \right)^{\alpha } x^{{\alpha C_{2} + 1}} x \in \left[ {0,L} \right]$$
(29)
$$\sigma_{{\text{s}}} \left( x \right) = \sigma_{{{\text{s}}0}} - \frac{{p\tau_{{\text{u}}} }}{{A_{{\text{s}}} \left( {\alpha C_{2} + 1} \right)}}\left( {\frac{{C_{1} }}{{\overline{s}}}} \right)^{\alpha } x^{{\alpha C_{2} + 1}} x \in \left[ {0,L} \right]$$
(30)

where \({\sigma }_{\mathrm{c}0}\) and \({\sigma }_{\mathrm{s}0}\) are the values of concrete and steel stresses in x = 0, and they are known, because in this section, perfect adherence is restored and the hypothesis of a plain section is valid:

$$\sigma_{{{\text{c0}}}} = \frac{N}{{nA_{{\text{s}}} + A_{{\text{c}}} }}$$
(31)
$$\sigma_{{{\text{s0}}}} = n\sigma_{{{\text{c0}}}}$$
(32)

being \(n={E}_{\mathrm{s}}/{E}_{\mathrm{c}}\), and N the axial force applied on concrete in x = L.

Finally, the expressions of concrete and steel strains, \({\varepsilon }_{\mathrm{c}}(x)\) and \({\varepsilon }_{\mathrm{s}}(x)\), are obtained considering the hypothesis of elastic behavior for both concrete and steel materials (\({{\varepsilon }_{\mathrm{c}}(x)=\sigma }_{\mathrm{c}}\left(x\right)/{E}_{\mathrm{c}}\) and \({{\varepsilon }_{\mathrm{s}}(x)=\sigma }_{\mathrm{s}}\left(x\right)/{E}_{\mathrm{s}}\)):

$$\varepsilon_{{\text{c}}} \left( x \right) = {{\left[ {\sigma_{{{\text{c}}0}} + \frac{{p\tau_{{\text{u}}} }}{{A_{{\text{c}}} \left( {\alpha C_{2} + 1} \right)}}\left( {\frac{{C_{1} }}{{\overline{s}}}} \right)^{\alpha } x^{{\alpha C_{2} + 1}} } \right]} \mathord{\left/ {\vphantom {{\left[ {\sigma_{{{\text{c}}0}} + \frac{{p\tau_{{\text{u}}} }}{{A_{{\text{c}}} \left( {\alpha C_{2} + 1} \right)}}\left( {\frac{{C_{1} }}{{\overline{s}}}} \right)^{\alpha } x^{{\alpha C_{2} + 1}} } \right]} {E_{{\text{c}}} }}} \right. \kern-\nulldelimiterspace} {E_{{\text{c}}} }} x \in \left[ {0,L} \right]$$
(33)
$$\varepsilon_{{\text{s}}} \left( x \right) = {{\left[ {\sigma_{{{\text{s}}0}} - \frac{{p\tau_{{\text{u}}} }}{{A_{{\text{s}}} \left( {\alpha C_{2} + 1} \right)}}\left( {\frac{{C_{1} }}{{\overline{s}}}} \right)^{\alpha } x^{{\alpha C_{2} + 1}} } \right]} \mathord{\left/ {\vphantom {{\left[ {\sigma_{{{\text{s}}0}} - \frac{{p\tau_{{\text{u}}} }}{{A_{{\text{s}}} \left( {\alpha C_{2} + 1} \right)}}\left( {\frac{{C_{1} }}{{\overline{s}}}} \right)^{\alpha } x^{{\alpha C_{2} + 1}} } \right]} {E_{{\text{s}}} }}} \right. \kern-\nulldelimiterspace} {E_{{\text{s}}} }} x \in \left[ {0,L} \right]$$
(34)

3.2 Case B: \(s\left( x \right) \le \bar s~~~{\rm{for}}~~x \in \left[ {0,{L_1}} \right];~~s\left( x \right) > \bar s~~~{\rm{for}}~~x \in \left[ {{L_1},L} \right]\)

This is the case in which the axial load on concrete is high enough to obtain a transferring length L that is divided in a first zone of amplitude L1, in which \(s\left(x\right)<\overline{s }\) (as in case A), and a second zone of amplitude L2 = L – L1, in which \(s\left(x\right)>\overline{s }\).

The differential problem in the first zone (\(x\in \left[0,{L}_{1}\right]\)) is formally analogous to that analysed in case A:

$$\left\{ {\begin{array}{*{20}l} {s^{\prime\prime}\left( x \right) = \frac{{\tau_{{\text{u}}} }}{{\overline{s}^{\alpha } }}\left( {\frac{p}{{E_{{\text{s}}} A_{{\text{s}}} }} + \frac{p}{{E_{{\text{c}}} A_{{\text{c}}} }}} \right)s\left( x \right)^{\alpha } x \in \left[ {0,L_{1} } \right]\quad \quad\quad\,\,\,\,(35) } \\ {s\left( 0 \right) = 0\quad\quad \quad\quad\quad \quad\quad \quad \quad\quad\quad \quad\quad\quad \quad\quad\quad\quad\,(36) } \\ {s^{\prime}\left( 0 \right) = 0\quad\quad \quad\quad\quad \quad\quad \quad \quad\quad\quad \quad\quad\quad \quad\quad\quad\quad (37) } \\ \end{array} } \right.$$

and its solution is also analogous to that expressed by Eq. (24):

$$s\left( x \right) = C_{1} x^{{C_{2} }} x \in \left[ {0,L_{1} } \right]$$
(38)

The values of slip and its derivates, calculated in x = L1, become the boundary conditions to solve the second-order differential problem in the second zone (\(x\in \left[{L}_{1},L\right]\)):

$$\left\{ {\begin{array}{*{20}l} {s^{\prime\prime}\left( x \right) = \left( {\frac{p}{{E_{{\text{s}}} A_{{\text{s}}} }} + \frac{p}{{E_{{\text{c}}} A_{{\text{c}}} }}} \right)\tau_{{\text{u}}} x \in \left[ {L_{1} ,L} \right]\quad\quad\quad\quad\,\,\, \,\,(39)} \\ {s\left( {L_{1} } \right) = \overline{s}\quad\quad\quad\quad \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\,\,\,\,\,\,\,\,(40) } \\ {s^{\prime}\left( {L_{1} } \right) = s^{\prime}_{L1} \quad\quad\quad\quad \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\,\, (41) } \\ \end{array} } \right.$$

where \(s^{\prime}_{L1}\) is the value of slip derivate obtained in x = L1 from the solution of the problem in the first zone. The solution of the system of equations is easily obtained by double integration:

$$s\left( x \right) = \frac{{C_{3} \overline{s}^{\alpha } }}{2}x^{2} + \left( {s^{\prime}_{L1} - C_{3} \overline{s}^{\alpha } L_{1} } \right)x + s_{L1} + \frac{{C_{3} \overline{s}^{\alpha } L_{1}^{2} }}{2} - L_{1} s^{\prime}_{L1} x \in \left[ {L_{1} ,L} \right]$$
(42)

where \(L={L}_{1}+{L}_{2}\) indicates the unknown transferring length.

The analogy in terms of slip solution between case A and the first zone of case B implies that the expressions of bond stress τ, concrete and steel stresses, \({\sigma }_{\mathrm{c}}\) and \({\sigma }_{\mathrm{s}},\) and strains \({\varepsilon }_{\mathrm{c}}\) and \({\varepsilon }_{\mathrm{s}}\), within transmission length domain [0;L1] are

$$\tau \left( x \right) = \frac{{\tau_{{\text{u}}} C_{1}^{\alpha } x^{{\alpha C_{2} }} }}{{\overline{s}^{\alpha } }}\quad x \in \left[ {0,L_{1} } \right]$$
(43)
$$\sigma_{{\text{c}}} \left( x \right) = \sigma_{{{\text{c}}0}} + \frac{{p\tau_{{\text{u}}} }}{{A_{{\text{c}}} \left( {\alpha C_{2} + 1} \right)}}\left( {\frac{{C_{1} }}{{\overline{s}}}} \right)^{\alpha } x^{{\alpha C_{2} + 1}} \quad x \in \left[ {0,L_{1} } \right]$$
(44)
$$\sigma_{{\text{s}}} \left( x \right) = \sigma_{{{\text{s}}0}} - \frac{{p\tau_{{\text{u}}} }}{{A_{{\text{s}}} \left( {\alpha C_{2} + 1} \right)}}\left( {\frac{{C_{1} }}{{\overline{s}}}} \right)^{\alpha } x^{{\alpha C_{2} + 1}} \quad x \in \left[ {0,L_{1} } \right]$$
(45)
$$\varepsilon_{{\text{c}}} \left( x \right) = [\sigma_{{{\text{c}}0}} + \frac{{p\tau_{{\text{u}}} }}{{A_{{\text{c}}} \left( {\alpha C_{2} + 1} \right)}}\left( {\frac{{C_{1} }}{{\overline{s}}}} \right)^{\alpha } x^{{\alpha C_{2} + 1}} \left] {/E_{{\text{c}}} x \in } \right[0,L_{1} ]$$
(46)
$$\varepsilon_{{\text{s}}} \left( x \right) = [\sigma_{{{\text{s}}0}} - \frac{{p\tau_{{\text{u}}} }}{{A_{{\text{s}}} \left( {\alpha C_{2} + 1} \right)}}\left( {\frac{{C_{1} }}{{\overline{s}}}} \right)^{\alpha } x^{{\alpha C_{2} + 1}} \left] {/E_{{\text{s}}} x \in } \right[0,L_{1} ]$$
(47)

Furthermore, the expressions of concrete and steel stresses are obtainable in the second zone (\(x\in \left[{L}_{1},L\right]\)) by integration of Eqs. (8) and (9) considering that \({\tau =\tau }_{\mathrm{u}}\) holds:

$$\sigma_{{\text{c}}} \left( x \right) = \sigma_{{\text{c}}} \left( {L_{1} } \right) + \frac{{p\tau_{{\text{u}}} }}{{A_{{\text{c}}} }}\left( {x - L_{1} } \right) \quad x \in \left[ {L_{1} ,L} \right]$$
(48)
$$\sigma_{{\text{s}}} \left( x \right) = \sigma_{{\text{s}}} \left( {L_{1} } \right) - \frac{{p\tau_{{\text{u}}} }}{{A_{{\text{s}}} }}\left( {x - L_{1} } \right) \quad x \in \left[ {L_{1} ,L} \right]$$
(49)

where \({\sigma }_{\mathrm{c}}\left({L}_{1}\right)\) and \({\sigma }_{\mathrm{s}}\left({L}_{1}\right)\) are the values of concrete and steel stresses in x = L1 obtained from Eqs. (44) and (45) calculated for x = L1.

Finally, considering the hypothesis of elastic behavior for both concrete and steel materials, the expressions of concrete and steel strains in the second zone (\(x\in \left[{L}_{1},L\right]\)) are the following:

$$\varepsilon_{{\text{c}}} \left( x \right) = {{\left[ {\sigma_{{\text{c}}} \left( {L_{1} } \right) + \frac{{p\tau_{{\text{u}}} }}{{A_{{\text{c}}} }}\left( {x - L_{1} } \right)} \right]} \mathord{\left/ {\vphantom {{\left[ {\sigma_{{\text{c}}} \left( {L_{1} } \right) + \frac{{p\tau_{{\text{u}}} }}{{A_{{\text{c}}} }}\left( {x - L_{1} } \right)} \right]} {E_{{\text{c}}} }}} \right. \kern-\nulldelimiterspace} {E_{{\text{c}}} }}\quad x \in \left[ {L_{1} ,L} \right]$$
(50)
$$\varepsilon_{{\text{s}}} \left( x \right) = {{\left[ {\sigma_{{\text{s}}} \left( {L_{1} } \right) - \frac{{p\tau_{{\text{u}}} }}{{A_{{\text{s}}} }}\left( {x - L_{1} } \right)} \right]} \mathord{\left/ {\vphantom {{\left[ {\sigma_{{\text{s}}} \left( {L_{1} } \right) - \frac{{p\tau_{{\text{u}}} }}{{A_{{\text{s}}} }}\left( {x - L_{1} } \right)} \right]} {E_{{\text{s}}} }}} \right. \kern-\nulldelimiterspace} {E_{{\text{s}}} }}\quad x \in \left[ {L_{1} ,L} \right]$$
(51)

It must be pointed out that the expressions of τ, \({\sigma }_{\mathrm{c}}\), \({\sigma }_{\mathrm{s}},\) \({\varepsilon }_{\mathrm{c}}\) and \({\varepsilon }_{\mathrm{s}}\), are directly derived through analytical considerations, and depend in both cases on the slip, s, within the transferring length, L.

4 Identification of the Transferring Length

To solve the differential problem introduced above, first of all it is necessary to establish whether \(s(x)\) is always smaller than limit slip \(\overline{s }\) within the entire transferring length (case A), or if \(s(x)\) is greater than \(\overline{s }\) in a portion \({L}_{2}\) of the transferring length. Considering the type \(2\) connection stated in the introduction, incremental load \(N\) is entirely applied on concrete in \(x=L\); then in this section, the steel jacked is unloaded:

$$\sigma_{{\text{s}}} \left( L \right) = 0$$
(52)

Considering that the abscissa, x, originates in the section, where perfect adherence between steel and concrete is restored (consistently with what was done in the previous paragraph), the transferring length \(L\) value is easily calculated both in the case in which \(\overline{s }\) is not reached within the transferring length (i.e., \(s\left(L\right)\le \overline{s }\)), by means of Eqs. (30) and (52), and in the case in which \(\overline{s }\) is reached within the transferring length (i.e., \(s\left(L\right)>\overline{s }\)), by means of Eqs. (45) and (52), as follows: first \(\overline{L }\) is defined as the length for which slip \(\overline{s }\) is reached, that is

$$s\left( {\overline{L}} \right) = \overline{s}$$
(53)

and by means of Eq. (24):

$$\overline{L} = \left( {\frac{{\overline{s}}}{{C_{1} }}} \right)^{{\frac{1}{{C_{2} }}}}$$
(54)

Second, on the basis of the first assumption in case A: the transferring length value \({L}_{\mathrm{A}}\) is calculated with Eq. (52) by considering Eq. (30):

$$L_{{\text{A}}} = \left[ {\sigma_{{{\text{s}}0}} \frac{{A_{{\text{s}}} \overline{s}^{\alpha } \left( {\alpha C_{2} + 1} \right)}}{{p\tau_{{\text{u}}} C_{1}^{{}} }}} \right]^{{\frac{1}{{C_{2} + 1}}}}$$
(55)

Therefore, by observing that \(s(x)\) [Eq. (24)] is monotonically increasing, the following considerations are reached: (a) If \({L}_{\mathrm{A}}<\overline{L }\), it results that \(s\left({L}_{\mathrm{A}}\right)<\overline{s }\) in case A, and then the transferring length solution L is equal to \({L}_{\mathrm{A}}\); (b) If \({L}_{\mathrm{A}}>\overline{L }\), it is case B, and then the transferring length solution L is equal to \({L}_{\mathrm{B}}\) calculated with Eq. (52) by considering Eq. (45):

$$L_{{\text{B}}} = \left( {\frac{p}{{A_{{\text{s}}} }}\tau_{{\text{u}}} L_{1} + \sigma_{{\text{s}}} \left( {L_{1} } \right)} \right)\frac{{A_{{\text{s}}} }}{{p\tau_{{\text{u}}} }}$$
(56)

where given the \(\overline{L }\) definition, it is clear that \({L}_{1}\)= \(\overline{L }\).

It should be noted that the calculation of the transferring length can be easily performed without any computational skills or instrumentation.

5 Model Accuracy

To check the accuracy of the analytical model proposed, extended research in the literature of experimental data regarding CFST push-out tests was performed. On the whole, 97 CCFTs and 35 RCFTs have been separately considered, as different expressions of \({\tau }_{\mathrm{u}}\) and have been taken into account here (Eqs. (4) and (5)). Comparison was performed between the ultimate load experimental and analytical values. The mechanical and geometrical properties of the specimens considered are reported in Tables 3 and 4 (see Appendix) for CCFT and RCFT, respectively. To check the accuracy of the model proposed here, ultimate load value \({N}_{\mathrm{u}}\) has been defined as the load that causes the achievement of local bond strength \({\tau }_{\mathrm{u}}\) in the applied load section, that is the load for which transferring length value \({L}_{\mathrm{A}}\) [Eq. (55)] equals length \(\overline{L }\) [Eq. (54)] for which slip \(\overline{s }\) is reached in the applied load section:

$$N_{{\text{u}}} = \frac{{\left( {\frac{{\overline{s}}}{{C_{1} }}} \right)^{{\frac{{\alpha C_{2} + 1}}{{C_{2} }}}} p\tau_{{\text{u}}} C_{1}^{\alpha } }}{{nA_{{\text{s}}} \overline{s}^{\alpha } \left( {\alpha C_{2} + 1} \right)}}\left( {nA_{{\text{s}}} + A_{{\text{c}}} } \right)$$
(57)

where Eqs. (31) and (32) are used to specify \({N}_{\mathrm{u}}\) and \({\tau }_{\mathrm{u}}\) they refer to Eq. (4) or (5) for CCFT or RCFT, respectively. The \({N}_{\mathrm{u}}\) values obtained with Eq. (57) and \({N}_{\mathrm{u}}\) values obtained with the empirical expression proposed by other authors (Tables 1 and 2 for CCFT and RCFT, respectively) have been compared with the experimental ultimate load, \({N}_{\mathrm{u},\mathrm{exp}}\), values obtained with Eq. (1) from the test data here considered Tables 3 and 4 in Appendix).

Table 1 Existing CCFT models: \({N}_{\mathrm{u}}\) [N], \(t\) [mm], \(d\) [mm], \(p\) [mm], \(l\) [mm]
Full size table
Table 2 Existing RCFT models: \({N}_{\mathrm{u}}\) [N], \(t\) [mm], \(h\) [mm], \(p\) [mm], \(l\) [mm], \(d\) [mm]
Full size table

The \({N}_{\mathrm{u}}\) values obtained have been compared with the experimental \({N}_{\mathrm{u},\mathrm{exp}}\) results for CCFTs and RCFTs.

In Tables 3 and 4 the average, AVG, and the coefficient of variation, COV, values of the ratio between the theoretical, \({N}_{\mathrm{u}}\), and experimental, \({N}_{\mathrm{u},\mathrm{exp}}\), ultimate load values have also been considered. The accuracy in the prediction is given by the AVG value: the closer to one, the more accurate the evaluation. The measure of the prediction uniformity is given by the COV value: the lower the value, the greater the uniformity. From the AVG and COV values reported in Tables 3 and 4, it is evident that the model proposed here leads not only to the highest accuracy but also to the most uniform predictions of the ultimate load both for CCFTs and RCFTs.

The above considerations are evident also when observing Fig. 4, where the \({N}_{\mathrm{u}}\) values calculated by means of Eqs. (57), (58), (59) and (60) are plotted vs. the experimental values obtained from 97 CCFT tests considered. In addition, in Fig. 5, the theoretical values obtained with Eqs. (63), (61), (62) and (63) are plotted vs. the experimental values for the 35 RCFT tests. In Figs. 4 and 5, in fact, the dots relative to the proposed model are concentrated along the entire bisector line, representing the perfect equality between theoretical and experimental values.

Fig. 4
figure 4

Theoretical vs. experimental ultimate load for CCFT push-out test

Full size image
Fig. 5
figure 5

Theoretical vs. experimental ultimate load for RCFT push-out test

Full size image

To further evaluate the accuracy of the analytical model, prominent evaluation parameters [23] such as \({R}^{2}\) (coefficient of determination), MSE (Mean Square Error), RMSE (Root-Mean-Square Error), MAE (Mean Absolute Error) and MAPE (Mean Absolute Percentage Error) have been calculated by means of Eqs. (64)–(68):

$$R^{2} = 1 - \frac{{\mathop \sum \nolimits_{i = 1}^{n} \left( {A_{i} - F_{i} } \right)^{2} }}{{\mathop \sum \nolimits_{i = 1}^{n} (A_{i} - \overline{A})^{2} }}$$
(64)
$${\text{MSE}} = \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \left( {A_{i} - F_{i} } \right)^{2}$$
(65)
$${\text{MRMSE}} = \sqrt {\frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \left( {A_{i} - F_{i} } \right)^{2} }$$
(66)
$${\text{MAE}} = \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \left| {A_{i} - F_{i} } \right|$$
(67)
$${\text{MAPE}} = \frac{1}{n}\left[ {\frac{{\mathop \sum \nolimits_{i = 1}^{n} \left| {A_{i} - F_{i} } \right|}}{{\mathop \sum \nolimits_{i = 1}^{n} \left| {A_{i} } \right|}}} \right] \cdot 100$$
(68)

where \({A}_{i}\) indicates the analysed value (\({N}_{\mathrm{u},\mathrm{exp}}\)), \({F}_{i}\) represents the estimated value (\({N}_{\mathrm{u}}\)), \(n\) is the number of the considered data and \(\overline{A }\) the mean analysed values.

Note that MSE, RMSE and MAE parameters are scale-dependent, whereas \({R}^{2}\) and MAPE are not and for this reason are much easier to interpret.

The results achieved are presented in Tables 5 and 6 for CCFTs and RCFTs, respectively. Here, a comparison with the existing models has also been developed.

As shown in Tables 5 and 6, \({R}^{2}\) of the analytical model for both CCFTs and RCFTs is higher than that of the existing models. In particular, an \({R}^{2}\) value of 0.30 obtained with the analytical model, vs. − 0.25, − 0.28 and − 1.82 values obtained by other authors for CCFTs and an \({R}^{2}\) value of 0.12 vs. − 0.62, 0.01 and 0.03 from others for RCFTs, demonstrate that the proposed model replicates the experimental values better. Note that with the coefficient of determination used, in Eq. (64), \({R}^{2}\) varies in range [− ∞,1]: when it is 1 the model perfectly represents the data, and a negative value (that is the case of existing analysed models) implies that the mean of experimental result data provides a better fit than the model itself. Results in terms of the MAPE parameter are good in CCFTs, where the 0.37% value obtained with the analytical model proposed are less than 0.41%, 0.45%, and 0.74% obtained from the existing models. As to RCFTs, the MAPE parameter obtained with the analytical model is equal to 1.44, while the existing models provide values of 1.59, 1.42 and 1.15. In the authors’ opinion, a better mean absolute percentage error for RCFTs could have been obtained on the basis of a greater number of experimental results; this aspect is confirmed by the \({R}^{2}\) analysis, according to which the proposed model better replicates the experimental values also for RCFTs, not in agreement with the MAPE results.

6 Application of the Proposed Calculation Method

In this paragraph, the analytical method proposed studies a numerical example of bond stress transfer in a CCFT. Both case A and case B introduced in paragraph 3 of this paper will be taken into account through a detailed explanation of the solution procedure. The following aims to underline how the method proposed is immediately applicable in both cases and is also useful in professional engineering practice.

For the numerical example, a CCFT with external jacket diameter d = 300 mm and jacket thickness t = 10 mm, axially loaded on concrete with a force of N = 200 kN and 900 kN was considered as an application of the proposed calculation method. The calculation of the transferring length and the study of slip, bond stress, steel and concrete stress trend within this domain, were carried out following the calculation model proposed here. For the concrete and steel moduli of elasticity, the values Ec = 30 GPa and Es = 210 GPa were used. The bond stress–slip relationships (Eqs. (2) and (3)), by means of Eq. (4) appear as follows:

$$\left\{ {\begin{array}{*{20}l} {\tau \left( x \right) = 0.896\left( {\frac{s\left( x \right)}{{0.084}}} \right)^{0.5} {\text{for}} s\left( x \right) \le \overline{s}\quad\quad\quad\quad (69)} \\ {\tau \left( x \right) = 0.896 {\text{for}} s\left( x \right) > \overline{s}\quad\quad\quad\quad\quad\quad\quad\quad\,\, (70)} \\ \end{array} } \right.$$

First, the length was calculated so as to reach slip \(\overline{s }\) [Eq. (54)]: \(\overline{L }=1099\mathrm{ mm}\). Thus, assuming that in case A, the transferring length, LA, would be [Eq. (55)]: \({L}_{\mathrm{A},200}=777\mathrm{ mm}\) for N = 200 kN, and \({L}_{\mathrm{A},900}=1282\mathrm{ mm}\) for N = 900 kN, it depends, in fact, on N by means of \({\sigma }_{s0}\) (Eqs. (31) and (32)). The comparison between \({L}_{A}\) and \(\overline{L }\) shows that: for N = 200 kN, LA,200 < \(\overline{L }\), hence \(s\left(L\right)<\overline{s }\) in case A, and for N = 900 kN, LA,900 > \(\overline{L }\), hence \(s\left(L\right)>\overline{s }\) (in case B), for which the transferring length must be calculated by means of Eq. (56). Furthermore, for N = 200 kN the transferring length is \({{L}_{200}=L}_{\mathrm{A},200}=777\mathrm{ mm}\), while for N = 900 KN, the transferring length is \({L}_{900}={L}_{\mathrm{B},900}=1314\mathrm{ mm}\).

The graphs of slip, bond stress, steel and concrete stresses and strains are reported in Figs. 6 and 7, respectively, for N = 200 kN and N = 900 kN. In particular, in observing the graphs regarding the application of load N = 900 kN (Fig. 7), it is important to emphasize that slip \(\overline{s }\) has been reached. In fact, there is a part of the transferring length near the applied load section (\(\overline{L }\) \(\le x\le\) LB,900), where bond stress is constant and equal to τu. The abscissa point corresponding to the achievement of τu (i.e., the starting point of the constant bond stress part), corresponds to the point at which \(s=\overline{s }\), that is \(x=\overline{L }=1086\) mm, as calculated above. Consistently with Eqs. (48), (49), (50) and (51), it can be observed that from this point up to the applied load section, in which \({\sigma }_{\mathrm{s}}=0\), the trend of steel and concrete stresses and strains are linear rather than polynomial.

Fig. 6
figure 6

Slip, bond stress, steel and concrete stresses and strains for N = 200 kN—case A: \(s\left(L\right)<\overline{s }\)

Full size image
Fig. 7
figure 7

Slip, bond stress, steel and concrete stress and strain for N = 900 kN—case B: \(s\left(L\right)>\overline{s }\)

Full size image

This paragraph aims to highlight the usefulness of the method in professional engineering practice. In addition, diagrams of the principal quantities (Figs. 6 and 7), involving the bond stress transfer problem within the transferring length, are plotted using the proposed analytical method which allows readers to notice the substantial difference, in terms of trends, between case A and case B: in case B slip \(s\) exceeds limit slip \(\overline{s }\) with \(x>\overline{L }\) and from this point it is clear that:

  • The bond–slip relationship plasticizes and value τ stops growing, thus remaining constant

  • Steel stress and strain decreases linearly

  • Concrete stress and strain increase linearly.

7 Conclusions

This paper presents a theoretical model for understanding the bond–slip behavior of the steel–concrete interface in CFSTs. The conclusions were based on the elasticity theory and on a nonlinear elastic-perfectly plastic steel–concrete bond–slip relationship. The peculiarity and highlight of the model proposed here are the following:

  • The model refers to a general case of load applied on concrete and gradually transferred onto a steel jacket, but it is not difficult to adapt to the case of load applied on steel and gradually transferred onto concrete.

  • The analytical formulation of the transferring length, that is the length within which the bond stress transfer develops, was obtained in a closed-form expression.

  • The analytical formulation of quantities involved in the problem: bond stress, slip on steel–concrete interface, concrete and steel stresses and strains, were also obtained in a closed-form expression.

  • To validate the model accuracy, the aforesaid formulas were used for the calculation of the ultimate load in CCFT and RCFT push-out samples, and the same ultimate loads were calculated also using empirical expressions of average uniform bond strength proposed in literature. Comparison with the analytical model proposed have led us to conclude that the results of the analytical model are more uniform and accurate. This conclusion indicates that the model is also valid for calculating the other mechanical quantities involved in the bond transferring mechanism between the concrete and steel in the concrete filled steel tubes.