Abstract
A distinctive slope stabilisation method that integrates two well-developed methods for slope stabilisation is analysed in this paper. The slope stabilisation method utilises embedded piles and geogrid-reinforced retaining walls with gabion basket wall facing. To study the effect of this integrated slope stabilisation method on the stability of the slope under the negative impacts of rainfall, a three-dimensional finite element model with fluid–solid coupling is adopted to indicate the rainfall infiltration process and investigate the corresponding slope responses. The shear strength reduction method is applied after fluid–solid coupling analysis to investigate the impact of various rainfall intensities and rainfall patterns on the stability of slopes with different configurations. The results from the comparison of slope responses among various configurations indicate that under the highest rainfall intensity, the integrated method improves the stability of the slope up to \(41.2\%\) and restrains the displacement increment of the road edge to a maximum of \(12.5\) mm. The most critical rainfall pattern for the stability of the slope has also been recognised in terms of the factor of safety and the variation in the negative pore-water pressure of the slope. The numerical results indicate that the back-loaded rainfall pattern always yields the lowest factor of safety and induces the highest loss of matric suction, which can be \(23\) kPa at the toe of the slope. Moreover, a comparison between two construction scenarios under various rainfall intensities was also conducted, which demonstrates that the reinforced filled slope configuration is preferable when the site conditions permit.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Slope failure imposes severe damage on civil structures, causing major economic losses and the losses of lives [1]. Slope instability may be induced by a wide variety of factors, including weather conditions, loss of vegetation, changing topography, unfavourable geological features, or a combination of these factors [2]. The influence of rainfall under unsaturated conditions is of particular importance for the evaluation of slope stability [3, 4]. A wide variety of analytical methods, therefore, have been established to relate the occurrence of slope failures to various rainfall characteristics. Based on historical analysis, landslide-triggering rainfall thresholds have been studied statistically [5,6,7]. Where there are only limited rainfall data or records of slope failure, the threshold of slope instability is identified by deterministic methods [8,9,10]. Where adequate data are available, the relation between rainfall and slope failure can be identified by probabilistic-based methods [11, 12]. The analytical methods mentioned above, however, may have their own limitations, including ignoring the ground conditions, various rainfall intensities, or most importantly, the permeability of the soil that is not constant but depends on the saturation degree of the soil [13]. These limitations may lead to misleading predictions of the slope behaviour, particularly for unsaturated soil. To overcome these limitations, finite element methods (FEMs) have been developed that can compute pore-water pressure and can also consider the coupled effect between the deformation and infiltration of unsaturated porous media [14]. Then, the strength reduction finite element technique can be utilised to evaluate and locate the factor of safety (FoS) of slopes and the corresponding critical slip surface [15].
The negative impact of rainfall on the stability of unsaturated soil slopes has been investigated in detail by FEMs due to its advantages. A previous study [16] investigated the relationship between climatic variables, soil hydraulic properties, and the initial conditions within the slope that may cause instability. A parametric study was conducted [17] to investigate the effect of rainfall intensity, soil properties, and the position of the groundwater table on slope stability. Another study [18] investigated the threshold of the instability of a clay soil slope located in the Mediterranean area induced by climatic variables, including rainfall, average temperature, and evapotranspiration. Moreover, researchers [19] have studied the effect of extreme storms on typical railway embankment stability by numerical simulations and investigated the effect of soil hydraulic characteristics under rainfall conditions.
Based on the studies mentioned above, rainfall significantly influences the unsaturated soil slope stability and can be described in terms of rainfall duration, intensity, and pattern. Regarding the influence of rainfall duration and intensity on unsaturated soil slope stability, a series of parametric studies have been conducted to investigate their effects on pore-water pressure and slope stability [15]. The pore-water pressure was computed by transient seepage analysis, and the stability of the slope was then evaluated by the reduced shear strength method. They concluded that slopes with large permeabilities are more prone to failure under rainfall events that have greater intensities and short durations, while slopes with low soil saturated permeability fail only when the rainfall has a long duration. In addition, researchers [20] also conducted parametric studies to investigate the relative importance of controlling parameters, including the rainfall intensity, in evaluating slope stability under various rainfall conditions. For each parametric study, the seepage analysis of the slope was first performed using the finite element method. Then, the slope stability analysis was conducted by Bishop’s simplified method considering the pore-water pressure obtained from the first step. They found that for a given rainfall duration, there is a threshold rainfall intensity that yields the lowest value of the factor of safety (FoS) of the slope; this value also increases with the increase in the soil saturated permeability. For the studies mentioned above, the research objective mainly focuses on the natural slope, whereas for the current study, the response of the natural slope, the slope with modified geometry for transportation purposes, and the slope with additional stabilisation reinforcement under various rainfall conditions have been investigated. The influence of changing the geometry of the slope and the effect of the slope stabilisation method utilised in the study area have also been investigated. Moreover, the effect of the rainfall pattern on the unsaturated soil slope stability has been studied through FEMs. A three-dimensional parametric study on the groundwater pressure responses of unsaturated cut slopes under typical Hong Kong rainfall patterns with various rainfall intensities, durations, and return periods has been conducted [21]. This study found that for a given rainfall amount and duration, patterns with a high initial intensity yielded the lowest FoS among the three rainfall patterns with the highest intensity at the beginning, middle and end of a rainfall event. Based on the response of groundwater pressure, they also concluded that prolonged rainfall with a relatively higher rainfall amount may induce slope failures at great depths. Another study [22] investigated the impact of antecedent rainfall patterns on the stability of slopes composed of soil with low and high permeabilities. Rainfall data from Singapore were analysed to identify the characteristics of the repeatable rainfall patterns. That study found that the rainfall pattern with the highest intensity at the end of the event resulted in the lowest FoS of the slope composed of high-permeability soil, whereas for the slope composed of low-permeability soil, the rainfall pattern with high initial intensity yielded the lowest FoS. They also concluded that, in general, the antecedent rainfall pattern influences the stability of the slope composed of low-permeability soil more significantly. Regarding the current study, the typical rainfall patterns in the study area have also been identified and then applied to various slope configurations based on the site conditions; therefore, the effect of the local rainfall patterns on the stability of the slopes within the study area can be clearly demonstrated.
This study considers the South Gippsland area of Victoria state, located in southeastern Australia. The annual mean precipitation and temperature in South Asia, including Australia, in the twenty-first century have been predicted by utilising the latest Coupled Model Intercomparison Project Phase 6 (CMIP6) dataset [23]. Based on the simulation results from the CMIP6 model, this study indicates that the predicted annual mean rainfall amount in South Asia will increase 10–20% in the near future. In addition, the predicted annual mean rainfall amount of the mid- and far-future periods will increase further to approximately 10–30%. Currently, in the study area, most road embankment and slope instabilities can be attributed to heavy rainfall [24, 25]. This phenomenon may be more severe based on the findings from the CMIP6 model [23]. Therefore, a distinctive slope stabilisation system comprising piles at the toe of gabion-faced geogrid-reinforced retaining walls (GF-GR-RWs) has been widely utilised to reinforce the slope and the road embankment to minimise the negative effect of rainfall [25]. Previous researchers [26] conducted a numerical study of this distinctive integrated slope stabilisation method by the FEM. The effectiveness of this integrated method was demonstrated by comparing various slope configurations, and an optimisation process for the critical design parameters of the integrated method was conducted by a series of parametric studies. This study found that the integrated method can improve the stability of the slope by approximately \(70.2\%\), and almost 1/3 of the material can be saved after the optimisation process. However, this study considers only the behaviour of the stabilised slope of the integrated method under the effect of gravity without the consideration of the rainfall effect, which is unfavourable for slope stability in the study area. Moreover, while the negative impact of rainfall on the natural slope stability has been investigated in detail by previous studies, the role of the road embankment infrastructure and slope stabilisation work under the impact of rainfall infiltration has received less attention in the literature. In addition, the response of the slopes within the study area that are subject to typical Australian rainfall patterns can be useful for understanding the slope instability situation in the study area, which has not been studied deeply.
In this study, the impact of rainfall on the road embankment infrastructure and the slope stabilisation work used in the Gippsland area to stabilise rainfall-induced slope failures are investigated. The rainfall intensities over a wide range are adopted first to investigate the effect of the distinctive integrated slope stabilisation method on FoS, the critical slip surface, the negative pore-water pressure, the maximum road edge displacement of the slope and the road embankment during the weakening of the soil under rainfall conditions. Three rainfall pattern designs derived from typical Australian patterns are then applied to each slope configuration, and the most critical rainfall pattern for the stability of the slope is recognised by considering the change in pore-water pressure during the saturation process and FoS of the slope. The results indicate that rainfall precipitation affects the stability of the slope configuration reinforced by the integrated method to a lesser extent, and the effect of the integrated system can be clearly demonstrated. Moreover, different responses of various slope configurations to the wide variety of rainfall conditions obtained from the numerical study can also be used as a reference for engineers to appropriately assess the rainfall-induced slope instability issue according to specific site conditions.
2 Study Site
2.1 Site Background
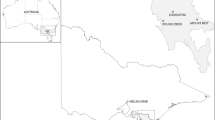
South Gippsland, located in Victoria state in Australia, is a region susceptible to rainfall-induced landslides (Fig. 1). In this area, the landscape mainly consists of maturely dissected, hilly, cleared terrain with some valleys that are relatively youthful, and the land surface is commonly stepped and hummocky. The sharp topographic expression of the fresh landslide becomes significantly subdued within a few decades through weathering or intentional ploughing, although the scars in the earth on the main scarps still remain the dominant features in this region over a longer period. Structurally, this area is composed of the dissected, elevated block of Lower Cretaceous rocks (Narracan Block), and the Lower Cretaceous rocks are also overlain by the Childers Formation sediment, which in turn is usually capped by the Tertiary older volcanic strata [24]. In addition, more than \(90\%\) of the Gippsland area was once covered by woodlands, but much of this has been cleared for the purpose of agriculture, which has imposed a long-term negative influence on slope instability in this area [27]. According to data from the Australian Bureau of Meteorology, Australia’s wettest \(24\)-month period was between April 2010 and March 2012. During this period, \(142\) slope failures occurred in the study area, according to records from the local government authority. In 2011, the occurrence of slope failure was concentrated on the 22nd of March and 21st of July, and the dates of the slope failures in 2012 were the 25th of May and the 4th and 22nd of June. According to the distribution of the large number of slope failures, \(30\%\) of the slope failures occurred around Mount Best (Upper Toora); therefore, the daily rainfall precipitation and the annually accumulated rainfall amounts from Mount Best in 2011 and 2012 are shown in Fig. 2. According to Fig. 2, the dates with high rainfall correspond with the dates of the occurrence of slope failures; therefore, the major reason for the large number of slope failures during 2011 and 2012 can be attributed to excessive rainfall. A review of the slope stability conditions in the study area was also conducted [24, 26], and the slope instability in the region can be explained through the following aspects: (1) steep slopes developed by fault escarpment and stream erosion; (2) the existence of residual soil with lower strength; (3) the existence of expansive clay soil; (4) fissures developed in clay soil that permit water to penetrate deeply into the soil; and (5) the infiltration of rainfall that increases the groundwater level and soil moisture content. Moreover, according to the results of laboratory soil tests and inspections of the soil exposed by the pile borehole at the site, the consistency grade of soils in the South Gippsland region ranges from very soft to stiff, and the consistency generally increases with depth. The soils with high plasticity are more likely to be involved in landslide activity than the other types of soil; however, slope failure was found to occur in the full range of soil types in the study area. The soils also generally have high plasticity and high clay content, and the shear strength of the soil is sensitive to the moisture content and the cohesion component of the soil is affected significantly by the clay content; therefore, the slope instability conditions become relatively worse under the rainfall conditions. In addition, the content of clay also increases with increasing depth, which indicates that slope failures are more likely to occur with the infiltration process of rainwater [24]. These features make the influence of rainfall on slope stability more significant. Therefore, a distinctive integrated slope stabilisation method that comprises conventional GF-GR-RWs with laterally loaded piles has been used widely in this area.
2.2 Stabilisation Construction
The borehole is drilled by a tractor-mounted auger to install the piles prior to constructing the retaining wall. The augering is continued in the weathered bedrock layer to form the space for the pile to embed. The I-beam post is then placed in each hole and supported when the borehole is backfilled by concrete. The I-beam post protrudes \(1\) metre above ground level and is then welded to the steel rail to form a fixed beam, which provides lateral support to the retaining wall.
Then, the GF-GR-RW is constructed adjoining the horizontal rail. Rocks are filled in gabion baskets, each of which is a 1 m cube. Each gabion basket is then connected horizontally with double twisted wire mesh to compose layers of wall facing. Five gabion basket layers are then stacked in a stepped pattern with a 5V:2H gradient. During the stacking process, the middle three layers of the gabion basket are wrapped by the geogrid, and then the tails of the geogrid are extended into the soil as it is backfilled.
2.3 Slope Configurations
The numerical model of each slope configuration is based on the site conditions. The natural slope configuration has a gradient of \(3\mathrm{V}:10\mathrm{H}\), as depicted in Fig. 3a, and then a cutting is made to create the road on the slope (Fig. 3b). An alternative way to construct the road on the slope is to involve filling on the slope (Fig. 3c). Based on these two construction scenarios, two different slope stabilisation configurations are used. For the cut slope configuration, the slope stabilisation system is installed above the road to stabilise the slope and the road embankment (Fig. 3d). For the filled slope configuration, the slope stabilisation system is installed below the road (Fig. 3e). For the reinforced slope configurations, the ratio of centre-to-centre spacing (\(S\)) to the pile diameter (\(D\)) adopted is \(3.5\), based on the site conditions (\(S=1.4 \mathrm{m},D=0.4 \mathrm{m}\)).
3 Theoretical Considerations
3.1 Water Flow in Unsaturated Soils
An empirical function has been used to describe the dependence of the permeability of the soil to water and air on the saturation degree [28]:
where \({a}_{\mathrm{w}}, {b}_{\mathrm{w}}, {c}_{\mathrm{w}}, {a}_{\mathrm{a}}, {b}_{\mathrm{a}}\) and \({c}_{\mathrm{a}}\) are fitting parameters; \({K}_{\mathrm{ws}}\) and \({K}_{\mathrm{as}}\) are the saturated permeability of the soil to water and air, respectively; \({u}_{\mathrm{w}}\) and \({u}_{\mathrm{a}}\) are the pore-water pressure and pore-air pressure; and \(\left({u}_{\mathrm{a}}-{u}_{\mathrm{w}}\right)\) represents the matric suction.
An empirical state surface equation is then adopted to represent the soil–water characteristic curve (SWCC) of unsaturated soil [28]:
where \({S}_{i}\) denotes the residual saturation degree, \({S}_{n}\) represents the maximum saturation degree, and \({a}_{\mathrm{s}}, {b}_{\mathrm{s}}, {c}_{\mathrm{s}}\) are the soil parameters.
The relation among the void ratio, the matric suction, and the net mean stress can be given by [28]:
where \({a}_{\mathrm{e}}\), \({b}_{\mathrm{e}}\), \({c}_{\mathrm{e}}\), and \({d}_{\mathrm{e}}\) are soil parameters, and \(p\) denotes the net mean stress.
The pore air is generally assumed to be connected with the atmosphere, i.e., \(\left({u}_{\mathrm{a}}=0\right)\), which means that the matric suction equals the pore-water pressure. Based on the typical site conditions, the main soil in the study area is clay; a previous study [28] summarises five typical sets of hydraulic parameters of the soil, including clay, to determine the relationship between the volumetric moisture content and matric suction and the relationship between the permeability coefficient and matric suction. The hydraulic characteristics of the clay soil at the slope site can then be determined (Table 1) [24, 25]. The derived curve of the SWCC and the soil permeability function are illustrated in Fig. 4. For the weathered rock layers, as they are still stable under hydraulic conditions, their hydraulic properties are therefore assumed to be the same as those of clay soil to simplify the iteration process, which also imposes a minor influence on the simulation results, except for the saturated coefficient of permeability, which is assumed to be \(1\times {10}^{-6}\) m/s based on the site conditions.
3.2 Shear Strength of Unsaturated Soils
The effective stress of the soil induced by the water flow can be given by [29]:
where \(\sigma \) is the total stress of the soil and \(\chi \) represents the saturation of the soil.
The Mohr–Coulomb failure criterion is used to represent the shear strength of the soil, which can be given by:
where \({\varphi }^{{\prime}}\) denotes the effective friction angle of the soil and \({c}^{{\prime}}\) is the effective cohesion.
Substituting Eqs. (5) into (6), the extended Mohr–Coulomb criterion [30] can be obtained as follows:
The pore air is assumed to be connected to the atmosphere; Eq. (7) can thus be simplified, and the shear strength of the unsaturated soil is as follows:
3.3 Strength Reduction Finite Element Method (SR-FEM)
The stability of the slope is evaluated by the SR-FEM after the seepage analysis. With the increase in the strength reduction factor, the original shear strength decreases continuously until slope failure occurs [31]. The occurrence of slope failure is determined by the nonconvergence of the simulation caused by an abrupt increase in the displacement of the characteristic node in the model [32]. \({c}_{\mathrm{r}}\) and \({\varphi }_{\mathrm{r}}\) after the strength reduction process are as follows:
where \(\mathrm{SRF}\) is the strength reduction factor. The strength reduction factor can be regarded as the FoS of the slope when the slope fails.
4 Numerical Modelling
4.1 Constitutive Models and Material Properties
The commercial finite element code Abaqus 2018 is used for the analysis. In the numerical simulation, the pile is modelled as an isotropic linear elastic material, and the nonlinear behaviour of the steel is modelled by the curve of ‘stress–strain’ [33]. The nonlinear feature of a woven polyester (PET) geogrid (GGW) is modelled by defining the curve of ‘stress–strain’ with a tensile limitation of \(150\) kN/m and a maximum strain of \(15\%\) [34]. Regarding the clay soil, gabion basket, and weathered bedrock, the perfectly elastoplastic model associated with the Mohr–Coulomb failure criterion is adopted and can be expressed as:
where c \(^{{\prime}}\)is the cohesion; \(\varphi ^{{\prime}}\) is the internal angle of friction; \(\theta \) is the Lode’s angle; \({I}_{1}\) is the first invariant of the effective stress tensor; and \({J}_{2}\) is the second invariant of the deviatoric stress tensor [35]. Based on the material characteristics, Table 2 summarises the properties for each component. For the strength properties of gabion baskets, the effective friction angle (\({\varphi }^{{\prime}}\)) and effective cohesion (\({c}^{{\prime}}\)) are determined as \(45^\circ \) and \(560\) kPa based on the direct shear test [36]. The clay soil dilation angle is determined as \(0^\circ \) according to the characteristic of the clay soil, which is normally consolidated [37].
4.2 Boundary Conditions
4.2.1 Displacement Boundary Conditions
For all the slope configurations involved in this study, the displacement of the bottom plane is fixed in all degrees of freedom. The side boundaries perpendicular to the base are constrained in the normal direction to restrict the horizontal displacement.
4.2.2 Hydraulic Boundary Conditions
According to the site conditions, the groundwater depth is \(8\) m for the left edge (designated as \({{H}_{\mathrm{w}}}^{1}\)) and \(5.7\) m for the right edge (designated as \({{H}_{\mathrm{w}}}^{2}\)) (Fig. 5). The contour of the groundwater is basically parallel to the slope surface. The slope surface is a flux boundary on which the surface pore fluid, which equals the rainfall intensity (\({I}_{\mathrm{r}}\)), is applied to represent the rainfall infiltration. The infiltration capacity, (\({f}_{\mathrm{p}}\)), which is the maximum rate of soil-absorbing water, is the highest at the beginning of the rainfall event, then gradually decreases with the infiltration process as the saturation degree of the soil increases, and finally reaches its minimum value, which equals the \({K}_{\mathrm{ws}}\) when the soils are saturated [38]. In addition, there are three following distinct cases of infiltration [39]: (a) \({I}_{\mathrm{r}}< {K}_{\mathrm{ws}}\). For this case, all rainfall infiltrates, and runoff does not occur. (b) \({K}_{\mathrm{ws}}<{I}_{\mathrm{r}}<{f}_{\mathrm{p}}\). During this stage, all rainfall still infiltrates into the soil without runoff. (c) \({K}_{\mathrm{ws}}<{f}_{\mathrm{p}}<{I}_{\mathrm{r}}\). In this case, surface ponding can occur, and due to the slope, runoff forms. To reflect the site conditions as much as possible, a hydraulic boundary with a zero pore-water pressure is applied on the surface of the slope for the following iterations when the third case occurs.
4.3 Interaction Properties and Mesh Configuration
The interface behaviour was modelled by defining the normal contact and tangential contact. The friction coefficient of the tangential contact, tan\(\delta ^{{\prime}}\), is calculated based on [40]as follows:
where \({\varphi ^{{\prime}}}_{\mathrm{min}}\) is the minimum friction angle of neighbouring materials. The surface contact property is summarised in Table 3. For the contact between the I-beam post and the concrete pile, the interaction is defined only as a normal contact and without the relative slide. In addition, the mesh arrangements and the connection within the system between each component are illustrated in Fig. 6. The 8-node brick element (C3D8) is used to discretise the I-beam post, the horizontal steel rail, the pile, the gabion basket wall facing, and the slope, while the 4-node membrane element (M3D4) is used to discretise the geogrid. The mesh arrangements of each component have been improved and optimised several times through the mesh refinement process under the rigorous frame of the contact definition; therefore, the separate mesh scheme for the component and the overall scheme of the mesh arrangement can indicate the site condition appropriately and effectively avoid discrepancies in the stress transmission during the simulation.
4.4 Validation
A typical experiment of saturated–unsaturated transient seepage in soil is simulated and compared to guarantee the effectiveness of the fluid–solid coupling conducted by Abaqus 2018. The simulation example is an experiment conducted on a soil flume [41]. The height, width, and length of this soil flume are \(0.33\) m, \(0.23\) m, and \(3.15\) m, respectively. Fine sand with a porous rate of \(0.44\) and a saturated permeability of 3.3E−3 m/s is used. The relation of the matric suction-saturation degree and the relation of the hydraulic conductivity-saturation degree is defined in Table 4. The hydrostatic condition is generated by a horizontal water table with a height of \(0.1\) m, and then the height of the left water table increases rapidly to \(0.3\) m. The phreatic surface within the soil thus develops over time and finally reaches a stable state. Then, a comparison of the phreatic surface at the different time frames between the experimental results and simulation results is conducted (Fig. 7). It is notable that the observed and simulated trends demonstrate good consistency. Therefore, the validity of Abaqus 2018 in conducting fluid–solid coupling simulations has been ensured.
5 Simulation Design
5.1 Rainfall Intensity
To investigate the influence of rainfall intensities on each slope configuration behaviour, the \(24\)-\(\mathrm{h}\) duration rainfalls with various intensities are determined and used. The various rainfall intensities are determined as a fraction of the soil saturated permeability. Therefore, the intensities of rainfall adopted equal \(3\) mm/h (\(0.083 {K}_{\mathrm{ws}}\)), 6 mm/h (\(0.16 {K}_{ws}\)), 9 mm/h (\(0.25 {K}_{\mathrm{ws}}\)), \(12\mathrm{ mm}/\mathrm{h }\) (\(0.33 {K}_{\mathrm{ws}}\)), \(15\mathrm{ mm}/\mathrm{h }\) (\(0.42 {K}_{\mathrm{ws}}\)), \(18\mathrm{ mm}/\mathrm{h }\) (\(0.5 {K}_{\mathrm{ws}}\)), \(21\mathrm{ mm}/\mathrm{h }\) (\(0.58 {K}_{\mathrm{ws}}\)), \(24\mathrm{ mm}/\mathrm{h }\) (\(0.66 {K}_{\mathrm{ws}}\)), \(27\mathrm{ mm}/\mathrm{h }\) (\(0.75 {K}_{\mathrm{ws}}\)), \(30\mathrm{ mm}/\mathrm{h }\) (\(0.83 {K}_{\mathrm{ws}}\)), and \(33\mathrm{ mm}/\mathrm{h }\) (\(0.92 {K}_{\mathrm{ws}}\)). Note that compared with the rainfall intensity data from the study area, some values of the rainfall intensity adopted in the analysis are relatively high, as the daily rainfall amount may occur in a short duration. This wide range of rainfall intensities can provide more possibilities to consider the extreme rainfall events with short durations. It is also worth noting that as the adopted rainfall intensities are lower than the soil saturated permeability, the rainfall amount is regarded as the net infiltration amount into the soil without consideration of the surface runoff. The rainfall intensities and corresponding rainfall amounts are summarised in Table 5.
5.2 Rainfall Pattern
According to [42], the temporal pattern of rainfall in Australia can be categorised into the following three groups based on the percentage of the time taken for \(50\%\) of the rainfall amount to occur: (a) front-loaded–\(0\) to \(40\%\) of the rainfall duration; (b) middle-loaded–\(40\%\) to \(60\%\) of the rainfall duration; and (c) back-loaded–\(60\%\) to \(100\%\) of the rainfall duration. These three typical Australian rainfall patterns are adopted for the distribution of \(490\mathrm{ mm}\) of rainfall with a \(120\)-\(\mathrm{h}\) duration. To magnify the feature of each rainfall pattern, three functional curves are used to make the \(50\%\) of rainfall occur within the corresponding time frame and to make the highest rainfall intensity, which is fixed at \(12\mathrm{ mm}/\mathrm{h }\), occur at the exact beginning, middle, and end of the rainfall for three patterns (Fig. 8). In South Gippsland, the occurrences of rainfall events (over a duration of 6 h) with front-loaded, middle-loaded and back-loaded rainfall patterns are \(22.7\%\), \(53.7\%\) and \(23.6\%\), respectively [42].
6 Analysis of Results
6.1 Effect of Various Rainfall Intensities
6.1.1 Effect on the FoS
The FoS of each slope configuration under various rainfall intensities was obtained through SR-FEM. Then, a comparison of the FoS was conducted between different slope configurations within each construction scenario to demonstrate the different responses of each slope configuration (Fig. 9). In addition, the effect of the integrated method on improving and maintaining the stability of the slope has been illustrated. Note that the value of the FoS of each slope configuration under various rainfall intensities is determined once the nonconvergence of the calculation occurs, as induced by the rapid displacement increase of the node at the crest of the slope.
Three slope configurations are involved in the first construction scenario, and the FoS of the natural slope configuration decreases from \(1.59\) to \(1.36\), with an increase in the intensity of rainfall from \(0\) to \(33\mathrm{ mm}/\mathrm{h }\) (Fig. 9a). Regarding the cut slope configuration, the FoS decreases gradually from \(1.36\) to \(1.18\). The FoS increases significantly to \(1.76\) after stabilisation by the integrated system under the condition of no rainfall. During the increase in rainfall intensity, the FoS drops to only \(1.66\). In addition, under the condition of maximum rainfall intensity (33 mm/h), such an increase in FoS is \(22.1\%\) between the reinforced cut slope configuration and natural slope configuration, and this value is \(40.7\%\) between the reinforced cut slope configuration and the cut slope configuration. The effect of this integrated method on improving and maintaining slope stability during rainfall infiltration has thus been demonstrated.
The second construction scenario involves filling on the natural slope. Regarding the filled slope configuration, when the intensity of the rainfall increases from \(0\) to \(33\mathrm{ mm}/\mathrm{h }\), the FoS decreases from \(1.31\) to \(1.19\) (Fig. 9b). The FoS of the filled slope configuration increases significantly to \(2.14\) after stabilisation by the integrated method. When the intensity of rainfall increases to 30 mm/h, the FoS of the reinforced filled slope configuration decreases gradually to \(1.94\). When rainfall intensity increases to \(33\mathrm{ mm}/\mathrm{h }\), the FoS decreases significantly to \(1.68\). This phenomenon indicates that the effect of rainfall on the stability of the reinforced filled slope configuration is more significant when the intensity of rainfall exceeds \(30\mathrm{ mm}/\mathrm{h }\). Compared with the filled slope configuration under a rainfall intensity of \(33\mathrm{ mm}/\mathrm{h }\), the FoS increases to \(1.68\) from \(1.19\) after being stabilised by the integrated method, and the increase in the FoS is \(41.2\%\). Therefore, the effect of the integrated method has been illustrated one step further.
6.1.2 Effect on the Critical Slip Surface
The influence of the rainfall intensity on the failure mechanisms has been analysed in this section. It is notable that the contour of the plastic strain is used to indicate the critical slip surface under various rainfall intensities for each slope configuration, and each critical slip surface corresponds to the value of FoS determined by the aforementioned criterion of SR-FEM. The results indicate that for a given duration, which is \(24\) h, the development mechanism of the slip surface of each slope configuration is different.
The critical slip surface of the natural slope configuration changes under various rainfall intensities (Fig. 10). When the rainfall intensity is 3 mm/h (Fig. 10a), the left end of the critical slip surface is at the slope crest, and the right end has a distance of 1/4 of the slope length to the toe of the slope. The contour between the two ends is basically along the interface between the stable and unstable layers. When the rainfall intensity increases to \(33\) mm/h (Fig. 10b), the critical slip surface moves downwards a follows: the left end has a distance of 1/3 of the slope length to the crest of the slope, and the right end is at the toe of the slope. The contour between the two ends is still along the interface.
Critical slip surface of the natural slope configuration: a under a rainfall intensity of \(3\) mm/h, b under a rainfall intensity of \(33\) mm/h (dimensions are illustrated in Fig. 3)
Regarding the cut slope configuration, the critical slip surface is basically the same under all rainfall intensities (Fig. 11a). According to Fig. 11a, the critical slip surface abuts the road embankment facing and develops in the upper part of the slope along a circular path from the toe of the road embankment. After being stabilised by the integrated method above the road, the critical slip surface is changed but remains the same under various rainfall intensities (Fig. 11b). The left end of the critical slip surface extends upwards to the slope crest along the interface between the two layers. It is notable that the critical slip surface exists in the upper part of the slope as the soil arching effect and the pile group effect restrains the unstable soil movements from the upper part to the lower part of the slope. In addition, the critical slip surface length increases significantly, which demonstrates that more soil shear strength is mobilised by the integrated method and contributes to the stability of the slope to a certain extent, and a higher FoS is then obtained.
Critical slip surface of the slope configuration of the first construction scenario under various rainfall intensities: a cut slope configuration, b reinforced cut slope configuration (dimensions are illustrated in Fig. 3)
For the filled slope configuration, the development of the critical slip surface under various rainfall intensities is different (Fig. 12). When the rainfall intensity is 3 mm/h (Fig. 12a), the left end of the critical slip surface is at the inner edge of the roads, and the right end has a distance of 2/3 of the lower slope length to the toe. The critical slip surface is circular within the layer of soil, and then the contour is along the interface between two layers as it reaches the rock layer. When the rainfall intensity increases to 33 mm/h (Fig. 12b), the right end of the critical slip surface extends further and has a distance of 1/4 of the lower slope length to the toe of the slope. The critical slip surface length under a rainfall intensity of \(33\) mm/h is almost twice the critical slip surface under a rainfall intensity of \(3\) mm/h.
Critical slip surface of the slope configuration of the second construction scenario: a filled slope configuration under a rainfall intensity of \(3\) mm/h, b filled slope configuration under a rainfall intensity of \(33\) mmm/h, c reinforced filled slope configuration under a rainfall intensity of \(3\) mm/h, d reinforced filled slope configuration under a rainfall intensity of \(33\) mm/h (dimensions are illustrated in Fig. 3)
After stabilisation by the integrated method, the critical slip surface changes significantly. When the rainfall intensity is \(3\mathrm{ mm}/\mathrm{h}\) (Fig. 12c), the slip surface almost passes through the entire slope. The critical slip surface left end is at the slope crest, and the right end has a distance of 1/4th of the lower slope length to the toe. Most of the slip surface is along the interface between rocks and the soil, except the area behind the embedded pile to the end of the reinforced soil zone, in which the critical slip surface is horizontal. This phenomenon can be attributed to the pronounced soil arching effect and pile group effect, which effectively restrains unstable soil movement; therefore, only the soil above this area can move horizontally. When the rainfall intensity increases to \(33\mathrm{ mm}/\mathrm{h }\) (Fig. 12d), the left end of the critical slip surface abuts the pile group, and the right end reaches almost the toe of the slope. The critical slip surface exists only in the lower part of the slope, which demonstrates that less soil shear strength is mobilised, and the rapid decrease in the FoS with the increase in the intensity of the rainfall from \(30\) to \(33\mathrm{ mm}/\mathrm{h}\) can be explained in this way.
6.1.3 Effect on the Negative Pore-Water Pressure
As the toe of the natural slope configuration has similar trends, the variation in the negative pore-water pressure at the natural slope configuration crest under different rainfall intensities is extracted and analysed (Fig. 13). For a rainfall intensity of 3 mm/h, the pore-water pressure increases to \(-96\) kPa from the initial pore-water pressure of \(-106\) kpa after the \(24\)-\(\mathrm{h}\) rainfall. When the intensity of rainfall reaches \(15\) mm/h, the pore-water pressure increases to \(-54\) kPa. For the maximum rainfall intensity adopted, \(33\) mm/h, the pore-water pressure increases to \(-25\) kPa. This phenomenon indicates that the rainfall intensity imposes a notable impact on the negative pore-water pressure within the slope, and the decrease in the FoS also confirms this relationship.
Pore-water pressure variation in the crest of the natural slope configuration caused by different rainfall intensities (Table 5)
6.1.4 Effect on Road Edge Displacement
The maximum displacement of the road edge of the reinforced cut slope configuration under various rainfall intensities has been compared and analysed (Fig. 14). For the horizontal displacement (Fig. 14a), the value of the inner edge increases from \(70.6\) mm/h under the condition of no rainfall to \(80.8 \mathrm{mm}\) under a rainfall intensity of \(33\) mm/h. Regarding the outer edge of the road, the horizontal displacement increases from \(26.8\) to \(39.3\) mm. The increments in horizontal displacements of the inner edge and outer edge of the road are \(10.2\) mm and \(12.5\) mm, respectively. For the vertical settlement of the road edge (Fig. 14b), the variation in the rainfall intensity has little effect on the inner edge of the road. The vertical settlement of the inner edge increases slightly from \(0.7\) to \(1.7\) mm with increasing rainfall intensity. For the outer edge of the road, the vertical settlement increases from \(32.4\) to \(43.5\) mm. With the increase in the rainfall intensity, the increments in the vertical settlement of the inner edge and the outer edge are \(1\) mm and \(11.1\) mm, respectively, which are acceptable compared with the width of the road.
6.2 Effect of Different Rainfall Patterns
6.2.1 Effect on the FoS
To investigate the effect of the rainfall pattern, the relation between the FoS and the horizontal nodal displacement of each slope configuration is established and compared (Fig. 15). Note that the certain characteristic node selected for all five slope configurations is the node of the slope crest.
For the natural slope configuration under three rainfall patterns (Fig. 15a), the FoS derived from the front-loaded pattern is \(1.58\), the FoS is \(1.56\) for the middle-loaded pattern, and the FoS is \(1.53\) for the back-loaded pattern. For the cut slope configuration (Fig. 15b), the FoS is \(1.33\) for the front-loaded pattern, and the FoS decreases to \(1.32\) for the middle-loaded pattern. The back-loaded pattern yields the smallest FoS, which is \(1.28\). Regarding the reinforced cut slope configuration (Fig. 15c), the FoS derived from the front-loaded pattern is \(1.74\). When the rainfall pattern changes to the middle-loaded pattern, the FoS decreases to \(1.73\). The FoS under the back-loaded pattern is still the smallest, which is \(1.70\). For the filled slope configuration (Fig. 15d), the front-loaded pattern still yields the highest FoS value, which is \(1.30\). The second largest FoS is \(1.29\), which is derived from the middle-loaded pattern. The FoS decreases to \(1.26\) when the back-loaded pattern is applied to the slope. For the reinforced filled slope configuration (Fig. 15e), the FoS is \(2.09\) under the front-loaded pattern. The middle-loaded pattern yields an FoS of \(2.07\). When the rainfall pattern changes to the back-loaded pattern, the FoS decreases to \(1.99\). The front-loaded pattern always yields the highest value of the FoS, followed by the middle-loaded pattern and the back-loaded pattern; therefore, the back-loaded pattern is determined as the most critical rainfall pattern.
6.2.2 Effect on Negative Pore-Water Pressure
To compare and illustrate the effect of the rainfall pattern, the negative pore-water pressure at the toe and crest of the natural slope configuration under different rainfall patterns are both extracted (Fig. 16). For the toe of the slope (Fig. 16a), when the front-loaded pattern is applied, the negative pore-water pressure increases from \(-40 \mathrm{kPa}\) when rainfall begins to \(-26\) kPa after \(49\) h, and then the negative pore-water pressure decreases to \(-30\mathrm{ kPa}\) at the end of the rainfall. Regarding the middle-loaded pattern, the negative pore-water pressure increases to \(-24\mathrm{ kPa}\) at \(t=69\) h. Then, the negative pore-water pressure decreases to \(-26\mathrm{ kPa}\) at the end of the rainfall. For the back-loaded pattern, the negative pore-water pressure increases gradually to \(-17\mathrm{ kPa}\) at the end of the rainfall. The overall reduction in the matric suction at the toe of the natural slope is \(10\mathrm{ kPa}\) for the front-loaded pattern, \(14\mathrm{ kPa}\) for the middle-loaded pattern, and \(23\mathrm{ kPa}\) for the back-loaded pattern. The reduction in the matric suction of the three rainfall patterns confirms the rationality of the FoS obtained from these three rainfall patterns.
Regarding the crest of the natural slope (Fig. 16b), when the front-loaded pattern is applied, the negative pore-water pressure increases rapidly from \(-108\mathrm{ kPa}\) when rainfall begins to \(-71\mathrm{ kPa}\) at \(t=22\) h. Then, the negative pore-water pressure decreases to \(-94\) kPa at the end of the rainfall. When the rainfall pattern changes to the middle-loaded pattern, the negative pore-water pressure increases to \(-64\mathrm{ kPa}\) at \(t=62\) h. The negative pore-water pressure then decreases to \(-89\) kPa. For the back-loaded pattern, the negative pore-water pressure at the slope crest increases to \(-57\mathrm{ kPa}\) at the end of the rainfall. It is worth noting that for the front-loaded and middle-loaded patterns, the negative pore-water pressure decreases again after the peak. This is because the negative pore-water pressure increases when the rainwater starts to infiltrate the slope. With the decrease in the rainfall intensity of the front-loaded and middle-loaded patterns, the infiltration rate of the rainwater through the surface is less than the percolation rate of the rainwater within the slope, and the pore-water pressure above the groundwater table level thus decreases again. Then, the matric suction recovers, and the soil shear strength increases. As a result, a higher FoS results for the front-loaded and the middle-loaded pattern. In other words, the rainfall patterns mainly influence the infiltration characteristics of the rainwater through the slope surface and thus influence the matric suction of slopes. The phenomenon that the front-loaded pattern yields the highest FoS for the five slope configurations, followed by the middle-loaded pattern and the back-loaded pattern, can be explained from this aspect.
7 Discussion
The response of each slope configuration to different rainfall intensities and different rainfall patterns has been studied by the SR-FEM with the consideration of fluid–solid coupling. In this section, the comparison of the FoS between two construction scenarios, the comparison of the development mechanism of the critical slip surface between each slope configuration, and the influence of the infiltrated rainwater amount on the stability of the slope are discussed.
The comparison of the FoS under different rainfall intensities between two slope configurations, the cut slope configuration and the filled slope configuration, is conducted (Fig. 17). The FoS values of the cut slope configuration are higher than that of the filled slope configuration under the conditions without rainfall, and they are \(1.36\) and \(1.31\), respectively. With the increase in rainfall intensity, the FoS of the cut slope configuration decreases to \(1.18\), while the FoS of the filled slope configuration decreases to \(1.19\). The reduction in the FoS of the cut slope configuration is \(0.18\), which is larger than that of the filled slope configuration, which is \(0.12\); therefore, the effect of the rainfall intensity on the cut slope configuration is more significant than that on the filled slope configuration.
After reinforcement by the integrated system (Fig. 18), the FoS of the reinforced cut slope configuration increases to \(1.76\) under the conditions without rainfall, and the FoS of the reinforced filled slope configuration increases to \(2.14\). The increase in the FoS of the reinforced filled slope configuration is \(0.83\), which is much larger than that of the reinforced cut slope configuration, which is \(0.39\). When the intensity of rainfall is less than \(30\) mm/h, the FoS of the reinforced filled slope configuration is larger than that of the reinforced cut slope configuration, and the difference is approximately \(0.30\). When the intensity of rainfall reaches \(33\) mm/h, the FoS of the reinforced filled slope configuration decreases significantly to \(1.68\), and the FoS values of the two slope configurations are basically the same, which indicates that a rainfall intensity larger than \(30\) mm/h influences the stability of the reinforced filled slope configuration more significantly. The rapid decrease in the FoS of the reinforced filled slope configuration when the rainfall intensity reaches \(33\) mm/h can be attributed to different failure mechanisms of the slope under various rainfall intensities. When the rainfall intensities range from \(3\) to \(30\) mm/h, a thorough critical slip surface along the full length of the slope is formed, which indicates that more shear strength of the soils has been mobilised and the integrated method also contributes effectively to the anti-sliding force. When the rainfall intensity increases to \(33\) mm/h, the lower part of the slope that abuts the integrated method slides first, and therefore, a rapid decrease in the FoS occurs. It is also worth noting that the reinforced cut slope configuration is more stable with the increase in rainfall intensity, as the overall reduction in the FoS is \(0.1\) for the reinforced cut slope configuration and \(0.46\) for the reinforced filled slope configuration.
The critical slip surface under different rainfall intensities is different for each slope configuration. For the cut slope configuration and the reinforced cut slope configuration, the critical slip surface is always kept the same. For the remaining three slope configurations involved, the natural slope configuration, the filled slope configuration, and the reinforced filled slope configuration, the critical slip surface changes with the variation in the rainfall intensity. This phenomenon can be attributed to different factors controlling the slope stability for each configuration. The gradient of the road embankment of the cut slope configuration and the reinforced cut slope configuration is relatively steep; therefore, the influence of this factor on the development mechanism of the critical slip surface is more significant than the negative pore-water pressure variation within the slope induced by rainwater infiltration. Regarding the other three slope configurations, the end and length of the critical slip surface change with the variation in rainfall intensity, which indicates that the loss of matric suction induced by the infiltrated rainwater is the factor controlling the development mechanism of the critical slip surface for these three slope configurations.
For a given rainfall amount, which is \(490\) mm distributed over \(120\)-\(\mathrm{h}\), the FoS values of the natural slope configuration induced by the three rainfall patterns are \(1.53\), \(1.56\) and \(1.58\). Compared with the rainfall amount, which is \(504\) mm distributed uniformly over \(24\)-\(\mathrm{h}\) (\(21\) mm/h) (No. 7 in Table 5), the FoS of the natural slope configuration is \(1.51\). The difference between these two rainfall amounts is \(14\) mm, and the corresponding difference in the FoS of the natural slope configuration between these two rainfall events ranges from \(0.02\) to \(0.07\). This phenomenon indicates that for a given initial groundwater level, the stability of the slope is mainly controlled by the infiltrated amount of rainwater under rainfall conditions.
8 Conclusion
To address the issue of the instability of the slope and the road embankment induced by rainfall precipitation in South Gippsland, an integrated slope stabilisation method that comprises a gabion-faced geogrid-reinforced retaining wall and embedded piles is used. In this study, the characteristics of the rainfall with respect to the rainfall intensity and the rainfall pattern were applied to various slope configurations in the study area. Then, the response of each slope configuration to various rainfall conditions was revealed, and the effect of the integrated method in improving and maintaining the stability of the slope under rainfall conditions was demonstrated. The most critical rainfall pattern for the slope stability was also recognised through the comparison of the representative hydraulic and mechanical indicators. The following conclusions can be drawn:
-
1.
For a given duration, the rainfall intensity imposes a significant impact on the representative indicators of the stability evaluation of each slope configuration. With the increase in rainfall intensity, the FoS of each slope configuration decreases continuously, the displacement of the road edge increases, and the loss of matric suction also increases rapidly. For the reinforced slope configuration, including the reinforced cut slope configuration and the reinforced filled slope configuration, the rainfall intensity influences the stability of the slope to a lesser extent.
-
2.
The failure mechanism of each slope configuration subjected to various rainfall intensities has different modes. For the cut slope configuration and the reinforced cut slope configuration, the critical slip surface is constant when the rainfall intensity increases. For the other three slope configurations, the pattern of the critical slip surface varies with the increase in rainfall intensity.
-
3.
For a given rainfall amount and duration, three designed rainfall patterns derived from Australian typical rainfall patterns, the front-loaded rainfall pattern, the middle-loaded rainfall pattern, and the back-loaded rainfall pattern, influence the stability of each slope configuration to various degrees. The front-loaded rainfall pattern always yields the highest FoS of the slope, followed by the middle-loaded rainfall pattern and the back-loaded rainfall pattern; therefore, the back-loaded rainfall pattern is recognised as the most critical rainfall pattern for the stability of the slope.
-
4.
At the crest and toe of the natural slope configuration, the variation in the negative pore-water pressure induced by the three typical rainfall patterns exhibits different tendencies. In general, the loss of the matric suction of each rainfall pattern at both the toe and crest can also confirm the most critical rainfall pattern for slope stability.
The response of each slope configuration subjected to various rainfall intensities and three typical rainfall patterns has been revealed, and the effectiveness of the integrated slope stabilisation method has also been illustrated clearly. For the site at which it is suitable to install the integrated slope stabilisation system both above or below the road, priority should be given to filled slope configurations, as it yields a relatively higher FoS in most cases within the range of the rainfall intensities adopted in this analysis. In addition, by understanding the failure mechanism of each slope configuration under various rainfall conditions through this study prior to the stabilisation of the slope, the scheme of the stabilisation of the slope can be improved and optimised by considering the specific surrounding conditions efficiently. As the tendency of extreme rainfall events with short durations (i.e., \(10\) and \(30\) min, and \(1\) and \(3\) h) is increasing in the Gippsland area [43], flash floods are likely to occur, and the stability of the slopes will also be influenced significantly. Therefore, further developments in the slope stability analysis for the study area with the consideration of rainfall precipitation should focus on the rainfall runoff on the slope surface.
References
Wu XZ (2015) Development of fragility functions for slope instability analysis. Landslides 12(1):165–175. https://doi.org/10.1007/s10346-014-0536-3
Arairo W, Prunier F, Djeran-Maigre I, Millard A (2014) Three-dimensional analysis of hydraulic effect on unsaturated slope stability. Environ Geotech 3(1):36–46. https://doi.org/10.1680/envgeo.13.00099
Vahedifard F, Mortezaei K, Leshchinsky BA, Leshchinsky S, Lu N (2016) Role of suction stress on service state behavior of geosynthetic-reinforced soil structures. Transp Geotech 8:45–56. https://doi.org/10.1016/j.trgeo.2016.02.002
Bordoloi S, Hussain R, Garg A, Sreedeep S, Zhou WH (2017) Infiltration characteristics of natural fiber reinforced soil. Environ Geotech 12:37–44. https://doi.org/10.1016/j.trgeo.2017.08.007
Terlien MT (1998) The determination of statistical and deterministic hydrological landslide-triggering thresholds. Eng Geol 35(2–3):124–130. https://doi.org/10.1007/s002540050299
Aleotti P (2004) A warning system for rainfall-induced shallow failures. Eng Geol 73(3):247–265. https://doi.org/10.1016/j.enggeo.2004.01.007
Martelloni G, Segoni S, Fanti R, Catani F (2012) Rainfall thresholds for the forecasting of landslide occurrence at regional scale. Landslides 9(4):485–495. https://doi.org/10.1007/s10346-011-0308-2
Gasmo JM, Rahardjo H, Leong EC (2000) Infiltration effects on stability of a residual soil slope. Comput Geotech 26(2):145–165. https://doi.org/10.1016/S0266-352X(99)00035-X
Claessens L, Schoorl JM, Veldkamp A (2007) Modelling the location of shallow landslides and their effects on landscape dynamics in large watersheds: an application for Northern New Zealand. Geomorphology 87(1–2):16–27. https://doi.org/10.1016/j.geomorph.2006.06.039
Harp EL, Reid ME, McKenna JP, Michael JA (2009) Mapping of hazard from rainfall-triggered landslides in developing countries: examples from Honduras and Micronesia. Eng Geol 104(3–4):295–311. https://doi.org/10.1016/j.enggeo.2008.11.010
Dai FC, Lee CF (2003) A spatiotemporal probabilistic modelling of storm-induced shallow landsliding using aerial photographs and logistic regression. Earth Surf Proc Land 28(5):527–545. https://doi.org/10.1002/esp.456
Berti M, Martina ML, Franceschini S, Pignone S, Simoni A, Pizziolo M (2012) Probabilistic rainfall thresholds for landslide occurrence using a Bayesian approach. J Geophys Res-Earth. https://doi.org/10.1029/2012JF002367
Ng CW, Shi Q (1998) A numerical investigation of the stability of unsaturated soil slopes subjected to transient seepage. Comput and Geotech 22(1):1–28. https://doi.org/10.1016/S0266-352X(97)00036-0
Wu LZ, Selvadurai AP (2016) Rainfall infiltration-induced groundwater table rise in an unsaturated porous medium. Environ Earth Sci 75(2):1–11. https://doi.org/10.1007/s12665-015-4890-9
Cai F, Ugai K (2004) Numerical analysis of rainfall effects on slope stability. Intl J Geomech 4(2):69–78. https://doi.org/10.1061/(ASCE)1532-3641(2004)4:2(69)
Tsaparas I, Rahardjo H, Toll DG, Leong EC (2002) Controlling parameters for rainfall-induced landslides. Comput Geotech 29(1):1–27. https://doi.org/10.1016/S0266-352X(01)00019-2
Rahardjo H, Nio AS, Leong EC, Song NY (2010) Effects of groundwater table position and soil properties on stability of slope during rainfall. J Geotech Geoenviron 136(11):1555–1564. https://doi.org/10.1061/(ASCE)GT.1943-5606.0000385
Pedone G, Ruggieri G, Trizzino R (2018) Characterisation of climatic variables aimed at identifying instability thresholds in clay slopes. Geotech Lett 8(3):231–239. https://doi.org/10.1680/jgele.18.00020
Feng JW, Zhang LL, Gao L, Feng SJ (2019) Stability of railway embankment of China under extreme storms. Environ Geotech 6(5):269–283. https://doi.org/10.1680/jenge.17.00043
Rahardjo H, Ong TH, Rezaur RB, Leong EC (2007) Factors controlling instability of homogeneous soil slopes under rainfall. J Geotech Geoenviron 133(12):1532–1543. https://doi.org/10.1061/(ASCE)1090-0241(2007)133:12(1532)
Ng CW, Wang B, Tung YK (2001) Three-dimensional numerical investigations of groundwater responses in an unsaturated slope subjected to various rainfall patterns. Can Geotech J 38(5):1049–1062. https://doi.org/10.1139/t01-057
Rahimi A, Rahardjo H, Leong EC (2011) Effect of antecedent rainfall patterns on rainfall-induced slope failure. J Geotech Geoenviron 137(5):483–491. https://doi.org/10.1061/(ASCE)GT.1943-5606.0000451
Almazroui M, Saeed S, Saeed F, Islam MN, Ismail M (2020) Projections of precipitation and temperature over the South Asian countries in CMIP6. Earth Syst Environ 4(2):297–320. https://doi.org/10.1007/s41748-020-00157-7
Brumley J (1983) Slope stability in the Strzelecki Ranges, Victoria. In: Knight MJ, Minty EJ, Smith RB (eds) Case studies in engineering geology, hydrogeology and environmental geology, Australia. Geological Society of Australia, Hornsby, pp 127–147
Smith J (2014) Rapid and progressive deterioration of local road assets caused by slope instability in regional Victoria, Australia. 1st international conference on infrastructure failures and consequences, July 16–20, Melbourne, Australia
Wang Y, Smith JV, Nazem M (2021) Optimisation of a slope-stabilisation system combining gabion-faced geogrid-reinforced retaining wall with embedded piles. KSCE J Civ Eng 25:4535–4551. https://doi.org/10.1007/s12205-021-1300-6
Adelana SM, Heaven MW, Dresel PE, Giri K, Holmberg M, Croatto G, Webb J (2020) Controls on species distribution and biogeochemical cycling in nitrate-contaminated groundwater and surface water, Southeastern Australia. Sci Total Environ 726:138426. https://doi.org/10.1016/j.scitotenv.2020.138426
Alonso E, Gens A, Lloret A, Delahaye C (1995) Effect of rain infiltration on the stability of slopes. In: 1st international conference on unsaturated soils, September 6–8, Paris, France
Wu TH (1967) Soil mechanics. Allyn and Bacon Inc, Boston
Fredlund DG, Rahardjo H (1993) Soil mechanics for unsaturated soils. Wiley, New York
Griffiths DV, Lane PA (1999) Slope stability analysis by finite elements. Geotechnique 49(3):387–403. https://doi.org/10.1680/geot.1999.49.3.387
Huang M, Jia CQ (2009) Strength reduction FEM in stability analysis of soil slopes subjected to transient unsaturated seepage. Comput Geotech 36(1–2):93–101. https://doi.org/10.1016/j.compgeo.2008.03.006
El-Reedy MA (2013) Concrete and steel construction: quality control and assurance. CRC Press, Boca Raton
Hussein MG, Meguid MA (2016) A three-dimensional finite element approach for modeling biaxial geogrid with application to geogrid-reinforced soils. Geotext Geomembranes 44(3):295–307. https://doi.org/10.1016/j.geotexmem.2015.12.004
Abaqus/Standard (2018) Abaqus version 6.18 user’s manual, Providence, Rhode Island, USA
Jiang Y, Wang X (2011) Stress-strain behavior of gabion in compression test and direct shear test. In: 3rd international conference on transportation engineering, July 23–25, Chengdu, China
Vermeer PA, De Borst R (1984) Non-associated plasticity for soils, concrete and rock. Heron 29(3):1–64
Delleur JW (2006) The handbook of groundwater engineering. CRC Press, Boca Raton
Mein RG, Larson CL (1973) Modeling infiltration during a steady rain. Water Resour Res 9(2):384–395. https://doi.org/10.1029/WR009i002p00384
Gu M, Collin JG, Han J, Zhang Z, Tanyu BF, Leshchinsky D, Ling HI, Rimoldi P (2017) Numerical analysis of instrumented mechanically stabilized gabion walls with large vertical reinforcement spacing. Geotext Geomembranes 45(4):294–306. https://doi.org/10.1016/j.geotexmem.2017.04.002
Akai K, Ohnishi Y, Nishigaki M (1977) Finite element analysis of saturated-unsaturated seepage in soil. Jpn Soc Civil Eng 264:87–96
Ball JE, Babister MK, Nathan R, Weinmann PE, Weeks W, Retallick M, Testoni I (2019) Australian rainfall and runoff: a guide to flood estimation. Commonwealth of Australia, Canberra
Yilmaz AG, Perera BJ (2015) Spatiotemporal trend analysis of extreme rainfall events in Victoria, Australia. Water Resour Manag 29(12):4465–4480. https://doi.org/10.1007/s11269-015-1070-3
Acknowledgements
The assistance from the South Gippsland Shire Council staff during the site visit is highly appreciated by the author. The numerical simulation was processed by the facility of NCI (National Computational Infrastructure) ANU.
Funding
Open Access funding enabled and organized by CAUL and its Member Institutions.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
On behalf of all authors, the corresponding author states that there is no conflict of interest.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Wang, Y., Smith, J.V. & Nazem, M. Effect of Various Rainfall Conditions on the Roadside Stabilisation of Slopes in Gippsland. Int J Civ Eng 21, 173–192 (2023). https://doi.org/10.1007/s40999-022-00752-x
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40999-022-00752-x