1 Introduction

In the context of modeling dynamic soil–structure interaction (SSI) systems, one method of substructuring the models is by calculation of impedance functions. Instead of computing the complete system, the model is subdivided and impedance functions are calculated from the soil–foundation subpart before being applied to the structure. In addition to efficiency, substructuring the system can also give better insight into the dynamic behavior of the soil–foundation system since it can be studied without the coupled effects of the structure.

The impedance function is commonly expressed in complex numbers:

$$\begin{aligned} Z(\omega )=k_{\text {d}}(\omega )+i\omega c_{\text {d}}(\omega ), \end{aligned}$$
(1)

where \(k_{\text {d}}\) is the dynamic stiffness coefficient, \(c_{\text {d}}\) is the dashpot coefficient, \(\omega\) is the cyclic frequency of excitation, and \(i=\sqrt{- \, 1}\). The soil–foundation system has different behaviors depending on whether the frequency of excitation is below or above the fundamental frequency [1]. At frequencies below the fundamental frequency, only material damping contributes to the imaginary part of the impedance function. At frequencies greater than the fundamental frequency, wave propagation adds high geometrical damping to the imaginary part. The difference in behavior can be crucial to the SSI response, and is especially relevant in the cases of shallow soil strata which can have relatively high fundamental frequencies.

Field experiments validating impedance functions are limited in number. Whereas some previous experiments have been performed at sites with substantial soil depths [2], others have included full-sized buildings [3] or both [4]. Recent studies have included complete SSI systems where minor structures are mounted to shallow foundations on top of well-investigated soil strata and exposed to controlled dynamic loading [5,6,7]. Many of these field tests are performed on deep strata of cohesive soil, and different results can be expected for shallow strata of frictional soil on bedrock.

A soil–foundation system is typically defined by a soil stratum and a massless and rigid foundation, and can be classified by its material and geometric characteristics [8] including the shape of the foundation, the embedment of the foundation, and the soil type profile (depth and the material properties). Impedance functions have been published in many journal papers and have been compiled in handbooks to give structural engineers simple tools to take SSI into account in design (collections of impedance functions can be found in Gazetas [9] or Sieffert [10]). Solutions for the impedance functions from the literature are, in many cases, given for a specific set of features, such as for circular surface foundations on layered media of infinite depth [11], circular embedded foundations on a homogeneous stratum on bedrock [12], and other specific assumptions [1, 13, 14]. Although the previously mentioned studies fully explore the effects of one or two of the specific features in each individual paper, when it comes to combinations of features that are not given in the literature, it may be difficult for the engineer to find the relevant model assumptions to use in a specific project and what consequences to expect. In order to fill that gap, this paper investigates the effects of the embedment of the foundation, the variation of the modulus with the depth, and the depth of the stratum on bedrock in different combinations. Further, the effects of applying a permanent load to the soil–foundation system and updating the spatial distribution before performing linear dynamic analyzes are introduced.

High-amplitude dynamic loading, such as earthquake loading, and dynamically sensitive soil–foundation systems, including poor soil conditions, result in high shear strains, and strains larger than \(10^{-5}\) induce nonlinear soil behavior [15]. Nonlinear [16, 17] or equivalent-linear [18, 19] models can be used to address this behavior. However, in many cases, the soil–foundation systems are less sensitive and the dynamic loads more modest, for example, bridge foundations on frictional soils exposed to train loading. In such cases, the shear strains due to dynamic loading remain in the elastic range [20], and a nonlinear dynamic analysis is uncalled-for. Furthermore, the structure’s self-weight may be relatively heavy, and the effect of permanent load on the modulus of the soil can be relevant. Empirical relationships describing the modulus nonlinearity can be used to calculate the modulus resulting from loading. Not only will the modulus be decreased from the shear strains, but it will also be increased due to the rise in mean effective stress. To the authors’ knowledge, the effect of permanent load on impedance functions have not been studied either numerically or experimentally.

The purpose of this article is to show the effects of model assumptions on the dynamic impedance functions of shallow foundations. The article aims at filling the gap in the literature by investigating the combined effects of model assumptions from a practical point of view. Two main objectives of the study are defined. The first was to study the implications of model assumptions, including the embedment of the foundation, the variation of the modulus with the depth, and the permanent load. Impedance functions calculated from the models with varying levels of idealization are compared in the paper. The second objective was to quantify the influence of permanent load in relation to the soil modulus coefficient and stratum depth. For this purpose, a parametric study was performed. To fulfill the objectives, numerical models using finite elements (FE) were created. The shallow foundation was given a fixed geometry and was assumed to be rigid and massless. The soil strata consisted of frictional soil supported by bedrock. Whereas the permanent load of the structure was included in the soil-foundation FE model in order to consider its effect on soil properties, the mass of the structure was not. This mass will be taken into account when the impedance functions are attached to the structure. The concrete slab and the concrete pier of the substructure are accordingly not introduced in the soil–foundation system; however, the geometry of the part of the substructure that is in contact with the soil is required to calculate the impedance functions. The spatial variation of the modulus of elasticity caused by the permanent load was updated for each element, considering low-strain modulus and modulus reduction relationships. Linear dynamic analyses were then performed on the updated models, and the impedance functions were calculated. The dynamic loading was assumed to affect the soil within the linear elastic range, and the impedance functions are valid in the serviceability limit state.

The soil and foundation parameters were chosen in the context of high-speed railway (HSR) bridges and Swedish soil conditions. Swedish geology is dominated by glacial soil masses on top of high-quality bedrock [21]. At many locations, lodgment moraine overlays bedrock, possibly covered by clay or silt layers. For shallow strata consisting of frictional soil, shallow foundations may be suitable for HSR bridges. Such soil deposits are limited in depth, and the maximum depth considered in this study was assumed to be 8 m. The embedment depth of a foundation is typically determined by the frost-free depth, which in Sweden is considered at 1.1-2.5 m.

The article has the following structure. In Sect. 2, empirical relationships of the modulus of frictional soils are presented. In Sect. 3, details of the numerical studies are given. In Sect. 4, the numerical model and the calculation procedure are described. The results are presented in Sect. 5. Finally, the study is summarized and conclusions are given in Sect. 6.

2 Soil Properties

2.1 Small-Strain Shear Modulus

The small-strain shear modulus of soil has been studied empirically by several authors for soil types ranging from cohesive to frictional, and many suggestions for formulas have been proposed [22,23,24]. Seed and Idriss [25] suggested a simplified formula for the small-strain shear modulus of frictional soil:

$$\begin{aligned} G_{{0}}=K_{{0}}(\sigma ')^{d} \end{aligned}$$
(2)

where \(K_{{0}}\) is the soil modulus coefficient, d is the stress exponent, and \(\sigma '\) is the mean effective stress. \(K_{{0}}\) and d are soil type specific constants. The Swedish design recommendations [26] have adopted this formula and adjusted it for Swedish conditions. In the recommendations, \(K_{{0}}\) ranges from 15,000 to 30,000 where the first value corresponds to sand and the latter to crushed fill material. Furthermore, \(d=1/2\) and the stress is inserted in kPa.

The mean effective stress \(\sigma '\) can be subdivided into two additive parts. For frictional soil, the stress in the undisturbed in situ soil is commonly estimated by the confined effective stress based on the coefficient of lateral earth pressure [27]:

$$\begin{aligned} \sigma '_{0}=\sigma '_{\text {v}} \frac{1+2k}{3}, \end{aligned}$$
(3a)

where this approximate relationship can be used:

$$\begin{aligned} k=1-\sin (\phi '), \end{aligned}$$
(3b)

Here, \(\sigma '_{\text {v}}\) is the effective vertical stress, k is the coefficient of lateral earth pressure, and \(\phi '\) is the drained friction angle. Assuming no ground water, the effective vertical stress \(\sigma '_{\text {v}}\) can be calculated with \(\rho g z\) where \(\rho\) is the density, g is the gravity constant, and z is the depth from the soil surface. External load adds to \(\sigma '\) by the mean effective stress

$$\begin{aligned} \sigma '_{\text {m}}=\dfrac{\sigma '_x+\sigma '_y+\sigma '_z}{3}, \end{aligned}$$
(4)

where \(\sigma '_x\), \(\sigma '_y\), and \(\sigma '_z\) are the effective normal stresses. Finally, the resulting stress becomes

$$\begin{aligned} \sigma '=\sigma '_{0}+\sigma '_{\text {m}}. \end{aligned}$$
(5)

2.2 Normalized Modulus Reduction

The reduction in modulus and increase in material damping ratio due to loading have been evaluated empirically in numerous studies for soil gradations ranging from cohesive to frictional soils [28,29,30]. In recent decades, researchers have aimed at collecting data from empirical studies and describing the nonlinear relationships using statistical tools. In Ref. [31], a statistical analysis of empirical data from resonant column tests was conducted. This produced a set of 18 dimensionless parameters describing the normalized modulus reduction curves and material damping ratio curves. The 18 parameters can be chosen to get either mean values or variances of the curves, and their values are dependent on the soil type. The normalized modulus reduction curve is calculated with

$$\begin{aligned} \frac{G}{G_{0}}=\frac{1}{1+\left( \frac{\gamma }{\gamma _{\text {r}}}\right) ^a}, \end{aligned}$$
(6)

where \(\gamma\) is the current shear strain, \(\gamma _{\text {r}}\) is the reference shear strain, and a is the curvature coefficient. The formulas for \(\gamma _{\text {r}}\) and a are found in [31] and require, in addition to the 18 dimensionless parameters, the plasticity index, over-consolidation ratio, and stress in the soil. Only soils with gradations ranging from clay to sand were included. However, the difference in normalized modulus reduction curves between different gradations of frictional soils is relatively small [30, 32]. A comparison between the mean normalized modulus reduction curve of gravelly soils by Rollins et al. [30] and the corresponding curve for sand in Ref. [31] shows good agreement.

The shear strain can be calculated from the effective octahedral shear strain [33],

$$\begin{aligned} \gamma =\frac{\alpha }{3}\sqrt{(\varepsilon _x-\varepsilon _y)^2+(\varepsilon _x-\varepsilon _z)^2+(\varepsilon _y-\varepsilon _z)^2+6(\gamma _{xy}^2+\gamma _{xz}^2+\gamma _{yz}^2)}, \end{aligned}$$
(7)

where \(\varepsilon _i\) and \(\gamma _{ij}\) are components of the strain vector and \(\alpha =0.65\). This shear strain measure has been used in previous studies [17, 19].

3 Numerical Studies

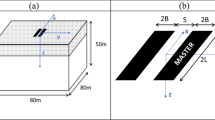
This paper presents two studies: a model assumptions study and a parametric study. A fixed geometry of the foundation was used in all numerical simulations, and an overview of the FE model including the dimensions of the foundation is presented in Fig. 1. The foundation was regarded as massless and rigid. The dimensions of the foundation are as follows: \(L=9.4\) m, \(B=3.3\) m, the thickness of the slab was 1.0 m, the length of the support wall was 7.0 m, and the thickness of the support wall was 0.9 m. \(H_{1}\) is the soil depth underneath the bottom of the foundation, \(H_{2}\) is the embedment depth and R is the radius of the FE model. The FE model is further described in Sect. 4.1.

Fig. 1
figure 1

A cross-section of the finite element model

Full size image

The material properties of the soil were chosen from typical values of frictional lodgment moraine [34] and were assumed constant in all calculations. The following material properties were chosen for all cases: material damping ratio \(\xi =\) 2.0%; density \(\rho =\) 2000 kg/m3; Poisson’s ratio \(\nu =\) 0.25; friction angle \(\phi '=\) 45 deg; stress exponent \(d=\) 1/2, and gravity constant \(g=\) 9.81 m/s2.

The permanent load was applied as a force P. In order to relate the load to the size of the foundation, the load is presented as a pressure q obtained from dividing the force P with the foundation’s bottom surface area. The following values were taken: \(q=\) (0, 220, 500) kPa. According to the Swedish design requirements, the upper limit on the pressure of shallow foundations on top of lodgment moraine on bedrock is 600 kPa [35].

The modulus at the surface of the stratum goes toward zero due to Eq. 2. This can cause poor conditioning of the elements because elements with high modulus are next to elements of low modulus, which can be particularly sensitive in calculation of impedance functions from surface foundations. In order to avoid this, a lower limit for the modulus corresponding to the value at a depth of 0.2 m was chosen.

3.1 Model Assumptions Study

The effects of the model assumptions on the impedance functions were studied by investigating four cases as shown in Fig. 2. It was decided that the fundamental frequency of all cases should be the same. This choice was made based on the fact that the behavior of the soil–foundation system is essentially different at frequencies below compared to above the fundamental frequency of the soil stratum, and fixing it was considered to be the best way to compare the models. In order to get the fundamental frequency of the homogeneous stratum to match the fundamental frequency of the stratum with a modulus varying with depth, the modulus value of the homogeneous soil stratum can be obtained by calculating an equivalent depth \(z_{\text {eq}}\) [36, 37]. \(z_{\text {eq}}\) determines the depth at which the equivalent modulus value \(G_{\text {eq}}\) of the modulus varying with the depth \(G(K_{{0}},\sigma '_{0})\) is taken from. \(G_{\text {eq}}\) is then applied to the homogeneous stratum and the equivalent wave speed \(v_{\text {eq}}\) gives the fundamental period \(T=4H/v_{\text {eq}}\), where H is the total stratum depth. With \(v_{\text {eq}}\) being the P-wave speed, T is the vertical fundamental period, and with \(v_{\text {eq}}\) being the S-wave speed, T is the horizontal fundamental period. In this work, since \(d=\) 1/2 in Eq. 2, the equivalent depth was calculated to \(z_{\text {eq}}= 0.64 H\).

Fig. 2
figure 2

Cases considered in the model assumptions study

Full size image

The model assumption cases had the following properties:

  • Case (a): Surface foundation on stratum of homogeneous soil. No permanent load.

  • Case (b): Embedded foundation in stratum of homogeneous soil. No permanent load.

  • Case (c): Surface foundation on stratum with modulus varying with the depth. Includes permanent load P.

  • Case (d): Embedded foundation in stratum with modulus varying with the depth. Includes permanent load P.

The following parameters were chosen for all the models: \(H_1=\) 8 m and \(K_{{0}}=\) 30,000, corresponding to a deep soil stratum consisting of stiff lodgment moraine. The embedment depth was fixed at \(H_2=\) 1.6 m. The modulus of Case (a) and Case (b) was calculated to \(G_{\text {eq}}\) = 240 MPa.

3.2 Parametric Study

The effect of permanent load was studied for the strata with varying depth \(H_1\) and soil modulus coefficient \(K_{{0}}\) in the parametric study. All the models had the configurations of Case (d) in Fig. 2. Eighteen combinations were analyzed based on the following parameters: \(q=\) (0, 220, 500) kPa, \(H_1=\) (2, 4, 8) m, and \(K_{{0}}=\) (15,000, 30,000). The embedment depth was fixed at \(H_2=\) 1.6 m.

4 Numerical Model

4.1 FE Model

The numerical model of the soil–foundation system was created in the commercial FE software Abaqus [38], and an overview of the FE model is presented in Fig. 1. The soil domain was created as a disk with a thickness equal to the stratum depth, and the bedrock was made infinitely stiff by constraining the bottom surface of the disk against translations. A void within the soil domain was created with the geometry of the embedded foundation. Then, rigid connections were applied to the surfaces of the soil facing the void linking them to a reference point (RP) positioned at midpoint on the bottom surface. In the case of a surface foundation, no void was created and the single surface at the interface between soil and foundation was rigidly connected to the RP. Loading was applied and output taken at the RP. The energy dissipation in soils at strains below \(10^{-3}\) is mostly rate-independent [15] and the rate-independent structural damping model was applied in the FE model, which is incorporated in the complex modulus as \(\varvec{K}^*=\varvec{K}(1+i2\xi )\), where \(\varvec{K}\) is the stiffness matrix.

Quadratic tetrahedral solid elements were used. The mesh size at the center of the soil domain at the foundation was 0.25 m. From the center, the mesh size was gradually enlarged along the radius toward the boundary of the model. The radius of the model was R = 200 m. At the boundary, the mesh size was 20 m. Due to the gradual enlargement of the elements, the computational time was reduced without causing spurious waves that can occur due to large size differences between elements. Infinite elements [39] were attached to the outer surface boundary of the model domain.

4.2 Verification

The verification of the FE model was performed for a flexible surface foundation on viscoelastic soil, and is illustrated in Fig. 3. Impedance functions were obtained from the semi-analytical solution of Kobori et al. [40] and compared to the calculated impedance functions of the FE model.

Fig. 3
figure 3

Verification case

Full size image

The chosen parameters in the analysis were \(B=\) 1 m, \(H=\) 4 m, \(G=\) 160 MPa, \(\rho =\) 2000 kg/m3, and \(\nu =\) 0.25. The viscosity \(\mu '\) was calculated as \(\mu '=\eta G B / v_s\) where \(\eta =2\xi\) is the loss factor and \(v_s=\sqrt{(G/\rho )}\). The configurations of the model were as described in Sect. 4.1. However, the rigid connections were removed, and a distributed surface load replaced the point load. The output was taken at midpoint of the surface. The resulting impedance functions are presented in Fig. 4, where v denotes the vertical direction and \({\text {h}}\) the horizontal direction. The results were normalized by \(\beta =H/GB^2\). The dimensionless frequency was \(a_{{0}}=\omega B/v_S\). The agreement between the finite element and the semi-analytical solutions was very good.

Fig. 4
figure 4

Verification results. Markers represent results from Kobori et al. [40] indicating the loss factor \(\eta\). Solid line indicates results from FE models

Full size image

4.3 Calculation Procedure

The updating of the G-modulus in each of the elements due to permanent load and the calculation of impedance functions were performed as follows:

  1. 1.

    Initially, the unloaded modulus was assigned: Calculate \(\sigma '_{0}\) (Eq. 3) and \(G_{0}\) (Eq. 2). In this state, \(G/G_{0}=\) 1 (Eq. 6), and the shear modulus is \(G=G_{0}\).

  2. 2.

    Apply permanent load P at the RP in Fig. 1 and run a static analysis.

  3. 3.

    Successively calculate: \(\sigma '_{0}\) (Eq. 3), \(\sigma '_{m}\) (Eq. 4), \(\sigma '\) (Eq. 5), \(G_{0}\) (Eq. 2), \(\gamma\) (Eq. 7), and G (Eq. 6).

  4. 4.

    Repeat steps 2 and 3 until convergence of the distribution of shear modulus G is reached.

  5. 5.

    Calculate impedance functions.

Direct steady-state calculations were performed in order to obtain the impedance functions. Harmonic unit loads were individually applied at the RP displayed in Fig. 1 to each of the six degrees of freedom in a given frequency range. The compliance functions U were obtained from the model. The impedance functions were then calculated by the inverse of the compliance functions \(Z=U^{-1}\). Only the values of the diagonal of the impedance function matrix were analyzed.

Fig. 5
figure 5

Updating of the shear modulus distribution due to permanent load. Values given in MPa. a \(H_1=\) 2 m, \(K_{{0}}=\) 30,000, b \(H_1=\) 8 m, \(K_{{0}}=\) 30,000 and c \(H_1=\) 8 m, \(K_{{0}}=\) 15,000. Dashed line indicates unloaded soil, solid line indicates updated soil

Full size image

The converged distributions of the shear modulus for three of the models are shown in Fig. 5, and the cuts are taken along the y–z plane. The models were configured as in Sect. 3.2 with \(q=\) 220 kPa. An increase in the permanent load results in two opposite effects on the modulus: an increase in \(G_{{0}}\) due to the increase in \(\sigma '\) and a reduction by \(G/G_{{0}}\) due to the increase in \(\gamma\). In the volume between the foundation and the bedrock, the permanent load caused an increase in the modulus. The influence is large for shallow stratum depths. Just outside of this volume, the modulus can be either reduced or increased from permanent load depending on the stress–shear strain interaction.

5 Results

The real part of the impedance function is denoted with \({\text {Re}}(Z_{j})\), whereas the imaginary part is denoted with \({\text {Im}}(Z_{j})\). The degrees of freedom are indicated by the subscript j and the coordinate axes are defined in Fig. 1. The compliance functions, \(|U_{j}|\), are denoted in the same way as the impedance functions and are given as absolute values. All functions are presented with the dimensionless frequency \(a_{{0}}=\omega w / v_s,{\text {eq}}\) where \(w = B/2\) and \(v_s,{\text {eq}}=\sqrt{G_{\text {eq}}/\rho }\) is the equivalent shear wave velocity of the strata (without the influence of the permanent load). Impedance functions are normalized with the static stiffness coefficients \(k_j,{\text {stat}}\), and the compliance functions are normalized by the static displacements \(u_j,{\text {stat}}\).

5.1 Model Assumptions Study

The normalized impedance functions from the model assumptions study are presented in Fig. 6. The corresponding static stiffness coefficients are given in Fig. 7. The results are presented in the x and z directions in order to show the principal effects of the model assumptions. The following observations are made:

  • In the pre-resonance state, i.e., before wave propagations are initiated, the impedance functions are proportional to the static properties of the soil–foundation system. The normalized impedance functions can be described by a single degree of freedom system. The real part of this system is \((k_{j,\text {stat}}-\omega ^2 m_{j,\text {stat}})/k_{z,\text {stat}}\), where \(m_{j,\text {stat}}\) is the mass of the system, and the imaginary part is constant and is equal to \(i2\xi\). The normalized impedance functions are thus very similar in the pre-resonance frequency range; however, they differ substantially at higher frequencies. At frequencies above the fundamental frequency, the impedance is highly influenced by the wave propagations and the single degree of freedom system is no longer valid. The imaginary part is increased significantly and the differences in impedance between the cases becomes obvious.

  • All cases have the same fundamental frequencies both in the vertical and in the horizontal direction which also coincide with the analytical fundamental frequencies of the soil strata [36]. The fluctuations in impedance that can be seen for all cases at \(a_0\approx 0.7\) in the x direction are due to the second mode of vibration of the soil, which for a homogeneous stratum has the natural frequency of three times the fundamental frequency according to \(T_n=(4H/v)/(2n-1)\) were v is the wave speed and n is the mode number. The natural frequencies of the second mode for the strata with modulus varying with the depth are somewhat lower than the natural frequencies of the strata with homogeneous soil. In the z direction, the frequency of the second mode of vibration is above the considered frequency range.

  • The embedment of the foundation increases the static stiffness coefficient as compared to the static stiffness coefficient of the corresponding surface foundation, as shown by comparing Case (a) to Case (b), and Case (c) to Case (d). This is explained by the reduced distance to the bedrock.

  • Strata with a modulus varying with the depth have lower static stiffness coefficients than strata with homogeneous modulus. This is evident when comparing Case (a) to Case (c) and Case (b) to Case (d). With increasing permanent load, the values of the static stiffness coefficients in Cases (c) and (d) are increased but they do not exceed the static stiffness coefficients of the homogeneous cases of (a) and (b).

  • As shown in Cases (c) and (d), the permanent load increases the static stiffness coefficient. The increase is, in some cases, more than 100%. Furthermore, the permanent load has a negligible effect on the fundamental frequency. The fundamental frequencies of the strata are thus not changed by the local influence that the permanent loads have on the soil moduli.

  • For surface foundations on top of strata with modulus varying with the depth, as in Case (c), very low static stiffness coefficients are obtained with \(q=\) 0. This shows the consequences of omitting permanent load in combination with very low modulus at the surface of the model. Adding permanent load to Case (c) increases the static stiffness coefficient considerably. This effect is also shown for the normalized impedance functions, where an increase in the permanent load leads to a decrease in the real part of the impedance and an increase in the imaginary part.

  • In this study, Case (a) gave static stiffness coefficients in the same order of magnitude as Case (d). The influence of the combination of the two model assumptions of Case (d), including the embedment of the foundation and the modulus varying with the depth, cancel each other out, resulting in similar static stiffness coefficients as in the simple case of Case (a). However, increasing the permanent load of Case (d) increases the differences between the cases. Further, the normalized impedance functions are largely different in the frequency range above the fundamental frequency.

Fig. 6
figure 6

Normalized impedance functions from the model assumptions study. Soild line indicates fundamental frequency

Full size image
Fig. 7
figure 7

Static stiffness coefficients of the four model cases

Full size image

In summary, the influence of the model assumptions on the normalized impedance functions are considerable in the post-resonance frequency range, and features such as the embedment of the foundation, the modulus varying with the depth, and the permanent load can affect the results. In the pre-resonance frequency range however, the normalized impedance functions were relatively similar for all the cases studied. The static stiffness coefficients of the cases differed with more than 100%. The model assumptions in this study did not have an effect on the fundamental frequency of the strata which were governed by the properties of the soil.

5.2 Parametric Study

Fig. 8
figure 8

Normalized impedance functions and the effects of permanent load

Full size image
Fig. 9
figure 9

Static stiffness coefficients normalized with \(k_{z,\text {stat},q = 0 kPa}\)

Full size image
Table 1 Static stiffness coefficients \(k_{z,\text {stat},q = 0 kPa}\). Values given in GN/m
Full size table
Fig. 10
figure 10

Normalized compliance functions from the parametric study

Full size image

Normalized impedance functions in the z direction are presented in Fig. 8. The static stiffness coefficients of each case, normalized with the static stiffness coefficients with q = 0 kPa, are given in Fig. 9. The static stiffness coefficients with q = 0 kPa are given in Table 1 as a reference. Normalized compliance functions are presented in Fig. 10. The effects of the permanent load on the impedance functions are similar in all degrees of freedom and for the sake of clarity, only the results in the vertical degree of freedom is presented. The following observations are made regarding the influence of the permanent load:

  • For most cases, the static stiffness coefficient increases with the permanent load, in particular for shallow strata with a high soil modulus coefficient, see Fig. 9. This can be explained by the high pressure and the small shear strain that mainly increase the modulus, see Fig. 5a, b. The maximum increase in static stiffness coefficient is 67%. In the case of the deep strata with a low soil modulus coefficient (\(H_1=\) 8 m and \(K_{{0}}=\) 15,000), the static stiffness coefficient decreases with increased permanent load. The reduction is small (4%) and is likely due to the high shear strains beside and under the foundation, which reduces the modulus (see Fig. 5c).

  • In the pre-resonance frequency range, the system acts as a single degree of freedom system, as described in Sect. 5.1. The real part of the normalized impedance can however be significantly influenced by the permanent load in this range, especially for shallower strata. This is clearly visible in Fig. 8 in the case of \(H_1=\)2 m where \((k_{j,\text {stat}}-\omega ^2 m_{j,\text {stat}})/k_{z,\text {stat}}\) is less steep for increasing permanent load, which is explained by a larger \(k_{z,\text {stat}}\) in relation to \(m_{z,\text {stat}}\). In the case of the deep soil, the effect of the permanent load on the pre-resonance impedance is low.

  • The effect of the permanent load on the fundamental frequency is small, see Fig 10. In the case of \(K_{{0}}=\) 15,000, the fundamental frequency decreases with an increasing permanent load, whereas it increases in the case of \(K_{{0}}=\) 30,000. The effect is smaller for deeper soil strata and increases with shallower depths. However, the variations of the fundamental frequency due to the permanent load are small when compared to the ones that are due to the stratum depth and the soil modulus coefficient.

  • In most cases, the resonances of the normalized compliance functions decrease with an increasing permanent load, see Fig. 10. The decrease is larger in the cases with stiffer and deeper soils. The resonance peaks for these cases are less distinct, whereas the resonance peaks become pointier for deeper and softer soils. The largest reduction in the normalized resonance peak is however observed in the case of the intermediate depth of \(H_1=\) 4 m with a stiff soil \(K_{{0}}=\) 30,000, and is 34%. In the case of the soft and deep soil stratum (\(H_1=\) 8 m with \(K_{{0}}=\) 15,000), a small increase in the normalized resonance (8%) due to the permanent load is observed. This particular case is also the only case where the static stiffness coefficient is reduced due to the permanent load.

  • In the frequency range above the fundamental frequency, the effect of the permanent load can lead to both an increase and a decrease in the normalized impedance at different frequency ranges. In the case of the shallower strata however, the real part of the normalized impedance is generally increased from additional permanent load, whereas the imaginary part is decreased. Whereas the effect of the permanent load on the static stiffness coefficients can be quite large, the effect on the normalized impedance functions is relatively small, especially for the deeper strata and at lower frequencies.

To summarize, the influence of the permanent load depends on the stratum depth and the soil modulus coefficient. In most cases, an increase in the permanent load led to an increase in the static stiffness coefficient. The maximum increase was 67% for \(H_1=\) 2 m and \(K_{{0}}=\) 30,000. However, in the case of the deep and soft soil (\(H_1=\) 8 m and \(K_{{0}}=\) 15,000), a decrease of 4% of the static stiffness coefficient was obtained. The effect of the permanent load on the normalized impedance functions is in some cases small, especially for deep strata and at lower frequencies. However, for shallower strata with higher soil modulus coefficients, the effect of permanent load on the normalized impedance functions is large. The largest decrease in the normalized compliance due to the permanent load was found at resonance and was 34% (\(H_1=\) 4 m and \(K_{{0}}=\) 30,000). The largest increase in the normalized compliance due to the permanent load was 8% (\(H_1=\) 8 m and \(K_{{0}}=\) 15,000).

6 Conclusions

The influence of model assumptions on the dynamic impedance functions of shallow foundations was investigated using finite elements. First, the influence of model assumptions, including embedment of the foundation, variation of the modulus with depth, and permanent load, were studied in a comparison of simple models to more detailed models. Second, a parametric study was conducted to investigate the influence of the permanent load in cases where the stratum depth and the soil modulus coefficient were varied. Small-strain modulus and modulus reduction relationships were used in an iterative process to update the modulus field due to permanent load, and impedance functions were then calculated. The conclusions from these studies are summarized in the following main points:

  1. 1.

    The model assumptions can have a great influence on the impedance functions. The considered combinations of model assumptions produced normalized impedance functions that were similar in the pre-resonance frequency range. However, in the frequency range above the fundamental frequency, the normalized impedance functions were very different. Further, the static stiffness coefficients of the models differed with more than 100%.

  2. 2.

    The parametric study showed that the permanent load has a significant influence on the normalized impedance functions, especially in the cases of shallow soil strata with high soil modulus coefficients. In most of the cases studied, an increase in the permanent load led to an increase in the static stiffness coefficient (with up to 67%). However, in the case of the deep and soft soil it led to a small decrease of 4%. The normalized impedance functions were in some cases relatively uniform, especially for the deeper strata. The maximum decrease in the normalized compliance occurred at the fundamental frequency and was 34%, whereas the maximum increase was 8%.

  3. 3.

    The permanent load had a small effect on the fundamental frequency of the soil–foundation system.

Finally, the present study assumes a frictional soil on bedrock and a fixed geometry for the foundation corresponding to railway bridges. Additional studies are therefore necessary to confirm the conclusions with different soils or dimensions for the foundation. However, the purpose of this paper was not to derive conclusions for all possible cases but to show that the assumptions made for the FE model and the permanent load may have an influence on the impedance functions and therefore the FE model should be defined carefully.