Highly Efficient AlGaN/GaN/InGaN Multi-quantum Well Ultraviolet Light-Emitting Diode

Abstract

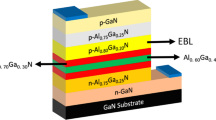
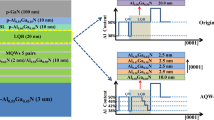
Nitride semiconductors have become the new generation of light sources for displays and optical storage. Nitride emitters are highly efficient, environmentally friendly and have a long device life. In this article, we have designed a new structure for ultraviolet light-emitting diode. The device consists of AlGaN/GaN/InGaN multi-quantum well structure. In this design, the quantum structure was engineered to increase the confinements of carriers in the quantum well. The more carrier’s confinement increases radiative recombination rate in the active region of the device and enhances the device performance. The proposed design and its performance are simulated and studied by numerical approach. Comparing to reported design, significant improvement in the intensity of output light and reduced electrical power consumption has been observed and the structure shows better performance at wavelength of 350–380 nm.

Appendix

In this section, the physical model of the device and the main parameters are reviewed briefly. Equations (1)–(35) have been used to simulate the presented device behavior. The details of physical modeling are available in references Bhattacharya (1994) and Yang (1988).

• A. Electroluminescence Spectrum

The spontaneous emission rate depends on the photon energy:

$$k_{\text{sp}} (\omega ) = \frac{1}{{\tau_{\text{R}} }}g_{\text{j}} (\omega )f_{\text{e}} (\hbar \omega )$$

(1)

where g_j(E) is the joint density of states and f_e(E) is the joint occupation probability for the valence and conduction bands also known as the emission condition. The joint density of states is analogous to the density of states for the conduction or valence band, but in this case, we are considering the number of states available to electrons and holes, which upon recombination would yield to photons of particular frequency. In order to determine the joint density of states, we use the parabolic approximation for the bands at the band edge. Recall that:

$$E_{1} = \frac{{\hbar^{2} k^{2} }}{{2m_{\text{V}}^{*} }}k$$

(2)

for hole in the valance band, and

$$E_{2} = \frac{{\hbar^{2} k^{2} }}{{2m_{{^{\text{C}} }}^{*} }}k + E_{\text{g}}$$

(3)

for electron in the conduction band.

Then, the energy of the photon emitted when the electron with energy E₂ recombines with the hole with energy E₁ is:

$$E = \hbar \omega = E_{2} - E_{1} = \frac{{\hbar^{2} k^{2} }}{{2m_{\text{r}} }} + E_{\text{g}}$$

(4)

where m_r is reduced mass and E is the energy of the emitting photon. Then, we can write the energies of the electron and the hole as:

$$E_{2} = E_{\text{C}} + \frac{{m_{r} }}{{m_{{^{\text{C}} }}^{*} }}(\hbar \omega - E_{\text{g}} )$$

(5)

$$E_{1} = E_{\text{V}} - \frac{{m_{\text{r}} }}{{m_{{^{\text{V}} }}^{*} }}(\hbar \omega - E_{\text{g}} ) = E_{2} - \hbar \omega$$

(6)

As the number of recombining electron hole pairs corresponds directly to the number of emitted photons, we can write that the total number of electrons dropping into the valence band and filling holes is exact same as number of photons in the ideal case, then:

$$g_{\text{C}} (E_{2} ){\text{d}}E_{2} = g_{\text{j}} (\omega ){\text{d}}\omega \Rightarrow g_{\text{j}} (\omega ) = g_{\text{C}} (E_{2} )\frac{{{\text{d}}E_{2} }}{{{\text{d}}\omega }}$$

(7)

where g_c(E) is:

$$g_{\text{C}} (E) = \frac{{(m_{\text{C}}^{*} )^{{\frac{3}{2}}} }}{{\pi^{2} \hbar^{3} }}\sqrt {2(E - E_{\text{C}} )}$$

(8)

Therefore:

$$g_{\text{j}} (\omega ) = \frac{{(m_{\text{r}} )^{{\frac{3}{2}}} }}{{\pi^{2} \hbar^{2} }}\sqrt {2(\hbar \omega - E_{\text{g}} )}$$

(9)

The emission condition is then expressed in terms of the Fermi distributions of the electrons and holes:

$$f_{\text{e}} (\hbar \omega ) = f_{\text{c}} (E_{2} )\left( {1 - f_{\text{v}} (E_{1} )} \right)$$

(10)

Here, f_c(E) and f_v(E) are the Fermi distribution functions for electrons and holes in the non-equilibrium injection conditions:

$$f_{\text{c}} (E) = \frac{1}{{1 + {\text{e}}^{{{\raise0.7ex\hbox{${E - E_{\text{Fc}} }$} \!\mathord{\left/ {\vphantom {{E - E_{\text{Fc}} } {k_{\text{B}} T}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${k_{\text{B}} T}$}}}} }}$$

(11)

$$1 - f_{\text{v}} (E) = \frac{1}{{1 + {\text{e}}^{{{\raise0.7ex\hbox{${E_{\text{Fv}} - E}$} \!\mathord{\left/ {\vphantom {{E_{\text{Fv}} - E} {k_{\text{B}} T}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${k_{\text{B}} T}$}}}} }}$$

(12)

where E_Fc and E_Fv are the non-equilibrium Fermi levels or quasi-Fermi levels (due to injection) for electrons and holes. During injection, the concentration of carries can be so high that the conduction band would have much higher concentration of electrons and the valence band would have much higher concentration of holes than they would have in thermal equilibrium, which can be expressed in terms of quasi-Fermi levels moving into the bands making the SC behaving almost like a metal.

We can determine the quasi-Fermi levels based on the injection concentrations. Remember how we can calculate carrier densities in equilibrium using D.O.S function and the Fermi distribution, so the same logic applies here:

$$n = n_{0} + \Delta n = \int\limits_{{E_{\text{c}} }}^{\infty } {g_{\text{c}} (E)f_{\text{c}} (E){\text{d}}E}$$

(13)

where

$$g_{\text{c}} (E) = \frac{{m_{\text{c}}^{*} }}{{\pi^{2} \hbar^{2} }}\sqrt {\frac{{2m_{\text{c}}^{*} (E - E_{\text{c}} )}}{{\hbar^{2} }}}$$

(14)

and

$$p = p_{0} + \Delta n = \int\limits_{ - \infty }^{{E_{\text{v}} }} {g_{\text{v}} (E)f_{\text{v}} (E){\text{d}}E}$$

(15)

where

$$g_{\text{v}} (E) = \frac{{m_{\text{v}}^{*} }}{{\pi^{2} \hbar^{2} }}\sqrt {\frac{{2m_{\text{v}}^{*} (E_{\text{v}} - E)}}{{\hbar^{2} }}}$$

(16)

In the conditions, when E₂ ≫  E_Fc, E₁ ≪  E_Fv the spontaneous emission rate can be found as:

$$k_{\text{sp}} (\omega ) = \frac{1}{{\tau_{\text{R}} }}g_{\text{j}} (\omega )f_{\text{e}} (\hbar \omega ) \approx D\sqrt {(\hbar \omega - E_{\text{g}} )} {\text{e}}^{{{{ - (\hbar \omega - E_{\text{g}} )} \mathord{\left/ {\vphantom {{ - (\hbar \omega - E_{\text{g}} )} {k_{\text{B}} T}}} \right. \kern-0pt} {k_{\text{B}} T}}}}$$

(17)

where

$$D = \frac{{\left( {2m_{\text{r}} } \right)^{{\frac{3}{2}}} }}{{2\pi^{2} \hbar^{2} \tau_{\text{R}} }}e^{{{{(E_{\text{Fc}} - E_{\text{Fv}} - E_{\text{g}} )} \mathord{\left/ {\vphantom {{(E_{\text{Fc}} - E_{\text{Fv}} - E_{\text{g}} )} {k_{\text{B}} T}}} \right. \kern-0pt} {k_{\text{B}} T}}}}$$

(18)

The spontaneous emission can be rewritten as wavelength function:

$$k_{\text{sp}} (\lambda ) = D\sqrt {\left( {\frac{hC}{\lambda } - E_{\text{g}} } \right)} {\text{e}}^{{{{ - ({{hC} \mathord{\left/ {\vphantom {{hC} {\lambda )}}} \right. \kern-0pt} {\lambda )}} - E_{\text{g}} )} \mathord{\left/ {\vphantom {{ - ({{hC} \mathord{\left/ {\vphantom {{hC} {\lambda )}}} \right. \kern-0pt} {\lambda )}} - E_{\text{g}} )} {k_{\text{B}} T}}} \right. \kern-0pt} {k_{\text{B}} T}}}}$$

(19)

• B. Optical power of LED

Depending on both the impurity profile and the external applied voltage, we can identify four current components in an LED under the forward-bias condition: (1) the electron diffusion current, (2) the hole diffusion current, (3) the space-charge-layer recombination current and (4) the tunneling current. The tunneling current is important only in a heavily doped pn junction at a small forward bias; thus, its effect is negligible in most LEDs at light-emitting current level. These current components are rewritten in the following:

$$I_{n} = \frac{{qD_{n} n_{i} }}{{L_{n} N_{a} }}^{2} ({\text{e}}^{{{{qv} \mathord{\left/ {\vphantom {{qv} {kT}}} \right. \kern-0pt} {kT}}}} - 1)$$

(20)

$$I_{p} = \frac{{qD_{p} n_{i} }}{{L_{p} N_{d} }}^{2} ({\text{e}}^{{{{qv} \mathord{\left/ {\vphantom {{qv} {kT}}} \right. \kern-0pt} {kT}}}} - 1)$$

(21)

$$I_{\text{rec}} = \frac{{qn_{i} x_{d} }}{2\tau }{\text{e}}^{{{{qv} \mathord{\left/ {\vphantom {{qv} {2kT}}} \right. \kern-0pt} {2kT}}}}$$

(22)

Recombination inside the space-charge layer is effective if trap levels exist near the center of the forbidden gap. This process is generally non-radiative, and the component I_rec does not contribute to the emission of light. Furthermore, luminescence originates from the electron diffusion current in the p side of the junction in most practical LEDs for reasons beyond the scope of present text. Consequently, we can define the current injection efficiency as:

$$\gamma = \frac{{I_{n} }}{{I_{n} + I_{p} + I_{\text{rec}} }}$$

(23)

Frequently, the hole diffusion current is negligible because of the high electron to hole mobility ratio; e.g., in GaAs, we have μ_n/μ_p = 30, and the foregoing equation can be simplified.

The injection efficiency indicates the percentage of diode current that can produce radiative recombination in the p side of the junction. The simplest recombination process is the band to band recombination, in which a free electron and a free hole recombine directly. The probable second process involves a shallow impurity state, where an electron recombines with a hole trapped on a shallow acceptor state. Alternatively, the process may involve a shallow acceptor and a shallow acceptor state. The photon energy generated in this process is smaller than E_g. In the third possibility process, via deep impurity states, photons may not be generated at all; even if photons are generated, their energy is much smaller than E_g.

To simplify the complex picture, let us take an elementary case where a non-radiative recombination process via an intermediate state is competing with the band to band radiative recombination. So, the radiative (U_r) and non-radiative recombination rates (U_nr) can be defined, respectively, as (for the p-type region):

$$U_{\text{r}} \equiv \frac{\Delta n}{{\tau_{\text{r}} }}$$

(24)

$$U_{\text{nr}} \equiv \frac{\Delta n}{{\tau_{\text{nr}} }}$$

(25)

where Δn is excess electron density, τ_r is radiative recombination lifetime, and τ_nr is non-radiative lifetime. The radiative efficiency is defined as the percentage of electron that recombine radiatively:

$$\eta = \frac{{U_{\text{r}} }}{{U_{\text{r}} + U_{\text{nr}} }} = \frac{\tau }{{\tau_{\text{r}} }}$$

(26)

where τ is the effective life time determined by:

$$\frac{1}{\tau } = \frac{1}{{\tau_{\text{r}} }} + \frac{1}{{\tau_{\text{nr}} }}$$

(27)

The overall internal quantum efficiency can now be written as:

$$\eta_{i} = \eta \gamma$$

(28)

The most important parameter of an LED is the external quantum efficiency. It may be significantly smaller than the internal quantum efficiency because of internal absorption and reflection of light. After photons are generated in the PN junction, they must pass through the crystal to reach the surface. Some of the emitted photons are reabsorbed by semiconductor. Furthermore, even after the photons have reached the surface, they may not be able to leave the semiconductor because of the large difference in the refractive indices of the semiconductor and air. According to the theory of optics, the critical angle at which total internal reflection occurs is determined by the Fresnel equation. All rays of light striking the surface at angles exceeding are reflected. Since refractive index ranges between 3.3 and 3.8 for a typical LED material, critical angle is calculated to be between 15 and 18. For the light striking within the critical angle, the portion that comes out is given approximately by the average transmissivity:

$$T = \frac{4n}{{(1 + n)^{2} }}$$

(29)

A simple expression relating the external quantum efficiency to the internal quantum efficiency is given by:

$$\eta_{\text{ext}} = \frac{{\eta_{i} }}{{1 + \alpha {{v_{ 0} } \mathord{\left/ {\vphantom {{v_{ 0} } {AT}}} \right. \kern-0pt} {AT}}}}$$

(30)

where α is average absorption coefficient, v₀ is diode volume, and A is emitting area.

The internal photon flux ϕ (photon per second), generated within a volume of the semiconductor, is directly proportional to the carrier injection rate R (pairs/cm³-s). The steady-state excess-carrier concentration Δn = Rτ (recombination rate = injection rate). Therefore, the photon flux can be expressed as:

$$\phi = \eta_{{_{\text{int}} }} RV = \eta_{\text{int}} {{V\Delta n} \mathord{\left/ {\vphantom {{V\Delta n} \tau }} \right. \kern-0pt} \tau } = \eta_{\text{int}} V{{({i \mathord{\left/ {\vphantom {i {e)}}} \right. \kern-0pt} {e)}}} \mathord{\left/ {\vphantom {{({i \mathord{\left/ {\vphantom {i {e)}}} \right. \kern-0pt} {e)}}} V}} \right. \kern-0pt} V} = \eta_{\text{int}} {i \mathord{\left/ {\vphantom {i e}} \right. \kern-0pt} e}$$

(31)

Now, the extracted photon flux from the structure is:

$$\phi_{0} = \eta_{e} \phi = \eta_{e} (\eta_{\text{int}} i/e)$$

(32)

where, the extraction efficiency specifies how much of the internal photon flux is transmitted out of the structure. A single quantum efficiency that accommodates both η_e and η_int is the external quantum efficiency η_ext:

$$\eta_{\text{ext}} \equiv \eta_{\text{e}} \eta_{\text{int}}$$

(33)

So, the LED output optical power P₀:

$$P_{0} = h\upsilon \phi_{0} = \eta_{\text{ext}} h\upsilon i/e$$

(34)

Equation (34) is used to calculate the output power of LED versus injected current.

• C. Current Voltage

The diode equation gives an expression for the current through a diode as a function of voltage. For a practical diode, expressed as:

$$I = I_{0} ({\text{e}}^{{\frac{qv}{nkt}}} - 1)$$

(35)

where, I is the net current flowing through the diode; I₀ is dark saturation current or the diode leakage current density in the absence of output light, v is applied voltage across the terminals of the diode, q is absolute value of electron charge, k is Boltzmann’s constant, t is absolute temperature (K) and n is ideality factor—a number between 1 and 2—which typically increases as the current decreases.

The dark saturation current (I₀) is an extremely important parameter which differentiates one diode from another. I₀ is a measure of the non-radiative recombination process in a device. A diode with a larger non-radiative recombination rate will have a larger I₀. The dark saturation current and the ideality factor (n) are declared by diode specification documents and different values at various operated conditions defined by diode manufacture which can be used on the expression.