Lattice Boltzmann Method Simulation of Nanofluid Natural Convection Heat Transfer in a Square Cavity with Constant Heat Flux at Walls

Abstract

In this study, for the first time, a nanofluid's natural convection heat transfer in a two-dimensional square cavity has been numerically investigated by use of the lattice Boltzmann method with the constant heat flux boundary condition. The horizontal walls of the cavity are insulated, and the vertical walls are kept at a constant heat flux. The diameters of the nanoparticles inside the cavity are the same and have a homogeneous distribution, and there is no chemical reaction between the particles. The flow is also assumed to be the steady state and two-dimensional. Constant temperature, streamlines, velocity, and average Nusselt have been investigated for different nanoparticle volume fractions and Rayleigh numbers. The results showed that the lattice Boltzmann method efficiently analyzes the natural heat transfer of nanofluids; moreover, by use of nanofluid in the cavity increases the heat transfer rate. With the increase in the nanoparticle volume fraction, the average Nusselt number on the right wall of the cavity increased. For a volume fraction of 20% with Grashof number 10⁵, the average Nusselt number increased by almost 50% compared to the base fluid at the same Grashof number. It has been observed that as the volume fraction of nanoparticles in the fluid increases, the fluid’s viscosity also increases; consequently, the velocity of the fluid is found to decrease.

1 Introduction

The natural convection in a square cavity is used in various applications, including solar energy collectors (Singh and Sharif 2003), non-Newtonian chemical processes (Patil and Kulkarni 2008; Lamsaadi et al. 2006), furnace engineering (Lim et al. 1999), domains affected by electromagnetic fields (Saha et al. 2007; Yan et al. 2004), cooling systems for electronic devices (Florio and Harnoy 2007), and chemical vapor deposition instruments (Iwanik and Chiu 2003). Therefore, enhancing the efficiency of natural convection in such cavities holds significant potential for energy and cost savings across these diverse industrial applications. The conventional heat transfer performance is limited by the low thermal conductivities of the most commonly used fluids, such as water, oil, and a mixture of ethylene–glycol. To overcome this limitation, nanofluids, consisting of nanoscale particles dispersed in a base fluid, have been proposed. In recent years, nanotechnology has been the subject of extensive research to improve the heat transfer rate of engineering systems (He et al. 2011; Tavousi et al. 2023a, 2023b, 2023c; Sudi et al. 2023).

The application of Cu-water nanofluid in a two-dimensional enclosure demonstrated an increase in the natural convection heat transfer efficiency with a rise in the volume fraction of nanoparticles (Khanafer et al. 2003). Subsequent research indicated that the size of nanoparticles in Al₂O₃-water nanofluid impacts natural convection heat transfer within horizontal and vertical rectangular enclosures. This study revealed a decrease in the heat transfer coefficient ratio as nanoparticle size increased (Wang et al. 2006). Additionally, analysis of the same nanofluid under laminar natural convection conditions highlighted the significance of viscosity and thermal conductivity in influencing natural convection heat transfer and fluid flow dynamics (Polidori et al. 2007). However, a study investigating Cu-water nanofluids across varied Grashof numbers and nanoparticle volume fractions found that the aspect ratio of the rectangular cavity did not significantly affect the enhancement of natural convection heat transfer (Jou and Tzeng 2006). A comparative study of natural convection in a cavity using three different water-based nanofluids Cu, Al₂O₃, and TiO₂ established that Cu nanofluids offered superior heat transfer enhancement relative to Al₂O₃ and TiO₂ (Oztop and Abu-Nada 2008).

The lattice Boltzmann method (LBM) has recently been recognized as a valuable numerical technique (Nemati et al. 2010; Zheng et al. 2010; Mohamad et al. 2010; Mussa et al. 2011; Choi et al. 2012; Choi and Kim 2011; Bararnia et al. 2011; Mondal and Mishra 2008; Zahedi and Vakili 2023). Compared to traditional computational fluid dynamic methods, the LBM approach is easier to use in complex geometries and multi-component flows (Jeong et al. 2010). This method can be used to simulate fluid flow in many applications of engineering, such as multiphase (Huang et al. 2009), porous media (Wu et al. 2005), and natural convection (Delavar et al. 2009). Recent research has demonstrated the utility of LBM in conjunction with the Immersed Boundary Method for analyzing radiative heat transfer, fluid-elastic body interactions, and particle distributions (Abaszadeh et al. 2022; Afra et al. 2022; Delouei et al. 2022).

In an investigation into SiO₂-water nanofluid within a tall enclosure, it was observed that the average Nusselt number escalates with the nanoparticle volume fraction across various aspect ratios and Rayleigh numbers (Kefayati et al. 2011). Additionally, LBM has been employed to examine the influence of the Prandtl number on natural convection in an open cavity containing liquid gallium, air, and water. This study revealed a decline in heat transfer correlating with an increase in Hartmann number (Kefayati et al. 2012). Furthermore, LBM was utilized to determine that at a constant Rayleigh number, the heat transfer rate diminishes, approaching the conduction limit, as the aspect ratio increases in an open enclosure (Mohamad et al. 2009). In a separate study, LBM was applied to analyze the interplay of surface radiation and natural convection heat transfer, coupled with entropy generation, in a two-dimensional rectangular cavity. It was found that an elevation in Rayleigh number intensifies the radiation entropy generation, contributing significantly to the total entropy generation (Abbasi et al. 2023). the use of LBM in studying natural convection in an open cavity filled with ethylene glycol-Al₂O₃ nanofluid indicated that the locally distributed Nusselt number amplifies with the rise in both Rayleigh number and the nanofluid’s volume fraction (Taher et al. 2022).

Upon reviewing the existing literature, it becomes evident that studies employing the LBM for cavities with constant heat flux at the walls, specifically utilizing Cu-water nanofluid, are conspicuously absent. This study aims to bridge this research gap by investigating the natural convection of Cu-water nanofluid within a square cavity, characterized by a constant heat flux boundary condition on its left and right walls. The LBM is meticulously applied to establish the boundary conditions and to facilitate the simulation of the problem. Furthermore, MATLAB programming is utilized to meticulously code and solve the governing equations, thereby providing a comprehensive understanding of the natural convection phenomena under study.

2 Problem Statement

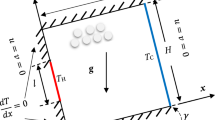
Figure 1 shows the schematic of the square cavity used in the simulation. The boundary conditions in this problem are constant heat flux at the left and right walls, and the bottom and top walls are considered adiabatic. The no-slip conditions were applied to the cavity’s walls. Pure water and Cu-water nanofluid are working fluids with volume fractions of 0.05, 0.1, and 0.2.

Fig. 1

Geometry of the problem with boundary conditions

3 Governing Equations

3.1 Lattice Boltzmann Method

This section describes the numerical methodology for natural convection heat transfer of a nanofluid using the lattice Boltzmann method in a square cavity. For simulating fluid flow, the relaxation time lattice Boltzmann method with the BGK approximation and the D₂Q₉ model configuration, as illustrated in Fig. 2, was utilized. Furthermore, for the temperature, the relaxation time lattice Boltzmann method with the BGK approximation and the D₂Q₅ model configuration, with a lattice arrangement depicted in Fig. 3, was employed.

Fig. 2

The two-dimensional lattice ${D}_{2}{D}_{9}$

Fig. 3

The two-dimensional lattice ${D}_{2}{D}_{5}$

The Boltzmann equation with external force term for flow and temperature field is defined as follows (Wang et al. 2013; Bararnia et al. 2011):

$${f}_{i}\left({\overrightarrow{x}}_{k}+{\overrightarrow{e}}_{i}\delta t,t+\delta t\right)-{f}_{i}\left({\overrightarrow{x}}_{k},t\right)=-\frac{1}{{\tau }_{v}}\left[{f}_{i}\left({\overrightarrow{x}}_{k},t\right)-{f}_{i}^{{\text{eq}}}\left({\overrightarrow{x}}_{k},t\right)\right]+\Delta t{\overrightarrow{e}}_{i}F$$

(1)

$${g}_{i}\left({\overrightarrow{x}}_{k}+{\overrightarrow{e}}_{i}\delta t,t+\delta t\right)-{g}_{i}\left({\overrightarrow{x}}_{k},t\right)=-\frac{1}{{\tau }_{T}}\left[{g}_{i}\left({\overrightarrow{x}}_{k},t\right)-{g}_{i}^{{\text{eq}}}\left({\overrightarrow{x}}_{k},t\right)\right]$$

(2)

where ${f}_{i}$, ${g}_{i}$, ${f}_{i}^{{\text{eq}}}$, ${g}_{i}^{{\text{eq}}}$, ${\tau }_{v}$, ${\tau }_{T}$, $\Delta t$ and $F$ are the distribution function, equilibrium distribution function, dimensionless relaxation time of the flow and temperature fields, time step and external forces exerted on flow, respectively.

Each of Eqs. 1 and 2 can be expressed as the collision and propagation steps (Mohamad 2011).

The collision step for the flow field:

$${\widetilde{f}}_{i}\left({\overrightarrow{x}}_{k},t+\delta t\right)-{f}_{i}\left({\overrightarrow{x}}_{k},t\right)=-\frac{1}{{\tau }_{v}}\left[{f}_{i}\left({\overrightarrow{x}}_{k},t\right)-{f}_{i}^{{\text{eq}}}\left({\overrightarrow{x}}_{k},t\right)\right]+\Delta t{\overrightarrow{e}}_{i}F$$

(3)

The propagation step for the flow field:

$${f}_{i}\left({\overrightarrow{x}}_{k}+{\overrightarrow{e}}_{i}\delta t,t+\delta t\right)={\widetilde{f}}_{i}\left({\overrightarrow{x}}_{k},t+\delta t\right)$$

(4)

The collision step for the temperature field:

$${\widetilde{g}}_{i}\left({\overrightarrow{x}}_{k},t+\delta t\right)-{g}_{i}\left({\overrightarrow{x}}_{k},t\right)=-\frac{1}{{\tau }_{T}}\left[{g}_{i}\left({\overrightarrow{x}}_{k},t\right)-{g}_{i}^{{\text{eq}}}\left({\overrightarrow{x}}_{k},t\right)\right]$$

(5)

The propagation step for the temperature field:

$${g}_{i}\left({\overrightarrow{x}}_{k}+{\overrightarrow{e}}_{i}\delta t,t+\delta t\right)={\widetilde{g}}_{i}\left({\overrightarrow{x}}_{k},t+\delta t\right)$$

(6)

where ${\widetilde{f}}_{i}$ and ${\widetilde{g}}_{i}$ are the flow and temperature fields after the collision, respectively.

The equilibrium distribution functions with the model of D₂Q₉ and D₂Q₅ (Fig. 3) for the flow and temperature fields are as follows (Mohamad 2011):

$${f}_{i}^{{\text{eq}}}=\rho .{w}_{i}\left[1+\frac{3}{{c}^{2}}{\overrightarrow{e}}_{i}.\overrightarrow{u}+\frac{9}{2{c}^{4}}{\left({\overrightarrow{e}}_{i}.\overrightarrow{u}\right)}^{2}-\frac{3}{2{c}^{2}}\overrightarrow{u}.\overrightarrow{u}\right]$$

(7)

$${g}_{i}^{{\text{eq}}}=T.{w}_{i}\left[1+\frac{3}{{c}^{2}}{\overrightarrow{e}}_{i}.\overrightarrow{u}\right]$$

(8)

where $\overrightarrow{u}$, $\rho$ and $T$ are the velocity, density, and temperature of the fluid, respectively.

The discrete velocity ${\overrightarrow{e}}_{i}$ of D₂Q₉ and D₂Q₅ for the flow and temperature fields are as follows (Mohamad 2011):

$$\vec{e}_{i} = \left\{ {\begin{array}{*{20}c} {\left( {{\text{0}},{\text{0}}} \right)i = 0} \\ {\left\{ {{\text{cos}}\left[ {\left( {i - 1} \right)\frac{\pi }{2}} \right],{\text{sin}}\left[ {\left( {i - 1} \right)\frac{\pi }{2}} \right]} \right\}.\;c\;\;\;i = {\text{1}},{\text{2}},{\text{3}},{\text{4}}} \\ {\left\{ {{\text{cos}}\left[ {\left( {2i - 9} \right)\frac{\pi }{4}} \right],{\text{sin}}\left[ {\left( {2i - 9} \right)\frac{\pi }{4}} \right]} \right\}.\;\sqrt 2 c\;\;\;i = {\text{5}},{\text{6}},{\text{7}},{\text{8}}} \\ \end{array} } \right.$$

(9)

$$\vec{e}_{i} = \left\{ {\begin{array}{*{20}c} {\left( {{\text{0}},{\text{0}}} \right)\;\;\;\;i = 0} \\ {\left\{ {{\text{cos}}\left[ {\left( {i - 1} \right)\frac{\pi }{2}} \right],{\text{sin}}\left[ {\left( {i - 1} \right)\frac{\pi }{2}} \right]} \right\}.\;c\;\;\;i = {\text{1}},{\text{2}},{\text{3}},{\text{4}}} \\ \end{array} } \right.$$

(10)

where c $=\frac{\delta x}{\delta t}$ is the speed of the lattice, and $\delta x$ and $\delta t$ are the space and time steps in the lattice.

The values of the coefficient of the discrete equilibrium distribution function (${w}_{i}$) in the direction of i for D₂Q₉ and D₂Q₅ are as follows:

$$w_{i} = \left\{ {\begin{array}{*{20}c} {\frac{4}{9}\;\;i = 0} \\ {\frac{1}{9}\;\;i = {\text{1}},{\text{2}},{\text{3}},{\text{4}}} \\ {\frac{1}{{36}}\;\;i = {\text{5}},{\text{6}},{\text{7}},{\text{8}}} \\ \end{array} } \right.$$

(11)

$$w_{i} = \left\{ {\begin{array}{*{20}c} {\frac{2}{6}\;\;i = 0} \\ {\frac{1}{6}\;\;\;i = 1,2,3,4} \\ \end{array} } \right.$$

(12)

${\tau }_{v}$ and ${\tau }_{T}$ in Eqs. 3 and 5 are the dimensionless relaxation time of flow and temperature that can be defined as follows (Kefayati et al. 2011):

$${\tau }_{v}=(3v+0.5)$$

(13)

$${\tau }_{T}=(3\alpha +0.5)$$

(14)

where $v$ and $\alpha$ are the kinematic viscosity and thermal diffusivity of fluid, respectively. The thermal diffusivity of fluid can be estimated as follows (Wang et al. 2013):

$$\alpha =\sqrt{3}\frac{(4+a)}{60}$$

(15)

where the value of a can be obtained from the following equation.

$$a=\frac{20 {\text{Ma}} \times {\text{Nx}}}{\sqrt{{\text{Ra}}\times {\text{Pr}}}}-4$$

(16)

where ${\text{Ma}}$, ${\text{Nx}}$, ${\text{Pr}}$, and ${\text{Ra}}$ are Mach number, number of nodes in the x direction, Prandtl number and Rayleigh number, respectively.

The Rayleigh number is defined as follows:

$${\text{Ra}}={\text{Gr}}\times {\text{Pr}}$$

(17)

where Grashof number is defined as follows:

$${\text{Gr}}= \frac{g\beta \Delta T {H}^{3}}{{v}^{2}}$$

(18)

where $g$, $\beta$, $\Delta T$, $H$, and $v$ are gravity acceleration, thermal expansion coefficient, the temperature difference of walls, the height of enclosure, and kinematic viscosity, respectively.

The velocity in the natural convection can be obtained from the following equation.

$$U= \sqrt{\alpha g\Delta T L}=\sqrt{\frac{{\text{Ra}}}{{\text{Pr}}}}\frac{v}{L}$$

(19)

The external force in the natural convection is the buoyancy force, so in Eqs. 1 and 3 the following equation can be used.

$${F}_{i}=3{w}_{i}g\beta \Delta T$$

(20)

where $g\beta$ can be calculated from the following equation.

$$g\beta =\frac{{\text{Ra}}\times v\times \alpha }{{H}^{3}}$$

(21)

3.2 Nanofluid Thermophysical Properties

The density of nanofluids can be obtained as follows (Xuan and Roetzel 2000):

$${\rho }_{{\text{nf}}}=\left(1-\varphi \right){\rho }_{{\text{bf}}}+\varphi {\rho }_{p}$$

(22)

The specific heat capacity of nanofluids is defined as follows (Pak and Cho 1998):

$$({\rho Cp)}_{{\text{nf}}}=\left(1-\varphi \right)(\rho {Cp)}_{{\text{bf}}}+\varphi ({\rho Cp)}_{P}$$

(23)

The viscosity of nanofluids can be calculated from the equation proposed by Brinkman (Brinkman 1952).

$${\mu }_{{\text{nf}}}=\frac{{\mu }_{{\text{bf}}}}{{\left(1-\varphi \right)}^{2.5}}$$

(24)

The thermal conductivity of nanofluid can be calculated from Maxwell’s equation (Hwang et al. 2007).

$${K}_{{\text{nf}}}=\frac{{K}_{p}+2{K}_{{\text{bf}}}+2\left({K}_{p}-{K}_{{\text{bf}}}\right)\varphi }{{K}_{p}+2{K}_{{\text{bf}}}-2\left({K}_{p}-{K}_{{\text{bf}}}\right)\varphi }{K}_{{\text{bf}}}$$

(25)

The thermal diffusivity is written as (Huminic and Huminic 2012).

$${\alpha }_{{\text{nf}}}=\frac{{K}_{{\text{nf}}}}{{(\rho {C}_{p})}_{{\text{nf}}}}$$

(26)

Thermophysical properties of copper and water are given in the (273 K as the reference temperature) Table 1.

Table 1 Thermophysical properties of copper and water (Khanafer et al. 2003)

After calculating the physical properties of the nanofluid and substituting them in place of the properties of base fluid, the resulting values will have an impact on the calculation of the Prandtl number, thermal conductivity, viscosity, thermal diffusivity, the hydrodynamic and thermal relaxation times (Bararnia et al. 2011; Kefayati et al. 2011).

$${Pr}_{{\text{nf}}}=\frac{{v}_{{\text{nf}}}}{{\alpha }_{{\text{nf}}}}$$

(27)

$${\tau }_{v}=(3{v}_{{\text{nf}}}+0.5)$$

(28)

$${\tau }_{T}=(3{\alpha }_{{\text{nf}}}+0.5)$$

(29)

3.3 Hydrodynamic and Thermal Boundary Conditions

The no-slip boundary condition is considered by the bounce-back boundary condition in the LBM for the flow in contact with the walls (Fig. 4).

Fig. 4

The bounce-back boundary condition in the LBM

Based on the bounce-back boundary condition, each distribution function that hits walls returns in the opposite direction, for example (Mohamad, 2011):

$$\left\{\begin{array}{c}{f}_{2}={f}_{4}\\ {f}_{5}={f}_{7} \\ {f}_{6}={f}_{8}\end{array}\right.$$

(30)

where the f₄, f₇, and f₈ are obtained from the propagation step.

The top and bottom walls are considered adiabatic boundary conditions with the form of bounce-back conditions in the LBM (Fig. 5).

Fig. 5

Thermal boundary conditions (Mohamad 2011)

For the top and bottom walls the following equations can be written (Mohamad 2011).

$${g}_{2}={g}_{4}$$

(31)

$${g}_{4}={g}_{2}$$

(32)

In this problem, the constant heat flux enters from the right wall and exits at the left wall. So, for the left wall, the unknown distribution function is cleared as (Bahoosh et al. 2021).

$${g}_{1}\left(0,j\right)= {g}_{1}\left(1,j\right)+\frac{(-{q}^{{\prime}{\prime}})\Delta {x}_{{\text{node}}}}{{k}_{{\text{nf}}}}$$

(33)

where ${k}_{{\text{nf}}}$, ${q}^{{\prime}{\prime}}$, $\Delta {x}_{{\text{node}}}$, j, and g are the thermal conductivity coefficient of nanofluid, constant heat flux at the left wall, lattice spacing, number of nodes, and temperature distribution function, respectively.

The unknown distribution function at the right wall is as follows (Bahoosh et al. 2021):

$${g}_{3}({N}_{i},{\text{j}})={g}_{3}\left({N}_{i}-1,j\right)+\frac{({q}^{{\prime}{\prime}})\Delta {x}_{{\text{node}}}}{{k}_{{\text{nf}}}}$$

(34)

The convergence criterion for flow and temperature fields based on the second-order of relative error (E₂) in velocity and the reduction in maximum temperature difference (E₁) throughout the computational domain is defined as follows (Wang et al. 2013):

$${E}_{2}=\sqrt{\frac{\sum_{{x}_{i}\in \Omega }\left[{\Vert {u}_{{x}_{i},t+1}-{u}_{{x}_{i},t}\Vert }^{2}+{\Vert {v}_{{x}_{i},t+1}-{v}_{{x}_{i},t}\Vert }^{2}\right]}{\sum_{{x}_{i}\in \Omega }{[\Vert {u}_{{x}_{i},t+1}\Vert }^{2}+{\Vert {v}_{{x}_{i},t+1}\Vert }^{2}]}} \le \varepsilon$$

(35)

$${E}_{1}={\text{Max}} |T\left(i,j,{t}_{n+1000}\right)-T\left(i,j,{t}_{n}\right)|\le \varepsilon$$

(36)

The velocity and temperature at each point can be obtained from the following equations (Wang et al. 2013, Mohamad 2011).

$$\rho ={\sum }_{i=0}^{8}{f}_{i}$$

(37)

$${\rho }_{0}u=\sum_{i=0}^{4}{\overrightarrow{e}}_{i}{f}_{i}$$

(38)

$$T={\sum }_{i=0}^{4}{g}_{i}$$

(39)

4 Results and Discussion

4.1 Grid Independence and Numerical Validation

Multiple grids were examined to guarantee the independence of results from the number of elements. Specifically, four distinct grids were utilized to simulate base fluid water with Pr = 7 and Ra = 3.5 × 10⁵, and the results of the Nusselt number were compared with the results from the analytical Eq. 40. The outcomes of these investigations are presented in Table 2. The 87 × 87 number of elements was selected to save cost and time to continue simulations (Kimura and Bejan 1984).

Table 2 Investigation of grid independence

$${\text{Nu}}=0.25\times {{\text{Ra}}}^{2/7}\times ({\frac{H}{L})}^{1/7}$$

(40)

The results of the Nusselt number from the present study were compared to the analytical results and numerical results of a published work (Table 3). The maximum difference observed was less than 9.5% when compared to both numerical and analytical results.

Table 3 Validation of the Nusselt number

4.2 Effect of Rayleigh Numbers on Flow and Natural Convection Heat Transfer for Water

Figure 6 shows the result of dimensionless temperature distribution, velocity, and streamlines for water and Ra^* = 3.5 × 10⁵ and Ra^* = 3 × 10⁶. It can be observed that isotherms near the vertical walls (right and left walls which are in the condition of constant heat flux) are almost parallel to the surfaces and perpendicular to the insulated walls of the cavity. Moreover, with an increase in the Rayleigh number, these lines approach the cavity walls, and their slope decreases, especially in the central regions of the cavity. For the velocity, as observed, the velocity is zero near the walls due to the no-slip condition. Additionally, the velocity is zero at the center of the vortices, and it increases as one moves away from the center of the vortices. For the streamlines near the hot wall (right wall), the fluid receives heat and tends to move upward. However, near the cold wall (left wall), the opposite happens, resulting in the formation of a counterclockwise flow in the cavity. As seen in Fig. 6, streamlines always have a counterclockwise direction, and with an increase in the Rayleigh number, the isotherm approaches the cavity walls. Additionally, for Ra* = 3.5 × 10⁵, only one vortex is observed in the middle of the flow, but for Ra* = 3.5 × 10⁶, more vortices are observed in the streamlines, and with an increase in the Rayleigh number, these vortices gradually move away from the center and approach the edges of the cavity.

Fig. 6

Temperature distribution, velocity and streamlines for water a Ra^* = 3.5 × 10⁵ and b Ra^* = 3 × 10⁶

4.3 Effect of Nanoparticles Volume Fraction on Flow and Natural Convection Heat Transfer

Figures 7, 8 and 9 illustrate the dimensionless temperature distribution and streamlines for different volume fractions (0.05, 0.1, and 0.2) of copper nanofluid at Grashof number 10³ and Prandtl number 6.2. In all figures, the solid lines represent pure water, while the dashed lines represent the nanofluid. As observed in these figures, for nanofluid with a low volume fraction (φ = 0.05), the difference between isotherms and streamlines is not significant compared to pure water. However, with an increase in the volume fraction, the difference between isotherms for the nanofluid and the pure water increase, particularly in the middle of the cavity.

Fig. 7

a isotherms (left) b streamlines (right) for φ = 0.05, Gr = 10³ and Pr = 6.2

Fig. 8

a isotherms (left) b streamlines (right) for φ = 0.1, Gr = 10³ and Pr = 6.2

Fig. 9

a isotherms (left) b streamlines (right) for φ = 0.2, Gr = 10³ and Pr = 6.2

4.4 Effect of Nanoparticles Volume Fraction and Grashof Number on Flow and Natural Convection Heat Transfer

Figures 10, 11, 12, 13, 14 and 15 depict the dimensionless temperature distribution and streamlines for various volume fractions of copper nanofluid at Grashof numbers 10⁴ and 10⁵ and the Prandtl number 6.2. The results indicate that for a constant Grashof number, an increase in the volume fractions of nanoparticles in the base fluid leads to a greater deviation of isotherms between the nanofluid and the base fluid. Additionally, an increase in the Rayleigh number intensifies the nanofluid's natural convection, and fluid moves faster. Consequently, figures show that the isotherms become more compact near the walls as the Rayleigh number increases. As the volume fraction of nanoparticles increases, the streamlines rotate in a counterclockwise direction and change their position. The displacement value in a specific Grashof number increases with an increase in nanoparticle volume fraction. Similarly, an increase in the Grashof number at a specific volume fraction results in a greater change in the position of streamlines. These displacements are more significant at the cavity's center than near the walls.

Fig. 10

a isotherms (left) b streamlines (right) for φ = 0.05, Gr = 10⁴ and Pr = 6.2

Fig. 11

a isotherms (left) b streamlines (right) for φ = 0.1, Gr = 10⁴ and Pr = 6.2

Fig. 12

a isotherms (left) b streamlines (right) for φ = 0.2, Gr = 10⁴ and Pr = 6.2

Fig. 13

a isotherms (left) b streamlines (right) for φ = 0.05, Gr = 10⁵ and Pr = 6.2

Fig. 14

a isotherms (left) b streamlines (right) for φ = 0.1, Gr = 10⁵ and Pr = 6.2

Fig. 15

a isotherms (left) b streamlines (right) for φ = 0.2, Gr = 10⁵ and Pr = 6.2

4.5 Effect of Grashof Number on the Flow Velocity of Nanofluid

Figures 16, 17 and 18 show the velocity fields in the cavity for the different volume fractions of nanoparticle and Grashof numbers. In all figures, lines and dashed are pure water and nanofluid, respectively. The results show that velocity in all Grashof numbers and volume fractions of nanoparticles is minimum near walls and in the center of the cavity. In addition, by increasing Grashof numbers, the minimum velocity area at the center of the cavity increases.

Fig. 16

The velocity fields for Gr = 10³, Pr = 6.2, and a φ = 0.05 b φ = 0.10 c φ = 0.20

Fig. 17

The velocity fields for Gr = 10⁴, Pr = 6.2, and a φ = 0.05 b φ = 0.10 c φ = 0.20

Fig. 18

The velocity fields for Gr = 10⁵, Pr = 6.2, and a φ = 0.05 b φ = 0.10 c φ = 0.20

4.6 Effect of Grashof Number and Different Volume Fractions on the Temperature Profile

Figures 19 and 20 show the temperature profile at $\frac{y}{H}=\frac{1}{2}$ (the middle horizontal line of the cavity) and $\frac{x}{L}=\frac{1}{2}$ (the middle vertical line of the cavity) for the different volume fractions of nanoparticles and Grashof numbers, respectively. As can be observed from the figures, with an increase in the Grashof number, the temperature difference of the centerline decreases for the nanofluid compared to the pure fluid. Additionally, with an increase in nanoparticle volume fraction, the temperature difference between the two walls on each surface decreases. According to the Nusselt number equation, this leads to an increase in the Nusselt number and, therefore, an increase in heat transfer. The graphs mentioned above are in perfect agreement with the results obtained from Alloui et al. (2012), which used the CFD method.

Fig. 19

The temperature profile at $\frac{y}{H}=\frac{1}{2}$, Pr = 6.2 and a 10³ b 10⁴ c 10⁵

Fig. 20

The temperature profile at $\frac{x}{L}=\frac{1}{2}$, Pr = 6.2 and a 10³ b 10⁴ c 10⁵

4.7 Effect of Grashof Number and Different Volume Fractions on the Velocity Profile

Figures 21 and 22 show the horizontal component velocity profile (u_x) at $\frac{y}{H}=\frac{1}{2}$ (the middle line of the cavity) and the vertical component velocity profile (u_y) at $\frac{y}{H}=\frac{1}{2}$ for different volume fractions of nanoparticles and Grashof numbers, respectively. As it can be concluded from the figures, the fluid velocity range has decreased with the increase in the volume fraction of nanoparticles. However, by increasing the nanoparticle volume fraction, the strength of convection heat transfer has decreased. The graphs are in perfect agreement with the results obtained from Alloui et al. (2012), which used the CFD method.

Fig. 21

The horizontal component velocity profile (u_x) at $\frac{y}{H}=\frac{1}{2}$, Pr = 6.2 and a 10³ b 10⁴ c 10⁵

Fig. 22

The vertical component velocity profile (u_y) at $\frac{y}{H}=\frac{1}{2}$, Pr = 6.2 and a 10³ b 10⁴ c 10⁵

Figure 23 shows the average Nusselt number at the right wall of the cavity for the different volume fractions of nanoparticles and Grashof numbers. It can be concluded that at a specific Grashof number, with increasing volume fraction of nanoparticles, the Nusselt number increases, which shows the increase in nanofluid heat transfer compared to pure fluid.

Fig. 23

The average Nusselt number at the right wall of the cavity for the different volume fractions of nanoparticles and Grashof numbers

5 Conclusions

This study used the lattice Boltzmann method to investigate the flow and heat transfer of a homogeneous nanofluid consisting of copper nanoparticles inside a square cavity. The horizontal walls of the cavity were kept insulated, while the vertical walls were subjected to constant heat flux. The nanofluid inside the cavity consisted of particles with the same diameter and a homogeneous distribution, and there was no chemical reaction between its components. The flow was assumed to be steady and two-dimensional. The effect of the volume concentration of nanoparticles on various dimensionless parameters related to the hydrodynamic and thermal behavior of the flow was evaluated. Based on the results obtained from this study, the following general conclusions were drawn:

• The results showed that the lattice Boltzmann method has considerable ability to predict free convection heat transfer and flow behavior in cavities under constant heat flux. Due to its simplicity, high speed, and independence of velocity on pressure, it is a more optimal method for investigating free convection heat transfer in cavities compared to other methods.

• It was observed that in a constant Grashof number, as the volume fraction of nanoparticles in the base fluid increases, the deviation of isotherms between the nanofluid and the base fluid increases. Additionally, as the Rayleigh number increases, the natural convection of the nanofluid increases, and the fluid moves faster. Therefore, isotherms become more compact near the cavity walls with an increase in the Rayleigh number.

• Furthermore, it was observed that with an increase in the volume fraction of nanoparticles, the streamlines rotate anticlockwise and change their location. The value of the displacement in a specific Grashof number increases with an increase in the volume fractions of nanoparticles. Also, as the Grashof number increases in a specific volume fraction of nanoparticles, the displacement of streamlines increases. These changes in the location of streamlines are more noticeable in the center of the cavity than near the walls.

• It has been shown that with an increase in the volume fraction of nanoparticles, the average Nusselt number on the right wall of the cavity has increased. For instance, for a volume fraction of 0.2 of nanoparticles in the Grashof number 10⁵, the average Nusselt number has increased by approximately 50% compared to the base fluid (water).

• Additionally, it was observed that at a constant Grashof number, the Nusselt number has increased with an increase in the volume fraction of nanoparticles, indicating an increase in the heat transfer of the nanofluid compared to the pure fluid.