1 Introduction

Magnetic drug targeting (MDT) is a method in which an external magnetic field guides magnetic drug carriers in the body to reach the target site. In this method, magnetic carriers are injected into the body through the arteries. Then, by applying an external magnetic field and creating a magnetic gradient in a specific area of the body, the magnetic carriers are transported to and captured at the target site (Liu et al. 2019a). Applications of targeted drug delivery systems include tumor treatment, targeting radioactive compounds, magnetic thermotherapy, and in vivo and in vitro diagnostics (Ahmad et al. 2013). The advantages of this method include therapeutic responses in the target organs at only one-tenth of the free drug dose, dissemination of the controlled drug in the target tissues at intervals of 30 min to 30 h, and prevention of acute drug toxicity directed toward endothelial cells and normal parenchyma (Aggarwal et al. 2012).

Many studies have been performed in the field of MDT in the last two decades. Experimental, numerical, and theoretical methods have been used to study different aspects of MDT (Kakavand et al. 2022; Avval et al. 2020; Liu et al. 2019b; Ranjbari et al. 2023; Koosha et al. 2022). The lattice-Boltzmann method (LBM) is a category of computational fluid dynamics (CFD) approaches to simulate flow fields. This novel emerging method has also been used by different authors in the field of drug delivery (Sajjadi et al. 2021, 2022; Kandelousi and Ellahi 2015). Shaw et al. (2013) presented a mathematical model for predicting targeted drug delivery in a permeable microvessel under the effect of a magnetic field. The blood behavior was modeled by the Casson model. It was observed that with an increase in the permeability of the microvessel wall, the tendency of the carrier particle to be captured at the tumor site decreased. Cherry et al. (2010) developed a physics-based model of a general MDT system. In this simulation, in addition to the dominant forces, interparticle forces were also considered. It was found that the particle retention rate increased with increasing particle diameter and magnetic field gradient strength and decreased with increasing bulk flow velocity. Bose and Banerjee (2015a) conducted a study on capturing magnetic particles flowing in a magnetic biofluid in a clogged bifurcated aortic vein under the influence of a nonuniform magnetic field. They found that there is an optimum value for parameters so that the maximum number of particles are captured at the tumor site. Guiding the spherical particles to the target location by obtaining the optimized magnetic field gradient was modeled by Lampropoulos et al. (2015). They reported that the proposed model could guide particles toward the desired direction with efficiency of over 90%. They also defined efficiency as the ratio of particles that remained in the desired trajectory (along the vessel and not stuck to the walls) to the total number of particles. Sharma et al. (2015) presented a mathematical model for the trajectories of magnetic nanoparticles in a vessel under the influence of a magnetic field. In this work, the magnet was located at the bottom of the vessel, and particles were trapped at the lower wall of the vessel. It was observed that if the magnet was located at a distance of 2.5 cm from the vessel, all the particles were trapped before or in the magnet's center. Rukshin et al. (2017) developed a mathematical model for tracking nanoparticles in blood flow in the presence of an applied magnetic field. In this research, magnetic force, power-law flow, interaction between particles and red blood cell (RBCs), and interaction between particles and blood were considered. Diffusion as a result of collisions with RBCs was found to overpower Brownian motion, emphasizing the importance of the role of RBCs as the source of diffusion. Calandrini et al. (2018) simulated MDT in the bloodstream by considering the fluid–structure interaction (FSI). In the CFD method, solid vessel deformation is ignored; however, it is considered in the FSI. It was concluded that FSI has an effect on the capture efficiency (CE), which is proportional to the inverse of Young’s modulus. Liu et al. (2018) proposed a three-dimensional multiscale LB-LDFootnote 1 approach for a nanoparticle (NP)–solvent system coupled with the LB–SLFootnote 2 method for RBC suspension to fully resolve NP transport in cellular blood flow. In this research, NP–cell interaction and NP–NP interaction were considered. As a result, Brownian motion was shown to be favorable for the margination of NPs in post-capillary vessels. Mohammadian and Pourmehran (2019) performed a study on MDT in the human lung under the influence of a nonuniform magnetic field, assuming the presence of a surface sound wave nebulizer. According to the results, the magnetic field strongly affects the deposition efficiency of particles. Manshadi et al. (2019) performed numerical modeling of MDT in a cancerous airway (lung cancer) using a permanent magnet. They found that optimizing the size of the magnet improved the CE by up to 68% and found that the use of MDT in the treatment of lung cancer was effective in delivering the drug to tumors located in the lower walls of airway branches. Majee and Shit (2020) investigated MDT in a vessel with stenosis using magnetic nanoparticles under the influence of a magnetic field. The results showed that with increasing nanoparticle aggregation, the Nusselt number increased, which in turn increased the heat transfer from the arterial wall to the surrounding tissues, thus killing the tumor and cancer cells without damaging healthy cells.

Investigation of the effects of the Saffman lift and buoyancy force on targeted drug delivery in a microstructure was addressed by Sutradhar (2021). In this study, essential factors affecting MDT in microsurgery were discussed. According to the obtained results, by considering the buoyancy and inertia force for larger nanoparticles, the CE of nanoparticles increases. Van Durme et al. (2021) proposed a model for directing and capturing magnetic nanoparticles at the desired target. The results show that the proposed method has an excellent ability to guide particles toward the desired location effectively. Ardalan et al. (2021) simulated the trajectories of magnetic nanoparticles in a stenosed vessel under the influence of an external magnetic field produced by a current-carrying wire. The results show that the CE of nanoparticles decreases with an increasing degree of constriction in the vessel. It was also found that by reducing the length of constriction in the vessel, the CE of nanoparticles increases. Fanelli et al. (2021) mathematically simulated targeted drug delivery in a vessel under the influence of an external magnetic field. The Newtonian and three different non-Newtonian models were used to model the blood. It was observed that a suitable non-Newtonian model for blood should be considered in order to model the balance between the hydrodynamic and magnetic forces properly. Camargo et al. (2021) investigated the CE of magnetic nanoparticles in a vessel with cancerous tumors in the breast under the influence of an external magnetic field. Blood flow was modeled as Newtonian. The results showed that 71% of the nanoparticles were captured at the tumor site by applying a magnetic field of 4 T, while this value was only 6% when no magnetic field was applied. Although the previous works have addressed many aspects of MDT, no studies have considered the RBC–particle interaction, considering blood as non-Newtonian.

From the literature, it can be found that the investigation of MDT considering RBC–particle interaction and particle–particle interaction as well as the non-Newtonian behavior of blood has not been addressed. Therefore, the present study aims to investigate the CE of carrier particles under the effect of a nonuniform magnetic field. Several factors, including RBC–particle and particle–particle interactions, carrier particle diameter, magnetic force, and non-Newtonian behavior of blood, have been considered. Results show that interaction forces and the non-Newtonian model significantly affect the CE of carrier particles.

2 Methodology

2.1 Model Geometry

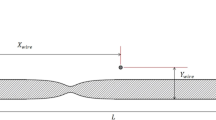
Figure 1 shows the geometry of the problem, which consists of a blood vessel and a permanent magnet. \({R}_{\mathrm{mag}}\), \({X}_{\mathrm{mag}}\), \(L\), and \({R}_{\mathrm{v}}\) are magnet radius, magnet's horizontal location, vessel length, and vessel radius, respectively, and \(d\) is the distance from the center of the magnet to the center of the vessel.

Fig. 1
figure 1

Geometry of the problem

Full size image

In the modeling, it is assumed that the fluid flow is fully developed. The boundary conditions governing the problem are as follows:

$$u = v = 0\quad \left\{ {\begin{array}{*{20}c} {0 < x < L,\quad y = R_{v} } \\ {0 < x < L,\quad y = - R_{v} } \\ \end{array} } \right.$$
(1)
$$\frac{\partial u}{{\partial y}} = 0\quad 0 < x < L,\;y = 0$$
(2)
$$P_{{{\text{out}}}} = 0\quad x = L{,} - R_{v} < y < R_{v}$$
(3)

where \(u\), \(v\), and \({P}_{\mathrm{out}}\) are the horizontal velocity, vertical velocity, and outlet pressure, respectively. The following assumptions are made to solve the problem:

  • RBCs and carrier particles are considered as solid spheres.

  • Newtonian and non-Newtonian blood flow is checked.

  • Incompressible flow.

  • No-slip condition on the wall.

  • Particles are randomly released.

  • The magnetic field is nonuniform.

2.2 Governing Equations

Different forces are applied to carrier particles due to the movement of magnetic carrier particles in the bloodstream. These forces include magnetic, drag, particle–RBC interaction, inertia, buoyancy, gravity, Brownian motion, particle–fluid interaction, interparticle effects, including magnetic dipole interaction, and van der Waals force (Furlani and Ng 2006). However, only the dominant forces, namely drag, magnetic, buoyancy, and RBC–particle and particle–particle interaction forces, have been considered in this study. It is assumed that there is a dilute mixture of particles at which the volumetric concentration of the particles is very low, i.e., \(c<<1\), where c is a volume occupied by the particles in a unit volume of fluid; thus, the effect of particles on the fluid can be neglected (Furlani and Ng 2006). In addition, Brownian diffusion is the dominant particle deposition mechanism for small particles (\({d}_{p}<100\,\mathrm{nm}\)), and as the particle size increases, the intensity of the Brownian force becomes rather small (Liu 2010; Ounis et al. 1991). Since in the present study the particle diameter is much larger than \(100\, \mathrm{nm}\), Brownian diffusion is neglected.

2.2.1 Fluid Flow

The governing equations of a fluid are continuity and momentum, which are in the form of Eqs. (4) and (5) (Bose and Banerjee 2015a):

$$\nabla \cdot u = 0$$
(4)
$$\rho \left( {\frac{\partial u}{{\partial t}} + u \times \nabla u} \right) = - \nabla p + \mu \left( {\nabla^{2} u} \right) + F$$
(5)

where \(\rho\), \(p\), and \(u\) are density, pressure, and velocity of the fluid, respectively, and \(F\) denotes the volumetric forces.

For modeling the non-Newtonian behavior of blood, the Carreau model is used, as follows (Bose and Banerjee 2015b):

$$\eta = \eta_{\infty } + \left( {\eta_{0} - \eta_{\infty } } \right)\left[ {1 + \left( {\lambda \dot{\gamma }} \right)^{2} } \right]^{{\frac{n - 1}{2}}}$$
(6)

where \(\eta_{\infty } = 0.0035\,{\text{Pa}}\,{\text{s}}\), \(\eta_{0} = 0.056\,{\text{Pa}}\,{\text{s}}\), \(\lambda = 3.313\,{\text{s}}\), and \(n = 0.3568\), and \(\dot{\gamma }\) is the shear strain rate of flow that depends on blood velocity and vessel diameter. The flow is assumed to be fully developed, and the velocity profile is in the form of Eq. (7) (Siebert and Fodor 2009):

$$u_{{\text{f}}} \left( y \right) = 2\overline{u}_{{\text{f}}} \left( {1 - \frac{{y^{2} }}{{R_{{\text{v}}}^{2} }}} \right)$$
(7)

where \(\overline{u}_{{\text{f}}} = 15\,{\text{mm}}/{\text{s}}\) is the average velocity of flow, and \(R_{{\text{v}}} = 75\,\upmu {\text{m}}\) is the vessel radius (Shazri and Idres 2017).

2.2.2 Carrier Particles

Newton's second law governs the motion of the carrier particles as follows:

$$m_{{\text{p}}} \frac{{{\text{d}}u_{{\text{p}}} }}{{{\text{d}}t}} = \sum F_{{{\text{ext}}}}$$
(8)

where \(m_{{\text{p}}}\) and \(u_{{\text{p}}}\) are the mass and velocity of carrier particles, respectively. Also, \(F_{{{\text{ext}}}}\) is the sum of forces acting on the carrier particles, including drag, magnetic, buoyancy, and interaction forces.

2.2.2.1 Drag Force

As mentioned earlier, because the volume fraction of carrier particles is very low, only the drag force acting on carrier particles by the fluid is considered. This drag force is defined as follows (Morsi and Alexander 1972):

$$F_{{\text{D}}} = \frac{{3\mu C_{{\text{D}}} {\text{Re}}_{{\text{p}}} .}}{{4\rho_{{\text{p}}} D_{{\text{p}}}^{2} }}\left( {u_{{\text{f}}} - u_{{\text{p}}} } \right)$$
(9)
$${\text{Re}}_{{\text{p}}} = \frac{{\rho \left| {u_{{\text{f}}} - u_{{\text{p}}} } \right|D_{{\text{p}}} }}{\mu }$$
(10)
$$C_{{\text{D}}} = a_{1} + \frac{{a_{2} }}{{{\text{Re}}_{{\text{p}}} }} + \frac{{a_{3} }}{{{\text{Re}}_{{\text{p}}}^{2} }}$$
(11)

where \(a_{1}\), \(a_{2}\), and \(a_{3}\) are constants. Besides, \(\rho_{{\text{p}}}\), \(D_{{\text{p}}}\), \(u_{{\text{f}}}\), \(u_{{\text{p}}}\), \(\rho\), and \(\mu\) are particle density, particle diameter, blood velocity, particle velocity, blood density, and blood viscosity, respectively.

2.2.2.2 Buoyancy Force

Buoyancy force is an upward force exerted on immersed objects. Therefore, buoyancy force applied on carrier particles flowing through blood is expressed by Eq. (12) (Sharma et al. 2015):

$$F_{{\text{b}}} = - V_{{\text{p}}} \left( {\rho_{{\text{p}}} - \rho_{{\text{f}}} } \right)g$$
(12)

where \(V_{{\text{p}}}\), \(\rho_{{\text{p}}}\), \(\rho_{{\text{f}}}\), and \(g\) are particle volume, particle density, fluid density, and gravitational constant, respectively.

2.2.2.3 Magnetic Force

A magnetic force produced by a permanent magnet exerting on a spherical particle is calculated by Eqs. (13)–(15) (Shazri and Idres 2017):

$$F_{m} = F_{mx} \hat{i} + F_{my} \hat{j}$$
(13)
$$F_{{{\text{m}}x}} = - 3\mu_{0} V_{{\text{p}}} M_{{\text{s}}}^{2} R_{{\text{m}}}^{4} \frac{{x - x_{{{\text{mag}}}} }}{{2\left[ {\left( {y - d} \right)^{2} + \left( {x - x_{{{\text{mag}}}} } \right)^{2} } \right]^{3} }}$$
(14)
$$F_{{{\text{m}}y}} = - 3\mu_{0} V_{{\text{p}}} \;M_{{\text{s}}}^{2} R_{{\text{m}}}^{4} \frac{y - d}{{2\left[ {\left( {y - d} \right)^{2} + \left( {x - x_{{{\text{mag}}}} } \right)^{2} } \right]^{3} }}$$
(15)

where \(\mu_{0} = 4\pi \times 10^{ - 7} \,{\text{H/m}}\) is the permeability of vacuum, and \(M_{{\text{s}}} = 10^{6} \,{\text{A/m}}\) is the magnetization of the magnet. In these equations, the proportionality constant, \(\chi\), is called the magnetic susceptibility. The magnetic susceptibility quantifies the tendency of a material to form magnetic dipoles. The effective susceptibility of spherical particles is related to their intrinsic susceptibility. Since we have assumed the particle is below saturation, the intrinsic susceptibility is \(\chi_{{{\text{eff}}}} = 3\) (Shazri and Idres 2017). Also, \(R_{{\text{m}}} = 2\,{\text{cm}}\) is the magnet radius, and \(x_{{{\text{mag}}}}\) is the horizontal components of the center of the magnet from the origin of the coordinate, which is \(6\,{\text{cm}}\).

2.2.2.4 Interaction Force

RBC–particle and particle–particle interactions happen in MDT. These forces indeed affect the capture of carrier particles at the region of interest (ROI). In this research, both particles and RBCs are considered solid spheres; thus, the RBC–particle and particle–particle interactions can be modeled by the Lennard–Jones model. This force is derived from the Lennard–Jones potential. Therefore, this potential can be used for the interaction between two spheres. The Lennard–Jones force is expressed as follows (Tan et al. 2012):

$$F\left( r \right) = \frac{24\varepsilon }{\sigma }\mathop \sum \limits_{j = 1}^{N} \left[ {2\left( {\frac{\sigma }{{\left| {r - r_{j} } \right|}}} \right)^{13} - \left( {\frac{\sigma }{{\left| {r - r_{j} } \right|}}} \right)^{7} } \right]\left( {\frac{{r - r_{j} }}{{\left| {r - r_{j} } \right|}}} \right)$$
(16)

where \(\varepsilon = 10^{ - 15} j\) is the strength of the potential energy, and \(\sigma = 200\,{\text{nm}}\) is the distance at which the particle–particle potential energy is zero. Also, N is the sum of the number of carrier particles (30) and the number of RBCs (30). Parameter \(r\) denotes the distance between the particles, and \(r_{j} \;\) is the position vector of the jth particle.

Finally, the capture efficiency of carrier particles is defined as the ratio of particles captured at the ROI to the total number of injected particles as follows (Banerjee et al. 2010):

$${\text{CE}} = \frac{{n_{{\text{t}}} - n_{{{\text{out}}}} }}{{n_{{\text{t}}} }}$$
(17)

where \(n_{{\text{t}}}\) and \(n_{{{\text{out}}}}\) denote the total number of injected particles and the number of particles that reach the outlet, respectively.

2.3 Numerical Procedure

The governing equations are solved using the finite element (FE) method. A continuous fluid flow is assumed, which is governed by the Navier–Stokes equations. The Paradiso and MUMPS solvers are used to determine the fluid flow and magnetic field, respectively. It is assumed that carrier particles are dispersed randomly at the inlet. COMSOL Multiphysics 5.5a is used to solve the equations. The hardware used to solve the equations includes an Intel® Core™ i5 CPU, 2.50 GHz, 16.00 GB RAM, and 500 GB SSD. The parameters used to solve the equations are provided in Table 1.

Table 1 Parameters and their values used in this study
Full size table

2.4 Mesh Convergence

Two types of meshes, i.e., mapped and triangle, are used to produce the grid. A mapped mesh is used for the vessel, and a triangle-type mesh is used for both the magnet and the environment. Five grids are considered to perform the grid independence study. The grids include G1 = 60,358, G2 = 121,632, G3 = 247,350, G4 = 501,246, and G6 = 1,056,322. The CE of carrier particles in terms of the number of elements is shown in Fig. 2. As can be seen from this figure, the CE is nearly the same for G4 and G5, and a further increase in the number of elements has almost no effect on CE; thus, to reduce the computational time and effort, G4 is used.

Fig. 2
figure 2

Grid independency

Full size image

3 Results and Discussion

3.1 Validation

The accuracy of the present study is validated by both numerical and experimental works. In the first step, the results of the present study are compared with the results reported by Shazri and Idres (2017), using the same parameters and geometry to check the accuracy of the results. It is assumed that \(d=2.5 \,\mathrm{cm}\) and \({D}_{\mathrm{p}}=500 \,\mathrm{nm}\). The trajectory of a particle released from the center of vessel is shown in Fig. 3. As can be seen, there is good agreement between both works.

Fig. 3
figure 3

Comparison of particle trajectory between the present study and Shazri and Idres (2017)

Full size image

In addition, the present work is validated by the experimental work done by Takeda et al. (2006). Again, the same geometry was used, and fluid velocity, vessel diameter, and nanoparticle diameter were set to \(20 \,\mathrm{cm}/\mathrm{s}\), \(2 \mathrm{mm}\), and \(2\,\mu \mathrm{m}\), respectively. The CE of carrier particles in the present results and Takeda et al. (2006) are 70% and 65%, respectively (see Table 2). There are two reasons for this deviation. First, Takeda et al. (2006) did not include RBC–particle interaction, which may decrease the CE of carrier particles. In addition, in the present study, non-Newtonian behavior is considered for blood. As a result, a deviation of 5% between the results is acceptable.

Table 2 Comparison of CE of nanoparticles in the present study and Takeda et al. (2006)
Full size table

3.2 Magnetic Field

In this study, a permanent (Nd-Fe-B) magnet is used to produce a nonuniform and constant magnetic field. The magnet is a cylindrical type with a radius of \({R}_{\mathrm{magnet}}=2 \,\mathrm{cm}\) and height of \({H}_{\mathrm{m}}=1 \,\mathrm{cm}\) which is located externally near the top vessel’s wall. The vertical location of the magnet is changed in order to adjust the strength of the magnetic field. The vertical distance from the center of the magnet to the center of the vessel, \(d\), is in the range of 2.5–5.5 cm. The variation in the magnetic flux density along the horizontal axis, i.e., (X,0,0), is plotted in Fig. 4a. The maximum field strength at the center of the vessel is nearly \(0.54 T\), which is in the safe range for the human body. The variation in the magnetic flux density along the vertical axis at the center of the vessel, i.e., \(({X}_{\mathrm{mag}},Y,0)\), is shown in Fig. 4b.

Fig. 4
figure 4

The magnetic flux density variation along the a horizontal and b vertical directions

Full size image

3.3 Interaction Forces

In this section, the effect of RBC–particle and particle–particle interactions on the location of carrier particles is investigated. A total of 30 RBCs and 30 particles are considered. The diameter of RBCs and particles are \({D}_{\mathrm{RBC}}=8 \,\mu\mathrm{m}\) and \({D}_{\mathrm{p}}=500-2000 \,\mathrm{nm}\), respectively. The Newtonian model is used for blood. RBCs are shown in the red sphere, while the carrier particles are shown in blue. To show the effect of RBC–particle interaction on the trajectory of particles, part of the vessel is shown at the same time. The whole length of the vessel is 12 cm, while in Figs. 5 and 6, only \(5.9 \,\mathrm{cm}\le X\le 6.55 \,\mathrm{cm}\) is shown. Figure 5a, b shows the location of particles with a diameter of \({D}_{\mathrm{p}}=500 \,\mathrm{nm}\) at time\(T=2.65\,\mathrm{s}\), and \(5.9 \,\mathrm{cm}\le X\le 5.97 \,\mathrm{cm}\). It can be seen from Fig. 5a, in which the interaction forces are considered, that there are one particle and five RBCs. However, in Fig. 5b, where interaction forces are neglected, there are three particles and five RBCs. Since all other forces are the same, it clearly shows the effect of interaction forces on the location of particles. However, because red blood cells are larger, they have a greater interaction force on the carrier particles, resulting in fewer carrier particles in the center of the vessel. The results are quite reasonable because particles experienced more variations in both direction and speed as RBC–particle collision occurs. This is the reason for the higher accumulation of particles and RBCs in the center of the vessel when there is no interaction force (see Fig. 5b).

Fig. 5
figure 5

Particle and RBC trajectories for \({D}_{\mathrm{p}}=500\,\mathrm{nm}\), \(d=4.5\,\mathrm{cm}\) a with interaction forces, b without interaction forces

Full size image
Fig. 6
figure 6

Particle and RBC trajectories for \({D}_{\mathrm{p}}=2000\,\mathrm{nm}\), \(d=5.5\,\mathrm{cm}\) a with interaction forces, b without interaction forces

Full size image

The location of carrier particles and RBCs is shown in Fig. 6a, b when \({D}_{\mathrm{p}}=2000 \,\mathrm{nm}\), \(d=5.5 \,\mathrm{cm}\), \(T=3 \mathrm{s}\), and \(6.34 \,\mathrm{cm}\le X\le 6.53 \,\mathrm{cm}\). When the interaction forces are neglected (see Fig. 6b), there are four particles and four RBCs; however, in Fig. 6a, in which interaction forces are considered, there are four particles and three RBCs. Again, because the RBC–particle interaction is higher, there are fewer particles near the RBCs when considering the interaction forces. As a result, the interaction forces have a significant effect on the location of carrier particles.

In the following sections, the effect of parameters including particle diameter, distance from the center of the magnet to the center of the vessel, interaction forces, and Newtonian and non-Newtonian models on the CE of carrier particles is investigated. Parameter values of \({D}_{\mathrm{p}}=500-2000 \,\mathrm{nm}\), \(d=2.5-5.5\,\mathrm{cm}\), \(L=12\,\mathrm{cm}\), \({R}_{\mathrm{v}}=75\,\mu\mathrm{ m}\), \({N}_{\mathrm{P}}=30\), and \({N}_{\mathrm{RBC}}=30\) are used. In addition, the carrier particles and RBCs are randomly dispersed at the vessel inlet so that the real condition is met. For better understanding and deeper insight, the results of the following sections are presented in the form of histograms. In MDT, the magnet is located just near the tumor site. Thus, in the present study, it is assumed that the tumor is located at the upper wall of the vessel with a size of nearly 4 cm. For a better understanding of the effect of particle diameter, with and without interaction forces, the vessel's upper wall is divided into ten regions, where R1 = 2 cm, R2 to R9 = 1 cm, and R10 = 2 cm. It is assumed that the tumor is located on the upper side of the wall in the R4–R7. The region where the tumor is located, i.e., R4–R7, is called the ROI. It should be noted that, since R1 = 2 cm and R10 = 2 cm are located at the inlet and outlet of the vessel where the magnetic field has the minimum value, because of the greater distance from the center of the magnet, they are not divided into four 1-cm regions for sake of simplicity. It should be noted that only the particles which are captured at the ROI are included in CE. Other regions are shown in histograms to see the displacement of carrier particles in different cases. It should be noted that for a better view, some parts in which the CE is zero are not shown in some of the figures. All histograms are presented for both cases, i.e., with and without considering interaction forces.

3.4 Particle Diameter

In this section, four particle diameters are used to determine the effect of particle diameter on the CE of carrier particles. The four diameters are \(500\,\mathrm{nm}\), \(1000\,\mathrm{nm}\), \(1500\,\mathrm{nm}\), and \(2000\,\mathrm{nm}\). Figures 7, 8, 9, and 10 show the histograms of CE of carrier particles in predefined regions, i.e., R1–R10, for different particle diameters for both with and without considering interaction forces. In all cases, the Newtonian model is used for the blood.

Fig. 7
figure 7

Comparison of CE of nanoparticle in predefined regions with and without considering interaction forces for \({D}_{\mathrm{p}}=500\,\mathrm{nm}\) and \(d=2.5\,\mathrm{cm}\)

Full size image
Fig. 8
figure 8

Comparison of CE of nanoparticle in predefined regions with and without considering interaction forces for \({D}_{\mathrm{p}}=1000\,\mathrm{nm}\) and \(d=2.5\,\mathrm{cm}\)

Full size image
Fig. 9
figure 9

Comparison of CE of nanoparticle in predefined regions with and without considering interaction forces for \({D}_{\mathrm{p}}=1500\,\mathrm{nm}\) and \(d=2.5\,\mathrm{cm}\)

Full size image
Fig. 10
figure 10

Comparison of CE of nanoparticle in predefined regions with and without considering interaction forces for \({D}_{\mathrm{p}}=2000\,\mathrm{nm}\) and \(d=2.5\,\mathrm{cm}\)

Full size image

Figure 7 is depicted to show the CE of carrier particles for \({D}_{\mathrm{p}}=500\,\mathrm{nm}\). As shown in the figure, all particles are captured at R1, R4, R6, and R7. The CE of carrier particles for the case considering interaction forces is 29%, while this value for the case without considering interaction forces is 42.1%. This reveals that considering interacting forces has led to a reduction in CE by 13%. Besides, it can be seen that in all regions, more particles are captured in the case without considering interaction forces. This difference is due to the sudden change in trajectories of carrier particles due to the interaction forces so that fewer particles are captured.

There is a direct relationship between particle diameter and drag force, so as the particle diameter increases, the drag force increases too. However, since the magnetic field is a function of \({D}_{\mathrm{p}}^{3}\) (Eqs. 14, 15, \({V}_{\mathrm{p}}\sim {D}_{\mathrm{p}}^{3}\)), the effect of particle diameter on the magnetic force is much more than the drag force. As a result, it is expected that the CE of carrier particles increases by increasing the particle diameter. Figures 8, 9, and 10 show the histograms of CE of carrier particles for \({D}_{\mathrm{p}}=1000\,\mathrm{nm}\), \({D}_{\mathrm{p}}=1500\,\mathrm{nm}\), and \({D}_{\mathrm{p}}=2000\,\mathrm{nm}\), respectively. By comparing the figures, it can be found that for \({D}_{\mathrm{p}}=1000\,\mathrm{nm}\), \({D}_{\mathrm{p}}=1500\,\mathrm{nm}\), and \({D}_{\mathrm{p}}=2000\,\mathrm{nm}\), the CE of carrier particles considering interaction forces are 44.1%, 47%, and 53%, respectively. On the other hand, these values for a case without considering interaction forces are 47%, 58%, and 70%, respectively. By comparing the results, it is revealed that the CE of carrier particles is reduced by considering the interaction forces for all diameters. The maximum difference between CE of carrier particles for a case with and without considering interaction forces corresponds to \({D}_{\mathrm{p}}=2000\,\mathrm{nm}\) with a value of approximately 17%. By looking at Fig. 8, it can be found that more particles are captured in some regions, i.e., R7 and R8, for the case with interaction compared to the case without interaction. The reason is that when collision occurs, whether particle–particle or RBC–particle, the direction of particles will change. Sometimes, this change in the direction of particles is desired so that the particles are deviated toward the vessel wall. In such cases, more particles are captured by considering the interaction forces. However, as can be seen from the figure, some particles are captured outside the ROI and are not included in the CE. This is why it can be concluded that by considering the interaction forces, the total number of particles captured at the ROI, i.e., R4–R7, is reduced compared to the case without interaction forces.

3.5 Non-Newtonian Behavior of Blood

In this section, the effect of non-Newtonian behavior of blood on the CE of carrier particles is investigated. The parameters used here are as follows: \({D}_{\mathrm{p}}=500-2000\,\mathrm{nm}\), \(d=2.5-5.5\,\mathrm{cm}\), \(L=12\,\mathrm{cm}\), and \({R}_{\mathrm{v}}=75\,\mu\mathrm{ m}\). Four cases are considered: case 1 (Newtonian model with interaction forces); case 2 (Newtonian model without interaction forces); case 3 (non-Newtonian model with interactions); and case 4 (non-Newtonian model without interaction forces). Figures 11 and 12 show the CE of carrier particles for all four cases for \({D}_{\mathrm{p}}=2000\,\mathrm{nm}\). It can be seen from Fig. 11 that for \(d=2.5\,\mathrm{cm}\), the maximum CE (70%) is related to case 2. The reason for this higher CE is due to the higher magnetic field, lower drag force (Newtonian case), and neglecting the interaction forces. With increasing \(d\), the CE of all cases decreases and approaches zero at \(d=4.5\,\mathrm{cm}\). This reveals that the dominant parameters are magnetic force, interaction forces, and non-Newtonian behavior of blood, respectively.

Fig. 11
figure 11

Comparison of CE of nanoparticles for four different cases in terms of distance from the center of the magnet to the center of the vessel for \({D}_{\mathrm{p}}=2000\,\mathrm{nm}\)

Full size image
Fig. 12
figure 12

Comparison of CE of nanoparticles for case 2 and case 3 for \({D}_{\mathrm{p}}=2000\,\mathrm{nm}\)

Full size image

Figure 12 shows the comparison of the real condition (case 3) and the ideal condition (case 2) in terms of \(d\). At \(d=2.5\,\mathrm{cm}\), it can be seen that the CE of the real condition is nearly 45%, while for the ideal condition, it is nearly 70%. The results show a 25% difference in CE when considering interaction forces and non-Newtonian behavior of blood. When the non-Newtonian model is used for blood, the drag force exerted on the particles increases, and thus fewer particles are captured. On the other hand, when interaction forces are considered, with every collision of particles with RBCs, the direction and speed of carrier particles are changed. Since the maximum magnetic force occurs near the magnet and at the ROI, the magnetic force cannot capture particles at the ROI when the collision occurs. As a result, some particles are either captured before or after the ROI, which are not included in the CE. Thus, as evident from the results, considering particle–RBC interaction will lead to a reduction in CE of carrier particles.

Figures 13 and 14 show the CE of carrier particles for Newtonian and non-Newtonian models for \({D}_{\mathrm{p}}=1500\,\mathrm{nm}\). It can be seen from Fig. 13 that for \(d=2.5\,\mathrm{cm}\), the maximum CE (58%) is related to case 2. The reason for this higher CE is due to the higher magnetic field, lower drag force (Newtonian case), and neglecting the interaction forces. With increasing \(d\), the CE of all cases decreases and approaches zero at \(d=5.5\,\mathrm{cm}\). It reveals that the dominant parameters are magnetic force, interaction forces, and non-Newtonian behavior of blood, respectively.

Fig. 13
figure 13

Comparison of CE of nanoparticles for four different cases in terms of distance from the center of the magnet to the center of the vessel for \({D}_{\mathrm{p}}=1500\,\mathrm{nm}\)

Full size image
Fig. 14
figure 14

Comparison of CE of nanoparticles for case 2 and case 3 for \({D}_{\mathrm{p}}=1500\,\mathrm{nm}\)

Full size image

Figure 14 shows a comparison of the real condition (case 3) and the ideal condition (case 2) in terms of \(d\). It can be seen that for \(d=2.5\,\mathrm{cm}\), the CE of the real condition is nearly 41%, while for the ideal condition it is nearly 58%, thus revealing a 17% difference in CE when considering interaction forces and non-Newtonian behavior of blood. When the non-Newtonian model is used for blood, the drag force exerted on the particles increases, and thus fewer particles are captured. On the other hand, when interaction forces are considered, the particle motion suddenly changes as the interaction occurs, resulting in fewer particles being captured.

4 Conclusions

In this study, the CE of magnetic carrier particles in a vessel containing blood flow under the influence of a nonuniform magnetic field was investigated. A total of 30 carrier particles and 30 RBCs were randomly dispersed at the inlet. Both RBCs and carrier particles were considered as solid spheres. The FEM method was used to solve the governing equations. The effect of several parameters, including particle diameter, non-Newtonian behavior of blood, distance from the center of the magnet to the center of the vessel, and RBC–particle and particle–particle interactions on the CE of carrier particles was investigated. The results are highlighted as follows:

  • As the diameter of the magnetic carrier particles increases, the magnetic force acting on them increases, and the particles are captured sooner.

  • By increasing the vertical distance from the magnet to the vessel, the intensity of the magnetic field decreases. The maximum magnetic field intensity is 0.54 T, which is within the safe range for human applications.

  • By increasing the magnet–vessel distance from 2.5 to 3.5 cm, the CE of nanoparticles for case 2 and case 3 decreased by 72% and 78%, respectively.

  • Considering the interaction forces has a considerable effect on the CE of carrier particles. It was observed that in all cases, by considering these forces, the CE is decreased. For example, for \({D}_{\mathrm{p}}=2000\,\mathrm{nm}\), the CE of carrier particles is decreased by 17% considering interaction forces, compared to the cases without interaction forces.

  • Among the cases studied in this research, the maximum (75%) and minimum (45%) CE values are found for case 2 and case 3, respectively.

  • It was observed that simultaneous consideration of the non-Newtonian model and interaction forces (case 3) significantly affects the CE of carrier particles. For example, for \({D}_{\mathrm{p}}=2000\,\mathrm{nm}\), the CE of carrier particles (for case 3) is decreased by 25% compared to case 2.

  • Since the maximum magnetic field is applied to the R4–R7 region, the maximum number of particles are captured at this region, i.e., ROI. For example, for \({D}_{\mathrm{p}}=500\,\mathrm{nm}\) and \(d=2.5\,\mathrm{cm}\), more than 40% of injected particles are captured in this region.

There are numerous cells and proteins suspended in blood. Blood is also a non-Newtonian shear-thinning fluid. As a result, the investigation of particle–particle and RBC–particle interactions and non-Newtonian model of blood can be considered one step further toward application of MDT in real in vitro applications. Therefore, the findings of the present study can provide a better understanding of the physics underlying how these parameters, i.e., interaction forces and non-Newtonian behavior, affect MDT. Further consideration of the effects of elasticity and deformation of RBCs on the CE of carrier particles remains for future work.