Durability and Compression Properties of High-Strength Concrete Reinforced with Steel Fibre and Multi-walled Carbon Nanotube

Abstract

High-strength concrete (HSC) reinforced with steel fibre (SF) and carbon nanotube (HSCRSC) is a new type of high-strength composite concrete with good fluidity, high strength, toughness, durability and other remarkable advantages. HSCRSC can be widely used in underground structures, such as wellbores. In this study, HSCs ranging from 70 to 100 MPa were designed, and the effects of fibre on the performance of the HSCs were compared and analysed through single-doped and double-mixed SF and multi-walled carbon nanotubes. Results showed that the fibre effectively improved the uniaxial and multiaxial compressive strengths and durability of HSCs and changed the failure mode from brittle to ductile, especially in the case of multiaxial compression failure. HSCs remained intact, but the plain concrete specimens had fractured forms, such as flakes, columns and layers. Moreover, the ultimate strength of the biaxial compression was between 1.10 and 1.39 times higher than that of the uniaxial compression, satisfying the Kufer–Gerstle criterion. The ultimate strength of the triaxial compression was between 1.24 and 2.55 times higher than that of the uniaxial compression, adhering to the Willam–Warnke meridian criterion. The modified B3 model met the prediction accuracy of shrinkage and creep for HSC and surpassed the biaxial and triaxial compression ultimate strength models provided in this study. The absolute value of the relative error was less than 6%, indicating that the model and test data were reliable. All test results showed that HSCRSC exhibited satisfactory comprehensive performance.

1 Introduction

Underground structures, such as coal mine shafts up to 1000 m deep, and ground structures, such as super high-rise buildings and super long-span bridges, have increasingly high requirements on the comprehensive performance of concrete. The requirements include good workability and high strength, toughness, durability and fluidity. Normal-weight concrete (NWC) has high brittleness (Seung et al. 2018), and its brittle fracture becomes much notable as strength grade increases. Adding steel fibre (SF), polypropylene fibre (PPF) and chopped basalt fibre (CBF) can resolve the brittleness of NWC and improve its toughness (Han et al. 2019; Castoldi et al. 2019; Caggiano et al. 2016; Zhu et al. 2019). Another type of fibre, namely multi-walled carbon nanotube (MWCN), has rarely been used in concrete because of its high price (Du et al. 2017). However, in recent years, the price of MWCN has dropped considerably due to the improvement of production technology. In the Chinese market, the price dropped from 15 ¥/g (RMB) in 2015 to 1 ¥/g in 2019, making the application of MWCN possible in special projects. The related research on carbon nanotube-modified cement-based composite material also shows that MWCN with a short length (0.5–2 μm) and a large diameter (20–30 nm) exerts the best strengthening effect on cementing materials (Cui et al. 2017). With these properties, MWCN exhibits increased compression strength (47%) and flexural strength (55%) compared with control samples with an optimal dosage of approximately 0.1% cement quality (Cui et al. 2017). Moreover, the mechanical properties of reactive powder concrete with heat curing are better than those with water curing. Heat curing is more conducive to improving the microstructure and mechanical properties of reactive powder concrete than water curing, thus promoting the combination of MWCN and reactive powder concrete (Ruan et al. 2018). Furthermore, the nano-core effect of MWCN can accelerate hydration, refine hydration products, improve the stiffness and hardness of cementing materials, and reduce internal defects. Adding MWCN can effectively reduce primary crack and make a structure compact by adsorption (Han et al. 2017). The contribution ratio of MWCN to strength is unremarkable due to MWCN’s microstructural characteristics. Nevertheless, the results of the present study show that MWCN strengthens the micro reinforcement of the concrete and exerts an adsorption effect on cement particles along with a pore-filling effect. Thus, MWCN can change the failure mode of specimens from brittle to plastic failure and demonstrates good durability resistance. This study also improves the physical and mechanical properties, durability, flowability and workability of HSC through MWCN combined with SF.

HSC has high heat release due to its large amount of cementing material resulting from a hydration exothermic reaction (Pan and Meng 2016). This reaction leads to an increase in the temperature difference between internal and external concrete, early age shrinkage and long-term creep (Pan and Meng 2016). Many factors adversely affect commonly used shrinkage and creep prediction models, such as CEB-FIP (1990) (Thomas 1993), B3 (Bažant and Baweja 1995) and GL2000 (Gardner and Zhao 1993), resulting in low prediction accuracy and limitations in model adaptation. In this study, the B3 model is appropriately modified to meet the prediction accuracy of shrinkage and creep for HSC.

Different from uniaxial compression and its failure modes, the lateral pressure increases the ultimate strength of concrete and changes the failure mode under multiaxial proportional loading (Rong et al. 2018). For example, tensile failure, columnar crush, layered splitting failure, diagonal shear failure or squeezing flow failure may occur in the case of multiaxial compression failure under different stress ratios (Song 2002). The description of the failure criteria of concrete, such as Mohr–Coulomb, Drucker–Prager and Willam–Warnke criteria, is complicated under complex stress conditions (Rong et al. 2018). We take the unified meridian equation as an example. The meridian equation must satisfy the characteristics of smoothness and convexity of the failure curve. According to the literature (Yang 2009), only the limit traces of the triaxial compression strength model on the off-plane satisfy these characteristics. Thus, the failure criteria can be described by the uniform meridian equation. The study found that under uniaxial compression, the stress–strain curve equation of HSC follows NWC. Similarly, the corresponding failure criterion form of HSC also adheres to NWC for proportional loading under multiaxial compression.

In this study, the effects on the strength of HSCs reinforced with single-doped and double-mixed SF and MWCN are compared using uniaxial mechanical property tests. Durability, shrinkage and creep tests are subsequently carried out. Finally, biaxial and real triaxial compression tests are conducted. The effects of SF and MWCN on the durability and multiaxial mechanical properties of HSC are analysed. The related experiments reveal that the macroscopic effect of SF, the microscopic effect of MWCN and their composite effects can effectively improve the physical and mechanical properties and durability of HSC. Experimental and theoretical bases for related research on and engineering application of high-strength, high-performance concrete are also provided.

2 Test Overview

2.1 Materials and Test Mix Proportion

• (1) Cement PO 52.5 cement, brand Jiangu (Jiaozuo, China), was used. The cement meets the Chinese national standard GB 175-2007 (2007).

• (2) Aggregates River sand from a local river that meets the Chinese national standard JGJ52-2006 (2006) was utilised. The fineness modulus (M_x) is 2.6 ≤ M_x ≤ 3.0. Crushed stone from a local quarry that meets the Chinese national standard GB T 14685-2011 (2011) was also adopted.

• (3) Fly ash Grade I fly ash made at Pingdingshan Yaomeng Power Plant (Pingdingshan, China) was used, and it meets the Chinese national standard GB/T 1596-2017 (2017).

• (4) Silica fume The silica fume was produced by Gongyi City (China). It contains over 92% active SiO₂ content and meets the Chinese national standard GB/T 18736-2017 (2017).

• (5) Superplasticizer Polycarboxylic acid superplasticizer produced by Henan Meiya Company (Zhengzhou, China) was used. It meets the Chinese national standard JGT 223-2017 (2017). The water-reducing rate is 30%, and the admixture is 1.6% of the cementitious material quality.

• (6) SF Corrugated SF produced by Zhengzhou Yujian Steel Fibre Limited Company (Zhengzhou, China) was used. It meets the Chinese national standard JG/T472-2015 (2015) and has a length (l_f) of 32 mm, an equivalent diameter (d_f) of 0.75 mm, an equivalent aspect ratio (l_f/d_f) of 42 and tensile strength greater than 800 MPa.

• (7) MWCN TNM8 produced by Chengdu Organic Chemistry Limited Company of the Chinese Academy of Sciences (Chengdu, China) was used. The outer diameter is more than 50 nm, the length is 10–20 µm, the purity is more than 95% and the bulk density is 180 kg/m³.

• (8) Water: Tap water used meets the Chinese national standard JGJ 63-2006 (2006).

The Chinese national standard JGJ 55-2011 (2011) was adopted as a reference through an orthogonal test and according to the requirements of pumping concrete. The optimal mix proportions ranged from 70 MPa to 100 MPa (see Table 1). The slump is 160–220 mm.

Table 1 Mix proportion (1 m³) of HSCs

2.2 Test Plan

In accordance with the Chinese national standard GB/T50081-2002 (2002), the mechanical property test specimens of concrete are in groups of three specimens which are in the same batch. Weight deviation of cement, water and admixture cannot exceed 0.5%, and aggregate deviation cannot exceed 1%. Vibration moulding was through vibration table. After moulding, the specimens were placed in a humid environment with a temperature of (20 ± 3) °C and a relative humidity of above 90% for curing.

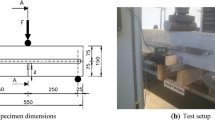
Table 2 presents the specimen size. The loading rate in the uniaxial compression test was 0.8 MPa/s to 1.0 MPa/s. The multiaxial compression test (equipment shown in Fig. 1) was loaded proportionally, and the loading rate in the σ₃ direction was 0.004 mm/s. The age of the multiaxial compression specimen was over 90 days. At this point, wear reduction measures should be taken. During the test of concrete cube specimens, the transverse friction constraint effect of the loading plate on the end face of the specimen can improve the strength of the specimen. Moreover, due to multiaxial loading, the loading head cannot automatically adjust the physical alignment in real time because of the frictional resistance between the loading head and the specimen interface. To ensure that the loading head can be fine-tuned in real time during multiaxial loading, as well as the physical and geometric alignment, the wear reduction measures must be taken during the multiaxial compression tests. Whether the wear reduction measures are appropriate depends on the uniaxial compression tests, that is, the cube compressive strength after the wear reduction measures should be the same as or close to the axial compressive strength. The test results of the relevant literature show that if no measures are taken to eliminate or reduce the frictional effect, then the strength of the specimen increases greatly, the test result is false and the test equipment may be damaged (Wang et al. 1978; Song 1994; Yang et al. 2016). In the present study, at least three specimens were used for each stress ratio in the multiaxial compression test. If the error exceeded the requirements of the Chinese national standard GB/T50081-2002 (2002), then the number of specimens was increased by three, the discrete values were deleted and the average value was obtained. The displacement was measured with a displacement sensor’s linear variable differential transformer (LVDT). The test was completed at the State Key Laboratory of Coastal and Offshore Engineering, Dalian University of Technology.

Table 2 List of tests and corresponding specifications and concrete types

Fig. 1

Sketch and photograph of a real triaxial testing machine for static and dynamic loading

Principal stress σ₁, σ₂ and σ₃ is specified as follows: the pull is denoted by ‘+’, the pressure is denoted by ‘−’ and σ₁ ≥ σ₂ ≥ σ₃. The symbols of stress and strain follow the same rules.

The shrinkage and creep tests used prismatic specimens. The creep test used prismatic specimens with dimensions of 100 mm × 100 mm × 400 mm. The relative humidity of the test environment was 60% ± 5%. Before the tests, the specimens were placed at room temperature (20 °C ± 2 °C) in a creep test room and loaded after maintenance for 28 days. In accordance with the Chinese national standard GB/T50082-2009 (2009), the stress σ_c of the creep test was 40% of axial compressive strength f_c, and the total holding time was 150 days. The shrinkage test used prismatic specimens with dimensions of 100 mm × 100 mm × 515 mm, and the test was carried out under constant temperature and humidity conditions with a relative humidity of 60% ± 5% and a temperature of (20 ± 2) °C. This test was completed at the Highway Science Research Institute of the Ministry of Transport of China.

HSC and HSCRSC (80 MPa) designed by the optimal mix proportion (seeing Table 1) were tested for frost resistance, impermeability and carbonation resistance. HSCs (80 MPa and 100 MPa) were tested for resistance to chloride ion erosion. The above tests were conducted according to the national standard GB/T50082-2009 (2009). The concrete impermeability test adopted the step-by-step pressurisation method. After the water pressure reached 1.3 MPa and was kept for 8 h, all specimens had no seepage and reached the highest impermeability grade of P12. To investigate the true impermeability of HSC, pressure was continued on this basis until the maximum compressive strength of the impermeability meter was 4 MPa. The average seepage height of the concrete specimen under constant water pressure was determined by the penetration height. The penetration height indicates the concrete resistance to water penetration. This test was completed at the Construction Engineering Quality Supervision and Inspection Station of Jiaozuo.

Given the many tests in this paper, Table 2 lists the specific tests and corresponding concrete types.

3 Test Results and Discussion

3.1 Uniaxial Compression Test

The mechanical properties of concrete specimens with different mix proportions in Table 1 were tested through uniaxial, biaxial and triaxial mechanical tests, durability tests and shrinkage and creep tests. The test results on the uniaxial mechanical property are shown in Table 3.

Table 3 Parameters of uniaxial mechanical performance

The results in Table 3 indicate that the early age strength of HSC developed rapidly. For example, with HSC-0-80 as the control group, the compressive strength of the four groups of concrete after 1 day reached 38.1–51.4% of that after 28 days. The compressive strength reached 77.8–83.1% after 7 days. The effect of adding MWCN on compressive strength was not obvious. However, with the composition of SF, the comprehensive performance of HSC became significant; for example, its tensile strength was 2.25 times that of the control group.

The other technical indexes in Table 3 were improved with the increase in concrete compressive strength. The ratio of axial compressive strength to cubic compressive strength, Poisson’s ratio, elastic modulus and peak strain were higher than those of NWC (i.e. 0.76, 0.2, 34.5 GPa and 0.002) (GB 50010-2010 2015). However, the dry apparent density was similar to 2400 kg/m³ specified in JGJ 55-2011 (2011).

With the form of splitting failure as an example (Fig. 2), HSC was accompanied with an explosive sound when it was destroyed, and the specimen was broken into two parts. The aggregates on the fracture surface were clearly visible (Fig. 2a). When the single-doped SF specimen was destroyed, the sound level was rather low, and the specimen remained intact with several small-width cracks (Fig. 2b). No sound was heard when the single-doped MWCN specimen was destroyed, and the specimen remained intact with only fine cracks visible on the surface (Fig. 2c). Owing to the long compression time, a visible crack appeared on the surface of the HSCRSC specimens after destruction, and SF crossed the crack.

Fig. 2

Photographs of failure modes of HSCs under splitting tensile stress

The uniaxial compressive stress–strain curve of concretes numbered HSC-0-70, 80, 90 and HSC-SC-70, 80, 90 are shown in Fig. 3.

Fig. 3

Stress–strain curves of HSCs under uniaxial compression

Given the lack of fibre constraints, the HSC specimens showed no signs before destruction. The destruction was accompanied with crisp and loud sounds and spallation. Eventually, the specimen broke into several pieces. The incomplete descending branch of curves in Fig. 3a reflects this phenomenon. Under the joint action of SF and MWCN, no oblique crack was visible on the surface before destruction, but the loading was accompanied with low-pitched noise. After the peak stress, visible oblique cracks appeared on the surface of the specimen quickly, and the angle between the oblique cracks and loading direction was approximately 30°. At this time, the specimen emitted a rapid and continuous crackle sound and finally cracked without breaking. The phenomenon indicates that HSCRSC has good ductility and toughness, and its failure mode is plastic.

As the strength grade increases, the brittleness of HSC increases as well and its toughness decreases. During the test, the descending section of the stress–strain curve is difficult to measure (see Fig. 3a). With the incorporation of fibres, especially SFs or composite fibres, the toughness of concrete can be effectively improved, making the descending section of the stress–strain curve easier to measure. This section also extends longer (i.e. the total strain increases, as shown in Fig. 3b), and the brittle failure of concrete is transformed into ductile failure.

The stress–strain curves of HSC and HSCRSC were described via a comparison and analysis of curve equations in different studies. The mathematical model (see Eqs. 1a, 1b) recommended by (Gao 1991) was suitable for this curve.

Ascending curve:

$$y = ax + (3 - 2a )x^{2} + (a - 2 )x^{3} ,\quad 0 \, \le x \le { 1},$$

(1a)

Descending curve:

$$y = \frac{x}{{b (x - 1 )^{2} + x}},\quad x > { 1},$$

(1b)

where x = ε₃/ε₀ and y = σ₃/f_c. a and b are fitting coefficients shown in Eqs. (1a) and (1b), respectively (see also Table 4).

Table 4 Fitting parameters of stress–strain curves for HSCs under uniaxial compression

According to the literature (Han et al. 2011), the physical (geometric) significance of the curve parameter a and b is that, if the value of the a is smaller and the value of the b is larger, then the curve is steeper and the area enclosed by the curve is smaller. These properties indicate that the plastic deformation of concrete is small, residual strength is low, the failure process is rapid and the material is brittle. Otherwise, the plastic deformation of concrete is large, the residual strength is high, the destruction is slow and the ductility is good. Table 4 shows that the value of the a in the rising section of the stress–strain curve of HSCRSC is larger than that of HSC, and the value of b in the descending segment of HSCRSC reduced from 3.59 to 3.16. Therefore, the plastic deformation of HSC is small. By contrast, HSCRSC has relatively high ductility and good toughness due to the addition of SF and MWCN.

3.2 Durability Test

In accordance with GB/T50082-2009 (2009), the specimens (HSC-0-80, HSC-0-100 and HSC-SC-80) were tested for anti-carbonation, impermeability, chloride penetration resistance, freeze–thaw resistance and sulphate resistance. The test results are shown in Tables 5 and 6.

Table 5 Parameters of durability for HSCs

Table 6 Test results of sulphate attack for HSC

Table 5 shows that HSCRSC exhibited good carbonation resistance, especially in the case of double-doped SF and MWCN. The carbonation depth before 14 days was 0 and only 0.5 mm at 28 days. The carbonation depth of HSC at 28 days was only 1.5 mm, which is smaller than the carbonation depth of NWC (2–3 mm) (Wang et al. 2017).

GB/T50082-2009 (2009) requires the step-by-step pressurisation method, and the highest water pressure is 1.3 MPa. If no water seepage occurred in each group after 8 h, then the highest grade of impermeability P12 was met. All of the specimens in this test did not show water seepage. Under the condition of breaking through the specification, the pressure continued until the highest pressure strength of the impermeability apparatus was 4 MPa, and it was stabilised for 8 h. The average seepage height (Eqs. 2a, 2b) of the concrete specimens under constant water pressure was measured with the permeability height method. The results showed that the penetration heights of HSC and HSCRSC were only 2 and 1.5 mm at a water pressure of 4 MPa, respectively.

The seepage height of a single specimen is

$$\overline{{h_{j} }} = \frac{1}{10}\sum\limits_{i = 1}^{10} {h_{i} } ,$$

(2a)

where $h_{i}$ stands for the height (mm) of seepage at the ith measurement point of the jth specimen and $h_{j}$ stands for the average seepage height (mm) of the jth specimen.

The average seepage height of a group of specimens is

$$\overline{h} = \frac{1}{6}\sum\limits_{j = 1}^{6} {\overline{{h_{j} }} } ,$$

(2b)

The relative dynamic elastic modulus after a freezing–thawing cycle was calculated according to the formula in GB/T50082-2009 (2009).

$$\Delta E_{\text{c}} = \frac{1}{3}\sum\limits_{i = 1}^{i = 3} {\frac{{f_{ni}^{2} }}{{f_{0i}^{2} }}} \times 100 ,$$

(3)

where f ²_ni stands for the transverse fundamental frequency (Hz) of the ith concrete specimen after n freezing–thawing cycles and f ²_0i stands for the transverse fundamental frequency initial value (Hz) of the ith concrete specimen before a freezing–thawing cycle.

For the chloride ion permeability resistance test, the permeability coefficient of NWC is 11.27 × 10⁻¹² (Zhang et al. 2018), which is higher than 2.57 × 10⁻¹² in this study. The coefficient decreased as the strength increased.

In the sulphate attack test, under the conditions of 120 and 150 times of dry–wet cycles, the apparent quality was intact (Fig. 4) with no loss of mass, and the resistance coefficients were all greater than 1 (both were similar). This result indicates that HSC has good resistance to chloride ion and sulphate attack.

Fig. 4

Photographs of specimens for control and after 150 wet–dry cycles corroded by sulphate

HSC has a large amount of cementing material and a low water-to-binder ratio, which leads to its low porosity and high compactness, thus improving its comprehensive strength and durability. Moreover, the connection effect of SF and its restraining effect on the microcrack propagation of concrete improve the strength of the concrete matrix. MWCN exerts a microfibre reinforcing effect and physically adsorbs the cement particles and fills the pores. The compactness and strength of the concrete matrix are improved, the porosity is reduced and the comprehensive strength and durability of the concrete are enhanced.

3.3 Shrinkage and Creep Tests

Shrinkage and creep tests were, respectively, carried out on representatives of HSC-0-80 and HSC-0-100. The test device is shown in Fig. 5, and the test results are provided in Table 7. The deformation was measured by LVDT with a scale distance of 200 mm.

Fig. 5

Photographs of creep and shrinkage tests under the same condition for HSC

Table 7 Experimental values of shrinkage and creep at different ages for HSC

Table 7 shows that the shrinkage of HSC developed rapidly in the first 3 days and stabilized at 28 days. As concrete strength grade increased, the higher the content of the cementing material, the higher the shrinkage value was. Creep is long-term deformation under the action of dead load, and the creep coefficient increases with age. A high-strength grade equates to a high elastic modulus, high deformation resistance and small creep coefficient.

Considering the complicated calculation of the shrinkage–creep prediction model, we calculated and analysed the CEB-FIP (1990) (Thomas 1993), GL2000 (Gardner and Zhao 1993) and B3 (Bažant and Baweja 1995) models. On the basis of the B3 model, the environment, temperature and materials were modified, the shrinkage formula was multiplied by 0.934 and the creep formula was multiplied by 0.921 (fitting coefficient). The absolute value of the relative error of shrinkage and creep was approximately 10%, which can satisfy the precision requirement in engineering. Therefore, the modified B3 model can be used to calculate the shrinkage and creep of HSC. The calculation results and relative errors are given in Table 8.

Table 8 Shrinkage strains, creep coefficients and relative errors calculated by different models for HSC

3.4 Biaxial Compression Performance

The results of the biaxial compression test are shown in Table 9 and Fig. 6. The calculated value of biaxial compression ultimate strength ($- \sigma^{\text{c}}_{30}$) was obtained with Eq. (4) (Yang et al. 2008).

Table 9 Test and calculated values of HSCs under biaxial compression

Fig. 6

Relationships amongst σ₃₀/f_c, ε₃₀/ε₀ and σ₂/σ₃ of HSCs under biaxial compression stresses

$$\sigma_{3} = \frac{{1 + \omega_{2} }}{{1 + \omega_{2}^{ - 1} }}\sigma_{2} ,\quad \omega_{2} = \frac{{\sigma_{3} }}{{\sigma_{2} }}$$

(4)

According to Table 9 and Fig. 6, the biaxial ultimate strength of concrete was higher than the uniaxial compressive strength under proportional loading. The multiple σ₃₀/f_c increased with the strength grade of concrete, but the maximum multiple was at a stress ratio of 0.5. When the stress ratio was less than 0.5, the ultimate strength increased with increasing stress; when it was greater than 0.5, the ultimate strength gradually decreased. For deformation, similar rules were observed. The biaxial strain was higher than the uniaxial one, and the multiple ε₃₀/ε₀ increased with the increase in the strength grade of the control concrete. However, the maximum multiple was at a stress ratio of 0.25. When the stress ratio was less than 0.25, the strain increased with stress; when greater than 0.25, the strain gradually decreased.

The ultimate strength calculation error showed that the absolute value of the relative error was less than 6%, indicating that the test results are accurate and reliable.

The failure state of the specimen under the condition of biaxial stresses (Fig. 7) shows that because SF and MWCN improved the toughness of the concrete matrix, a sound was heard during loading. The sound was loud but dull. After the specimen broke, the surface showed many cracks, which increased with the stress ratio, but the specimen remained intact. Before the ultimate stress was reached, the HSC specimen emitted an explosive sound, and a few visible cracks existed on the surface. After reaching the ultimate stress, the crack surface was formed at an angle to the free surface.

Fig. 7

Photographs of failure modes of specimens for HSCs under biaxial compression. Note: (b₆) was not unloaded in time after the specimen was destroyed, but the connection effect of SF was observed

The failure mode of HSC shows that the lateral compressive stress was small, and the specimen was divided into three pieces along the free surface. A number of vertical cracks were observed on the active surface of σ₃ (Fig. 7a₁). At a stress ratio of 0.25, the edge of the specimen was damaged and split into four parts, additional visible cracks existed and the fracture interface roughly formed a 30° angle with the vertical direction (Fig. 7a₂). As the stress ratio increased, the specimen could only produce a large tensile strain on the free surface such that flake failure occurred parallel to the principal stress acting surface. The number of broken pieces of the specimen increased.

3.5 Triaxial Compression Performance

The test results of triaxial compression are shown in Table 10 and Fig. 8. The calculated values ($- \sigma^{\text{c}}_{30}$) of triaxial compression ultimate strength were obtained with Eq. (5) (Yang et al. 2008).

Table 10 Test and calculated values of HSCs under real triaxial compression

Fig. 8

Effect of intermediate principal stress on ultimate strength under real triaxial compression

$$\sigma_{3} = \frac{{\sqrt {\sigma_{1} \sigma_{2} (1 + \omega_{1} + \omega_{3} )(1 + \omega_{2} + \omega_{3}^{ - 1} )} }}{{1 + \omega_{1}^{ - 1} + \omega_{2}^{ - 1} }},\omega_{1} = \frac{{\sigma_{3} }}{{\sigma_{1} }},\omega_{3} = \frac{{\sigma_{2} }}{{\sigma_{1} }}$$

(5)

According to Table 10 and Fig. 8, the ultimate strength of triaxial compression was determined by lateral stresses under proportional loading. In this test, the ultimate strength was the maximum strength when σ₃:σ₂:σ₁ = 1:1:0.1, which indicates the significant influence of the intermediate principal stress on the ultimate strength. However, the influence trend of intermediate principal stress on ultimate strength did not vary with the strength grade nor with the presence or absence of fibre.

Compared with the increasing multiple of the ultimate strength in the case of biaxial compression, that of triaxial compression was improved but not obviously. The relative error analysis of the ultimate strength indicated that the absolute values of the relative error were less than 6%, revealing that the test data are accurate and reliable. The model can reflect the relationship between the ultimate strength and intermediate principal stress under triaxial compression.

The failure state of specimens under triaxial compression (Fig. 9) showed that although the differences in the failure mode of HSC and fibre-reinforced concrete were not obvious, due to the effect of SF, the specimen remained intact after being destroyed. SF could effectively improve the toughness of the concrete matrix. Moreover, the failure modes of specimens were typically represented by columnar cracking (Fig. 9a₁, a₂), layered cracking (Fig. 9b₁, b₂) and oblique shear failure (Fig. 9c₁, c₂).

Fig. 9

Photographs of failure modes of specimens for HSCs under real triaxial compression

3.6 Multiaxial Compression Failure Criteria

According to the analysis of different failure criteria for concrete under biaxial compression, the Kufer–Gerstle criterion (Kupfer and Gerstle 1973) (Eq. (6a)) can describe the test results well. Equation (6a) can be converted to Eq. (6b) to reflect the effect of the stress ratio on the ultimate strength of biaxial compression.

$$\left( {\frac{{\sigma_{3 0} }}{{f_{\text{c}} }} + \frac{{\sigma_{2 0} }}{{f_{\text{c}} }}} \right)^{2} + m\frac{{\sigma_{3 0} }}{{f_{\text{c}} }} + n\frac{{\sigma_{2 0} }}{{f_{\text{c}} }} = 0,$$

(6a)

$$\frac{{\sigma_{3 0} }}{{f_{\text{c}} }} = \frac{{m + n/\omega_{2} }}{{\left( {1 + \omega_{2}^{ - 1} } \right)^{2} }},$$

(6b)

where m and n are undetermined coefficients.

On the basis of the test data in Table 9, regression analysis was performed with the least squares method. The fitting parameters and correlation coefficient results are shown in Table 11, and the failure envelope curve is shown in Fig. 10.

Table 11 Fitting parameters and correlation coefficients of Eq. (5)

Fig. 10

Strength envelopes of HSCs by the Kufer–Gerstle criterion under biaxial compression

Figure 10 shows that the Kupfer–Gerstle criterion can be adopted for HSC, and the envelope curve with high strength surrounds the low-strength envelope curve with the highest strength on the outermost side.

For triaxial compression, according to the ultimate trace analysis of Eqs. (4) and (5) on the off-plane in the literature (Zhang et al. 2018) and the basic conditions that must be satisfied by the unified meridian, only the triaxial compression strength model of concrete meets the smooth and convex features on the plane (Fig. 11). The triaxial compression can be expressed by the meridian equation, as shown in Eqs. (7a) and (7b) (Argyris et al. 1974).

$$\frac{{\tau_{\text{mt}} }}{{f_{\text{c}} }} = \frac{{\rho_{t} }}{{\sqrt 5 f_{\text{c}} }} = a_{0} + a_{1} \frac{{\sigma_{\text{m}} }}{{f_{\text{c}} }} + a_{2} \left( {\frac{{\sigma_{\text{m}} }}{{f_{\text{c}} }}} \right)^{2} , \, \theta = 0^{ \circ } ,$$

(7a)

$$\frac{{\tau_{\text{mc}} }}{{f_{\text{c}} }} = \frac{{\rho_{\text{c}} }}{{\sqrt 5 f_{\text{c}} }} = b_{0} + b_{1} \frac{{\sigma_{m} }}{{f_{\text{c}} }} + b_{2} \left( {\frac{{\sigma_{\text{m}} }}{{f_{\text{c}} }}} \right)^{2} ,\quad \theta = 60^{ \circ } ,$$

(7b)

where τ_mt and τ_mc represent the average shear stress τ_m value of θ = 0° and θ = 60°, respectively (θ is the stress lode angle) [Eq. (7c)]. σ_m is the average or octahedral normal stress, i.e. σ_oct or σ₈ [Eq. (7d)]. ρ_t and ρ_c are the characteristic lengths of pulling and pressing meridians, respectively. a_i and b_i (i = 0, 1, 2) are the undetermined coefficients (determined by the characteristic test point).

Fig. 11

Limited trace of strength model Eq. (4) on the deviatoric stress plane

$$\tau_{\text{m}} = \frac{1}{{\sqrt {15} }}\sqrt { (\sigma_{1} - \sigma_{2} )^{2} + (\sigma_{2} - \sigma_{3} )^{2} + (\sigma_{3} - \sigma_{1} )^{2} } = \frac{3}{{\sqrt {15} }}\tau_{8} {\text{ (or}}\; \, \tau_{\text{oct}} ) ,$$

(7c)

$$\sigma_{\text{m}} = \sigma_{8} = \sigma_{\text{oct}} = \frac{1}{3}(\sigma_{1} + \sigma_{2} + \sigma_{3} ),$$

(7d)

The meridian equation for triaxial compression of concrete is shown in Fig. 12.

Fig. 12

Compressive and tensile meridians of HSCs under real triaxial compression

Figure 12 shows that τ_oct/f_c increased with the increase in the absolute value of σ_oct/f_c, and the pulling and pressing meridians expanded outward along the direction of the hydrostatic pressure axis. This result indicates that the fracture surface of HSC expanded outward, which is the same as NWC. At the same time, the envelope curve traces on the off-plane also expanded outward. We inferred that the strength envelope surface of HSC also expanded outward with the increase in concrete strength grade, and the envelope curve with high strength enveloped the low-strength one. However, as illustrated in Fig. 12a, b, the influence of strength grade on the envelope curve was very small because the pulling and pressing meridians almost overlapped.

Figure 12c) reveals that although SF can effectively increase the strength of the concrete matrix, the influence on the pulling and pressing meridians is not significant and only slightly improved, that is, the strength envelope curve surrounded that of HSC.

4 Conclusions

This study used HSCs of 70 MPa, 80 MPa, 90 MPa and 100 MPa as reference. HSCs with different strength grades were prepared by single-doped and double-mixed SF and MWCN. Durability, shrinkage and creep and uniaxial and multiaxial strength tests were conducted using several mix proportions. Through a comparative analysis, the following conclusions were obtained.

• (1) SF and MWCN effectively improved the uniaxial and multiaxial compressive strength and durability of HSC and changed the failure mode of specimens, especially when SF and MWCN were mixed simultaneously.

• (2) HSC and HSCRSC specimens were accompanied with explosive sounds under uniaxial and multiaxial compression, but the sound was dull when SF and MWCN were single- or double-doped. The failure mode could be changed at the same time, that is, from brittle to ductile failure. The specimen remained intact after failure. HSC showed flake damage under biaxial compression and was characterised by columnar, layered and oblique shear damage under triaxial compression.

• (3) After the B3 model was modified in terms of environment, temperature and material and multiplied by the corresponding fitting coefficients, it met the requirements of the shrinkage and creep prediction model of HSC. The absolute value of the relative error was approximately 10%, which meets engineering accuracy requirements.

• (4) The strength models of biaxial and triaxial compression fully reflected the relationship between ultimate strength, intermediate principal stress and stress ratio. The prediction results were relatively accurate. The absolute value of the relative error was less than 6%, indicating that the test results are accurate and reliable.

• (5) With the increase in lateral stress, the ultimate strength of concrete increased with the strength grade, and both were higher than the uniaxial compressive strength. The multiple σ₃₀/f_c was between 1.10 and 1.39 times under biaxial compression and between 1.24 and 2.55 times under triaxial compression. The maximum ultimate strength was at the point where σ₃:σ₂ = 1:0.5 under biaxial compression and σ₃:σ₂:σ₁ = 1:1:0.1 under triaxial compression.

• (6) The biaxial compression failure satisfied the Kufer–Gerstle criterion, and the triaxial compression failure satisfied the Willam–Warnke tensile–pressure meridian criterion. The failure envelope curve with high strength enveloped the low-strength one. Strength grade was not sensitive to the influence of the pulling and pressing meridians, that is, all the pulling and pressing meridians almost overlapped.

Appendix

The following is a detailed description of the relevant test standards.

• (1) Cube compressive strength test according to GB/T50081-2002 (2002).

The cube compressive strength test must be carried out by the following steps:

• 1) When the specimen reaches the test ages, it should be taken out from the curing site to check its size and shape and tested as soon as possible.

• 2) Wipe the specimen surface, upper and lower pressure plate clean.

• 3) Take the side of the specimen forming as the pressure surface. The specimen should be placed on the lower pressing plate or backing plate of the testing machine, the centre of the specimen should be aligned with the centre of the lower press plate of the testing machine.

• 4) Starting the machine, the surface of the specimen should be in even contact with the upper and lower pressure plate or the steel backing plate.

• 5) During the test, continuous and uniform loading should be conducted, and the loading speed should be 0.3–1.0 MPa/s. When the compressive strength of the cube is less than 30 MPa, the loading speed should be 0.3–0.5 MPa/s. When the compressive strength of the cube is 30–60 MPa, the loading speed should be 0.5–0.8 MPa/s. When the compressive strength of the cube is not less than 60 MPa, the loading speed should be 0.8–1.0 MPa/s.

• 6) When manually controlling the loading speed of the press, stop adjusting the throttle of the testing machine when the specimen approaches failure and starts sharp deformation. Until the specimen break down, the failure load is recorded.

• 7) The compressive strength of the cube specimen should be calculated by the following formula:

  $$f_{\text{cu}} = F_{\hbox{max} } /A,$$

  (8)

  where F_max stands for failure load (N) of specimen. A stands for Bearing area (mm²) of specimen.

• 8. The determination of compressive strength value about cube specimens should comply with the following provisions:

  • 1. Take the arithmetic mean value of the measured values about three specimens as the strength value of this set of specimens.

  • 2. When the maximum or minimum value differs from the median by more than 15% of the median, exclude the maximum and minimum values and take the intermediate value as the compressive strength value of this group.

  • 3. When the maximum and minimum values differ from the median by more than 15% of the median, the results of this group’s tests are invalid.

• 9) When the concrete strength grade is less than 60 MPa, the strength value measured with non-standard test pieces should be multiplied by the size conversion factor, which can be taken as 1.05 for 200 mm × 200 mm × 200 mm and 0.95 for 100 mm × 100 mm × 100 mm.

• 10) When the concrete strength grade is not less than 60 MPa, the standard test piece 150 mm × 150 mm × 150 mm should be used. When using non-standard test pieces and the strength grade is not greater than 100 MPa, the size conversion factor should be determined by testing. In the case of no test determination, the conversion factor for the size of 100 mm × 100 mm × 100 mm specimens can be taken as 0.95. When the concrete strength grade is greater than 100 MPa, the size conversion factor should be determined through tests.

(2) Axial compressive strength test according to GB/T50081-2002 (2002).

The axial compressive strength test should be carried out by the following steps:

• 1) to 6) Same as above (1): 1) to 6).

• 7) The axial compressive strength should be calculated by the following formula:

  $$f_{\text{c}} = F_{ \hbox{max} } /A,$$

  (9)

• 8) Same as above (1): 8).

• 9) When the concrete strength grade is less than 60 MPa, the strength value measured with non-standard test pieces should be multiplied by the size conversion factor, 1.05 for 200 mm × 200 mm × 400 mm and 0.95 for 100 mm × 100 mm × 300 mm. When the concrete strength grade is not less than 60 MPa, the standard test piece 150 mm × 150 mm × 300 mm should be used. When using non-standard test pieces, the size conversion factor should be determined by testing.

(3) Splitting tensile test according to GB/T50081-2002 (2002)

The splitting tensile strength test should follow the following steps:

• 1) Same as above (1): 1).

• 2) Wipe the specimen surface, upper. Parallel lines are drawn in the middle of the top and bottom surfaces to determine the position of the splitting surface.

• 3) Place the test piece in the centre of the pressure plate under the test machine, the splitting pressure surface and the splitting surface should be perpendicular to the top surface of the specimen. Between the upper and lower pressing plate and the specimen, a circular shaped cushion block and a cushion strip are placed. The block and strip should be aligned with the centre line above and below the specimen and should be perpendicular to the top surface of the moulding. Installing the strip and specimen on the positioning frame is advisable (Fig. 13).

  Fig. 13

  

  Positioning bracket (1-spacer; 2-filler strip; 3-support)

• 4) Same as above (1): 4).

• 5) Continuous and uniform loading during the test. When the compressive strength of the corresponding cube is less than 30 MPa, the loading speed should be 0.02–0.05 MPa/s. When the compressive strength of the corresponding cube is 30–60 MPa, the loading speed should be 0.05–0.08 MPa/s. When the compressive strength of the corresponding cube is not less than 60 MPa, the loading speed should be 0.08–0.10 MPa/s.

• 6) Same as above (1): 6).

• 7) The fracture surface of the specimen should be perpendicular to the pressure surface; when it is not, it should be recorded.

• 8) The split tensile strength of concrete should be calculated according to the following formula:

  $$f_{\text{ts}} = 2F_{ \hbox{max} } /\left( {\pi A} \right) = 0. 6 3 7F_{ \hbox{max} } /A,$$

  (10)

• 9) Same as above (1): 8).

• 10) The value of splitting tensile strength measured by 100 mm × 100 mm × 100 mm non-standard specimen should be multiplied by the size conversion coefficient of 0.85. When the concrete strength grade is not less than 60 MPa, the standard specimen 150 mm × 150 mm × 150 mm should be used.

(4) Flexural test according to GB/T50081-2002 (2002)

The concrete flexural test procedure is as follows:

• 1) Same as above (1): 1).

• 2) Clean the surface of the specimen and draw the loading line on the side of the specimen.

• 3) The test device is shown in Fig. 14, and the mounting size deviation should not be greater than 1 mm. The bearing surface of the specimen is the side of the specimen when it is formed, and the bearing and contact surface between the bearing surface and cylinder should be stable and even.

  Fig. 14

  

  Test equipment

• 4) and 5) Same as above (5): 5) and 6).

• 5) The flexural strength f_bs (MPa) should be calculated as follows:

  $$f_{\text{bs}} = F_{\hbox{max} } l/ \, \left( {bh^{2} } \right),$$

  (11)

  where l represents the span between supports (mm), b represents the section width of the specimen (mm) and h represents the section height of the specimen (mm).

• 6) Same as above (3): 9).

• 7) When the specimen size is 100 mm × 100 mm × 400 mm non-standard specimen, the size conversion coefficient should be multiplied by 0.85. When the strength grade of concrete is not less than 60 MPa, using the standard specimen (150 mm × 150 mm × 600 mm or 150 mm × 150 mm × 550 mm) is advisable. When non-standard specimens are used, the size conversion factor should be determined by the test.

(5) Modulus of elasticity test according to GB/T50081-2002 (2002)

The test should be carried out according to the following steps:

• 1) to 4) Same as above (1): 1) to 4).

• 5) It should be loaded to F₀, the initial load value of the reference stress of 0.5 MPa. The constant load should be maintained for 60 s (s) and the deformation reading ε₀ of each measurement point should be recorded in the next 30 s. The load should be continuously and evenly applied to F_a (1/3 axial compressive strength f_c), and the constant load should be maintained for 60 s. The deformation reading ε_a of each measurement point should be recorded in the next 30 s.

• 6) If the ratio of the difference between the deformation values of the left and right sides and their average value is greater than 20%, then the provisions of 5) of this article should be repeated for the middle specimen. When it cannot be reduced to less than 20%, the test is invalid.

• 7) After confirming that the specimen alignment conforms to the provisions of paragraph 8) of this article, the specimen is unloaded to the reference stress of 0.5 MPa (F₀) at the same speed as the loading speed, with a constant load of 60 s. Repeat preloading at least twice with the same loading and unloading speeds. After the last preloading is completed, the load should be held for 60 s at the reference stress of 0.5 MPa (F₀). In the later 30 s in the deformation of each measuring point reading epsilon ε, apply the same loading speed to F_a, hold the load for 60, and record the deformation reading a at each measuring point for the next 30 s (Fig. 15).

  Fig. 15

  

  Test loading scheme

• 8) Remove the deformation measuring instrument, load at the same speed until the failure, and record the failure load. When the difference between the compressive strength and f_c after measuring the elastic modulus is more than 20% of f_c, it should be noted in the report.

• 9) The elastic modulus of concrete should be calculated according to the following formula:

  $$E_{\text{c}} = \, \left( {F_{\text{a}} {-\!\!-}F_{0} } \right)L/\left( {\left( {\varepsilon_{\text{a}} {-\!\!-}\varepsilon_{0} } \right)A} \right),$$

  (12)

• 10) In Formula 12, F_a represents the load when the stress is 1/3 of the axial compressive strength (N). F₀ represents the initial load (N) when the stress is 0.5 MPa. A represents specimen bearing area (mm²). L represents measuring distance (mm). ε_a represents mean value of deformation on both sides of specimen under F_a (mm). And ε₀ represents mean value of deformation on both sides of specimen under F₀ (mm).

• 11) The elastic modulus value of this set of specimens should be taken as the arithmetic mean value of the measured values of three specimens, which is accurate to 100 MPa. When the difference between the axial compressive strength value after measuring the elastic modulus of one specimen and the axial compressive strength value used to determine the test control load is more than 20% of the latter, the elastic modulus value should be calculated according to the arithmetic mean value of the measured values of the other two specimens. The test is invalid when the difference is more than 20% of the latter.

(6) Frost resistance test according to GB/T 50082-2009 (2009)

Adopt the quick-freezing method, and the frost resistance of concrete is expressed by the number of freezing–thawing cycles. The test steps are as follows:

• 1) When the curing age of the specimen in standard culture or in the same condition is 24 days, the specimen should be taken out of the curing room and then soaked in water at (20 ± 2) °C. The soaking water surface should be 20–30 mm higher than the top surface of the specimen.

• 2) After soaking for 4 days, remove the specimen and wipe the surface moisture with a wet cloth, then observe the appearance and measure the size and number and weigh the initial mass of the specimen. The initial value of transverse fundamental frequency should be determined according to the regulation of dynamic elastic modulus test of concrete.

• 3) Put the specimen into the specimen box, then put the specimen box into the specimen frame in the freeze–thaw box and inject water into the specimen box. During the entire test, the height of water level in the box should always be more than 5 mm higher than the top surface of the specimen. The temperature measuring box should be placed in the centre of the freeze–thaw box.

• 4) The freezing–thawing cycle should comply with the following provisions:

  • 1. Each freezing–thawing cycle should be completed within 2–4 h, and the melting time should not be less than 1/4 of the whole freezing–thawing cycle time.

  • 2. During freezing and melting, the minimum and maximum temperature of the specimen centre should be controlled within (−18 ± 2) °C and (5 ± 2) °C, respectively. At any time, the temperature of the specimen centre should be lower than 7 °C and higher than −20 °C.

  • 3. The time taken for each specimen to drop from 3 to −16 °C should be more than 1/2 of the freezing time. The time taken for each specimen to rise from −16 to 3 °C should also be greater than 1/2 of the whole melting time. The temperature difference between the inside and outside of the specimen should not exceed 28 °C.

  • 4. The conversion time between freezing and melting should not be greater than 10 min.

• 5) Transverse fundamental frequency of the test piece every 25 freezing–thawing cycles. Before the measurement, the scum on the surface of the specimen should be cleaned and the water on the surface dried, then the external damage should be checked and the quality of the specimen weighed.

• 6) When one of the following situations occurs in the freezing–thawing cycle, the test can be stopped:

  • 1. Reach the specified freezing–thawing cycle times.

  • 2. The relative dynamic elastic modulus of the specimen decreased to 60%.

  • 3. The mass loss rate of the specimen was up to 5%.

• 7) The relative dynamic elastic modulus of concrete should be calculated according to the following formula:

  $$\Delta E_{\text{c}} = \, \left( {f_{n,i} /f_{0,i} } \right)^{2} \times 100\% ,$$

  (13)

  The mass loss rate of a single test piece should be calculated according to the following formula:

  $$\Delta m = \, (m_{0,i} - m_{n,i} ) \, /m_{0,i} ,$$

  (14)

  where $\Delta m$ represents mass loss rate (%) of the ith concrete specimen after n freezing–thawing cycles. m_{0, i} represents mass (g) of the ith concrete specimen before freezing–thawing cycle. m_{n, i} represents mass (g) of the ith concrete specimen after n freezing–thawing cycles.

(7) Impermeability test according to GB/T 50082-2009 (2009)

The test is an integrated method using stepwise pressure method and penetration height method. The specific test steps are as follows:

• 1) Water pressure should be 0.1–0.2 MPa. A round table test model with the upper diameter d_T = 175 mm, the lower diameter d_B = 185 mm, and the height h = 150 mm was used. The sealing material is cement and butter. The trapezoid plate is a transparent material of 200 mm × 200 mm and is drawn with ten parallel lines of equal spacing, as shown in Fig. 16.

  Fig. 16

  

  Schematic of trapezoidal board

• 2) The impermeability test consists of six specimens in each group. After the moulds are removed, the cement slurry film on both ends of the specimen is removed with a wire brush and then are placed in the curing room for curing. The age is 28 days.

• 3) Take out the specimen and wipe it when it is cured to 27 days. After drying, seal it with cement and butter, the mass ratio of cement to butter is 2.5:1. When sealing, the sealing material should be evenly scraped on the side of the test piece with a triangle knife, the thickness should be controlled between 1 and 2 mm. The test mould is placed and pressed into the test piece. The bottom of the specimen and the mould must be flat.

• 4) After the specimen is installed, open the water test valve. The water leaking out of the six holes should fill the test pit, and then close the valve. Then, place the test piece on the impermeability meter, open the valve and increase the seepage pressure to 4 MPa according to the impermeability of the high-strength concrete. Afterwards, observe the water seepage. It lasts for 24 h, and the pressurisation cannot exceed 5 min. Record the test piece from the time when the stable pressure is reached. The test device is shown in Fig. 17.

  Fig. 17

  

  Concrete permeability test

• 5) During the test, if water seepage is observed at the end of any specimen, then the test of the specimen should be stopped, the time should be recorded and the height of the specimen should be taken as the water seepage height. For the specimens without water seepage, a split test should be performed after 24 h. Use a waterproof pen to trace water marks on the cross section of the specimen.

• 6) Place the trapezoidal plate on the cross section of the test piece and measure the height of the traced water mark at 10 measuring points with a steel ruler. The reading is accurate to 1 mm.

• 7) Calculate the measured water seepage height.

The seepage height of a single specimen is expressed as follows:

$$\overline{{h_{j} }} { = }\frac{1}{10}\sum\limits_{{i{ = }1}}^{10} {h_{i} } ,$$

(15)

The average seepage height of a group of specimens is given as follows:

$$\overline{h} { = }\frac{1}{ 6}\sum\limits_{{j{ = }1}}^{6} {\overline{{h_{j} }} } ,$$

(16)

(8) Carbonation resistance test according to GB/T 50082-2009 (2009)

The carbonation specimen generally adopts standard curing, and the age of the specimen should generally reach 28 days. The concrete with additional admixture can determine the curing age before carbonation according to its characteristics. Remove from the standard curing room 2 days before testing. It was then baked at a constant temperature of 60 °C for 48 h. After the drying treatment, all surfaces of the specimen should be sealed with heated paraffin except one or two opposite sides. Parallel lines with spacing of 10 mm are drawn with a pencil along the length of the side to predetermine the measuring point of carbonation depth. The specific test steps are as follows:

• 1) The treated carbonation resistant specimen should be placed on the iron frame in the carbonation box, and the distance between the carbonized surfaces of each specimen should not be less than 50 mm.

• 2) Seal the carbonation box cover tightly. Mechanical or oil seals can be used, but water seals must not be used as they may affect the humidity regulation in the box. Start the gas convection device in the box, slowly in CO₂, and measure the concentration of CO₂ in the box, and gradually adjust the flow of CO₂ to keep the concentration of CO₂ in the box at 20% ± 3%. During the entire test, a dehumidifier or silica gel can be used to control the relative humidity in the box within the range of 70% ± 5%. The carbonation test should be carried out at a temperature of (20 ± 5) °C.

• 3) The concentration of CO₂, temperature and humidity in the chamber are measured at regular intervals. Generally, it is measured every 2 h at 1 to 2 days, and every 4 h thereafter. According to the measured CO₂ concentration to adjust its flow size at any time.

• 4) When the carbonation progresses to 3, 7, 14 and 28 days, take out the specimen and break the shape to determine the carbonation depth.

• 5) Scrape part of the obtained test piece to remove the powder remaining on the section, and then spray with a 1% phenolphthalein alcohol solution (containing 20% distilled water). After 30 s, the carbonation depth of measuring points on both sides was measured with the measuring scale of carbonation depth according to each 10 mm measuring point originally marked.

• 6) The average carbonation depth of concrete at different ages should be calculated according to the following formula, which is accurate to 0.1 mm.

  $$h_{\text{c}} = \frac{{\sum\nolimits_{i = 1}^{n} {h_{i} } }}{n} ,$$

  (17)

  where h_i represents carbonation depth (mm) of each measuring point on two sides and n represents the total number of side points on both sides.

The average carbonation depth of 28 days per three test specimens under standard conditions was used as the concrete carbonation value, and the value was used to compare the carbonation resistance of various concretes.

(9) Resistance to chloride penetration test according to GB/T 50082-2009 (2009)

For the rapid chloride permeability test method, the following steps are carried out:

• 1) The concrete cylinder specimens with a diameter of 95 mm and a thickness of 51 mm and cultured for 28 days. During the test, three specimens were used as a group.

• 2) The specimen surface was dried in the air until the surface was dry, and the resin sealing material was applied to the side of the specimen. Before the test, the specimens should be put into the beaker (1000 ml) and then into the vacuum dryer. The vacuum pump should be started and the vacuum degree should be less than 13 Pa.

• 3) After the vacuum was maintained for 3 h, the vacuum was maintained, and enough distilled water was injected until the specimen was submerged. After soaking for 1 h, the pressure returned to normal pressure, and then the sample was soaked for another (18 ± 2) h.

• 4) Remove the specimen from the water, wipe off the excess water, install the specimen in the test tank, seal with rubber sealing ring and clamp the two test tanks and the specimen with screw to ensure no leakage. Following this, put the test device in the flowing cold water tank at 20–23 °C.. The water surface should be 5 mm lower than the top surface of the device. The temperature should be maintained at 20–25 °C during the test.

• 5) Solution (0.3 mol of NaOH and 3.0% NaCl solution) are injected into the test tank. The copper network in the test tank where NaOH solution is injected is connected to the positive electrode of the power supply. The copper network in the test tank where NaCl solution is injected is connected to the negative electrode of the power supply.

• 6) Plug in and apply constant voltage of 30 V to the two copper grids. Record the initial current reading I₀, energising and keeping the test tank full of solution. The test device is shown in Fig. 18.

  Fig. 18

  

  Resistance to chloride ion penetration test device RCM method

• 7) The chloride ion transfer coefficient of concrete is calculated according to the following formula:

  $$\psi_{\text{s}} = \frac{{0.0239 \times \left( {273 + T} \right)}}{{\left( {U - 2} \right)t}}\left( {X_{\text{d}} - 0.0238\sqrt {\frac{{(273 + T)LX_{\text{d}} }}{U - 2}} } \right) ,$$

  (18)

  where U represents the absolute value of the voltage used (V). T represents the mean of the initial temperature and the end temperature of the anode solution. L represents specimen thickness (mm), with an accuracy of 0.1 mm. X_d represents average chloride penetration depth (mm), with an accuracy of 0.1 mm. t represents duration (h) of test.

• 8) The arithmetic mean value of chloride ion migration coefficient of three samples should be taken as the measured value of chloride ion migration coefficient of each group. When the difference between the maximum or minimum value and the median value exceeds 15% of the median value, this value should be removed and the average value of the other two values should be taken as the measured value. When the maximum value and the minimum value both exceed 15% of the median value, the median value should be taken as the measured value.

(10) Resistance to sulphate attack test according to GB/T 50082-2009 (2009)

Use wet–dry cycle method. The test steps are as follows:

• 1) After the specimen was put into the specimen box, the configured 5% Na₂SO₄ solution was put into the specimen box. The liquid level of the solution should exceed the surface of the topmost specimen by no less than 20 mm. The time from the beginning of the specimen to the end of soaking should be (15 ± 0.5) h. The infusion time should not exceed 30 min. The soaking age should be measured from the time when the concrete specimen is moved into 5% Na₂SO₄ solution. The specimen should be inspected and adjusted regularly. The pH value of the solution stays between 6 and 8. The temperature of the solution should be controlled at 25–30 °C.

• 2) Natural drying: After soaking, the lifting switch is automatically opened, and the specimen is lifted and dried within 2 min. It takes an hour.

• 3) Stoving: After drying, the temperature of the specimen rose to (80 ± 5) °C and remained at 6 h.

• 4) Specimen cooling: After stoving, the refrigeration system starts. The surface temperature of the specimen in the specimen chamber was cooled to 25–30 °C, and the total time was 2 h.

• 5) After the specimen is cooled to room temperature, a dry–wet cycle test is completed. Add the solution. The next dry–wet cycle is performed according to steps (1) to (4) above.

• 6) The weighing test of the tested part is conducted every 10 dry–wet cycles. At the same time, a group of compressive strength tests are carried out, and the surface damage is observed.

• 7) During the dry–wet cycle test, standard curing should be carried out for the other two groups of comparison specimens. Compared with the specimen after the completion of the dry and wet cycle. The corrosion resistance coefficient of concrete compressive strength is obtained. The corrosion resistance coefficient is calculated as follows:

  $$K_{\text{f}} = \left( {f_{{{\text{c}},n}} /f_{{{\text{c}},0}} } \right) \times 100,$$

  (19)

  where f_c,n represents the compressive strength (MPa) of a group of concrete specimens corroded by sulphate after n times of dry–wet cycling. f_{c, 0} represents the compressive strength (MPa) of a group of concrete specimens subjected to sulphate corrosion was compared with that of standard curing at the same age.

When the test meets any of the following conditions, the test can be stopped:

• 1. Mass corrosion resistance coefficient is less than 95%.

• 2. The corrosion resistance coefficient of compressive strength is less than 75%.

• 3. The number of dry and wet cycles reaches 150.

(11) Shrinkage test according to GB/T 50082-2009 (2009)

The steps of shrinkage test are as follows:

• 1) The shrinkage test should be conducted in a constant temperature and humidity environment, with room temperature maintained at (20 ± 2) °C and relative humidity at 60% ± 5%. The specimens should be placed on shelves that do not absorb water, and the bottom surface should be elevated. The clearance between each specimen should be greater than 30 mm.

• 2) When determining the characteristic value representing the shrinkage performance of a certain concrete, the specimen should be removed from the standard curing room at the age of three days (calculated from the time when concrete is mixed with water). It should be immediately transferred to the constant temperature and humidity chamber to measure its initial length, and thereafter its deformation reading should be measured at least at the time interval specified as follows: 1, 3, 7, 14, 28, 45, 60, 90, 120, 150, 180 and 360 days (from the time of moving into the constant temperature and humidity chamber).

• 3) When determining the relative shrinkage value of concrete under a specific condition, the test should be carried out according to the required conditions. For non-standard curing specimens, when they need to be transferred to a constant temperature and humidity room for testing, they should be pre-set in the room for 4 h before the initial value is measured. The initial dry and wet state of the specimen should be recorded during measurement.

• 4) The zero point of the instrument should be corrected with a standard rod before the shrinkage measurement and should be rechecked at least once or twice during the measurement. One test was conducted after reading all the specimens. When the deviation between zero and the original value is more than ± 0.001 mm, it should be adjusted to 0 and then measured again.

• 5) The position and direction of the specimen placed on the horizontal contract meter should be consistent each time. The corresponding direction marks should be marked on the specimen. The specimen should be placed and taken out carefully and should not collide with the table rack and table bar. After a collision, the specimen should be removed and the zero should be rechecked with a par.

• 6) When using the vertical concrete shrinkage meter, the entire set of test equipment should be placed where not be susceptible to external vibration. When reading, tap the meter or slide the probe up and down. A test bench for installing a vertical concrete shrinkage meter should have a damping device.

• 7) When measuring with contact method extensometer, the position and direction of specimen and instrument should be kept fixed. Repeat each reading three times.

• 8) The shrinkage rate of concrete should be calculated according to the following formula:

  $$\varepsilon_{\text{st}} = (\Delta \varepsilon_{\text{st}} - \Delta \varepsilon_{s0} )/L_{0} ,$$

  (20)

  where ε_st represents shrinkage of concrete after loading for t days. ∆ε_st represents concrete micrometre reading (mm) after the day. ∆ε_s0 represents concrete initial micrometre reading (mm). L₀ represents shrinkage measuring range (mm).

• 9) The arithmetic mean value of three specimens in each group should be taken as the measured value of shrinkage of concrete specimens in this group, and the calculation is accurate to 1.0 × 10⁻⁶.

(12) Creep test according to GB/T 50082-2009 (2009)

The creep test should meet the following requirements:

• 1) The probe or measuring point should be glued 1 day before the test, and the instrument should be carefully checked after installation without any loosening or abnormal observation.

• 2) Before loading, the compressive strength of the prismatic body should be tested.

• 3) When the probe and the meter are ready, the creep specimen should be placed on the lower pressure plate of the creep meter, and the axes of the specimen, loading device, dynamometer and creep meter should be aligned. The zeroing of the deformation measuring instrument should be checked again and the initial reading should be recorded.

• 4) After the specimen is placed, loading should start in time. When there is no special requirement, the creep stress should be 40% of the measured compressive strength of the prism.

• 5) The deformation value of the specimen should be measured at 1, 3, 7, 14, 28, 45, 60, 90, 120, 150, 180, 270 and 360 days after loading.

• 6) While reading the deformation reading of the creep specimen, the shrinkage value of the shrinkage specimen with reference to the same condition should be measured.

• 7) After loading, the specimen should be inspected regularly for load maintenance, which should be checked once at 7, 28, 60 and 90 days after loading. If the load change is more than 2%, it should be made up. When using a spring-loaded rack, adjustments can be made by applying the correct load and tightening the nuts on the screw.

• 8) Creep coefficient should be calculated according to the following formulas:

  $$\varphi_{t} = \varepsilon_{c,t } /\varepsilon_{0} ,$$

  (21)
  $$\varepsilon_{0} = \Delta L_{0} /L_{\text{b}} ,$$

  (22)

  where φ_t represents creep coefficient after loading t days. ε_{c, t} represents creep strain (mm/m) after loading t days (with an accuracy of 0.001 mm/m). ε₀ represents the initial strain (mm/m) measured during loading (with an accuracy of 0.001 mm/m). ∆L₀ represents the initial deformation value measured during loading (mm) (with an accuracy of 0.001 mm). L_b represents measuring range (mm) (with an accuracy of 1 mm).

• 9) The creep coefficient of each group should be determined by the arithmetic mean value of three specimens.