1 Introduction

Count data are commonly encountered in everyday life phenomena, including insurance, economics, social sciences, medicines, transport and among an unlimited number of areas. In these applications, the count observations are normally expressed as positive integers that are collected on a daily, weekly, or monthly sequential basis. Hence, such repeated observations are more likely serially correlated. On the other side, these series of counts are commonly over-dispersed due to some outliers or presence of physical or latent effects and, in some cases, can be equi-dispersed or under-dispersed as well. Thus, there is an important need to appropriately model the series of counts via the suitable distribution that can accommodate as fully as possible different statistical features.

The prevalent probability models in the literature include the geometric, Poisson, Poisson mixtures (Karlis and Xekalaki 2005), Conway–Maxwell Poisson (Shmueli et al. 2005; Sellers and Shmueli 2010; Sellers et al. 2012) distributions. However, owing to the complex nature and some unique properties of the natural phenomena, such as skewness, dispersion, monotone or unimodal failure rate, inflation or deflation, these conventional density functions may not be fully relevant, as similarly argued in El-Morshedy et al. (2020), Eliwa and El-Morshedy (2021) and the references therein. This leads to introducing some other more flexible distributions for positive counts that emerge from discretizing some continuous functions. Examples of such distributions have been comprehensively studied by Gómez-Déniz and Calderín-Ojeda (2011), Chakraborty and Chakravarty (2012), Nekoukhou et al. (2013), Bakouch et al. (2014), Hussain et al. (2016), Bahti and Bakouch (2019), Altun (2020) and references therein.

In this same sense, this paper introduces a modified discrete Burr–Hatke (BH) model, based on the transmuted record type (TRT) constructor introduced by Shakil and Ahsanullah (2011). The discrete version of BH model has been recently proposed by El-Morshedy et al. (2020) to model count events exhibiting huge over-dispersion with various skewness features. The discrete version of BH stands out as a main competitor to the traditional count models as it yields far more superior fitting criteria. This paper focuses on the TRT construction strategy because it leads to skewed distributions and is compatible with one side long-tailed data. The transmuted distributions are special cases of extremal distributions (Kozubowski and Podgórski 2016).

Further to the choice of the probability model, there is a need to investigate the relevant time series structures related to the counts of correlated nature. For repeated count observations, McKenzie (1986), McKenzie (1988) and Al-Osh and Alzaid (1987) introduced the thinning-based INAR(1) processes. The classical INAR(1) model consists of two important components: a survival part that relates the current observation with its previous lagged via the thinning, in particular, the binomial thinning operation (Steutel and van Harn 1979) and a random innovation or error component. In the original INAR(1) model, the innovation was allowed to follow the benchmark Poisson, while the binomial thinning was defined with the fixed or random coefficient.

Over the years, in view of obtaining better fitting criteria or information criteria in severely over-dispersed or zero inflated data series, several authors have proposed a vast number of alterations to either the innovation terms. The INAR(1) model based on the geometric innovations was introduced by Jazi et al. (2012), which can handle the over-dispersed count data sets. The INAR(1) model with the binomial thinning operator and Poisson–Lindley innovation was established by Lívio et al. (2018), and several estimation methods, including the conditional least squares, Yule–Walker and conditional maximum likelihood, were used for estimating the parameters.

Recently, to cover some unique properties of real data sets, other distributions were designated for innovation of the IANR(1) models, such as power series (Bourguignon and Vasconcellos 2015), Poisson-transmuted exponential (Altun and Mamode Khan 2021) and Bell (Huang and Zhu 2021).

Borges et al. (2017) introduced a new operator called \(\rho\)-negative binomial thinning operator and provided a new INAR(1) process with geometric marginals that can be applied for phenomena with excess zeros. Liu and Zhu (2021) introduced a new flexible thinning operator named extended binomial that has two parameters. Considering the extended binomial operator, they defined a new INAR(1) model and estimated the unknown parameters through the two-step conditional least squares and conditional maximum likelihood methods.

Ristić et al. (2013) were the first to propose the INAR(1) process having a dependent count series. Shirozhan et al. (2019) combined the Pegram operator with the dependent thinning operator. A new dependent negative binomial thinning operator based on the inflated geometric counting series is introduced by Shamma et al. (2020).

In classical models, the counting series are expected to be independent, which is not often the case in real-world situations like contagious diseases. Also, the binomial thinning operator is not suitable for zero inflated demands. After an outbreak has gone, we occasionally come across data sets with too many zeros. As a result, we need a count model that can deal with zero inflation. All earlier drawbacks stimulate us to introduce a new INAR(1) model based on the generalized negative binomial (GNB) thinning operator with flexible discrete innovations. The most notable feature of the utilized thinning operator is that it may be used for data sets with additional observations. The principal aim of this paper is devoted to introducing an INAR(1) model with dependent counting series with flexible innovations, where the dependency of the count series makes the thinning operator more suitable for modeling practical count data sets. Some clinical data sets demonstrate the applicability of the suggested model.

The following is the outline of the paper. Section 2 introduces a distribution using the TRT approach and the discrete BH baseline distribution. Also, the survival, hazard rate, probability generating functions and non-central moments of the proposed distribution are provided. The GNB thinning operator is reviewed in Sect. 3. With the proposed discrete innovations, the INAR(1) process is developed, which is based on the GNB thinning operator, and some properties of the process are investigated, including the conditional mean and variance. Several parametric and nonparametric estimation methods for the proposed INAR(1) process are reported in Sect. 4. Finally, in Sect. 5, two real-life count data are utilized to analyze the application of the introduced INAR(1) model, demonstrating our model’s suitability in contrast to several relevant INAR(1) models.

2 A Modified Version of Discrete Burr–Hatke Distribution

In this section, we provide a modified discrete distribution based on transmuted record type method and discrete Burr–Hatke baseline distribution. The survival and hazard rate function, along with some statistical properties of the distribution, are also given.

First, we consider the DBH distribution, which is introduced by El-Morshedy et al. (2020). The cumulative distribution function (CDF) and probability mass function (PMF) of DBH distribution are represented, respectively, as

$$\begin{aligned} H_{_Y}(y,\lambda )&= 1-\dfrac{\lambda ^{y+1}}{y+2}, \quad 0<\lambda <1 ,\;\; y=0,1,2,\ldots ,\\ h_{_Y}(y,\lambda )&= \Big (\frac{1}{y+1}-\frac{\lambda }{y+2}\Big )\lambda ^y. \end{aligned}$$

Now, we review the TRT method, which is defined as

$$\begin{aligned} Z\overset{d}{=}\ \left\{ \begin{array}{ll} Y_{U_{(1)}} &{} \text { w.p. } \;\;1-\gamma \\ Y_{U_{(2)}} &{} \text { w.p. } \;\; \gamma \end{array} \right. , \qquad 0<\gamma <1, \end{aligned}$$

where \(Y_{U_{(1)}}\) and \(Y_{U_{(2)}}\) are, respectively, the first and second upper records [for more details, see Shakil and Ahsanullah (2011)].

Hence, the CDF of TRT distribution is shown as

$$\begin{aligned} F_{_Z}(z,\lambda ,\gamma )=H_{_Y}(z)+\gamma (1-H_{_Y}(z))\ln (1-H_{_Y}(z)), \end{aligned}$$

where \(H_{_Y}(z)\) is an arbitrary CDF baseline distribution. Consider the DBH baseline distribution, the CDF of the proposed distribution is represented as

$$\begin{aligned} F_{_Z}(z,\lambda ,\gamma )&= 1-\dfrac{\lambda ^{z+1}}{z+2}+\gamma \Big (\dfrac{\lambda ^{z+1}}{z+2}\Big ) \ln \Big (\dfrac{\lambda ^{z+1}}{z+2}\Big )\\&= 1-\dfrac{\lambda ^{z+1}}{z+2}\Big [1-\gamma \ln \Big (\dfrac{\lambda ^{z+1}}{z+2}\Big ) \Big ], \end{aligned}$$

and the PMF is

$$\begin{aligned} f_{_Z}(z,\lambda ,\gamma )&= F_{_Z}(z,\lambda ,\gamma )-F_{_Z}(z-1,\lambda ,\gamma )\\&= \lambda ^{z}\bigg [\dfrac{1}{z+1}-\dfrac{\lambda }{z+2}-\gamma \bigg (\dfrac{1}{z+1}\ln \Big ( \dfrac{\lambda ^{z}}{z+1}\Big )\\ &\quad -\,\frac{\lambda }{z+2}\ln \Big (\dfrac{\lambda ^{z+1}}{z+2}\Big )\bigg )\bigg ]. \end{aligned}$$

We call this distribution as the transmuted record type-discrete Burr–Hatke.

The survival and hazard rate functions (HRF) of the TRT-DBH are demonstrated as below

$$\begin{aligned} S(z,\lambda ,\gamma )&= \dfrac{\lambda ^{z+1}}{z+2}\Big [1-\gamma \ln \Big (\dfrac{\lambda ^{z+1}}{z+2}\Big ) \Big ],\\ \text { HRF }(z,\lambda ,\gamma )&= \dfrac{f_{_Z}(z,\lambda ,\gamma )}{S(z-1,\lambda ,\gamma )}\\&= 1-\dfrac{\lambda (z+1)\bigg (1-\gamma \ln \Big (\dfrac{\lambda ^{z+1}}{z+2}\Big )\bigg )}{(z+2)\bigg (1-\gamma \ln \Big (\dfrac{\lambda ^{z}}{z+1}\Big ) \bigg )}. \end{aligned}$$

The PMF and HRF plots of TRT-DBH distribution are depicted in Figs. 1 and 2, for different combinations of the parameters.

Fig. 1
figure 1

The PMF plots for TRT-DBH distribution with different combinations of parameters \((\lambda ,\gamma )\)

Full size image
Fig. 2
figure 2

The HRF plots for TRT-DBH distribution with different combinations of parameters \((\lambda ,\gamma )\)

Full size image

It is clear that the HRF of TRT-DBH distribution has different shapes, including decreasing and unimodal, which dedicate the capability of TRT-DBH distribution to model different types of data sets.

2.1 Some Statistical Properties of TRT-DBH Distribution

Now, some properties of the TRT-DBH distribution are investigated, such as the probability generating function, r-th non-central moments, and so on.

Let Z follow the TRT-DBH distribution with the parameters \((\lambda ,\gamma )\), then its probability generating function is obtained as follows

$$\begin{aligned} G_{_Z}(s)&= E(S^Z)\\&= \sum _{z=0}^{\infty }s^z\Big [\dfrac{\lambda ^ z}{z+1}-\dfrac{\lambda ^{z+1}}{z+2}\Big ]-\gamma \sum _{z=0}^{\infty }s^z\\ &\quad \quad \bigg [\dfrac{\lambda ^z}{z+1}\ln \Big (\dfrac{\lambda ^ z}{z+1}\Big )-\dfrac{\lambda ^{z+1}}{z+2}\ln \Big (\dfrac{\lambda ^{z+1}}{z+2}\Big ) \bigg ]\\&= \dfrac{1}{S\lambda }\Big (1-\frac{1}{s}\Big )\sum _{z=0}^{\infty }\dfrac{(s\lambda )^{z+1}}{z+1}+\dfrac{1}{s}\\ &\quad -\,\gamma \ln (\lambda )\Big (1-\frac{1}{s}\Big )\sum _{z=0}^{\infty }\Big (1-\frac{1}{z+1}\Big )(S\lambda )^{z}\\ &\quad +\,\gamma \Big (1-\frac{1}{s}\Big )\sum _{z=0}^{\infty }\frac{\ln (z+1)(s\lambda )^{z}}{z+1}\\&= \Big (1-\frac{1}{s}\Big )\bigg \{\dfrac{-1}{s\lambda }\ln (1-s\lambda )-\gamma \ln (\lambda )\\ &\quad \quad \Big [\frac{1}{1-s\lambda }-\frac{1}{s\lambda }\ln (1-s\lambda ) \Big ]\\ &\quad -\,\gamma S\lambda \, \Phi '(s\lambda ,1,2) \bigg \}+\dfrac{1}{s}, \qquad \vert s\vert <1 \end{aligned}$$

where \(\Phi (a,b,c)=\sum _{n=0}^{\infty }\dfrac{a^n}{(n+c)^b}, \;\vert a \vert <1\) is the LerchPhi function and we denote its derivative as

$$\begin{aligned} \Phi ^{'}(a,b,c)=\frac{\partial }{\partial b}\Phi ^{(0,1,0)}(a,b=b_0,c)\mid _{b=b_0}. \end{aligned}$$

Noted that both \(\lambda\) and s are restricted \((0<\lambda<1,\vert s\vert <1)\); hence, the condition of the LerchPhi function is satisfied.

The r-th non-central moments of TRT-DBH distribution are represented as

$$\begin{aligned} E(Z^r)&=\sum _{z=0}^{\infty }z^r f_{_Z}(z,\lambda ,\gamma )\\&= \sum _{z=0}^{\infty }\Big (z^r-(z-1)^r\Big ) \dfrac{\lambda ^ z}{z+1}\\ &\quad -\,\gamma \sum _{z=0}^{\infty }\Big (z^r-(z-1)^r\Big ) \dfrac{\lambda ^z}{z+1}\ln \Big (\dfrac{\lambda ^ z}{z+1}\Big ). \end{aligned}$$

It is concluded that the first and second moments of the TRT-DBH distribution are as follows

$$\begin{aligned} \mu _{_Z}&= E(Z)= -1-\frac{\ln (1-\lambda )}{\lambda }-\gamma \Big [\ln (\lambda ) \nonumber \\ &\quad \qquad \Big (\frac{1}{1-\lambda }+\frac{\ln (1-\lambda )}{\lambda }\Big )+ \lambda \, \Phi '(\lambda ,1,2)\Big ],\nonumber \\ E(Z^2)&= \frac{3-\lambda }{1-\lambda }+\frac{3 \ln (1-\lambda )}{\lambda }\nonumber \\ & \quad -\,\gamma \ln (\lambda )\bigg (\frac{5\lambda -3}{(1-\lambda )^2}-\frac{3\ln (1-\lambda )}{\lambda }\bigg )\nonumber \\ &\quad -\,\gamma \Big (2\, \Phi '(\lambda ,0,1)-3\lambda \,\Phi '(\lambda ,1,2)\Big ) . \end{aligned}$$
(1)

Accordingly, based on the first and second moments, the variance of TRT-DBH distribution can be obtained in closed form. The Fisher dispersion index (FDI) is defined as the variance to mean ratio, which indicates whether a certain distribution is suitable for under or over-dispersed data sets. If FDI \(<(>)1\), the distribution is under-dispersed (over-dispersed).

The numerical mean, variance, skewness, kurtosis and FDI of TRT-DBH distribution are provided in Table 1, for different combinations of the parameters. Based on Table 1, the mean and variance of TRT-DBH are increased by increasing values of parameters \(\lambda\) and \(\gamma\). Also, for small values of \(\lambda\) and large values of \(\gamma\), the FDI measure is near to one, which indicates the equi-dispersion of TRT-DBH distribution. For other combinations of \((\lambda ,\gamma )\), the FDI measure is more than one, so the TRT-DBH distribution is over-dispersion. The TRT-DBH distribution is severely skewed to right and leptokurtic. So, TRT-DBH distribution also has a perfect fit for right long-tailed data.

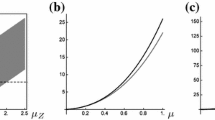
Based on Fig. 3, the values of \(Var(Z)-E(Z)\) are always positive, which confirms the results of Table 1 and the over-dispersion nature of the TRT-DBH model.

Table 1 Some statistical properties of the TRT-DBH distribution
Full size table
Fig. 3
figure 3

The \(Var(Z)-E(Z)\) plots for TRT-DBH distribution with different combinations of parameters \((\lambda ,\gamma )\)

Full size image

3 Formulation of the INAR(1) Model with TRT-DBH Innovation

The purpose of this section is to introduce an INAR(1) time series model based on the TRT-DBH distribution. First, we review the definition of the GNB thinning operator defined by Shamma et al. (2020), and then, an INAR(1) model with TRT-DBH innovation is constructed.

Definition 1

(Shamma et al. 2020) Consider a sequence of independent identically distributed (iid) geometric random variables \(\{V_i\}_{i\in {\mathbb {N}}}\) with parameter \(\frac{\theta }{1+\theta }\) and Bernoulli random variable W with parameter \(\frac{\alpha }{\theta }\), \(0\le \alpha \le \theta \le 1\), where \(V_i\) and W are independent for all \(i\in {\mathbb {N}}\). Define a sequence of dependent random variables \(\{U_i\}_{i\in {\mathbb {N}}}\) as \(U_i=V_iW ,\; i\in {\mathbb {N}}\). It can be verified \(U_i\) has a mixture distribution as follows

$$\begin{aligned} P(U_i=u)=\left\{ \begin{array}{ll} 1-\frac{\alpha }{1+\theta } &{} u=0\\ (\frac{\alpha }{\theta })\frac{\theta ^{u}}{(1+\theta )^{u+1}}&{} u=1,2,\ldots \end{array}\right. , \end{aligned}$$
(2)

denoted as zero inflated geometric distribution \(\big (ZIG(1-\frac{\alpha }{\theta },\frac{\theta }{1+\theta })\big )\).

Also,

$$\begin{aligned} E(U_{i})&= \alpha , Var(U_{i})=\alpha (2\theta -\alpha +1),\\ Cov(U_{i},U_{j})&= \alpha (\theta -\alpha ),\;i\ne j. \end{aligned}$$

The random variable \(\sum \nolimits _{i=1}^{n}U_{i}\) is a mixture of zero and negative binomial \((n,\frac{\theta }{1+\theta })\) distributed random variables with proportions \(1-\frac{\alpha }{\theta }\) and \(\frac{\alpha }{\theta }\), respectively, and the zero inflated negative binomial distribution is the name given to it.

Definition 2

(GNB thinning operator) Let X be a non-negative integer valued random variable and \(\left\{ {U_{i},\;i\in {\mathbb {N}}}\right\}\) as noted above by (2). The operator “\(\alpha *_{\theta }\)”\(,\;0\le \alpha \le \theta \le 1\), defined as \(\alpha *_{\theta }X_{t-1}= \sum _{i=1}^{X_{t-1}} U_{i,t}\) is called the GNB thinning operator.

Shamma et al. (2020) outlined the properties of the GNB thinning operator

3.1 The Proposed INAR(1) Model

The following recursive equation introduces the proposed stationary INAR(1) process \(\{X_{t}\}\) as

$$\begin{aligned} X_t=\alpha *_{\theta }X_{t-1}+Z_t, \qquad \alpha<\theta <1,\;\; t\ge 1, \end{aligned}$$
(3)

where “\(*_{\theta }\)” is the GNB thinning operator, \(\{Z _{t}\}\) be a sequence of TRT-DBH random variables with parameters \((\lambda ,\gamma )\) and given \(X_{t-1}\), the random variables \(\alpha *_{\theta }X_{t-1}\) and \(Z_{t}\) are independent of each other. We shall refer to this model as TRBH-INAR(1).

The one-step transition probabilities are

$$\begin{aligned} P_{0j}=P\left( X_{t}=j\vert X_{t-1}=0\right) =P(Z_{t}=j), \end{aligned}$$

and for \(i\ge 1\), we get

$$\begin{aligned} P_{ij}&= P\left( X_{t}=j\vert X_{t-1}=i\right) =(1-\frac{\alpha }{\theta })P(Z_t=j)\nonumber \\ &\quad +\,\frac{\alpha }{\theta }\sum _{k=0}^{j}\left( {\begin{array}{c}i-1\\ i+k-1\end{array}}\right) \frac{\theta ^{k}}{(1+\theta )^{i+k}} P(Z_t=j-k), \end{aligned}$$
(4)

where

$$\begin{aligned} P(Z_{t}=j)&= \lambda ^{j}\bigg [\dfrac{1}{j+1}-\dfrac{\lambda }{j+2}-\gamma \bigg (\dfrac{1}{j+1}\ln \Big ( \dfrac{\lambda ^{j}}{j+1}\Big )\\ &\quad -\,\frac{\lambda }{j+2}\ln \Big (\dfrac{\lambda ^{j+1}}{j+2}\Big )\bigg )\bigg ]. \end{aligned}$$

This model may be fitted to infectious illness data and can be used to describe the disease’s transmission as follows: In the case of the INAR(1) model, if \(X_{t-1}\) represents the number of new patients throughout the time span \((t-2, t-1]\), \(\alpha *_\theta X_{t-1}\) will be the number of surviving patients from the previous month, which may stimulate new patients or likely cure, and \(\{Z_t\}\) will be the number of new patients infected in the current period.

Remark 1

Shamma et al. (2020) provided several properties of the GNB thinning operator as follows

  1. (i)

    \(E\left( \alpha *_{\theta }X\mid X \right) =\alpha X\),

  2. (ii)

    \(Var\left( \alpha *_{\theta }X\mid X \right) =\alpha (\theta -\alpha ) X +\alpha (\theta +1)X\),

  3. (iii)

    \(E\left( \alpha *_{\theta }X\right) =\alpha E(X)\),

  4. (iv)

    \(E\left( \alpha *_{\theta }X \right) =\alpha (\theta -\alpha ) E^2(X) +\alpha (\theta +1)E(X)+\alpha \theta \, Var(X)\).

The expectation and variance of the process \(\{X_t\}\) is obtained as

$$\begin{aligned} E(X)&= \frac{\mu _{_Z}}{1-\alpha },\\ Var(X)&= \dfrac{\alpha \mu _{_Z} (1+\theta )}{(1-\alpha )(1-\alpha \theta )}+\dfrac{\alpha (\theta -\alpha )\mu ^2_{_Z}}{(1-\alpha )^2 (1-\alpha \theta )}\\ &\quad +\,\dfrac{\sigma ^2_{Z}}{1-\alpha \theta }, \end{aligned}$$

where \(\mu _{_Z}\) and \(\sigma ^2_{Z}\) are the mean and variance of TRT-DBH distribution, respectively.

Proposition 1

The Fisher dispersion index of \(\{X_t\}\) is obtained as

$$\begin{aligned} I_X&= \frac{Var(X)}{E(X)}\\&= \frac{\alpha (\theta -\alpha )\mu ^2_{_Z}+\alpha (\theta +1)(1-\alpha )\mu _{_Z}+(1-\alpha )^2\sigma ^2_Z}{(1-\alpha \theta )(1-\alpha )\mu _{_Z}}. \end{aligned}$$

This readily demonstrates that \(I_X\) is more than one and obviously is over-dispersed.

Proof

In order to confirm \(I_ZX\ge 1\), it is required to show \(Var(X)- E(X)\ge 0\). Hence, we show the following inequality always holds

$$\begin{aligned} \alpha (\theta -\alpha )\mu ^2_{_Z}+(1-\alpha )(2\alpha \theta -1+\alpha )\mu _{_Z}+(1-\alpha )^2\sigma ^2_Z \ge 0, \end{aligned}$$

which can be rewritten as

$$\begin{aligned} \alpha (\theta -\alpha )\mu ^2_{_Z}+(1-\alpha )^2\Big (\sigma ^2_Z- \mu _{_Z}\Big )+2\alpha \theta (1-\alpha )\mu _{_Z}\ge 0. \end{aligned}$$

Since the TRT-DBH model is over-dispersed or equi-dispersed, so \(I_Z>1\) (i.e., \(\sigma ^2_{_Z}-\mu _{_Z}\ge 0\)), and the proof is concluded. \(\square\)

Proposition 2

Suppose \(\{X_{t}\}\) is a stationary process defined by (3), then for \(\alpha<\theta <1\) and \(t\ge 1\),

  1. (i)

    The conditional expectation is

    $$\begin{aligned} E\left( X_{t}\mid X_{t-k}\right) =\alpha ^{k}X_{t-k}+\dfrac{1-\alpha ^{k}}{1-\alpha }\mu _{_Z} . \end{aligned}$$
    (5)

    When \(k\rightarrow \infty\), then \(\lim _{k\rightarrow \infty }E\left( X_{t}\mid X_{t-k}\right) =\dfrac{\mu _{_Z}}{1-\alpha }\), which is the process’s unconditional expectation.

  2. (ii)

    The conditional variance is

    $$\begin{aligned} Var(X_{t}\mid X_{t-1})=\alpha (\theta -\alpha )X_{t-1}^{2}+\alpha (\theta +1)X_{t-1}+\sigma ^2_{Z}, \end{aligned}$$
    (6)

    and

    $$\begin{aligned} Var\left( X_{t}\mid X_{t-k}\right)&= \alpha ^k\left( \theta ^k-\alpha ^k\right) X_{t-k}^{2}+\alpha ^{k}\frac{(1+\theta )(1-\theta ^k)}{1-\theta } X_{t-k}\\ &\quad +\,2\mu _{_Z} \alpha ^k\Big (\dfrac{1-\theta ^k}{1-\theta } -\dfrac{1-\alpha ^k}{1-\alpha }\Big ) X_{t-k}\\ &\quad +\,\dfrac{\alpha \mu _{_Z}(1+\theta )}{1-\theta } \Big (\dfrac{1-\alpha ^{k-1}}{1-\alpha }-\dfrac{\theta (1-(\alpha \theta )^{k-1})}{1-\alpha \theta }\Big )\\ &\quad +\,\mu ^2_{_Z}\Big ( \dfrac{1-(\alpha \theta )^{k-1}}{1-\alpha \theta } -\dfrac{1-\alpha ^{2k-2}}{1-\alpha ^2} \Big ) \\ &\quad +\, 2\alpha \mu ^2_{_Z}\bigg [\frac{\theta }{1-\theta }\Big (\dfrac{\alpha (1-\alpha ^{k-1})}{1-\alpha }-\dfrac{\alpha \theta (1-(\alpha \theta )^{k-1})}{1-\alpha \theta }\Big ) \\ &\quad -\,\dfrac{\alpha }{1-\alpha }\Big (\dfrac{\alpha (1-\alpha ^{k-1})}{1-\alpha }-\dfrac{\alpha \theta (1-\alpha ^{2k-2})}{1-\alpha ^2}\Big )\bigg ]\\ &\quad +\,\sigma ^2_{Z}\dfrac{1-(\alpha \theta )^k}{1-\alpha \theta }. \end{aligned}$$

    hence,

    $$\begin{aligned} \lim _{k\rightarrow \infty }Var\left( X_{t}\mid X_{t-k}\right)&= \dfrac{\alpha \mu _{_Z} (1+\theta )}{(1-\alpha )(1-\alpha \theta )}\\ &\quad +\,\dfrac{\alpha (\theta -\alpha )\mu ^2_{_Z}}{(1-\alpha )^2 (1-\alpha \theta )}+\dfrac{\sigma ^2_{Z}}{1-\alpha \theta }, \end{aligned}$$

    which is the process’s unconditional variance.

  3. (iii)

    The autocorrelation function of the process \(\left\{ X_{t}\right\}\) is represented as

    $$\begin{aligned} \rho (k)=Corr(X_t,X_{t-k})=\alpha ^{k}. \end{aligned}$$

Proof

See Appendix A. \(\square\)

3.2 Different Estimation Method

The conditional maximum likelihood, modified conditional least square, modified maximum empirical likelihood, and Yule–Walker estimation procedures for the parameters of the TRBH-INAR(1) model are discussed in this section.

3.2.1 Conditional Maximum Likelihood Estimation

The log-likelihood function is maximized in terms of the model parameters \(\varvec{\delta }=\) \((\alpha ,\theta ,\lambda ,\gamma )\) in order to produce conditional maximum likelihood (CML) estimators. The log-likelihood function for sample observation \(X_{1},\ldots ,X_{n}\) from the TRBH-INAR(1) model can be written as

$$\begin{aligned} \ell \left( \varvec{\delta } \right)&= \log L\left( \varvec{\delta }\mid X_{2},\ldots ,X_{n}\ \right) \\&= \sum \limits _{t=2}^{n}\log P\left( X_{t}=j \mid X_{t-1}=i\right) , \end{aligned}$$

where \(P\left( X_{t}=j\mid X_{t-1}=i\right)\) is transition probability given by (4). The CML estimator of the unknown parameters are numerically obtained by maximizing the log-likelihood function with commands “nlm” or “optim” from statistical package “R”.

3.2.2 Modified Conditional Least Square Estimation

The modified conditional least squares (MCLS) estimators of the parameters \(\alpha ,\mu _{_Z}\) are found by minimizing the expression below

$$\begin{aligned} Q(\alpha ,\mu _{_Z} )&= \sum _{t=2}^{n}\left( X_{t}-E(X_{t}\mid X_{t-1})\right) ^{2}\nonumber \\&= \sum _{t=2}^{n}\left( X_{t}-\alpha X_{t-1}-\mu _{_Z} \right) ^{2}, \end{aligned}$$
(7)

where \(\mu _{_Z}\) is a function of the parameters \((\lambda ,\gamma )\). The estimators are given by

$$\begin{aligned} {\hat{\alpha }}_{_{MCLS}}=\dfrac{(n-1)\sum \nolimits _{t=2}^n X_t X_{t-1}-\sum \nolimits _{t=2}^nX_t\sum \nolimits _{t=2}^nX_{t-1}}{(n-1)\sum \nolimits _{t=2}^nX_{t-1}^{2}-( \sum \nolimits _{t=2}^n X_{t-1})^2}, \end{aligned}$$

and

$$\begin{aligned} {\hat{\mu }}_{_{Z, MCLS}}=\dfrac{\sum \nolimits _{t=2}^{n}X_{t}-{\hat{\alpha }}_{_{MCLS}}\sum \nolimits _{t=2}^{n}X_{t-1}}{n-1}. \end{aligned}$$

It is worth mention that the MCLS estimation of parameters \((\lambda ,\gamma )\) is obtained by finding the root of the equation (1) equal to the estimation of the \({\hat{\mu }}_{_{Z, MCLS}}\).

The one-step conditional expectation of the process depends only on the parameters \(\alpha\) and \(\mu _{_Z}\) and is not possible to use it for the estimation of the parameter \(\theta\). Hence, the parameter \(\theta\) can be estimated under the modified method proposed by Karlsen and Tjøstheim (1988). The parameter \(\theta\) can be estimated by minimizing the following expression

$$\begin{aligned} T(\theta )=\sum _{t=2}^{n}\left( V_{t}-Var(X_{t}\vert X_{t-1})\right) ^2, \end{aligned}$$
(8)

where

$$\begin{aligned} V_{t}&= (X_{t}-E(X_{t}\vert X_{t-1}))^{2}\\&= \left( X_{t}-{\hat{\alpha }}_{_{MCLS}} X_{t-1}-{\hat{\mu }}_{_{Z, MCLS}} \right) ^{2}, \end{aligned}$$

and \(Var(X_{t}\vert X_{t-1})\) is defined in (6) with estimated values of the parameters \((\alpha ,\lambda ,\gamma )\) as below

$$\begin{aligned} Var(X_{t}\mid X_{t-1})&= {\hat{\alpha }}_{_{MCLS}}(\theta -{\hat{\alpha }}_{_{MCLS}} )X_{t-1}^{2}\\ &\quad +\,{\hat{\alpha }}_{_{MCLS}} (\theta +1)X_{t-1}+{\hat{\sigma }}^2_{_{Z, MCLS}}, \end{aligned}$$

where \(\sigma ^2_{Z}\) is a function of the parameters \((\lambda ,\gamma )\) and can be estimated easily by \(({\hat{\lambda }}_{_{MCLS}},{\hat{\gamma }}_{_{MCLS}})\).

3.2.3 Modified Maximum Empirical Likelihood Estimation

The nonparametric modified empirical likelihood (MEL) technique for the TRBH-INAR(1) model is discussed in this section, which comprises two phases. In the first step, we obtain the maximum MEL estimators for the parameters \(\alpha\) and \(\mu _{_Z}\) as follows. By taking the derivative of \(Q(\alpha ,\mu _{_Z})\) defined in (7) with respect to \(\varvec{\beta }=(\alpha ,\mu _{_Z})\), we have the estimating equation

$$\begin{aligned} \frac{-1}{2}\dfrac{\partial Q(\varvec{\beta } )}{\partial \varvec{\beta }}=\sum _{t=2}^{n}m_{t}(\varvec{\beta })=0, \end{aligned}$$

where \(m_{t}(\varvec{\beta } )=(m_{1,t}(\varvec{\beta }),m_{2,t}(\varvec{\beta }))^{\prime }\) with \(m_{1,t}(\varvec{\beta } )=X_{t-1}(X_{t}-\alpha X_{t-1}-\mu _{_Z})\), \(m_{2,t}(\varvec{\beta })=X_{t}-\alpha X_{t-1}-\mu _{_Z}\). Following Qin and Lawless (1994), we can define the log MEL function as

$$\begin{aligned} L_{ME}(\varvec{\beta })=\sum _{t=1}^{n}\log \big (1+d^{\prime }(\varvec{\beta } )m_{t}(\varvec{\beta })\big ), \end{aligned}$$

where \(d(\varvec{\beta } )\) satisfies

$$\begin{aligned} \frac{1}{n}\sum _{t=1}^{n}\frac{m_{t}(\varvec{\beta })}{1+d^{\prime }(\varvec{\beta })m_{t}(\varvec{\beta })}=\varvec{0}. \end{aligned}$$

The maximum MEL estimator (MMELE) for the parameter \(\varvec{\beta }\) is defined by minimizing the above equation, i.e.,

$$\begin{aligned} \hat{\varvec{\beta }}_{_{mmel}}=\arg \min _{\varvec{\beta } }L_{ME}(\varvec{\beta } ). \end{aligned}$$

The MMEL estimation of the parameters \((\lambda ,\gamma )\) can be easily obtained based on the \({\hat{\mu }}_{_{Z ,mmel}}\) and finding the root of the Eq. (1).

The maximum MEL estimator for the parameter \(\theta\) is obtained in the second phase. By considering the function \(T(\theta )\) which is defined in (8), we have

$$\begin{aligned} \frac{-1}{2}\dfrac{\partial T(\theta )}{\partial \theta }=\sum _{t=2}^{n}m_{t}(\theta ), \end{aligned}$$

where \(m_{t}(\theta )={\hat{\alpha }}_{_{mmel}}X_{t-1}(X_{t-1}+1)\Big [V_{t}-{\hat{\alpha }}_{_{mmel}}(\theta -{\hat{\alpha }}_{_{mmel}})X_{t-1}^{2} -{\hat{\alpha }}_{_{mmel}}(\theta +1)X_{t-1}-{\hat{\sigma }}^2_{_{Z,mmel}}\Big ],\) and \(V_{t}=\left( X_{t}-{\hat{\alpha }}_{_{mmel}}X_{t-1}-{\hat{\mu }}_{_{Z,mmel}}\right) ^{2}\). The MMELE for the parameter \(\theta\) will be obtained by minimizing log MEL function.

3.2.4 Yule–Walker Estimation

The Yule–Walker (YW) estimators of the unknown vector \(\varvec{\delta }\) are obtained as follows. Using the fact that \(E(X_{t})=\dfrac{\mu _{_Z}}{1-\alpha }\) and \(Corr(X_{t},X_{t-1})= \alpha\), the YW estimations of the parameters \((\alpha ,\mu _{_Z})\) are generated using the sample mean and sample autocorrelation function as follows:

$$\begin{aligned} {\hat{\alpha }}_{{YW}}&= \dfrac{\sum _{t=2}^{n}(X_{t}-{\overline{X}})(X_{t-1}-{\overline{X}})}{\sum _{t=1}^{n}(X_{t}-{\overline{X}})^{2}},\\ {\hat{\mu }}_{_{Z, YW}}&= {\overline{X}}(1-{\hat{\alpha }}_{{YW}} ). \end{aligned}$$

Similarly, the YW estimation of the parameters \((\lambda ,\gamma )\) is performed using the \({\hat{\mu }}_{_{Z ,mmel}}\), and finding the equation’s root (1).

We utilize the second moment of the procedure to estimate the parameter \(\theta\) as follows:

$$\begin{aligned} E(X_{t}^{2})&= \alpha \theta E(X_{t}^2)+\alpha (1+\theta )E(X_t)\\ &\quad +\,E(Z^2_t) +2\alpha \mu _{_Z} E(X_t)\\&= \dfrac{\alpha (1+\theta )}{1-\alpha \theta }E(X_t)+\dfrac{E(Z^2_t)}{1-\alpha \theta }+\dfrac{2\alpha \mu _{_Z} E(X_t)}{1-\alpha \theta }, \end{aligned}$$

which is obtained based on Remark 1. Let \(\overline{X^2}=\frac{1}{n}\sum _{t=1}^n X_t^2\), then

$$\begin{aligned} \overline{X^2}= \dfrac{{\hat{\alpha }}_{{YW}} (1+\theta )}{1-{\hat{\alpha }}_{{YW}} \theta }{\overline{X}}+\dfrac{{\hat{\mu }}_{_{Z, YW}} ^2+ {\hat{\sigma }}_{_{Z, YW}}}{1-{\hat{\alpha }}_{{YW}} \theta }+\dfrac{2{\hat{\alpha }}_{{YW}} {\hat{\mu }}_{_{Z, YW}} {\overline{X}}}{1-{\hat{\alpha }}_{{YW}} \theta }, \end{aligned}$$
(9)

as a result, estimate of the parameter \(\theta\) is determined by computing the root of the Eq. (9) numerically.

4 Simulation Approach

We examine the efficiency of the parameter estimate approaches for the TRBH-INAR(1) model using Monte Carlo simulation, under different sample sizes \(\varvec{n}=(100,200,500, 1000)\) over \(h=1000\) iterations. Two distinct parameter combinations are evaluated as \(\left( \alpha ,\theta ,\lambda \right) =\left( 0.4,0.8,0.7,0.3\right)\) and \(\left( 0.2,0.4,0.9,0.6 \right)\). We use the mean squared error (MSE) metric to assess the estimators’ performance. The results are summarized in Tables 2 and 3, where represent that all estimates of the parameters are convergent to their actual values. Furthermore, when the sample size grows larger, the MSE decreases. Among different kinds of estimation methods, the CML and MMEL provide better performance than MCLs and YW estimations, since they have small MSE for all parameters. In comparison among the CML and MMEL methods, we provide the computer running time (R.time), which indicates that the MMEL method is faster than CML and as well as CML in MSE measure. As a result, the nonparametric MMEL technique outperforms other methods of estimation.

Table 2 Results of simulations of the TRBH-INAR(1) model’s parameter estimations
Full size table
Table 3 Results of simulations of the TRBH-INAR(1) model’s parameter estimations
Full size table

5 Application of Real-World Data

In this section, we investigate the application of the TRBH-INAR(1) process by using two types of clinical count data.

The first data set is devoted to daily counts of death from the COVID-19 disease, reported from Netherland and consists of 46 observations, from second July until 16-th August at 2021, by the World Health Organization (https://covid19.who.int).

The second data set represents the weekly counts of Tularemia disease, reported from Bavaria, and it consists of 48 observations, from first week until 48-th week on 2020, from the Robert Koch Institute: SurvStat@RKI 2.0 (https://survstat.rki.de) site.

Fig. 4
figure 4

The sample path, ACF and PACF of both data sets

Full size image

Figure 4 depicts the sample path, autocorrelation function (ACF), and partial autocorrelation function (PACF) of the two data series, indicating that the data sets should be modeled using a first-order autoregressive model. Furthermore, the augmented Dickey–Fuller test is used to justify stationarity of the two clinical data sets, where the p-value of augmented Dickey–Fuller test for COVID-19 data is less than 0.01 and for Tularemia data is equal 0.022, which confirm the stationarity of both data sets.

The mean, variance and autocorrelation of the two data sets are (3.565, 7.717, 0.557) and (2.125, 5.047, 0.310), respectively. Both data series are empirically over-dispersed with dispersion indices \(\hat{\mathrm{I}}_{X}=(2.164,2.375) \), respectively.

We compare the TRBH-INAR(1) model to some competitive INAR(1) models as:

PINAR(1) (Al-Osh and Alzaid 1987), GINAR(1) (Alzaid and Al-Osh 1988), NBIINAR(1) (Al-Osh and Aly 1992), GPQINAR(1) (Alzaid and Al-Osh 1993), NBRCINAR(1) (Weiß 2008), NGINAR(1) (Ristić et al. 2009), DCGINAR(1) (Ristić et al. 2013), NDCINAR(1) (Miletić Ilić 2016), \(\rho\)-NGINAR(1) (Borges et al. 2017), GADCINAR(1) (Nastić et al. 2017) and GNBINAR(1) (Shamma et al. 2020).

We reported the CML estimates, the information criterion (IC) statistics as AIC, BIC, HQIC and CAIC, and the root mean squares of differences of observations and predicted values (RMS) for each INAR model. Tables 4 and 5 show the results for two different data series. Regarding Tables 4 and 5, the values of the IC and RMS are the smallest for the TRBH-INAR(1) model. Therefore, we can conclude that the TRBH-INAR(1) model provides the best loss information among other competitive INAR(1) models.

Table 4 The CML estimates and some IC measures of COVID-19 data
Full size table
Table 5 The CML estimates and some IC measures of Tularemia data
Full size table

5.1 The Clinical Data Sets’ Residual Analysis

We provide the results of a residual analysis of clinical data sets, which confirmed the suitability of the proposed model. The Pearson residuals are defined as

$$\begin{aligned} e_t=\frac{X_t-E(X_t\mid X_{t-1})}{\sqrt{Var(X_t \mid X_{t-1})}}, \end{aligned}$$

where \(E(X_t\mid X_{t-1})\) and \(Var(X_t\mid X_{t-1})\) are defined in (5) and (6), respectively. Note that, estimation of the parameters of the TRBH-INAR(1) model are substituted in each \(E(X_t\mid X_{t-1})\) and \(Var(X_t\mid X_{t-1})\) to compute the Pearson residuals.

The Pearson residuals ACF of both data sets is shown in Fig. 5. The residuals are non-correlated, as shown in Fig. 5, and the results are supported by the Ljung-Box test p-values (0.679, 0.935). Figure 6 shows the Pearson residuals cumulative periodogram, which shows how residuals are distributed randomly and without trend.

Figure 7 shows the result of the parametric re-sampling method. First, 5000 data sets with bootstrap sample size \(\varvec{n}=(46,48)\) are obtained using the fitted TRBH-INAR(1) model (with CML estimates of the parameters of each data set). Second, using the bootstrap samples, the ACF of each specific lag is calculated. The acceptance bounds \(100(0.975)\%\) and \(100(0.025)\%\) quantiles are shown as “\(+\)”, and the samples ACF are presented by “\(\bullet\)” symbols, in Fig. 7. According to Fig. 7, all of the sample autocorrelations were assigned between the acceptance boundaries, indicating that the model was adequate.

Fig. 5
figure 5

The Pearson residuals ACF for the two data sets

Full size image
Fig. 6
figure 6

The Pearson residuals cumulative periodogram for the two data sets

Full size image
Fig. 7
figure 7

The acceptance areas and the bootstrap ACF

Full size image

5.2 Methods of Forecasting

To test the TRBH-INAR(1) model’s appropriateness and predictability, we present forecasts of the specified data sets using both the traditional and modified Sieve bootstrap approaches.

The k-step ahead classical predictor of the TRBH-INAR(1) model is represented as

$$\begin{aligned} {\hat{X}}_{t}=E\left( X_{t}\mid X_{t-k}\right) =\alpha ^{k}X_{t-k}+\dfrac{1-\alpha ^{k}}{1-\alpha }\mu _{_Z}, \end{aligned}$$

where unknown parameters \(\alpha\) and \(\mu _{_Z}\) are substituted by the related CML estimates.

5.2.1 Modified Sieve Bootstrap Approach

The integer nature of the count data is not preserved by the classical predictor, despite the fact that the count time series is an integer. The Sieve bootstrap technique is a distribution-free predictor that preserves the integer nature of the count data. Hence, we modified the bootstrap approach proposed by Pascual et al. (2004) to apply for the TRBH-INAR(1) model via the following steps. Since \(\alpha *_{\theta }\left( \alpha *_{\theta }X\right) \overset{d}{\ne }\alpha ^{2}*_{\theta }X\), we can only provide the one-step modified Sieve bootstrap prediction.

  1. 1.

    The thinning parameters \((\alpha ,\theta )\) are estimated based on the YW estimation approach.

  2. 2.

    Compute residuals \({\hat{Z}}_{t}=X_{t}-{\hat{\alpha }}X_{t-1},\) for \(t=2,...,n\).

  3. 3.

    The empirical distribution of the modified residuals \({\tilde{Z}}_{t}\) is provided, where \({\tilde{Z}}_{t}=\left[ {\hat{Z}}_t\right]\), and \([\cdot ]\) shows the nearest integer value.

  4. 4.

    The bootstrap series \(X_{t}^{b}\) is given by

    $$\begin{aligned} X_{t}^{b}={\hat{\alpha }}*_{{\hat{\theta }}} X_{t-1}^{b}+Z_{t}^{b}, \qquad b=1,\ldots ,B, \end{aligned}$$

    where B is the bootstrap sample size that was chosen to be \(B=500\), and \(Z_{t}^{b}\) is generated from the empirical distribution in step 3, for \(t=1,2,...,n\).

  5. 5.

    The YW estimation of the parameters \(({\hat{\alpha }}_{{YW}},{\hat{\theta }}_{{YW}})\) is obtained by inserting the sample mean, variance, and solving the following equations

    $$\begin{aligned} E\left( X_{t}\right) (1-\alpha )&= E\left( Z_{t}\right) \\ Var(X_{t})&= \dfrac{\alpha (\theta -\alpha )\mu ^2_{_Z}}{(1-\alpha )^2(1-\alpha \theta )}\\ &\quad +\,\dfrac{\alpha (\theta +1)\mu _{_Z}}{(1-\alpha )(1-\alpha \theta )} +\dfrac{\sigma ^2_{Z}}{1-\alpha \theta }. \end{aligned}$$
  6. 6.

    Based on the sample means \({\hat{\alpha }}=\frac{1}{B}\sum _{i=1}^{B}{\hat{\alpha }}_{_{i,YW}}\) and \({\hat{\theta }}= \frac{1}{B}\sum _{i=1}^{B} {\hat{\theta }}_{_{i,YW}}\), the parameters \(\left( \alpha ,\theta \right)\) are estimated.

  7. 7.

    The recursion method is used to acquire future bootstrap observations by the expression

    $$\begin{aligned} {\hat{X}}_{t+1}^{b}={\hat{\alpha }}*_{{\hat{\theta }}}X_{t}^{b}+Z_{t+1}^{b}. \end{aligned}$$

The traditional and modified Sieve bootstrap predictions of the relevant data series, for which we know the observed values, are provided in Table 6 as a result of evaluating two prediction approaches. When there are zero or near-zero data demands, the symmetric mean absolute percent error (SMAPE) is applied to compare the forecast systems. The less SMAPE value leads to a better forecasting scheme. According to Table 6, the modified Sieve bootstrap predictors’ SMAPE values are lower than classical, and the modified Sieve bootstrap predictors are integers, which are consistent with the nature of actual data.

Table 6 The k-step ahead predictions of clinical data series
Full size table

6 Conclusions

We provide a first-order integer-valued autoregressive [INAR(1)] time series model based on the transmuted record type-discrete Burr–Hatke (TRT-DBH) distribution, which is a more flexible version of the discrete Burr–Hatke distribution. The TRT-DBH distribution is proved to over-dispersed, asymmetric and leptokurtic. The hazard rate function of the proposed distribution has different shapes as monotone and unimodal. The applicability of the TRT-DBH distribution is demonstrated in time series modeling based on an INAR(1) model with TRT-DBH distributed innovations. Properties of the model are studied as well as different estimation approaches for the model parameters. The assessment of the properties and estimation approaches is conducted via some simulation studies. The adequacy of fit of the proposed INAR(1) model is checked via two clinical data sets, including the Covid-19 series and is compared with other competitive models. For both clinical data sets, we perform the residual analysis (Pearson residuals), as well as traditional and modified Sieve bootstrap forecasting methods.