1 Introduction

Presently, research on activated carbon development is closely associated with the investigation of various precursors, including agricultural wastes (Leite et al. 2018; Nworie et al. 2022; Malesic-Eleftheriadou et al. 2022; Liu et al. 2023), invasive forest fruits or trees (Lazarotto et al. 2022), and their interaction with contaminants present in the environment. Nevertheless, the core issue lies in the composition of water, as contaminated water harbours a mixture of pollutants resulting from industrial discharges, untreated agricultural runoff, and domestic waste (da Silva Santos et al. 2021; Ismail et al. 2022). Therefore, it is crucial to direct activated carbon research towards addressing the simultaneous removal of numerous pollutants, rather than considering it as an ideal scenario with controlled variables. In this regard, only a limited number of studies have undertaken the formidable challenge of addressing this issue. For instance, Aichour and Zaghouane-Boudiaf (2020) discussed the mechanism of adsorption using two cationic dyes as pollutants from single and binary solutions onto activated carbon from citrus peel. Yazidi et al. (2020) studied the competitive adsorption phenomenon using durian shell as a precursor for activated carbon to adsorb amoxicillin and tetracycline. They obtained a better adsorption capacity for amoxicillin than tetracycline using their material. Chandrasekaran et al. (2020) prepared activated carbon from Prosopis juliflora wood for ciprofloxacin and amoxicillin adsorption in single and binary systems. They revealed that ciprofloxacin has an antagonistic effect on amoxicillin adsorption in binary system. Other studies have reported the use of lignocellulosic biomass such as, avocado seed (Zhu et al. 2018), coconut shell (Qin et al. 2018), a mixture of almond and apricot stone shell (Kılıç and Orhan 2019), tree pods from Erythrina speciosa (Bouzidi et al. 2023) to carry out binary adsorption of pollutants simultaneously or in parallel. Furthermore, removing contaminants from water has been elucidated theoretically using density functional theory to simulate the interaction of water molecule and contaminants considering Van der Waals dispersion interaction (Nematov et al. 2022).

Contaminants include heavy metals, rare earth metals (Iftekhar et al. 2022), or organic molecules that exist as cationic, anionic, or ionic species upon contact with water. The challenge lies in the fact that the efficiency of the adsorbent for a specific pollutant (be it cationic, anionic, or an ionic molecule) depends on factors such as the precursor used, textural characteristics, and the presence of functional groups (carboxylic, phenolic, quinones) on the surface of the activated carbon (Nayagam and Prasanna 2022). This implies that multiple activated carbons would be necessary for each type of pollutant, leading to a cost-intensive process of pollutant removal using activated carbons. However, parallel adsorption using a single adsorbent has shown that, in addition to the mentioned functional groups, the presence of heteroatoms like nitrogen, sulphur, phosphorus, and even trace inorganic elements in the carbon could enhance the removal of more than one pollutant (Figueiredo and Pereira 2012; Sun et al. 2019). Moreover, the implementation of binary adsorption involving both anions and cations can contribute to a better understanding of the mechanisms governing the selection process when activated carbon interacts with pollutants of varying polarities.

The development of multifunctional activated carbon from abundant lignocellulosic biomasses, capable of simultaneous multi-pollutant adsorption, has the potential to enhance overall wastewater secondary and tertiary treatment processes. Macadamia nutshell, a lignocellulosic biomass considered as residue, constitutes approximately one-third of the total mass of the fruit. In Mexico, the production of macadamia nuts in 2021 reached 21.58 tons per hectare, contributing to a total production of approximately 32,205.77 tons of this product (Servicio de Información Agroalimentaria y Pesquera 2023). Likewise, the worldwide production was about 369,491 tons in the same year (SAMAC. Macadamias South Africa NPC 2023). Therefore, the substantial production of macadamia nuts has resulted in a significant quantity of residual shells. Limited studies have reported the utilization of activated carbon derived from macadamia nutshell, primarily focusing on the removal of a single pollutant. This adsorbent has predominantly been employed for the removal of dyes and tetracycline. For instance, Martins et al. (2015) prepared activated carbon from macadamia nut shells using NaOH as an activating agent for the removal of tetracycline antibiotics, obtaining a maximum adsorption capacity of 455.33 mg/g. Dao and Le Luu (2020) activated macadamia nutshell using H2SO4 and K2CO3 for the removal of methylene blue in the water. Wongcharee et al. (2019) produced activated carbon from macadamia nutshell and zeolite composite via the physical activation method with CO2. The activated carbon was deployed to remove methylene blue (MB) from water. They reported a low maximum adsorption capacity of 97 mg/g. The same research group examined a common precursor, employing it as a hybrid magnetic nanosorbent material for the adsorption of synthetic melanoidin. Their findings revealed that the adsorbent achieved a capacity of 14.87 mg/g (Wongcharee and Aravinthan 2020). In contrast, Du et al. produced activated carbon from macadamia nutshell through KOH activation, utilizing microwave radiation for the adsorption of Reactive Blue 19 dye. Their results indicated that the material reached a maximum adsorption capacity of 376.81 mg/g (Du et al. 2017). Hence, the significance and novelty of our work lie in the fact that to the best of our knowledge, there is no available study on the removal of amoxicillin (AMX) using activated carbon derived from macadamia nutshell. Besides, to the best of our knowledge there are no studies on the binary removal of methylene blue and amoxicillin using activated carbon from macadamia nutshell.

Antibiotics are used extensively to treat bacterial infections. According to Word Health Organization (WHO), amoxicillin and amoxicillin/clavulanic acid are the most frequently consumed antibiotics globally (World Health Organization 2018). Similarly, AMX is used for veterinary bacterial infection treatment (Putra et al. 2009). The high demand for antibiotics has resulted in unregulated disposal, which could lead to drug resistance, skin irritation, nausea, stomachache, and diarrhea (Suárez and Gudiol 2009; Moura et al. 2018). Studies have shown that after the consumption of amoxicillin in humans, about 86 ± 8% is excreted through the urine (Pezoti et al. 2016). Moreso, high accumulation could result in an overdose, which is harmful to human beings and animals.

On the other hand, methylene blue (MB), with a chemical formula C16H18ClN3S is a cationic dye extensively used in the textile industry, surgical procedures, to treat some illnesses, and for veterinary purposes (Borghei et al. 2021; Gupta et al. 2022). At high concentrations, MB could result in heart disease, skin irritation, vomiting, and headache and could be hazardous to the aquatic system (Al-Ghouti and Sweleh 2019; Xue et al. 2022). Hence, it is important to develop an effective adsorbent that is capable of removing both AMX and MB from aqueous solution in a binary system (Rodrigues et al. 2020).

To address the challenges associated with concurrently describing the adsorption of two pollutants in a binary solution using a sustainable adsorbent, we present the synthesis of activated carbon from macadamia nutshell. This process involves one-step chemical activation with K2CO3 as an environmentally friendly activating agent. The generated activated carbon was applied for the simultaneous removal of AMX and MB in a binary solution (BS). A comprehensive characterization of the developed activated carbon was conducted to elucidate the structural-performance relationship. The study involved the evaluation of the effects of pH, temperature, pollutant concentration, and contact time. Furthermore, the kinetics mechanism, three isotherm models, and the thermodynamics of the adsorption process were investigated.

2 Materials and methods

2.1 Materials

Amoxicillin, AMX (C16H19N3O5S, molecular weight = 365.40 g/mol) and methylene blue, MB (C16H18ClN3S, molecular weight = 319.85 g/mol), were purchased from Merck. HCl (98% purity), NaOH (99% purity), and K2CO3 anhydrous were all purchased from Sigma-Aldrich. The macadamia nutshell was provided to us by local farmers in Tepoztlán, Morelos, Mexico.

2.2 Activated carbon production

The experimental design employed the Box–Behnken approach to elucidate the impact of factors such as precursor:K2CO3 (× 1), activation temperature (× 2), activation time (× 3), and molar ratios on both the adsorption capacity of the binary solution (BS) and the carbon yield. The detailed experimental design is presented in Table 1. Box–Behnken designs are known for their efficiency and cost-effectiveness when compared to many 3 k factorial designs. The design allows for the selection of points from three-level factorial arrangements, and the experimental points can be situated on a hypersphere equidistant from the central points. Additionally, the use of an experimental design minimizes material waste and enables the use of milder conditions. Fifteen experimental runs were generated, with three of them being central points to measure the reproducibility and consistency of the data. The interaction factors and ANOVA analysis, with a model confidence level of 0.05 p-value, were elucidated.

Table 1 Levels of experimental factors in Box–Behnken design
Full size table

Chemical activation was employed in the preparation of activated carbon from macadamia nutshell (MNS). Approximately 20 g of finely ground macadamia nutshell was impregnated with varying amounts of K2CO3 in a weight ratio ranging from 1:1 to 1:3 (K2CO3:precursor) in 200 mL of deionized water. The resulting slurry was heated to 85 °C for 4 h under vigorous stirring. Subsequently, the impregnated MNS with K2CO3 was dried at 105 °C in an oven overnight to eliminate excess moisture. Activation was carried out in an electrical tubular furnace (Linderberg Blue M) under a N2 atmosphere (100 mL/min). Various conditions of temperature (ranging from 700 to 900 °C), with a heating rate of 20 °C/min, and residence time (between 1–2 h) were applied. The resultant carbon was washed with 1 M HCl to neutralize excess alkali salt and open the pores of the carbon. Following this, it was washed with deionized water until a neutral pH was achieved and subsequently dried in an oven at 105 °C for 2 h. The yield of the activated carbon was calculated using Eq. 1.

$$\mathrm{Yield} \,(\%)=\frac{\mathrm{MNS}-\mathrm{AC} (g)}{\mathrm{MNS} (g)}\times 100$$
(1)

where MNS-AC (g), represents the resulting activated carbon of each run, and MNS (g) is the initial weight of the raw biomass.

2.3 Activated carbon characterization

The sample that presented the best behaviour was characterized by scanning electron microscopy (SEM) S-5500 (Hitachi) model series. The morphology was obtained at different magnifications from 15,000× to 50,000×. The elemental analysis was obtained using the energy dispersive X-ray spectroscopy (EDX, Bruker) attached to the SEM. Fourier transform infrared spectroscopy (FTIR, Nicolet iS50) was used to evaluate the functional groups associated with the adsorbent. The data was recorded in the wavenumber range from 4000 to 400 cm−1. The nitrogen physisorption isotherm at 77 K was investigated using NOVA 2200e Quantachrome equipment. The specific surface area was calculated using Brunauer–Emmett–Teller (BET) and density functional theory (QS-DFT) models. The pore distribution was obtained using the QS-DFT method.

2.4 Batch adsorption experiments

The binary solution (BS) utilized to evaluate the adsorption capacity of the activated carbons comprised of an equal concentration of AMX and MB dissolved in deionized water. The experimental design was adapted from Wei et al. (2022). The conditions were tailored according to the adsorption capacity of the best-activated carbon sample, considering that the binary solution contains two pollutants. The total concentration was 400 mg/L, i.e. 200 mg/L of MB and 200 mg/L of AMX. The solution was refrigerated to avoid the degradation of AMX. Then, batch experiments were conducted by adding 100 mL of the 400 mg/L BS and 0.1 g of the MNSAC in Erlenmeyer flasks. The flasks were inserted in a thermostat shaker (Julabo-SW series) and were subjected to agitation at 150 rpm for 12 h at room temperature. Thereafter, the residual concentration was measured in a UV-visible spectrophotometer (Shimadzu UV-1900) at a range placed from 230 to 664 nm based on the calibration curve.

The percentage removal was calculated using Eq. 2.

$$\mathrm{Removal}\, [\%]=\frac{{C}_{0}-{C}_{f}}{{C}_{0}}\times 100$$
(2)

where \({C}_{0}\) and \({C}_{f}\) are the initial and final concentrations of BS in mg/L, respectively.

2.5 Influence of pH and pHpzc value

The pH was evaluated by placing 200 mg/L of each pollutant, i.e. a total of 400 mg/L of BS and 0.1 g of the best activated carbon sample in Erlenmeyer flasks. The solution pH was adjusted using 0.1 M NaOH and 0.1 M HCl and left to equilibrate at 30 °C for 24 h under an agitation speed of 150 rpm. The initial and final pH was determined by a Sper Scientific Benchtop Meter potentiometer. The point of zero charge pHpzc was determined where the initial pH (pHi) intersects the final pH (pHf), i.e. pHi = pHf.

2.6 BS adsorption equilibrium and kinetics studies

Equilibrium adsorption at different initial concentrations of the BS (50 mg/L to 800 mg/L) was conducted to investigate the adsorption kinetics. This was achieved by placing 200 mg/L of different BS concentrations in a flask and then adding 0.2 g of the best MNS-AC sample (this was determined from the adsorption capacity and the activated carbon yield). The solutions were heated at 30 °C for 24 h under constant agitation of 150 rpm. The removal with respect to time was determined by taking measurements at different time intervals. This procedure was repeated for different temperatures of 40 °C and 50 °C.

The amount of BS adsorbed at a time (t) in mg/g (qt) was determined from Eq. 3.

$${q}_{t}=\frac{\left({C}_{0}-{C}_{t}\right)V}{W}$$
(3)

where V (L) is the volume of the BS solution, W (g) is the weight of the activated carbon sample added, and Ct is the concentration at time t in mg/L. Also, using the concentration at the equilibrium (Ce) it is possible to calculate the quantity of BS adsorbed at the equilibrium in mg/g (qe) as shown in Eq. 4.

$${q}_{e}=\frac{\left({C}_{0}-{C}_{e}\right)V}{W}$$
(4)

Kinetics studies were estimated from qe data and time t collected for each concentration of BS and were fitted to pseudo-first-order (PFO), pseudo-second-order (PSO), and Elovich models shown in Eqs. 5 (Lagergren 1907), 6 (Ho and Mckay 1999), and 7 (Elovich and Larinov 1962).

$$\mathrm{PFO}{q}_{t}={q}_{e}(1-{e}^{-{k}_{1}t})$$
(5)
$$\mathrm{PSO}{q}_{t}=\frac{{k}_{2}{q}_{e}^{2}t}{(1+{k}_{2}{q}_{e}t)}$$
(6)
$$\mathrm{Elovich}{q}_{t}=\frac{1}{\beta }\mathrm{ln}(\alpha \beta )+\frac{1}{\beta }\mathrm{ln}t$$
(7)

where, k1 (1/min) and k2 (g/mg·min) are the rate constants for PFO and PSO, respectively, at time t. The α and β are constants of the Elovich kinetics model, the first one refers to the initial adsorption rate, whereas the latter is the desorption constant. The interparticle diffusion by Weber and Morris (1962) was determined from Eq. 8.

$${q}_{t}={k}_{p}{t}^{1/2}$$
(8)

where t is the time in min and k is the constant intrinsic to the interparticle diffusion equation. To correlate the experimental data with PFO and PSO, all the values obtained were validated using the coefficient of determination R2 (Eq. 9), root mean square error RMSE (Eq. 10), and average relative error ARE (Eq. 11).

$${R}^{2}=1-\frac{{\sum }_{i=1}^{n}{({y}_{i}-{\widehat{y}}_{i})}^{2}}{{\sum }_{i=1}^{n}{({y}_{i}-\overline{y })}^{2}}$$
(9)
$$\mathrm{RMSE}=\sqrt{\frac{1}{n-1}{\sum }_{i=1}^{n}{({y}_{i}-{\widehat{y}}_{i})}^{2}}$$
(10)
$$\mathrm{ARE}=\frac{1}{n}\sum_{i=1}^{n}\left|\frac{{y}_{i}-{\widehat{y}}_{i}}{{y}_{i}}\right|$$
(11)

2.7 Adsorption equilibrium isotherms

Experimental data from the kinetics studies were also used to analyse the adsorption isotherm models. To achieve this purpose, Origin software was used to find all the constants needed to fit experimental data to isotherms models. The models evaluated in this paper were Langmuir (1916) (Eq. 12), Freundlich (1906) (Eq. 13), and Khan (Eq. 14).

$${q}_{e}=\frac{{q}_{m}{k}_{L}{C}_{e}}{1+{k}_{L}{C}_{e}}$$
(12)
$${q}_{e}={K}_{F}{C}_{e}^{1/nF}$$
(13)
$${q}_{e}=\frac{{q}_{m}{k}_{K}{C}_{e}}{{(1+{k}_{K}{C}_{e})}^{nK}}$$
(14)

where qm is the maximum adsorption capacity of the adsorbent (mg/g), all K and n parameters refer to the equilibrium constant (L/mg) and dimensionless exponent from each isotherm, respectively. R is the universal gas constant (kJ/mol·K) and T corresponds to the temperature (K).

2.8 Adsorption thermodynamic parameters

Thermodynamic behaviour of the adsorption process and the interaction between BS and the best MNS-AC sample were investigated. The Gibbs free energy (ΔG°), enthalpy (ΔH°), and entropy (ΔS°) are calculated using the following Eqs. (15) and (16).

$$\Delta G^\circ =-RT\mathrm{ln}{K}_{L}$$
(15)
$$\mathrm{ln}{K}_{L}=\frac{\Delta S^\circ }{R}-\frac{\Delta H^\circ }{RT}$$
(16)

where KL is the equilibrium constant from Langmuir isotherm, R is the ideal gas constant (8.314 J/mol·K), and T (K) is the temperature of the adsorption process.

3 Results and discussion

3.1 Effect of factors on the activation process over yield and BS adsorption

Response surface methodology, implemented with the Box–Behnken design, was employed to investigate the impact of activation factors on the yield and adsorption capacity of the BS. The obtained results revealed that the activation time and the K2CO3:precursor molar ratio are not significantly influential in the model prediction, as indicated by the p-values obtained from ANOVA. Consequently, these factors do not significantly affect the adsorption of the BS and the yield of activated carbon, contrary to initial expectations. However, the activation temperature exhibited high significance in the model prediction, with a p-value of 0.004, which is lower than the 0.005 significance level. This signifies that the activation temperature significantly contributes to both the yield of activated carbon and the adsorption of the BS.

Factors interaction was very evident only for the BS adsorption, with the strongest interaction found for temperature–time. The Eqs. (17) and (18) represent the regression equation of the yield and BS adsorption, respectively.

$$\mathrm{Yield}=25.33+0.633x1-3.663x2+0.302x3-0.67{x1}^{2}-1.03{x2}^{2}+0.02{x3}^{2}+1.75x1x2-0.91x1x3+1.15x2x3$$
(17)
$$\mathrm{BSads}=64.84+2.77x1+15.39x2+2.1x3+3.68{x1}^{2}-9.36{x2}^{2}-8.37{x3}^{2}-3.41x1x2+0.36x1x3-3.97x2x3$$
(18)

The range of activated carbon yield found was from 16.47% (Run 8) to 28.08% (Run 3). For BS adsorption, the results varied from 25.89% (Run 1) to 73.72% (Run 2) (Table 2). Based on the removal percentage and low activating agent and activation time, Run 2 (R2-MNS) was selected. Besides, time and K2CO3:precursor do not significantly influence the response variables and the model; therefore, it is not necessary to employ more resources, which will increase materials and operational costs. The central points (Run 13, 14, and 15) of the Box–Behnken 33 experimental design have a standard deviation of 1.081 for yield and 2.215 for BS adsorption. These values show good correlation, indicating consistency and reproducibility of the performance of the experiment.

Table 2 Extended Box–Behnken design matrix for K2CO3 chemical activation and the influence of factors over BS removal and yield
Full size table

3.2 Characterization of R2-MNS

The chemical composition of R2-MNS was determined by EDX analysis. The sample predominantly comprises of carbon (85.55%), followed by oxygen (7.78%), nitrogen (3.20%), silica (2.18%), and potassium (1.29%). It is noteworthy to mention that the impurities of silicon (Si) and potassium (K) likely originated from the intrinsic composition of the macadamia nutshell biomass and possibly from the activating agent. The micrographs of the R2-MNS at different magnifications were obtained from the SEM images. The 1500× micrograph (Fig. 1a) shows the porosity distribution throughout the R2-MNS surface. From Figs. 1b and c, it is possible to notice the non-homogeneous distribution of porosity of the sample of activated carbon. Additionally, the surface of R2-MNS exhibits slit pores and cracks, showcasing various types of pores. The white deposits observed on the surface correspond to inorganic elements, specifically silica and potassium, as indicated in the EDS analysis.

Fig. 1
figure 1

Micrographs from SEM at: a 1500×, b 5000× and c 20,000× magnifications

Full size image

FTIR analysis presented in Fig. 2 showcases the spectra from R2 and R4, both exhibiting superior behaviour in terms of adsorption uptake and yield. Additionally, samples with lower adsorption and yield (R1 and R3) were included for comparative purposes. All four samples display a similar signal at ~ 3430 cm−1, corresponding to the combined hydroxyl functional group and pyrrole (N–H) vibrations, as documented by Wong et al. (2018). Furthermore, the samples exhibit an intense response at ~ 1560 cm−1, identified as the carboxyl functional group (C=O) (Lang et al. 2021). The peaks at 814 cm−1 and 1107 cm−1 are due to C–O bonding, typical carboxylic acids (Wei et al. 2022). However, for R1 and R3 at 1107 cm−1, the peaks vibrate slightly out-of-phase compared to the best samples (R2 and R4). The mentioned delay is caused by the displacement of the central atom of the functional group. In this case, the mentioned out-of-phase vibration could affect the interaction of the surface chemistry and pollutants of BS (Larkin 2011). Additionally, a high amount of these functional groups could influence the adsorption processes because of the hydrogen bonds formed between the water and oxygenated functional groups, which block the access of pollutants to the porosity of activated carbon (Alagarsamy 2011).

Fig. 2
figure 2

FTIR spectra for macadamia nutshell activated carbon samples

Full size image

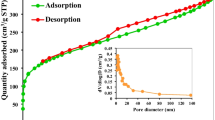
The physisorption isotherm was obtained for the optimal sample, R2-MNS. According to the BET model, it exhibited a surface area of 1225 m2/g, while the QS-DFT (Quenched State Density Functional Theory) surface area was slightly higher at 1239 m2/g. Additionally, R2-MNS displayed a pore volume of 0.801 cm3/g and an average pore size of 0.463 nm. Figure 3a displays the isotherm shape of R2-MNS. Clearly, the isotherm shows a combination of Type II and IV accompanied by adsorption–desorption hysteresis of Type H4 according to IUPAC nomenclature. The characteristics of these isotherms are primarily composed of micropores and mesopores. The pore width presented in Fig. 3b shows two peaks, which correspond mainly to mesopores, with a small contribution of micropores, confirming the isotherm trend.

Fig. 3
figure 3

a R2-MNS adsorption–desorption isotherm, and b pore size distribution following DFT methodology

Full size image

3.3 Effect of PH and determination of pHpzc

It is well established that pH significantly influences the adsorption mechanism by regulating the charges on the adsorbent surface and participating in the degree of ionization of the solution components (Jeirani et al. 2017). On the other hand, the pHpzc is the point when the surface charge on the activated carbon is neutral. In this work, the pHpzc of R2-MNS is 4.5, indicating an acidic behaviour of this sample (Fig. 4a). At a pH higher than pHpzc (pH > 4.5), the surface of R2-MNS is negatively charged and could promote affinity of the surface to attract more cations in the BS, i.e. the MB (Kılıç and Orhan 2019). When the pH is less than 4.5 the opposite phenomenon occurs and more anions would be preferably adsorbed on the carbon surface, in this case, represented by AMX.

Fig. 4
figure 4

Effect of pH in adsorption of BS. a Determination of pHpzc for R2-MNS in BS, and b Percentage of binary solution removed at different pH values

Full size image

Figure 4b illustrates the impact of the pH of the binary solution (BS) on the adsorption capacity, covering a pH range from 2 to 12. The results distinctly indicate that R2-MNS exhibits favourable adsorption capacity across a broad pH spectrum; however, a notable decline in pollutant removal is observed in a highly alkaline environment. The optimum adsorption occurred at a pH of 6, achieving a 77.53% removal of BS (comprising 55.85% removal of AMX and 99.98% removal of MB). Conversely, the least effective behaviour was observed at pH 10 and 12, yielding 63.69% and 63.66% removal of BS, respectively.

Also, Fig. 5 shows the quantity of each component of BS adsorbed at different pH values. Evidently, there are no changes in MB removal percentage in all the tested pH range, which suggests that the forces involved here are mostly π–π interaction (Lyu et al. 2018; Esvandi et al. 2020). Also, this indicates that AMX has a synergistic behaviour towards MB, hence, it is not affected by the presence of AMX (Martínez et al. 2023). On the other hand, it is expected that AMX would have a better adsorption capacity at acidic pH, however, the optimal pH for AMX removal in BS was pH 6. Under acidic conditions, the AMX molecule is found in its negative form (with –COOH already converted to –COO–) and the surface of R2-MNS is positively charged (pH < 4.5), hence, the predominant adsorption mechanism is mainly through electrostatic forces (Homem et al. 2010). When the pH was increased, the surface of R2-MNS becomes negatively charged (pH > 4.5), which causes electrostatic repulsion of mentioned anions, and initiates a competitive adsorption process between the OH− groups from the alkalinity of the solution and –COO– functional groups from AMX (Imanipoor et al. 2021).

Fig. 5
figure 5

Removal of each pollutant from BS at the corresponding pH

Full size image

3.4 Effect of R2-MNS dosage

The concentration of R2-MNS was varied from 0.10 to 0.30 g to investigate the effect of the adsorbent dose. The experiment was conducted using 100 mL of 400 mg/L of BS under 24 h as shown in Fig. 6. Notably, the percentage uptake was measured for each pollutant in parallel and simultaneously at their respective wavelengths. At a dosage of 0.10 g, a noticeable contrast in the uptake percentage between MB and AMX is evident. The removal percentages for MB and AMX are approximately 95% and 46%, respectively. Upon increasing the dosage of R2-MNS, the removal capacity for BS exhibits a linear increase. The adsorption of MB reaches 100% at the initial R2-MNS dose, and this saturation point is sustained even at higher doses. This phenomenon can be attributed to the higher affinity of MB for the activated carbon sample, resulting in its preferential adsorption, influenced by competitive adsorption dynamics. Consequently, AMX becomes available to be adsorbed at the remaining vacant active sites. In this context, the uptake of AMX by R2-MNS increases with an increase in the carbon dosage, indicating that additional active sites are still needed to effectively remove AMX. In other words, the AMX adsorption is proportional to the concentration of R2-MNS. This process primarily occurs in the micropore region, where the greatest number of active sites for adsorption in aqueous solutions can be found. Considering the results and associated costs in producing activated carbon, a working dosage of 0.2 g was selected to carry out the rest of the experiments. This amount was chosen because the adsorbent shows an adequate adsorption capacity without spending lots of activated carbon.

Fig. 6
figure 6

Effect of R2-MNS concentration on adsorption processes at 150 rpm for 12 h and room temperature

Full size image

3.5 Effect of temperature

Temperature is an important parameter that affects principally the rate and range of the adsorption. In this case, the influence of temperature was investigated from 30 to 50 °C and the result is shown in Fig. 7. Parameters such as pH, R2-MNS dosage, and concentration of BS were maintained at the optimal conditions already selected in previous sections (0.2 g of R2-MNS and neutral pH). Usually, an increase in temperature is expected to promote adsorption mechanisms (Bergmann et al. 2015). This is because increasing temperature decreases the viscosity and increases molecular motion allowing the pollutants to adsorb on the activated carbon. Above 40 °C, the equilibrium adsorption was slightly enhanced, approximately 10 mg/g. Further increase in temperature above 50 °C will promote the reversibility of the adsorption equilibrium (Foo and Hameed 2010). From the viewpoint of the input energy and resources employed, a temperature of 40 °C was selected as the best temperature for the rest of the experiments.

Fig. 7
figure 7

Effect of temperature for BS adsorption with R2-MNS probed at 30, 40, and 50 °C, for 24 h and 150 rpm

Full size image

3.6 Effect of contact time and kinetic of adsorption

Sufficient contact time is crucial to ensure that the adsorbent reaches adsorption equilibrium. In this study, experiments were conducted at various concentrations of BS ranging from 50 to 800 mg/L. An equal proportion of AMX and MB in each experiment were consistently maintained. For instance, a 50 mg/L solution of BS was prepared by adding 25 mg/L of MB and 25 mg/L of AMX. Simultaneously, the optimal temperature (40 °C) and pH (neutral), as discussed in previous sections, were employed. Figure 8 shows that BS adsorption increases with time until equilibrium is reached. For all experiments, a notable trend was observed, characterized by robust adsorption initially, followed by a more gradual adsorption thereafter. Notably, at the lowest concentrations of BS (50 mg/L and 100 mg/L), equilibrium was achieved within the first 2 min. This rapid equilibrium can be attributed to the abundant free active sites present on the activated carbon material. As the concentration increased from 200 to 800 mg/L, equilibrium was reached after 400 min. This prolonged equilibrium time corresponds to the saturation point of active sites on the adsorbent, considering the impact of competitive adsorption. The observed adsorption behaviour in these experiments can be interpreted as an initial intense adsorption phase, primarily driven by the availability of free active sites on the surface of R2-MNS.

Fig. 8
figure 8

Effect of contact time in the removal of BS using 0.2 g of R2-MNS at 40 °C, neutral pH

Full size image

Additionally, interparticle diffusion could support the adsorption rate of the samples. Using the initial adsorption factor (Ri) obtained from the Weber-Morris methodology (Weber and Morris 1962), it was found that experiments at concentrations from 50 to 600 mg/L of BS demonstrate strong initial adsorption (Ri value between 0.5 and 0.1), see Fig. 9. Meanwhile, at 800 mg/L the behaviour was described better as intermediately initial adsorption (Ri value between 0.9 and 0.5) (Wu et al. 2009).

Fig. 9
figure 9

Adsorption behaviour of adsorption experiments from Weber-Morris’ methodology

Full size image

On the other hand, it was also found that the maximum adsorption capacity at 40 °C was 578.925 mg/g from an initial concentration of 800 mg/L of BS in approximately 24 h. The experimental kinetic data were fitted with pseudo-first-order kinetic (PFO), pseudo-second-order kinetic (PSO), and Elovich models. The results of the fitting are shown in Fig. 10. Observably, the PSO model best described the variation in the experimental data followed by the Elovich and then PFO. This was validated by the range of coefficients of determination R2 and the error analysis based on root-mean-square error (RMSE) and absolute relative error (ARE) at different initial BS concentrations (Table 3). The PFO has RMSE in the range of 1.511–109.502, ARE range of 0.022–0.225, and R2 in the range of 0.991–0.842. The PSO presented RMSE, ARE, and R2 ranges of 0.937–64.349, 0.015–0.103, and 0.999–0.869, respectively. Whereas, the Elovich model has RMSE of 1.032–14.472, ARE of 0.013–0.029, and R2 of 0.997–0.991. The superior fit obtained from PSO compared to PFO implies that the interaction mechanism between R2-MNS and BS predominantly occurs through chemisorption. Additionally, the successful adaptation of the Elovich model to the kinetic data, characterized by minimal error and a high R2 value, signifies heterogeneous adsorption on the surface of R2-MNS (Terdputtakun et al. 2017; Sahoo and Prelot 2020; Wang and Guo 2020; Revellame et al. 2020). It is worth noting that PSO performs well for low-concentration solutions, and this could be a primary reason for its less than perfect adaptation to the higher concentrations employed in this experimental study (Wang and Guo 2020).

Fig. 10
figure 10

PFO, PSO, and Elovich kinetics modelling fitted to experimental data from different initial concentrations at 40 °C and neutral pH

Full size image
Table 3 Parameters and errors obtained from the adsorption kinetics models from real data
Full size table

3.7 Isotherm modelling

Adsorption isotherm models could be used to describe the interaction mechanism occurring between the R2-MNS and BS. Also, the parameters obtained from these models provide information on the values of maximum adsorption capacity, energy, surface properties, etc. (Bonilla-Petriciolet et al. 2017). In this study, eight isotherm models were evaluated, and the result was correlated and validated by R2.

The best fitting was Khan isotherm (followed by Freundlich, and Langmuir models) according to the R2 value in all temperatures, which is close to unity (Table 4). Besides, the Khan isotherm model is a combined Langmuir and Temkin isotherm that has been specifically used for pure substances adsorption (bi-adsorbate adsorption), which is the phenomenon described in the present work (Mozaffari Majd et al. 2022). In the same sense, the Freundlich isotherm reveals valuable insights into the characteristics of the adsorbent surface. In this instance, a value of 1/nF < 1 was obtained, as all the values for nF (the strength constant) exceeded unity. This underscores the adsorbent's effectiveness when in contact with low-concentration solutions (Nguyen et al. 2022). Similarly, the Langmuir model is well-suited to elucidate the behaviour of the adsorption phenomena in these experiments. Conversely, the Langmuir isotherm characterizes homogeneous monolayer adsorption, assuming the absence of lateral interactions between the adsorbate and adsorbent (Kalam et al. 2021).

Table 4 Data obtained from evaluated isotherm models at different temperatures
Full size table

Additionally, separation factor (RL) from this isotherm was evaluated at different temperatures and initial BS concentrations to study the nature of the adsorption process and to describe the affinity of BS molecules to the R2-MNS surface (Fig. 11). RL values obtained were between 0 and 1, these values exponentially decrease as the initial concentration increases, indicating favourable adsorption (Al-Ghouti and Da’ana 2020). In addition, the adsorption intensity values (1/nF) obtained in this work were less than zero in all temperatures, which indicates that the adsorption processes are favourable (Kalam et al. 2021).

Fig. 11
figure 11

Separation factor evaluated at different temperatures

Full size image

3.8 Adsorption thermodynamics

The thermodynamics parameters in Table 5 could give an idea of the spontaneous or nonspontaneous nature of adsorption, and the viability of the adsorption process (Ray et al. 2020). The Gibb’s free energy (Δ°G) enthalpy (Δ°H) and entropy (Δ°S) were obtained.

Table 5 Thermodynamics parameters of the adsorption process
Full size table

The negative value of enthalpy (− 30.404 kJ/mol) suggests exothermic adsorption, whereas the negative value of entropy (− 104.38 J/mol) indicates less disorder in the process. For Gibb’s energy (Δ°G), positives values of 1.038 kJ/mol, 2.661 kJ/mol, and 3.101 kJ/mol, were obtained at temperatures of 303 K, 313 K and 323 K, respectively, indicating a nonspontaneous reaction (Ebelegi et al. 2020). Additionally, the activation energy value calculated through the Arrhenius equation was 51.68 kJ/mol, which means that the process involved in this work was essentially chemisorption (Inglezakis and Zorpas 2012).

Table 6 provides knowledge about previous recent works where macadamia nutshell was used as a precursor. Data presented in the table contains information regarding the maximum removal capacity reached through using their methods for primarily one pollutant, which in all cases are lesser than the results shown in the presented work.

Table 6 Adsorption capacity comparisons with adsorbents made from macadamia nutshell
Full size table

4 Conclusions

In conclusion, microporous activated carbon was developed from macadamia nutshell using potassium carbonate as an eco-friendly activation agent. The Box–Behnken toolbox allowed for the generation of experimental design (15 experimental runs) to evaluate the influence of factors such as K2CO3:precursor ratio, activation temperature, and activation time on the response surface for binary adsorption of cationic methylene blue dye and ionic amoxicillin antibiotics. Under optimal conditions of 900 °C, 1 h, and K2CO3:precursor ratio of 2:1, the R2-MNS revealed a specific surface area of 1225 m2/g, pore volume of 0.801 cm3/g, and an average pore width of 0.406 nm. The R2-MNS activated carbon realized a maximum adsorption capacity of 578.9 mg/g under the best conditions of 40 °C and neutral pH. The pseudo-second-order adsorption kinetic model adequately described the experimental data with RMSE, ARE, and R2 in the range of 0.937–64.349, 0.015–0.103, and 0.999–0.869, which indicates a chemisorption mechanism. Evaluated isotherm models revealed that Khan isotherm used for pure substances best described the variation in the data. Thermodynamic studies show exothermic adsorption. Overall, value-added activated carbon can be derived from macadamia nutshell for multipollutant removal in a single stage adsorption. Studies on waste integration for activated carbon production and atomistic evaluation of possible interactions of the pollutants in the solution is recommended to enhance the understanding of this process.