1 Introduction

Increasing energy efficiency in every sector is an important pillar of the European energy policy to combat climate change and increase the security of supply. Industry accounts for a quarter of the EU’s final energy demand. More than 70% of this is used for the provision of heating and cooling, of which more than 80% is used to produce process heat (EC 2016), whereby industrial excess heat is generated. From a technical point of view, industrial excess heat can be described as unwanted heat generated by an industrial process (Pehnt 2010). From a societal perspective, it can be described as heat that is a by-product of industrial processes and is currently not used, but which could be used in the future by society and industry to increase energy efficiency (Broberg Viklund and Johansson 2014). In this context, our paper deals with the quantification of the excess heat potentials for Baden-Württemberg, Germany. For this purpose, we evaluated the emission declarations of production sites and applied a bottom-up method to estimate the excess heat potentials. Unlike previous theoretical potential estimates, however, we also included the corrosiveness of exhaust gases in our estimation. We are therefore able to show the relevance of considering corrosion when estimating excess heat potentials. In our analysis, we do this by considering whether sulphuric acid is present in the exhaust gases, because this is the main cause of corrosion in exhaust gases besides water.

The paper is structured as follows. The remainder of Sect. 1 presents the literature review, the problem with excess heat and corrosion, the identified research gap and our contribution. Section 2 describes the data from the emission declarations and our method. Section 3 contains the results. A discussion of our findings is provided in Sect. 4, and the paper finishes with a summary and conclusions in Sect. 5.

1.1 Literature review

The topic of industrial excess heat utilisation has a long history. Bergmeier (2003) summarised the history of waste energy recovery in Germany starting in 1920. As early as the 1920s, numerous journals were already addressing the topic of ‘heat management’ and discussing measures to increase energy efficiency by harnessing industrial excess heat. Additional particularly relevant impulses followed in the 1970s and 1980s. The oil crises of 1973 and 1979 forced energy-intensive companies in the chemical and petrochemical industry to look for ways to reduce their energy consumption (Klemeš and Kravanja 2013). This led to significant progress in the field of heat integration, a term used for concepts that combine processes for the purpose of heat recovery, which can be understood as a formalised method for realising excess heat potentials (Klemeš and Kravanja 2013). One milestone was the development of the pinch analysis by Linnhoff and Flower (1978). This method included a structured approach to the design of heat exchanger networks and to the recording and realisation of excess heat potentials in production plants. Subsequently, numerous articles appeared in technical journals, which quantified the potentials due to heat integration for individual case studies (cf. Aydemir 2018).

At the end of the 1990s and the beginning of the new millennium, more and more articles followed that explored excess heat potentials not only for individual case studies but also for larger geographical regions. Bonilla et al. (1997) quantified the industrial excess heat potential for the Basque Province in Spain. This was followed by two studies by Pellegrino et al. (2004) and Viswanathan et al. (2006), which were taken up by Johnson et al. (2008) and resulted in an estimate of the industrial excess heat potential for the USA. McKenna and Norman (2010) estimated the industrial excess heat potential for the UK, and Pehnt et al. (2011) for Germany. Rattner and Garimella (2011) again estimated the potential for the USA, followed by Persson et al. (2014) for the EU-27. Finally, Miró et al. (2015) extracted the results of previous studies and compiled estimates of the industrial excess heat for the European Union including Norway and Turkey, Japan and Korea, and the USA and Canada. This was followed in 2016 by Forman et al.’s (2016) estimate of the global excess heat potential. In 2017, Brueckner et al. (2017) then presented an additional estimate of the potential for Germany, followed by two further estimates for Europe in 2018 and 2019 (cf. Papapetrou et al. 2018; Bianchi et al. 2019).

The studies mentioned above are based on different methodological approaches. Brueckner et al. (2014) propose three categories for the classification of excess heat studies: the scope of the study, the method of data collection (survey or estimate) and the approach for generating results (top-down or bottom-up). Estimates based on surveys are always bottom-up. Company data, e.g. mandatory reports, are usually assigned to surveys, and studies based on these are thus classified in the bottom-up category.

Many of the estimates mentioned above are based on CO2 emission data from production sites and are therefore assigned to the bottom-up category. The first work in this area was initiated by McKenna and Norman (2010), whose study forms the data basis for Hammond and Norman (2014). Both studies use data from the EU Emissions Trading Scheme (ETS), which includes reported CO2 emissions from production sites operating installations covered by the ETS. These emissions can in turn be attributed to specific industrial sectors and the corresponding production processes. To estimate industrial excess heat, McKenna and Norman (2010) first calculate an emission factor per industrial sector (tonnes of CO2 per energy input) based on the statistical energy carrier mix of the sectors. This is then used to estimate fuel consumption for the production sites in the ETS. On this basis, the excess heat of the sites is then determined taking the underlying production processes into account. Persson et al. (2014) also follow this approach, with the difference that the underlying CO2 emissions per site are taken from the European Pollutant Emission Register. Manz et al. (2018) also use the European Pollutant Emission Register to estimate industrial excess heat. In contrast to McKenna and Norman (2010), however, they do not estimate the fuel consumption per site directly on the basis of CO2 emissions, but on the basis of estimated production quantities. For this purpose, they first construct a national specific CO2 emission factor for the manufacture of certain products. In principle, the national production quantity for a specific product (e.g. tonnes of glass) is related to the CO2 emissions of the corresponding industrial sector. This factor is then used to estimate the production quantities of the production sites, which in turn are used to estimate the fuel consumption of the sites. Finally, similar to McKenna and Norman (2010), excess heat is estimated considering the technological characteristics of the underlying production processes.

A further approach in the bottom-up category was presented by Brueckner et al. (2017) for Germany. Here, exhaust gas data from production sites are used to estimate industrial excess heat. In contrast to the approaches presented above, the data used here enable a direct estimation of industrial excess heat from exhaust gases. Brueckner et al. (2017) use emission reports for this purpose, which are mandatory for certain plants in Germany and in which the temperature, volume flow rate and operating time of the exhaust gas flows must be specified. The evaluated production sites account for about 58% of the industrial fuel consumption in Germany. Brueckner et al. calculate a theoretical excess heat potential of 35 TWh, which corresponds to about 13% of the fuel consumption. It should be emphasised that this estimate focuses exclusively on the excess heat in exhaust gases. This also applies to the other approaches from the bottom-up category described above. Estimates of excess heat from other sources, e.g. diffuse excess heat, excess heat in by-products such as slag, waste water, etc., have not yet been carried out for larger geographical regions or are not known. Here, estimates are more likely to be found in industry-specific sector reports, which would have to be extended to the spatial level.

1.2 Excess heat and corrosion

In industry, heat is mainly provided by the combustion of fuels (cf. Rehfeldt et al. 2018). However, only some of this heat is used for the required process heat. The rest of the heat generated is contained as excess heat in the output materials or in the exhaust gas. This results in exhaust gases or output materials, whose temperatures are significantly higher than the ambient temperature in many cases. In our analyses, we focus on the excess heat potential of exhaust gases and use real data from the emission declarations of production sites. In order to tap the energetic potential of the exhaust gases, heat exchangers are necessary, which are usually made of metal. These heat exchangers are susceptible to corrosive components of the exhaust gases. In practice, corrosion aspects are therefore taken into account when estimating the usable excess heat potential (cf. Johnson et al. 2008; Saechsische Energieagentur GmbH 2012).

Corrosion is the chemical reaction of a metallic substance with its environment that leads to a change in its properties and can impair the function of a metallic component or the associated system. Corrosion is an electrochemical reaction when metals come into contact with ion-conducting media, in most cases, water (cf. Weißbach et al. 2015). Corrosion is thus caused by the presence of a substance that triggers corrosion. The reaction partners are called agents, oxidised and reduced agents, which form the so-called RedOx system to produce the corrosion. It is the interaction of the individual substances and not the properties with each other that determine whether and to what extent corrosion occurs (cf. Hirzel 2017). When excess heat from exhaust gases is used, the corrosion system thus consists of the exhaust gas and the corrosion-promoting substances it contains, as well as the material of the heat exchanger, usually metal. The corrosion-triggering substances contained in the exhaust gases due to the combustion of fuels include water, sulphuric and sulphurous acid, hydrogen chloride, hydrogen fluoride, etc. (cf. Herzog et al. 2012). If the temperature of the exhaust gas falls below the temperature of the dew point of these substances, the substances condense and corrosion occurs. In practice, the dew points of two substances are particularly relevant: water and sulphuric acid.

For sulphur-free fuels, water and thus the water dew point is corrosion relevant. The corresponding dew point varies between 45 and 60 °C depending on the fuel and air-to-fuel ratio. However, condensing water vapour is not as critical for excess heat utilisation as acidic condensates. Condensing boilers, for example, which use the condensation heat of steam are widely established. Therefore, this paper focuses on the possible limitations resulting from acidic condensates, in our case, sulphuric acid.

Sulphuric acid has dew points that are higher than those of other acids and water. In the case of exhaust gases from the combustion of fuels containing sulphur, corrosion problems in practice are attributed to sulphuric acid (cf. Herzog et al. 2012). The dew point of sulphuric acid is therefore a relevant parameter when estimating the usable energetic potentials when cooling the exhaust gases is involved (cf. Effenberger 2000). If the temperature of an exhaust gas stream containing sulphuric acid falls below the dew point temperature of the sulphuric acid, the acid condenses and corrosion occurs. In principle, it is possible to use the condensation enthalpy from such condensation and the energy of the exhaust gas below the dew point. However, this requires using materials for the heat exchangers that are considerably more expensive and, in addition, must consider the boundary conditions of subsequent processes which may restrict such a design (cf. Bornemann 2017). This can lead to a situation where using the excess heat from exhaust gases becomes either less economical or uneconomical (cf. Johnson et al. 2008). In addition, in individual cases, state environmental authorities may require minimum exhaust gas temperatures for exhaust gases containing sulphuric acid in order to reduce the risk of pollution in adjacent areas (cf. personal communication). It can therefore be assumed that, in practice, the dew point of sulphuric acid represents a threshold, which differentiates easy from difficult to use excess heat potentials from exhaust gases. This is indicated by manuals in the field of industrial excess heat utilisation (cf. Johnson et al. (2008); Saechsische Energieagentur GmbH 2012), technical books (cf. Effenberger 2000) and project reports (cf. Deutsche Bundesstiftung Umwelt 2002). The sulphuric acid dew point depends on the humidity of the exhaust gas, the concentration of sulphuric acid in the exhaust gas, and the pressure. The corresponding dew point in a technical system is usually between 120 and 150 °C (cf. Effenberger 2000).

1.3 Motivation and research gap

The excess heat potential from exhaust gases estimated by Brueckner et al. (2017) is a theoretical one since it does not include any aspects of technical usability. Methodologically, the excess heat of the exhaust gas flows is calculated based on temperature differences to the environment and assumptions about the specific heat capacity (cf. Eq. 1).

$$E = m \cdot c_{\text{p}} \cdot \Delta T$$
(1)

where E (kJ) is the energy quantity of the excess heat source, \(c_{\text{p}}\) (kJ/kg K) is the specific heat capacity of the gas under consideration and \(\Delta T\) (K) is the temperature difference to the environment.

Central to this are the assumptions that the specific heat capacity of nitrogen is assumed uniformly for the exhaust gas flows and that 35 °C is always assumed as the lower reference temperature for \(\Delta T\). The choice of the lower reference temperature of 35 °C is one of the reasons why the estimation in Brueckner et al. (2017) is consistently referred to as a theoretical potential.

When estimating excess heat potentials, three dimensions are usually used in the literature, which are explained and critically reflected below:

  • The theoretical excess heat potential. This is the sum of the available potential in the observation area. In relation to excess heat, this can be understood as the maximum amount of energy contained in the excess heat.

  • The technical excess heat potential. This is the proportion of the theoretical potential that can be used taking into account technical and environmental restrictions. In the context of excess heat utilisation, for example, the losses due to heat transfer and heat transport play a role.

  • The economic excess heat potential. This is the part of the technical potential that can be used economically.

Concrete criteria are necessary to determine the boundaries. In technical discussions with experts from the manufacturing industry, the pollution of exhaust gases with sulphuric acid was repeatedly mentioned as a central criterion that limits the theoretical potential (cf. Aydemir et al. 2019). This motivated our analysis, which is described below.

Our analysis distinguishes the excess heat potentials of exhaust gases by the dew point of sulphuric acid. We perform a bottom-up analysis to determine the excess heat of exhaust gases. As in Brueckner et al. (2017), we use emission declarations in accordance with the Federal Immission Control Ordinance (BImSchV). Methodologically, we evaluate the energy content similar to Brueckner et al. (2017), but show the effect of taking corrosive components into account by considering the sulphur content of the exhaust gases. This shows how much the theoretical potential is reduced if the energy content of the sulphur-containing exhaust gases is only used up to the dew point of sulphuric acid. On the one hand, this shows how much of the theoretical potential can be used in heat exchangers with comparatively little effort, since no corrosive components are present. On the other hand, it also shows when more advanced technical solutions are necessary, since corrosive media are treated. This aspect has not yet been taken into account in the existing bottom-up analyses that estimate the excess heat potential on the basis of emission reports and represents the identified research gap. Our contribution is therefore a novel method, which also takes the corrosive component of sulphuric acid into account when estimating the available excess heat based on emission reports.

2 Data and methodology

2.1 Data

All plant operators subject to licensing pursuant to the fourth German Federal Immission Control Ordinance (4. BImSchV) must submit an emission declaration every 4 years (cf. 11. BImSchV). In this study, we use data from emission declarations for Baden-Württemberg, Germany, for the year 2012. The data were provided by the Baden-Württemberg State Institute for the Environment, Survey and Nature Conservation (LUBW). The data contained in the emissions declarations are structured according to the identification number of the production site in which a so-called plant requiring a permit is operated. A ‘plant requiring a permit’ could be, for example, a furnace within this production site. As the data are reported by the enterprises themselves, it can be assumed that the data, at least to a large extent, reflect real on-site conditions.

Figure 1 shows the data structure of the data set used. One production site contains one or more plants. In the figure, ‘Fuel’ represents a fuel entering a plant, and therefore the production site, which is characterised by a certain fuel consumption (in ton) in the reporting year. The plant, and therefore the production site, emits exhaust gases into the atmosphere via certain points at the system boundary (e.g. chimneys). These points are designated as sources in the figure. Since the production sites can be subject to different operating modes (full load, partial load, etc.), different data are also reported for different operating periods, which are then reflected in different so-called emission-causing processes (ECPs) for each source. The ECPs are uniquely numerically coded.

Fig. 1
figure 1

Data structure of data set used

Full size image

The data used contain 6771 ECPs for 455 production sites from the manufacturing sector. The data contain different variables, of which the variables in Table 1 are relevant for this paper. In principle, these data can be divided into four groups: exhaust gas, fuels, pollutants and the industry sector.

Table 1 Groups in used data set
Full size table

In principle, the data are used in our analysis per production site as follows. The energy content of the exhaust gas streams is estimated from data for the exhaust gas group. Fuel consumption is estimated from the data for the fuels group. The data for the pollutants group are used to analyse whether sulphuric acid is present in the exhaust gas.

The data had to be adjusted for the analysis, since not all ECPs were complete. Some of the data records are generated automatically by software to close data gaps in the reporting. These data sets are generated based on the energy consumption of a production site and do not contain any information on temperature, volume flow or operating time. In the first step of data preparation, these automatically generated data were excluded from the data set for further analysis. This reduced the data set by 3565 ECPs and 1 production site. In the second step, all data records were removed that had missing items concerning temperature, volume flow or operating time. Figure 2 shows the missing records and the remaining data set.

Fig. 2
figure 2

Missing records of the data set

Full size image

The lower left of the diagram shows the missing data for each variable. Most of the missing data concern the temperature. A total of 333 entries were missing here. In the middle of the diagram, the missing variables are shown in combination, or the missing variables for one case only. For example, the temperature variable was missing in a total of 333 cases, but this variable on its own was only missing in 28 cases. This means that the temperature was missing in these 28 cases, but the other variables were present. The volume flow of the exhaust gas was also often missing, in 310 entries in total and in 287 entries in combination with the temperature. The operating time was only missing in a total of 21 entries. By excluding the incomplete data, the data set was further reduced by an additional 341 ECPs and 15 production sites to 2865 ECPs and 439 production sites.

In the third step, we removed all data sets in which the temperature of the exhaust gas was lower than 36 °C, since the temperature of the exhaust gas can be reduced to 35 °C in our analyses in order to estimate the amount of excess heat. In total, 1244 ECPs remained for 363 production sites for our analysis.

2.2 Methodology

The values are presented as follows: For an ‘emission-causing process’ (ECP) with number i belonging to the excess heat source with number j, which in turn belongs to the production site with number a, \(V_{a,j,i}\) denotes the volume flow, \(B_{a,j,i}\) the operating time and \(T_{a,j,i}\) the temperature. The data were evaluated in three steps to determine the excess heat from the exhaust gases of the production sites concerned.

In the first step, all the ECPs were energetically evaluated using Eq. 2. We assumed that the density and specific heat capacity of the exhaust gas flows could be approximated to the density and specific heat capacity of nitrogen. In addition, we assumed that the specific heat capacity is independent of the temperature.

$$E_{a,j,i} = V_{a,j,i} \cdot B_{a,j,i} \cdot 1.3 \left( {\frac{\text{kg}}{{{\text{m}}^{3} }}} \right) \cdot 1.007 \left( {\frac{\text{kJ}}{{{\text{kg}} \cdot {\text{K}}}}} \right) \cdot \left( {T_{a,j,i} - T_{u} } \right)$$
(2)

where \(E_{a,j,i}\) (kJ) is the energy quantity, \(V_{a,j,i}\) (m3/h) is the volume flow, \(T_{a,j,i}\) (K) is the temperature and \(B_{a,j,i}\) (h) is the operating time of the exhaust gas under consideration for the emission-causing process with number i, belonging to the excess heat source with number j, which in turn belongs to the production site with number a. \(T_{\text{U}}\) denotes the temperature down to which the exhaust gas is cooled for heat recovery.

The amount of energy from exhaust gases for the excess heat source under consideration is then determined using Eq. 3.

$$Q_{a,j} = \mathop \sum \limits_{i} E_{a,j,i}$$
(3)

where \(Q_{a,j}\) (kJ) is the energy quantity for the excess heat source with number j, which belongs to the production site numbered a. \(E_{a,j,i}\) (kJ) is the energy quantity of the associated emission-causing processes as in Eq. 2.

The excess heat from the exhaust gases for the entire production site is calculated according to Eq. 4.

$$Q_{a} = \mathop \sum \limits_{j} Q_{a,j}$$
(4)

where \(Q_{a}\) (kJ) is the energy quantity for excess heat for the entire production site numbered a. \(Q_{a,j}\) (kJ) are the associated emission-causing processes as in Eq. 3.

The first step is visualised in Fig. 3.

Fig. 3
figure 3

Visualisation of step 1 of the methodology

Full size image

In the second step, the energy content of the fuels used at the production sites was calculated according to Eq. 5.

$${\text{EN}}_{a,e} = M_{a,e} \cdot H_{e }$$
(5)

where \({\text{EN}}_{a,e}\) (kJ) is the energy content of fuel with number e used at production site a. \(M_{a,e}\) is the annual quantity (ton) used at production site a and \(H_{e }\) (kJ/ton) is the net calorific value of fuel numbered e.

The total energy consumption resulting from the use of the fuels for production site a is then determined by summation according to Eq. 6:

$${\text{AE}}_{a} = \mathop \sum \limits_{e} {\text{EN}}_{a,e}$$
(6)

where \({\text{AE}}_{a}\) is the energy content of all fuels used at production site a. \({\text{EN}}_{a,e}\) is the energy content of the associated fuels at production site a as in Eq. 5.

In the third step, an excess heat quota was formed for each production site, which relates the total excess heat from exhaust gases determined for each production site to the total energy consumption:

$${\text{EQ}}_{a} = \frac{{Q_{a} }}{{{\text{AE}}_{a} }}$$
(7)

where \({\text{EQ}}_{a}\) is the excess heat quota for production site numbered a. \(Q_{a}\) is the energy quantity for excess heat for the entire production site numbered a.\({\text{AE}}_{a}\) is the energy content of all fuels used at production site a.

The exhaust gas quota serves as a plausibility check of the values. In this step, all production sites with a quota above a threshold value were sorted out. This was done because we assumed that the reported data may be incorrect or incomplete if the excess heat quota is particularly high. We selected a threshold value of 60% for our analysis, as particularly old furnaces can achieve such high excess heat quotas (cf. Johnson et al. 2008).

With regard to the procedure described so far, it should be mentioned that the data refer exclusively to (guided) exhaust gas flows that are discharged to the environment at the system boundary. Therefore, we only determine the potential for industrial excess heat from exhaust gas flows. Excess heat flows from other sources (diffuse excess heat, waste water, etc.) and the energy loss that the excess heat gas flows experience within the system boundary are not determined. The above-described procedure was used for the following two cases.

Theoretical potential (TP) 35 °C is assumed for \(T_{\text{u}}\) for the TP case in Eq. 2. \(T_{\text{u}}\) represents the assumed ambient temperature on particularly hot days in summer, with the aim of ensuring that the heat source can be used all year round. The theoretical maximum usable energy potential is therefore determined against this background.

Low hanging potential (LP) For the LP case in Eq. 2, 135 °C is assumed for \(T_{\text{u}}\) for all \(E_{a,j,i}\) which contain sulphuric acid in the exhaust gas, i.e. corrosive components. Only the comparatively easily accessible part is calculated for these exhaust gas flows, and this potential is referred to as the ‘low hanging potential’. 135 °C was chosen for the reference case as this is in the middle of the range for the sulphuric acid dew point (120–150 °C).

For \(E_{a,j,i}\), where only water is the corrosive substance, \(T_{\text{u}}\) was still assumed to be 35 °C. The reason for this is that the use of excess heat from the condensation of water vapour is the state of the art (e.g. in condensing boilers). We did not take into account the latent heat of the condensation of water in our analyses, as the data used do not contain any information on the water content of the exhaust gases.

The potential for the LP case was also calculated for two additional sulphuric acid dew point temperatures, 120 °C and 150 °C, to show the sensitivity of the analysis.

3 Results

The first section of the results shows the excess heat potential considering the corrosion aspect. The second section analyses the three biggest industrial sectors of the data set, because these account for about 73% of the determined excess heat. The third section performs a sensitivity analysis with a variable dew point of sulphur. We also show the determined excess heat of the exhaust gases as a function of the exhaust quotas.

3.1 Excess heat potential considering corrosion

After applying the method described above, 292 production sites remain with 876 excess heat sources for which the excess heat from exhaust gases was determined. A fuel demand of about 18.9 TWh was calculated for these 292 production sites. This corresponds to about 56% of the industrial fuel demand in Baden-Württemberg. It should be noted that the economic activity ‘production of coke and petroleum products’ (NACE 19) is not included as this sector is normally included in the German energy balance under the energy transformation sector.

Figure 4 shows the excess heat determined from the exhaust gases for the 292 production sites for the TP and LP cases. In the TP case, the calculated excess heat potential is 2.2 TWh. This is equivalent to 11.8% of the calculated fuel demand. This calculated value is in line with the results of Brueckner et al. (2017) and Bloemer et al. (2019). Based on a fuel demand of 19.4 TWh, Brueckner et al. (2017) estimated a theoretical potential of about 2.5 TWh for excess heat from exhaust gases for Baden-Württemberg. This corresponds to about 12.8% of the fuel demand. Bloemer et al. (2019) calculated a potential of 1.9 TWh for Baden-Württemberg, but do not indicate the associated fuel demand. Overall, therefore, all three analyses (including this one) calculate a potential for excess heat from exhaust gases that is comparable in terms of magnitude. In the LP case, the calculated excess heat potential is 1.3 TWh. This is equivalent to 7.0% of the calculated fuel demand. The excess heat potential for the LP case is thus approx. 40% lower than for the TP case in our analysis.

Fig. 4
figure 4

Estimated excess heat for analysed cases

Full size image

Figure 5 shows the determined excess heat from exhaust gases as a function of the temperature for both cases investigated. About 85% of the excess heat from exhaust gases is attributable to exhaust gas flows with a temperature up to 250 °C in the TP case (red line) and 77% in the LP case (pink line). In addition, about 30% of the excess heat occurs at temperatures below 100 °C in the TP case. In the LP case, this is 38%. These results show that excess heat recovery is particularly relevant for low-temperature applications. Additionally, the figure reveals the difference between the LP and TP cases (black line). It can be seen that the difference is most apparent in the temperature range between 100 and 200 °C. This is due to the fact that these temperature ranges mainly feature excess heat from companies using sulphur-containing fuels. The delta remains almost constant in the high-temperature ranges, because natural gas, which does not contain sulphur, is mainly used for to supply process heat here (at least in our records). It should be pointed out that these results depend on the industries involved. Baden-Württemberg is a federal state that is not as strongly influenced by heavy industry as other federal states in Germany. In other federal states, e.g. North Rhine-Westphalia, where many blast furnaces are operated for steel production, the results could be considerably different with regard to the curve.

Fig. 5
figure 5

Cumulated excess heat as a function of temperature

Full size image

3.2 Analysis of the biggest industry sectors in the data set

Within our analysis, three industry sectors account for a large proportion of the excess heat from exhaust gases. In the TP case, three industry sectors account for about 73% of the determined excess heat: manufacture of non-metallic mineral products, manufacture of pulp and paper products and manufacture of basic metals. In the LP case, this is approx. 70%. However, these three sectors only account for 68% of fuel consumption. Moreover, only 44% of production sites are in these three sectors. Therefore, production sites from these three sectors must be larger sites with high energy consumption, which tend to have more excess heat than the others in the data set.

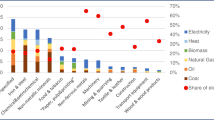
Figure 6 shows the calculated excess heat from exhaust gases for the six industry sectors with the highest excess heat for the TP and LP cases. Together, they cover about 90% of the estimated excess heat. It also shows the relative difference between TP and LP for these sectors, which is the difference between the excess heat for cases TP and LP in relation to the excess heat of case TP in per cent. Of the three largest sectors of the economy with the highest quantities of excess heat from exhaust gases, the manufacture of non-metallic mineral products sector has the highest relative difference with 68%, followed by the manufacture of pulp and paper products sector with 35% and the manufacture of basic metals sector with 6%. The relative difference for the next two sectors (manufacture of chemical products and textiles) is again relatively high at 34% and 41%, respectively. For the manufacture of transport equipment, etc. (NACE 29), the relative difference is only about 10%. In our analysis, excess heat was also estimated for 12 other sectors whose relative differences are not shown in the figure, as these sectors have a comparatively small share in the total estimated excess heat and their relative differences therefore do not strongly influence the results in absolute terms.

Fig. 6
figure 6

Excess heat per case and industry sector

Full size image

The results in Fig. 6 show that the relative differences between TP and LP vary widely by sector. These large differences result from the varying sulphur content of the fuel inputs in the different sectors. We therefore analysed the fuel input for the three largest sectors. Figure 7 shows the fuel input for the three industry sectors with the highest excess heat. Fuels with high sulphur contents are highlighted. This shows that industries that have a large difference in the calculated excess heat potential between TP and LP also used relatively more sulphurous fuels. For example, the difference between the potentials is 68% in the sector manufacture of non-metallic mineral products, and almost 70% of the fuel demand in this sector is for sulphur-containing fuels. In the steel sector, there is only a 6% reduction in the excess heat between TP and LP, which also corresponds to the fuel composition. About 80% of the fuel demand in this sector is covered by natural gas, which is low sulphur or sulphur-free. Regional aspects are particularly relevant here. In Baden-Württemberg, there is no blast furnace route for steel production, only electric arc furnaces and numerous foundries.

Fig. 7
figure 7

Fuel composition of the three industry sectors with the most excess heat

Full size image

3.3 Sensitivity analysis and exhaust gas quotas

To validate the robustness of the results, we additionally calculated the low hanging potential for the acid dew point temperatures of 120 °C and 150 °C. A potential of 1.4 TWh was determined for the LP case with a dew point temperature of 120 °C and about 1.3 TWh for the 150 °C dew point temperature. The potential for the 135 °C analysis was also approximately 1.3 TWh. This shows that the determined excess heat is comparable for the whole range of considered dew point temperatures.

Finally, Fig. 8 shows the determined excess heat plotted against the excess heat quotas of the production sites for the TP case. This shows the excess heat in absolute terms and relative to the determined total excess heat. It can be seen that 50% of the excess heat is generated by production sites with excess heat quotas of up to 17%. Another 25% of excess heat is generated by production sites with excess heat quotas of up to 34%. The remaining 25% of excess heat is generated by production sites with excess heat quotas of up to 59%.

Fig. 8
figure 8

Cumulated excess heat as a function of the excess heat quota for the production sites

Full size image

4 Discussion

Our analysis is based on emission declarations for 455 production sites in Baden-Württemberg, Germany that contain information about exhaust gases, fuels, pollutants and industry sector among other things. We adjusted the data set, since not all data entries were complete, so that 361 production sites were considered for the energy evaluation. An additional 69 production sites were excluded when applying the method, where data errors in the emission declarations were suspected. In the end, the excess heat potential was estimated for 292 production sites. Therefore, our estimate covers only some of the excess heat available from exhaust gases in Baden-Württemberg. If complete and corrected emission declarations were available for the production sites not considered here, the absolute potential would be higher.

In order to exclude potentially erroneous data, we selected a threshold value of 60% for the excess heat quota, since old furnaces in particular can achieve such high excess heat quotas (cf. Johnson et al. 2008). This step led to the above-mentioned exclusion of 69 production sites. However, we cannot rule out the possibility of correct data being excluded. The reason is that the data only include the fuel consumption of the production sites and not the electricity consumed to supply process heat. For production sites that use a particularly large amount of electricity, such as an electric steel plant, such high excess heat quotas may be plausible. However, this step only reduces the size of the data set. Furthermore, it was assumed that the case described above does not occur at a particularly large number of production sites, as fuels are currently still predominantly used to provide process heat. We therefore do not expect the results to change considerably if this could be taken into account. We treat the data as correct for production sites at which the excess heat quota does not exceed the threshold value after evaluation of the data. This seems justified since companies must report these data to the environmental authorities. Therefore, even though these data could in principle contain errors, we assumed that data quality is high.

We then calculated how much the theoretical potential would be reduced if the energy content of sulphur-containing exhaust gases were only used up to the sulphuric acid dew point to avoid corrosion. This calculation involved further assumptions that are discussed below.

It was assumed that the density and specific heat capacity of the exhaust gas flows can be approximated to the density and specific heat capacity of nitrogen. This assumption is sufficient for an aggregated estimate, but if analyses were carried out at site level, the exact composition of the exhaust gas would be known. In addition, it was assumed that the specific heat capacity is independent of temperature. In reality, however, the heat capacity is different for different temperatures. The difference is about 10% for nitrogen when comparing 35–500 °C. However, the difference between 35 and 200 °C is only about 1%. Since most of the excess heat is generated within this range, it can be assumed that this will not have a significant influence on the results.

Our analyses do not consider the latent heat of condensation of water vapour in the exhaust gas. Water vapour contains a large amount of energy released by condensation. Condensation of water vapour is the state-of-the-art technology (e.g. in condensing boilers). However, our data do not contain any information about the water content of the exhaust gases. One possibility would be to estimate the water content of the individual exhaust gases based on process-specific parameters. However, using real data represents a strength of our analysis, which is why we did not supplement them with estimates. Future research could include this aspect in the analyses, but the corresponding data must be collected.

Based on the literature, we assumed the dew temperature of sulphuric acid to range from 120 to 150 °C. We addressed the uncertainty of the exact dew temperature by analysing three different cases with different acid dew temperatures to test the robustness of our findings. We are aware that the acid dew point temperature may also lie outside this range depending on the framework conditions (e.g. fuel composition). However, we assumed that this is not particularly frequent, as the bandwidth used represents a common corridor for technical systems in Germany according to Effenberger (2000).

Our analysis shows the relevance of considering the sulphur dew point when calculating excess heat potentials, as this can be a relevant limiting factor in practice for the use of excess heat. However, we do not regard this as an absolute technical limit. In individual cases, it may be advisable to fall below the dew point of sulphur and install corrosion-resistant materials. However, this goes beyond the scope of our analysis, which is not case-specific but considers the data for 455 production sites in a geographically defined area.

The estimated excess heat potential from exhaust gases in Baden-Württemberg in our analysis is about 40% lower than the theoretical potential due to our consideration of corrosive components in the exhaust gases. These results show how relevant it is to consider corrosive components when determining excess heat potentials. However, many more parameters would be needed to determine the real technical and economic potential. For example, constraints imposed by other processes could additionally limit the technical and economic potential. In addition, there could be regulatory restrictions to set the minimum temperature of exhaust gases in order to reduce the risk of pollution to adjacent areas. These factors were not part of our analysis.

The method used in our analysis can be applied to the whole of Germany, as the underlying data are collected by the environmental agencies of the different federal states within the framework of the Federal Immission Control Act. In order to assess whether the applied method can be transferred to other countries, it would be necessary to examine the data collected in other countries within the context of emission control. For the EU countries, it would be particularly interesting to evaluate how other member states implement the Industrial Emissions Directive, especially in the area of monitoring.

It is not possible to directly apply the method used in our paper to the European Pollutant Emission Register (E-PRTR), since neither temperature nor volume flow is recorded in the E-PRTR. The same applies to data from the Emission Trading System (ETS). In principle, however, our method could be used to derive characteristic values for industry sectors, which could then be transferred to other countries. Specifically, the share of excess heat in relation to fuel consumption could be calculated differentiated by industry sector. This could then be used together with energy statistics from other countries to estimate industrial excess heat. Brueckner et al. (2017) have already done this as part of their estimation of the theoretical potential for Germany, in order to transfer the results of their bottom-up analysis, which covered only part of the production sites in Germany, to the whole of Germany. However, such an estimate is then no longer a purely bottom-up estimate, but a combination of bottom-up and top-down calculations. Papapetrou et al. (2018) have also done this by using bottom-up values from Hammond and Norman (2014) for British industry to estimate the excess heat for Europe. For such approaches, however, it must be critically examined to what extent the industrial structure differs between countries, and which systematic errors can be caused by applying indicators from other countries.

5 Conclusions

In this paper, we calculated the excess heat potentials from the exhaust gas data of about 300 production sites in Baden-Württemberg, Germany. In addition to the theoretical potential, a so-called low hanging potential was determined. The low hanging potential is based on the assumption that the excess heat from exhaust gases containing sulphuric acid is only used up to the dew point of sulphuric acid. The results of our analysis show that the low hanging potential is about 60% of the theoretical potential. This means that fewer restrictions due to corrosion are expected and the potentials can be tapped with comparatively less effort for 60% of the excess heat from exhaust gases. Conversely, this also shows that exploiting the remaining 40% is likely to require equipment that can withstand corrosive acidic substances. However, this may render the energy potential below the acid dew point uneconomical or less economical, which is an obstacle to fully exploiting the excess heat potential.

Overall, therefore, our analysis shows that considering the corrosive effect of sulphuric acid can have considerable influence when estimating excess heat potentials. Since sulphuric acid is a pollutant, this indicates that pollutants in general could be important when estimating excess heat potentials. Future work may take this into account, especially when quantifying the technical and economic potentials for using excess heat. However, this is not the only additional aspect required to determine the actual technical and economic potential. Further research should therefore aim at developing more advanced methods to estimate the technical and economic excess heat potential. For Germany, in particular, these should be developed on the basis of emission declarations, as these are updated every 4 years. In this context, the temporal development of excess heat utilisation could therefore also be assessed. In addition, existing studies estimating the excess heat from industry for geographically defined areas have so far been mainly limited to exhaust gas-based flows. Further work could complement this by considering diffuse excess heat, excess heat from waste water and products or by-products such as slag. With regard to promoting the use of excess heat potentials, future analyses should aim at determining which factors favour excess heat utilisation. It is of particular interest to identify which policy measures effectively promote the use of excess heat, e.g. by removing obstacles in a targeted manner.