1 Introduction and motivation

Additive manufacturing is an essential tool in innovative production processes. The extended degrees of freedom offer much potential in usage, construction, and product design [1]. Rising raw material and energy costs, constantly increasing environmental requirements, and the increasing demand for resource-saving products represent a paradigm shift in classic production processes [2].

In addition to the purely energetic evaluation, developing energy models is a method to determine energy consumption and reduce it in the long term. The specific energy consumption model, also known as the SEC model, allows a quick estimation of energy consumption by multiplying the SEC with a unit like the mass of the workpiece, the manufacturing time, or the exposed area [3]. Here, high dependence on the used machine, the considered peripheral devices, and the geometry are noticeable.

Previous studies, such as those by Kellens et al. [4] and Baumers et al. [5], have laid the basis for understanding the energy demands of PBF-LB/M processes. Various energy models have subsequently been proposed, including those by Paul and Anand [6], Yi et al. [7], Lv et al. [3], and Hui et al. [8]. These models are often limited by their specificity to sub-processes or subsystems. This results in limitations in their applicability to other manufacturing machines or inaccuracies in energy consumption predictions. The simulation accuracy ACC is mostly in the range of 90% [3, 5, 9] with the limitation of small sample sizes. Moreover, nearly, all these models rely heavily on process time information, making the accuracy of their simulations largely dependent on the quality of the underlying time model.

In the following study, two manufacturing machines of the PBF-LB/M process are analyzed and compared with other studies. The aim is to analyze the power and resource consumption to use these data to build an improved energy model with a high accuracy, which can be used as an additional parameter in the adapted design methodology. Furthermore, potential savings are derived from the load curves.

2 Definitions

2.1 Selective laser melting

Additive manufacturing encloses a wide range of possibilities for manufacturing different materials. This study aims to investigate the resource and energy consumption of metal additive manufacturing processes especially using the selective laser melting (SLM) process, also known as laser powder bed fusion or PBF-LB/M. Other methods such as FDM or SLS processes with an additional step of sintering are not considered.

Two production machines operating according to the PBF-LB/M principle are used to investigate the material and energy flows. A Renishaw AM400 and a newly developed MPrint from the company One Click Metal. Both operate with single-fiber lasers, the AM400 with a 400 W and the Mprint with a 200 W power laser. In addition to the building space parameters, the simple powder handling, and the compact dimensions of the MPrint are significant differences from the AM400 (Table 1).

Table 1 Comparison of the additive manufacturing machines used in the test series
Full size table

The layer-by-layer structure, in which a controlled laser selectively welds metal powder in layers, produces complex three-dimensional structures. Kellens [4] divides the PBF-LB/M (SLM) process into four phases:

  1. 1.

    Prepare: initializing, preheating, inerting

  2. 2.

    Exposure: selective melting of the metal powder

  3. 3.

    Recoating: recoating with new powder

  4. 4.

    Post-processing: unpacking, separation from the construction platform, cleaning, and machine restoration.

The four steps are identical in both manufacturing machines, with only the inertization differing significantly. In the AM400, a vacuum is initially created in the build chamber by extracting the air. This is followed by flooding the chamber with Argon inert gas until the limit value of 1000 ppm is reached. The MPrint only inertizes based on the displacement principle with nitrogen up to an oxygen content of 6000 ppm. The unpacking occurs after the build process (phases 2 and 3).

2.2 Energy modeling

Based on Hui’s [8] research, energy models can be divided into three categories: specific energy models (SEC), phase-based energy models and subsystem-based energy models.

Specific energy models use specific energy consumption multiplied by a characteristic value, such as mass or volume. Other attributes could be the exposure area or time, though only the area considers workpiece geometry, layer thickness, and orientation [6].

A sub-phase model, like that developed by Yi et al., divides the process into particular time and power model for each phase, such as preparation or cooling, allowing precise determination of energy requirements per step [7, 9].

Sub-system models differentiate between energy-related subsystems. Often, the equipment parts of the production machine are considered, such as the cooling unit, laser unit and the process computer [3]. The simulation accuracy depends on the level of detail of the modeling of the subsystems.

2.3 Experimental setup

This study uses standard tensile specimens like Fig. 1 according to the standard dimensions of the DIN 50125 [10] to ensure workpiece and process quality when process parameters are varied. The energetic comparison and the analysis of the material flows of the two PBF-LB/M machines are carried out with three different standard tensile specimens shown in Table 2 manufactured from 316L, a stainless-steel material.

Fig. 1
figure 1

Design of a standard tensile test specimen in the Form of type E and a test length of 25 mm

Full size image
Table 2 Standard tensile test samples. A testing of round samples is recommended by the VDI 3405  [11] and is used additionly to the already used flat specimen
Full size table

The specimens are manufactured with the standard process parameters of the manufacturer on both machines in different orientations: horizontal, upright and 45°, as it is described by the VDI 3405 [11].

The load curves are recorded with energy data loggers Fluke 1730 and Emonio P3 in the temporal resolution of 1 s. If possible, the different system parts are recorded separately. A higher resolution can be achieved with an oscilloscope, as shown in the study by Brinkmann [12] on the influence of jump times on energy modeling. The oscilloscope allows precise laser power determination at the different scan parameters, strategies, and geometries. Jump times, the phase in which the laser is repositioned until the following point exposure, are largely not considered in previous models but lead to increased simulation accuracy (Table 3).

Table 3 Measurement of resource flows
Full size table

An exemplary mass study is carried out on both machines with the material 316 l to determine the metal powder flows. Faludi [13] calculates a loss of approx. 18% for the AM250, which is identical to the AM400 except for the laser power. This agrees with other studies, which determine a loss of up to over 20% [4] related to the fused metal powder, especially with the production machines without integrated powder handling. Manual sieving is more tending to make mistakes, so it can be expected that the MPrint’s cartridge system will result in less loss. Initially, powder quantities are weighed for filling the cartridges and silos. Both machines are filled to the maximum. After production, all containers are again emptied, sieved, and weighed before restoring the initial state. The complete powder stream’s recycling degree is determined in this case, which varies from Faludi and Kellen’s approach [4, 13].

Simulation accuracy has to be defined to compare the energy models' accuracy. The ACC is introduced by Yi et al. [9] and calculated as shown in Eq. 2.1 with Eexp as the measured energy consumption and Esim for the simulated energy consumption:

$${\text{ACC}}=\left(1-\frac{\left|{E}_{{\text{exp}}}\right.-\left.{E}_{{\text{sim}}}\right|}{{E}_{{\text{exp}}}}\right)\cdot 100 \%$$
(2.1)

3 Main chapter(s)

3.1 Determination of the material flows and process gases

The AM400 is initially filled with 103.7 kg of metal powder. The production process melts 1.2 kg, and after unpacking, sieving, and refilling, losses of 1.8 kg are determined. Due to the small sample quantity at MPrint, two build jobs with standard tensile samples were weighed together. With a total powder quantity of 39.6 kg, the value of the waste powder is 398 g, corresponding to a value of around 1% of the total amount sieved. The recycling rates of the AM400, with 97%, are comparable to the MPrint, with 98%, despite manual powder handling. The comparison of all measured weights is shown in Table 4. The waste powder rates related to the components are up to 150%, significantly higher than the values of Faludi and Kellens [4, 13].

Table 4 Comparison of the metal powder and waste powder of the AM400 and the MPrint. The recycling rate relates to the whole infilled powder mass
Full size table

Table 5 compares two the principles and built time of tensile specimens. In the AM400, after the vacuum process, inert gas is pulsed in only to maintain pressure and atmosphere. Vacuuming is efficient concerning the required inert gas but requires additional electrical energy.

Table 5 Comparison of the build time and process gas values
Full size table

3.2 Analysis of the load curves

The load studies were performed with data loggers with a resolution of 1 s. The high resolution shows individual layers’ power curve but does not precisely reflect the laser power since the exposure times are well below 1 s. The load curve of the AM400 shows the different phases of the manufacturing process, as in Fig. 2 visible.

Fig. 2
figure 2

Analysis of the load curve of the AM400. The different phases of the manufacturing process are visible

Full size image

After the start-up of all systems, the base load is approximately constant at 350 W. The inertization process starts at minute 6 when the vacuum pump shows a significant power curve. The deflection at minute 15 is another short activation of the vacuum pump, minutes 16 and 18, and the constant load beginning in minute 19 results from the process gas fan. From minute 30, the melting process starts. The individual layers are recognizable due to the volatile high power above 1000 W, generated by the pulsing laser, as well as the drop in power during the coating process. The layer time, starting with the support structures, is 90 s, and the recoater time is 8.5 s (Fig. 3).

Fig. 3
figure 3

Comparison of the load curve of the AM400 with and without heating the build plate

Full size image

The dryer and cooling unit are external devices and are recorded separately. Figure 3 shows two complete, identical build jobs, each with the AM400 and the cooling and drying unit measured. The power of the cooling and drying unit can be reported as approximately constant at 1900 W. In build job 2, the build platform heating was additionally activated, which heats the build space to 150 °C. In addition to the higher energy requirement, the processing time is extended due to the heating and cooling phases.

The MPrint does not require an external cooling unit. The load curve, shown in Fig. 4, can also be divided into different phases, although less clearly compared to Fig. 2.

Fig. 4
figure 4

Analysis of the load curve of the MPrint

Full size image

The base load is approx. 160 W. From minute two, flooding with nitrogen starts with a slightly increased power of 300 W–350 W. The melting process starts from minute 8:30. The layers are also clearly visible here with a maximum capacity of up to 1200 W. In the comparison of both production machines, the maximum power in the production process is up to 1200 W. The manufacturing parameters are similar due to the same tensile specimens and material. The base load of the AM400 is higher than that of the MPrint, which does not require an external cooling unit. If this is included with the AM400, the production process’s power rises to 3500 W. The slightly longer vacuuming and flooding process of the AM400 saves inert gas by a factor of four, although the volume to be inerted is six times higher.

3.3 Energy consumption

The energy consumption of both additive manufacturing machines is comparable, although the consumption of the AM400 is higher in all sub-phases, as shown in Fig. 5. Without considering the cooling unit, the consumption of 9.4 kWh of the AM400 is higher than that of the Mprint, with 7.4 kWh building the same built job. One reason is the bigger size of the AM400, which also leads to bigger process fans, drivers, and a higher-powered computer and laser system.

Fig. 5
figure 5

Comparison of the energy consumption of the AM400 and the Mprint in the sub phases. Obviously, the consumption of the cooling unit is higher than the production process itself

Full size image

3.4 Energy model

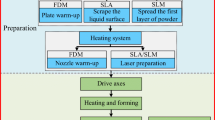
The analysis of the load curve helps to understand and optimize an energy model. In contrast to static models, such as the SEC model, this energy model is more based on the analysis of the system and power curves. The model can be described more like the sub-system models but also has characteristics of the sub-phase models due to its division into phases like it is shown in Fig. 6:

Fig. 6
figure 6

Example of the sub phase and sub system energy model of the AM400

Full size image
$${t}_{{\text{total}}}= {t}_{{\text{Uprep}}}+{t}_{{\text{vac}}}+{t}_{{\text{Mprep}}}+{t}_{{\text{built}}}$$
(3.1)

The preparation phase is further subdivided into operator preparation phase tUprep, vacuum phase tvac, and machine preparation phase tMprep. Together with the build phase, this results in the total printing duration ttotal as defined by Eq. 3.1.

The AM400’s cooling and drying unit is considered as a sub-system, depending on the build time. Power functions are developed for the sub-phases, as in the detailed modeling of Yi et al. [9]. The workpiece geometry and process parameters define the properties of the build phase. Therefor a specific time model is necessary with the results from the times of one layer. A special feature is the consideration of jump times [12], which can further increase the accuracy of the energy model. The jump times depend on the scan strategy and the geometry itself. In this case, the energy model is more accurate due to the detailed time models and the consideration of the parts geometry. The innovation of this model and the higher accuracy is mostly driven by the combination of the consideration of the geometry of the parts using the built file and the detailed separation of the different sub systems and phases.

The quality of the energy model can be classified by comparing it to the other studies. As shown in Table 6, the ACC of the developed energy model is comparable to the other studies. Considering the jump times and the part's geometry, a higher ACC up to 95.4% is reachable, although the values of Yi and Baumers are higher. However, it is necessary to note that Yi's results were validated only through a case study with a single workpiece. The present study's findings indicate that the simulation accuracy of all examined energy models is subject to workpiece-dependent fluctuations, thus limiting the significance of samples with few workpieces.

Table 6 Comparison of the ACC of different energy models
Full size table

4 Discussion

In the study of the resource efficiency of AM processes, electrical energy, process gas, and metal powder are the primary resources.

The mass study shows a high degree of recycling for both units and high losses concerning the component weight. It must be differentiated here that the study’s objective was the recycling rate, which is why all the metal powder was sieved. With the AM400, the mass study was carried out highly efficiently and without errors, which can only sometimes be guaranteed. Therefore, it can be challenging to transfer these values to the industry. The integrated powder handling of the MPrint has a similarly high value of the recycling rate and the process can be transferred easily to an industrial process.

The production of high-purity process gases such as nitrogen and argon are very energy-intensive [14]. Additional vacuuming shows a high savings potential compared to the pure displacement of oxygen, with an energy consumption of the vacuum pump of approximately 0.1 kWh per build job. Further savings potential can be found in the design of the process gas flow and the design of the installation space. Flow-optimized channels reduce the energy consumption of the circulation and the oxygen residual formation. Despite identical installation space, the value of up to 0.75 m3 of the AM400 observed over several construction jobs is significantly different from Faludi’s estimate of 0.208 m3 [13]. His estimate is based only on the double calculated volume of the build chamber with 0.11 m3. It does not consider the likewise evacuated volume of the platform chamber with an additional 0.25 m3. A total of 0.36 m3 has to be evacuated, and neither process air, filters, hoses, the set value of oxygen content in ppm, nor the displacement are taken into account. Nevertheless, the comparison shows that the usage of a vacuumization reduces the usage of process gases significantly.

The examination of the load curve shows a high dependence of the energy demand on the build time. During recoating and the jumps, no production takes place despite the increased energy demand. Optimizations are possible here, especially in the design and preparation phase. Implementing a design methodology adapted to AM [15] can lead to significant savings.

Upon analyzing the systems, it is noticeable that the cooling unit of AM400 utilizes a consistent 1900 W of power regardless of the build process’s power parameters. A controlled alternative or a cooling water system connection offers a high savings potential.

A high level of detail in the time model of the energy simulation leads to improved simulation accuracy compared to pure SEC models and the parameter-based simulation of the partial phases. The comparison of the SEC in Table 7 shows that the MPrint lies with the upper value in the range of the Baumers study [5]. The minimum value of 60.9 MJ/kg is not comparable to other research, although the batch size of two must also be considered here. The values of the AM400, on the other hand, are verified by a sample of seven build jobs examined and are in the range of the current study by Kellens [16].

Table 7 Specific energy consumption (SEC) for different studies
Full size table

5 Conclusion and outlook

The additive manufacturing process is a resource-intensive manufacturing process [17] representing an innovative tool in various manufacturing systems. Compared to conventional manufacturing systems, the extended degrees of freedom can lead to high savings already in the design phase.

Our research shows high potential for the further development and optimization of system components concerning resource requirements such as electricity or inert gases. Considering component geometry, the methodology for accurate simulation of energy consumption offers additional potential that can be realized directly in the design phase. The transformation process towards climate-friendly and sustainable manufacturing of efficient products can be significantly supported by applying a design methodology adapted to additive manufacturing in combination with resource-efficient design. In particular, the metals industry and manufacturing processes are energy-intensive and have high CO2 emissions. Optimizations based on our simulation of resource consumption support the transformation process towards climate-friendly production.