1 Introduction

The metal powder bed fusion (PBF) processes, electron beam powder bed fusion (PBF-EB) and laser powder bed fusion (PBF-LB), produce near net-shape parts in a layer-by-layer fashion from a powder bed [1]. 3D CAD parts are sliced and the resulting 2Ds are filled with precisely aligned micro-meter wide weld seams (or points [2]) which fuse applied powder layers by remelting the previous layer partially [3, 4].

Due to its layer-wise production paradigm, metal PBF provides unique access to inspect and control the manufacturing process. Consequently, the academic and industrial interest in process monitoring and control topics continues to be high, as can be seen from the high number of recent review articles [5,6,7,8,9].

The level-terminology proposed by Grasso et al. [9] allows to classify process monitoring approaches. Level 1 systems observe the quality of the powder bed and the printed slice and obtain either images or height maps of the build surface in situ, depending on the implemented principle of measurement. Obtained images can be post processed to analyse the dimensional accuracy of printed parts [10] or to analyse the powder bed [11]. Table 1 shows that a lower number of studies obtains the height map or surface topography of the build surface, which may underline the added complexity of measuring the build surface topography quantitatively instead of recording a simple image. This is especially true in PBF-EB, where any process monitoring method has to cope additionally with exceptionally high build temperatures [12], X-rays [13] and metal evaporation [14].

Table 1 Number of studies in [9] describing level 1 process monitoring methods in PBF-EB or PBF-LB broken down according to the observation result: image or height map of the build surface
Full size table

In PBF-EB, the developing surface topography of the printed slice is of immanent interest for process parameter development, quality inspection and control applications. Naturally, the topography of the powder bed, especially its homogeneity and coverage of the printed parts, is highly important for a successful build [5].

Liu et al. [15] developed a fringe projection prototype system using a CCD camera and a projector attached to the vacuum chamber of an PBF-EB machine via optical ports, which allowed to measure the build surface topography. Additionally, a calibration method for the said method has been developed [16]. However, PBF-EB build surfaces are difficult to measure with optical methods since highly reflective metal surfaces (the molten parts) are present next to the highly diffusive powder bed which leads ultimately to intensity saturation issues. Improving the dynamic range of the CCD camera chips can solve the problem on the hardware level. Another option is to extend traditional fringe projection systems with machine learning algorithms which enable to adapt exposure parameters dynamically during the process due to surface classification results [17]. But still, the hard process conditions inherent to PBF-EB plague any process monitoring method based on optical imaging, since optical view ports have to be protected from coating due to metal vapour originating from the melt pool.

Electron optical (ELO) imaging prevents these challenges using back scattered electrons to obtain information from the build surface. 2D images are computed from 1D time series voltage data recorded at robust detector systems during scans of the build surface in a line-by-line fashion with a low-power, focused electron beam. So far, single ELO detector systems have been used to classify surface morphologies of printed parts for fast process parameter development [18], analyse the dimensional accuracy of parts based on their contour in 2D [10] and in 3D [19] (by stacking extracted 2D contours in build direction). Additionally, the method has been investigated for in situ pore detection [20,21,22]. The capabilities of ELO imaging to measure material contrast has been demonstrated in [23] and exploited in a recent study on powder contamination [24].

In scanning electron microscopy (SEM), multi-detector systems are known to facilitate the usage of material and topographical contrast [25, 26]. This motivates the usage of multi-detector systems in PBF-EB. Zhao et al. pioneered the usage of a two-detector system, showing that the sum image contains material information whereas the difference image is proportional to the height gradient of printed cubes [27]. Bäreis et al. tested a four-detector system on a Freemelt ONE (Freemelt AB, Mölndal, Sweden) machine by printing cuboid samples of the Ni-base superalloy CMSX-4 at temperatures \(>{1000\,\mathrm{{}^{\circ }\text {C}}}\) for over 30 h. Then cracks on the samples surface formed and were observed in situ in a mean image of all four detectors or the sum image formed by opposite detectors [28]. The same four-detector system has been used by Ye et al. to detect the evolution of the smoke phenomena [29].

This work demonstrates for the first time, that it is possible to measure the build surface topography quantitatively and reliable every layer of a PBF-EB build process using a multi-detector ELO imaging system. The basis for this study is previous work of the authors. Renner et al. [30] demonstrate surface topography reconstruction in a PBF-EB machine by surface gradient computation of ELO measurements from an experimental four-detector system. A raytracing model of ELO imaging presented in [31] allows to simplify the gradient computation step and to rationalize multi-detector design in terms of detector positioning and heat shield dimensioning.

This work presents an newly developed four-detector system and a cuboid heat shield following the previously formulated design guide lines. In addition, the PBF-EB process cycle is extended and contains an ELO scan of the applied powder layer (termed powder scan) and the melt surfaces (termed melt scan), which allows to reconstruct the respective build surface topographies. To account for measurement uncertainties, a pre-existing surface reconstruction (or normal integration) algorithm is used which implements Tikhonov regularization. The optimal regularization parameter is determined with the help of the ex situ determined surface topography of a printed part. Finally, potential applications with respect to super-elevated edges are outlined and the sensitivity of surface topography changes of single parts to process parameter changes is demonstrated.

2 Methods

2.1 Detector system

Fig. 1
figure 1

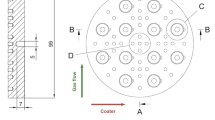
Four-detector ELO imaging system. a Overview, displaying the cuboid shaped heat shield, reduced powder tanks and a part of the detector system with Kapton cable connections (above the heat shield). b The four-detector system, as seen from the build surface, showing disk shaped detectors. c View with removed front part of the heat shield illustrating a heat protection sheet in-between the detectors. d Close-up of the front detector, showing the ceramic insulation of the holders and and a connected Kapton cable

Full size image

Figure 1 displays the newly developed four-detector system used in this work. The detector system has been tailored to the geometric constraints of the machine ATHENE, following the design guidelines formulated in [30, 31]. In short, the right and left detector need to be aligned with the x-axis and the front and back detector need to be aligned with the y-axis of the machine coordinate system. Heat shields should be designed to minimize the influence of multiple scattering events on ELO images recorded by the single detectors. Detectors should be small to be susceptible to local normal vector changes on the imaged area, but big enough to keep a high signal-to-noise ratio. Detectors need to be placed high above the build surface so that masking (back scattered electrons cannot reach the detector since the build surface itself is an obstacle in their pathway) is diminished as much as possible. In addition, detectors pairs need to be as far apart as possible to enhance ELO image contrast. Naturally, some of these design guide lines are contradictory and a compromise, keeping a machines specific geometric constraints in mind, has to be found.

The heat shield displayed in Fig. 1a has a cuboid shape and is centered with the machine coordinate system. While this does not minimize the impact of multiple scattering events, it keeps the image contribution of multiple scattering events equal for each single detector. The standard Arcam S12 powder tanks have been scaled down, so that each single detector can be placed at a height of \(d_h={342\,\mathrm{\text {m}\text {m}}}\) and \(d_w={120\,\mathrm{\text {m}\text {m}}}\) distant from the z-axis, while providing enough powder supply for big parts. \(D_h\) and \(d_w\) are defined in Fig. 2c. The detector discs (Fig. 1b–d) have a diameter of \({50\,\mathrm{\text {m}\text {m}}}\), are fabricated from stainless steel and their normal vectors point towards the machine coordinate system center (Fig. 2c). Figure 1c shows the detector system with the front part of the heat shield removed as seen from the vacuum chamber door. A thin stainless steel sheet protects the electron beam gun from heat radiation during the build. The detector discs are attached to a holding plate with holders, which are isolated from machine ground by thick ceramic washers (Fig. 1d). This guarantees, that the detector system is robust to short-circuiting due to metal evaporation which develops during the process.

2.2 Experimental procedure

Fig. 2
figure 2

a Extended PBF-EB process cycle containing an ELO powder and melt scan. Every process phase in which ELO imaging has (published) applications is indicated. b Dimensions of the cube and cross specimen. The hatch pattern rotates with layer n. c Positioning of a single detector in the machine coordinate system

Full size image

The experiment consists of building 6 cubes and a cross using the extended process cycle (two ELO imaging steps instead of one) depicted in Fig. 2a. After each powder layer deposition and preheating step an ELO powder scan is performed to observe the applied powder layer. Then the parts are hatched. Subsequently, the ELO melt scan is performed to control the quality of the melt surfaces of the parts. Afterwards the build table moves down by \({50\,\mathrm{\upmu \text {m}}}\) resulting in the same nominal layer height and the process cycle begins anew for the next layer.

The dimensions of the parts and the rotation of the hatch patterns are defined in Fig. 2b. While the cubes are standard parts in process parameter development, the cross is chosen to provoke trailing, partially persistent and fully persistent melt pools, as described in [32, 33]. All parts are hatched with a snake-hatch pattern using a line offset \(l_o\) of \({100\,\mathrm{\upmu \text {m}}}\). The hatch pattern of the cubes is rotated by \({90\,\mathrm{{}^{\circ }}}\) every layer, whereas the hatch pattern of the cross is rotated by \({180\,\mathrm{{}^{\circ }}}\), as indicated by the schematic.

The build is conducted on the machine ATHENE (an Arcam S12 machine body retrofitted by the company pro-beam GmbH & Co. KGaA), which offers a standard electron beam gun with a fixed acceleration voltage \(U={60\,\mathrm{\text {k}\text {V}}}\) and the possibility to freely program the beam path. Its rake system is still the original and can be seen in Fig. 1a. It consist of a triangular prism serving as a holder for \(2 \times 2\) thin metal sheets, which are perforated with a one sided grating for flexibility. Ti–6Al–4V, grade 23 ELI powder with a particle size distribution between 45 and 105 mm (Tekna Advanced Materials Inc.) is used as feedstock and distributed by the rake system. In each layer, the rake moves once over the build surface, in positive or negative x-direction.

Before process begin, a controlled helium atmosphere of \({3\times 10^{-3}}\,\hbox {mbar}\) is applied by evacuating the vacuum chamber to \(\sim {1\times 10^{-5}}\,\hbox {mbar}\) and subsequent flooding with helium. The build consists of 60 layers of point supports printed on a steel start plate at a starting temperature of \({750\,\mathrm{{}^{\circ }\text {C}}}\), followed by 220 layers with the varying beam powers P described in Table 2. Additionally, the scan velocity \(v_s\) is changed. From layer 60 to 160, each part is built with a different “slow” scan velocity, layer 161 to 270 use a different "fast" scan velocity. Whereas the area energies \(E_A\) vary moderately, the lateral velocities \(v_{\text {lat}}\) vary drastically, especially in the cross geometry. \(V_{\text {lat}}\) describes how the melt pool moves perpendicular to the scan direction and is computed by

$$\begin{aligned} v_{\text {lat}} = \frac{v_s l_o}{l_h}~~~, \end{aligned}$$
(1)

where \(l_h\) is the hatch length. \(E_A\) extends the concept of line energy \(E_L = P / v_s\) with the line offset and is computed by

$$\begin{aligned} E_A = \frac{P}{v_s l_o}~~~. \end{aligned}$$
(2)

Tables 3 and 4 summarize all lateral velocities and area energies. To summarize, the process parameters are varied intentionally in the described manner to induce surface topography changes. In the same spirit, the hatch pattern of the cross specimen is rotated by 180 \({}^{\circ }\) to keep \(v_{\text {lat}}\) constant in the short side arms and the body for the respective process parameter regimes.

Table 2 Beam power P in \({\text {W}}\), set per layer for all parts
Full size table
Table 3 Lateral velocities \(v_{\text {lat}}\) of all parts in \(\hbox {mm}\, \hbox {s}^{-1}\)
Full size table
Table 4 Area energies \(E_A\) of all parts in \(\hbox {J mm}^{-2}\)
Full size table

The measurement chain for multi-detector ELO imaging is identical to the one described in [30], this includes digitizer and amplifier settings. ELO imaging parameters for the powder and the melt scan are equal. A maximally focused beam at a beam current of \({3\,\mathrm{\text {m}\text {A}}}\) is used, which results in a Gaussian beam profile and a full width half max (FWHM) diameter of \({270\,\mathrm{\upmu \text {m}}}\) (measured with a pinhole beam measurement device by the company pro-beam GmbH & Co. KGaA and analysed with in-house software). The beam moves at \(v_s = {75\,\mathrm{\text {m}\text {s}^{-1}}}\) and covers an area of \(90 \times 90\,\hbox {mm}^{-2}\) in 1500 single scan lines. These settings result in a pixel side length of \({60\,\mathrm{\upmu \text {m}}}\).

After the build process, all parts are extracted from the sinter cake. The last layer of the cross is used for validation purposes by measuring its surface height map with the optical profilometer Keyence VR-6200 with a pixel side length of \({14.8\,\mathrm{\upmu \text {m}}}\).

2.3 Software

All code written for this work uses libraries of the scientific Python universe. NumPy [34] and SciPy are used for general computing purposes and for the implementation of the surface reconstruction algorithm described in Sect. 3.3. Matplotlib [35], PyVista [36] and Cmasher [37] are used for visualization. The point cloud library Open3D [38] is used to register reconstructed surface topographies with validation measurements of the same surface. The library scikit-image [39] is used for basic image processing tasks.

3 Theory

Fig. 3
figure 3

Graphical abstract of the computation chain illustrating the single steps described in Sect. 3. All ELO images are recorded from the melt scan of layer 246

Full size image

This sections builds heavily on previous works [30, 31] of the authors. Only the key results necessary for this work are repeated, for the sake of readability. A complete computation chain was developed in [30], starting with four single ELO images, surface tilt and solid angle (STSA) contrast correction, surface gradient (or normal vector field) computation and culminating in the height map of a Ti–6Al–4V melt plate, which was obtained using an integration algorithm. The computation of the surface gradients was greatly simplified in [31]. This work utilizes the new gradient computation procedure and a variant of the previous integration algorithm.

3.1 Computation chain

The graphical abstract in Fig. 3 summarizes the computation chain. At first, four square-shaped ELO images are recorded by the left, right, back and front detectors of the detector system at the powder or melt scan of a given layer. Each single ELO image is STSA contrast corrected by division with the respective correction image. The correction images are obtained either from the sintered powder bed during the process or from an even plate made from the same alloy as the powder. The resulting STSA-corrected ELO images are used to compute the surface gradient (normal vector) field of the build surface \(-\nabla {\overline{Z}}(x,y) = [n_{Sx}, n_{Sy}]^T\) and the detector positioning, as explained in Sect. 3.2. Subsequently, the gradient field is used as input to the surface reconstruction (or integration) algorithm described in Sect. 3.3. The result is the in situ measured height map or surface topography of the build surface \({\overline{Z}}(x,y)\). Naturally, all computation steps have to be repeated for every ELO scan every layer.

3.2 Gradient computation

The single STSA corrected ELO images of the right, left, back and front detector \(R^C, L^C, B^C\) and \(F^C\) are the basis of the computation of the normalized difference images \(M_x\) and \(M_y\) as

$$\begin{aligned} \begin{aligned} M_x&= \frac{R^C - L^C}{R^C + L^C} \\ M_y&= \frac{B^C - F^C}{B^C + F^C}. \end{aligned} \end{aligned}$$
(3)

Using the detector height \(d_h\) and width \(d_w\) allows to compute the surface gradient field \(-\nabla {\overline{Z}}(x,y) = [n_{Sx}, n_{Sy}]^T\) as

$$\begin{aligned} \begin{aligned} -\frac{\partial {\overline{Z}}(x,y)}{\partial x} = n_{Sx}&= \frac{M_x d_h}{d_w + xM_x + yM_y} \\ -\frac{\partial {\overline{Z}}(x,y)}{\partial y} = n_{Sy}&= \frac{M_y d_h}{d_w + xM_x + yM_y}. \end{aligned} \end{aligned}$$
(4)

The measured gradient field is then used as input for the following surface reconstruction algorithm. Further calibration steps might be necessary, but were not required in the experimental part of this work.

3.3 Surface reconstruction with Tikhonov regularization

This work uses the surface reconstruction (or normal integration) approach described in Harker et al. [40, 41]. For the sake of readability, the main points are outlined below. Surface reconstruction from a measured gradient field can be solved efficiently by finding the minima of a global least squares cost function directly, by rewriting the problem in terms of a Sylvester equation. To this end, the unknown height map Z(x, y) and the measured gradients \(\nabla {\overline{Z}}(x,y)\) are written in discrete form as matrices \({\textbf{Z}}\), \(\mathbf {{\overline{Z}}_x}\) and \(\mathbf {{\overline{Z}}_y}\). Using the numerical differentiation matrices \({\textbf{D}}_x\) and \({\textbf{D}}_y\) allows to approximate the true gradient with the measured gradient field: \(\mathbf {{\overline{Z}}}_x \approx {\textbf{Z}}{\textbf{D}}_x^T\) and \(\mathbf {{\overline{Z}}}_y \approx {\textbf{D}}_y {\textbf{Z}}\). Now, a global least squares cost function \(\epsilon ({\textbf{Z}})\) is formulated, which enforces that the difference between the true and the measured gradient is minimal.

Tikhonov regularization is used to cope for measurement noise in the STSA corrected ELO images and global bias in the gradient field due to positioning inaccuracies of electron gun, build plane and multi-detector system in the common machine coordinate system. \(\lambda \Vert {\textbf{Z}} - {\textbf{Z}}_0 \Vert _F^2\) is added to the cost function, where \(\Vert \cdot \Vert _F^2\) is the Frobenius norm and \({\textbf{Z}}_0\) is the a priori estimate of the unknown height map. This is a simple regularization term, implying that that all matrices are square and the regularization parameter \(\lambda\) is equal for the x- and y-direction. Choosing \({\textbf{Z}}_0=0\) is domain-specific to PBF-EB. Acceptable height elevations of specimens (\(Z(x,y)>0\)) are approximately 3 orders of magnitude smaller than the side length of the build surface. Otherwise, the rake will make hard contact during powder layer application and the build process fails. The simplified regularization term \(\lambda \Vert {\textbf{Z}} \Vert _F^2\) bounds the solution \({\textbf{Z}}\) to its norm. Following [41], the cost function \(\epsilon ({\textbf{Z}})\) is then written as

$$\begin{aligned} \begin{aligned} \epsilon ({\textbf{Z}})&= \Vert {\textbf{D}}_y{\textbf{Z}} - \overline{{\textbf{Z}}}_y\Vert _F^2 + \Vert {\textbf{Z}}{\textbf{D}}_x^T - \overline{{\textbf{Z}}}_x\Vert _F^2 \\&~~~+ 2 \lambda \Vert {\textbf{Z}} \Vert _F^2. \end{aligned} \end{aligned}$$
(5)

The minimum of Eq. (5) is found by differentiation with respect to \({\textbf{Z}}\) and equating the result to 0. The result is the following Sylvester equation

$$\begin{aligned} \begin{aligned}\left( {\textbf{D}}_y^T {\textbf{D}}_y + \lambda {\textbf{I}} \right) {\textbf{Z}} + {\textbf{Z}}\left( {\textbf{D}}_x^T {\textbf{D}}_x + \lambda {\textbf{I}} \right) - {\textbf{D}}_y^T \mathbf {{\overline{Z}}_y} - \mathbf {{\overline{Z}}_x} {\textbf{D}}_x = 0. \end{aligned} \end{aligned}$$
(6)

As usual, the identity matrix is denoted by \({\textbf{I}}\). There are sophisticated approaches which help to find an optimal value for \(\lambda\) [41], but this work uses validation measurements of as-built cross specimen surface to determine \(\lambda\) once (for a given detector system).

4 Results and discussion

4.1 ELO powder scan

To the authors knowledge, this work shows multi-detector ELO imaging applied to observe the quality of the applied powder layer for the first time. Figure 4b depicts all four recorded STSA corrected images of the powder bed of layer 246. Areas of sintered powder aside the specimen appear dark, but with varying intensity. Two, intertwined, explanations for the intensity variation come into mind. First, local density variations in the even sintered powder bed may lead to a varying effective back scattering coefficient and consequently varying local intensity. And second, the local powder particle stacking leads to a mean normal vector under the beam profile, which is representative of the locally uneven powder surface topography, and changes the measurement result at the detectors. Both scenarios are explained by the model equations in [30, 31]. Whereas the 1st explanation would lead to approximately the same image of the local powder bed recorded by all four detectors, the 2nd explanation would lead to four different images due to the positioning of the detectors. Figure 4a enlarges the inlets of b and displays that each detector images the same powder area differently. This might be an indication that the 2nd explanation dominates the image generation.

The specimens are not evenly covered by powder, as can be clearly seen in the pixel intensity variations on top of the specimens in Fig. 4b. Especially the cross specimen’s right side appears brighter, which indicates that it is only sparsely covered with powder. In this layer, the rake comes from the positive x-direction (or from right to left in the images) and applies the powder layer. When the rake blades touches elevated parts of the right specimen borders, it bows back and scratches the elevated part free of powder. Since the rake moves on continuously, the rake blade jumps back to its original position, like a spring, which disturbs the application of an even powder layer. This is called powder flicking [42]. On the other side of the part, the left specimen borders act as a barrier for the rake blade which compacts the powder locally.

Figure 4c displays the measured gradients \(-\nabla {\overline{Z}}(x,y)\), computed with Eqs. (3) and (4), using the STSA corrected ELO images in Fig. 4b. Even though the pixel intensity of the sintered powder bed is lower than that of the specimens, there is no perceptible difference in the gradient images looking at the transition zone between sintered powder bed and specimens. This is quite an astonishing result, but already predicted and explained by the model of multi-detector ELO image formation derived in [30] and expanded on in [31]. In short, the electron beam scans the build surface line by line. Every, single build surface location is convoluted with the beam profile and acts as single signal source simultaneously for all four detectors. Therefore, any local build surface characteristic like density (or powder coverage), material composition and surface topography defines the raw signals and the reconstructed ELO images. Subsequently, the proposed gradient computation method removes influences of the detector’s solid angle, material dependencies magnitude of the imaging beam current by STSA contrast correction. The only remaining information is the gradient of the current build surface at the time of ELO image recording. In the case of Fig. 4c, this is the newly applied and preheated powder layer.

Fig. 4
figure 4

ELO Images recorded from the powder scan of layer 246. a Enlargements of the marked areas in (b), which shows all four STSA corrected ELO images. c Display of the gradient field \(-\nabla {\overline{Z}}(x,y)\) computed from the four ELO images in (b) by Eq. (4)

Full size image

4.2 Determination of regularization parameter and validation

The best regularization parameter \(\lambda\) is determined pragmatically by comparing the as-built surface of the cross part with surface topography reconstructions obtained by various regularization parameters \(\lambda\). After the build, the cross is extracted from the sinter cake and its surface topography measured. This measurement is taken to be the true surface Z(x, y), since its resolution is high. The in situ surface topography reconstructions are denoted with \({\overline{Z}}(x,y)\), originate in this section from the ELO melt scan of layer 270 and span the whole build surface. \({\overline{Z}}(x,y)\) is first cropped to the same dimensions of Z(x, y). Then, a clean binary segmentation mask is subsequently obtained from the sum images [30, 31] of opposite detectors and classical Otsu’s thresholding, as implemented in [39]. This allows to set the powder areas artificially to a height of 0. Subsequently, both surfaces are converted to point clouds and then registered using the iterative closest point algorithm described in [43] and implemented in Open3D. Plotting the absolute difference \(|Z(x,y) - {\overline{Z}}(x,y)|\) over various regularization parameters \(\lambda\) results in the box plots of Fig. 5a. Clearly \(\lambda = 0.4\) results in the smallest interquartile range (\({}{17.4}{}-{4.5\,\mathrm{\upmu \text {m}}}\)), the smallest median (\({9.9\,\mathrm{\upmu \text {m}}}\)) and mean value (\({14.4\,\mathrm{\upmu \text {m}}}\)). Therefore, all further results in this study use \(\lambda =0.4\).

Figure 5b compares the ex situ measured surface of the cross Z(x, y) with the in situ surface topography reconstruction \({\overline{Z}}(x,y)\). Clearly, both surfaces show the same features. Indeed, the in situ measured \({\overline{Z}}(x,y)\) matches Z(x, y) to an astonishing degree. Zooming in allows to observe that \({\overline{Z}}(x,y)\) is slightly blurred. The reason is of course, that every ELO image recording is given basically by the convolution of the true specimen surface with the electron beam profile [44]. Since the electron beam profile is described by a FWHM diameter of \({270\,\mathrm{\upmu \text {m}}}\), fine details, for example topographies of a single scan line, are blurred out. This is as well the reason, that the biggest errors in magnitude occur in steep hills and valleys with small lateral extension as can be seen in the areal difference \(Z(x,y)-{\overline{Z}}(x,y)\) in Fig. 5b.

The profiles in Fig. 5c underline the same point, but illustrate that valleys are overestimated by the represented method. A possible explanation is that valleys swallow back scattered electrons (masking) or lead to multiple scattering events, which both result in a lower local ELO signal, steeper gradients and consequently deeper valleys. Overall, it is clear in situ surface topography reconstructions from multi-detector ELO images provide high-quality information. This method has the potential for even higher accuracies, when beam diameters of future machines get smaller.

Fig. 5
figure 5

Determination of the best regularization parameter \(\lambda\) and validation measurements. a Box plots of \(|Z-{\overline{Z}}|\) computed from the complete build surface with varying regularization parameters \(\lambda\). \({\textbf {b}}\) Comparison of surface topographies of the cross obtained by microscope and in situ with \(\lambda =0.4\). \({\textbf {c}}\) Profiles along x at \(y=0\) and along y at \(x=0\) of the surface topographies above

Full size image

4.3 Build surface topographies

Fig. 6
figure 6

Height maps computed from the ELO a) melt scan of layer 243, b) the powder scan of layer 244 and c) the subsequent melt scan of the same layer

Full size image

The height maps in Fig. 6 display the complete build surface and are computed from ELO melt and powder scans of the layers 243 and 244. The renderings on the left give a visual impression of the height maps on the right. Clearly, the melt surfaces of the cross and cube 3 in Fig. 6a show the biggest magnitude variations. Since the local energy input is high in all parts, the applied powder layer (rake moves from right to left) depicted in Fig. 6b cannot cover the parts completely. The dominant hills in the short arms of the cross persist but show a lower magnitude, since the build table is lowered by \({50\,\mathrm{\upmu \text {m}}}\). As can be clearly observed in Fig. 6c, the power change from \({}{1260}{}\) to \({1440\,\mathrm{\text {W}}}\) (Table 2) results in an instant surface topography change in all cubes. The cubes are hatched in the \(n + 2\) direction defined in Fig. 2b. Due to the high lateral velocity \(v_{\text {lat}}\) and high area energy \(E_A\), the melt pool develops to be persistently liquid over multiple scan lines [32]. After solidification, the last completely liquid melt pool can be observed in each cube on the left side. Each cube forms two to three dominant elevations which span the cube approximately parallel to the x-direction. The cross on the other hand does not show such a drastic surface morphology change, which might be explained by the combination of hatch pattern and part boundaries.

While a first promising mechanism is developed which describes surface topography evolution in PBF-EB by melt pool type [33], it falls short to explain all details seen in this work. Clearly, surface topography development is connected to fluid dynamics. Especially the stability of thin fluid films, in combination with the local temperature field and the part boundaries are postulated to play a dominant role. For example, the following current numerical study investigates the effect of local substrate temperature on surface morphology [45].

Tracking the surface topography from layer to layer allows to compute the following quantities. The difference of powder scan topography \(n+1\) and melt scan topography n gives access to the local powder thickness. The difference from melt scan topographies \(n+1\) and n allows to isolate height differences to melt pool movements, which might allow to investigate hard to control geometrical features of complex parts in situ. Analysing the powder and melt scan topographies of layer \(n+1\) in combination gives access to mass transport phenomena.

It has to be noted that the melt surface topographies of all cubes (in Fig. 6a, c) seem to be slightly tilted towards the build surface boundaries. The reason for the phenomena is unclear at the point of writing. Possibly, the build surface bends globally build surface due to temperature differences between preheated build surface and the colder surrounding, but it could be as well a measurement artefact in ELO images, the computed gradients or the integration algorithm. None of the above could be be excluded or confirmed by the validation study of Sect. 4.2, since it has been conducted only on the cross part. Including the whole build surface in method validation might be possible, but is experimentally challenging and out of the scope this work. Additionally, any validation study on build surface topographies in additive manufacturing (AM) using ex situ measured surface topographies is forced to neglect the influence of temperature.

4.4 Surface topography and melt pool behaviour

Figure 7 tracks the evolution of surface topographies of powder and melt scan of the cross specimen from layers 158 to 163. The white arrows in the ELO images \(L^C\) and the black arrows in the height maps of the respective powder scans indicate, that the specimen borders are not as densely covered than the rest of the specimen. This behaviour alternates from left to right with the layer number and correlates with the rake movement, as explained in Sect. 4.1. But now, the previous observation can be quantified with the help of the surface topography of the powder scan. For example in layer 158, the rake moves from right to left over the elevated right edge of the cross which has a height of \(\sim {50\,\mathrm{\upmu \text {m}}}\). The depression to its left (black arrow) forms due the powder flicking phenomena explained above. Interestingly, the depression deepens due to melting, which can be quantified by the height map of the melt scan of layer 158 but cannot be observed in a single ELO image alone. Significant material transport has to occur, since the depressions and elevations at the \({10\,\mathrm{\text {m}\text {m}}}\) edges of the cross increase in magnitude. The same behaviour can be observed in the following layers.

Up to layer 160, the middle part of the cross shows a different surface morphology than the side arms, which can be explained by the difference in lateral velocity \(v_\text {lat}\). As described schematically in [33], trailing melt pools transport material predominantly in opposite scan direction, whereas partially permanent to permanent melt pools transport material backwards, orthogonal to the hatch direction.

The \({10\,\mathrm{\text {m}\text {m}}}\) sides of the cross allow to observe the effect of a trailing to partial permanent melt pool. The super-elevated edges form due to material deposition at the turning points. Contrarily, the side arms of the cross show swelling in their interior and depressions at the part boundaries, which indicates a permanent melt pool.

The surface topographies of the short arms of the cross transform immediately after layer 160, since the \(v_\text {lat}\) change (from 50 to \({130\,\mathrm{\text {m}\text {s}^{-1}}}\)) exceeds the local stability limit of the fluid films [33]. The topography of the middle part stays qualitatively the same, but the super-elevated edges shrink in height whereas the neighbouring depressions grow wider and less deep. A potential cause is that the \(v_\text {lat}\) change transforms the melt pool from a trailing to a partially persistent melt pool, which is known to produce smooth surfaces.

As indicated in Sect. 4.3, quantitative descriptors for the above topography changes can be computed by taking two subsequent (or more) layers into account. Using these, it might be possible to identify local melt pool behaviour in complex parts from the surface topographies obtained by powder and melt scans.

Fig. 7
figure 7

Layers 158 to 163 of the cross part. STSA corrected ELO images of the left detector and the respective surface topographies computed from powder and melt scan are shown

Full size image
Fig. 8
figure 8

Evolution of a the histogram of the height maps Z(x, y) of the melt surfaces of the cross and b the standard deviations of all parts as function of the layer number. Process parameter changes are indicated by grey vertical lines

Full size image

4.5 Sensitivity of surface topography to power changes

This section investigates surface topography evolution across the whole build, starting from the first stable layer up to the last layer of the build (layer numbers: 64–270). Figure 8a depicts the layer wise height map histogram evolution of the melt surfaces of the cross, similar as a spectrogram. Each height map forms a single color-encoded histogram, which is placed vertically in an image at the row position of the respective layer. The colormap depicts the probability that a measured surface point is found in a height bin. The single height maps of the cross have been obtained equivalent to Sect. 4.2. Clearly and as expected, the majority of the part is at a height of 0. At process begin, the minimal and maximal detected heights first shrink to then settle at approximately \(\pm {100\,\mathrm{\upmu \text {m}}}\). The process parameter change at layer 161 increase the width of the respective histograms. Interestingly, a substructure (at \(\sim {}{1e-2}{}\) and indicated by black arrows) forms in the spectrogram, which is roughly proportional to the standard deviations of the histograms and susceptible to the process parameter changes indicated by the gray lines.

Going further, Fig. 8b illustrates the evolution of the standard deviation \(\sigma\) of all parts (segmented in the same way as the cross) with the layer number. The parts are ordered after increasing \(v_\text {lat}\) and therefore decreasing \(E_A\). The \(v_\text {lat}\) change at layer 161 lowers the measured \(\sigma\) for all cubes, except cube 3 and the cross. The effect can be rationalized again by the smoothing effect of a partial permanent melt pool. All subsequent process parameter changes induce a standard deviation increase. The huge increase at layer 244 is depicted in the height maps of Fig. 6. At layer 255, the beam power is reverted to \({960\,\mathrm{\text {W}}}\) and the standard deviation rapidly recover the previous levels. This demonstrates a healing effect and underlines the importance of in situ surface topography reconstruction in layer-based control applications.

In summary, this section demonstrates the susceptibility of the surface topography of individual parts to all process parameter changes in this study. The potential of multi-detector ELO imaging to quantify surface topography changes locally, as well in complex parts, is obvious. But, clearly more work has to be done to develop a satisfactory descriptor (going beyond the standard deviation) which enables the connection of process parameters and surface topography locally.

5 Conclusion

This work is a first-time demonstration of in situ build surface topography measurements in PBF-EB using multi-detector ELO imaging. Accurate height maps of the whole build surface can be reliably obtained every layer of a build process. The method is validated successfully with an ex situ measured surface of an as-built part. Additionally, first applications are shown, which demonstrate that plenty of process relevant information can be gathered from the surface topography reconstructions of ELO powder and melt scans. The results underline the applicability of multi-detector ELO monitoring for future layer-based control applications.

Naturally, many new questions are raised by this study and are posed in the following in loose order. The depth resolution of the method depends on the lateral resolution of the gradient field and thereby on the lateral resolution of single ELO images. However, right now it is unknown how pixel dimension, beam profile and ELO imaging parameters interplay to limit the depth and lateral resolving capabilities of the method. To change that, accurate beam profile measurements need to be conducted in combination with ELO imaging parameter tests on defined specimens like the corrugated sheet metal object in [31]. To extent the proposed method to bigger build area sizes, it might be advantageous to test different surface reconstruction algorithms.. And most importantly, surface topographies of complex parts need to be connected to the locally applied process parameters via descriptors which allow future layer-based control applications.