Simulation-based process parameter optimization for wire arc additive manufacturing

Abstract

During manufacturing of components using wire arc additive manufacturing, specific cooling times are required to prevent overheating of the structure and geometrical distortions. Currently, these cooling times are inserted based on experience at certain interlayer temperatures — which reduces the reproducibility, leads to unwanted component properties, and increases the process time. In this contribution, instationary thermal finite element simulations are applied to compute the temperature evolution of additively manufactured components using the inactive element method. This allows to optimize the process parameters, which are — in our considerations here — the welding velocity and the cooling time of each layer, to reduce the total process time while achieving sufficient component properties. The optimization is carried out with the gradient-free Nelder–Mead simplex algorithm, where certain constraints of the process parameters are considered via penalty functions. To obtain reasonable simulation results, the temperature-dependent heat transfer of the experimental setup is modeled and calibrated with experimental data beforehand. It becomes apparent that thermal finite element simulations combined with a gradient-free optimization procedure are a suitable numerical tool to perform the optimization of process parameters for wire arc additive manufacturing. The optimized process parameters fulfill certain requirements regarding the cooling of the manufactured component. Moreover, the optimized parameters can significantly reduce the process time compared to manually chosen parameters. In our example, this is around 48 %.

1 Introduction

Among the continuously increasing number of additive manufacturing processes, wire arc additive manufacturing (WAAM) has gained significant interest in research and industry in recent years. WAAM is a metal additive manufacturing process that belongs to the group of directed energy deposition processes, see [18]. The general process can be described concisely: A wire filler material is fed through a nozzle and melted in an electric arc. Then, the liquefied material is deposited layer-wise on the component or base plate. The key advantages of WAAM are, among others, high deposition rates and the possibility to manufacture multi-material components. Comprehensive reviews of the current state-of-the-art for WAAM are provided by [45, 50]. Similar to joint welding processes, WAAM involves numerous process parameters. Determining a feasible parameter set necessitates either resource- and time-consuming experimental tests or numerical simulations. In recent literature, both experimental and numerical studies to improve the process parameters are covered.

[34] carried out an experimental study by varying the wire feed rate and the energy input while investigating microstructure and mechanical properties. Moreover, [55] investigated arc current, arc voltage, and welding velocity as process parameters based on the effective area of deposition. In their study, the authors adjusted the parameters on a single-layer bead and transferred the results to a thin wall. The layer geometry was also studied by [8] in a purely experimental study. Because of the layer-wise manufacturing process, WAAM-manufactured components can show an anisotropic mechanical behavior. Thus, [1] studied different inclination angles to reduce the anisotropy of the mechanical properties. A comprehensive experimental study was carried out by [57], wherein the authors investigated the influence of wire feed rate, welding velocity, and deposition strategy on the microstructure, mechanical properties, and weld bead geometry. Further, [32] employed Gaussian process regression to improve the productivity and shape quality of WAAM-manufactured components taking into account wire feed rate, welding velocity, and interlayer time. Of course, the different process parameters are influencing each other. Considering this, [49] investigated the combined effect of interlayer temperature and welding velocity for different cooling strategies.

In contrast to the aforementioned experimental studies, numerical simulations are also applied in several contributions to study the process parameters of WAAM or even to perform parameter optimization. In this context, [46] provide a comprehensive review of the state-of-the-art in modeling WAAM processes. The objectives of the reported process parameter studies using numerical simulation differ, for example, reduction of residual stresses or improving the geometrical accuracy of the manufactured components. Among others, [47] conducted a trajectory optimization of a single layer to control the temperature of the manufactured component. Therefore, the authors used mixed-integer optimization with partial differential equation constraints, see also [9] for a similar approach. Path planning for WAAM with finite elements to reduce residual stresses is also covered by [4]. In contrast, [59] focused on the part distortions and studied different deposition patterns and shell thicknesses of a half-cylindrical shell. Further studies dealing with the geometrical accuracy of the deposited layers are provided by [2, 60], where the interlayer temperature and wire feed rate [60] or the arc voltage [2] were considered as process parameters. It is well known that the thermal history significantly influences the microstructure of the manufactured component. Thus, [37] determine local solid-state phase fractions to finally predict the hardness of the material, whereas [56] varied the substrate preheating temperature to decrease temperature gradients. In another study, [42] provide an attempt to modify the process parameters of each layer through observation of the molten pool size to reduce both total part distortions and residual stresses. The optimization is based on adjusting the heat source power input, which is also done by [48]. Viola et al. [54] estimated the manufacturing time based on interlayer time using an analytical model for the thermal analysis of a single layer. Even neural networks can be utilized for predicting cooling times, as demonstrated by [16].

As mentioned above, the cooling time (also denoted as idle time, interlayer time, or interpass time), i.e. the cooling time after welding a layer, is important to prevent overheating of the structure, which leads to residual stresses due to thermal gradients that influence microstructural evolution. Prior research has shown that fixed cooling times are not advisable, because of the heat conduction in the build direction, see, for instance, [41, 53]. Therefore, it is recommended that cooling times are adjusted to increase with growing part height [58]. Apart from residual stresses, controlling the interlayer temperature, which is closely related to the choice of cooling time, is important to prevent bead solidification defects and to obtain adequate material properties [17]. Thus, in this work, we consider the welding velocity and the cooling time of each layer as parameters during the optimization. Numerical investigations of the cooling time in WAAM processes were performed, among others, by [33, 40]. However, some authors focused solely on the effect of the cooling time on thermal gradients [33]. Then, the cooling time was selected based on numerical simulations, but without taking into account additional process parameters or constraints on the cooling of the component.

In contrast to the aforementioned studies, we perform iterative optimization of the process parameters using thermal finite element simulations of the WAAM process. Moreover, apart from only reducing the overall process time, particular requirements regarding the cooling of the structure are considered during the optimization to also ensure sufficient material properties. This differs significantly from the studies in the current literature.

To achieve this, the basic optimization problem is formulated first in Sect 2. Afterwards, in Sect. 3, the numerical procedure to perform the simulations is recapped where finite elements and the so-called inactive element method are employed. Of course, reliable thermal simulations of the WAAM process require a calibration of the numerical model. Thus, in Sect. 4, the heat exchange of the welding setup with the environment is calibrated by drawing on experimental temperature data of a multilayer weld. Finally, the welding process parameters of each layer — welding velocity and cooling time — are optimized using a gradient-free optimization technique in Sect. 5 , and the manufacturability of the optimized parameters is validated with an experiment.

The applied notation is defined in the following manner: geometrical vectors are denoted as $\vec {a}$, column vectors and matrices at the global finite element level are indicated by bold-type italic letters , whereas column vectors and matrices on the local element level are represented by bold-type Roman letters .

2 Basic optimization problem

First of all, the basic problem is formulated based on the transient heat conduction equation

$$\begin{aligned} \rho (\vec {x}) c_{\text {p}}(\Theta ) \dot{\Theta }(\vec {x},t) = - {{\,\textrm{div}\,}}\vec {q}(\vec {x},t) + r_{\Theta }(\vec {x},t), \end{aligned}$$

(1)

where $\rho$ denotes the mass density, $c_{\text {p}}(\Theta )$ defines the temperature-dependent specific heat capacity, $\Theta$ symbolizes the absolute temperature, $\vec {q}$ the heat flux vector, and $r_{\Theta }$ represents a volumetric heat source. The heat flux vector is provided by Fourier’s model

$$\begin{aligned} \vec {q}(\vec {x},t) = -\kappa (\Theta ) {{\,\textrm{grad}\,}}\Theta (\vec {x},t) \end{aligned}$$

(2)

with the temperature-dependent thermal conductivity $\kappa (\Theta )$, which is assumed, for the first instance, to be isotropic and thus only a scalar quantity. Both the specific heat capacity $c_{\text {p}}(\Theta )$ and the thermal conductivity $\kappa (\Theta )$ are modeled by interpolating experimental data for mild steel from Brown and Song [12] according to App. A.

To solve the parabolic partial differential equation Eq. (1), boundary conditions and initial conditions are required,

$$\begin{aligned} \Theta (\vec {x},t)&= \overline{\Theta }(\vec {x},t){} & {} \quad \text {on} \; A^\Theta (t), \end{aligned}$$

(3)

$$\begin{aligned} \vec {q}(\vec {x},t) \cdot \vec {n}(\vec {x})&= \overline{q}(\Theta (\vec {x},t)){} & {} \quad \text {on} \; A^\text {q}(t), \end{aligned}$$

(4)

$$\begin{aligned} \vec {q}(\vec {x},t) \cdot \vec {n}(\vec {x})&= \hat{q}(\vec {x},t){} & {} \quad \text {on} \; A^\text {w}(t), \end{aligned}$$

(5)

$$\begin{aligned} \Theta (\vec {x},t_0)&= \Theta _0(\vec {x}){} & {} \quad \text {at} \; t_0. \end{aligned}$$

(6)

Dirichlet boundary conditions prescribing the temperature on the surface $A^\Theta$ are denoted by $\overline{\Theta }$. Moreover, $\vec {n}$ symbolizes the normal vector on the surface of the material body. The prescribed heat flux $\overline{q}$ on the surface $A^\text {q}$ for the case of convection and radiation reads

$$\begin{aligned} \overline{q}(\Theta ) = h(\Theta ) \left( \Theta - \Theta _\infty \right) + \sigma \epsilon (\Theta ) \left( \Theta ^4 - \Theta _\infty ^4\right) , \end{aligned}$$

(7)

see, for example, [26]. In Eq. (7), $h(\Theta )$ denotes the convection coefficient, which is temperature dependent. This is usually neglected in recent literature — which, however, is questionable from the authors’ point of view (as will be explained later on). Further parameters are the Stefan-Boltzmann constant $\sigma = 5.67 \times 10^{-8}\text { W m}^{-2}\,\text {K}^{-4}$ and the temperature-dependent surface emissivity $\epsilon (\Theta )$. Similar to the specific heat capacity and the thermal conductivity, the temperature dependence of the emissivity is modeled using experimental data and is described in App. A. It should be noted that the specific emissivity values depend on surface roughness, wavelength, etc. In Eq. (7), we do not distinguish between the temperature of the ambient air (in the convection term) and the temperature of surrounding surfaces (in the radiation term), but simply use $\Theta _\infty$. It is worth mentioning that $\overline{q}(\Theta )$ represents a temperature-dependent prescribed heat flux. Hence, this is denoted as a mixed boundary condition. Moreover, $\hat{q}$ in Eq. (5) defines a prescribed surface heat flux (Neumann boundary condition) which can be used as a heat source, see [19] for example. However, in this work, we apply a volumetric heat source $r_{\Theta }$ for the energy input, i.e. $\hat{q} = 0$. Instead of applying heat source models prescribing the heat flux, it is also possible to prescribe certain temperatures to consider the energy input from the welding arc, see [19, 35] for details regarding different models. Finally, Eq. (6) defines the initial temperatures at time $t_0$.

Fig. 1

Time-dependent domains of a material body

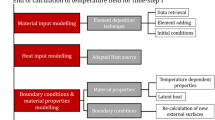
Figure 1 shows the domains of a material body under consideration of the entire surface A(t), which decomposes into the surface $A^\Theta (t)$, where the temperature is prescribed, the surface part $A^\text {q}(t)$, where non-linear boundary conditions are applied, and $A^\text {w}(t)$, where a heat source can be applied to model the energy input from the arc. For the entire surface, $A(t) = A^\Theta (t) \cup A^\text {q}(t) \cup A^\text {w}(t)$ holds. Since the structure evolves during an additive manufacturing process, all surface regions are functions of the time t. Of course, this holds for the volume V(t) as well, which decomposes into a region $V^\text {w}(t)$, where a volumetric heat source $r_{\Theta }$ is applied, and the remaining region $V^\text {d}(t)$, $V(t) = V^\text {d}(t) \cup V^\text {w}(t)$.

Fig. 2

a Heat source movement during WAAM process, b discrete welding bead with arc length s(t) and aligned marching cuboid for element activation

The movement of the heat source, which models the energy input from the welding arc in the real process, can be described with an arc length s(t), i.e. the distance covered by the welding arc during the process. In this work, we assume a constant welding velocity $v_{\text {w}}$ of the heat source during welding of one layer and $v_{\text {w}}= 0$ during cooling, see Fig. 2a. Of course, $v(t) = \dot{s}(t) \ge 0$ holds. During the real WAAM process, the movement of the welding robot is controlled with three-dimensional coordinate data in a G-code file. Here, this G-code information is used for the heat source movement in the numerical simulation. Thus, the movement of the heat source can be applied to perform the element activation that accounts for the evolution of the structure during the process. In this work, the inactive element method is employed for the finite element simulations using an in-house finite element code. Here, we refer to [36] regarding an overview of different element activation techniques in additive manufacturing process simulation. The particular methodology of the G-code-based element activation is explained in [51], where a continuous interpolation of the discrete G-code data is performed and an aligned marching cuboid is used for the element activation, see Fig. 2b. Moreover, [30] report similar steps towards an automation of finite element simulations for directed energy deposition processes. In this respect, the current position of the arc is modeled with the vector $\vec {r}_{\text {w}}(t) = \tilde{\vec {r}}_{\text {w}}(s(t)) = x_k(t) \vec {e}_k$, with the motion $x_k(t) = \tilde{x}_k(s(t))$.

In this contribution, we use finite elements to describe the evolution of the domain V(t) on the one hand and to provide information for the optimization of the process parameters , here the welding velocity $v_{\text {w}}(t)$ in each layer and cooling time after each layer, on the other hand. Hence, the total process time T, $t \in [t_0,T]$, should be minimized,

(8)

However, there are some process-related inequality constraints. First, the welding velocity $v_{\text {w}}(t)$ must be in a certain range. If the welding velocity is too small, then the weld pool dimensions increase and geometrical deviations occur. If it is too large, defects arise and the so-called humping can be observed. Thus,

$$\begin{aligned} v_{\text {w}}(t) \ge v_{\text {w,min}}, \qquad v_{\text {w}}(t) \le v_{\text {w,max}}\end{aligned}$$

(9)

with $v_{\text {w,min}}< v_{\text {w,max}}$, $v_{\text {w,min}}\ge 0$, and $v_{\text {w,max}}\ge 0$. Second, the cooling times $\Delta t_{\text {c}}$ should be positive,

$$\begin{aligned} \Delta t_{\text {c}}\ge 0. \end{aligned}$$

(10)

Besides constraining the process parameters $v_{\text {w}}$ and $\Delta t_{\text {c}}$, there are certain requirements to consider regarding the cooling of the structure. From materials science, it is known that the cooling time $\Delta t_{\text {8/5}}$ between ${800}\,^{\circ }\text {C}$ and ${500}\,^{\circ }\text {C}$ should not exceed a certain limit (maximum) $\Delta t_{\text {8/5,max}}$,

$$\begin{aligned} \Delta t_{\text {8/5}}\le \Delta t_{\text {8/5,max}}. \end{aligned}$$

(11)

Otherwise, coarse grains are obtained in the microstructure, leading to undesired component properties, e.g. brittleness, see [25] in the context of WAAM, for example. Moreover, to reduce thermal gradients and thus residual stresses in the manufactured structure, the interlayer temperature $\Theta _{\text {int}}$ should be below a certain limit $\Theta _{\text {int,max}}$,

$$\begin{aligned} \Theta _{\text {int}}\le \Theta _{\text {int,max}}. \end{aligned}$$

(12)

To summarize, in this work, we minimize the overall process time T of a wire arc additive manufacturing process while considering certain constraints of the process parameters, Eqs. (9) and (10), and requirements to the cooling of the manufactured structure itself, Eqs. (11) and (12).

3 Thermal finite element formulation for additive manufacturing processes

To solve the parabolic partial differential Eq. (1), we draw on a variational formulation yielding the weak form, which, according to [5], is denoted as principle of virtual temperatures in analogy to the well-known principle of virtual displacements in solid mechanics. Thus, virtual temperatures (test functions) $\delta \Theta (\vec {x})$ are introduced, which are assumed to be arbitrary, but zero at positions $\vec {x}$, where Dirichlet boundary conditions are present, i.e. $\delta \Theta = 0$ on $A^\Theta$. The principle of virtual temperatures reads

$$\begin{aligned} \pi _{\Theta }(t,\Theta ,\delta \Theta )&= \int _V \rho \, c_{\text{ p }}\, \dot{\Theta } \, \delta \Theta \, \text {d}V\nonumber \\ {}&\quad + \int _V \kappa {{\,\text {grad}\,}}\Theta \cdot {{\,\text {grad}\,}}\delta \Theta \, \text {d}V\nonumber \\ {}&\quad + \int _{A^\text{ q }} \overline{q} \, \delta \Theta \, \text {d}A^\text{ q } + \int _{A^\text{ w }} \hat{q} \, \delta \Theta \, \text {d}A^\text{ w }\nonumber \\ {}&\quad - \int _{V^\text{ w }} \rho \, r_{\Theta }\, \delta \Theta \, \text {d}V^\text{ w }= 0. \end{aligned}$$

(13)

Following the method of lines, the spatial discretization is carried out first, drawing on isoparametric finite elements according to the Bubnov–Galerkin method. Then, the temporal discretization is performed. Because of the spatial discretization, the volume V(t) and surface A(t) of the evolving structure change over to the approximations $\Omega (t)$ and $\Gamma (t)$, respectively. Moreover, a consistent matrix notation is applied in the following. Shape functions for temperature,

(14)

and the virtual temperature,

(15)

are introduced, where are the coordinates. As mentioned before, the virtual temperatures vanish at positions with prescribed temperatures, . Here, a decomposition into unknown nodal temperatures $\varvec{\Theta }{\, \in \mathbb {R}}^{n_{\Theta }}$ and prescribed nodal temperatures $\overline{\varvec{\Theta }}{\, \in \mathbb {R}}^{n_{\overline{\Theta }}}$ is already done. and denote vectors of shape functions. ${n_{\text {dof}}}= n_{\Theta } + n_{\overline{\Theta }}$ defines the temperature degrees of freedom. The temperature gradients and gradient of the virtual temperatures are required in Eq. (13). Thus,

(16)

and . Inserting these quantities into the weak form (13) and utilizing the arbitrariness of the virtual temperatures $\delta \varvec{\Theta }$ yields a large-scale system of first-order ordinary differential equations (ODEs),

(17)

However, since the domain of the material body expands during the additive manufacturing process, the matrices introduced in the ODE (17) differ from the classical formulation for thermal finite element simulations, see [44], for example. If the domain $\Omega _{n}$ is present at time $t_{n}$, then the domain extension at $t_{n+1}$ is considered with an increment $\Delta \Omega _{n}$, yielding $\Omega _{n+1}= \Omega _{n}\cup \Delta \Omega _{n}$. As a result, the matrices in Eq. (17) read

(18)

(19)

The quantity abbreviates the temperature-dependent heat flux from the boundary conditions (4) and (5) as well as the heat source term,

(20)

Further, it has to be considered that piecewise-defined initial conditions for each time-step from $t_{n}$ to $t_{n+1}$ are present,

(21)

The temperature $\Theta$ is obtained from the solution $\varvec{\Theta }$ of the previous time-step, and $\Theta _0$ corresponds to the given initial temperature.

For non-additive manufacturing applications, time-adaptive stiffly accurate diagonally implicit Runge–Kutta methods can be applied for the time discretization, see [44], whereas the non-smoothness of the initial data after domain extensions requires different strategies for additive manufacturing process simulation, see [28], where the time integration for evolving domains in additive manufacturing is studied. Based on the given temperatures $\varvec{\Theta }_{n}$ at time $t_{n}$ on $\Omega _{n}$, the aim is to determine the nodal temperatures $\varvec{\Theta }_{n+1}$ at $t_{n+1}$ on $\Omega _{n+1}$. In this work, we draw on the well-known Backward-Euler method. Then, for a given time-step size $\Delta t_n= t_{n+1}- t_{n}$,

$$\begin{aligned} \varvec{\Theta }_{n+1}= \varvec{\Theta }_{n}+ \Delta t_n\,\varvec{\dot{\Theta }}_{n+1}\end{aligned}$$

(22)

is obtained. In order to compute $\varvec{\Theta }_{n+1}$, a system of non-linear equations

(23)

has to be solved at each time $t_{n+1}$, where we apply the Newton–Raphson method.

In the aforementioned equations, it is apparent that the latent heat from phase changes is not yet considered. In general, there exist different techniques to account for latent heat effects, see [24] for a review. The apparent heat capacity concept is based on modifying the specific heat capacity. However, as [43] investigated, there are more suitable techniques, especially for simulating metal additive manufacturing processes, such as the proposed modified heat integration scheme. Moreover, [29] applied a method developed by [13] for the simulation of selective laser melting. Here, we use the approach by [39], where latent heat effects are considered by prescribing an additional heat contribution $r_{\text {lat}}$ that is proportional to the temperature velocity,

(24)

(25)

where $\Theta _\text {sol}$ and $\Theta _\text {liq}$ are the solidus temperature and liquidus temperature, respectively. The latent heat of fusion between the liquid and solid phase of the material is denoted with $h_{\text {lat}}$. The additional heat contribution $r_{\text {lat}}$ is then considered together with the volumetric heat source $r_{\Theta }$, $\tilde{r}_{\Theta }= r_{\text {lat}}+ r_{\Theta }$.

Moreover, it is worth mentioning that we apply the volumetric heat source on top of the previous layer, as indicated in Fig. 2b. Although this is quite common in WAAM process simulation, there are studies in which the heat source is placed on top of the current layer, see, for example, [42]. We refer to [39] for a discussion regarding the positioning of the heat source and follow the explanations therein to justify the position on the previous layer.

4 Model calibration

The numerical model for the process simulation has to be calibrated to yield reasonable results. This can be carried out by calibrating the heat source parameters representing the energy input [35, Sect. 8.5.2]. Moreover, the heat exchange with the environment should be considered as well. In this work, we take the heat source parameters from experimental data and accordingly calibrate only the heat exchange. First, the experimental setup is briefly explained, where the temperature is measured at two points on the base plate during welding of a thin vertical wall. Then, the numerical model for the calibration is described. Afterwards, the applied non-linear least-squares method is briefly recapped and the calibration results are provided, together with an uncertainty quantification.

Fig. 3

Geometry of experimental three-layer setup for model calibration with two thermocouples (blue)

4.1 Experimental setup

The calibration of the numerical model is done with temperature data from a three-layer weld. The geometry of the experimental setup is shown in Fig. 3, where the two thermocouples on the base plate are indicated by blue lines. The thermocouples were positioned at distances of 5 and 10 mm from the weld. The WAAM-process was performed with arc voltage $U = {17.7}\,\text {V}$ and arc current $I = {147}\,\text {A}$. Further, the wire feed rate $v_{\text {f}}= {4}\,\text {m/min}$ and welding velocity $v_{\text {w}}= {50\,\mathrm{\text {cm}\min }}$ were chosen representing common settings in WAAM. The zigzag lay-up strategy was used and an interlayer temperature $\Theta _{\text {int}}= {180}\,^{\circ }\text {C}$ was prescribed, yielding a total process time of 131 s for the three-layer weld. The welding filler material ISO 14341-A G 50 7 M21 4Mo was used with M21 shielding gas. It is worth mentioning that the cooling time after each layer, which is later on considered as process parameter in the optimization procedure, is not prescribed during this experiment. Instead, the interlayer temperature is experimentally measured at the end of the previously manufactured layer using a thermometer and the process is continued after reaching $\Theta _{\text {int}}$.

4.2 Numerical setup

According to [19], surface heat sources are suitable for welds with a small penetration depth. However, for the wire arc additive manufacturing process at hand, a moving volumetric heat source model is preferable. In this work, we choose the well-known Goldak model introduced by [20], which is frequently applied even for additive manufacturing process simulation, see [3] for a review. Geometrically, the Goldak model for additive manufacturing comprises two half-ellipsoids, confer [46], for example. The ellipsoid halves are distinguished into a front and a rear part, wherein the volumetric heat flux $r_{\Theta }$ in Eq. (1) is prescribed with a Gaussian distribution. For the front part

$$\begin{aligned} r_{\Theta }= & {} r_{\Theta ,\text {f}}(\hat{x}_1,\hat{x}_2,\hat{x}_3) \nonumber \\= & {} \displaystyle \frac{6\sqrt{3}f_{\text {f}}\, Q}{a_{\text {f}}\, b \, c \,\pi \sqrt{\pi }} \, \exp \!\left( -3\frac{\hat{x}_1^2}{a_{\text {f}}^2}-3\frac{\hat{x}_2^2}{b^2}-3\frac{\hat{x}_3^2}{c^2}\right) \end{aligned}$$

(26)

and rear part

$$\begin{aligned} r_{\Theta }= & {} r_{\Theta ,\text {r}}(\hat{x}_1,\hat{x}_2,\hat{x}_3) \nonumber \\= & {} \displaystyle \frac{6\sqrt{3}f_{\text {r}}\, Q}{a_{\text {r}}\, b \, c \,\pi \sqrt{\pi }} \, \exp \!\left( -3\frac{\hat{x}_1^2}{a_{\text {r}}^2}-3\frac{\hat{x}_2^2}{b^2}-3\frac{\hat{x}_3^2}{c^2}\right) \end{aligned}$$

(27)

hold. The moving coordinate system of the heat source is represented by the coordinates $\hat{x}_1$, $\hat{x}_2$, and $\hat{x}_3$. The factors $f_{\text {f}}$ and $f_{\text {r}}$ describe fractions of the deposited heat, yielding the continuity of the model with respect to the welding direction,

$$\begin{aligned} f_{\text {f}}= \displaystyle \frac{2a_{\text {f}}}{a_{\text {f}}+a_{\text {r}}}, \quad f_{\text {r}}= \displaystyle \frac{2a_{\text {r}}}{a_{\text {f}}+a_{\text {r}}}, \quad \end{aligned}$$

(28)

where $f_{\text {f}}+ f_{\text {r}}= 2$ holds. The total power input $Q = \eta \,UI$ is obtained with the arc efficiency $\eta$, arc voltage U, and arc current I. The geometry is described with $a_{\text {f}}$ and $a_{\text {r}}$, which are the ellipsoid semi-axis parameters in welding direction for the front and rear part, respectively. Accordingly, b and c are the semi-axis parameters of the width and depth directions. It is worth mentioning that the transient behavior of the weld pool length is usually neglected, confer [7]. Later on, the arc orientation is orthogonal to the welding direction in the experiments. Otherwise, the general double ellipsoidal model proposed by [15] has to be considered instead of the model given above.

The heat exchange of the structure with the environment is done by convection and radiation, see Eq. (7). In recent literature, a broad range of convection coefficients is reported for the simulation of WAAM processes, see [6, 14, 22, 39, 40] to name only a few. Usually, the convection coefficients are assumed to be temperature-independent — which, from the authors’ point of view, is questionable due to the large temperature range during welding, see the discussion in [21] as well. In this work, we thus apply temperature-dependent convection coefficients $h(\Theta )$, where the ansatz

$$\begin{aligned} h(\Theta ) = c_1\tanh (c_2\Theta ) + c_3 \end{aligned}$$

(29)

is chosen, i.e. the convection coefficient saturates at very high temperatures, which is in contrast to the polynomial ansatz chosen by [21]. As a result, the three coefficients $c_1$, $c_2$, and $c_3$ have to be calibrated with experimental data.

The geometrical parameters of the applied heat source model should approximately represent the weld pool dimensions and are prescribed based on literature data with comparable weld bead dimensions, [39]. Moreover, arc voltage U and arc current I are taken from the aforementioned experimental setup, while the arc efficiency $\eta = 0.8$ is chosen as a common value for gas metal arc welding processes. The heat source parameters are compiled in Table 1.

Table 1 Heat source parameters of Goldak model

The experimental geometry from Fig. 3 is spatially discretized with ${n_{\text {e}}}= 7280$ 20-noded hexahedral elements, leading to $n_\text {nodes}= 36743$. As shown in Fig. 4, the symmetry in $\vec {e}_3$-direction is employed and only one half of the structure is modeled. Since the inactive element method according to [36] is applied, the nodes and elements are subsequently activated depending on the heat source position. It should be noted that the convection and radiation boundary conditions on the interface between active and inactive elements of the evolving structure are considered in this work as well, see [51] for details of the procedure. An adiabatic boundary condition is assigned to the symmetry plane in $\vec {e}_3$-direction, i.e. $\overline{q} = 0$. At the bottom of the base plate, a prescribed heat transfer coefficient $\overline{h} = {100}\,\text {W m}^{-2}\,\text {K}^{-1}$ is considered to account for the contact between base plate and welding table, which is not modeled in detail here. All remaining surfaces are exposed to temperature-dependent convection and radiation boundary conditions compliant with Eq. (7). The ambient temperature is set to $\Theta _\infty = {23.5}\,^{\circ }\text {C}$, which is also the initial temperature of the newly activated elements. The time integration is done with the Backward-Euler method and a fixed time-step size $\Delta t \,= {0.4\,\mathrm{\text {s}}}$.

Fig. 4

Spatially discretized numerical model with boundary conditions

The material parameters, specific heat capacity $c_{\text {p}}$ and thermal conductivity $\kappa$ are modeled temperature-dependent according to App. A. The density $\rho = {7.85}\,\text {kg dm}^{-3}$ of the material is assumed to be temperature-independent. The latent heat of fusion $h_{\text {lat}}= {250}\,\text {J g}^{-1}$, solidus temperature $\Theta _\text {sol}= {1469}\,^{\circ }\text {C}$, and liquidus temperature $\Theta _\text {liq}= {1512}\,^{\circ }\text {C}$ in Eq. (24) are estimated from the values in [27] for steel.

4.3 Calibration with non-linear least-squares method

During the model calibration, i.e. the calibration of the parameters $\varvec{\beta }= \lbrace c_1, c_2, c_3 \rbrace ^T$, $\varvec{\beta }{\, \in \mathbb {R}}^{n_{\beta }}$, describing the temperature-dependent convection coefficient (29), the solution of Eq. (13) is required. For that purpose, we introduce the solution operator $S^{\, \text {LS}}$ assigning a unique temperature solution in time and space to each parameter set $\varvec{\beta }$,

$$\begin{aligned} \varvec{\beta }\mapsto S^{\, \text {LS}}(\varvec{\beta },.,.), \quad {\left\{ \begin{array}{ll} \text {where}\, \Theta =S^{\, \text {LS}}(\varvec{\beta },\vec {x},t) \, \text {satisfies }(3)\text { and }(13)\\ \qquad \qquad \qquad \text { for all }\delta \Theta \text { and }t\in \left[ t_0,T\right] , \\ \text {where}\, \Theta =S^{\, \text {LS}}(\varvec{\beta },\vec {x},t_0) \, \text {satisfies }(6). \end{array}\right. } \end{aligned}$$

(30)

However, as explained in Sect. 3, solving Eq. (13) with boundary conditions (3) and initial conditions (6) is carried out in a discrete manner using finite elements. Thus, we denote the solution operator , where N represents the total number of spatial and temporal temperature degrees of freedom.

The non-linear least-squares method serves to calibrate the numerical model, which is based on the convection model (29), based on the experimental temperature data. The objective function reads

(31)

where is the residuum vector. The observation operator extracts the temperatures at the experimental thermocouple positions from the numerical results. Further, $\vert \vert \cdot \vert \vert$ is the Euclidean norm. The experimental temperatures , , are measured at the thermocouple positions and then linearly interpolated, successively, to the simulated time points. Thus, data from $n_\text {t} = 219$ time points of the simulation are considered for the calibration, i.e. ${n_{\text {d}}}= 2n_\text {t}$. The aim is to minimize the discrepancy between experimental and simulation data,

$$\begin{aligned} \min _{\varvec{\beta }} f(\varvec{\beta }) \quad \text {i.e.} \quad \varvec{\beta }^* = \underset{\varvec{\beta }}{\text {arg min}}\, f(\varvec{\beta }), \end{aligned}$$

(32)

to obtain the solution $\varvec{\beta }^*$. The so-called normal equation

(33)

is received from the necessary condition of a (local) minimum — a vanishing gradient of the objective function. As a result, (33) represents a system of non-linear equations, where the Jacobian reads

(34)

. In this work, the solution of the optimization problem is conducted with the Nelder–Mead simplex algorithm from the MATLAB routine fminsearch, which is a gradient-free optimization method for unconstrained problems. The applied termination criteria read $\textrm{tol}_f = 0.1$ and $\textrm{tol}_{\varvec{\beta }} = 0.1$. Note that gradient-based optimization techniques could be applied as well for the model calibration.

The calibrated temperature cycles are shown in Fig. 5, where the subscript 1 indicates the thermocouple with 5 mm distance to the weld and, accordingly, the subscript 2 refers to the second thermocouple. It is evident that errors in the temperature peaks, which occur when the arc passes the thermocouple position, are present even for the calibrated model. In contrast, the cooling is well-captured, especially, for the first thermocouple. The obtained results are sufficient for the present work since the cooling of the structure has a significant influence on the process parameter optimization. The calibrated parameter set reads .

Fig. 5

Measured and computed temperature–time data at two points on the base plate

4.4 Uncertainty quantification

Besides obtaining a solution $\varvec{\beta }^*$ from the optimizing scheme, it is of particular interest to evaluate the quality of the fit and the reliability of the solution. This leads to the evaluation of quality measures and is established in the context of parameter identification for constitutive models, see, for example, [23, 52], but can easily be transferred to the model calibration in this work as well.

The Jacobian is evaluated in the solution $\varvec{\beta }^*$ by drawing on numerical differentiation, for which a central difference quotient is chosen. Then, the Hessian can be approximated

(35)

which is justified since in the solution holds. The evaluation of the Hessian is closely related to the issue of local identifiability of parameters. Therein, the solution $\varvec{\beta }^*$ is a suitable minimum of the objective function (31) if neither the determinant of the Hessian nor any sub-determinant vanishes, i.e. is positive definite. Another possibility to check the suitability of the obtained solution $\varvec{\beta }^*$ is the so-called statistical stability, which is explained in [11], which is beyond the scope of the present contribution. Moreover, the quality of the fit can be evaluated with the covariance matrix

(36)

$s^2$ denotes an estimate of the unknown variance of the residuals. The variances of the parameters $\varvec{\beta }$ in the solution $\varvec{\beta }^*$, i.e. the diagonal entries of the covariance matrix , allow to compute the parameter uncertainties $\Delta \varvec{\beta }^*$. As a result, a confidence interval with ${68.3\,\mathrm{\%}}$ confidence level is obtained for each parameter,

$$\begin{aligned} \varvec{\beta }_\text{ conf }= \varvec{\beta }^* \pm \Delta \varvec{\beta }^* \, \text{ with } \, \Delta \beta _i^*= \sqrt{P_{ii}}, \, i = 1,\ldots ,n_{\beta }. \end{aligned}$$

(37)

For the model calibration at hand, the smallest sub-determinant of the Hessian is obtained as $3 \times 10^{6}\,{m}^{4}\,^{\circ }\text {C}\,\text {K}^{2}\,\text {W}^{-2}$. Thus, the solution $\varvec{\beta }^*$ is a (local) minimum. The uncertainties of the parameters for a confidence level of 68.3 % are depicted in Table 2. During the model calibration, the process parameters, i.e. $v_{\text {w}}$ and $\Delta t_{\text {c}}$, are fixed from the experiment. Hence, the activation time of each element and the number of discrete time-points $n_{\text {t}}$ do not change during model calibration. This leads to smoothness of , which allows to compute for uncertainty quantification. The temperature-dependent convection coefficient according to Eq. (29) is visualized in Fig. 6, where the shaded area indicates the estimated uncertainty.

Table 2 Confidence intervals of the identified parameters for the model calibration

Fig. 6

Calibrated temperature-dependent convection coefficient $h(\Theta )$ with uncertainty (confidence level ${68.3\,\mathrm{\%}}$)

5 Optimization of process parameters

The main scope of this contribution is the optimization of the WAAM process parameters to minimize the overall process time T, which is simply the sum of welding $\Delta t_{\text {w}}^{(i)}$ and cooling times $\Delta t_{\text {c}}^{(i)}$ over all layers i, $i = 1,\ldots ,n_{\text {l}}$. Again, we draw on a three-layer vertical wall, $n_{\text {l}}= 3$, see Fig. 4, as an application example. It is worth mentioning that, of course, the general method is applicable to a higher number of welds or more complex geometries as well. Here, are the process parameters considered in the optimization, where the cooling after the last layer is not of interest, i.e. $\Delta t_{\text {c}}^{(n_{\text {l}})} = 0$. The solution operator S relates the process parameters to the temperature,

(38)

Since finite elements are applied in this work, the solution operator S is applied in a discrete setting for the process optimization, as explained in Sect. 3, leading to .

The objective function for the process parameter optimization reads

(39)

and should be minimized

(40)

The welding time $\Delta t_{\text {w}}^{(i)}$ is calculated from the welding velocity $v_{\text {w}}^{(i)}$ and the layer length L under the assumption of a constant velocity in each layer i, compare Fig. 2a. As already explained in Sect. 2, different constraints of the process parameters and constraints concerning the cooling of the structure have to be considered during the optimization. These are enforced using a penalty factor p in the objective function (39). $\langle \cdot \rangle$ are the Macaulay-brackets with the properties $g(x) = \langle x \rangle$, $g(x) = 0$ for $x < 0$ and $g(x) = x$ for $x \ge 0$. Wherever possible, time quantities are employed in the objective function. Thus, the constraints (9) concerning the welding velocity are re-formulated

$$\begin{aligned} \Delta t_{\text {w,min}}= \frac{L}{v_{\text {w,max}}}, \qquad \Delta t_{\text {w,max}}= \frac{L}{v_{\text {min}}}. \end{aligned}$$

(41)

The restriction to positive cooling times $\Delta t_{\text {c}}^{(i)}$ is enforced with a penalty term as well.

Moreover, the constraints regarding the cooling of the structure, $\Delta t_{\text {8/5,max}}$ (11) and $\Theta _{\text {int,max}}$ (12), are considered in the objective function (39). The evaluation of $\Delta t_{\text {8/5}}^{(i)}$ is performed on top of layer i, centered in length and thickness direction. Here, represents the cooling time between ${800}\,^{\circ }\text {C}$ and ${500}\,^{\circ }\text {C}$ for layer i, which is extracted from the numerical results by means of the observation operator $O_{\text {8/5}}^{(i)}:\mathbb {R}^{N}\rightarrow \mathbb {R}$. The interlayer temperatures $\Theta _{\text {int}}^{(j)}$ are determined in a similar manner at the end of layer j, right before the welding of the next layer begins, i.e. the temperature is evaluated at time $t_{\text {int}}^{(j)} = \sum _{k=1}^j(\Delta t_{\text {w}}^{(k)}+\Delta t_{\text {c}}^{(k)})$. Again, an observation operator $O_{\text {int}}^{(j)}:\mathbb {R}^{N}\rightarrow \mathbb {R}$ is used to determine the required interlayer temperatures from the numerically computed results, . The numerical setup described in Sect. 4.2 is used unchanged with the calibrated heat exchange. Moreover, $w_{\text {t}}= 1 {\text {s}^{-1}}$ and $w_{\Theta }= 1\,{{{}^{\circ }\text {C}}^{-1}}$ are introduced as weighting factors to obtain a dimensionless objective function (39).

The optimization is once again done with the Nelder–Mead simplex algorithm since the penalty terms and the element activation lead to non-differentiabilities in the objective function and the solution operator . To be more specific, in contrast to the model calibration, where a certain element has a fixed activation time, the process parameter optimization leads to different activation times of an element during optimization. Moreover, it is important to note that if larger problems, e.g. with several welding layers, are considered, the rather simple derivative-free optimization method would have to be replaced, because it does not admit any theoretical complexity guarantees and the runtime for more degrees of freedom becomes quickly prohibitive in practice. In this case, derivative-based optimization methods need to be employed for efficiency. They require the efficient computation of the derivatives of the objective function, which is subject to further research.

The welding velocity $v_{\text {w}}^{(i)}$ can be different in each layer, but is restricted with $v_{\text {w,min}}= {5}\,\text {mm s}^{-1}$ and $v_{\text {w,max}}= {10}\,\text {mm s}^{-1}$. Furthermore, $\Delta t_{\text {8/5,max}}= {20\,\mathrm{\text {s}}}$ and $\Theta _{\text {int,max}}= {180}\,^{\circ }\text {C}$ are chosen for the steel under consideration. To achieve constraint satisfaction, a penalty factor of $p = 1000$ was found to be sufficient during pre-tests, where it was observed that $p=10$ and $p=100$ does not lead to exact constraint satisfaction. For simplicity, the same penalty factor is used for all terms in the objective function (39). Of course, different penalty terms could be used instead, whereas the specific choice depends on the problem at hand.

The optimization scheme yields the solution . The welding times $\Delta t_{\text {w}}^{(i)}$ in correspond to the welding velocities $v_{\text {w}}^{(1)} = {10}\,\text {mm s}^{-1}$, $v_{\text {w}}^{(2)} = {6.95}\text { mm s}^{-1}$, and $v_{\text {w}}^{(3)} = {7.56}\text { mm s}^{-1}$. The process time $T = {50.6\,\mathrm{\text {s}}}$ is minimized, while all constraints regarding the process parameters and cooling are sufficiently satisfied. The cooling behavior of the layers is shown in Fig. 7. The peak temperatures, where the heat source moves across the nodes, are quite high — which is in accordance with the current literature on the Goldak heat source, see the remarks in [38, 46], for example. Moreover, the interlayer temperatures right before starting the next layer are shown in Fig. 8. It should be mentioned that there are regions of the previous layer that slightly exceed the maximum interlayer temperature $\Theta _{\text {int,max}}$. However, as the start of the next layer is considered in the optimization scheme, these points fulfill constraint (12). The interlayer temperatures with the optimized parameter set are $\Theta _{\text {int}}^{(1)} = {174}\,^{\circ }\text {C}$ and $\Theta _{\text {int}}^{(2)} = {180}\,^{\circ }\text {C}$ for the first and second layer, respectively. The cooling time between ${800}\,^{\circ }\text {C}$ and ${500}\,^{\circ }\text {C}$ is quite similar for all three layers, $\Delta t_{\text {8/5}}= {3\,\mathrm{\text {s}}}$, see Fig. 7.

Fig. 7

Cooling behavior of the layers for optimized process parameters

Fig. 8

Temperature distribution after cooling of a first layer and b second layer

Fig. 9

Three-layer vertical wall welded with optimized process parameters

Although specific constraints of the process parameters are incorporated into the objective function (39), the optimization procedure might lead to a parameter set, which is not suitable for real-world application. To show the manufacturability of the optimized process parameters, Fig. 9 visualizes the three-layer vertical wall manufactured with the optimized set of process parameters . Thus, it is evident that suitable process parameters for wire arc additive manufacturing processes can be obtained from an iterative optimization procedure using thermal finite element simulations. Moreover, the process parameters for the model calibration in Sect. 4.1 were chosen manually in the experiment, under consideration of an interlayer temperature $\Theta _{\text {int,max}}= {180}\,^{\circ }\text {C}$ leading to a process time of 98.5 s. In contrast, the optimized process parameters result in a process time $T = {50.6}\,\text {s}$. Hence, the process time is reduced by 48 % compared to the manually chosen parameters, which have to be carefully selected based on experience to prevent overheating of the structure.

6 Conclusions

The present contribution provides a novel attempt for the process parameter optimization of wire arc additive manufacturing processes. The process parameters under investigation are the welding velocity and cooling time of each layer, where the latter are usually chosen manually based on experience. In this work, the process parameter optimization is iteratively carried out using a gradient-free optimization scheme. For this purpose, thermal finite element simulations are performed using the inactive element method and a G-code-based element activation. It turns out that, once the numerical model is calibrated with experimental data, the process parameter optimization yields reliable results and allows a significant reduction of the total process time compared to manually selected process parameters without numerical simulations. Simultaneously, desired material properties are ensured with particular constraints regarding both the process parameters and the cooling of the manufactured structure itself, which are sufficiently satisfied in the optimized parameter set. The manufacturability of the optimized parameters is demonstrated for the investigated geometry of a three-layered thin vertical wall.

Fig. 10

Temperature-dependent thermal material properties from Brown and Song [12] for mild steel with calibrated fit for numerical simulation

Appendix A: Temperature-dependent material properties

With regard to the numerical simulation of a welding process, the thermal material parameters — specific heat capacity $c_{\text {p}}(\Theta )$ and thermal conductivity $\kappa (\Theta )$ — and the surface emissivity $\epsilon (\Theta )$ as additional parameter, are required. Because of the broad temperature range in welding simulations, the temperature-dependence of the material parameters has to be considered. For this purpose, in a first step, reference is made to the data in [12], see Fig. 10. Above a certain temperature, a phase transition in the solid state takes place in steels. Thus, the material properties exhibit a kink. For smoothing, we use the concept of logarithmic interpolation of Kreisselmeier and Steinhauser [31], see also the discussion of the interpolation properties in [10]. A similar approach to the proposal outlined below has already been described in [44]. The logarithmic interpolation

$$\begin{aligned} f(x) = -c \ln \left( \frac{e^{-f_1(x)/c} + e^{-f_2(x)/c}}{2}\right) \end{aligned}$$

(A1)

has the property that, for a positive value c, the function f(x) tends to the function with lower function values. Thus, c controls the smoothness at the intersection point $x_0$, i.e. where $f(x_0) = f_1(x_0) = f_2(x_0)$. In the case of the specific heat capacity $c_{\text {p}}(\Theta )$, the ansatz

$$\begin{aligned} c_{\text {p}}(\Theta ) = -c_{\text {c}}\ln \left( \frac{e^{-c_{\text {p}1}(\Theta )/c_{\text {c}}} + e^{-c_{\text {p}2}(\Theta )/c_{\text {c}}}}{2}\right) \end{aligned}$$

(A2)

with the functions

$$\begin{aligned} c_{\text {p}1}(\Theta )&= a_1 e^{a_2 \Theta } + a_3, \quad \text {and}\nonumber \\ c_{\text {p}2}(\Theta )&= a_4 e^{a_5 (\Theta - a_6)} + a_7 \end{aligned}$$

(A3)

is chosen. The interpolation factor $c_{\text {c}}= 20$, the curve parameters $a_3 = {400}\,\text {J kg}^{-1}\,\text {K}^{-1}$ and $a_7 = {400}\,\text {J kg}^{-1}\,\text {K}^{-1}$ for the constant values, and $a_6 = {725}\,^{\circ }\text {C}$ describing the transition temperature, are fixed. Then, the calibration of the remaining parameters is done using a non-linear least-squares approach, confer Subsect. 4.3, and the Nelder–Mead simplex algorithm, which is implemented in the MATLAB routine fminsearch. The parameters $a_1 = {22.061}\,\text {J kg}^{-1}\,\text {K}^{-1}$, $a_2 = {5e-3\,\mathrm{{{}^{\circ }\text {C}}^{-1}}}$, $a_4 = {1376.36}\,\text {J kg}^{-1}\,\text {K}^{-1}$, and $a_5 = {0.0189\,\mathrm{{{}^{\circ }\text {C}}^{-1}}}$ are obtained. Here, the original data is assumed to be constant for $\Theta > {1500}\,^{\circ }\text {C}$ in the calibration. For the procedure and discussions later on, the accuracy of the calibration is assumed to be sufficient.

Next, the heat conductivity $\kappa (\Theta )$ is considered. The experimental data in Fig. 10b indicates that the first function should have a saturation value and the second function is assumed to be linear

$$\begin{aligned} \kappa (\Theta ) = c_{\kappa }\ln \left( \frac{e^{\kappa _{1}(\Theta )/c_{\kappa }} + e^{\kappa _{2}(\Theta )/c_{\kappa }}}{2}\right) \end{aligned}$$

(A4)

with $c_{\kappa }= 1$ and the functions

$$\begin{aligned} \kappa _{1}(\Theta )&= \frac{b_1}{2} (1 - \tanh (b_2(\Theta -b_3))) \quad \text {and} \nonumber \\ \kappa _{2}(\Theta )&= b_4 \Theta + b_5. \end{aligned}$$

(A5)

The calibration yields the parameters $b_1 = {57.385}\,\text {W m}^{-1}\text { K}^{-1}$, $b_2 = 1.6 \times 10^{-3}\,^{\circ }\text {C}^{-1}$, $b_3 = {765.2}\,^{\circ }\text {C}$, $b_4 = 5.9 \times 10^{-3}\,\text {W m}^{-1}\,^{\circ }\text {C}^{-1}\,\text {K}^{-1}$, and $b_5 = {21.6}\,\text {W m}^{-1}\,\text {K}^{-1}$.

The emissivity $\epsilon (\Theta )$ is modeled without logarithmic interpolation since the experimental data in Fig. 10c shows a saturation behavior with increasing temperature. Thus, the ansatz

$$\begin{aligned} \epsilon (\Theta ) = \frac{c_1}{2} (1 + \tanh (c_2 \Theta )) - c_3 \end{aligned}$$

(A6)

is chosen, where the parameters $c_1 = {}{0.710}{}$, $c_2 = {3.58e-3\,\mathrm{{{}^{\circ }\text {C}}^{-1}}}$, and $c_3 = {}{0.128}{}$ are determined. The response of the calibrated models (A2), (A4), and (A6) are shown in Fig. 10a–c.