Abstract
A crucial step in the powder bed metal additive manufacturing process is the formation of a thin layer of powder on top of the existing material. The propensity of the powder to form thin layers under the conditions used in additive manufacturing is critically important, but no test method has yet been established to measure this characteristic, which is sometimes referred to as spreadability. The current work spreads a single layer of powder using commercial equipment from the paint and food industries and derives the density of a layer of powder, which is of a similar thickness to that in additive manufacturing. Twenty-four powders from eight suppliers have been tested and the density of the layers has been measured as a function of various parameters. Twenty-two of the powders successfully form thin layers, with a density of at least 40% of each powder’s apparent density. Hall flow time did not correlate with the spread layer density, although the two powders that did not spread did not pass through the Hall funnel. The roughness of the plate onto which the powder was spread, the recoater speed, the layer thickness, particle size and aspect ratio all affect the measured layer density. Results of the new test are repeatable and reproducible. These findings can be used to develop a test for spreadability for metal powders that can be used for additive manufacturing, which will help to improve the quality of printed components.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In powder bed fusion processes, powder is spread into thin (< 100 µm) layers. This layer is melted by a heat source or fused using a binder to build a component. The spreading of the powder is crucial but is much less studied than other process steps. There is no established technique or metric for quantitative analysis of a powder when it is spread. Even relevant standards for the characterisation of feedstock for additive manufacturing either omit the word “spread” [1] or state that measurement techniques are under development [2]. The degree to which a powder may be spread into thin layers under the action of an externally applied force, such as from a blade or roller, is often called “spreadability”, although no exact definition of the term has yet been agreed or standardised.
The behaviour of a powder ensemble when it is compelled to move by an external force is known as flowability, which is taken to be high when powder moves easily under an external force. A more detailed definition of “flowability” depends on the test technique used to quantify it. There are already many techniques to measure powder flowability. In literature, the suitability for powder in additive manufacturing has been related to flowability but not to spreadability, including early relevant publications [3,4,5,6,7]. However, “layer quality” or “layer density” is sometimes mentioned as important for the final quality or density of printed parts. Some studies mention powder spreading, but few consider this as a characteristic like a flowability [8, 9].
Flowability and spreadability both require the motion of particles past each other, and each may be representative of the other, but this is not yet established. In polymer powders, spreading is used as a measure of flow behaviour [10]. However, for metals, the relevant standard states: “Flowability … is not necessarily correlated to spreadability” [2]. Therefore, dedicated measurements of spreadability must be made. If spreadability cannot be measured, the development of new powders for additive manufacturing will be slower and more expensive. The expected growth of additive manufacturing would then be restricted.
There has been recent progress to develop a robust and convenient spreadability test. Spreadability has been shown to depend on the blade used to spread the powder [11], particle size distribution [12] and moisture content [13, 14]. Spreadability measurements can be used to infer print performance in-situ [15]. A review of possible techniques indicates that image analysis or mass-based measurements using an automated spreading machine are sufficient to indicate spread quality [16, 17]. To ensure that a test could be implemented easily in a laboratory or industry, one proposal is to spread powder manually and classify the powder layer appearance [18]. This is likely to be sufficient for an approximate qualitative indication, but perhaps not for the qualification of new powders. Furthermore, the need for manual spreading might make the technique difficult to repeat or reproduce. X-ray imaging provides very detailed information about the layer thickness and surface condition, which is very good for fundamental knowledge but requires specialist X-ray equipment [19]. This is, therefore, likely to be impractical for day-to-day testing and evaluation. Surface analysis using 3D scanning is promising, but it requires detailed post-processing and may be too slow and expensive for day-to-day research, which may demand a simpler experimental procedure. Recent work, for example, uses a document scanner head to capture the whole powder layer [20]. Alternative studies have assessed powder layers in various situations using digital cameras [21,22,23], three-dimensional scanning [24], interferometry [25,26,27] and thermal measurements [28].
The current study presents the development of a simple, inexpensive and semi-automated test based on equipment from the paint/food industries and simple laboratory equipment that calculates the density of powder in a thin layer [14]. To ensure clarity and provide sufficient detail, the current article aims only to present the method thoroughly and benchmark it against a traditional test, namely the Hall flowmeter [29], as well as demonstrate that the technique is sensitive to changes in common powder characteristics. Future articles will analyse the behaviour of specific powders during this test, analyse the reasons for such behaviour and present detailed comparisons with a theoretical foundation between this test and other common tests for powders used in additive manufacturing, such as powder rheometry and rotating powder analysis [2, 5, 30, 31].
2 Materials and methods
2.1 Powders
Twenty-four commercially available powders were tested, including steels, a nickel-base superalloy, a titanium alloy and an aluminium alloy (Table 1). These powders represent a variety of powders that are used in powder bed additive manufacturing processes and allow the sensitivity of the test to changes in powder characteristics, such as size distribution and chemistry, to be tested. Since this study aims to derive a test methodology, not to explain or justify any correlations, detailed characterisation of each powder (e.g. satellites, surface condition) is not presented here.
During the initial development of the test method, powders G and K were used most extensively, as it was already known from experience that they should spread well under conditions used in this study. The other powders were then used to test the method and investigate its sensitivity.
2.2 Size distribution and shape
Particle size distribution and shape were determined using dynamic image analysis in a Camsizer XT (Retsch GmbH, Germany) with the X-Jet module. Each powder sample was approximately 10 g for steel powders and an equivalent volume for the nickel and aluminium-based powders. The size of each particle is defined as the shortest possible Martin diameter. The aspect ratio is defined in this study as each particle’s shortest possible Martin diameter divided by its longest possible Martin diameter. For each powder, the mean aspect ratio of all particles measured in the ensemble is reported. The number of particles tested was well in excess of the minimum number required by the relevant global standards (ISO 13322-2:2014 and ISO13322-1:2014). Samples were taken from larger batches using riffling, in accordance with the relevant standard (ISO 14488:2007).
2.3 Spreadability test
Spreadability tests were performed using a TQC Sheen (Metamora, Michigan, USA) AB4120 Automatic Film Applicator with a custom-made 316L steel plate as a surface onto which the powders were spread (Fig. 1). One side of the plate was milled to a fine finish, the other was left in the as-received condition. A through-thickness square section was removed from the plate using wire electro-discharge machining (Fig. 2). This section is wider than the powder layer that will be formed, so excess powder from the entire width of the layer may be collected in a container placed beneath the hole.
Elcometer 3560/1 and 3560/2 gap applicators (Elcometer Ltd, Manchester, UK) were used to spread the powders, with adhesive tape to restrict each layer to 50 mm width (Fig. 3). The edges of these spreaders are higher in the centre to allow powder to pass out of a central hole and be spread into a thin layer. Each edge is machined to a different height above the base of the spreader. The tape was folded such that the amount of powder adhering to the tape was minimised and the resulting arrangement was measured using a micrometer to be (50 ± 2) µm thick. Adding the tape to the quoted height of the layers formed by each of the four edges of the applicators, the resulting layer thicknesses available were 80 μm, 110 μm, 140 μm or 170 μm (3560/1) and 100 µm, 150 μm, 200 μm or 250 μm (3560/2). Both applicators were demagnetised using a commercial instrument (Bekker Magnetics BV, Eindhoven, Netherlands). The applicator is placed in front of the spreading bar (Fig. 1), which pushes the applicator during the spreading operation and leaves a powder layer behind. These gap applicators are compliant with the relevant standard for the formation of thin films of paints and coatings (ASTM D823-18) [32].
Elcometer 3560/2 gap applicator (a) top/bottom view without tape, showing the as-received geometry; b side view showing the possible layer heights in the as-received condition; c top/bottom view with tape added to reduce the transverse width of the spread layer to 50 mm and d side view of the spreader with tape added, showing the effect on the layer heights formed by each spreading edge
Recoater speeds from 1 mm s−1 to 500 mm s−1 were used, which is the entire range of speeds available with the equipment used in this study. The speed of the recoater mechanism was validated using a SICK DT20 Hi (Sick AG, Waldkirch, Germany) laser distance meter capable of measuring the entire spreading operation.
The roughness of the plate onto which the powders were spread was measured using an Alicona InfiniteFocusSL 3D measurement system (Alicona Imaging GmbH, Graz, Austria). Each measurement covers \(50\text{ mm}\times 50\text{ mm}\), with a minimum height resolution of 0.1 µm and minimum measurable arithmetic mean roughness of 0.15 (using “\(\times 10\)” magnification).
A sample of powder is first weighed using a Precisa BJ 1000C balance with a tolerance of ± 0.01 g (equivalent to approximately ± 0.05% in density within the layer). It is then poured into the gap applicator to an approximately even height across the entire width. To simplify the process, the thickness of the poured powder is not controlled precisely (cf. the procedure to pour powder in a Hall flow test). However, if the starting volume is twice the layer volume, the spread layer properties were found to be independent of pouring. The spreading bar is then moved across the base plate at the desired speed. A small mass of powder forms a thin layer on the base plate; excess powder is recovered in a plastic container that is placed under the hole cut into the base plate (Fig. 2). Some powder also adheres to the gap applicator during each spreading operation. Both the container (with the excess powder in it) and the gap applicator are weighed using the same balance that was used to weigh the initial powder sample. Before this weighing, the balance is tared with both the clean gap applicator and the empty container, so that the mass of excess powder may be measured directly. By subtracting this from the initial mass of powder, it is possible to determine the mass of the powder in the layer. The nominal width (reduced to 50 mm using the tape), length (393 mm due to the position of the spreading bar and the size of the base plate) and thickness of the spread layer are known, so the spread layer density may be calculated. The geometry of the spread layer was also measured independently using an ATOS Core 200 three-dimensional scanner (GOM GmbH, Braunschweig, Germany) with a point spacing of 0.08 mm. This instrument is not as precise as the Alicona InfiniteFocusSL but can be used to perform measurements on freestanding objects, while any object must be placed on the stage of the Alicona instrument for measurement. Transferring the base plate onto the measurement stage of the Alicona instrument is likely to disturb the powder layer and lead to inaccurate results, so the ATOS instrument was preferred.
The theoretical volume of a layer 500 µm (0.5 mm) thick–the maximum envisaged in future tests–has a volume of \(393\times 50\times 0.5=9800 \, {\text{mm}}^{3}=9.8 \,{\text{cm}}^{3}\). Therefore, 25 cm3 was selected as the starting volume to ensure more than double the layer volume will be used while limiting the amount of powder required. The gap applicators used in this study have a maximum capacity of 50 cm3, so if a thicker or wider layer is required, the starting volume can be adjusted accordingly within this limit.
2.4 Flowability measurements
Flowability was measured using a Hall flow meter (ACuPowder International LLC, Union City, USA), in accordance with the relevant industry standards (ASTM B212-17 and ISO 4490:2018) [29, 33]. Three tests were performed for each sample.
2.5 Density measurements
The apparent density was measured using a 25 cm3 cup below the Hall flow funnel (Sect. 2.4), in accordance with the relevant standard (ASTM B212-17) [29]. Three measurements were taken for each sample.
Tap density was measured after 3000 taps using a Quantachrome Autotap Tap density tester with a 25 cm3 cylinder (Anton Paar GmbH, Graz, Austria), in accordance with the relevant standard (ISO 3953:2011) [34].
Layer density was calculated by weighing the mass of powder that did not form part of the layer and subtracting this from the starting mass of powder. The resulting mass was then divided by the nominal layer volume, calculated from the nominal thickness and area.
3 Results
3.1 Layer profile
Profilometry data plotted for powder G along the transverse (\(x\)) direction (Fig. 1), at positions 5 cm and 10 cm from the start of the spread layer in the spreading (\(y\)) direction spread to various nominal thicknesses at \(150\text{ mm }{\text{s}}^{-1}\), show that the layers are all very close to the nominal width of \(50\text{ mm}\); the sides of the layers are steep (Fig. 4). The average measured thickness (\(z\)-dimension) of the layer is close to the nominal thickness in each case except 100 µm (Table 2). The powder and recoater speed were selected arbitrarily and other data indicate that these results apply to all powders and recoater speeds used in this study.
3.2 Base plate roughness
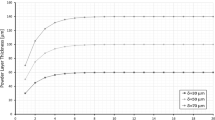
Roughness measurements for both faces of the base plate show that the milling gave a significantly smoother surface (Fig. 5, Table 3). The roughness of the build plate leads to a boost in measured layer density for thin layers but seems to be detrimental to layer density in thicker layers (Fig. 6).
3.3 Recoater speed
Increasing the recoater speed leads to a decrease in measured density. This effect is much more pronounced for the milled side of the plate. At the lowest recoater speeds and using the side of the plate in the as-received condition, the layer density exceeded the apparent density (Fig. 7). This plot is representative of all powders used in this study.
3.4 Layer dimensions
The measured areas of all layers were slightly greater than the nominal area. Since the areas and thicknesses of all layers above 100 µm nominal thickness are close to the measured values, the volumes and densities are also similar (Table 4). All layers had an area close to the nominal value.
On the as-received surface, layer thickness has no systematic influence on the measured density of powder G for layer thicknesses above 80 µm. The measured layer density increases systematically with layer thickness on the milled surface (Figs. 6, 8). This was consistent for all powders in this study.
3.5 Repeatability and reproducibility
One dataset within this study was taken a second time by an independent operator to assess the reproducibility of the method. All measurements lay within one standard deviation of the mean for each operative and the two mean results agreed within standard deviation (Table 5).
Data taken in this study show that the method described here gives similar results to other sources (Fig. 9).
3.6 Spreadability metrics
It is evident from the layer densities measured for all powders in this study that two powders (H and X) have extremely low spreadability, while the remaining powders exhibit similar performance (Fig. 10, where the height of the bar for each powder is the median value of eight measurements and error bars show the range of the measurements; powders that flowed through the Hall funnel are filled in solid and those that did not are hashed).
By combining the median layer density and other powder characteristics, it is possible to show that the results of the method described here are affected by commonly reported powder characteristics: an increase in \({d}_{50}\) seems to lead to a decrease in tap density and layer density but an increase in apparent density (Fig. 11a). An increase in aspect ratio seems to lead to an increase in all density metrics (Fig. 11b).
3.7 Relation to performance in a 3D printer
To test the applicability of the test method to additive manufacturing, one of the powders in this study was used as feedstock in an EOS M290 3D printer, which operated at a recoater speed of 150 mm s−1 (Fig. 12). Most of the powders in this study were of insufficient mass to be spread in the printer, but alloy X was available in suitable quantity. Another powder that was known to spread well in the printer was also used to show that the print conditions can generate good layers if the powder is suitable.
4 Discussion
Three-dimensional optical profilometry (3D scanning) shows that the layers have a width that is very close to the desired 50 mm and have steep sides (Fig. 4). This justifies the assumption that is used in the density calculations that the layers are cuboidal to a good approximation. The length of the layer is fixed by the starting point and the edge of the plate. Profilometry also shows that the layer thicknesses are close to the nominal values above 100 µm. Since the gap applicators had tape added to the bottom of them to limit the lateral spread of the powder which raised them (Fig. 3), the minimum thickness that was achievable was 80 µm, even though the spreader is sold with the capacity to form a 30 µm layer.
The larger discrepancy between nominal and measured layer thickness in the 100 µm (nominally) thick layer (Table 2) has not been explained. However, it is believed that this effect is caused by the fact that the layer thickness is only a small multiple of the size of many particles in the powder used for these measurements (powder G). This powder has a d50=28 µm and a d90=41 µm. Therefore, in the case of a layer formed from a 100 µm gap it will contain many particles that have a diameter around half the nominal layer thickness. This could cause many particles to be pushed ahead of the gap applicator. Thicker layers may avoid this affect due to the greater gap through which particles can pass. Such behaviour is not yet fully understood and this explanation is merely conjecture at this time, but it is a topic that should be further investigated in dedicated experiments or computer simulations using techniques such as discrete element modelling.
It has been shown that the test method of collecting powder, weighing it and deriving the density of the powder in the spread layer may be repeatable and reproducible (Table 5). Comparing the current results to other studies shows that the results are consistent with other measurements (Fig. 9). This implies that the proposed methodology gives representative and reasonable results. Further tests are required with more operators using a range of test parameters and materials to increase the confidence in the repeatability and reproducibility of the test and analysis methods.
The surface on which the powder is spread clearly influences layer density. Rough surfaces allow particles to sit in the low regions, which will allow the incorporation of fine particles into the layer. The plate in the as-received condition has low regions that are 27 µm below the mean level, while milling reduces this to only 4 µm (Fig. 5, Table 3). A study of the effect of plate roughness was performed on powder G, which contains particles that are 15 µm diameter and can occupy the low regions on the plate only in as-received condition (Table 1). This is the probable cause for the increase in density when the as-received side of the plate is used to spread a 150 µm thick layer (Fig. 7).
Increasing recoater speed seems to lead to a reduction in layer density for both the as-received and milled surfaces, although this dependence is weaker for the as-received surface, which is presumably due to the extra grip of the rougher surface and the greater relative importance of powder filling of scratches and pits in the as-received case (Fig. 7). The reduction in layer density at higher recoater speeds is seen widely in literature, and is rationalised as the faster speed giving less time for particles to rearrange themselves and pass below the blade. Increasing layer thickness above 140 µm improved the layer density on both surfaces (Fig. 6). The layer density of the thinnest layers is higher for the side of the plate in the as-received condition, presumably as a larger fraction of the particles were able to sit in the low regions of the plate (Fig. 6). This increase of density is not a true reflection of the layer quality, since it is an artefact caused by roughness in the plate. However, it may possibly give an indication of the ability of a powder to fill defects in pre-existing sintered layers in the powder bed fusion process, although this is conjecture and must be tested thoroughly before being accepted or assumed.
Increasing particle size (characterised by the mean particle diameter, \({d}_{50}\)) leads to a decrease in layer density. A higher \({d}_{50}\) leads to larger interstices between particles. Since the volume of the layer is fixed, these larger interstices result in less space being filled by the particles and a lower density (Fig. 11a). The trend in tap density supports this. Apparent density does not follow this pattern. It is very sensitive to cohesive forces between particles, such as van der Waals forces, which are more significant at lower particle sizes. This is because van der Waals forces scale with particle diameter, but particle mass depends on the diameter cubed [37, 38]. Therefore, gravitational and inertial forces are less significant for small particles, which causes the apparent density to be lower at small particle sizes, as flow takes place only under gravity and over a short time. However, during the tap density test, there is sufficient time and kinetic energy to overcome these cohesive forces and achieve a high density at a low particle size. The particle shape affects apparent density, tap density and layer density similarly: a higher aspect ratio (more spherical particles) leads to higher densities (Fig. 11b). Since the method derived here has been shown to be sensitive to particle size and shape metrics, further investigation and theoretical consideration of the method could reveal and explain the dependence of spreadability on particle size and shape.
Examining the powders studied in the current work, it is apparent that some powders cannot be spread (Fig. 10, powders H and X). All other powders could be spread into a continuous layer. Powder X could also not be spread in an EOS M290 printer, which implies that the test could be representative of the printing process. However, more spreading trials using various combinations of powders and printers are required to assess this rigorously. While it is unfortunate that it is not possible to report the composition of powder X, it is still useful to note that the test derived here showed that it could not be spread and this was found to be the case in print trials.
Comparing the layer density to the various other densities, the authors propose three possible criteria to qualify a powder as spreadable: 20% of the bulk (solid) density, 30% of the tap density or 40% of the apparent density. Most powders in this study meet these criteria. However, not all layers are equally suitable. A more stringent set of criteria, with higher fractions of densities, or based on an inspection of defects, may be more suitable in practice. A comparison of the spread densities to performance in additive manufacturing would be required to decide on these limits. The effects of different layer thicknesses and recoating speeds on printability can then be investigated to discover the influences of particle size and particle shape. For example, applicators that can form layers of 50 µm or 30 µm would lead to different behaviour for fine and coarse size distributions. However, it is not fair to simply run the test proposed in this study at the nominal layer thickness of a given printing process, as spreading on a melted surface leads to a larger effective layer density, as some particles spread in any given layer fill defects in previous layers. This effect stabilises after approximately ten layers [12]. Other conditions, such as the roughness of the surface onto which the powder is spread, recoater speed, vibrations and humidity can also be investigated.
Some spreadable powders flow freely through the Hall funnel, while others do not. Both powders H and X, which did not spread, also fail to flow through the Hall funnel. This can be interpreted as implying that a powder that passes a Hall flow test will spread, but that a high layer density is not guaranteed. In fact, some of the highest layer densities were achieved by powders that failed the Hall flow test (Fig. 10). Other flowability measurement techniques that are recognised as being more diagnostic in the assessment of additive manufacturing powders, such as rotating powder analysis and powder rheometry should be investigated to see if they correlate to the current test. However, neither of those methods is standardised (unlike the Hall flowmeter) and it is rare to find such metrics in materials specifications, so the relevance to current practice will be limited. Future developments in testing and standards may allow these methods to be used more widely in powder specifications, so such a study is still useful, as well as providing more insight into physical processes.
Powders C and D have very similar characteristics (Table 1). It is encouraging to see that their spread layer density was similar (Fig. 10). This suggests that the current test can identify powders that are alike. Also, powders L, P and T are all 316L stainless steel of similar particle size and show similar spreading performance (Table 1 cf. Fig. 10), despite coming from three different suppliers. There is a slight variation in aspect ratio between the three powders, but this seems to be unimportant for determining spread density. Similarly, powders that are different also show different performances in the current test. Increasing the size fraction of 316L powder (and decreasing the aspect ratio, as is generally expected for larger particles), leads to degradation in the spread density. Amongst powders N, R and U, all are 316L steel and have the same size range and similar \({d}_{50}\) but powder N has a significantly higher aspect ratio (Table 1). Powder N also performs markedly better than the other two during spread trials (Fig. 10). However, in the largest size ranges for the 316L powders (90 ≤ d/µm ≤ 150; powders O, S and W), powder O has a smaller \({d}_{50}\) than the others and exhibits the lowest spread density. This contravenes the overall trend observed during this study (Fig. 11a). Such discrepancies are not entirely surprising, as the powders have not been characterised in detail and factors such as the surface condition, moisture and the presence of satellites are unknown. Indeed, of these latest three powders, only powder S failed to pass through the Hall funnel, so some properties of that powder must be different to the other two (Fig. 10). Such investigations are ongoing and shall be reported in the future.
A simple visual comparison of the performance of powders during spreading in the proposed test and during print operations suggest that the test is representative of spreading during printing in the cases tested (Fig. 12). A more detailed and wide-ranging comparison with print trials will be required once the test method is finalised.
5 Conclusions
This study examined twenty-four powders in a spreadability test that measures the mass of powder in a layer of known nominal dimensions. Key findings were:
-
Nominal layer dimensions were close to the measured values. The density of the powder in the layer can, therefore, be calculated based on nominal dimensions.
-
The test was repeatable and reproducible. It also generated results that are consistent with other data published in literature.
-
The as-received (rougher) surface led to higher densities. This effect diminished for thicker layers, where the fraction of powders in contact with the plate is less.
-
As particle size, measured by \({d}_{50}\), increased, the layer density and tap density decreased, but the apparent density increased.
-
Powders with a higher aspect ratio led to higher layer density, apparent density and tap density.
-
A simple criterion could classify a powder as spreadable if the layer density exceeds some fraction of the apparent density, tap density or bulk density. More work is required to derive useful limits, but the initial work suggests that 40% of apparent density may be suitable.
Now that the applicability of the spreading test has been established, several areas in which further work is required may be identified:
-
The effect of spreading multiple layers on the layer density and the formation of defects should be investigated.
-
The effect of base plate roughness should be investigated more thoroughly, using a range of roughnesses and machining techniques to generate the base plate surface.
-
The shape of layers at various recoater speeds, layer heights and with different powders should be studied using 3D-profilometry or a similar technique to ensure that the analysis procedure is valid under wider range of conditions than is shown in this article.
-
A wider study is needed to determine the effect of the roughness of the surface onto which the powder is spread and the effect of the gap size when the powder contains particles with a diameter that is a large fraction of the nominal layer thickness.
-
Hall flow is unsuitable to predict spreadability. Other flow metrics should also be tested and compared to the test proposed here.
-
More spreading devices should be tested in this equipment, such as rollers or rakes to see if the test is still applicable.
-
More thorough study of the influence of powder characteristics on spreading behaviour must be undertaken, including explanations that are consistent with theory.
-
A more thorough study of the repeatability and reproducibility of the test and analysis methods should be undertaken, using more independent operators and a range of test parameters and powders.
-
The use of more layer thicknesses, especially thinner layers to give a more faithful representation of many powder bed additive manufacturing processes, to show the applicability of the current methodology to such tests.
Availability of data and material
The data in this study are available upon request to the corresponding authors. The material used in this study is not available for distribution.
Code availability
Not applicable.
References
ASTM International (2014) ASTM F3049-14: standard guide for characterizing properties of metal powders used for additive manufacturing processes. ASTM International, West Conshohocken
International Standards Organisation (2020) ISO/ASTM 52907:2020 Additive manufacturing–feedstock materials–methods to characterize metal powders. International Standards Organisation, Geneva
Murr LE (2018) A metallographic review of 3D printing/additive manufacturing of metal and alloy products and components. Metallogr Microstruct Anal 7:103–132. https://doi.org/10.1007/s13632-018-0433-6
Schmelzer J, Rittinghaus SK, Weisheit A et al (2019) Printability of gas atomized Mo-Si-B powders by laser metal deposition. Int J Refract Met Hard Mater 78:123–126. https://doi.org/10.1016/j.ijrmhm.2018.08.016
Yun H, Dong L, Wang W et al (2018) Study on the flowability of TC4 alloy powder for 3D Printing. IOP Conf Ser Mater Sci Eng. https://doi.org/10.1088/1757-899X/439/4/042006
Ma Y, Evans TM, Philips N, Cunningham N (2020) Numerical simulation of the effect of fine fraction on the flowability of powders in additive manufacturing. Powder Technol 360:608–621. https://doi.org/10.1016/j.powtec.2019.10.041
Peter R, Baker J (1997) Three dimentional printing with fine metal powders. Diss. Massachusetts Institute of Technology, Cambridge
Zhang W, Mehta A, Desai PS, Fred Higgs C (2017) Machine learning enabled powder spreading process map for metal additive manufacturing (AM). In: solid freeform fabrication 2017: proceedings of the 28th annual international solid freeform fabrication symposium–an additive manufacturing conference, University of Texas, Austin, p 1235–1249
Haferkamp L, Haudenschild L, Spierings A et al (2021) The influence of particle shape, powder flowability, and powder layer density on part density in laser powder bed fusion. Metals (Basel) 11:1–15. https://doi.org/10.3390/met11030418
Van den Eynde M, Verbelen L, Van Puyvelde P (2015) Assessing polymer powder flow for the application of laser sintering. Powder Technol 286:151–155. https://doi.org/10.1016/j.powtec.2015.08.004
Mitterlehner M, Danninger H, Gierl-Mayer C et al (2020) Study on the influence of the blade on powder layers built in powder bed fusion processes for additive manufacturing. BHM Berg- Huettenmaenn Monatsh 165:157–163. https://doi.org/10.1007/s00501-020-00955-6
Jacob G, Brown CU, Donmez A (2018) The influence of spreading metal powders with different particle size distributions on the powder bed density in laser-based powder bed fusion processes. US Department of Commerce, National Institute of Standards and Technology, Gaithersburg
Mitterlehner M, Danninger H, Gierl-Mayer C, Gschiel H (2021) Investigation of the influence of powder moisture on the spreadability using the spreading tester. BHM Berg- Huettenmaenn Monatsh 166:14–22. https://doi.org/10.1007/s00501-020-01067-x
Mellin P, Rashidi M, Fischer M et al (2021) Moisture in metal powder and its implication for processability in L-PBF and elsewhere. BHM Berg- Huettenmaenn Monatsh 166:33–39. https://doi.org/10.1007/s00501-020-01070-2
Snow Z, Diehl B, Reutzel EW, Nassar A (2021) Toward in-situ flaw detection in laser powder bed fusion additive manufacturing through layerwise imagery and machine learning. J Manuf Syst 59:12–26. https://doi.org/10.1016/j.jmsy.2021.01.008
Snow Z (2018) Understanding powder spreadability in powder bed fusion. The Pennsylvania State University, State College
Snow Z, Martukanitz R, Joshi S (2019) On the development of powder spreadability metrics and feedstock requirements for powder bed fusion additive manufacturing. Addit Manuf 28:78–86. https://doi.org/10.1016/j.addma.2019.04.017
Ahmed M, Pasha M, Nan W, Ghadiri M (2020) A simple method for assessing powder spreadability for additive manufacturing. Powder Technol 367:671–679. https://doi.org/10.1016/j.powtec.2020.04.033
Escano LI, Parab ND, Xiong L et al (2018) Revealing particle-scale powder spreading dynamics in powder-bed-based additive manufacturing process by high-speed x-ray imaging. Sci Rep 8:1–11. https://doi.org/10.1038/s41598-018-33376-0
Le T-P, Wang X, Davidson KP et al (2021) Experimental analysis of powder layer quality as a function of feedstock and recoating strategies. Addit Manuf 39:101890. https://doi.org/10.1016/j.addma.2021.101890
Lu QY, Nguyen NV, Hum AJW et al (2019) Optical in-situ monitoring and correlation of density and mechanical properties of stainless steel parts produced by selective laser melting process based on varied energy density. J Mater Process Technol 271:520–531. https://doi.org/10.1016/j.jmatprotec.2019.04.026
Abdelrahman M, Reutzel EW, Nassar AR, Starr TL (2017) Flaw detection in powder bed fusion using optical imaging. Addit Manuf 15:1–11. https://doi.org/10.1016/j.addma.2017.02.001
Caltanissetta F, Grasso M, Petrò S, Colosimo BM (2018) Characterization of in-situ measurements based on layerwise imaging in laser powder bed fusion. Addit Manuf 24:183–199. https://doi.org/10.1016/j.addma.2018.09.017
Zhang B, Ziegert J, Farahi F, Davies A (2016) In situ surface topography of laser powder bed fusion using fringe projection. Addit Manuf 12:100–107. https://doi.org/10.1016/j.addma.2016.08.001
Kanko JA, Sibley AP, Fraser JM (2016) In situ morphology-based defect detection of selective laser melting through inline coherent imaging. J Mater Process Technol 231:488–500. https://doi.org/10.1016/j.jmatprotec.2015.12.024
Neef A, Seyda V, Herzog D et al (2014) Low coherence interferometry in selective laser melting. Phys Procedia 56:82–89. https://doi.org/10.1016/j.phpro.2014.08.100
DePond PJ, Guss G, Ly S et al (2018) In situ measurements of layer roughness during laser powder bed fusion additive manufacturing using low coherence scanning interferometry. Mater Des 154:347–359. https://doi.org/10.1016/j.matdes.2018.05.050
Krauss H, Zeugner T, Zaeh MF (2014) Layerwise monitoring of the selective laser melting process by thermography. Phys Procedia 56:64–71. https://doi.org/10.1016/j.phpro.2014.08.097
ASTM International (2017) ASTM B212-17: standard test method for apparent density of free-flowing metal powders using the hall flowmeter funnel. ASTM International, West Conshohocken
Mussatto A, Groarke R, O’Neill A et al (2021) Influences of powder morphology and spreading parameters on the powder bed topography uniformity in powder bed fusion metal additive manufacturing. Addit Manuf 38:101807. https://doi.org/10.1016/j.addma.2020.101807
Kiani P, ScipioniBertoli U, Dupuy AD et al (2020) A statistical analysis of powder flowability in metal additive manufacturing. Adv Eng Mater 22:1–6. https://doi.org/10.1002/adem.202000022
ASTM International (2018) ASTM D823-18: Standard Practices for Producing Films of Uniform Thickness of Paint, Coatings and Related Products on Test Panels. ASTM International, West Conshohocken
International Standards Organisation (2018) ISO 4490:2018 metallic powders–determination of flow rate by means of a calibrated funnel (Hall flowmeter). International Standards Organisation, Geneva
International Standards Organisation (2011) ISO 3953:2011 metallic powders–determination of tap density. International Standards Organisation, Geneva
Lidman L (2019) Characteristics and properties for iron powder with flow additives. Lund Universitet, Lund
Cordova L, Bor T, de Smit M et al (2020) Measuring the spreadability of pre-treated and moisturized powders for laser powder bed fusion. Addit Manuf 32:101082. https://doi.org/10.1016/j.addma.2020.101082
Turner GA, Balasubramanian M (1974) Investigations of the contributions to the tensile strength of weak particulate masses. Powder Technol 10:121–127. https://doi.org/10.1016/0032-5910(74)80037-9
Tomas J, Kleinschmidt S (2009) Improvement of flowability of fine cohesive powders by flow additives. Chem Eng Technol 32:1470–1483. https://doi.org/10.1002/ceat.200900173
Funding
Open access funding provided by KTH Royal Institute of Technology.
Author information
Authors and Affiliations
Contributions
All authors contributed to the study’s conception and design. Material was provided by KS, SDG, SS, VP, AM, KJ and FM. Data collection and analysis were performed by CH, PM, LM, VH, MU, ES. The first draft of the manuscript was written by CH and PM and all authors commented on previous versions of the manuscript. All authors read and approved the final manuscript. CH and PM contributed equally to this work and share first authorship.
Corresponding author
Ethics declarations
Conflict of interest
The authors have no competing interests to declare that are relevant to the content of this article.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Hulme, C.N., Mellin, P., Marchetti, L. et al. A practicable and reliable test for metal powder spreadability: development of test and analysis technique. Prog Addit Manuf 8, 505–517 (2023). https://doi.org/10.1007/s40964-022-00341-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40964-022-00341-3