1 Introduction

Laser powder bed fusion (L-PBF) is an additive manufacturing (AM) technology that fuses layer by layer based on metal powder using a laser beam [1, 2]. This process is capable of producing complex shapes based on computer-aided design software (CAD) that minimizes the time to market and maximizes material savings [3, 4]. Lattice structures are periodic open-cell structures that allow the production of components with the same mechanical properties but decreasing material weight [3]. In these structures, there is a designed porosity (nominal interconnected porosity) that is inherent to the part and a non-designed porosity (closed porosity) that results from the process used to manufacture the part [5]. The metrology procedures involved in measuring the lattice structures are of great interest when arrangements in the micro-size regime are produced. Some researchers have studied the deviation between CAD files and parts produced with additive technologies. For example, Grunsven et al. [6], compared the accuracy among the CAD file and the real part using a µCT and a scanning electron microscopy (SEM) in pieces fabricated with electron beam melting (EBM). They found that the difference between the designed and fabricated strut thickness is approximately 200 µm. Shah et al. [7] worked with SLS, FDM, and SLA technologies, their experiment consisted of measuring samples comparing a coordinate measuring machine (CMM) and computer tomography (CT) to study dimensional accuracy. Rashid et al. [8] found that the scan strategy in L-PBF can influence the dimensional accuracy of the built sample. Their results indicated that samples fabricated with different strategies can promote overgrowth in some regions of the printed surfaces. Campanelli et al. [9] made a study about the dimensional accuracy of the unit cell length of the printed Ti6Al4V pieces on L-PBF measured with a CMM. Their results indicated deviations from model dimensions of less than 50 µm. Teeter et al. [10] created a metrology test object, varying dimensions, and including holes, cylinders, rectangles, gaps, and lattices to verify the AM in metals for biomedical applications. Yan et al. [11] fabricated gyroid lattices in AISI 316 L material, resulting in an as-built strut size slightly higher than the design and having constant deviation among each sample. Rupal et al. proposed an innovative methodology that includes geometric tolerances for metal AM parts and assemblies. Their experiments were performed with Inconel 718 and samples resulted in a size error of 0.75% for holes and 0.63% for pin components [12]. According to Weidmann et al., significant deviations occur from nominal geometry when several segments of hexagons merge from a single node which can be also observed with thin lattice structures [13]. Additionally, Großmann et al. studied the impact of both, laser power and scan speed on the strut diameter of truss lattice structures [14]. Their results indicate that increasing the laser power or decreasing the scanning speed increases strut diameter of thin-walled lattice structures.

Several metrology techniques have been used to study specimens fabricated in the L-PBF process. Optical techniques have been used for measuring complex freeform parts produced using AM involving issues such as getting the object coverage and allowing sensors to be repositioned without recalibration [15]. Therefore, optical technologies as confocal microscopy and focus variation microscopy (FVM) gained interest due to their significantly reduced acquisition time [16]. Micro-computed tomography (µCT) is defined as a non-destructive method in which the object is irradiated with X-rays or gamma rays and mathematical algorithms are used to create a cross-sectional image or a sequence of such images [17]. Carlton et al. [18] measured 3D pore volume and morphology in additively manufactured stainless steel. The results indicated that the internal porosity influences fracture mechanisms and consequently, in their mechanical behavior. Siddique et al. [19] reported a study of porosity inside a solid specimen. Their results reveal that pores influence crack initiation. When these pores are close to the surface, they tend to reduce the fatigue life of the specimens. Table 1 presents the literature review of the measurement of lattices structures. According to Teeter et al. [10], the differences between the target and the measured dimension are greater in the smallest dimension. This trend follows the standard deviation, which increased from the largest to the smallest dimension. Additionally, Yan et al. found that the experimental strut sizes were larger than the designed values (i.e., from the designed strut of 0.50–0.42 mm) [11]. While Sing et al. made measurements of strut diameter which resulted smaller than the designed value (i.e., from the designed strut of 0.6–0.335 mm) [20]. The characterization of cell lattices has many challenges related to powder sticking to part surfaces and process parameter selection. The study aimed to analyze the process capability and to compare between metrology techniques for dimensional characterization of neck fatigue specimens. Cell length and strut width were measured in cubic and hexagonal lattice structures to study the geometrical restrictions achievable by L-PBF.

Table 1 Dimensional metrology of lattice structures for L-PBF
Full size table

2 Materials and methods

2.1 Raw material

The material used for the experimental trials was AISI316L (designation SS 316L-0410, Renishaw-United Kingdom) stainless steel powder. The powder morphology was qualitatively characterized through a scanning electron microscope (SEM) (Carl Zeiss EVO MA25, Germany). Several images were acquired, and 30 particles were measured to quantify the particle’s size diameter. From the SEM study, powder particles are mostly spherical with a low presence of satellites, and based on the obtained micrographs the average particle size diameter (i.e., quantified from all particles measured) was found to be 25.2 ± 7.9 µm. Figure 1 presents the (a) particle morphology and (b) size distribution.

Fig. 1
figure 1

Particle distribution in stainless steel 316L a micrograph of stainless steel powder and b particle size distribution

Full size image

2.2 Experimental setup

QuantAM 4.1.0.76 software was used to program the L-PBF process parameters, orientation, and piece supports. A L-PBF machine (Renishaw AM400, Gloucestershire, UK) was used for experimental trials. Considering the angle between the longitudinal axis of the specimens and the building plate three replicates were manufactured in a horizontal (0°) and vertical (90°) orientation. The selected parameters and scanning strategy were selected based on the previous work of Ramirez et al. [23] for wall width tests and lattice structures (Table 2). The layer thickness was reduced from 50 µm down to 40 µm compared to our previous work. It was performed to get higher accuracy and denser pieces; [24] further experiments must be performed to analyze the influence of layer thickness in the manufacture of micro-geometries. For wall width experiments, no supports were added, and samples were removed by wire-EDM. For lattice structures supports with circular cross-section (diameter of 0.6 mm and height of 0.7 mm) were added and samples were removed from the plate by eliminating the supports manually. Samples were cleaned in an ultrasonic bath to eliminate the powder trapped between the lattice structures.

Table 2 L-PBF parameters used for specimens
Full size table

2.3 Wall width manufacture and characterization

A geometric validation of samples created with L-PBF was performed to determine the machine’s process capability. A block with dimensions of 30 mm in length, 21 mm in width, and height of 5 mm was fabricated. Figure 2 presents the block manufactured with two orientations (horizontal (Fig. 2a) and vertical (Fig. 2b), with designed wall widths (\({W}_{\mathrm{w}}\)) between 200 µm and 1000 µm. A wall width (\({W}_{\mathrm{w}}=1000 \mathrm{\mu m})\) is illustrated in Fig. 2 in both orientations. Three replications of each printing were performed and measured in a front-facing view. A focus variation microscope, FVM (Infinite FocusXL200, Alicona, Austria) was employed to measure wall width using a 5 × lens to determine the level of variation on the strut’s width based on the build orientation. Wall characterization was used to select geometrical features (i.e., strut width) of cell lattices.

Fig. 2
figure 2

Samples for metrology testing were manufactured in a a horizontal (0°) and b vertical (90°) orientation

Full size image

2.4 Lattice structures design

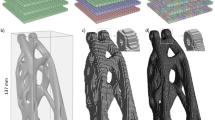
The overall sample geometry was based on the neck region of rotary beam fatigue experiments (see Fig. 3a). Solid and lattice structures were used as test samples in this study (see Fig. 3b–d). A CAD file was created in SolidWorks 2018 (Solidworks, USA) based on a rotating-beam fatigue specimen (ISO 1143:2010). Software Element 1.23.0 (nTopology) was used to create the lattice structures. In this software, cubic edge and Hex prism edge were selected and warped to fit the lattice around the volume. Additionally, a uniform thickness was chosen in nTopology for strut width and the file was exported with a.STL file format. Lattice structures based on struts are manufactured by periodic cell structures, which makes them interesting for their simplicity [25]. Therefore, cubic and hexagonal unit cells were explored with a designed unit cell (\({C}_{\mathrm{dl}})\) of 1000 µm and designed strut width \(\left({U}_{\mathrm{dw}}\right)\) of 250 µm and 500 µm. Once lattice structures were created, unit cell length and strut width size are distorted to fit the neck volume. Table 3 shows the cell length and strut width dimensions after meshing specimens using nTopology (i.e., nominal values) software. The reference geometry to study relative errors are the nominal values indicated in Table 3, for both the fine and coarse cell designs. These variables (i.e., \({C}_{\mathrm{wf}}, {C}_{\mathrm{lf}}, {H}_{\mathrm{wf}}, {H}_{\mathrm{lf}}, \mathrm{and} {C}_{\mathrm{wc}}, {C}_{\mathrm{lc}}, {H}_{\mathrm{wc}}, {H}_{\mathrm{lc}})\) were measured in nTopology before manufacturing and correspond to the dimensions of manufactured pieces after distortion caused by necking. Cell length refers to one side of the cube and hexagonal cells measured from vertex to vertex while strut width corresponds to the distance measured in a lateral view. Figure 3a presents a rotating-beam fatigue specimen and Fig. 3b illustrates the solid neck specimen. Figure 3c, d shows cubic and hexagonal cells in fine configuration \(({U}_{\mathrm{dw}} =\)250 µm), respectively. Figure 3e, f shows the schematics of the path performed by the laser during the fabrication process. It is noted that in such regions, where the diameter of the strut is wider, the laser performs a regular hatching-borders process. Figure 4 presents the cell lattice measurements after neck distortion to illustrate measured variables.

Fig. 3
figure 3

a Reference rotating-beam fatigue specimen and manufactured samples (only neck region): b solid, c cubic unit cell and d hexagonal unit cell. Schematics of the laser path for the building of the e cubic and f hexagonal unit cells

Full size image
Table 3 Nominal strut width and unit cell length (i.e. after meshing in nTopology software) vs. designed dimensions before distortion
Full size table
Fig. 4
figure 4

Cell lattice representation after meshing with N-Topology software a cubic cell, b hexagonal cell

Full size image

2.5 Dimensional characterization of lattice structures

Lattice cell and strut width were characterized using three tools: an optical microscope (OM) (Toolmaker, Mitutoyo, USA); a micro-computer tomography scanner, µCT (SkyScan 1172, Bruker, USA), and a focus variation microscope, (FVM) (Infinite FocusXL200, Alicona, Austria). The OM technique has a resolution between 1 and 2 µm and was used with a 15 × lens and no external software. The sample was placed on the stage and positioned with stage adjustment knobs. A digital display was used to select the unit system (i.e., mm). Intersecting lines were used to measure cell length and strut width from the desired start point (i.e., zero absolute) to the endpoint manually. OM microscope was pre-calibrated by the supplier. The FVM technique was set with a Measure Suite 5.3 software; samples were observed with a 5 × lens and a vertical resolution of 0.84 µm, a lateral resolution of 7.83 µm, and an exposure time of 12.8 ms. FVM calibration was performed with the stage initialization process to position the microscope at the start position. The sample was placed on stage and positioned with joystick control and coaxial light was selected. Two planes were chosen in the Z-axis in upper and lower levels until a blurry image was shown in the software. Fifty profiles were selected to identify the valleys and ridges of the sample (i.e., measured cell length and strut width) using the profile form measurement tool. According to the FVM supplier, the maximum permissible length measurement error is 0.15 µm with a standard deviation of 0.01 µm when the height step is 1 µm, which corresponds to the selected value for this study. The µCT technique has a resolution of 26.8 µm and the software SkyScan 1172, NRecon, and CTAn. Preliminary validation of this resolution was performed in equipment using cylindrical gages (vermont gage, Swanton, VT, USA) to confirm their diameter. An Al + Cu filter, a voltage of 55 kV, a current of 181 µA, an exposure time of 900 ms, and a power of 10 W were selected in µCT. Measured specimens (Fig. 3b–d) were placed in a vertical position (Z-axis) and one 3D image (~ 1000 pictures) was taken by sample with three replicates. The µCT measurements were done with a 0.5 µm voxel size. The software used for dimensional assessment was the SkyScan 1172 to extract dimensional and porosity information. Skyscan 1172 data was exported to NRecon software to create.bmp images of the area of interest. A cross-section plane was placed in the middle of the sample and two crossing lines were used to identify the unit cell of the center and measured samples dimensionally. For dimensional analysis, two measurements were performed by plane (i.e., OM and FVM microscope 2 external planes) and three measurements for µCT (2 external planes and middle planes). These planes were identified previously in samples. Unit cell length and strut width were measured as is shown in Fig. 4. The dimensional analysis of cell length and strut width was evaluated with the relative of error \(\% {\varepsilon }_{\mathrm{r}}\) (Eq. 1):

$${\varepsilon }_{\mathrm{r}}=\left|\frac{{v}_{\mathrm{m}}-{v}_{\mathrm{n}}}{{v}_{\mathrm{n}}}\right|\times 100,$$
(1)

where \({v}_{\mathrm{m}}\) is the measured value and \({v}_{\mathrm{n}}\) the nominal value.

2.6 Experimental overall porosity

Besides dimensional assessment, a porosity characterization was performed as a complementary technique to correlate product integrity with the type of cell and building orientations. Images obtained with NRecon software in µCT were used to create a 3D model reconstruction (.STL file) and to analyze porosity using CTAn software (CT Analyser 1.14.4.1). A table with values of total volume, object volume, and percentage of object volume was obtained to calculate porosity. Additionally, CTvol was used to visualize the 3D model, and the data viewer was allowed to study samples internally. The overall porosity \({(P}_{\mathrm{o}})\) inside the volume of interest (VOI) was calculated according to Eq. 2. Where %OV is the object volume percentage.

$${P}_{\mathrm{o}}=100-\%\mathrm{OV}.$$
(2)

The overall porosity includes the interconnected porosity according to each cell configuration and the closed porosity caused by processing. It was calculated using neck fatigue volume from testing specimens (3 samples). This object volume percentage is calculated with Eq. (3);

$$\%\mathrm{OV}=\frac{\mathrm{OV}}{\mathrm{VOI}},$$
(3)

where \(\mathrm{OV}\) is the object volume and \(\mathrm{VOI}\) is the volume of interest selected by the user. In this work, we calculated the nominal interconnected porosity, which corresponds to the volume fraction compared to a solid neck sample of designed samples, and defined by the difference of the nominal volume and the proportion of the volume within the lattice structure. This term differs from relative density due to it is defined by the proportion of the material (dry weight) with a total specimen volume [26].

3 Results

3.1 Wall width characterization

Several designed wall width values were established to explore process capability. Figure 5 presents the relative error of measured wall width (average of three samples for each orientation). Table 4 presents the raw data plotted in Fig. 5. In terms of overall trends, we can observe that for larger wall dimensions the relative error tends to decrease (i.e., a designed wall width greater than 350 µm). For example, wall widths larger than 750 µm in the vertical orientation seem to generate better results in terms of dimensional variations, with relative errors below ~ 10%. Even with the largest dimensions in all width, the horizontally built orientation generates relative errors of around ~ 9% or higher. Samples with a wall width of 250 µm and 500 µm showed relative errors between 13 and 16%. Although other samples have a relative error lower than these values. These struts sizes show the lowest difference between horizontal and vertical orientations. Therefore, these dimensions (250 and 500 µm) were selected as the strut-designed size for cell lattices experiments.

Fig. 5
figure 5

Dimensional variations for straight wall specimens (average of three replications for each build orientation)

Full size image
Table 4 Data set of experimental wall width
Full size table

3.2 Dimensional characterization of lattice structures

The first analysis was an aggregate of relative errors for strut width (fine and coarse strut sizes) and cell length, as shown in Fig. 6. In this case, the data for both cubic and hexagonal cell structures were combined. It is clear that the cells with fine struts are pushing the limits of the process and, therefore, the relative error is significant (between 5 and 25%). Once we proceed with the coarse strut dimensions the relative error drops to levels below ~ 3%. Interestingly, the cell length shows relative errors below ~ 5%. This trend is explained by the relatively large dimension of the cell lengths (760 and 830 µm). The overall pattern in relative errors with this aggregate analysis is the same independent of the metrology technique used.

Fig. 6
figure 6

Dimensional relative error based on the type of equipment (metrology technique). Metrology equipment (techniques): OM (optical microscope), µCT (micro-computerized tomography), FVM (focus variation microscopy)

Full size image

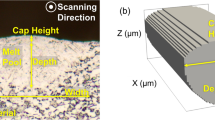
Cell length was measured with three different equipment in cubic and hexagonal lattices. All of them work based on different principles. For FVM and OM, measurements were obtained in the front and backplane. Figure 6 presents the results for cubic cells. Our results show the differences among equipment with the same specimen. For cell length measurement (Fig. 7a) in a vertical orientation, OM and FVM showed a maximum relative error of 4.5% and 4.1%, respectively, with a \({U}_{\mathrm{dw}}\) of 250 µm. While µCT presented a maximum relative error of 4.7% in the horizontally built orientation. For strut width of 190 µm (Fig. 7b) and manufactured in a vertical orientation resulted in a maximum relative error of 23.7, 10.4, and 22.3% for µCT, OM, and FVM, respectively. When nominal strut width was increased (\({C}_{\mathrm{wc}}\)=478 µm), relative errors were reduced to values lower than 4.1% in both orientations. For the hexagonal cell (Fig. 8), our results indicate that when \({U}_{\mathrm{dw}}\) is 500 µm, the cell length measurements (Fig. 8a) are up to our target in contrast when \({U}_{\mathrm{dw}}\) is 250 µm cell length measurements are below our target. This trend was not observed in the cubic cell. OM and FVM showed a maximum relative error of 3.5% and 3.2% in the horizontally built orientation, respectively. While µCT resulted in a relative error of 9.1% in the same orientation. For samples fabricated in a vertical orientation, measured strut width (Fig. 8b) resulted in a maximum relative error of 50, 3, and 66% with µCT, OM, and FVM, respectively. When nominal strut width was increased, relative errors were reduced to values lower than 4.7% in both orientations. Additionally, both cell types showed strut widths greater than our nominal values. Figure 9 illustrates the images obtained with (a) µCT (micro-computerized tomography), (b) OM (optical microscope), (c) FVM (focus variation microscopy) of a hexagonal cell with designed strut width of 500 µm.

Fig. 7
figure 7

Cubic cells: a cell length and strut width evaluation. Note: metrology equipment (techniques): OM (optical microscope), µCT (micro-computerized tomography), FVM (focus variation microscopy), built orientation: H [horizontal (0°)], V [vertical (90°)]

Full size image
Fig. 8
figure 8

Hexagonal cells: cell length (a) and strut width evaluation (b). Metrology equipment (techniques): OM (optical microscope), µCT (micro-computerized tomography), FVM (focus variation microscopy), built orientation: H [horizontal (0°)], V [vertical (90°)]

Full size image
Fig. 9
figure 9

Images obtained of hexagonal cell (\({U}_{\mathrm{dw}}=\) 500 µm) with a µCT (micro-computerized tomography), b OM (optical microscope), c FVM (focus variation microscopy)

Full size image

Tables 5 and 6 present the analysis of variance for each set of measurements. The significant p values were highlighted in bold. ANOVA test was performed for each cell type and designed strut width. Orientation was analyzed for horizontal and vertical positions while the three equipment were considered for the study. For cubic cell structures, both the orientation and the measurement equipment are significant factors for cell length, independent of fine or coarse strut size. Additionally, the orientation is a significant factor for nominal strut width of 478 µm in cubic cell type. For hexagonal cells, only the equipment is a significant factor for nominal cell length of 760 µm in coarse strut type.

Table 5 Cubic cell structures: analysis of variance
Full size table
Table 6 Hexagonal cell structures: analysis of variance
Full size table

3.3 Experimental overall porosity

Table 7 presents the porosity characterization results. The manufactured piece resulted in a wider strut, which tends to close the reticular cell and consequently reduce the interconnected porosity. Our report includes the interconnected porosity and the closed porosity caused by the process itself, which causes the overall porosity. Both structures have similar results in porosity percentage. Cubic cells resulted with a relative error between ~ 3 and 19%, and hexagonal the cell with a relative error between 12 and 27% concerning the interconnected porosity. Samples with maximum relative errors are highlighted in bold in Table 7. For solid samples, closed porosity resulted lower in horizontally built orientation (0°).

Table 7 Porosity characterization results
Full size table

4 Discussion

Manufacturing lattice structures has resulted in great interest for several authors, analyzing surface roughness, porosity, and dimensions. Dallago et al. explained that the discrepancies between the designed and built strut thickness are of great importance in the study of the influence of geometric features on mechanical properties [27]. In our work and according with their approach, we designed a fatigue neck specimen with the objective to compare among three technologies to dimensionally characterize additively manufactured lattices structures, particularly strut widths. Regarding the dimensional assessment, we found that the fabricated wall dimensions and deviations are dependent on the selected building orientation for relatively large features. The orientation building showed significance (Fig. 5) for a designed wall width between 200 and 350 µm in both orientations, which resulted in a relative error between 9 and 38%. Additionally, dimensions up to 750 µm in vertical orientation follow a relative error trend down until ~ 2.3%, while samples manufactured in horizontal orientation have a steady error trend after 600 µm (relative error between 9.4 and 14.4%). Weißmann et al. [28] characterized the effect of Ti6Al4V samples orientation on the measurement of the diameter in single struts fabricated by SLM and EBM process. They found that samples oriented at a 45° angle resulted always in larger dimensions compared to the nominal CAD data and to samples oriented at a 0° angle. While dimensional deviations tend to decrease in larger diameters manufactured by SLM. Our experiments were performed using the parameter set of Table 2. Further trials can be performed to modify variables including the inclination angle, and to analyze their influence on wall width dimensions. Additionally, thin walls can be manufactured at different levels of laser power and scanning speed to evaluate the influence of heat input in thin walls. According to Großmann et al., a high level of energy results in high particle adhesion on the down skin surface while for very low energies, high surface tension gradients are present in the melt zone, which promotes a balling phenomenon [14]. Supplementary to the particle adhesion, there are inherent variations in build plate position caused by the accuracy provided by linear guide and other actuators, which induced a sinusoidal motion [29]. In our experiments, some particle adhesion was observed in cell lattices causing cell occlusion. Laser scanning parameters (i.e., beam compensation, hatch distance, fill contour, and border contours) are of great importance when small features are manufactured. For example, hatch distance (i.e., the distance between line vector of point exposures) can influence the geometrical error on samples due to attached particles on the sample [30]. Besides, hatch distance has an impact on thermal gradients which promotes a volatile melt pool in the beginning, ending and turning of a scanline [31]. In our experiments, the reduction on the relative error as the wall thickness increases can be explained by the path created by the laser during the melting process. For example, scan paths observed in the samples with a wall width of 250 μm, shows that, the laser acted as a single vector, with border parameter. As the wall width increases, the volume space on which the laser can perform a volume scan also increases. Additionally, in terms of beam compensation as well as the making of border and fill contours, there is a minimum wall width which is related to the relative errors observed in Fig. 5.

For lattice structures, the smallest nominal strut widths (170 µm and 190 µm) resulted in a relative error of 18.8% and 40% for a hexagonal and cubic cell, respectively, both with vertical orientation. Even though, the horizontally built orientation presented a relative error of 10.4% and 2.8% for hexagonal and cubic cell, respectively. The L-PBF machine used for these experiments can get a resolution from 20 to 100 µm in z-axis (building direction), depending on the established layer thickness, which also depends on the average particle size of the selected powder. Regarding the x–y resolution, it is dependent on the process parameters, the particles adhered at the cell surface in the x–y direction (horizontal) and the melt pool which is larger than the laser focus diameter (~ 77 µm). According to Yang et al., the accuracy and the efficiency of the L-PBF process is determined by the melt pool width which has an effect on strut thickness [32]. In horizontal orientation, lattice structures (hexagonal and cubic) resulted in more precise measurements according to our dimensional characterization. Additionally, it is in accordance to our dimensional characterization (Fig. 5) wherein both designed dimensions (250 and 500 µm), vertical orientation resulted in higher relative error compared with horizontal orientation. Notwithstanding, samples vertically built-in dimensional characterization (Fig. 5) got the lowest dimensional error for the designed wall width up to 750 µm. Our metrology results are in agreement to every equipment resolution and the measured dimension. Strut width for fine cell type resulted in maximum relative errors using different techniques. While FVM and OM resulted in a lower relative error in comparison to μCT when the measured dimensions were above 500 µm. It is worth mentioning that this latter technique is very useful when measuring internal features, difficult to characterize with other methods. Moreover, some measurement errors can be caused by a larger expanded uncertainty, scatter radiation, and beam hardening [33].

Regarding product integrity, Carlton et al. [18] performed some experimental tests in fatigue specimens and their results revealed a higher porosity in as-built AM specimens (~ 2.4%) in comparison to their annealed condition (~ 2.2%). According to Sola et al. [34], a pretreatment of feedstock to eliminate moisture and the process parameter optimization can reach density values higher than 99.5%. Our characterization for solid parts, resulted in an experimental overall porosity between ~ 2.7 and 7.8% in a horizontal (0°) and vertical orientation (90°), respectively, indicating that the porosity that can be achieved is in the same order of magnitude as in the literature for solid samples. Further experiments must be performed to modify process parameters (i.e. laser power, hatching distance, and scanning speed) to reduce closed porosity. For the results shown in the experimental overall porosity for the lattice specimens, the overall porosity resulted lower than the nominal interconnected porosity and hexagonal lattice structures resulted with the highest difference. This can be explained by the occlusion of the lattice cell. Similar results were obtained by Hollander et al. [35], who produced discs with parallel cylindrical pores of 500, 700, and 1000 µm, and observed a rim pore reduction of 150 µm. The results shown in this work are focused on the dimensional analysis of fatigue specimens; it can be of great interest to test specimens with cell lattices. In particular, Tridello et al. demonstrated that build orientation affects mechanical performance in very-high-cycle-fatigue testing (VHCF) [36]. Their results indicated that the VHCF strength of horizontally built specimens is higher than vertical orientation which is correlated with the defect size found in vertically built specimens. Our results indicated that lattices manufactured in horizontal position resulted in the lowest dimensional error, and further tests must be performed to evaluate structure strength.

5 Conclusions

Summarizing, a detailed investigation on the influence of building orientation and feature dimensions in L-PBF parts was presented, with the following conclusions:

  • For straight wall specimens, only features larger than 750 µm show acceptable levels of dimensional relative error (~ 2% to ~ 15%) for vertical orientation. For horizontally built orientation, the achieved relative error lies between 9.4 and 14.4% for designed wall width up to 600 µm. The build orientation does not show significant influence on dimensional relative error for features smaller than 750 µm.

  • For lattice structures, the finer struts (250 µm) show a significant level of dimensional average relative error (~ 3% to ~ 40%) in a hexagonal structure. This additive manufacturing process delivers more consistent dimensions for coarser struts (500 µm), with average relative errors between ~ 1 and ~ 4% for both manufactured cell structure. All metrology techniques showed the same trends in terms of capturing the dimensional variations for fine and coarse struts.

  • Hexagonal and cubic lattice structures were fabricated in horizontal and vertical orientations. Our results show that the dimensional relative error varies from different feature sizes, unit cell type and orientation.

  • Cubic cell lattice structures had the highest relative errors (relative error range between 1.1 and 40%) compared to hexagonal cell lattice structures (relative error range between 0.97 and 18.8%) in dimensional characterization (i.e., cell length and strut width measurements). The maximum relative errors were found in the vertically built orientation in both types of unit cell.

  • The OM and the FVM resulted in the lowest relative measuring error, which meets the resolution specified by the equipment. The µCT did not present acceptable results for dimensional analysis; however, it resulted useful as a non-destructive method to porosity analysis/quantification in lattice structures fabrication.

  • The hexagonal lattice structure resulted in a higher experimental overall porosity compared to the cubic structure. Additionally, vertical orientation resulted in higher experimental porosity compared to horizontal orientation.

  • The porosity analysis showed that the vertical orientation gave us samples with higher values of experimental overall porosity up to 2.8 times compared to the horizontally built orientation porosity in solid samples.