Introduction

Regardless of the casting technology used for manufacturing cast components, liquid metal quality has an essential role in providing high structural integrity, mechanical performance, and the avoidance of casting defects such as porosity, leakage, hot tears, and cracks.1,2,3 Even the first of the well-known ten rules, created by Campbell4,5 to provide the fundamental requirements for the manufacture of high-quality metal castings, emphasizes the importance of “starting with a good-quality melt.” To accomplish this, the melting, melt transfer, and melt processing steps need to be carefully selected, executed, and controlled. However, the quality of the ingots produced by different primary or secondary alloy suppliers can differ remarkably. In this way, the melt quality is affected by the impurity content of the ingots used as charge material.6 Not all ingots are created the same way: Quality ingot producers use in-line degassing and filters. If the selected supplier is not using appropriate melt treatment, the foundries need to modify their melt treatment methods to avoid an increase in porosity- and oxide-related scrap.7 Another critical issue is the casting method of the ingots. If the casting of ingots is performed by pouring turbulently, the effects of melt treatments can be hindered.8

The production methods of remelt aluminum and aluminum alloy ingots were comprehensively reviewed by Grandfield.9 The most common technology to produce foundry alloy ingots is gravity casting into open molds that are typically assembled into an ingot conveyor line (Figure 1a). Cast iron or steel molds are generally used for this purpose, and the filling is executed through a casting wheel or automated casting ladles. The speed of the conveyor line is usually optimized to maximize productivity, while the solidification rate also needs to be considered. For this reason, the molds are often water-cooled to achieve higher production rates. In terms of metal quality and dross formation during filling, the design of the casting wheel or ladle and the upstream melt handling and treatment methods are the main influences. Ingot producers are mainly interested in maintaining high-production rates, while dross formation during pouring is kept at a minimum. There are numerous studies,10,11,12 which showed that by optimizing the filling stage, dross formation and oxide entrainment can be effectively lowered. However, even when optimized mold filling is utilized, the method itself is not free of oxide and air entrainment, especially at the common production rates applied by the industry. Another common problem of gravity cast ingots is that they usually have shrinkage cavities, which can even contain water as a result of applying water cooling directly on the ingot or as a result of inappropriate storage.13 This clearly holds the risk of explosions if water-contaminated ingots are charged directly to liquid metal.14 There has been a growing trend to apply in-line degassing and ceramic foam filters before gravity casting of the ingots, which could help in lowering the inclusion content of the metal.7,9

Figure 1
figure 1

Schematic illustration of (a) gravity casting (GC) into open molds and (b) horizontal direct-chill casting (HDC).

Full size image

Horizontal direct-chill casting (HDC) is another common technology to produce foundry ingots. HDC is a continuous casting process in which liquid metal is fed from the tundish to water-cooled molds through a refractory transfer tube and an orifice plate (Figure 1b). The withdrawal roll is driven at the required casting speed. HDC cast bars have tight dimensional controls and usually no cracks or shrinkage cavities. As the process does not involve any pouring action and there is no free-falling liquid metal, there is much lower dross and entrained oxide concentration than in open mold casting. At the required lengths, the bars are cut with a cut-off saw, which is synchronized with the withdrawal roll.9,15 The casting machines are generally connected to the melting furnaces through a metal launder system which involves in-line degassing units and filter boxes.16,17

The detection and quantification of impurities present in ingots should be considered as an important task when the supplier of the charge material is selected. There are different approaches available in the literature for this task. Most of these characterization methods are based on the reduced pressure test (RPT). Fox and Campbell18,19 reported that RPT can be an effective tool in the evaluation of liquid metal quality. During solidification under reduced pressure, the entrained gases between the layers of bifilm defects are expanded.20 In addition, the solubility of hydrogen in the alloy is reduced by the lower hydrogen partial pressure, which results in enhanced H2 precipitation.21 The consequence of these factors is that double oxide film defects inside the RPT samples are expanded, which allows easier detection by X-ray radiography or quantitative image analysis on a polished section.18 Dispinar and Campbell22 introduced the so-called bifilm index (BI) which can be used to quantify the bifilm content of the molten metal based on the sum of the maximum lengths of pores found on the cross section of RPT samples.

Dispinar and Campbell23 investigated the effects of reducing the free-falling height and the turbulence inside the casting launder on the quality of gravity cast secondary foundry ingots. Their characterization method involved the remelting of the ingots in an induction furnace and taking RPT samples, then the density and the bifilm index values were evaluated. There was a clear improvement in the metal quality by reducing the falling height and by improving the flow inside the launder by design modifications: The density of the RPT samples increased, while the bifilm index was effectively reduced. However, the production rate was lowered by the modifications, which tends to be a more important parameter for some ingot suppliers than metal quality. Erzi et al.6 proposed a relatively complex method for assessing the quality of ingots from different suppliers. 10 kg charges are prepared from the investigated ingots, and after melting, RPT, spiral fluidity, and tensile test specimens are cast. The so-called supplier’s quality index is then calculated from the bifilm index, fluidity length, and tensile properties. The method of Erzi and Tiryakioǧlu24 involves cutting out a sample from the middle of the investigated ingot and machining it to the exact size of the RPT sampling cup. The specimen is melted inside the cup and solidified in a partial vacuum. Then, the detection and quantification of pores in the sample are conducted with either metallographic methods or computed tomography (CT). By comparing the results of the image analysis of the cross section of the RPT samples and the CT porosity analysis, Erzi and Tiryakioǧlu concluded that both methods yield similar results. A similar approach was utilized by Hsu and Li,25 who used remelted RPT samples for the characterization of the effect of different gating system designs and ceramic foam filters on the metal quality. Their method involved sectioning small samples (3 × 3 × 7 cm) and remelting them in the RPT sampling cups at 700 °C with a furnace residence time of 1 hour.

Fox and Campbell19 also mention that during the development of their remelting tests, initial trials were carried out with the same method suggested by Erzi and Tiryakioǧlu24 (i.e., machining a sample to the exact size of the RPT sampling cup and remelting in it), which were time-consuming and can result in air pockets being trapped between the sample and the crucible wall, which can cause air entrainment during remelting. For this reason, Fox and Campbell suggested the use of a porous medium such as sand or alumina that can support the specimen in a small container like a steel cup during remelting. To the best of our knowledge, this method was not adopted by any published research work yet and its detailed technical parameters that allow proper investigation of metal quality are not clarified in the literature. According to the mentioned authors, any sample geometry can be used for this method. However, it would be practical to use a sample geometry, remelting temperature, and porous medium quantity that allows a similar solidification rate as in the case of traditional RPT samples. The solidification rate is a critical factor in porosity formation.26,27,28 Too high solidification speed can hinder pore growth, while too slow solidification under partial vacuum can result in gas removal in the form of bubble bursting on the surface (similarly to vacuum degassing).29 Consequently, the present research work aimed to test the method of Fox and Campbell for the characterization of the quality of aluminum alloy ingots and to investigate the solidification conditions during the utilization of the method. For this, solidification simulations were conducted, and the selected parameters were tested by investigating the quality of primary aluminum alloy ingots produced by different technologies. The results were compared with the melt quality assessment of as-melted batches made from the ingots.

Materials and Experimental Procedure

The proposed remelting procedure is schematically illustrated in Figure 2. Small samples are machined from the investigated alloy ingots and melted in silica sand at 700 °C. We used unbonded loose silica sand as a melting medium with an average grain size of 0.35 mm. For these tests, 20 × 20 × 10 mm sample size was selected, which fit easily into the RPT sample cup. After melting, the sample is taken to the vacuum chamber of the RPT apparatus. Following solidification, the specimens can be investigated by computed tomography or by the image analysis of cross-sectional images made after appropriate metallographic preparation. The latter approach was chosen in this work.

Figure 2
figure 2

The scheme of the quality assessment of the ingot material.

Full size image

The selection of loose sand as a melting medium was based on the work by Fox and Campbell19 who reported that remelting samples (which are machined to the exact size of the steel cups) in steel cups can result in air pockets being trapped between the sample and the crucible wall, which can cause air entrainment during remelting. As loose sand has high gas permeability, the air between the sand grains surrounding the metal sample cannot enter the metal sample, as it would require more pressure to enter the liquid metal through the surface oxide layer than escaping through the pores between the sand grains.

As the first step of our investigation, we conducted solidification simulations with the aid of the gravity casting module of the NovaFlow&Solid simulation software, to investigate the differences between the solidification rates of traditional and remelt RPT samples. First, the solidification of a traditional RPT sample (Figure 3a) cast from Al–9.5%Si–0.4%Mn–0.15%Fe (weighing 90 g) was simulated with a casting temperature of 700 °C. The mold was selected to be a steel cup (with a thermal conductivity of 26 W/m·K) preheated to 300 °C with a 0.8-mm-thick refractory coating (with a thermal conductivity of 0.25 W/m·K). Then, the solidification of a remelted sample with sizes of 20 × 20 × 10 mm was simulated with silica sand mold material (with a selected thermal conductivity of 0.3 W/m·K30) and the RPT steel cup as a container (Figure 3b and c). The starting temperature of the sample and the mold was 700 °C. During the simulations, two sand quantities were tested: 55 g (Figure 3b), which is enough to completely fill the steel cup, and 30 g (Figure 3c), which was selected in an attempt to decrease solidification time. For real-life experiments, the 30-g sand quantity was chosen. The reason for this choice is that it was found during preliminary tests with sampling cups filled fully with sand that the top surface of the specimen was completely liquid even after 1.5 minutes and gas bubbles were bursting at the top of the sample, which can seriously alter the accuracy of quality evaluation.

Figure 3
figure 3

Cross-sectional view of the geometries used for solidification simulations, (a) RPT specimen and (b, c) samples remelted in sand support.

Full size image

The investigated AlSi9Mn ingots were manufactured by two different technologies: horizontal direct-chill casting (Figure 4a and b) and open mold gravity casting (Figure 4c and d). Two 1-cm-thick slices were cut from both types of ingots, and then, five samples were extracted from each slice as shown in Figure 4b and d (10 samples for both ingot types). Before melting, the samples were held at 500 °C for 1 h in a muffle furnace to remove any possible contaminations and hydroxides formed during the cutting of the samples. Before the first use, the sand that was used as a melting medium was preheated and held at 700 °C for 1 h to remove any possible volatile impurities and to facilitate the melting process of the alloy samples. The alloy samples were plugged into the preheated sand and were held at 700 °C for 15 minutes. The relative humidity levels in the workshop were between 50 % and 60 % during all experimental steps.

Figure 4
figure 4

(a, b) Direct-chill cast and (c, d) gravity cast ingots; sampling places are indicated in (b) and (d).

Full size image

Based on preliminary thermal analysis, 15 minutes is enough for the specimens to melt and reach the temperature of the sand. The samples solidified in the vacuum chamber of an RPT apparatus with 80 mbar pressure and 6 minutes of residence time. Although no binder was used to cure the sand, the shape retention of the specimens was excellent (Figure 5).

Figure 5
figure 5

Shape retention during remelting and solidification under reduced pressure.

Full size image

As an additional test, traditional RPT samples were taken from ingot samples (weighing 500 g), which were melted in a clay-graphite crucible at 700 °C. Three samples were cast immediately after reaching the casting temperature. The sampling method is described in detail in Ref. 31. The chemical composition of the ingot samples was analyzed with optical emission spectroscopy, which showed a minimal difference between the two types of ingots (Table 1).

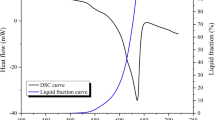
Table 1 Concentration of the Alloying Elements of the Studied Aluminum Alloy Ingots (wt. %)
Full size table

Thermal analysis tests were conducted on samples with the traditional RPT and remelt sample geometries. For these tests, a K-type thermocouple with a 1-mm diameter was used, which was protected by a stainless steel sheath. In both cases, the RPT cups were placed on an insulating refractory block. Before the thermocouple was vertically lowered into the remelted RPT sample, it was preheated to approximately 650 °C with a blow torch, to avoid excess heat extraction from the small-sized sample. In the case of the traditional RPT geometry, the steel cup was preheated to 300 °C. The temperature data were collected by a data acquisition system (National Instruments NI-9211) linked to a personal computer at a 4-Hz sampling frequency.

The RPT samples (both remelted and traditional) were cut in half and were ground with SiC grinding papers with grit sizes 180, 320, and 500. A scanner was used to make cross-sectional images with 1000 dpi resolution, and then, the MATLAB Image Processing Toolbox™ software was used for image analysis (as described in Ref. 32). Pores with an area smaller than 30 pixels (0.0194 mm2) were not taken into account. For microstructural analysis, samples were further ground up to 2400 grit size and polished with 3- and 1-μm diamond suspensions. Secondary dendrite arm spacing (SDAS) measurements were conducted. The average SDAS was evaluated by micrographs made from the cross sections of remelted and traditional RPT samples. For each specimen, 20 measurements were made in 4 different fields of view (80 measurements/sample).

Based on the results of the image analysis, bifilm index (BI [mm]) was calculated as33:

$${\text{BI}} = \sum L_{\max }$$
(1)

where \({L}_{\mathrm{max}}\) is the maximum length (major axis length) of pores [mm]. Bifilm index normalized to sample area (NBI [mm/cm2]) was evaluated as:

$${\text{NBI}} = \frac{{\sum L_{\max } }}{{A_{{{\text{Sample}}}} }}$$
(2)

where \(A_{{{\text{Sample}}}}\) [cm2] is the cross-sectional area of the samples. The pore number density (\({\text{N}}_{{\text{d}}}\) [cm−2]):

$$N_{{\text{d}}} = { }\frac{N}{{A_{{{\text{Sample}}}} }}$$
(3)

where \(N\) [−] is the total number of pores. The pore area fraction (\(A_{f}\) [%]):

$$A_{f} = \frac{{\sum A_{P} }}{{A_{{{\text{Sample}}}} }} \cdot 100$$
(4)

where \(A_{P}\) [cm2] is the area of a pore. Additionally, the normalized total pore perimeter (NTPP) [mm/cm2] was also calculated as:

$${\text{NTPP}} = \frac{{\sum P_{P} }}{{A_{{{\text{Sample}}}} }}$$
(5)

where \(P_{p}\) [mm] is the perimeter of a pore. The shape factor (SF) of the pores was calculated as33:

$$S_{F} = \frac{{4\pi A_{P} }}{{P_{p}^{2} }}$$
(6)

where a perfect circle would have an SF of 1.

Results and Discussion

Solidification Simulations

Figure 6 shows the simulated temperature distributions at the cross sections of traditional (Figure 6a) and remelted RPT samples (Figure 6b and c) at different stages of the solidification. Figure 6b presents the case when 55 g of silica sand was used as a porous medium, and Figure 6c presents the case when 30 g of silica sand was used as a porous medium. In all cases, the starting temperature of the liquid metal was 700 °C in accordance with the experimental parameters. The mold temperature, however, was rather different: The steel cup of the traditional RPT sample was set to 300 °C, while the sand support and steel cup of the remelted specimens were set to 700 °C.

Figure 6
figure 6

Cross-sectional view of the temperature distribution according to solidification simulations of (a) traditional and (b, c) remelted RPT samples at different stages of the solidification process. (b) presents the case when 55 g of silica sand was used as a melting medium and (c) presents the case when 30 g of silica sand was used as a melting medium.

Full size image

Figure 7 summarizes the local solidification times (Figure 7a–c) and solidification times (Figure 7d–f) at the cross sections of the samples. Local solidification time (tf [s]) is defined as the time taken at a given location in a casting for the temperature to fall from the liquidus to the non-equilibrium solidus, while solidification time (tsol [s]) is interpreted as the time needed at a given location in a casting for the temperature to fall from the casting temperature to the non-equilibrium solidus. The total solidification time (ttotal [s]) is the time needed to reach 0 % liquid phase fraction in the whole casting, starting from the moment of casting. The remelted samples start to solidify later than the traditional RPT specimen, which is a consequence of the preheated sand filling. In the case of using 55 g sand, a hot spot is formed under the specimen (Figure 6b), which increases the solidification time and results in a total solidification time of 297 s (Figure 7e). On the other hand, applying 30 g sand as a filler results in a rather similar total solidification time as in the case of the traditional RPT (with a 9 s difference).

Figure 7
figure 7

(a-c) Local solidification times and (d-f) solidification times at the cross sections of (a, d) traditional RPT specimens and samples remelted in (b, e) 55 g and (c, f) 30 g silica sand.

Full size image

Although the total solidification times of traditional RPT specimens and samples remelted in 30 g sand are rather similar, the local solidification time is remarkably less for the remelted piece (Figure 7c). As the fineness of the microstructure is controlled by the local solidification time, based solely on the simulations, using 55 g sand would be a better choice in terms of providing similar solidification conditions as in the case of traditional RPT. On the other hand, preliminary tests revealed that using sampling cups filled fully with sand results in a more significant bubble bursting at the top of the samples due to the delayed start of the solidification process. For this reason, 30 g of sand filling was used during real-life experiments.

Microstructural Investigation and Thermal Analysis

To investigate whether the local solidification times of remelted samples were indeed similar to that of the traditional RPT samples, SDAS measurements were conducted. Evaluating SDAS is a useful tool, which can be used for the prediction of local solidification times of different alloys.34,35,36 The average SDAS was calculated by measurements made on micrographs taken from remelted (Figure 8a and c) and traditional RPT samples (Figure 8b and d). In each case, the average SDAS is around 50 μm with negligible variation, which means the differences in the local solidification times indicated by the simulations do not have a significant effect on the secondary dendrite arm spacings of the samples.

Figure 8
figure 8

Microstructural images of the investigated samples: (a) HDC cast remelted, (b) HDC cast traditional, (c) gravity cast remelted and (d) gravity cast traditional.

Full size image

Similar to the simulations, the thermal analysis results also indicate a remarkable difference in the local solidification times (about 56 s), while there is a smaller difference in total solidification times (Figure 9). It should be noted that the difference could be less significant during solidification without thermocouples, as some heat may be conducted away by the thermocouple, whose effect is more significant in the case of the small-sized remelted sample.

Figure 9
figure 9

Cooling curves of traditional and remelt RPT samples.

Full size image

It is well known that the secondary dendrite arm spacing (SDAS [m]) can be estimated from the local solidification times (tf [s]) according to the following formula37:

$${\text{SDAS}} = K\left( {Mt_{f} } \right)^{1/3}$$
(7)

where

$$M = - \frac{\Gamma D}{{m\left( {1 - k} \right)\left( {c_{E} - c_{0} } \right)}}\ln \left( {\frac{{c_{E} }}{{c_{0} }}} \right)$$
(8)

\(K\) is a numerical constant, which is 5.5 according to Feurer and Wunderlin,38 and 1281/3 \(\approx\) 5.0 according to Kirkwood.39 \(\Gamma\) is the Gibbs–Thomson coefficient [K·m], \(D\) is the diffusivity of solute atoms in liquid [m2/s], \({\mathrm{c}}_{\mathrm{E}}\) denotes the eutectic composition (12.6 wt. % in the Al–Si system), \({c}_{0}\) is the solute concentration (9 wt. %), \(m\) is the slope of the liquidus curve (6.6 °C/wt. % for Al–Si) and \(\mathrm{k}\) is the distribution coefficient, which is 0.13 for Si in Al.34 \(\Gamma\) is given as

$${\Gamma } = { }\frac{{\sigma_{{{\text{SL}}}} }}{{\Delta S_{f} }}$$
(9)

where \({\sigma }_{\mathrm{SL}}\) is the solid/liquid interfacial energy [J/m2] and \(\Delta {S}_{f}\) is the entropy of fusion [J/Km3]. Using \({\sigma }_{\mathrm{SL}}\)=0.15 J/m240 and \(\Delta {S}_{f}\)=1.112·106 J/Km3,41 \(\Gamma\) is 1.349·10−7 Km. If \(\mathrm{D}\)=2.05·10−9 m2/s (which was calculated at 590 °C liquidus temperature based on Ref. 42), the experimentally measured 50 μm SDAS is given by Eqn. 7 at \({t}_{\mathrm{f}}=\) 223 s when \(K=\) 5.0 and \({t}_{\mathrm{f}}=\) 167 s when \(K=\) 5.5. By comparing the measured and calculated local solidification times (Table 2), the matching between the values is relatively good when the numerical constant of Kirkwood39 is used. Also, it is worth noting that the local and total solidification times acquired by solidification simulations are also in accordance with the experimental results. Based on the results detailed above, it can be said that there are some differences between the local solidification times of traditional and remelted RPT samples, but these differences are too small to be evinced by microstructural investigations. This means that pore formation is not affected notably by the differences in the local solidification rates.

Table 2 Comparison of Measured and Calculated Solidification Times
Full size table

Quality Evaluation

Table 3 summarizes the image analysis results of remelted RPT samples, while Figure 10 shows the comparison of the individual parameters evaluated during the analysis. Figure 11 summarizes the distribution of maximum pore diameters (Figure 11a and b) and shape factors (Figure 11c and d) of the pores found within the 10 DC and 10 GC remelted samples. The compiled results in Table 3 show clear differences between the porosity parameters of the specimens extracted from the ingots cast by the two technologies: The gravity cast ingots possess higher values, which indicates higher impurity content. The average pore area fraction is almost double and the average BI is more than one and a half times the values of the direct-chill cast ingot. Based on this, the bifilm and gas content (solute hydrogen and entrained air) of the gravity cast ingot is remarkably higher, which is in agreement with the results of Erzi and Tiryakioǧlu,24 who found that the quality of DC cast AlSi7Mg0.3 ingots was more favorable than that of the gravity cast ingots. According to Uludağ et al.43, the melt quality can be categorized by the BI values as follows:

  • 0 mm ≤ BI ≤ 10 mm: high-quality melt,

  • 10 mm ≤ BI ≤ 25 mm: good quality,

  • 25 mm ≤ BI ≤ 50 mm: average quality,

  • 50 mm ≤ BI ≤ 100 mm: unacceptable quality,

  • BI ≥ 100 mm: bad quality that should be avoided.

Table 3 Image Analysis Results of Remelted Samples
Full size table
Figure 10
figure 10

(a-f) Comparison of different parameters evaluated by the image analysis of remelted samples (DC: direct-chill cast, GC: gravity cast ingot).

Full size image
Figure 11
figure 11

Distribution of (a, b) maximum pore diameters (c, d) and pore shape factors in (a, c) HDC and (b, c) gravity cast samples. For the analysis, the pore data of the 10–10 remelted samples were merged.

Full size image

Based on solely this scale, the DC cast ingot falls into the “average quality,” while the gravity cast ingot belongs to the “unacceptable quality” category. However, it should be emphasized the remelted samples of this study have a smaller cross section than traditional RPT samples, which were presumably used for the establishment of the quality scale of Uludağ et al., so even stricter BI limits should be used for the categorization in our case. There are several studies22,44,45,46,47,48,49 that showed that BI values correlate with mechanical properties, which means that the mechanical properties of castings made from the two investigated types of ingots could differ (using the same technological parameters). This presumption will be investigated in a future study.

Because the cross-sectional area of the samples was relatively constant, there is a strong correlation between BI and NBI values (Figure 10a). By comparing pore number density and NBI results (Figure 10b), we only found a poor correlation, which is in accordance with the results of Uludağ et al.43, but somewhat contradicts the results of Dispinar and Campbell44,49 who found a strong linear correlation between the number of pores and BI values for different alloys. However, it is worth noting that the number of pores and total pore diameter (BI) are not necessarily interrelated. A strong correlation is expected when most of the pores have similar diameters. However, in theory, the same BI can be reached with numerous small pores or with a few larger ones. By looking at the cross-sectional images in Figure 10a–d, one can see that there are cases when the differences in the sizes of the pores are remarkable, which explains the poor correlation in Figure 10b. It was reported that in most cases, the diameter of the pores in RPT samples follows the lognormal distribution,43,50 and it is common that most of the pores have a similar diameter, which means that some type of correlation between the number of pores and BI can be expected. However, there could be circumstances, which can contribute to non-uniform pore size distribution as it was reported by LaOrchan et al.51 In the case of short-freezing range alloys (like 413), a solid shell may form on the surface of the RPT sample, which can result in a large central pore caused by shrinkage. In our case, the distribution of maximum pore diameters (Figure 11a and b) shows that most of the pores fall into the size range of 0.2–0.4 mm for both HDC and GC samples. However, there is a significant fraction within the size range of 1–2 mm, especially in the case of GC specimens, which explains the poor fitting in Figure 10b.

There is an excellent linear correlation between NBI and NTPP with an R2 value of 0.9527 (Figure 10c). It was reported by Uludağ et al.43 that there is a strong relationship between the total volume of pores and BI. However, a relationship between the total pore perimeter (and its normalized values) and BI was not published yet. Dispinar and Campbell52 highlighted that maximum pore diameter is an approximation of bifilm length. Based on this assumption, the main idea behind NTPP is that pore perimeter can be used as a rough two-dimensional approximation of bifilm surface area (naturally it is an overestimate as bifilms are expanded during solidification). From this point of view, NTPP is a two-dimensional version of the bifilm spatial index (BSI) introduced by Song et al.53 If we assume that each pore has a perfectly circular cross section, the relationship between the total pore perimeter and BI (and their normalized values) should be simply a factor equal to the value of π (Figure 12a). In this case, NBI should be π−1 = 0.3183 times NTPP. If we force the regression line to intercept the axis of ordinates at 0, we get a relationship, which is pretty close to the theoretical one: NBI = 0.2937NTPP. The difference is mainly caused by the fact that pores are not perfectly spherical, and their cross sections are not perfectly circular. We can see in Figure 12a that the values of GC samples differ more significantly from the theoretical relationship meaning that the pores are less spherical in these specimens. This is supported by the shape factor data in Figure 11c and d, which shows that there are more pores in HDC samples, which have a shape factor between 0.9 and 1.0. The average shape factor of the pores found in HDC and GC specimens is 0.65 and 0.57, respectively.

Figure 12
figure 12

Relationship between NBI and NTPP in the theoretical case, when the pores are perfectly spherical (black line) compared with the experimental data.

Full size image

The pore area fraction results correlate poorly with normalized BI (Figure 10d) and NTPP (Figure 10e), which can also be explained by the deviation of the pores from the spherical shape. No relationship was found between pore number density and pore area fraction (Figure 10f). Note that in theory, each relationship presented in Figure 10 should intercept the axis of ordinates at 0. However, to get representative R2 values, the regression lines were not forced to intercept at 0.

Traditional RPT Samples

The results of the image analysis of traditional RPT samples (Figure 13) cast from remelted ingot pieces show a similar difference between DC and gravity cast ingots as in Table 3. Almost every investigated parameter is higher for gravity cast ingot samples (Figure 13a), which indicates higher bifilm and gas content. The only exception is the pore number density, which is higher in the case of DC cast ingot (Figure 13b). This higher number of pores is most probably a result of the higher tendency to shrinkage porosity formation in traditional RPT samples. In our previous study,54 we found that after multiple rotary degassing treatments (with Ar purging gas) a large central shrinkage pore formed in a traditional RPT sample as a result of low hydrogen and bifilm content. However, this central shrinkage pore may appear as several small pores on a sectioned sample surface. In this case, especially for the 3rd DC RPT sample, the situation is similar: There is a central shrinkage pore, which appears as separate pores on the cross section, which increases pore number density.

Figure 13
figure 13

Results of the image analysis of RPT pieces cast from remelted (a) gravity cast and (b) HDC cast ingot samples.

Full size image

NBI, Af, and NTPP results correlate well with that of the remelted samples, and it is evident that the HDC cast ingot possesses lower oxide and gas concentration. This can be traced back to the differences in the melt preparation and casting technologies. As is highlighted in introduction, the HDC casting process does not involve any pouring action and there is no free-falling liquid metal, so there is no bifilm formation during casting. Also, the casting units are generally connected to the melting furnaces through a metal launder system which involves in-line degassing units and filter boxes.16,17 For these reasons, metal cleanliness is often superior to gravity cast ingots, which is supported by our experimental results.

Possible Sources of Error in Quality Evaluation

Tiryakioğlu et al.55 reported that there are bifilms in RPT samples that fail to open up and inflate into pores during solidification. For this reason, it is stated by Olofsson et al.56 that porosity is only the visible (or the more easily detectable) part of the entrainment damage. This indicates that RPT tends to underestimate bifilm quantity. The number of unopened bifilms (hidden entrainment damage) can be especially high when the solute hydrogen content is low.57 Based on this, there could be unopened bifilms in the samples that were not detected during our investigation, which means that only those bifilms are quantified that can form pores during solidification. This uncertainty currently applies to most (if not all) melt quality evaluation methods, which rely on reduced pressure tests. However, it should be highlighted that the pores have grown larger in remelted samples compared to traditional RPT specimens, which can be directly seen in the higher pore area fraction values of remelt samples (Table 3 and Figure 13). The possible reason for this is that initially, the remelted samples stay in the liquid state for a longer time (Figure 9), which allows a more complete bifilm inflation. From this point of view, remelted samples provide more accurate information about the bifilm content than traditional RPT specimens.

As the remelted samples are relatively small, the suspicion arises that the liquid metal may absorb hydrogen from the furnace atmosphere, or it may lose hydrogen due to natural degassing.58 The former possibility was tested by remelting a sample extracted from a degassed batch that had a density of 2.67 g/cm3. After remelting and solidifying in a vacuum chamber at 80 mbar, the density of the sample remained the same, which indicates that hydrogen absorption was not an issue during the 15 minutes of the melting procedure. It is the authors’ opinion that natural degassing is also negligible taking into account that a relatively thick oxide layer forms on the sample surface during the 1-hour long preheating at 500 °C and the melting procedure. It was reported that the absorption and desorption rates of hydrogen through an undisturbed oxide layer of liquid Al at temperatures below 800 °C are about 1–3 ml·m−2·h−1. This reaction rate is increased to 104 or 105 ml·m−2·h−1 by the continuous disturbance of the melt surface.59 In the examined case, the practical meaning of this is that unless the oxide layer on the melt surface is disturbed, hydrogen transport between the sample and the furnace atmosphere can be neglected. By taking traditional RPT specimens, it appears that with time, natural degassing occurred to some degree as the pore area fraction was significantly less in the case of the third RPT samples, which were cast approximately 15 minutes after taking the first samples (Figure 13). From this point of view, remelted samples provide more accurate results.

It is also worth noting that for the remelting investigations, the parts with shrinkage cavities on the central region of the ingot were not considered (Figure 4d). These, if they are connected to the surface (or initiated by a bifilm), already have an oxidized surface, which increases the oxide load of the batches made by melting these ingots. This is clearly not reflected by this investigation method.

Conclusion

Based on the experimental results detailed in this study, the following conclusions can be drawn:

  • The quality evaluation method proposed by Fox and Campbell19 can be successfully applied for the characterization of the bifilm and gas (hydrogen and entrained air) content of solid ingot materials. The method holds the potential to be applicable for the quality evaluation of any type of solid samples such as sections of cast parts or running systems.

  • Solidification simulations, thermal analysis, and microstructural investigations revealed that by using the proposed sample geometry and remelting technique, the differences in the solidification conditions of traditional and remelt RPT samples are too small to be uncovered by microstructural investigations.

  • HDC cast ingots possess lower bifilm and gas concentrations, which can be traced back to the differences in the casting technologies of the ingots: Gravity cast ingots are poured turbulently, which results in more severe air and oxide film entrainment. Shrinkage cavities in gravity cast ingots also contribute to lesser metal quality.

  • There is a strong linear correlation between the normalized values of bifilm index and the total pore perimeter, which indicates that bifilm index can be used for the prediction of total pore surface area.