Introduction

High-pressure die casting (HPDC) is an important process for the manufacture of Mg components in the automotive and handheld tools industries. This is due to that HPDC allows cost-effective near-net-shape manufacture of parts with complex geometries in a single operation.1 Among the Mg-based alloys, AZ91 accounted for more than 50% of all HPDC components due to an excellent combination of properties.2

Optimization of processing parameters (such as intensification pressure, ejection force and time, die geometry and temperature, cooling time) is critical to producing high-quality HPDC castings and is usually a complex exercise where the different parameters interact.3 If parameters are not carefully controlled, the castings will turn out defective. The most typical defect in HPDC components is porosity,4,5,6,7,8 which substantially degrades properties. Adamane et al.6 reviewed the effects of the injection parameters on the porosity and tensile properties of the die castings and suggested optimal values for the gate velocity and intensification pressure for an aluminum alloy. Yalçin et al.9 reported that the vacuum application to the die cavity is more important and effective than injection pressure to decrease porosity of A380 aluminum alloy. Moreover, they reported that the casting with a high injection velocity cannot be preferred together with high pouring temperature, a high-pressure injection with vacuum. Lee et al.7 showed that for magnesium alloy porosity is reduced with increasing intensification pressure, but increased with increasing casting second-phase injections speed.

Besides porosity, distortion (warping) of the casting is another cause of rejection for HPDC parts. A component may exceed the accepted tolerance allowance due to distortion.10 Distortions in castings are usually due to variation of cooling rates in different regimes or due to variation of section thicknesses.11 Castings contract during solidification and cooling. This contraction interacts with constraints such as die walls and generates residual stresses and a complex springback and continued warping during post-die ejection cooling.12 For complex-shaped castings, non-uniform cooling conditions may create plastic strain that results in permanent distortion.13

Solidification and cooling in the HPDC process lead to the development of residual stresses within the surface layers of the cast component. This has a negative influence on, for instance, fatigue life.14 Not only the level of stress, but also the type of stress (tensile or compressive) is critical factors to understand in the formation of residual stress. A surface with tensile residual stress induced by the casting process will be more prone to fatigue failure than a surface with compressive residual stress.15 Moreover, if substantial residual stress exists in a casting, there is potential that at high temperatures residual stress may relax, resulting in part distortion.16 Hence, understanding of residual stress distribution and the distortion pattern of HPDC cast AZ91D parts could enable reduced shape deviation from design specification, through improved process control and better die design. This would also improve productivity and reduce cost. Hence, to increase the process efficiency a fundamental understanding of component distortion and residual stress is an important topic to study. Specifying the appropriate set of process parameters, which provides a high-quality HPDC product, is a key concern for engineers and researchers.

The main objective of present work was to get a detailed map and to understand the effect of HPDC process parameters on both distortion and residual stress response of an AZ91D component. The studied parameters were first-phase injection speed, the temperature difference between the two die halves through variation of the temperature of fixed half of the die, cooling time and intensification pressure. The distortion and residual stress of the finished products were measured. Furthermore, analysis of variance (ANOVA) was used to find the effect of casting parameters on the performance characteristics.

Experimental Procedure

Component Casting

The case study of this paper is an engine crank case of a chain saw, as shown in Figure 1. The composition of the alloy was measured using an optical emission spectroscopy (OES) (SpectroMaxCCD LMXM3, SPECTRO Analytical Instruments Inc, Germany), as given in Table 1. Crank cases were manufactured at Husqvarna AB using a Buhler SC-D42 machine with 4000kN locking force, and the protecting gas was a mixture of 0.5% SO2 and dry air. The experimental window for the design is shown in Table 2.

Figure 1
figure 1

Illustration of the crank case. The right picture is moving side and the left picture is fixed side of the crank case. The points for distortion measurements are indicated as D1, D2, D3, D4 and D5. The locations for residual stress measurements are indicated as R1, R2 and R3.

Full size image
Table 1 Chemical Composition of the AZ91D Alloy (wt%) Established Through OES
Full size table
Table 2 Design Scheme of High-Pressure Die-Cast Parameters and Their Minimum and Maximum Levels Together with Average of Reference Level Parameters for References Cast Sample
Full size table

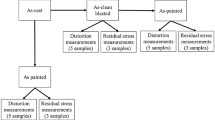
In HPDC, there are a number of parameters that may influence component characteristics and performance. Hence, investigating the best combinations of process parameters and their changing quantities in order to obtain results statistically reliable is crucial. In the current study, a response surface method was used through a D-optimal approach allowing for an effective design capable of a quadratic response surface with three replications and three runs for the lack of fit. To create this design of experiments (DOE), DesignExpert™ software (Stat-Ease) was used for both the DOE and the regression analysis and analysis of variance (ANOVA). In current work, four principal casting parameters (A) first-phase injection speed, (B) temperature of fixed half of the die, (C) cooling time and (D) intensification pressure were specified as the varied casting parameters. The choice of omitting the second-phase injection speed was based on the fact that the dwell time in the shot sleeve is of the order 70 times longer than the duration of the second phase resulting in that the temperature loss during the process is dominated by the shot-chamber dwell time. The interfacial heat flux in the shot sleeve is of the order of 2 MW/m2 17 and in order of 6 MW/m2 18 in the die cavity during filling; hence, shot-sleeve dwell time is the dominating parameter for final part temperature during processing. The minimum and maximum levels of HPDC parameters are identified as given in Table 2. The interaction between these parameters was studied as well. It should be mentioned that intensification pressure was applied immediately after the second stage and for the full duration of the cooling time. To assure that components were cast under stable conditions, parts from the first ten shots were scrapped and subsequently components were sampled. Moreover, it was assured that all the test conditions made acceptable cast components without apparent casting defects and within dimensional tolerances.

The experimental design and results are collated in Tables 3 and 4 for distortion and residual stress measurements, respectively. For distortion measurements, each run condition was repeated ten times to acquire sufficient statistics for the response. Residual stress was measured for components cast by eight different run conditions where each run was repeated three times, see Table 4.

Table 3 Experimental Layout Using Quadratic Method Through DOE Together with Distortion Responses at Different Reference Points
Full size table
Table 4 Experimental Layout and Responses for Residual Stresses
Full size table

Component Distortion Measurements

The distortion value was measured by using the standard in-house quality assurance tool, as shown in Figure 2. The distortion values were obtained through the comparison of dimensional measurement between actual HPDC part and design specification at five critical reference points D1, D2, D3, D4 and D5, see Figures 1 and 2. The measured direction was along the normal vector of surface, and the value measured was the positive (toward fixed side) or negative (toward moving side) deviation away from the zero plane.

Figure 2
figure 2

The standard in-house quality assurance tool applied for measuring the distortion value. D1, D2, D3, D4 and D5 are the five reference points.

Full size image

Residual Stress Measurements

The prism hole-drilling system (Stresstech Group Company) was employed to measure residual stresses. The hole-drilling technique involves drilling a hole in the component and measuring the resulting strain near the hole. The hole-drilling technique is based on the fact that if a stressed material is removed from its surroundings, the equilibrium of the surrounding material must readjust its stress state to attain a new equilibrium. In the conventional technique using strain gages, surface distortion is measured as a change in electrical resistance.19 Prism measures surface distortion using laser light (ESPI—electronic speckle pattern interferometry).20 Images from before drilling are compared with those after each incremental drilling. Every condition is described by a set of four images, each taken with the reference beam phase-shifted a different amount: 0°, 90°, 180° and 270°.

Data analysis includes all pixels in a ring-shaped region around the hole, described by the inner and outer integration radius (the inner radius was twice that of the hole radius and the outer radius was four times of the hole radius). The area immediately next to the edge does not provide useful information because the drilling process disturbs this part of the surface. Eventually, the results were treated with an unwrapping algorithm to produce the displacement map for each of the three variables of the planar stress state. Furthermore, together with the elastic material parameters, Young’s modulus and Poisson’s ratio, this generates the stress values.

The maximum useful hole depth is dependent on hole diameter. The numerical models developed for prism support drilling between drilling between 0.1 < h/d < 0.6. The end mills with 0.8 mm dimeter were used in this study.

In current study, residual stresses were measured at three different locations, points R1, R2 and R3, as shown in Figure 1. These points are the critical points, which have shown failure (creep and/or fatigue) problem during operation. The maximum residual stress value at any depth was adopted as the residual stress value of the whole product in this process. The drilling rig was programmed to reach the final depth of 0.5 mm in 14 equidistant steps. The drilling feed rate was 0.05 mm/s, and after every drilling step, the drilling was stopped for about 60 s before taking a first set of images; a second image set was taken about 30 s; after that, illumination alpha rotation angle was 50° and video alpha rotation angle was 30° for all measurements. Stresses were calculated using a Poisson’s ratio of 0.3 and a Young’s modulus of 45,000 MPa.

In this study, the signed von Mises stress (SVM) was used for the residual stresses quantification, see Eq. 1. The SVM represents the sign (positive or negative) of the absolute maximum principal stress to include the influence of tension and compression in the effective stress.

$$ \sigma_{\text{svm}} \, = \,{\text{sign}}(I_{1} ) \cdot \sigma_{\text{vm}} $$
(1)

where \( \sigma_{\text{vm}} \) is the von Mises stress and \( I_{1} = \sigma_{x} + \sigma_{y} + \sigma_{z} \)

Result and Discussion

Analysis of Distortion

The average distortion (together with standard errors) responses at each reference points (see Figure 1) are collated in Table 3. The distortion direction was also taken into consideration. To model the significance of HPDC process parameters and their interactions on distortion responses at different reference points, regression analysis was applied through ANOVA. However, no statistically significant regression model was realized for the distortion responses at points D1, D2, D3 and D4. The reason for this could be related to the relatively small changes in distortion responses of these points by varying the cast conditions, see Table 3.

On the other hand, for distortion responses at point D5, the ANOVA was conducted and the results are given in Table 5. The temperature of fixed half of the die, (B), and intensification pressure parameter, (D), were statistically significant model terms. Moreover, the parameters (B2) and (D2) were also statistically significant. Based on ANOVA results, the interaction between the temperature of fixed half of the die parameter (B) and intensification pressure parameter (D) was kept to keep model hierarchy to allow retransformation from the normalized terms used in the evaluation. It should be mentioned that another model where parameters (A) and (C) were statistically significant could be obtained but removed as they had no physically significant impact on distortion.

Table 5 ANOVA Response Surface Reduced Quadratic Model for Distortion Response at Point D5
Full size table

The impact of the intensification pressure on distortion responses is plotted in Figure 3a. Increasing the intensification pressure generated less distortion at point D5. Increasing the intensification pressure will increase heat transfer between the part and the die. This will allow the part rib structure on the moving side to bend the part toward the moving side.

Figure 3
figure 3

The effect of (a) parameter (D) = intensification on distortion response and (b) interaction of parameters (B) = temperature of fixed half of the die and parameter (D) on distortion response at point D5. Centerline is the actual trend. Dash lines are the 95% confidence intervals.

Full size image

Figure 3b shows the impact of the interaction of the temperature of fixed half of the die, (B), and intensification pressure, (D), on distortion responses at point D5. The temperature of the moving side was kept constant at 150 °C during the experimental campaign. It was observed that as the temperature difference between the two die halves (fixed and moving side) increased, the distortion response was such that the distortion tended to be toward the moving side at point D5.

The largest distortion in the part was at point D3. The distortions did not significantly change with casting conditions, see Table 3. Moreover, no statistically significant model was obtained for distortion responses at this point. It should, however, be noted that point D3 was adjacent to two ejector pins and there was a rib structure on the moving side that could contribute to this distortion. The exact cause of this large distortion could not be positively identified.

Analysis of Residual Stress Measurements Analysis

Figure 4a–c shows the SVM stresses at the locations points R1, R2 and R3 with locations shown in Figure 1. The maximum value of von Mises (VM) stress at any depth was identified and the SVM value of that VM stress was considered as the residual stress value of the component. The residual stress responses are collated in Table 4. It was observed that at all points R1, R2 and R3 the maximum value of |SVM| was at the very surface (depth of 0.025–0.05 mm) and these stresses were tensile. Moreover, the residual stresses tended toward zero at depths greater than 0.5 mm.

Figure 4
figure 4

Trends of residual stress profiles of the SVM stress at (a) point 1, (b) point 2 and (c) point 3. The run conditions are given in Table 4.

Full size image

Hofer et al.11 suggested that residual stress for HPDC cast parts could be due to cooling and solidification as the solidified surface gains mechanical stability and shrinks. As the interior of the casting solidifies and cools, the initially solidified surface is put under compression. Secondary residual stresses are related to the geometry of the component.21 For the mechanism suggested by Hofer et al.,11 some degree of thermal gradient is required to allow a surface layer to solidify. However, in this study, tensile stress was observed in all cases at the surface. Thermal gradients in a solid layer are characterized by the Biot number, hL/k, where h is the heat transfer coefficient, L the characteristic length and k the thermal conductivity. Estimating the Biot number with h = 112 kW/m2 K (at peak value), k = 72 Wm−1 K−1 22 and L = 0.5 mm (typical half cross-sectional thickness at the region of interest) leads to a Biot number of 0.77. This Biot number suggests that there might be a temperature gradient in the surface layer. However, no compressive stress identified at the surface, which means that the magnitude of tensile residual stress at the surface was bigger than the residual stress induced due to the solidification.

From Table 4, it is understood that increasing the intensification pressure led to an increase in tensile residual stress responses at all locations of R1, R2 and R3 at the very surface.

The maximum SVM stress responses for three different points are collated in Table 4. ANOVA of the residual stress (SVM) for points R1, R2 and R3 (Figure 1) is given in Tables 6, 7 and 8 respectively.

Table 6 ANOVA Response Surface Reduced Quadratic Model for Residual Stress Responses for Point R1
Full size table
Table 7 ANOVA Response Surface Reduced Quadratic Model for Residual Stress Responses for Point R2
Full size table
Table 8 ANOVA Response Surface Reduced Quadratic Model for Residual Stress Responses for Point R3
Full size table

The parameters (B) and (D) were found statistically significant model terms for residual stress at point R1, see Table 6. Interaction between parameters (B) and (D) was kept to keep model hierarchy as (D2) was statistically significant. The effect of temperature of fixed half of the die (B) and intensification pressure (D) on residual stress at point R1 is plotted in Figure 5a, b, respectively. Increasing the temperature of fixed half of the die slightly reduced residual stress at point R1, see Figure 5a. However, an increased intensification pressure strongly increased residual stress at point R1, see Figure 5b. The interaction of parameters (B) and (D) is shown in Figure 5c. The dominating effect is that of the intensification pressure (D). It is worthwhile noting that at low intensification pressure the effect of the temperature of fixed half of the die at residual stress of point R1 was less than at high intensification pressure. At high intensification pressure (D), an increased fixed half temperature (B) reduced residual stress, suggesting that relaxation takes place in contact with the die and that the nature of contact is changed between the die and the component. A similar in-die relaxation was observed by Jarfors23 revealing itself as a change in the early-stage hardening in the stress–strain behavior of thin-walled AZ91D test samples.

Figure 5
figure 5

(a) The effect of parameter (B) temperature of fixed half of the die, (b) the effect of intensification pressure parameter (D) and (c) the interaction of parameters (B) and (D). Dash lines are the 95% confidence intervals.

Full size image

Table 7 shows ANOVA for residual stress at point R2. Parameters (B), (C), (C2) and (D) showed significant effect on the model responses. Figure 6a–c shows the effect of temperature of fixed half of the die, cooling time and intensification pressure on the residual stress responses at point R2. Influence of parameters (B) and (D) at point R2 is similar to the point R1 responses. Decreasing the temperature of fixed half of the die and increasing the intensification pressure induced more residual stress at this point. Here, like point R1, the effect of intensification pressure on residual stress was stronger compared to effect of the temperature of fixed half of the die. At point R2, cooling time (C) was statistically significant where an increased cooling time up to 10 s resulted in less residual stress supporting an in-die relaxation for point R1. Cooling times beyond 10 s showed no physically significant change in residual stress. It should be noted that the point R2 is adjacent to the gating system and will experience higher temperature than the rest of the investigated location.

Figure 6
figure 6

(a) The effect of parameter (B) temperature of fixed half of the die, (b) the effect of intensification pressure parameter (D) and (c) the effect of cooling time on residual stress responses at point R2. Centerline is the actual trend. Dash lines are the 95% confidence intervals.

Full size image

Table 8 shows ANOVA for residual stress at point R3. The parameters (B) and (D) are the significant model terms. Similar to the points R1 and R2, increasing the temperature of fixed half of the die slightly reduced the residual stress, suggesting in-die relaxation. An increased intensification pressure increased the residual stress at this point, see Figure 7a, b.

Figure 7
figure 7

(a) The effect of parameter (B) temperature of fixed half of the die and (b) the effect of intensification pressure parameter (D) on residual stress responses at point R3. Centerline is the actual trend. Dash lines are the 95% confidence intervals.

Full size image

Comparing the results from the distortion and residual stress analysis showed that the most dominant parameter was intensification pressure. An increased intensification pressure reduced distortion and increased residual stress near the surface. The distortion showed a maximum on the fixed half of the die when the temperature difference was at a minimum between the two halves. The distortion is toward the fixed side as the geometry of the part is such that it forms a cup around the protruding parts of the fixed side. Residual stress tended to be reduced with increasing moving side temperature supporting an in-die relaxation which also was supported by a reduction of residual stress with increased cooling tome for point R2. It should be noted that the maximum values of SVM were all tensile stress close to the surface (0.025 mm depth). Pure solidification from the wall should result in compressive stresses.24 This supports that the residual stress formation is dominated by the part lateral contraction and part distortion around the fixed side during cooling, opposing the finding of Hofer et al.11

Conclusions

High-pressure die casting is a complex manufacturing process with many sub-processes or variables. An experimental parametric study was carried out to quantitatively characterize the effects of temperature of fixed half of the die, cooling time, the first-phase injection speed and intensification pressure on the distortion and residual stress formation in the high-pressure die-cast AZ91D Mg alloy. The collated and presented data lead to the following important observations and conclusions.

The most important process parameter affecting the distortion and residual stress near the surface was intensification pressure. It was clearly observed that increasing the intensification pressure decreased the components’ distortion at point D5. Besides, application of intensification pressure significantly increased the residual stress values near the surface.

Significant statistical model for distortion responses were only obtained for distortion results at point D5. It appeared evident that temperature difference between two halves of the die is an important parameter to consider in tolerance management. An increase in the temperature of fixed half of the die increased the total amount of distortion in components, and the distortion is toward the fixed side. On the other hand, increasing the moving side temperature decreased the residual stress of the components due to in-die relaxation.

The other two process parameters, first-phase injection speed and cooling time, were found to be relatively less influential.

The obtained maximum SVM was all tensile close to the surface, which means that the residual stress formation is dominated by the part lateral contraction and part distortion around the fixed side during cooling.

The identification of critical process parameters can help foundrymen for better planning the casting process of castings which tend to the formation of distortion and residual stresses.