Introduction

This paper analyses the time series properties of tax revenues over the period from 1965 to 2021 in a set of 21 OECD countries. For this purpose we use a fractional integration framework which is more general than the standard one based on the stationary I(0) versus non-stationary I(1) dichotomy. In particular, it allows the differencing parameter d to take any real value, including fractional ones, as opposed to integers only. As a result, it allows for a much wider range of stochastic processes. Moreover, the estimated parameter d measures the degree of persistence of the series and sheds light on whether or not it is mean reverting. This provides useful information on whether the effects of shocks to the series will be transitory of permanent which cannot be found in other studies using different methods such as unobserved components (Koopman and Ooms 2003).

Given the recent surge in inflation, we also examine whether there exists a long-run relationship linking this variable to taxation. For instance, Patoli et al. (2012) found that they are positively correlated in Pakistan; Sunday (2015) also found a long-term association in the case of Nigeria; Wang and Han (2018) provided evidence of unidirectional causality running from taxation to inflation in China. In the present study, we test for mean reversion in the differences between the tax series and inflation to establish whether they are linked.

The layout of the paper is the following: Sect. “Methodology” outlines the methodology; Sect. “Data” describes the data, Sect. “Empirical Results” reports the results, and Sect. “Conclusions” offers some concluding remarks.

Methodology

As mentioned before, we use fractional integration or I(d) techniques. These belong to a broader category called long-memory processes, which are characterised by a spectral density function which is unbounded at one or more frequencies in the spectrum. Alternatively, they are defined in the time domain as processes for which the infinite sum of the autocovariances is infinite. Within this category, a process is said to be fractionally integrated or integrated of order d, denoted by I(d), and where d can be any real number, if can be expressed as

$$(1-L{)}^{d}x(t)=u(t), t=1, 2, \dots ,$$
(1)

where L is the backshift operator (Lx(t) = x(t–1)) and u(t) is short memory or integrated of order 0, also denoted as I(0). For such a process the spectral density function is positive and bounded at all frequencies; this category includes the white noise and the stationary Auto Regressive Moving Average (ARMA) class of models. However, if d > 0 in (1), x(t) becomes long memory because its spectral density function, f(.), tends to infinity as the frequency (λ) approaches zero, i.e.,

$$f\left(\lambda \right)\to \infty , as \lambda \to {0}^{+}.$$
(2)

Fractional integration was originally introduced in Granger (1980) as a result of the observation that many aggregated data displayed a periodogram (which is an estimator of the spectral density function) with a very large value around the zero frequency, suggesting that the series should be differenced; however, after differentiation, the periodogram of the differenced series shows a value close to zero at such frequency, which is an indication of over-differentiation. Thus, the order of integration should be an intermediate value between 0 and 1. In an earlier study, Robinson (1978) had justified the existence of this type of processes by means of aggregation of heterogeneous autoregressive (AR) ones, and similar arguments (based on aggregation) have been made by many other authors, including Taqqu et al. (1997), Chambers (1998), Parke (1999), Souza (2008), Hassler (2011), Shi and Sun (2016), etc. Nowadays, fractional integration is widely used in the analysis of aggregated time series data (see, e.g., Gil-Alana and Robinson 1997; Gil-Alana and Moreno 2012; Abbritti et al. 2016; 2023; etc.).

The estimation of the differencing parameter is carried out here by means of the Whittle function, which is an approximation to the likelihood function of a stationary Gaussian time series in the frequency domain, using a version of a testing approach developed by Robinson (1994). This procedure has a number of appealing features, namely it has a standard null limit distribution, and it allows to consider any real value d, including those outside the stationary region (d ≥ 0.5); in addition, it is the most efficient method against local departures from the null hypothesis that d is a given real value.

Data

The series used for the analysis are total tax revenue, VAT, and tax on income (both personal and corporate) in 21 OECD countries (Austria, Belgium, Canada, Denmark, Finland, France, Geermany, Greece, Ireland, Italy, Luxembourg, Netherlands, New Zealand, Norway, Portugal, tSpain, Sweden, Switzerland, Turkey, UK, US) at an annual frequency over the period 1965–2021. We also construct inflation series as the percentage change in the Consumer Price Index (CPI) over the same period. All series are taken from the Organisation for Economic Co-Operation and Development (OECD) database (https://data.oecd.org/). Since the original tax series are denominated in their national currency, to make them comparable they have been converted into euros for the countries with a different currency using the following exchange rates:

  • Canada: 1 CAD = 0.68 EUR

  • Denmark: 1 DKK = 0.13 EUR

  • Japan: 1 JPY = 0.0068 EUR

  • New Zealand: 1 NZD = 0.57 EUR

  • Norway: 1 NOK = 0.087 EUR

  • Sweden: 1 SEK = 0.088 EUR

  • Switzerland: 1 CHF = 1.02 EUR

  • Türkiye: 1 TRY = 0.047 EUR

  • United Kingdom: 1 GBP = 1.14 EUR

  • United States: 1 USD = 0.91 EUR

Figure 1 plots the total tax revenue, the US having the highest one.

Fig. 1
figure 1

Time series of the total tax revenues in euros from the OECD countries with data since 1965

Full size image

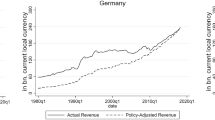
Figure 2 displays instead the Value Added Tax (VAT) series. This source of tax revenue is highest in Germany.Footnote 1

Fig. 2
figure 2

Time series corresponding to 1965–2021 value added taxes revenue of each OECD country in euros

Full size image

Figure 3 plots income tax revenue, with the US again having the largest one.

Fig. 3
figure 3

Time series of taxes on income, profits and capital gains revenues from OECD countries in euros until 2021

Full size image

Empirical Results

For our purposes, we examine the following model:

$$y\left(t\right)={\beta }_{0}+{\beta }_{1}t+x\left(t\right), (1-L{)}^{d}x(t)=u(t), t=1, 2,\dots$$
(3)

where y(t) refers to the observed data, β0 and β1 are the coefficients corresponding respectively to the intercept and a linear time trend, and x(t) is assumed to be I(d), where d is another parameter that is also estimated from the data. The error term u(t) is assumed to be a white noise process with zero mean and constant variance.

We estimate the differencing parameter d using three different model specifications:

i) With β0 and β1 being unknown and estimated alongside d,

ii)With β1 = 0 a priori, thus including an intercept only in the model, and

iii)With both β0 and β1 equal to zero a priori, thus not including any deterministic terms.Footnote 2

The best specification is chosen by testing with t-values the significance of the respective coefficients.

Tables 1, 2, and 3 display the estimates of d along with the confidence bands corresponding to the non-rejection values of d at the 95% level for total, VAT, and tax on income revenues respectively. For each series, the coefficients in bold are those from the selected specification.

Table 1 Estimates of the differencing parameter: total revenue
Full size table
Table 2 Estimates of the differencing parameter: VAT
Full size table
Table 3 Estimates of the differencing parameter: tax on income
Full size table

For total revenue (Table 1), the time trend is significant in all cases except for Greece and Turkey, where the constant is also insignificant. For VAT (Table 2), the only series with an insignificant trend is insignificant is the Netherlands. Finally, in the case of tax on income (Table 3), there are no significant deterministic term in the model for Japan, and the time trend is insignificant in Greece, New Zealand, and Turkey.

The values correspond to the estimates of the differencing parameter. In parenthesis, the 95% confidence intervals for the values of d. In bold, the values corresponding to the selected model for each series

aIndicates evidence of mean reversion at the 5% level

Regarding persistence as measured by the differencing parameter d, it can be seen that for total revenue the unit root null hypothesis, i.e., d = 1, cannot be rejected for most of the series, this hypothesis being rejected in favour of d > 1 only for Greece (d = 1.39), Italy (1.25), Luxembourg (1.31), and Portugal (1.25). Moreover, evidence of mean reversion (d < 1) is found only in the case of Switzerland (0.80). For VAT, the values are generally lower, and mean reversion now takes place for Belgium (d = 0.72), Italy (0.69), and Spain (surprisingly with a large negative value, − 0.64Footnote 3); for New Zealand, d is found to be significantly higher than 1, while for the rest of the cases, the values of d are in the I(1) interval. Concerning the tax on income, evidence of mean reversion is now obtained for Austria (d = 0.74), Belgium (0.41), Finland (0.54), Spain (0.59), Sweden (0.32), and USA (0.51). Evidence of d above 1 is found for Greece (1.35), Luxembourg (1.29), and Turkey (1.56). For the rest of the cases the unit root null hypothesis cannot be rejected.

Table 4 summarises the results obtained so far; there are a few cases of mean reversion: one for total revenue (Switzerland); three for VAT (Belgium, Italy, and Spain), and six for tax on income (Austria, Belgium, Finland, Spain, Sweden and USA).

Table 4 Summary of the results for d
Full size table

Next, we incorporate inflation into the analysis. Figure 4 shows that Turkey has the highest rate among the 21 countries considered.

Fig. 4
figure 4

Time series of the OECD countries’ annual inflation rate since 1965

Full size image

Tables 5 and 6 report respectively the estimates of d from the three specifications being considered and the corresponding estimates from each regression model. Again, the coefficients in bold are those from the selected specification.

Table 5 Estimates of the differencing parameter: inflation
Full size table
Table 6 Estimated coefficients of the selected models: inflation
Full size table

It can be seen that the time trend is significant only in the case of Korea, with intercept being the only significant deterministic term in most cases. Concerning the differencing parameter, d, only for Korea (d = 0.48), Iceland (0.75), Norway (0.63), and Sweden (0.89) the unit root null hypothesis is rejected in favour of mean reversion. In all the other cases, the estimated order of integration is within the unit root interval, the highest values being estimated for Italy (1.02), France (1.04), and Luxembourg (1.05).

Next, we focus on whether there is a relationship linking the tax series and inflation. Table 7 shows the correlation coefficients for each of the 21 OECD countries considered. It can be seen that all the values are positive and close 1, which indicates a very strong correlation.

Table 7 Correlation between inflation and revenues
Full size table

To test more rigorously for the existence of a long-run relationship between tax revenues and inflation one could use fractional cointegration methods. Engle and Granger (1987) defined cointegration in a bivariate context as a situation where the two individual series are integrated of order d, i.e., I(d), but there exists a linear combination of the two which is integration of a smaller order, say, d – b with b > 0. Though they define this concept for any real values, d and b, most of the empirical analysis carried out since then, however, has been conducted for the integer case, i.e., with d = b = 1, or, in other words, with I(1) individual series, and I(0) cointegrating errors. Engle and Granger (1987) proposed a two-step approach, testing first the order of integration of the individual series, and then, in a second step, the order of integration of the cointegrating residuals (see also Cheung and Lai 1993, and Gil-Alana 2003). However, this approach has the disadvantage of using estimated values rather than observed ones in the second step. To avoid this, we test instead for mean reversion in the difference between the tax revenue series and inflation.

The values correspond to the estimates of the differencing parameter. In parenthesis, the 95% confidence intervals for the values of d. In bold, the values corresponding to the selected model for each series

aIndicates evidence of mean reversion at the 5% level

In the case of the total revenue-inflation differential (Table 8), the time trend is found to be significant in all countries except one (Greece), and mean reversion is only statistically significant in Austria, with an estimated value of d of 0.66. For the rest of the countries, the unit root null hypothesis cannot be rejected, which implies lack of reversion to the mean. Thus, cointegration between total revenue and inflation only occurs in the case of Austria.

Table 8 Estimates of the differencing parameter: REVENUE—INFLATION
Full size table

For the VAT-inflation differential (Table 9), we find evidence of mean reversion in a number of cases: UK (d = 0.37), for which the I(0) hypothesis cannot be rejected), Austria and Belgium (d = 0.50), Canada (0.51), and Italy (0.69). This represents evidence of a long-run equilibrium relationship, except for Italy, where the order of integration is the same as for the VAT series itself.

Table 9 Estimates of the differencing parameter: VAT—inflation
Full size table

The values correspond to the estimates of the differencing parameter. In parenthesis, the 95% confidence intervals for the values of d. In bold, the values corresponding to the selected model for each series

aIndicates evidence of mean reversion at the 5% level

Finally, for the tax on income-inflation differential (Table 10), the mean reversion hypothesis cannot be rejected in the cases of Austria (d = 0.42), Portugal (0.73), and Switzerland (0.78), where this differential exhibits a lower degree of integration compared to the tax series itself.

Table 10 Estimates of the differencing parameter: tax on income-inflation
Full size table

A summary of the results for the three differentials is presented in Table 11. To sum up, mean reversion is found only in Austria in the case of deflated total revenues; in Austria, Belgium, Canada, Italy and the UK in the case of deflated VAT; in Austria, Portugal and Switzerland in the case of deflated tax on income.

Table 11 Summary of the results for d: deflated series
Full size table

Conclusions

This paper examines the stochastic behaviour of tax revenues in 21 OECD countries over the period 1965–2021 using a fractional integration approach. More specifically, the fractional differencing parameter d is a measure of persistence; it also sheds light on whether or not mean reversion occurs and shocks have transitory or permanent effects. The results indicate that most of series exhibit long memory. Also, in most cases the selected model specification includes a time trend, the exceptions being the Netherlands in the case of the VAT series, Greece and Turkey in the case of both total tax revenue and tax on income, Japan and New Zealand in the latter case only. In most cases the unit root null hypothesis cannot be rejected, and in a few cases such as the Netherlands and New Zealand d is even above 1.

As for the inflation series, the I(1) hypothesis cannot be rejected for the majority of the countries, mean reversion only occurring in the cases of Korea, Iceland, Norway and Sweden. However, stronger evidence of mean reversion is found for the differences between the three original tax series and inflation compared to the tax series themselves, which points to the existence of a linkage between taxation and inflation, especially in the case of VAT and tax on income.

These findings add to the existing body of knowledge by providing more extensive evidence on the stochastic properties of tax revenues and inflation as well as on their linkages. They also suggest future avenues for research and have crucial policy implications. Particularly important is the evidence concerning the existence of a significant relationship between taxes and inflation, as the tax system is typically not neutral with respect to inflation (Beer et al. 2023). Specifically, its effects on incentives and tax burdens change with inflation and can create distortions such as the failure to adjust some parameters of the tax system (for instance, tax thresholds) in line with inflation, timing effects concerning tax collection and refunds, as well as the taxation of (both household and corporate) nominal rather than real gains and profits. Therefore it is essential that fiscal policy in the OECD countries should address these issues. This might require adjusting tax thresholds and other tax parameters in line with inflation; further, withholding taxes and advance corporate income taxes might be required to solve timing issues, and corporate cash-flow taxes might also be useful to reduce distortions (Beer et al. 2023). Thus OECD tax authorities should consider introducing such changes, and academic research should investigate further the issue of tax distortions and their effects.

It should be noted that the analysis conducted in this paper has some limitations which could be overcome in future work extending it in several directions. In particular, the reasons for the rejection of the unit root null hypothesis for both tax revenues and inflation in a number of cases could be investigated. In addition, tests for structural breaks could be carried out using the method of Bai and Perron (2003) and/or its adaptation to the specific case of fractional integration developed by Gil-Alana (2008)—this is an important issue because overlooking structural breaks can produce spurious long-memory (see, e.g., Diebold and Inoue 2001; Granger and Hyung 2004; etc.). Finally, possible nonlinearities could be modelled using an appropriate framework such as Chebyshev polynomials in time (Cuestas and Gil-Alana 2016), Fourier functions (Caporale et al. 2024) or neural networks (Gil-Alana and Yaya 2021) in the context of fractional integration.