1 Introduction

Constitutive models, also known as material models, are mathematical formulations which describe the relation between stresses and deformation within the scope of any material. These models facilitate an understanding of how materials respond to external forces and thermal loading under diverse loading conditions. Constitutive models include several parts such as Equation of State (EOS), strength model, and failure criterion. Examples of constitutive models tailored for brittle materials include the Mohr–Coulomb model, Von Mises, Johnson–Holmquist–Cook (JHC), Johnson-Holmquist (JH), Karagozian and Case (K&C), and Riedel, Thoma, and Hiermaier (RHT). These models have been proposed for addressing brittle material challenges (Johnson and Holmquist 1992; Malvar et al. 1997; Riedel et al. 1999; Ma and An 2008). Their application extends to various simulations, encompassing drop weight impact (Baranowski et al. 2020), blast analysis (Xie et al. 2017; Sunita et al. 2022), rock cutting analysis (Rutten et al. 2019; Wang et al. 2022), and numerous other scenarios where the behavior of these materials is simulated using these models.

Nowadays, the prevalence of advanced numerical methods has led many researchers and engineers to employ numerical simulations, utilizing numerical tools, for solving their models. Two crucial points in the application of numerical methods involve the selection of a suitable constitutive model and determination of its input parameters. In the recently conducted research JHC model was recognized as an efficient rock material model(Fang et al. 2014; Kang et al. 2014; Xie et al. 2019; C D Lou 2021; Kucewicz et al. 2021; Lou et al. 2021). This material model has been employed successfully for a wide range of brittle materials in different physical problems like impact (Mata 2017), penetration (Polanco-Loria et al. 2008; ISLAM et al. 2012; Kong et al. 2016), blasting (Tai et al., 2011; J. Wang et al. 2021), rock breakage (Liu et al. 2016), wave propagation (Xie et al. 2020), etc. JHC constitutive model offers key advantages, including a three-range equation of EOS and the incorporation of both volumetric and equivalent plastic strains in damage calculation. Despite these advantages, JHC material model has certain limitations, such as the representation of tensile damage (Johnson and Holmquist 1994; Ren et al. 2017). Users can minimize these limitations by employing suggested techniques. One approach involves defining a pre-existing failure surface with a user-defined interface (Kong et al. 2016; Li and Shi 2017; Ren et al. 2017). The other method considers the finite element erosion method, which may be more practical than the first approach (Wang et al. 2007).

The selected model is not only chosen for its efficiency but is also preferred due to its straightforward implementation in comparison to other similar models, making it the main subject of this research. Various advanced constitutive models have been developed for brittle materials, including the Riedel–Hiermaier–Thoma (RHT) (Riedel et al. 1999), continuous surface cap (CSC) model(Murray 2007), and Johnson–Holmquist-ceramic (JH-2) (Johnson and Holmquist 1999), among others. While these models have demonstrated effectiveness in addressing different problems, they share common drawbacks, such as numerous input parameters and sophisticated determination procedures (Huang et al. 2022). These challenges hinder users from incorporating them easily with existing information. Acknowledging these limitations and recognizing the excellent performance of the JHC constitutive model, this paper seeks to provide a procedure for parameter determination of the JHC model for a widely studied rock type called Indiana Limestone with existing data. Indiana Limestone rocks were selected because they are widespread kinds of carbonate rocks that contribute to different projects. Also, it has been modeled in lots of numerical simulations recently (Kim 2010; Kim et al. 2012, 2021). The current study aims to collect experimental data, conduct analysis on achieved data, and determine constitutive model parameters through statistical analysis, numerical back analysis, and calibration. Ultimately, providing a well-defined set of parameters for the JHC constitutive model serves as a valuable resource for future numerical simulations involving Indiana Limestone rocks and elucidates how to use existing data for the determination of JHC constitutive model parameters.

JHC model's parameters have been determined by several researchers for some kinds of rock like Dolomite, Limestone, Jinping Marble, Coal, and concrete (Fang et al. 2014; Kang et al. 2014; Xie et al. 2019; Kucewicz et al. 2021; Lou et al. 2021). Additionally, Kong and Hao determined JHC parameters for Indiana Limestone considering its precise strength and properties for a specific rock (Fang et al. 2014). However, in this study considering that Indiana Limestone exhibits a range of strengths and specifications, the aim is to determine the input parameters of the JHC model for a wider range of properties. Although the previous researchers had to do some laboratory tests on their target specimens, the distinct characteristic of the present paper is that all required information was extracted from existing resources. During the parameter determination stage, a combination of static and dynamic test results, including uniaxial compression strength (UCS), triaxial compression tests (TCS), cyclic loading tests, split Hopkinson pressure bar (SHPB), and impact tests, are employed to obtain accurate and comprehensive results. Following the parameter determination, a calibration and validation process is implemented to achieve more precise results of the JHC model and show the accuracy of input parameters.

2 Description of the Johnson–Holmquist–Cook constitutive model

The JHC model was developed by Johnson, Holmquist, and Cook before the introduction of the JH-2 model (Johnson and Holmquist 1992). These scientists aimed to formulate a constitutive model to predict the behavior of concrete under conditions of large deformation, high strain rate, and high pressure (LHH). While originally designed for concrete, this model finds widespread application in simulating rocks subjected to LHH (Holmquist and Johnson 2008; Kang et al. 2014; Liu et al. 2015, 2023; Xie et al. 2019; C D Lou 2021; Kucewicz et al. 2021; Wang et al. 2021; Tian et al. 2022). The model in question can effectively simulate rocks due to the shared brittle nature of rocks and concrete, resulting in similar failure mechanisms. It's important to note that while concrete is an engineered material with precise control over its components, rocks are natural materials. Additionally, the planar structure prevalent in many rocks introduces anisotropic behavior, adding complexity to their simulation.

2.1 Strength model

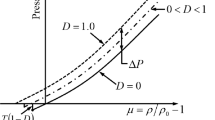
JHC constitutive model considers strength of rock and other brittle material behavior as an asymmetric perspective which means it is signifying distinct compression and tensile strengths within the model. Figure 1 illustrates the failure surface in the JHC material model. Visualized failure surface is described with Eq. 1 which is called a constitutive model.

Fig. 1
figure 1

JHC strength model Johnson and Holmquist (1992)

Full size image
$${\sigma }^{*}=\left[A\left(1-D\right)+B{P}^{*N}\right]\left(1+C\text{ln}\dot{{\varepsilon }^{*}}\right)$$
(1)

In Eq. 1, the constants A, B, and N are components of the failure criterion. Between those three constants, A refers to normalized cohesion which is the amount of theoretical stress that causes material fracture through shearing. constants B and N serve as the coefficient and exponent, respectively, for the hardening of normalized pressure. In the latter part of Eq. 1, C represents the strain rate coefficient. \({P}^{*}\) is the normalized pressure and is defined by Eq. 2. Additionally, \(\dot{{\varepsilon }^{*}}\) is the normalized strain rate which is expressed with Eq. 3. In the end, \({\sigma }^{*}\) is equivalent to normalized stress which is shown by Eq. 4.

$${P}^{*}=\frac{\text{P}}{{f}_{C}}=\frac{\frac{\left({\upsigma }_{1}+{\upsigma }_{2}+{\upsigma }_{3}\right)}{3}}{{f}_{C}}=\frac{{I}_{1}}{{f}_{C}}$$
(2)

where \(\text{P}\) and \({f}_{C}\) represent pressure and uniaxial compression strength respectively. Pressure is the average of normal stresses which is called the first invariant of stress tensor (\({I}_{1}\)).

$$\dot{{\varepsilon }^{*}}=\dot{\varepsilon }/{\dot{\varepsilon }}_{0}$$
(3)

where \(\dot{\varepsilon }\) and \({\dot{\varepsilon }}_{0}\) are strain rate and reference strain rate respectively.

Johnson and Holmquist suggested 1 s−1 as reference strain rate which has been used in all simulations with the JHC constitutive model (Johnson and Holmquist 1992).

$${\sigma }^{*}=\upsigma /{f}_{C}$$
(4)

where σ denotes stress.

2.2 Damage

Equation 1 contains accumulated damage parameter (D), ranging from 0 to 1. The amount of D for intact rock and fully fractured rock will be 0 and 1, respectively. As illustrated in Fig. 1, the damage parameter reduces material strength, and ultimately when D = 1, strength degrades to residual strength. At this point, the JHC model indicates a lack of tensile strength, which is in total agreement with reality.

As depicted in Fig. 2, the damage parameter (D) in the JHC material model is a function of plastic strain and plastic volumetric strain. The inclusion of plastic volumetric strain in the calculation of the damage parameter accounts for hydrostatic compressibility. According to Johnson and Holmquist, the damage parameter is obtained following Eq. 5 (Johnson and Holmquist 1992):

$$D=\sum \frac{\Delta {\varepsilon }_{p}+\Delta {\mu }_{p}}{{\varepsilon }_{p}^{f}+{\mu }_{p}^{f}}$$
(5)

where \(\Delta {\varepsilon }_{p}\) and \(\Delta {\mu }_{p}\) are increments of effective plastic strain and volumetric plastic strains during a cycle of integration, respectively. \({\varepsilon }_{p}^{f}+{\mu }_{p}^{f}\) is the total plastic strain under a constant pressure until fracture and it is calculated using Eq. 6.

$${\varepsilon }_{p}^{f}+{\mu }_{p}^{f}={D}_{1}{\left({P}^{*}+{T}^{*}\right)}^{{D}_{2}}\ge EFMIN$$
(6)

where \({D}_{1}\) and \({D}_{2}\) are damage constants, \(EFMIN\) is the minimum plastic strain (the minimum plastic strain before fracture), \({T}^{*}\) is the normalized maximum stretching hydrostatic pressure. This normalized parameter can be derived from Eq. 7.

$${T}^{*}=\frac{T}{{f}_{C}}$$
(7)

where \(T\) is the material's tensile strength.

Fig. 2
figure 2

Damage model Johnson and Holmquist (1992)

Full size image

2.3 Equation of state (EOS)

According to (Johnson and Holmquist 1992), the JHC model distinguishes between hydrostatic and deviatoric stresses. Consequently, it appears feasible to incorporate an equation of state (EOS) into this model. An EOS defines the relationship between pressure and volumetric strain. It is shown in Fig. 3 that the relation between pressure and volumetric strain is formulated in three distinct stages while distinguishing between loading and unloading paths. These stages are summarized below:

Fig. 3
figure 3

Equation of State (EOS) in the JHC model Johnson and Holmquist (1992)

Full size image

The first stage (OA): this stage, because of reversible deformations, is also known as the elastic stage. This stage begins from tensile cutoff (\(-T(1-D)\)) and extends to the elastic limit (\({P}_{c}\)) which is equal to the pressure at uniaxial compression Strength. During this stage, the loading and unloading equations are the same, expressed in Eq. 8.

$$P=K\mu$$
(8)
$$K=E/\left[3(1-2\nu )\right]$$

where \(K\) and \(E\) are elastic modules of bulk and elastic, respectively, and \(\nu\) refers to the poison ratio and \(\mu\) is the volumetric strain.

Second stage (AB): This phase serves as a transition between the elastic and locking stages. The reduction of stiffness, due to the collapse of air-void pores, is the most important event in this stage. However, strength increases until reaching the locking pressure (\({P}_{lock}\)). The gas and liquid in pores are gradually squeezed out and plastic strain is produced at the same time which is expressed by the following equation:

$$P={P}_{c}+{K}_{l}(\mu -{\mu }_{c})$$
(9)

where \({K}_{l}\) is the volumetric module in the transition stage, and \({\mu }_{c}\) is the volumetric strain in the crushing stage.

It is important to emphasize that users cannot directly control this part and it is an interpolation between the linear stage and the third stage. Johnson and Holmquist have warned that the slope of this stage should be lower than the elastic stage (Johnson and Holmquist 1992).

The unloading path in this stage, unlike the first stage, differs from the loading path. This path is determined by interpolating a path between adjacent regions. The equation of state during this unloading phase is as follows:

$$P=\left[\left(1-F\right)K+F.{K}_{p}\right].\mu$$
(10)

where F is the interpolating factor, which is calculated by Eq. 11, \({K}_{p}\) is plastic bulk modulus (Eq. 12), and \({\mu }_{pl}\) is compaction volume strain (Liu et al. 2023).

$$F=\left({\mu }_{max}-{\mu }_{c}\right)/\left({\mu }_{pl}-{\mu }_{c}\right)$$
(11)
$${K}_{p}=\left({P}_{l}-{P}_{c}\right)/\left({\mu }_{pl}-{\mu }_{c}\right)$$
(12)

where \({\mu }_{max}\) is the maximum volume strain reached before unloading.

Third stage (BC): according to (Johnson and Holmquist 1992), this stage represents the strength of fully crushed and poreless material. As depicted in Eq. 13, it follows a third-order expression. This range describes the pressure-volumetric strain relation for the significantly high pressures.

$$P={K}_{1}\overline{\mu }+{K}_{2}{\overline{\mu }}^{2}+{K}_{3}{\overline{\mu }}^{3}$$
(13)
$$\overline{\mu }=\frac{\left(\mu -{\mu }_{l}\right)}{\left(1+{\mu }_{l}\right)}$$

where \(\overline{\mu }\) is a modified volumetric strain.

3 JHC constitutive model parameter determination

The JHC constitutive model requires the determination of several parameters for its application to a specific rock type. These parameters, as listed in Table 1, are categorized into six groups. While some of these parameters can be obtained from existing literature or through mechanical tests, others necessitate more complex determination methods. In addition to the 19 primary parameters, the LS-DYNA software incorporates 2 additional parameters, which are included in the final section of Table 1 (Holmquist and Johnson 2011).

Table 1 JHC constitutive model parameters classification
Full size table

To determine the parameters of the JHC model, certain parameters are established through the proposed approaches outlined in the original JHC constitutive model paper (Johnson and Holmquist 1992). Additionally, other parameters are determined using commonly adopted methods for parameter determination in constitutive models, as employed by various researchers for determining parameters of different material models (ISLAM et al. 2012; Baranowski et al. 2020; Kucewicz et al. 2021). Figure 4 presents a flowchart that delineates the sequential process of parameter determination for the JHC model, highlighting the requisite calculations and key considerations. The individual steps of this process will be thoroughly discussed in Sects. 3.1 to 3.4, 4.1 and 4.2. In the process of determining parameters of JHC material model for Indiana Limestone, efforts have been made to compile a comprehensive database using existing data for Indiana Limestone (Russell Lamont; Wu 1971; Heard 1974; Furnish 1994; Ai and Ahrens 2004; Vajdova et al. 2004; Zhou et al. 2009; You 2010; Chakraborty 2013; Janmahomed 2016; Li and Ghassemi 2021). Table 2 presents a summary of the properties of various Indiana Limestone samples. Considering this table, it is evident that the diverse samples of Indiana Limestone exhibit relatively consistent properties. Therefore, through parameter determination using this data, the findings can be applied to various types of Indiana Limestones. This implies a general parameter determination for different Indiana Limestones. Consequently, users have the flexibility to apply the JHC material model to different varieties of Indiana Limestones based on their general information, such as the physical and mechanical properties outlined in Table 1.

Fig. 4
figure 4

The flowchart of parameter determination for the JHC model

Full size image
Table 2 Indiana limestone database
Full size table

3.1 Strain rate coefficient

It is widely accepted that rocks under various loading conditions and consequently under different strain rates, respond differently. As a result, a term known as the dynamic increase factor (DIF) has been introduced. This factor is defined as the proportion of strength at a specific strain rate to the material's strength at the static strain rate. Dynamic increase factors of rocks in compression and tension are shown in Figs. 5 and 6, respectively. Two noteworthy observations emerge. Firstly, rock's responses to compression and tension are quite different. Kucewicz et al. claimed that this distinct behavior is due to the occurrence of Intergranular and Transgranular fractures (Kucewicz et al. 2021). The other notable observation is the nonlinear behavior of dynamic strength which is shown in Fig. 6.

Fig. 5
figure 5

Compression strength of rocks as a function of strain rate Liu et al. (2018)

Full size image
Fig. 6
figure 6

Tensile strength of rocks as a function of strain rate Liu et al. (2018)

Full size image

Researchers acknowledge that the strength of rocks and other brittle materials is influenced by the strain rate (Lajtai et al. 1991; Shojaei and Voyiadjis 2017). Figure 7 illustrates three regimes depicting the dynamic strength dependence on strain rate. In the low strain rate region, material strength exhibits a gradual increase with the rise in strain rate (up to \({10}^{2} {\text{s}}^{-1}\)). In regime 2, there is a notable surge in strength as the strain rate increases from \({10}^{2} {\text{s}}^{-1}\) to \({10}^{3} {\text{s}}^{-1}\). In the final regime, the behavior of material concerning strain rate is similar to the first regime, with a reduced dependency, although an increasing trend is observed (Qi et al. 2009). It should be noted that Figs. 5 and 6 do not contain any data or reports pertaining to regime 3.

Fig. 7
figure 7

Dependence of dynamical strength on strain rates of brittle materials (\({\dot{\varepsilon }}_{1}\approx {10}^{0}-{10}^{2}{s}^{-1}, {\dot{\varepsilon }}_{s}\approx {10}^{3}{s}^{-1}; {\dot{\varepsilon }}_{2}\approx {10}^{4}{s}^{-1}\)) (Qi et al. 2009)

Full size image

In the JHC constitutive model (Eq. 1), C represents a strain rate dependency. It is customary to determine a unit strain rate coefficient applicable across all strain rate ranges (Johnson and Holmquist 1992). Considering the explanation provided for Fig. 7, it appears that this may not be an appropriate tool for illustrating the strain rate effect on strength. On account of the nonlinear behavior of dynamic strength dependency to strain rate, strain rate ranges are divided into two static (\(\dot{\varepsilon }\le 1\)) and dynamic (\(\dot{\varepsilon }>1\)) parts. Ultimately, strain rate coefficients are determined in these two regions.

The JHC material model does not directly scale the tensile strength of the material as the strain rate increases. However, by examining Eq. 6, it becomes evident that the normalized maximum stretching hydrostatic pressure (\({T}^{*}\)) plays a role in damage calculation. Therefore, it becomes crucial to precisely consider this factor in the calculation of the strain rate parameter. According to Eq. 7, the normalized maximum stretching hydrostatic pressure is computed using Eq. 14, where \({f}_{tdynamic}\) represents dynamic tensile strength.

$${\text{T}}_{dynamic}^{*}=\frac{\frac{{f}_{tdynamic}}{3}}{{f}_{c}}$$
(14)

Uniaxial compression tests result in low strain rates, and Split Hopkinson Pressure Bar (SHPB) results in high strain rates are used for determination of strain rate coefficient. Frew et al. have conducted dynamic tests on Indiana Limestone and reported obtained properties in Table 3 (Frew et al. 2001).

Table 3 Characteristics of SHPB tests and Indiana limestone properties
Full size table

In the first step of strain rate coefficient determination, all reported results at various strain rates for Indiana Limestone were normalized to uniaxial compression strength (\({f}_{c}=64.6 MPa\)) subsequently, all points were to the normalized maximum stretching hydrostatic pressure in normalized pressure- normalized stress system (\({T}^{*}-{\sigma }^{*}\)) and all are shown in Fig. 8. It is important to highlight that the strengths of Indiana Limestone presented in Fig. 8 are outcomes of diverse strain rates. As these varied strengths are related to different hydrostatic pressures, it is crucial to recognize that all results are influenced by this parameter. Consequently, this chart does not accurately depict the pure effect of strain rate. To depict strength just as a function of strain rate, all lines in Fig. 8 were cut by \({P}^{*}=\frac{\frac{{f}_{c}}{3}}{{f}_{c}}=\frac{1}{3}\) and results are shown in Fig. 9.

Fig. 8
figure 8

Normalized Pressure- Normalized Stress at different strain rates

Full size image
Fig. 9
figure 9

Normalized Pressure- Normalized Stress at different strain rates at \({P}^{*}=\frac{1}{3}\)

Full size image

Considering Fig. 5, it is evident that the relationship between DIF and stain rate can be determined using a bilinear chart in static and dynamic strain rates. The results depicted in Fig. 9 were transformed to the strain rate- equivalent stress (\(\dot{\varepsilon }-{\sigma }^{*}\)) system to static and dynamic strain rates, respectively as shown in Figs. 10 and 11. A logarithmic function was fitted to each of them, as indicated by Eq. 1. As it is illustrated in Fig. 11, \(1 {\text{s}}^{-1}\) serves as a transient strain rate connecting the two strain rate ranges. Figure 12 shows that strain rate effects in the dynamic range is more than in the static range, confirming findings according to Liu et al. (2018). Eventually, strain rate parameters are determined as \({C}_{static}=0.017\) for static strain rate and \({C}_{dynamic}=0.0205\) for dynamic strain rates. It is noteworthy that the selection of \({C}_{static}\) or \({C}_{dynamic}\) as an input for the C parameter in the model is contingent upon whether the numerical model operates under static or dynamic conditions. This distinction is made by the user, who then inputs the appropriate value.

Fig. 10
figure 10

Strain rate- equivalent stress in the static strain range

Full size image
Fig. 11
figure 11

Strain rate- equivalent stress in static dynamic range

Full size image
Fig. 12
figure 12

Strain rate- equivalent stress

Full size image

3.2 Material strength parameters

3.2.1 Normalized cohesive strength (A)

In a static condition (elimination of strain rate) for an intact rock (\(D=0\)) JHC constitutive model in Eq. 1 can be simplified as shown in Eq. 15.

$${\sigma }^{*}=A+B{P}^{*N}$$
(15)

In this state, according to plasticity, the JHC constitutive model and Mohr–Coulomb model act similarly and cross pure shear and uniaxial compression on the compression meridian plane (Kucewicz et al. 2021; Lou et al. 2021; Polanco-Loria et al. 2008). Mohr–Coulomb model in the principal stress coordinate system is defined based on Eq. 16.

$${\sigma }_{1}=\frac{1+\text{sin}\varphi }{1-\text{sin}\varphi }{\sigma }_{3}+\frac{2c\text{cos}\varphi }{1-\text{sin}\varphi }$$
(16)

where c is cohesion, and \(\varphi\) is the angle of internal friction angle (Goodman 1991).

Based on the Mohr–Coulomb model, the cohesion is determined as interception of failure envelop on several triaxial compression tests in Mohr's circles. As shown in Fig. 13, triaxial compression tests were conducted on Indiana Limestone under different confining pressures (You 2010). Concerning Fig. 13, cohesion obtained about 24.3 MPa so normalized cohesive strength (A) was calculated as shown in Eq. 16.

Fig. 13
figure 13

Mohr circles of triaxial compression tests conducted on Indiana Limestone

Full size image
$$A=\frac{C}{{f}_{C}}=\frac{24.3}{64.6}=0.38$$
(17)

3.2.2 Normalized pressure hardening coefficient (B) and Pressure hardening index (N)

Following Eq. 16, Fig. 14 demonstrates a linear correlation between confining pressure and axial stress in a triaxial test performed on Indiana Limestone. In conventional triaxial tests, axial stress is equal to the first principal stress (\({\sigma }_{1}\)) and confining pressure is equal to the third principal stress (\({\sigma }_{3}\)) which itself is the same as the average principal stress (\({\sigma }_{2}\)). Reported principle stresses in Fig. 14 can be transformed to \({P}^{*}-{\sigma }^{*}\) system using Eqs. 16–18 and are shown in Fig. 15. The data in Fig. 15 were fitted by Eq. 15, considering a normalized cohesive strength (\(A=0.38\)). As a result, \(B=0.9619\) and \(N=0.4993\) were obtained. In the end, by increasing \({P}^{*}\) the limited value for \({\sigma }^{*}\) determined approximately \(SFMAX=4\).

Fig. 14
figure 14

Triaxial compression tests conducted on Indian Limestone in Principal stresses system

Full size image
Fig. 15
figure 15

Yield surface fitting

Full size image
$${\text{J}}_{2}=\frac{1}{6}\left[{\left({\upsigma }_{1}-{\upsigma }_{2}\right)}^{2}+{\left({\upsigma }_{1}-{\upsigma }_{3}\right)}^{2}+{\left({\upsigma }_{2}-{\upsigma }_{3}\right)}^{2}\right]\stackrel{{\upsigma }_{2}={\upsigma }_{3}}{\Rightarrow }{\text{J}}_{2}=\frac{1}{3}{\left({\upsigma }_{1}-{\upsigma }_{3}\right)}^{2}$$
(18)
$${\sigma }^{*}=\frac{\sqrt{3{\text{J}}_{2}}}{{\text{f}}_{\text{c}}} \stackrel{{\text{J}}_{2}=\frac{1}{3}{\left({\upsigma }_{1}-{\upsigma }_{3}\right)}^{2}}{\Rightarrow } {\sigma }^{*}=\frac{\left({\upsigma }_{1}-{\upsigma }_{3}\right)}{{\text{f}}_{\text{c}}}$$
(19)
$${P}^{*}=\frac{\text{P}}{{f}_{C}}=\frac{\frac{\left({\upsigma }_{1}+{\upsigma }_{2}+{\upsigma }_{3}\right)}{3}}{{f}_{C}} \stackrel{{\upsigma }_{2}={\upsigma }_{3}}{\Rightarrow } \frac{\left({\upsigma }_{1}+2{\upsigma }_{3}\right)}{{3f}_{C}}$$
(20)

3.3 Material equation of state parameters

Referring to Sect. 2.3, the equation of state shows the relationship between pressure and volumetric strain, and in the JHC material model is divided into three parts. Various methodologies exist for determining EOS parameters, particularly when laboratory data is available or in the absence of experimental information for a specific material. A primary approach for EOS parameter determination is through hydrostatic compression tests, also known as uniaxial strain compression and Holmquist claimed that this approach is the most appropriate approach for EOS parameters determination(Johnson and Holmquist 1992). In the present study, this method has been employed, since uniaxial strain compression data is available for Indiana Limestone.

In the absence of uniaxial strain compression, two alternative approaches have been suggested. The first involves utilizing uniaxial shock data obtained from flyer plate impact tests conducted by some researchers (Wang et al. 2018; Baranowski et al. 2020; Kucewicz et al. 2021). In the worst-case scenario, when data from flyer plate impact tests and uniaxial strain compression tests are both unavailable, another way of determining EOS parameters is using Eq. 19, as shown in Eq. 19 (Lou et al. 2021):

$$\text{P}=\frac{{C}^{2}\rho \mu \left(1+\mu \right)}{{\left[\left(1-S\right)\mu +1\right]}^{2}}$$
(21)

where \(c\) and \(s\) are empirical constants which refer to the properties of the material. Los Alamos National Laboratory has released the values of these constants for some rocks (Lou et al. 2021).

As mentioned above, the uniaxial strain test results, measured by Heard (1974), were used for EOS parameters determination. Figure 16 illustrates the data of the uniaxial strain test on Indiana Limestone. The first region of the equation of state of the JHC model is an irreversible elastic part and bulk modulus in this part was obtained according to elasticity using Eq. 8 and with respect to Table 3 (\(K=26.67 \text{GPa}\)). When rock reaches the elastic limit, based on Polanco-Loria et al., volumetric pressure is determined using Eq. 20 (Polanco-Loria et al. 2008). Considering Eq. 8 and Fig. 3, the amount of and \({\mu }_{c}\) were calculated as Eq. 21:

Fig. 16
figure 16

Uniaxial strain test on Indiana Limestone (Heard 1974)

Full size image
$${P}_{c}=\frac{{f}_{c}}{3}=\frac{64.6}{3}=21.53 \text{MPa}$$
(22)
$${\mu }_{c}=\frac{{P}_{c}}{K}=\frac{21.53\times {10}^{-3}}{26.67}=8.1\times {10}^{-4}$$
(23)

One of the shortcomings of the JHC constitutive model is its inability to predict the hardening behavior as the confining pressure increases. To address this limitation, some researchers have taken an average of elastic modulus in uniaxial and triaxial compression strength tests to compensate this drawback (Kucewicz et al. 2021).

Considering Eq. 13, the third part of the equation of state is a third-order polynomial equation in which the variable is modified volumetric strain (\(\overline{\mu }\)). The reason for utilizing modified volumetric strain is approaching the equation of state toward zero when volumetric strain tends toward \({\mu }_{lock}\). \({\mu }_{lock}\) is equal to the void ratio and obtained using particle density (\({\rho }_{g}\)) and bulk density (\(\rho\)) reported in Table 2 using Eq. 22:

$${\mu }_{l}=\frac{{\rho }_{g}}{{\rho }_{0}}-1=\frac{2.61}{2.3}-1=0.135$$
(24)

So, in this stage, uniaxial strain data in Fig. 16 were fitted with a third-order polynomial, and the following constants were found for it; \({K}_{1}=119.1\text{ GPa},{K}_{2}=-1901\text{ GPa}\) and \({K}_{3}=20030\text{ GPa}\).

In the last part of EOS parameters determination, the transient region was obtained interpolating the first and the third part of EOS. Due to pores being destroyed, the stiffness of rock reduces. Therefore, bulk modulus in the transient region is computed as 85% of the elastic bulk modulus, expressed as follows:

$${K}_{transient}=0.85*{K}_{elastic}=0.85*26.67=22.67 \text{GPa}$$
(25)

Then the intersection of two transient and 3rd-order parts of the equation of state was gained (\({\mu }_{plock}=0.202\)). Using the obtained intersection point, the pressure in the locking stage of the equation of state was calculated using Eq. 24 as mentioned below:

$${\text{P}}_{\text{l}}={\text{P}}_{\text{c}}+\left({\text{K}}_{\text{t}}\times \left({\upmu }_{\text{pl}}-{\upmu }_{\text{c}}\right)\right)=0.02153+\left(22.67\times \left(0.202-0.00081\right)\right)=4.58\text{ GPa}$$
(26)

Finally, the EOS is depicted in Fig. 17.

Fig. 17
figure 17

JHC material model's EOS for Indiana Limestone

Full size image

3.4 Damage parameter determination

There are two main methods for damage parameter determination. The first approach involves utilizing cyclic compression test results, that has been used by Johnson and Holmquist for the first time for the JHC constitutive model (Johnson and Holmquist 1992). This approach needs a cyclic compression test which is commonly not available. As a consequence, another method has been used for JHC damage parameters determination by some researchers which is numerical calibration. This method has demonstrated favorable results and serves as a viable alternative when cyclic compression test data is unavailable for certain rock types (Baranowski et al. 2020; Kucewicz et al. 2021).

Here, a combination of the first and second approaches is employed. Firstly, damage parameters are calculated by utilizing cyclic compression test results conducted on Indiana Limestone by Janmahomad (Janmahomed 2016), contributing to one of the damage parameters (\({D}_{1}\)). Subsequently, employing a calibration technique, the determination of another damage parameter is achieved (\({D}_{2}\)). This combined approach leverages both experimental data and numerical calibration for a more comprehensive understanding of the material's behavior.

Figure 18 illustrates the cyclic compression test conducted on Indiana Limestone alongside a hypothetical line assumed to be fitted on the failure point in this graph. To calculate the first damage parameter with this method, several assumptions have been made as outlined below:

  • The longitudinal elastic strain of the specimen is disregarded.

  • The volumetric plastic strain is very small and it is negligible.

  • The assumption is made that the strength of Indiana Limestone degrades as predicted in Fig. 18.

Fig. 18
figure 18

Cyclic compression test on Indian Limestone (Janmahomed 2016)

Full size image

This is noteworthy that the first assumption due to that the elastic range is small can be considered true. The second assumption because of the nature of the cyclic test which does not produce high pressure, seems to be acceptable. So, the pointed strain at zero stress level in Fig. 18 can be considered as plastic strain (\({\varepsilon }_{p}^{f}=EFMIN=0.0115\)). Considering these notes, Eq. 6 rearranges as shown in Eq. 25.

$${\varepsilon }_{p}^{f}=0.0115={D}_{1}{\left({P}^{*}+{T}^{*}\right)}^{{D}_{2}}$$
(27)

As mentioned earlier, \({D}_{2}\) was calculated using calibration techniques and at this stage, it is assumed to be one. Concerning Eqs. 2, 7, and Table 3, normalized maximum stretching hydrostatic pressure (\({T}^{*}\)) and normalized pressure (\({P}^{*}\)) were calculated and are shown in Fig. 19 with considering graph of damage in Fig. 2 linear. Consequently, the first damage parameter is determined (\({D}_{1}=0.055\)).

Fig. 19
figure 19

Damage function in JHC constitutive model for Indiana Limestone

Full size image

3.4.1 Damage parameter calibration

Damage parameters significantly influence the post-peak behavior of rock. Therefore, for the calibration of these parameters, reference is made to triaxial compression tests conducted on Indiana Limestone, as presented in the study by Walton et al. (2017). The results of these triaxial compression tests are depicted in Fig. 20. The findings indicate that as confining pressure increases, the Indiana Limestone exhibits higher strength, and the failure mode transitions from brittle to ductile. The reason why the uniaxial compression strength test was not used is its inability to predict of softening behavior of rock after failure. In the next step, a numerical simulation of the triaxial compression test was built and compared to the experimental results of Indiana Limestone.

Fig. 20
figure 20

Indiana Limestone triaxial compression test (Walton et al. 2017)

Full size image

Figure 21 displays the cylindrical specimen modeled in LS-DYNA software, with a diameter of 50 mm and a length of 100 mm, mirroring the dimensions of the actual experimental specimen. The cylinder is positioned between two caps, with the lower cap fixed in all directions, and the upper cap fixed in all directions except the one aligned with the specimen's axial direction. The upper cap moves downward with a prescribed velocity based on Walton et al. (2017). The specimen consisted of 51,800 cubic meshes. The simulation is conducted in two phases: initially, the confining pressure is applied, and subsequently, axial loading is introduced. Confining pressure is implemented using a segment set and defined pressure curve.

Fig. 21
figure 21

Triaxial compression test in LS-DYNA

Full size image

Figure 22 depicts strain–stress curves with different damage parameters (D2). It is shown that there is a 1.5% error in the peak point of stress–strain prediction in comparison to the experimental data. But on the other hand, it is clear that with an increase in D2 from 0.5 to 1.5, the amount of residual strength decreases. Finally, D2 = 15 is the most appropriate input to this parameter and predicts the post-peak behavior of Indiana Limestone under 10 MPa confining pressure.

Fig. 22
figure 22

Numerical and experimental results of triaxial strength test on Indiana Limestone at confining pressure of 10 MPa

Full size image

4 Validation

4.1 Uniaxial compression strength test

Frew et al. (2001) conducted a quasi-static uniaxial compression strength test on a specific Indiana Limestone. To facilitate a comparison between the uniaxial compression strength test results of the specimen and the JHC numerical simulation modeling, a numerical simulation of the specimen is performed utilizing the commercial finite element software, LS-DYNA. All simulation setups employed are identical to those outlined in Sect. 3.4.1, which pertains to a triaxial compression strength test. The only difference is that, for the uniaxial compression test, no confining pressure was applied. It is important to note that, given the quasi-static nature of the loading in the uniaxial compression strength test (with a strain rate of approximately \(\dot{\varepsilon }={10}^{-5} {s}^{-1}\), the \({C}_{static}\) was implanted for this simulation. The experimentally determined value for the UCS is 64.6 MPa as noted in Table 4.

Table 4 Material and geometrical setup of SHPB test
Full size table

Figure 23 depicts the numerical and experimental uniaxial compression strength of Indiana Limestone. Notably, the illustration highlights a satisfactory agreement between the experimental and numerical results of the uniaxial compression strength test. The numerical model, employing the JHC constitutive model, successfully predicts both the peak strength and stiffness of Indiana Limestone under uniaxial conditions.

Fig. 23
figure 23

Comparisons of the simulated and experimental values of uniaxial compression strength of Indiana Limestone

Full size image

4.2 Split Hopkinson Pressure Bar

The dynamic uniaxial compression test, commonly known as the Kolsky bar or Split-Hopkinson Pressure Bar (SHPB), stands as a widely used method for characterizing the dynamic properties of materials, including rocks and other brittle substances. Frew et al. conducted dynamic impact tests on Indiana Limestone (Frew et al. 2001). To emulate this, a numerical simulation of an SHPB test was executed in LS-DYNA, as illustrated in Fig. 24. The Kolsky bar setup, as per Frew et al.'s configuration, comprises four parts: the impact bar, incident bar, specimen, and transmitted bar. Material parameters and geometric dimensions of the experimental setup are detailed in Table 5.

Fig. 24
figure 24

Schematic of SHPB test

Full size image
Table 5 Johnson–Holmquist–Cook constitutive model parameters for Indiana Limestone
Full size table

During the test, the impact bar with a speed of 13.9 m s−1 collides with the incident bar which initiates the elastic wave propagation. In this study, the stress resulting from this impact was imported to the incident bar due to simplification in numerical simulation which is shown in Fig. 25.

Fig. 25
figure 25

Incident pulse with an annealed copper pulse shaper (Frew et al. 2001)

Full size image

Figure 26 presents the experimental and numerical incident, reflected, and transmitted strains in an SHPB test on Indiana Limestone. There is excellent agreement between the experimental and numerical results. Despite neglecting dispersions of elastic waves caused by the Pochhammer–Chree effect related to bar geometry (attributed to the assumption of an instantaneous rising time, which deviates from experimental conditions), the average mechanical behavior of Indiana Limestone under dynamic loading conditions (such as the stress–strain curve), is characterized using determined strains in Fig. 26, characteristics reported in Table 5, and following Equation (Eqs. 27, 28). Additionally, the strain rate in each increment can be calculated using Eq. 29.

Fig. 26
figure 26

Numerical and experimental Strain–time signals of SHPB on Indiana Limestone

Full size image
$$\sigma \left(t\right)={E}_{S}{\left(\frac{{D}_{steel}}{{D}_{specimen}}\right)}^{2}{\varepsilon }_{T}(t)$$
(28)
$$\varepsilon \left(t\right)=\frac{2.{C}_{S}}{{L}_{sp}}{\int }_{0}^{t}{\varepsilon }_{R}(t)dt$$
(29)
$$\dot{\varepsilon }\left(t\right)=\frac{2.{C}_{S}}{{L}_{sp}}{\varepsilon }_{R}(t)$$
(30)

According to Fig. 27, there are noticeable discrepancies in the prediction of the dynamic compression strength of Indiana Limestone. It is important to recognize that these underestimations may stem from the simplifications inherent in the numerical simulation process, which can be considered acceptable within certain limits.

Fig. 27
figure 27

Numerical and experimental stress–strain comparison of SHPB test on Indiana Limestone

Full size image

Despite these deviations between the simulated and experimental stress wave results, they demonstrated an overall agreement. Consequently, the simulation results can be considered accurate and reasonable within the context of the model's limitations.

4.3 Triaxial compression strength test

In this section, some of the experimental triaxial tests shown in Fig. 28 are simulated to check the validity of the determined values for the JHC parameters. It is worth noting that the second damage parameter is set to 1.5, as determined in Sect. 3.4.1. Figure 28 illustrates the comparison between the results of triaxial compression tests and the numerical models for the Indiana Limestone. As shown, there is good agreement between the two, ensuring the accuracy of the determined JHC parameters.

Fig. 28
figure 28

Numerical and experimental results of triaxial strength tests under different confining pressures (P)

Full size image

4.4 Sensitivity analysis of key JHC material model parameters

In this section, a sensitivity analysis is performed on the most influential parameters of the JHC model using the base information of the specimen noted in Table 4 to identify which parameter has the greatest impact on the model's results. UCS test, as previously described, is utilized for this purpose. Figure 29 illustrates the changes in UCS values based on the variation of different parameters. Five key parameters including A, B, N, \({P}_{L}\) and \({P}_{C}\) are examined in this analysis, all of which have been introduced in Table 1. According to Fig. 29, strength model parameters (A, B, N) have a more significant impact on the rock's strength compared to the material pressure parameters (\({P}_{L}\) and \({P}_{C}\)). Among these parameters, B exhibits the most substantial influence on the rock's strength.

Fig. 29
figure 29

Sensitivity analysis of key parameters in the JHC model for the UCS test

Full size image

5 Conclusion

In this paper, a literature-based parameter determination method for the Johnson–Holmquist–Cook (JHC) constitutive model is proposed specifically for Indiana Limestone rocks. The parameter determination approach involves assembling a comprehensive dataset, conducting statistical analyses, performing analytical derivations, and employing numerical back analysis techniques. All parameters, except one of the damage parameters, are determined through analytical derivations. Due to the scarcity of data for one of the damage parameters, it is determined via calibration using numerical simulations of triaxial compression strength data obtained from experimental results.

The accuracy of the determined JHC constitutive model parameters for Indiana Limestone rocks is validated through a series of static and dynamic loading tests. Static loading is accomplished using uniaxial and triaxial compression strength tests, while dynamic testing is carried out using the Split Hopkinson Pressure Bar (SHPB) test. The JHC constitutive model, employing the determined input parameters, exhibits a realistic estimation of Indiana Limestone's behavior.

During the parameter determination process for the JHC constitutive model of Indiana Limestone, additional insights are uncovered. It is found that the strain rate effect on Indiana Limestone rocks is more pronounced under dynamic strain rates compared to the static region, which aligns with the response patterns observed for brittle materials under varying loading rates. In the determination of damage parameters, a significant impact of the second damage parameter on the post-peak behavior of the rock is observed, with an increase in the second damage parameter (\({D}_{2}\)) corresponding to a decrease in the residual strength of Indiana Limestone.

In conclusion, a cost-effective and efficient method for determining parameters of the Johnson–Holmquist–Cook constitutive model is presented, eliminating the need for conducting expensive laboratory tests. This approach enhances the overall efficiency of numerical methods and demonstrates the adaptability of the determined dataset for Indiana Limestone rocks to other Indiana Limestone samples by adjusting basic properties such as shear modulus, compression and tensile strengths, and density. The insights provided by this study serve as valuable guidance for numerical modeling of Indiana Limestone and other similar rocks. Further validations are still required to examine the applicability of the JHC model in various failure mechanisms not discussed in this paper.