Stability of highly inclined non-circular wellbores in isotropic formations

Abstract

The shear and tensile stabilities of highly inclined non-circular wellbores are investigated in this study. Using the equivalent-ellipse hypothesis, the non-circular geometry was approximated as an ellipse, and the corresponding stress concentration equations are presented. With the new set of stress concentration equations, a comprehensive study of the tensile and shear stabilities of an elliptical borehole was conducted, including the impact of well inclination and azimuthal angles, horizontal stress difference, degree of ellipticity, and orientation of the maximum horizontal stress to the major axis of the ellipse. Using five commonly used shear failure criteria, we observed that both Mohr–Coulomb and Drucker Prager (inscribed) failure criteria predicted higher collapse pressures, relative to the others including Drucker Prager (inscribed), Mogi-Coulomb, and Modified Lade. While Drucker Prager's (circumscribed) failure criterion underestimates the collapse pressure. Both the linear elastic and poroelastic models were used in investigating the fracture initiation orientation and pressure of highly inclined elliptical boreholes. The prediction from the poroelastic model is always less than the linear elastic model. In some instances, they predict different fracture initiation orientations. From this study, we observed that generally, a near-circular wellbore is more stable than elliptical borehole in both shear and tension. Nevertheless, there are some well inclination and azimuthal angles than can make an elliptical borehole have more shear and tensile stabilities than a near-circular wellbore.

Article Highlights

• Easy-to-compute stress concentration equations around a highly inclined elliptical wellbore are presented in this work.

• Conducting both tensile and shear stability studies, it was observed that generally near circular wellbores are more stable than elliptical boreholes.

• For some combinations of well inclination and azimuthal angles elliptical boreholes can have more shear and tensile stabilities than near-circular wellbores.

1 Introduction

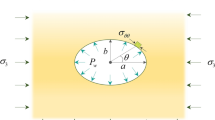
The cross-sections of drilled wellbores for oil and gas exploration, waste disposal, and geothermal energy extraction are not circular as reported in some field studies (Chen et al. 2020), Aadnoy and Angell-Olsen 1995). One of the major factors contributing to a non-circular wellbore geometry is wellbore deformation and failure due to mechanical stresses and chemical actions. In most conventional and unconventional drilling operations, the boreholes are designed to be “circular” in cross-section. In some formations, such as hard rocks with non-uniform stress conditions, the relatively circular geometry may not be stable because the stresses may cause the portions of the formation to break from the wall. Wellbore breakout, which occurs because of compressive shear failure, produces a pronounced non-circular geometry. As the well angle increases, the propensity for shear failure increases. Breakout due to compressive shear failure generally occurs when the wellbore pressure is below a critical value. A major consequence of significant breakout along the length of the wellbore is a prolonged non-productive time. At the onset of modeling wellbore breakout, in an isotropic formation, a dog-eared shape, occurring along the orientation of maximum compressive stress is assumed (Cox 1970; Bell and Gough 1979; Plumb et al. 1985). But as observed by Zoback et al. (1985), breakouts are enlarged sections of the wellbore with broad and flat curvilinear surfaces, orientated in the direction of maximum horizontal compression (Fig. 1). Although the actual shape of the wellbore section is not exactly elliptical, it was approximated as a doubly symmetric hole by Cheatham (1993) and Exadaktylos et al. (2002). Assuming the breakout geometry to be an ellipse is a further approximation of the actual geometry for an easy computation of the stress concentration. Exadaktylos et al. (2002) presented a semi-analytical plane elasticity solution of a circular hole with diametrically opposed notches in a homogeneous and isotropic geomaterial. Their solution compared very well with Mitchell’s (1966)) work on equivalent-ellipse. Hence, suggesting that the use of the equivalent ellipse hypothesis (Fig. 2) provides a means of describing analytically the stress concentration around a non-circular wellbore (within a linear elastic framework), provided there is no damage around the wellbore.

Fig. 1

A representative breakout shape as observed by Zoback et al. ( (Zoback et al. 1985)) in wells drilled in a Nevada test site

Fig. 2

A schematic representation of the application of the equivalent ellipse hypothesis for approximating the geometry of a wellbore with breakout with an ellipse having similar stress concentration

Second, well design is another key factor that impacts the geometry of the wellbore. For example, to prevent uncontrolled breakout, especially in high-angle wells, an elliptical well section is created in an orientation that relieves the stresses in the formation (Lund 2000). More so, the junctions of multi-laterals are elliptical or oval and present borehole instability problems (Hovda et al. 1998 and Brister 1997). In the development of a closed-loop geothermal system, many open-hole laterals are needed to make the system economical. At the junction of each lateral to the main borehole, the cross-section is not circular and may suffer from instability if not carefully addressed.

A discriminate enlargement of the hole in the direction of maximum compression may occur, as shown in Fig. 3, even when the wellbore pressure is above the critical collapse pressure. This is because around and along the orientation of maximum compression, the formation of cracks due to the actions of the in-situ stresses is highest. For softer formation, this incident can be very catastrophic (Zhu and Liu 2013). The authors demonstrated that significant wellbore enlargement can occur because of the impacts of the drillstring. Unfortunately, the catastrophic impact of drillstring vibration, especially chaotic whirling, on wellbore stability is often of low priority in many well designs and drilling operations. In fact, very limited studies have been conducted on the impact of drillstring vibration on wellbore stability (Placido et al. 2002 and Khaled and Shokir 2017, Khaled (2017), Vijayan et al. (2017), Saleh and Mitchell ( 1989), Santos et al. (1999). This is not the primary focus of this paper, but it is worth mentioning.

Fig. 3

A sketch of wellbore enlargement caused by a forward and b backward whirl of the BHA

With the understanding that the cross sections of highly inclined wellbores can be non-circular, based on the reasons mentioned above, it is important to investigate the shear and tensile stabilities of such boreholes. To investigate the stability of a highly inclined elliptical borehole, in an isotropic formation, it is needful to first derive tractable stress concentration equations around such a hole. Although several authors have published stress distributions around a non-circular borehole in an isotropic material (Inglis 1913; Stevenson 1945; Maugis Maugis 1992; Muskhelishvili 1963; and Setiawan and Zimmerman 2020), unfortunately, these models are primarily applicable to vertical and low-angle wells, as the out-of-plane shear stresses are disregarded. However, Qi et al. (2018) presented stress concentration equations around an elliptical hole in an anisotropic plate, using conformal mapping method. Though their solution can be reduced to an isotropic plate case, the set of equations are not tractable. Luo and Wang (2009) used complex variable method to determine the stress concentration around an elliptical hole in an infinite matrix with remote anti-plane shear stress loading, but their solution is not as simple as the one presented here. Therefore, we present in this paper, an easy-to compute a set of stress concentration equations, accounting for both in-plane and anti-plane stresses.

Hence, knowing the stress concentrations around the borehole, the tensile and shear stabilities can be assessed, using the well-known continuum-based approaches. Although a few studies on the stability of elliptical wellbores have been done by past authors, unfortunately, these models are primarily applicable to vertical and low-angle wells, as the out-of-plane shear stresses are disregarded (Aadnoy and Angell-Olsen 1995, Aadnoy and Edland ( 2001), Chen et al. (2019), Cheng et al. (2019). For high-angle wells, the anti-plane shear stresses significantly impact the stability of the well, and thus cannot be neglected for rigorous stability analyses.

Compressive shear failure around a borehole occurs when the wellbore pressure falls below a critical value. And at a specific orientation around the wellbore, the maximum principal stress is highest, causing significant damage and breakout, which strongly depends on the strength of the rock. In this work, we are focused on the onset of shear failure of an elliptical borehole. The breakout morphology around an elliptical borehole is not considered in this work.

Tensile failure of the wellbore occurs intentionally or unintentionally during drilling. The unintentional fracture of the wellbore is usually undesired, as it could lead to loss circulation and eventually blowout. During drilling, a leak-off test is often conducted, after each casing is set, to examine the strength of the open-hole interval below the casing. The goal of the leak-off test is to ensure the strength of the rock in the openhole interval is sufficient to handle the mud program designed for the openhole section. This is an example of intentional fracturing scheme. Similarly, in unconventional resource development, the well stimulation by hydraulic fracturing leads to intentional fracturing of the wellbore.

Wellbore fracturing is initiated when the wellbore stresses change from compression to tension. This occurs when the wellbore pressure is excessively high and/or the wellbore fluid is colder than the rock, thus reducing the hoops stress. To model the critical pressure at which fracture initiation occurs around the wellbore, continuum mechanics-based approaches have often been used. Hubbert and Willis (1957) proposed the first set of fracturing pressure for vertical wells, stating that tensile failure will occur if the acting fluid pressure exceeds the minimum tangential stress. From their proposition, some authors have presented similar fracture initiation models for circular borehole with penetrating and non-penetrating borehole conditions (Hiramatsu and Oka 1962, 1968); Daneshy 1973; Bradley 1979; Amadei 1983; Huang et al. 2012; Aadnoy and Looyeh 2010; Aadnoy 1998; Fjaer et al. 2008; Cui et al. 1997; and Abousleiman and Cui 1998). Many of these past studies neglect the presence of pre-existing fractures around the wellbore and assume an undamaged circular wellbore in their models. And the tensile failure initiation is determined when the effective minimal principal stress is equal to the tensile strength of the formation. But this is usually not the case, as observed in formation image log and core analysis, as naturally and./or induced fractures are often observed intersecting the wellbore (Bunger et al. 2010). However, for near-borehole fracturing there are two stages of tensile failure—fracture initiation and reopening of pre-existing cracks/fractures. The use of continuum mechanics approach is appropriate for estimating fracture initiation if the right constitutive model is used. For brittle rocks, the use of linear elastic model may prove reasonable. But for ductile and quasi-ductile rocks, the use of elastoplastic model assumption is advised. Aadnoy and Belayneh (2004) presented an elastoplastic fracturing model for a circular wellbore, assuming a non-penetrating wellbore wall condition. Despite these limitations, we proceed in this work to use the continuum approach for estimating fracture initiation pressure around highly inclined elliptical wellbore.

This paper is arranged such that we first present the stress concentrations around an elliptically shaped wellbore by subdividing the 3D problem into in-plane and out-of-plane subproblems. In the subsequent sections following, the model formulations for shear and tensile stabilities are presented. Next, the accuracy of the proposed equations was validated with field and experimental data, and some sensitivity studies were conducted on key parameters that affect both the shear and tensile stabilities of an elliptical borehole.

2 Stresses around an elliptical borehole

Kirsch (1898) equations are mostly used for wellbore stability analyses in the oil and gas industry today because circular geometry of the wellbore is assumed, which may be valid in some cases. From the foregoing, it is obvious that the complexity of the wellbore geometry introduces additional complexity into wellbore stability analyses. To understand the stability of the borehole, determining the total stresses acting around the wellbore is very essential. In the previous sections of this paper, the induced stress concentrations from several mechanical loadings of the formations have been considered individually. Now, based on the assumption that the associated deformations to these loadings are small, the superposition theorem is applied. In that case, stresses with the same line of action can be summed linearly together.

The stress concentrations around an elliptical borehole in a saturated rock formation are derived in Appendix A.

2.1 Hoop stress at the wellbore wall

The combined hoop stress is the superposition of the induced hoop stresses by the mechanical loadings.

$${\upsigma }_{\eta \eta }^{\prime}={\sigma }_{\eta \eta }^{(\mathrm{1,1},1)^{\prime}}+{\sigma }_{\eta \eta }^{(\mathrm{1,1},2)^{\prime}}+{\sigma }_{\eta \eta }^{(\mathrm{1,2},1)^{\prime}}+{\sigma }_{\eta \eta }^{(\mathrm{1,2},2)^{\prime}}+{\sigma }_{\eta \eta }^{(\mathrm{1,3},1)^{\prime}}+{\sigma }_{\eta \eta }^{(\mathrm{1,3},2)^{\prime}}$$

(1)

$${\upsigma }_{\eta \eta }^{\prime}=\left[\begin{array}{l}\frac{\left({\upsigma }_{yy}^{\prime}+{\upsigma }_{xx}^{\prime}\right){\text{sinh}}2{\varsigma }_{0}-\left({\upsigma }_{xx}^{\prime}-{\upsigma }_{yy}^{\prime}\right)\left({\text{cos}}2\alpha +{e}^{2{\varsigma }_{0}}{\text{cos}}2\left(\alpha -\eta \right)\right)}{{\text{cosh}}2{\varsigma }_{0}-{\text{cos}}2\eta }\\ -2{\sigma }_{xy}\left\{\frac{{e}^{2{\varsigma }_{0}}{\text{sin}}2\eta -{\text{sin}}2\alpha }{{\text{cosh}}2{\varsigma }_{0}-{\text{cos}}2\eta }\right\}-\Delta {p}_{w}\left\{\frac{2{\text{sinh}}2{\varsigma }_{0}}{{\text{cosh}}2{\varsigma }_{0}-{\text{cos}}2\eta }-1\right\}\end{array}\right]$$

(2)

It shows from Eq. (2) that the induced hoop stress by the in-plane shear stress is independent of the orientation of the major axis of the ellipse with respect to the horizontal. When $\alpha =0 \mathrm{or }\pi /2$ and ${\zeta }_{0}\to \infty$, then Eq. (2) reduces to the hoop stress around a wellbore with circular geometry.

2.2 Axial stress at the wellbore wall

From Eq. (A.26) the axial stress at the wellbore wall is derived as

$${\upsigma }_{zz}^{\prime}={{\text{S}}}_{zz}^{\prime}-v\left[\begin{array}{l}\left({\upsigma }_{xx}^{\prime}-{\upsigma }_{yy}^{\prime}\right)\left\{\frac{{e}^{2{\varsigma }_{0}}\left({\text{cos}}2\alpha {\text{sinh}}2{\varsigma }_{0}+{\text{sin}}2\alpha {\text{sin}}2\eta \right)}{{\text{cosh}}2{\varsigma }_{0}-{\text{cos}}2\eta }\right\}\\ -\frac{{e}^{2{\varsigma }_{0}}\left({\upsigma }_{xx}^{\prime}-{\upsigma }_{yy}^{\prime}\right){\text{cos}}2\alpha \left({\text{cosh}}2{\varsigma }_{0}-{\text{cos}}2\eta \right)}{{\text{cosh}}2{\varsigma }_{0}-{\text{cos}}2\eta }\\ +2{e}^{2{\varsigma }_{0}}{\sigma }_{xy}\left\{\frac{{\text{cos}}2\alpha {\text{sin}}2\eta +{\text{sin}}2\alpha {\text{sinh}}2{\varsigma }_{0}-\left({\text{cosh}}2{\varsigma }_{0}-{\text{cos}}2\eta \right){\text{sin}}2\alpha }{{\text{cosh}}2{\varsigma }_{0}-{\text{cos}}2\eta }\right\}\\ -{\Delta p}_{w}\left(\frac{2{\text{sinh}}2{\varsigma }_{0}}{{\text{cosh}}2{\varsigma }_{0}-{\text{cos}}2\eta }-2\right)\end{array}\right]$$

(3)

Equation (3) shows the dependence of axial stress on wellbore pressure with increasing ellipticity, and it reduces to Kirsch’s solution when ${\mathrm{tan\zeta }}_{0}=1$. This additional effect is not present when the wellbore is perfectly circular.

2.3 Stress in the confocal ellipse direction

This is equivalent to the radial stress for a circular wellbore geometry

$${\upsigma }_{\varsigma \varsigma }^{\prime}={p}_{w}-{p}_{0}$$

(4)

2.4 Anti-plane hoop shear stress at the wellbore wall

$${\sigma }_{\eta z}=\frac{\left(1+{\text{tanh}}{\varsigma }_{0}\right)}{\sqrt{{{\text{sin}}}^{2}\left(\eta \right)+{{\text{tanh}}}^{4}{\varsigma }_{0}{{\text{cos}}}^{2}\left(\eta \right)}}\left\{{\sigma }_{yz}{\text{cos}}\left(\eta +\alpha \right)-{\sigma }_{xz}{\text{sin}}\left(\eta +\alpha \right)\right\}$$

(5)

2.5 Anti-plane shear stress in the direction of the confocal ellipse

$${\sigma }_{\varsigma z}=0$$

(6)

2.6 In-plane shear stress at the wellbore wall

$${\sigma }_{\varsigma \eta }=0$$

(7)

2.7 Thermal loading of the wellbore

The induced stress concentration from thermal loading of the near-wellbore region can be added linearly to the stress concentrations from mechanical loadings, based on the principle of superposition. The thermal loading of the near-wellbore region is highly driven by the difference between the temperature of the rock and wellbore fluid, and the thermal and mechanical properties of the rock (specifically Young’s modulus, Poisson ratio, and thermal linear expansivity).

Thermal stresses are generally tensile or compressive but may generate shear stresses if the temperature field is nonlinear, as the principal strains will vary across the material body. More so, if there are non-local effects or intrinsic or stress-induced anisotropy in the material, shear stresses can be generated. But in this study, these secondary effects are not considered. The temperature loading of the wellbore wall is uniform, and no shear stresses are induced from thermal loading.

When the wellbore fluid is colder than the in-situ formation temperature the induced thermal stresses are tensile at all wellbore azimuths. Although the effect of temperature is time-dependent, steady-state is assumed to have been reached between the wellbore fluid and the formation. The induced thermal stresses at the wellbore wall are.

Induced thermal hoop stress

$$\Delta \sigma_{\eta \eta }^{T} = \frac{{\alpha_{t} E\left( {T - T_{0} } \right)}}{1 - v}$$

(8)

Induced thermal axial stress

$$\Delta \sigma_{zz}^{T} = \frac{{\alpha_{t} E\left( {T - T_{0} } \right)}}{1 - v}$$

(9)

The induced thermal stress in the confocal ellipse direction, at the wellbore wall, is zero. T is the temperature of the wellbore fluid and ${T}_{0}$ is the virgin in-situ temperature of the formation. At the wellbore wall, both the fluid and the rock grains in contact are assumed to be in thermal equilibrium, so that Eqs. (8) and (9) hold.

From Eqs. (8) and  (9), it is evident that a decrease in the temperature of the wellbore fluid induces tensile thermal stress on the near region of the wellbore. And as documented by Zoback (2010), the cooling of the wellbore generates drilling-induced tensile fractures around the near region of the well.

Hence, from the foregoing, the induced stress concentrations at the wellbore wall due to both mechanical and thermal loading of the formation are presented.

2.8 Comparing proposed hoop stress equation with a published solution.

We further compare the reduced form of the hoop stress derived in this study with Lekhnitskii (1956) solution, which was recast by Aadnoy and Angell-Olsen (1995) in Fig. 4.

Fig. 4

Comparing the hoop stress distribution predicted with the proposed equation in this study and Aadnoy and Angell-Olsen (1995), with dimensionless parameter a $c=0.6$, b $c=0.7$, c $c=0.8$, d $c=0.9$, and e $c=1$. It should be noted that the solution provided by Aadnoy and Angell-Olsen (1995) is only applicable to vertical wellbores, and it is a series approximation of the stress distribution

The figure shows that the difference between the two solutions over the entire orientation span of the wellbore is negligible. The figure was plotted assuming the in-situ stresses are 65 Mpa and 45 Mpa, a range of the dimensionless parameter labeled as c by Aadnoy and Angell-Olsen (1995) from 0.6 to 1, which is equivalent to ${Tanh}^{-1}(c)$ in this study, pore pressure is 0 Mpa, and the wellbore pressure is 40 Mpa. At the value of c = 1, both solutions converge accurately to the Kirsch’s solution.

It should be noted that we rotated the coordinate system by $\alpha =\frac{\pi }{2}$ so as to have the same orientation angles as the set of equations by Kirsch (1898) and Aadnoy and Angell-Olsen (1995). As shown in Fig. 5 the proposed coordinate system in this paper starts with $\eta =0$ at the major axis of the ellipse. While in Aadnoy and Angell-Olsen (1995) and Kirsch (recast by Aadnoy and Looyeh (2010) the major axis of the ellipse is expected at $\eta =\frac{\pi }{2}$.

Fig. 5

The orientation of the principal stresses at the wellbore wall at fracture initiation. The fracture initiates in a direction perpendicular to the minimum principal stress

It is worth mentioning at this point that there are other relevant studies on hoops stress distribution around an elliptical borehole. Jaeger et al. (2007) and Savin (1961) presented hoop stress equations for an elliptical hole in an isotropic body, subjected to a uniaxial far-field loading, with an arbitrary inclination angle to the horizontal axis. Setiawan and Zimmerman (2020)) provided a complete in-plane stress solution around an arbitrary-shaped hole. Their solution will not be able to address stability analysis for highly inclined wells.

3 Mechanical stability

Wellbore stability analysis during drilling and the entire life of the well have been extensively addressed by many authors, hence, we would not be providing an extensive literature review on this topic; the reader is advised to check other published works on this area including Aadnoy and Looyeh (2010) and Fjar et al. (2008) for detailed background. But the goal of this section of the paper is to provide solutions to some well engineering questions. First, what is the impact of wellbore ellipticity on the shear and tensile failures of the wellbore? Can the state of stress around the wellbore, after the occurrence of breakout in a highly deviated wellbore, be estimated analytically without using an expensive finite element simulator? What is the impact of wellbore ellipticity on in-situ horizontal stress measurements?

Conventional pre-drill wellbore stability studies often assume linear elastic or poroelastic behavior of the rock (Zoback 2010). The linear elastic assumption provides a good prediction of the onset of failure around the well but overestimates the behavior of the near-well region after failure, especially in ductile formations.

Analytical models for investigating instabilities around wellbores may indeed have some inherent limitations, such as the inability to capture complex stress distributions around non-circular geometry and inelastic rock behavior. Yet, they provide a powerful tool for sensitivity analyses and calibration of numerical models, in some cases. Most studies conducted on the post-failure stability analysis of the wellbore have been based on finite element analysis (Tsopela et al. 2020; Li et al. 2020; Lin et al. 2020; Cheng et al. 2019; Zhang et al. 2019; Li et al. 2017; and Li et al. 2016), except the notable semi-analytical model for stress distribution around a notched circular opening presented by Exadaktylos et al. (2002) and analytical models, for the same problem, conducted by Muskheishvilli (1963)) and Mitchell (1966).

Hence, in this study, we present an analytical approach for estimating the stability of elliptical wellbores—collapsed and deformed wellbores, using the equations presented above, in Sect. 2. The onset of the shear failure and fracture initiation around such wellbores are considered in the subsequent sections of this paper. Although Aadnoy and Edland (2001) and Aadnoy and Angell-Olsen (1995) have presented similar solutions for predicting the stability of non-circular wellbore geometry, the studies are only applicable to the vertical section of the wellbore.Dyskin

3.1 Shear failure

Shear failure of the wellbore is associated with low wellbore pressures. A lower wellbore pressure increases the hoop stress, while the radial stress (hyperbolic for elliptical wellbore) reduces at the same rate as the wellbore pressure. In the same vein, a higher wellbore fluid temperature compared to formation fluid can also cause the hoop stress to increase. The considerable difference between the hoop stress and hyperbolic stress (radial for circular wellbore) leads to higher shear stress acting on the wellbore wall. Above a critical stress level, compressive shear failure will occur, and some regions around the wellbore will breakout. The prediction of breakout shapes has been extensively addressed by Gough and Bell (1982), Ewy and Cook (1990), Zoback et al. (1985), Stacey and Jongh (1977), Ortlepp (1987), and Oyedokun and Schubert (2016).

These studies predicted that breakout shapes can be generally flat-bottomed or triangular for brittle geomaterials. Hence, the shear failure of the wellbore under anisotropic stress loading will often generate a non-circular wellbore shape—a notched circular borehole. Although other studies applied the fracture mechanics approach to understanding the mechanics of borehole breakouts (Fairhust and Cook1966); Horii and Nemat-Nasset 1985; Dyskin and Germanovich 1999; Germanovich and Dyskin 2000; and Nemat-Nasser and Horii 1982), they still predicted similar notched-shape patterns.

According to Etchecopar et al. (1999), Guenot and Santarelli (1988), and Maury (1992), the shear rupture modes around the wellbore can be classified into three major categories—A, B, and C. Only two of these rupture categories will cause the wellbore geometry to be elliptic—classes A and B, if the initial shape was perfectly circular at all. But as mentioned earlier, most drilled boreholes are not perfectly circular; there is a measure of ellipticity to the cross-section.

As will be shown later in this study, the stress concentrations around a collapsed wellbore (categories A and B especially) can be adequately predicted by adopting equations presented above to Mitchell (1966) equivalent ellipse hypothesis. This is where the importance of these equations can be best appreciated in wellbore stability analysis.

3.1.1 Shear failure orientation

In a vertical well, shear failure occurs in the direction of the minimum horizontal in-situ stress. But in a deviated well, the orientation of shear failures significantly depends on the state of stress around the wellbore, which is a function of well angles (inclination, azimuth) and in-situ stresses.

Typically, the principal stresses at the wellbore wall are

$${\upsigma }_{1}^{\prime}=\frac{1}{2}\left({\upsigma }_{\eta \eta }^{\prime}+{\upsigma }_{zz}^{\prime}\right)+\frac{1}{2}\sqrt{{\left({\upsigma }_{\eta \eta }^{\prime}-{\upsigma }_{zz}^{\prime}\right)}^{2}+4{\sigma }_{\eta z}^{2}}$$

(10)

$${\upsigma }_{2}^{\prime}=\frac{1}{2}\left({\upsigma }_{\eta \eta }^{\prime}+{\upsigma }_{zz}^{\prime}\right)-\frac{1}{2}\sqrt{{\left({\upsigma }_{\eta \eta }^{\prime}-{\upsigma }_{zz}^{\prime}\right)}^{2}+4{\sigma }_{\eta z}^{2}}$$

(11)

$${\upsigma }_{3}^{\prime}={\Delta p}_{w}$$

(12)

where ${\sigma }_{1}^{\prime}$ is the effective maximum principal stress and ${\sigma }_{3}^{\prime}$ the least principal stress.

The orientation where collapse will occur is determined by the value of $\eta$ that maximizes the maximum principal stress at the wellbore wall:

$$\frac{\partial {\upsigma }_{1}^{\prime}}{\partial \eta }=\frac{1}{2}\sqrt{{\left({\upsigma }_{\eta \eta }^{\prime}-{\upsigma }_{zz}^{\prime}\right)}^{2}+4{\sigma }_{\eta z}^{2}}\left\{\frac{\partial {\upsigma }_{\eta \eta }^{\prime}}{\partial \eta }+\frac{\partial {\upsigma }_{zz}^{\prime}}{\partial \eta }\right\}+\frac{1}{2}\left({\upsigma }_{\eta \eta }^{\prime}-{\upsigma }_{zz}^{\prime}\right)\left\{\frac{\partial {\upsigma }_{\eta \eta }^{\prime}}{\partial \eta }-\frac{\partial {\upsigma }_{zz}^{\prime}}{\partial \eta }\right\}+2{\sigma }_{\eta z}\frac{\partial {\sigma }_{\eta z}}{\partial \eta }=0$$

(13)

However, the full solution is very complex and difficult to manage. But for type A breakout mode, the hoop stress is much higher than other prevailing stresses at the wellbore wall. Hence, to overcome this limitation, it is often assumed that $\frac{\partial {\upsigma }_{1}^{\prime}}{\partial \eta }\approx \frac{\partial {\upsigma }_{\eta \eta }^{\prime}}{\partial \eta }$. In the same vein, for type B breakout, the axial stress is the highest and the approximation $\frac{\partial {\upsigma }_{1}^{\prime}}{\partial \eta }\approx \frac{\partial {\upsigma }_{zz}^{\prime}}{\partial \eta }$ may seem reasonable. It should be noted that these approximations disregard the influence of the anti-plane shear stresses on the orientation of wellbore breakouts in deviated wellbores.

This assumption generally works but, on some occasions, it may be possible to observe a different failure orientation based on the failure criterion selected. Also, it is worth noting that it is possible that Eq. (11) may represent the least effective principal stress for a well with high anti-plane shear stresses.

3.1.2 Shear failure criteria

Knowing the appropriate critical collapse mud weight, which is highly dependent on the rock failure model, is very essential in wellbore stability analysis. Many failure criteria models have been proposed, but only a few of these are often used geomechanical analyses in the oil and gas industry—linearized Mogi-Coulomb (by Al-Ajmi and Zimmerman (2005), Mohr–Coulomb, Inscribed Drucker-Prager, Circumscribed Drucker-Prager, and Modified Lade (expressed by Ewy (1999)).

All the failure criteria can be categorized into two main groups, based on how they can be fitted to the triaxial test data (Colmenares and Zoback 2002); Benz and Schwab 2008) and accurately predict the critical collapse mud weight. The study by Mclean and Addis (1990) concluded that some failure criteria can predict unrealistic results for some stress states while performing very well in other stress conditions. And as studied by Yi et al. (2005), any failure criterion that can fit well to the polyaxial test data will perform very well in predicting the shear failure of the rock, thus providing a reliable collapse mud weight.

The shear failure criteria, which specify the stress conditions at failure, can also be classified into two categories based on the linearity or nonlinearity of the governing equations and consideration for the effect of intermediate principal stress in the governing equations. From the investigation conducted by Morita and Nagano (2016), using a failure criterion with a linear stress–strain requires adjusting the unconfined compressive strength of the rock to match the failure observed on image logs. They further mentioned that (1) any failure surface should be expressible with stress or strain invariants and (2) stress states exceeding the failure point should depart from the failure surface with significant distance. With this in mind, the modified Lade criterion (expressed by Ewy) does not satisfy condition (1). Hence, extreme caution should be exercised, as the criterion’s prediction may be inaccurate in some cases. In the same vein, the Mohr–Coulomb failure criterion overestimates the critical mud weight because it neglects the impact of the intermediate principal stress. While the Drucker-Prager criterion underestimates the critical collapse mud weight because it exaggerates the influence of the intermediate principal stress. On the other hand, the predictions from Mogi-Coulomb are close to field and laboratory data (Rahimi and Nygaard 2015; Zhang et al. 2010; Morita and Nagano Morita and Nagano 2016). It should be noted that there are other studies on this subject that have used other failure criteria, different from the ones mentioned above we are highlighting the notable ones, relevant to this study. Table 1 below provides a summary of the five main failure theories, which are under consideration.

Table 1 A summary of the four commonly used rock shear failure criteria

3.1.3 Critical collapse pressure

The state of stress and the mechanical properties of the rock around the wellbore significantly dominate when and how wellbore collapses occur. Selecting the best model to capture the nonlinear elastic and inelastic behaviors of the near-well region has received a lot of interest from many authors. For brittle rocks, which fail with a small reduction in strength, the use of elastoplastic models is unnecessary, despite exhibiting second-order effects. But for young, weak rocks that are which are under compacted, the use of the elastoplastic model is appropriate.

However, most of the analytical models give predictions close to the field and laboratory data, especially when the Mogi-Coulomb failure criterion is used. And in this study, the performance of these failure criteria (listed in Table 1), using the proposed equations above, are compared with published laboratory studies conducted by Salisbury et al. (1991), Abdulhadi (2009), Islam and Skalle (2011), Nes et al. (2015), Marsden et al. (1996), and Gabrielsen et al. (2010) and a field study by Rahimi and Nygaard (2015)).

When modeling shear failure in ductile formations, the considerations of the intermediate principal stress alone is not sufficient. The use of elastoplastic models to simulate yield zones around the wellbore has been attempted by Huang et al. (2018), Li and Tang (2016), Kang et al. (2009), Aadnoy and Belayneh ( 2004), Ronglin et al. (1998), Zervos et al. (1998), Veeken et al. (1989), Jiang et al. (2009), and Westergaard (1940). Despite the use of the elastoplastic models, the predictions from most of the failure criteria listed above are within an error margin (on the average) of 0.1lbm/gal mud weight when compared, especially for brittle and less ductile rocks. We are in no wise trying to downgrade the use of the elastoplastic models, but the realistic application of these models is still complex and computationally expensive to deploy.

Chemical agents and wellbore hydraulics have been observed to significantly influence collapse shape (Li et al. 2020; Mody and Hale 1993; Chenevert and Pernot 1998; Pašić et al. 2007; Xu 2007; Lal Lal 1999; Cheatham 1984; Chen et al. 2003; Chenevert 1970). Although the chemical effect can be significant when drilling through chemical active shale zones, we will not be considering both factors (chemical and hydraulics effects) in this study.

3.2 Tensile failure

Tensile failure occurs when and where the least principal stress becomes most tensile. For a wellbore with no pre-existing fracture/crack, a small crack is first initiated at this orientation. And for a wellbore with pre-existing cracks/fractures emanating from the wellbore into the near-region, fracture reopening occurs at the azimuth where the strain energy release rate exceeds the critical strain energy release rate at the tip of the crack. In some cases, multiple fractures can propagate at the same time. In a vertical well, tensile failure occurs in the orientation of the maximum horizontal in-situ stress. But in a deviated well, the orientation of tensile failure depends on the state of stress around the wellbore, which is a function of well angles (inclination, azimuth) and in-situ stresses.

Using the continuum mechanics approach, the principal stresses at the wellbore wall at the point of tensile failure are

$${\upsigma }_{3}^{\prime}=\frac{1}{2}\left({\upsigma }_{\eta \eta }^{\prime}+{\upsigma }_{zz}^{\prime}\right)-\frac{1}{2}\sqrt{{\left({\upsigma }_{\eta \eta }^{\prime}-{\upsigma }_{zz}^{\prime}\right)}^{2}+4{\sigma }_{\eta z}^{2}}$$

(14)

$${\upsigma }_{2}^{\prime}=\frac{1}{2}\left({\upsigma }_{\eta \eta }^{\prime}+{\upsigma }_{zz}^{\prime}\right)+\frac{1}{2}\sqrt{{\left({\upsigma }_{\eta \eta }^{\prime}-{\upsigma }_{zz}^{\prime}\right)}^{2}+4{\sigma }_{\eta z}^{2}}$$

(15)

$${\upsigma }_{1}^{\prime}={\Delta p}_{w}$$

(16)

where ${\upsigma }_{1}^{\prime}$ is the effective maximum principal stress and ${\upsigma }_{3}^{\prime}$ the effective least principal stress. The orientation where tensile failure will occur, is determined by the value of $\eta$ that minimizes the minimum principal stress at the wellbore wall:

$$\frac{\partial {\upsigma }_{3}^{\prime}}{\partial \eta }=0$$

(17)

3.2.1 Fracture pressure

Fracture initiation pressure can be very different from the breakdown pressure value in some cases. From the definition of fracture initiation pressure, which is the pressure at which a small initial defect at the wellbore wall starts to propagate or a defect develops, can vary from the breakdown pressure of the formation depending on the non-linear material behavior. If there is a substantial non-linearity in the mechanical response of the host rock, during the loading, the difference between the two pressure values can be significant, and vice versa. Haimson and Fairhust (1967) developed an expression relating the breakdown pressure with fracture initiation pressure, for a poroelastic solid.

Breakdown pressure, on the other hand, is a critical pressure at which there is a failure at the tip of a pre-existing fracture. According to classical approach, breakdown characterizes the end of the elastic response of the rock to tensile loading, and an immediate initiation of tensile failure dominance. Although nonlinear response of the rock to the load cannot be disregarded, as there could be variation of the borehole diameter with pressure. Thus, suggesting that the fracture could initiate before the borehole pressure reaches its peak.

In this paper, the linear elastic and poroelastic fracture initiation models, and fracture mechanics-based model for breakdown pressure, for an elliptical borehole are presented. And the effects of wellbore ellipticity and its rotation in the stress field are emphasized.

3.2.2 Linear elastic-based model for fracture initiation

The key criterion for fracturing, based on this model assumption, is

$${\sigma }_{3}^{\prime}={\sigma }_{t}$$

(18)

where ${\sigma }_{3}^{\prime}$ and ${\sigma }_{t}$ are the effective minimum principal stress and rock tensile strength.

3.2.3 Poroelastic model for fracture initiation

The model presented in Sect. 3.2.2 is mostly applicable to impermeable rocks, subjected to a high pressurization rate. For a vertical well, with circular cross section, the solution reduces to Hubbert and Willis (1957)) equation. One key observation of this model is its independence of the pressurization rate, which is contrary to experimental findings (Haimson and Zhao 1991; Schmitt and Zoback 1992; Detournay and Cheng 1992; Detournay and Carbonell 1994). Detournay and Cheng (1992) and Detournay and Carbonell (1994) showed that the fracture models by Hubbert and Willis (1957) and Haimson and Fairhurst (1967) corresponds respectively to slow and fast asymptotic regimes of well pressurization rate, assuming the pre-existing defect or micro-crack is small compared to the well radius. Garagash and Detournay (1996) developed a mathematical model accounting for the influence of pressurization on fracture pressure of a wellbore with pre-existing micro-cracks.

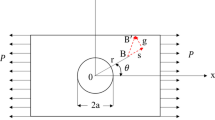
Using the modeling framework presented by Detournay and Cheng (1992) the dependence of fracture initiation pressure, at the boundary of an elliptical borehole with high inclination angle, on pressurization rate in a permeable rock is presented. But in this study, the length scale characterizing the tensile failure process takes place when the effective minimum principal stress, averaged over the length scale, reaches the tensile strength of the rock. It is assumed the rock is isotropic, and the micro-crack initiates in the direction normal to the orientation of the minimum principal stress at the wellbore wall Fig. 5.

In the vicinity of the wellbore wall, the minimum principal stress is taken to be a superposition of the purely elastic and poroelastic contribution from the change in pore pressure, triggered by the fluid boundary condition, at the onset of fracture initiation.

By extending the work of Detournay and Cheng (1992) to a highly inclined wellbore, the effective minimum principal stress at the borehole wall, in a poroelastic solid, is presented as

$${\sigma }_{3}^{\prime}={\tilde{\sigma }}_{3}+2\mu \left({p}_{w}-{p}_{0}\right)f\left(\tau \right)-\left[{p}_{0}+\left({p}_{w}-{p}_{0}\right)f\left(\tau \right)\right]$$

(19)

The first term on the right-hand side of Eq. (19) is the linear elastic contribution, the second term represents the contribution induced by pore pressure, and the third component is the pore pressure required to transform from a total to an effective stress. It should be noted that the modeling assumes a constant pressurization rate, $A$. It is assumed that at the initial condition, $t=0,$ the borehole pressure, ${p}_{w}$, is increased through this relation, ${p}_{w}-{p}_{0}=At$; ${p}_{0}$ is the far-field pore pressure. $\mu$ is a poroelastic parameter, defined as $\mu ={\alpha }_{b}(1-2v)/2\left(1-v\right),$ where $0<{\alpha }_{b}\le 1$ is the Biot’s coefficient. $f(\tau )$ is the influence function defined in Duhamel’s theorem; it is a function of the dimensionless fluid diffusion time around the wellbore. This function varies between $0$ and $1$, as the dimensionless time increases from 0 to $\infty$.

The underlying assumption of Eq. (19) is that the principal stress concentration is averaged over the length scale of the microcrack, a condition that is valid in elastic boundary value problems, provided the size of the microcrack is much lesser than the wellbore size.

At fracture initiation, the effective minimum principal stress is equal to the tensile strength of the rock, and ${p}_{w}={p}_{wf}$. From Eqs. (18) and (19), the implicit fracture initiation pressure equation is presented

$${p}_{wf}=\frac{{\tilde{\sigma }}_{3}-{\sigma }_{t}+{p}_{wf}-2{p}_{0}}{1+\left(1-2\mu \right)f\left({\tau }^{*}\right)}+{p}_{0}$$

(20)

For slow pressurization rate to failure $f\left({\tau }^{*}\right)=1$. But when $f\left({\tau }^{*}\right)=0$, the solution reduces to the linear elastic model, implying an infinitely fast pressurization rate. The influence function at failure, $f\left({\tau }^{*}\right)$, is defined as

$$f\left({\tau }^{*}\right)=\frac{1}{{\tau }^{*}}\underset{0}{\overset{{\tau }^{*}}{\int }}g(\tau -{\tau }^{\prime})d{\tau }^{\prime}$$

(21)

and function $g(\tau )$ is defined as

$$g\left(\tau \right)=\sqrt{\frac{\tau }{\pi }}\left[1-{\text{exp}}\left(\frac{-1}{\tau }\right)\right]+\left[1-{\text{erf}}\left(\frac{1}{\sqrt{\tau }}\right)\right]$$

(22)

The dimensionless time to failure, ${\tau }^{*}$, is given as ${\tau }^{*}=\frac{4c({p}_{wf}-{p}_{0})}{A{\lambda }^{2}}$, where $\lambda$ is the size of the microcrack, and c is the diffusivity coefficient.

4 Model validation with field and laboratory data

In this section of the paper, we compare shear and tensile stability predictions based on the set of stress concentration equations with available field and laboratory data.

4.1 Shear stability model validation

To validate the predictions from the proposed equations above, the predicted collapse pressures from each of the failure criteria are compared with the results from Kirsch solutions, assuming the well is almost circular. This reduction to a circular geometry is based on two reasons: (1) to compare the predictions with Kirsch solutions, and (2) the available laboratory and field studies, which we intend to validate the model with, are based on almost circular borehole cross-sections.

4.1.1 Field data

The performance of the reduced form of the proposed model is compared with Kirsch’s solutions using data from several field studies. Assuming a minor breakout width of less than 60⁰ to be the onset of shear failure is sometimes practiced in field analyses (Zoback, 2007). But without caliper logs, the onset of shear failure can be inferred from drilling events. In the quest of comparing our analytical predictions with the field-reported mud weights, this criterion was considered.

4.1.1.1 Tullich field, North Sea

Shear failure was observed along the horizontal section of the well through a sandstone reservoir with inter-bedded claystone. The stress regime in this area was reported to be a normal faulting and the orientation of the maximum horizontal stress is between 40° and 60° (Russel et al. 2006) Table 2. below provides the summary of the rock properties and stress data for the reservoir zone of interest in this field.

Table 2 Stress state and rock mechanical properties for Well 9/23a-T2

Using the field data presented in Table 2 to compute the critical mud weights from each of the failure criteria. In this computation, we assume ${\varsigma }_{0}=\frac{23\pi }{24}$ (ratio of minor to major axis is 0.995). Figure 6 shows a sensitivity study on the impact of the choice of ${\varsigma }_{0}$ on the predicted stress value (maximum principal stress in this case). The figure also brings to fore that the choice of ${\varsigma }_{0}$ (for circular geometry assumption) will not significantly affect the result, as long as ${\varsigma }_{0}\gg \frac{\pi }{2}$ or the ratio of the minor to major axis is greater than 0.894.

Fig. 6

A sensitivity study, with Well 9/23a-T2 data, showing the impact the choice of ${\varsigma }_{0}$ has on the stress distribution, in this case the effective maximum principal stress. The stress distribution around the elliptical hole is compared with Kirsch solution when a ${\varsigma }_{0}=\frac{\pi }{4}$, b${\varsigma }_{0}=\frac{\pi }{2}$, c${\varsigma }_{0}=\frac{3\pi }{4}$, and d ${\varsigma }_{0}=\pi$

Figure 7 shows the computed collapse pressure variation around the wellbore for each of the failure criteria. From the plots, the predictions from the proposed equations match Kirsch solutions, when the appropriate ${\varsigma }_{0}$ value is chosen. In this field case, Eq. (10–12) adequately represent the effective principal stresses at the wellbore wall. And the predicted failure orientations from each of the failure criteria are the same, as shown in Fig. 7.

Fig. 7

Using data from Well 9/23a-T2, the estimated collapse pressure and orientation is predicted using a Mohr–Coulomb, b Mogi-Coulomb, c Modified Lade, d Drucker Prager (inscribed), and e Drucker Prager (circumscribed) failure criteria

From Table 3, it is evident that the predicted mudweights from the proposed equations are similar to the mudweights predicted with Kirsch’s solution for each of the shear failure criteria. The goal of this paper is not to select the best failure criterion but to show the performance of the proposed equations. When the appropriate ${\varsigma }_{0}$ is selected to represent the geometry of a circular wellbore the results are similar to Kirsch’s.

Table 3 Predicted mud weights for Well 9/23a-T2

4.1.2 Northwest shelf, Australia

The two wells of interest, Well A-1 and Well B-4 are in different stress regimes. Field A is located in a normal-strike slip faulting regime and the well was drilled in the direction of the minimum horizontal stress to reduce the risk of wellbore instability. On the other hand, field B is located in a normal faulting regime. Well B-4 experienced severe instabilities due to insufficient mud weight at about 9.6ppg while Well-A-1 experienced minor instabilities at a mud weight of 10.44ppg. Table 4 presents the rock properties and stress states at the depths of failure in the two wells (Chen et al. 2002).

Table 4 Stress state and rock mechanical properties for wells A-1 and B-4

Figure 8 shows a sensitivity study on the impact of the choice of ${\varsigma }_{0}$ on the predicted stress value (maximum principal stress in this case as well). Thus, emphasizing the point that the choice of ${\varsigma }_{0}$ (for circular geometry assumption) will not significantly affect the wellbore stability analysis, as long as ${\varsigma }_{0}\gg \frac{\pi }{2}$.

Fig. 8

A sensitivity study, with Well A-1 data, showing the impact the choice of ${\varsigma }_{0}$ has on the stress distribution, in this case the maximum principal stress. The stress distribution around the elliptical hole is compared with Kirsch solution when a ${\varsigma }_{0}=\frac{\pi }{4}$, b${\varsigma }_{0}=\frac{\pi }{2}$, c${\varsigma }_{0}=\frac{3\pi }{4}$, and d ${\varsigma }_{0}=\pi$

Figures 9 and 10 with Table 5 similarly show that the proposed stress equations can accurately describe the stability of both highly inclined circular and elliptical boreholes.

Fig. 9

Using data from Well A-1, the estimated collapse pressure and orientation is predicted using a Mohr–Coulomb, b Mogi-Coulomb, c Modified Lade, d Drucker Prager (inscribed), and e Drucker Prager (circumscribed) failure criteria

Fig. 10

Using data from Well B-4, the estimated collapse pressure and orientation is predicted using a Mohr-Coulomb, b Mogi-Coulomb, c Modified Lade, d Drucker Prager (inscribed), and e Drucker Prager (circumscribed) failure criteria.

Fig. 11

Fracture initiation pressure predicted with the poroelastic and linear elastic models, using the proposed set of stress concentration equations. These are plotted with data from Test # a 1, b 2, c 3, d 4, e 13, and f 16

Table 5 Predicted mudweights for wells A-1 and B-4

4.1.3 Laboratory studies

In this section, we want to further investigate the performance of the proposed solution on how adequately it can represent the state of stress around a borehole with a circular cross-section with results from published laboratory experiments.

4.1.3.1 Islam and Skalle (2011)

The authors presented results from HC tests conducted under underbalanced conditions on Pierre-1 shale samples drilled parallel and normal to the bedding. In the borehole collapse tests, isotropic loads were first applied on the sample to achieve initial stress conditions, and subsequently the borehole pressure was decreased while keeping the cell pressure constant. To define the failure initiation point, the authors marked the stress state at the onset of accelerated deformation of the borehole wall. This approach is similar to the observation and proposition of Dyskin et al. (1999). Using dipole asymptotic and beam approximation, they (Dyskin et al.) showed that the onset of collapse around the wellbore is at the inception of the unstable crack growth.

The mechanical properties of the test samples are presented in Table 6. The recorded failure pressure for the test specimen sampled in the orientation parallel to the bedding plane was 22.4 Mpa and the failure pressure for the specimen sampled in the direction normal to the bedding plane was 19 Mpa.

Table 6 Rock mechanical properties and loading condition for the test sample

The authors did not provide the yield pressure of the samples. At the onset of the rapid growth of cracks around the borehole, the material constitutive relation cannot be represented by linear elastic behavior and the commonly used shear failure criteria will not apply. Comparing the predictions from the failure criteria with the observed ultimate collapse pressure, it is evident that the test samples experienced softening before ultimate failure. Table 7 shows the estimated collapse pressure using the five failure criteria.

Table 7 Predicted collapse pressures for the two borehole tests

4.1.3.2 Marsden and Dennis (1996)

The authors conducted thick-walled hollow cylinder tests on smectite mudrock to investigate the instability mechanisms of soft rocks. In the tests, the confining stresses were constant while the conditions of axial plane strain were maintained, and the internal pressure of the cell was gradually reduced under undrained conditions until the samples yielded and collapsed. The authors characterized failure by pairs of conjugate shear surfaces propagating away from the borehole with wedges of intact material in-between. During the loading process, it was seen that closure commenced with a relatively stiff, slightly nonlinear response before yielding. Then followed by softening with relatively linear behavior before ultimately collapsing. For tests in which there was a gradual transition from pre- to post-yield, the failure initiation pressure is approximated as the intersection of the two limbs of the curves; it should be noted that the yield pressure was chosen as the onset of failure in this laboratory experiment. In some of the HC tests conducted, the failure of the sample were more distinct, occurring immediately after yielding. As the borehole pressure decreased below the yield pressure, the deviatoric stress components within the test samples increased and failure propagated from the internal borehole surface towards the outer boundary of the sample, resulting in the complete collapse of the samples. During this process, the confining pressure was reduced and was monitored through the confining pressure control device, thus, providing a means to accurately determine the ultimate collapse pressure. The failure pattern observed in these tests was different from breakouts observed in competent sedimentary rocks, as the shear failure surfaces were not localized but continuous and accompanied by large shear displacements from plastic deformation. We are using only one of the tests conducted in this experiment and Table 8 presents the mechanical properties and loading conditions for HC1 test. The recorded ultimate collapse pressure from the experiment was 24.9 Mpa, while the sample began to yield at a pressure of 28.6 Mpa. Using the proposed equations and Kirsch solutions, the predicted collapse pressures for each of the five failure criteria are presented in Table 9.

Table 8 Rock mechanical properties and loading condition for test HC1

Table 9 Predicted onset of collapse for HC1 test sample

From the foregoing analysis, it is worth noting that the commonly used shear failure criteria predict the onset of failure or yielding of the borehole. In essence, the shear failure criteria will perform well in predicting the onset of failure for both brittle and ductile rocks. For brittle rocks, the yielding and ultimate collapse pressure are almost the same, as yielding is not pronounced. But for ductile formations, the yielding is pronounced, and the ultimate collapse pressure can be significantly different from the yielding pressure.

4.2 Tensile stability model validation

In this section, we compared the fracture initiation pressure predicted from the linear elastic and poroelastic models with the data collected from the field and laboratory experiments.

4.2.1 Laboratory study by Liu et al. (2022)

They conducted both numerical and experimental studies on fracture initiation around an elliptical shaped borehole. Although the experiment is limited to a vertical well, the variation of $\alpha$ in this experiment further provides a robust means of validating the proposed equations.

In this experiment, three mutually perpendicular loads were applied on the specimens through a servo-controlled pressurizing device. Water was used as the fracturing fluid, and the specimens were predominantly sandstone. This suggests that the poroelastic model may be a more suitable model for comparison. The fluid injection was done at a constant rate until the pressure peaked, and each of the experiments ended when the injection pressure dropped. A plain strain condition was improvised in the experiment by using a displacement-controlled loading mode in the vertical stress direction. Note that the pore pressure in this case is 0 Mpa. The authors mentioned that the Poisson’s ratio, elastic modulus, and UCS of the sandstone specimens are 0.34, 12.4 Gpa, and 75.16 Mpa respectively.

The different loading schemes, geometries and orientations of the elliptical holes used in this experiment, and the predictions with linear elastic and poroelastic models are shown in Table 10 below.

Table 10 comparing the poroelastic and linear elastic model predictions with experimental data from Liu et al. (2022)

$a$ and $b$ in the Table 10 are the half lengths of the major and minor axes of the ellipse respectively. The results from the linear elastic model are far off from the observed data from the experiments, as expected. Therefore, we decided not to include them in this specific example. The fracture initiation orientations, predicted with the proposed equations, especially with the poroelastic model, align very well with the observations from the work of Liu et al. (2022), as shown in Fig. 11.

From this experiment, it is evident that an elliptical wellbore is more stable in tension than a near-circular wellbore, as the horizontal stress ratio decreases (see Test cases 1–9). But in an isotropic horizontal stress loading the reverse is the case (see Test cases 9–12). In the same vein, the orientation of the fracture initiation.

Also, we observed from this experiment (both modeling and experimental data agree) that the orientation of fracture initiation can be different for similar elliptical holes in different isotropic media (having different tensile strengths), and under the same loading condition. This thus suggests that fracture initiation around an elliptical wellbore is very sensitive to the magnitude of the tensile strength of the medium (see Figs. 11d and 12). But for near-circular holes, this was not observed. This observation could only be predicted with the poroelastic fracture initiation model.

Fig. 12

A hypothetical test case for experiment 4, where the tensile strength of the host rock is assumed to be 4.44 MPa. The orientation of fracture initiation is different when compared with the actual Test case 4

4.2.2 Field study by Naidu and Rylance (2017)

The authors collected data (Leak Off Tests, Extended Leak Off Tests, Diagnostic Fracture Injection Tests, Wireline Formation Tests, and Formation Pressure Integrity Tests) from several wells in Khazzan gas field and inferred the fracture initiation and breakdown pressures from these tests.

They first determined the bulk modulus of the initial system volume and picked the fracture initiation pressure as the pressure value corresponding to reduced value in the bulk modulus of the system and breakdown pressure was picked as the peak pressure in the tests; only the fracture initiation pressures will be compared in this section. The prevailing stress conditions, rock strength and pressurization rate for the injection tests are presented in Table 11. The models capturing the two extreme cases of slow and fast pressurization rates are compared with the observed/picked fracture initiation pressures from these tests.

Table 11 State of stress, rock strength, and pressurization rates for injection tests conducted in a vertical well in Khazzan gas field

Since the boreholes in this field are almost circular in cross section, and we intend to validate the predictions from the poroelastic and linear elastic models with the observed data, the wellbore shape is now assumed to be ${\varsigma }_{0}=\frac{23\pi }{24}$ (the ratio of the length of the minor to major axis is 0.995), which is nearly circular. As observed in Table 12, the predictions from the poroelastic model closely align with the observed field data, while the linear elastic model overpredicts the fracture initiation pressure. Although as suggested by some authors in the literature, the poroelastic model should converge to the linear elastic model at high pressurization rate, the predicted fracture initiation pressure at a high pressurization rate, in this case, does not agree with the observed field data. This further confirms the limitation of the linear elastic model in predicting fracture initiation pressure, especially for circular boreholes (Aadnoy and Belayneh 2004). Garagash and Detournay (1997) has concluded that there is no fast limit of fracture initiation pressure, although a slow limit exists. This is a direct consequence of the incompressibility of the fluid and suggests a large negative pressure in the micro-crack with increasing pressurization rate, and the fracture pressure will become unbounded as the pressurization rate increases. Thus, this condition of negative pressure in the microcrack is meaningless since the fluid cannot sustain tension. Hence, the pure linear elastic model does not represent the true upper limit of the fracture initiation pressure, and its results can be misleading.

Table 12 Comparing results of linear elastic and poroelastic fracture initiation models with data from Khazzan gas field

5 Sensitivity studies

The proposed stress concentration equations, with the resulting fracture initiation an collapse pressure models, have been validated with field and laboratory data in the previous section of this paper. In this section, we investigate the impacts of key stress and well parameters on both tensile and shear stabilities of inclined wellbores with elliptical and near-circular cross sections.

5.1 Variation of collapse pressure with $\boldsymbol{\alpha }$ and wellbore ellipticity

Using the field data from Well 9/23a-T2, we conducted a sensitivity analysis on the impact of wellbore ellipticity index on the magnitude of the collapse pressure. The Mogi-Coulomb failure criterion is selected in this case.

From Fig. 13, based on the prevailing well profile and stress data, it can be inferred that the wellbore becomes less stable in shear as its geometry becomes more elliptical, provided the prevailing in-situ stresses and wellbore orientation remain unchanged. But it should be noted that this conclusion is based purely on a linear elastic theory.

Fig. 13

A sensitivity study, with Well 9/23a-T2 data, showing the variation of wellbore collapse pressure with wellbore ellipticity index, ${\varsigma }_{0}$ and$\alpha$. In test a$\alpha ={0}^{0}, {\varsigma }_{0}=\frac{\pi }{4}$, b$\alpha ={0}^{0}$,${\varsigma }_{0}=\frac{3\pi }{4}$, c$\alpha ={45}^{0}$, ${\varsigma }_{0}=\frac{\pi }{4}$ d$\alpha ={45}^{0}$, ${\varsigma }_{0}=\frac{3\pi }{4}$ e$\alpha ={90}^{0}$, ${\varsigma }_{0}=\frac{\pi }{8}$ f$\alpha =9{0}^{0}$,${\varsigma }_{0}=\frac{3\pi }{4}$, g$\alpha ={135}^{0}$, ${\varsigma }_{0}=\frac{\pi }{4}$ h$\alpha ={135}^{0}$, ${\varsigma }_{0}=\frac{3\pi }{4}$

In addition, this figure further supports the conclusion reached earlier that as long as ${\varsigma }_{0}\gg \frac{\pi }{2}$ (the ratio of the minor to major axis is greater than 0.92), the choice of the ellipticity index can represent a circular geometry with minimal error.

The shear stability of the elliptical wellbore is enhanced when $\alpha =0$, i.e. when the maximum horizontal stress aligns with the orientation of the major axis; Fig. 13a, b show that an elliptical-shaped wellbore is more stable than a near-circular wellbore in this scenario. An elliptical wellbore is very unstable, in shear, when the minimum horizontal stress aligns with the major axis, and the ratio of the minor to major axis is less than 0.92; the farther the ratio is to this value, the less stable is the borehole in shear, based on linear elastic framework.

5.2 Variation of collapse pressure with horizontal stress loading

In this case, we assume $\alpha =90^\circ$. The vertical stress value, well angles, and the rock properties from Well 9/23a-T2, in Table 2, are used in this analysis.

From Fig. 14 it is evident that with increased horizontal stress difference, the shear stability of the wellbore reduces. The shear stability of the elliptical hole, in this case also, is lower than the near-circular wellbore. When the maximum horizontal stress is more than twice the magnitude of the minimum horizontal stress, in this example, there is a rotation in the orientation of the shear failure around the elliptical wellbore (Fig. 21e).

Fig. 14

A sensitivity study, with Well 9/23a-T2 data, showing the variation of wellbore collapse pressure with horizontal stress loading. In test a ${S}_{H}=3750, {S}_{h}=3747.47, {\varsigma }_{0}=\frac{\pi }{4}$ b${S}_{H}=3750, {S}_{h}=3747.47, {\varsigma }_{0}=\frac{3\pi }{4}$, c ${S}_{H}=5750, {S}_{h}=3747.47,{\varsigma }_{0}=\frac{\pi }{4}$ d ${S}_{H}=5750, {S}_{h}=3747.47, {\varsigma }_{0}=\frac{3\pi }{4}$ e ${S}_{H}=7750, {S}_{h}=3747.47,{\varsigma }_{0}=\frac{\pi }{4}$ f ${S}_{H}=7750, {S}_{h}=3747.47, {\varsigma }_{0}=\frac{3\pi }{4}$

Shear failure is seen occurring in the direction parallel to the maximum horizontal stress. But when the wellbore approaches a near-circular geometry, the well is infinitely unstable in shear over a wide range of wellbore orientational angles, in the vicinity of the maximum horizontal stress direction (Fig. 14f). In other cases, the shear failure occurs in the direction of the minimum horizontal stress.

5.3 Variation of collapse pressure with wellbore inclination and azimuthal angles

In this case, we assume$\alpha =90^\circ$. The vertical and horizontal stress values and the rock properties from Well 9/23a-T2, in Table 2, are also used in this analysis. The well inclination angles used in this analysis are a low angle of 10°, 50° for medium high-angle wells, and 90° for high angle wells, and the azimuthal angle from 0° to 360°. Figure 15 shows the variation of collapse pressure with azimuthal angle and ellipticity index for a low well inclination angle of 10°. The general trend from this sensitivity study is that the shear stability of the wellbore increases as it approaches a near-circular cross section. There are instances where the elliptical hole is very unstable, in shear, along the edges of the major axis. This occurs, especially when the well azimuth is around ${45}^{0}+{90}^{0}n,$ where $n=\mathrm{0,1},2,\dots$. The cases in Fig. 15g and o are good examples.

Fig. 15

A sensitivity study, with Well 9/23a-T2 data, showing the variation of wellbore collapse pressure with well azimuthal angle, $\vartheta$. The well inclination for this test is ${10}^{0}$, when the azimuthal angle is a $\vartheta ={0}^{0}, {\varsigma }_{0}=\frac{\pi }{4}$, b $\vartheta ={0}^{0}, {\varsigma }_{0}=\frac{3\pi }{4}$, c $\vartheta ={45}^{0}, {\varsigma }_{0}=\frac{\pi }{4}$, d $\vartheta ={45}^{0}, {\varsigma }_{0}=\frac{3\pi }{4}$ e $\vartheta ={90}^{0}, {\varsigma }_{0}=\frac{\pi }{4}$, f $\vartheta ={90}^{0}, {\varsigma }_{0}=\frac{3\pi }{4}$ g $\vartheta ={135}^{0}, {\varsigma }_{0}=\frac{\pi }{4}$, h $\vartheta ={135}^{0}, {\varsigma }_{0}=\frac{3\pi }{4}$, i $\vartheta ={180}^{0}, {\varsigma }_{0}=\frac{\pi }{4}$, j $\vartheta ={180}^{0}, {\varsigma }_{0}=\frac{3\pi }{4}$, k $\vartheta ={225}^{0}, {\varsigma }_{0}=\frac{\pi }{4}$, l $\vartheta ={225}^{0}, {\varsigma }_{0}=\frac{3\pi }{4}$, m $\vartheta ={270}^{0}, {\varsigma }_{0}=\frac{\pi }{4}$, n $\vartheta ={270}^{0}, {\varsigma }_{0}=\frac{3\pi }{4}$, o $\vartheta ={315}^{0}, {\varsigma }_{0}=\frac{\pi }{4}$, p $\vartheta ={315}^{0}, {\varsigma }_{0}=\frac{3\pi }{4}$, q $\vartheta ={360}^{0}, {\varsigma }_{0}=\frac{\pi }{4}$, and r $\vartheta ={360}^{0}, {\varsigma }_{0}=\frac{3\pi }{4}$

With increased well inclination angle, the shear stability of both elliptical and near-circular holes decreases. For mediumly inclined wells ($40^\circ \le \gamma <65^\circ$), of which $\gamma =50^\circ$ is one, the shear stability of the well drastically worsens, especially with some combinations of well azimuthal angles, as seen in Fig. 16. Such combinations must be avoided in well design.

Fig. 16

A sensitivity study, with Well 9/23a-T2 data, showing the variation of wellbore collapse pressure with well azimuthal angle, $\vartheta$. The well inclination for this test is ${50}^{0}$, when the azimuthal angle is a $\vartheta ={0}^{0}, {\varsigma }_{0}=\frac{\pi }{4}$, b $\vartheta ={0}^{0}, {\varsigma }_{0}=\frac{3\pi }{4}$, c $\vartheta ={45}^{0}, {\varsigma }_{0}=\frac{\pi }{4}$, d $\vartheta ={45}^{0}, {\varsigma }_{0}=\frac{3\pi }{4}$ e $\vartheta ={90}^{0}, {\varsigma }_{0}=\frac{\pi }{4}$, f $\vartheta ={90}^{0}, {\varsigma }_{0}=\frac{3\pi }{4}$ g $\vartheta ={135}^{0}, {\varsigma }_{0}=\frac{\pi }{4}$, h $\vartheta ={135}^{0}, {\varsigma }_{0}=\frac{3\pi }{4}$, i $\vartheta ={180}^{0}, {\varsigma }_{0}=\frac{\pi }{4}$, j $\vartheta ={180}^{0}, {\varsigma }_{0}=\frac{3\pi }{4}$, k $\vartheta ={225}^{0}, {\varsigma }_{0}=\frac{\pi }{4}$, l $\vartheta ={225}^{0}, {\varsigma }_{0}=\frac{3\pi }{4}$, m $\vartheta ={270}^{0}, {\varsigma }_{0}=\frac{\pi }{4}$, n $\vartheta ={270}^{0}, {\varsigma }_{0}=\frac{3\pi }{4}$,o $\vartheta ={315}^{0}, {\varsigma }_{0}=\frac{\pi }{4}$, p $\vartheta ={315}^{0}, {\varsigma }_{0}=\frac{3\pi }{4}$, q $\vartheta ={360}^{0}, {\varsigma }_{0}=\frac{\pi }{4}$, and r $\vartheta ={360}^{0}, {\varsigma }_{0}=\frac{3\pi }{4}.$

With higher inclined angles $\gamma >65^\circ$, in this case $\gamma =90^\circ$, higher mud-weights are required to keep the different well configurations from failing in shear (Fig. 17). No catastrophic shear failure was observed for the different well configurations having an inclination angle of ${90}^{0}$ with different well azimuthal values.

Fig. 17

A sensitivity study, with Well 9/23a-T2 data, showing the variation of wellbore collapse pressure with well azimuthal angle, $\vartheta$. The well inclination for this test is ${90}^{0}$, when the azimuthal angle is a $\vartheta ={0}^{0}, {\varsigma }_{0}=\frac{\pi }{4}$, b $\vartheta ={0}^{0}, {\varsigma }_{0}=\frac{3\pi }{4}$, c $\vartheta ={45}^{0}, {\varsigma }_{0}=\frac{\pi }{4}$, d $\vartheta ={45}^{0}, {\varsigma }_{0}=\frac{3\pi }{4}$ e $\vartheta ={90}^{0}, {\varsigma }_{0}=\frac{\pi }{4}$, f $\vartheta ={90}^{0}, {\varsigma }_{0}=\frac{3\pi }{4}$ g $\vartheta ={135}^{0}, {\varsigma }_{0}=\frac{\pi }{4}$, h $\vartheta ={135}^{0}, {\varsigma }_{0}=\frac{3\pi }{4}$, i $\vartheta ={180}^{0}, {\varsigma }_{0}=\frac{\pi }{4}$, j $\vartheta ={180}^{0}, {\varsigma }_{0}=\frac{3\pi }{4}$, k $\vartheta ={225}^{0}, {\varsigma }_{0}=\frac{\pi }{4}$, l $\vartheta ={225}^{0}, {\varsigma }_{0}=\frac{3\pi }{4}$, m $\vartheta ={270}^{0}, {\varsigma }_{0}=\frac{\pi }{4}$, n $\vartheta ={270}^{0}, {\varsigma }_{0}=\frac{3\pi }{4}$, o $\vartheta ={315}^{0}, {\varsigma }_{0}=\frac{\pi }{4}$, p $\vartheta ={315}^{0}, {\varsigma }_{0}=\frac{3\pi }{4}$, q $\vartheta ={360}^{0}, {\varsigma }_{0}=\frac{\pi }{4}$, and r $\vartheta ={360}^{0}, {\varsigma }_{0}=\frac{3\pi }{4}$

5.4 Variation of fracture initiation pressure with $\boldsymbol{\alpha }$ and wellbore ellipticity

Using the field data in Table 2 to conduct a sensitivity study, the trend shows that the poroelastic model yields a lower bound of the fracture initiation pressure (Fig. 18), which has been generally observed with the model presented by Haimson and Fairhurst (1967), a reduced form of the model. Both the shape and rotation of the major axis of the ellipse, $\alpha$, influence the tensile failure orientation and its magnitude. The fracture initiation pressure for each case study is the minimum pressure value, as shown in the plots.

Fig. 18

Comparing the fracture initiation pressure predictions from the poroelastic solution with linear elastic model, using the field data from Well 9/23a-T2. The rotation angle of the wellbore axis and ellipticity index for each scenario are a$\alpha ={0}^{0}$, ${\varsigma }_{0}=\frac{\pi }{4}$ b $\alpha ={0}^{0}{\varsigma }_{0}=\frac{3\pi }{4}$, c$\alpha ={45}^{0}$, ${\varsigma }_{0}=\frac{\pi }{4}$ d $\alpha ={45}^{0}{\varsigma }_{0}=\frac{3\pi }{4}$ e$\alpha ={90}^{0}$, ${\varsigma }_{0}=\frac{\pi }{4}$ f$\alpha =9{0}^{0}$,${\varsigma }_{0}=\frac{3\pi }{4}$, g $\alpha ={135}^{0}$, ${\varsigma }_{0}=\frac{\pi }{4}$ h$\alpha ={135}^{0}$, ${\varsigma }_{0}=\frac{3\pi }{4}$

From this data example, fracture initiation occurs in the direction of the maximum horizontal stress. Furthermore, this sensitivity study emphasizes the need to conduct numerical studies for each design or field scenario, and not make a general conclusion that could be dangerous and costly. Based on linear elastic assumption, we demonstrated that the tensile stability of a borehole generally reduces with increased ellipticity, especially when the maximum horizontal stress direction aligns with the orientation of the major axis of the ellipse. This finding agrees with the work of Scheldt et al. (2020). Nevertheless, when the direction of the maximum horizontal stress is not parallel to the orientation of the major axis, the tensile stability of the elliptical hole may be enhanced (Fig. 18c, e, g).

5.5 Variation of fracture initiation pressure with horizontal stress loading

The same field data, presented in Table 2, is used in this sensitivity study. The horizontal stresses and wellbore ellipticity index are varied in this analysis. We assumed $\alpha =90^\circ$. From Fig. 19 the elliptical hole becomes more stable than a near-circular wellbore as the horizontal stress difference increases. The orientation of fracture initiation remained unchanged as the stress difference increased. On the contrary, when the direction of the maximum horizontal stress aligns with the orientation of the major axis, the near-circular wellbore is seen to be more stable than an elliptical hole, for all the cases of stress difference tested in this analysis (Fig. 20). We only presented the first two pair cases in Fig. 20 since there was no significant change in the results when the stress ratio was 3.

Fig. 19

A sensitivity study, with Well 9/23a-T2 data, showing the variation of fracture initiation pressure with horizontal stress loading for a horizontal well. In this test $\alpha ={90}^{0}$ for a${S}_{H}=3750, {S}_{h}=3747.47, {\varsigma }_{0}=\frac{\pi }{4}$ b ${S}_{H}=3750, {S}_{h}=3747.47, {\varsigma }_{0}=\frac{3\pi }{4}$, c ${S}_{H}=5750, {S}_{h}=3747.47,{\varsigma }_{0}=\frac{\pi }{4}$ d ${S}_{H}=5750, {S}_{h}=3747.47, {\varsigma }_{0}=\frac{3\pi }{4}$ e ${S}_{H}=7750, {S}_{h}=3747.47,{\varsigma }_{0}=\frac{\pi }{4}$ f ${S}_{H}=7750, {S}_{h}=3747.47, {\varsigma }_{0}=\frac{3\pi }{4}$

Fig. 20

A sensitivity study, with Well 9/23a-T2 data, showing the variation of fracture initiation pressure with horizontal stress loading for a horizontal well. In this test $\alpha ={0}^{0}$ for a ${S}_{H}=3750, {S}_{h}=3747.47, {\varsigma }_{0}=\frac{\pi }{4}$ b ${S}_{H}=3750, {S}_{h}=3747.47, {\varsigma }_{0}=\frac{3\pi }{4}$, c ${S}_{H}=5750, {S}_{h}=3747.47,{\varsigma }_{0}=\frac{\pi }{4}$ d ${S}_{H}=5750, {S}_{h}=3747.47, {\varsigma }_{0}=\frac{3\pi }{4}$

In the same vein, for a vertical well the same pattern or trend was observed (Fig. 21); the elliptical hole is more stable as the stress difference increases. When there is almost an isotropic horizontal loading, fracture initiation is seen to occur at any orientation around the near-circular wellbore (Fig. 21b). But for an elliptical hole, the fracture initiation aligns with the direction of the maximum horizontal stress (Fig. 21a).

Fig. 21

A sensitivity study, with Well 9/23a-T2 data, showing the variation of fracture initiation pressure with horizontal stress loading for a vertical well. In this test $\alpha ={90}^{0}$ for a ${S}_{H}=3750, {S}_{h}=3747.47, {\varsigma }_{0}=\frac{\pi }{4}$ (b) ${S}_{H}=3750, {S}_{h}=3747.47, {\varsigma }_{0}=\frac{3\pi }{4}$, c ${S}_{H}=5750, {S}_{h}=3747.47,{\varsigma }_{0}=\frac{\pi }{4}$ d ${S}_{H}=5750, {S}_{h}=3747.47, {\varsigma }_{0}=\frac{3\pi }{4}$ (e)${S}_{H}=7750, {S}_{h}=3747.47,{\varsigma }_{0}=\frac{\pi }{4}$ f ${S}_{H}=7750, {S}_{h}=3747.47, {\varsigma }_{0}=\frac{3\pi }{4}$

5.6 Variation of fracture initiation pressure with wellbore inclination and azimuthal angles

Using the data for Well 9/23a-T2 presented in Table 2, we assessed the variation of fracture initiation pressure with well azimuthal angle for low, medium, and high inclination angles. The general observation from this study is that the near-circular wellbore is more stable than an elliptical borehole. Nevertheless, there are several combinations of well inclination and azimuthal angles that could make an elliptical borehole have a higher fracture initiation pressure than a near-circular wellbore (Figs. 22, 23, 24).

Fig. 22

A sensitivity study, with Well 9/23a-T2 data, showing the variation of fracture initiation pressure with well azimuthal angle, $\vartheta$. The well inclination for this test is ${10}^{0}$, when the azimuthal angle is a $\vartheta ={0}^{0}, {\varsigma }_{0}=\frac{\pi }{4}$, b $\vartheta ={0}^{0}, {\varsigma }_{0}=\frac{3\pi }{4}$, c $\vartheta ={45}^{0}, {\varsigma }_{0}=\frac{\pi }{4}$, (d)$\vartheta ={45}^{0}, {\varsigma }_{0}=\frac{3\pi }{4}$(e)$\vartheta ={90}^{0}, {\varsigma }_{0}=\frac{\pi }{4}$, (f)$\vartheta ={90}^{0}, {\varsigma }_{0}=\frac{3\pi }{4}$ g $\vartheta ={135}^{0}, {\varsigma }_{0}=\frac{\pi }{4}$, h $\vartheta ={135}^{0}, {\varsigma }_{0}=\frac{3\pi }{4}$, i $\vartheta ={180}^{0}, {\varsigma }_{0}=\frac{\pi }{4}$, j $\vartheta ={180}^{0}, {\varsigma }_{0}=\frac{3\pi }{4}$, k $\vartheta ={225}^{0}, {\varsigma }_{0}=\frac{\pi }{4}$, l $\vartheta ={225}^{0}, {\varsigma }_{0}=\frac{3\pi }{4}$, (m)$\vartheta ={270}^{0}, {\varsigma }_{0}=\frac{\pi }{4}$, n $\vartheta ={270}^{0}, {\varsigma }_{0}=\frac{3\pi }{4}$, o $\vartheta ={315}^{0}, {\varsigma }_{0}=\frac{\pi }{4}$, p$\boldsymbol{ }\vartheta ={315}^{0}, {\varsigma }_{0}=\frac{3\pi }{4}$, q $\vartheta ={360}^{0}, {\varsigma }_{0}=\frac{\pi }{4}$, and (r) $\vartheta ={360}^{0}, {\varsigma }_{0}=\frac{3\pi }{4}$

Fig. 23

A sensitivity study, with Well 9/23a-T2 data, showing the variation of fracture initiation pressure with well azimuthal angle, $\vartheta$. The well inclination for this test is ${50}^{0}$, when the azimuthal angle is a $\vartheta ={0}^{0}, {\varsigma }_{0}=\frac{\pi }{4}$, b $\vartheta ={0}^{0}, {\varsigma }_{0}=\frac{3\pi }{4}$, c $\vartheta ={45}^{0}, {\varsigma }_{0}=\frac{\pi }{4}$, d $\vartheta ={45}^{0}, {\varsigma }_{0}=\frac{3\pi }{4}$(e)$\vartheta ={90}^{0}, {\varsigma }_{0}=\frac{\pi }{4}$, f $\vartheta ={90}^{0}, {\varsigma }_{0}=\frac{3\pi }{4}$(g)$\vartheta ={135}^{0}, {\varsigma }_{0}=\frac{\pi }{4}$, h $\vartheta ={135}^{0}, {\varsigma }_{0}=\frac{3\pi }{4}$, i $\vartheta ={180}^{0}, {\varsigma }_{0}=\frac{\pi }{4}$, j $\vartheta ={180}^{0}, {\varsigma }_{0}=\frac{3\pi }{4}$, k $\vartheta ={225}^{0}, {\varsigma }_{0}=\frac{\pi }{4}$, l $\vartheta ={225}^{0}, {\varsigma }_{0}=\frac{3\pi }{4}$, m $\vartheta ={270}^{0}, {\varsigma }_{0}=\frac{\pi }{4}$, n $\vartheta ={270}^{0}, {\varsigma }_{0}=\frac{3\pi }{4}$, o $\vartheta ={315}^{0}, {\varsigma }_{0}=\frac{\pi }{4}$, p$\vartheta ={315}^{0}, {\varsigma }_{0}=\frac{3\pi }{4}$, q $\vartheta ={360}^{0}, {\varsigma }_{0}=\frac{\pi }{4}$, and r $\vartheta ={360}^{0}, {\varsigma }_{0}=\frac{3\pi }{4}$

Fig. 24

A sensitivity study, with Well 9/23a-T2 data, showing the variation of fracture initiation pressure with well azimuthal angle, $\vartheta$. The well inclination for this test is ${90}^{0}$, when the azimuthal angle is a $\vartheta ={0}^{0}, {\varsigma }_{0}=\frac{\pi }{4}$, b$\vartheta ={0}^{0}, {\varsigma }_{0}=\frac{3\pi }{4}$, c $\vartheta ={45}^{0}, {\varsigma }_{0}=\frac{\pi }{4}$, d $\vartheta ={45}^{0}, {\varsigma }_{0}=\frac{3\pi }{4}$ e$\vartheta ={90}^{0}, {\varsigma }_{0}=\frac{\pi }{4}$, f$\vartheta ={90}^{0}, {\varsigma }_{0}=\frac{3\pi }{4}$ g $\vartheta ={135}^{0}, {\varsigma }_{0}=\frac{\pi }{4}$, h $\vartheta ={135}^{0}, {\varsigma }_{0}=\frac{3\pi }{4}$, i $\vartheta ={180}^{0}, {\varsigma }_{0}=\frac{\pi }{4}$, j $\vartheta ={180}^{0}, {\varsigma }_{0}=\frac{3\pi }{4}$, k $\vartheta ={225}^{0}, {\varsigma }_{0}=\frac{\pi }{4}$, l $\vartheta ={225}^{0}, {\varsigma }_{0}=\frac{3\pi }{4}$, m $\vartheta ={270}^{0}, {\varsigma }_{0}=\frac{\pi }{4}$, n $\vartheta ={270}^{0}, {\varsigma }_{0}=\frac{3\pi }{4}$, o $\vartheta ={315}^{0}, {\varsigma }_{0}=\frac{\pi }{4}$, p $\vartheta ={315}^{0}, {\varsigma }_{0}=\frac{3\pi }{4}$, q $\vartheta ={360}^{0}, {\varsigma }_{0}=\frac{\pi }{4}$, and r $\vartheta ={360}^{0}, {\varsigma }_{0}=\frac{3\pi }{4}$

6 Conclusions

A set of equations describing the stress concentrations around an elliptically shaped and highly inclined wellbore has been presented in this paper. When the ellipticity parameter, governing the shape of the wellbore, is adjusted such that the shape of the wellbore becomes almost/fully circular, the predicted stress concentrations agree very well with the known Kirsch solutions. Subsequently, the proposed equations were validated by investigating the shear and tensile stabilities of elliptical and near-circular wellbores from the field and laboratory experiments. From this study, the following key conclusions are drawn.

• 1. As the elliptical hole becomes narrower, the hoop stress at the orientation of the major axis of the ellipse increases, which agrees with experimental results and other numerical and analytical observations. Though both near-circular and elliptical boreholes experience catastrophic shear failure for some combinations of well inclination and azimuthal angles (especially medium inclination angles), such failures are more common with elliptical holes. Furthermore, With increased horizontal stress difference, the shear stability of an elliptical borehole reduces while its tensile stability increases, provided the orientation of the maximum horizontal stress is perpendicular to the orientation of the major axis of the ellipse. On the other hand, when the orientation of the maximum horizontal stress aligns with the orientation of the major axis, the near-circular (or circular) borehole becomes more stable.

• 2. A near-circular wellbore is more stable than elliptical borehole in both shear and tension. Nevertheless, we were able to show quantitatively that an elliptical borehole can have more shear and tensile stabilities than a near-circular wellbore for some well inclination and azimuthal angles. The shear stability of the elliptical wellbore is enhanced when the direction of the maximum horizontal stress aligns with the orientation of the major axis. On the contrary, the tensile stability of an elliptical borehole worsens when the direction of the maximum horizontal stress is parallel to the orientation of the major axis.

• 3. From this study, we were able to discover that Kirsch solution can still be used for some elliptical-shaped wellbores, with very minimal error, for as long as the ellipticity index is greater than $\frac{\pi }{2}$, i.e., the ratio of the minor to major axis should be greater than 0.92. This threshold was not determined by a rigorous mathematical process, but by a trial-by-error.

• 4. The commonly used shear failure criteria predict the onset of failure or yielding of the borehole. In essence, the shear failure criteria will perform well in predicting the onset of failure for both brittle and ductile rocks. For brittle rocks, the yielding and ultimate collapse pressure is almost the same, as yielding is not pronounced. But for ductile formations, the yielding is pronounced, and the ultimate collapse pressure can be significantly different from the yielding pressure. Out of the five commonly used shear failure criteria for wellbore stability analysis—Mohr–Coulomb, Mogi-Coulomb, Modified Lade, Druger Prager (Inscribed), and Druger Prager (Circumscribed), we observed that both Mohr–Coulomb and Drucker Prager (inscribed) failure criteria predicted higher collapse pressures, relative to the rest. Thus, affirming the generally observed performances of these criteria.

• 5. The fracture initiation pressure predicted from the poroelastic model is always lower than the linear elastic model. In addition, the tensile stability of a highly inclined elliptical borehole may be enhanced when the direction of the maximum horizontal stress does not align with the orientation of the major axis of the ellipse.

Appendix A: Derivation of stress concentrations around an elliptical borehole

Consider a wellbore inclined with respect to the cartesian coordinate system ${X}^{\prime}, {Y}^{\prime},{Z}^{\prime}$ as shown in Fig. 

Fig. 25

A representation of an inclined wellbore in an isotropic formation where ${S}_{v}, {S}_{H}, {S}_{h}$ are the in-situ stresses

25 below. For generality, the in-situ maximum horizontal stress is oriented in a direction that is ${\vartheta }_{0}$ from ${X}^{\prime}-$ axis. The in-situ stresses can be transformed to local coordinate system $\overline{x },\overline{y },\overline{z }$ through the tensor transformation relation ${\sigma }_{ij}={Q}_{mi}{Q}_{nj}{S}_{mn}$, where ${Q}_{mi}$ is the cosines matrix of the coordinate axes of the reference frame with respect to the local axis to the wellbore, ${S}_{mn}$ are the in-situ stresses, and ${\sigma }_{ij}$ are the transformed stresses.

The z-axis of the local system coincides with the wellbore axis. The directions of the transformed stress components depend on the wellbore inclination angle (from vertical), $\gamma ,$ azimuthal angle referenced from the orientation of maximum horizontal stress, and the wellbore position from the x-axis, $\theta$.

The effective in-situ stress ${\sigma }_{xx}^{\prime}$ is oriented at an arbitrary angle $\alpha$ with the x-axis as shown in Fig. 

Fig. 26

A schematic representation of the cross section of the wellbore and the transformed effective in-situ stresses in wellbore local cartesian coordinates. The stresses around the wellbore azimuth are represented using elliptical coordinate system $(\zeta , \eta$)

26. The ellipticity parameter at the wellbore wall is ${\zeta }_{0}$.

The model development is based on the following assumptions:

• a. The formation matrix is homogeneous and isotropic.

• b. The rock behaves as a linearly elastic material.

• c. The deformations are small.

• d. The principal in-situ stresses do not align with the borehole axes.

• e. The complex potential functions are independent of origin. This indicates homogeneity and isotropy of the formation. The stresses and displacements will be periodic in $\eta$, for continuity of stress and displacement.

• f. Inside the elliptical cavity acts a fluid pressure, ${p}_{w}$, and no fluid transfer is assumed between the cavity and the host material body (the rock formation).

• g. The size of the hole is very small compared to the size of the linearly elastic material body; in fact, it is assumed infinite.

• h. Compressive stress is assumed to be positive while tensile stress is taken to be negative in this study.

The foregoing problem can be further decomposed into three (3) main subproblems, and since small deformations are assumed, the total stress components acting on the infinite material body is the linear superposition of the stresses from each subproblem. Hence, the complex potential functions will be determined for each of the subproblems.

Since the boundary of the hole is elliptical, an elliptical coordinate system is used for convenience. However, the Cartesian system is also employed because it is easy to visualize. The Cartesian system consists of orthogonal sets of straight lines $x={\text{const}}.$ and $y={\text{const}}$, while the elliptical coordinate system consists of the set of confocal ellipses and confocal hyperbolae. At every point $(\zeta ,\eta )$ the intersecting ellipse and hyperbola are orthogonal. And along an elliptical boundary, $\eta$ ranges from ${0}^{0}$ to ${90}^{0}$ (from $+x$ axis to $+y$ axis). Along a hyperbola, $\zeta$ ranges from 0 at the intersection with the major axis of the ellipse to infinity.

As shown by Stevenson (1945), the stress transformation from cartesian plane to an elliptical coordinate system, for a porous solid, is derived as

$${\upsigma }_{\varsigma \varsigma }^{\prime}+{\upsigma }_{\eta \eta }^{\prime}={\upsigma }_{xx}^{\prime}+{\upsigma }_{yy}^{\prime}$$

(A.1)

$${\upsigma }_{\eta \eta }^{\prime}-{\upsigma }_{\varsigma \varsigma }^{\prime}+2i{\sigma }_{\varsigma \eta }={e}^{i2\alpha }\left({\upsigma }_{yy}^{\prime}-{\upsigma }_{xx}^{\prime}+i2{\sigma }_{xy}\right)$$

(A.2)

and the elliptic coordinates $\zeta , \eta$ are defined by

$$Z=f{\text{cosh}}\xi$$

(A.3)

$$\xi =\zeta +i\eta$$

(A.4)

$$\overline{\xi }=\zeta -i\eta$$

(A.5)

$$\left.\begin{array}{l}\frac{dZ}{d\xi }=fsinh\xi \\ Z\frac{d\xi }{dZ}=coth\xi \end{array}\right\}$$

(A.6)

Choosing complex potential functions, ($\Omega , \varpi ),$ that give single-valued displacement function or dislocation type at most. Hence, Stevenson (1945) showed that equations (A.1) and (A.2) can be re-written as

$${\upsigma }_{\varsigma \varsigma }^{\prime}+{\upsigma }_{\eta \eta }^{\prime}=\frac{1}{2}\left\{{\Omega }^{\prime}(Z)+{\overline{\Omega } }^{\prime}(\overline{Z })\right\}$$

(A.7)

$${\upsigma }_{\eta \eta }^{\prime}-{\upsigma }_{\varsigma \varsigma }^{\prime}+i2{\sigma }_{\varsigma \eta }=-\frac{1}{2}\frac{d\xi }{dZ}\frac{d}{d\overline{\xi }}\left\{Z{\overline{\Omega } }^{\prime}(Z)+{\overline{\varpi } }^{\prime}(Z)\right\}$$

(A.8)

Noting that

$$\frac{d\xi }{dZ}\frac{d\overline{Z}}{d\overline{\xi } }={e}^{-2i\alpha }$$

(A.9)

where $\overline{Z }$ is the complex conjugate of $Z$, and $\overline{\xi }$, the complex conjugate of $\xi$. Hence, summing equations (A.7) and (A.8) yields

$$4\left({\upsigma }_{\varsigma \varsigma }^{\prime}+{\upsigma }_{\eta \eta }^{\prime}\right)=\left\{\Omega ^{\prime}(Z)+\overline{\Omega }^{\prime}(\overline{Z })-\frac{d\xi }{dZ}\frac{d}{d\overline{\xi }}\left(Z\overline{\Omega }^{\prime}(Z)+\overline{\varpi }^{\prime}(Z)\right)\right\}$$

(A.10)

And by substituting Eq. (A.6) into Eq. (A.10) yields

$$4\left({\upsigma }_{\varsigma \varsigma }^{\prime}-i{\sigma }_{\varsigma \eta }\right)={\Omega }^{\prime}(Z)+{\overline{\Omega } }^{\prime}(\overline{Z })-\frac{d{\Omega }^{\prime}(Z)}{d\xi }{\text{coth}}\overline{\xi }-\frac{1}{f}\frac{d{\overline{\varpi } }^{\prime}(Z)}{d\xi }{\text{cosech}}\overline{\xi }$$

(A.11)

The advantages of this method over the use of Airy stress function include the ease of making a rapid change from one set of an orthogonal coordinate systems to another, and thus, provides an operation that does not involve the solution of new differential equations when the coordinates are transformed. Although it is well known that 2-D plane strain isotropic elasticity problems can be solved using the complex variable function, points of application of force corresponding to poles and logarithmic singularities of these functions, though conserved in conformal mappings, these mappings lack good correspondence, as they do not transform a traction-free boundary into a traction-free boundary, for example. Though this limitation has restricted the use of complex functions to the study of isolated nuclei of strain, the strength of the complex variable method used in this work is such that it overcomes these drawbacks (Fig. 

Fig. 27

A schematic representation of the associated subproblems in Subproblem-1

27).

1.1 Sub-problem-1

In this subproblem, only the normal stresses in the plane $x-y$ and the in-plane shear stress act throughout the infinite material plate, while the wellbore pressure act in the cavity. A plane strain assumption is imposed for this subproblem. The in-situ anti-plane shear stresses and vertical stresses are disregarded. However, using the superposition theorem, sub-problem-1 is further divided into three, as shown in Eq. (A.6).

2.1.1.1 Sub-Problem-1.1.1. In this subproblem, only the transformed effective in-situ stress ${\sigma }_{xx}^{\prime}$ is acting throughout the infinite plate and there is no pressure acting in the cavity/hole. As mentioned earlier, the in-situ effective stress is oriented at an arbitrary angle $\alpha$ with the x-axis. This problem, which was first solved by Inglis (1913)) using the Airy stress functions, has been addressed by other authors as well. Stevenson (1945) and Maugis (1992)) used complex potential functions based on an elliptical coordinate system, and Muskhelishvili (1963) used the conformal mapping method.

The complex potential functions derived by Stevenson (1945) were

$$\Omega \left(Z\right)={\sigma }_{xx}^{\prime}f\left\{{e}^{2{\varsigma }_{0}}\mathit{cos}2\alpha \mathit{cos}h\xi +\left(1-{e}^{2{\varsigma }_{0}+i2\alpha }\right)\mathit{sin}h\xi \right\}$$

(A.12a)

$$\varpi (Z)=-{\sigma }_{xx}^{\prime}{f}^{2}\left\{\left(\mathit{cos}h2{\varsigma }_{0}-\mathit{cos}2\alpha \right)\xi +\frac{1}{2}{e}^{2{\varsigma }_{0}}\mathit{cos}h2\left(\xi -{\varsigma }_{0}-i\alpha \right)\right\}$$

(A.12a)

These potential functions have been observed by Maugis (1992)) to yield the correct stresses but give rise to unwanted rotation at infinity. Nevertheless, they have been used in this work, as the focus is not on the displacements around the hole, but the stresses.

Therefore, substituting the complex potential functions in Eq. (A.12) and their derivatives into Eq. (A.11) and noting that along $\zeta ={\zeta }_{0}$, $\xi ={\zeta }_{0}+i\eta$, $\overline{\xi }={\zeta }_{0}-i\eta$. It thus implies that, $2\overline{\xi }={2\zeta }_{0}-\xi$. Hence, the stress relations in Eq. (A.11) for subproblem 1.1.1 becomes

$$4\left({\sigma }_{\varsigma \varsigma }^{(\mathrm{1,1},1)^{\prime}}-i{\sigma }_{\varsigma \eta }^{\mathrm{1,1},1}\right)=\left[\begin{array}{l}{\sigma }_{xx}^{\prime}\left\{{e}^{2{\varsigma }_{0}}\mathit{cos}2\alpha +\left(1-{e}^{2{\varsigma }_{0}+i2\alpha }\right)\mathit{cot}h\xi \right\}\\ +{\sigma }_{xx}^{\prime}\left\{{e}^{2{\varsigma }_{0}}\mathit{cos}2\alpha +\left(1-{e}^{2{\varsigma }_{0}-i2\alpha }\right)\mathit{cot}h\left(2{\varsigma }_{0}-\xi \right)\right\}\\ +{\sigma }_{xx}^{\prime}\mathit{cot}h\left(2{\varsigma }_{0}-\xi \right)\left\{\left(1-{e}^{2{\varsigma }_{0}+i2\alpha }\right){\mathit{cosec}h}^{2}\xi \right\}\\ +{\sigma }_{xx}^{\prime}\mathit{cosec}h\left(2{\varsigma }_{0}-\xi \right)\left\{\begin{array}{l}-\left(\mathit{cos}h2{\varsigma }_{0}-\mathit{cos}2\alpha \right)\mathit{cot}h\xi \mathit{cosec}h\xi \\ +2{e}^{2{\varsigma }_{0}}\mathit{cos}h2\left(\xi -{\varsigma }_{0}-i\alpha \right)\mathit{cosec}h\xi \\ -{e}^{2{\varsigma }_{0}}\mathit{cot}h\xi \mathit{cosec}h\xi \mathit{sin}h2\left(\xi -{\varsigma }_{0}-i\alpha \right)\end{array}\right\}\end{array}\right]$$

(A.13)

And,

$${\sigma }_{\varsigma \varsigma }^{(\mathrm{1,1},1)^{\prime}}+{\sigma }_{\eta \eta }^{(\mathrm{1,1},1)^{\prime}}=\frac{1}{2}\left\{{\Omega }^{\prime}(Z)+{\overline{\Omega } }^{\prime}(\overline{Z })\right\}={\text{Re}}\left\{{\Omega }^{\prime}(Z)\right\}$$

(A.14)

For stability analysis, the states of the stresses at the wellbore wall are of prime interest, hence, the hoop stress at the wellbore wall is determined as

$${\left.{\sigma }_{\eta \eta }^{(\mathrm{1,1},1)^{\prime}}\right|}_{{\varsigma }_{0}}={\sigma }_{xx}^{\prime}\left\{\frac{{\text{sinh}}2{\varsigma }_{0}+{\text{cos}}2\alpha -{e}^{2{\varsigma }_{0}}{\text{cos}}2\left(\alpha -\eta \right)}{{\text{cosh}}2{\varsigma }_{0}-{\text{cos}}2\eta }\right\}$$

(A.15)

2.1.1.2 Sub-Problem-1.1.2

Like subproblem-1.1.1, only the transformed in-situ stress ${\sigma }_{yy}^{\prime}$ is acting throughout the infinite material body and the wellbore pressure is also disregarded. By choosing the same potential functions in Eq. (A.12) and following the same procedure as shown in subproblem-1.1.1, the stress relations for this subproblem becomes

$$\begin{array}{l}4\left({\sigma }_{\varsigma \varsigma }^{(\mathrm{1,1},2)^{\prime}}-i{\sigma }_{\varsigma \eta }^{\mathrm{1,1},2}\right)=\left[\begin{array}{l}{\sigma }_{yy}^{\prime}\left\{{e}^{2{\varsigma }_{0}}{\text{cos}}2\beta +\left(1-{e}^{2{\varsigma }_{0}+i2\beta }\right){\text{coth}}\xi \right\}\\ +{\sigma }_{yy}^{\prime}\left\{{e}^{2{\varsigma }_{0}}{\text{cos}}2\beta +\left(1-{e}^{2{\varsigma }_{0}-i2\beta }\right){\text{coth}}\left(2{\varsigma }_{0}-\xi \right)\right\}\\ +{\sigma }_{yy}^{\prime}coth\left(2{\varsigma }_{0}-\xi \right)\left\{\left(1-{e}^{2{\varsigma }_{0}+i2\beta }\right){{\text{cosech}}}^{2}\xi \right\}\\ +{\sigma }_{yy}^{\prime}cosech\left(2{\varsigma }_{0}-\xi \right)\left\{\begin{array}{l}-\left({\text{cosh}}2{\varsigma }_{0}-{\text{cos}}2\beta \right)coth\xi cosech\xi \\ +2{e}^{2{\varsigma }_{0}}cosh2\left(\xi -{\varsigma }_{0}-i\beta \right)cosech\xi \\ -{e}^{2{\varsigma }_{0}}coth\xi cosech\xi sinh2\left(\xi -{\varsigma }_{0}-i\beta \right)\end{array}\right\}\end{array}\right]\\ \end{array}$$

(A.16)

where $\beta =\alpha +\frac{\pi }{2}$. Thus, the effective hoop stress at the wellbore wall is

$${\left.{\sigma }_{\eta \eta }^{(\mathrm{1,1},2)^{\prime}}\right|}_{{\varsigma }_{0}}={\sigma }_{yy}^{\prime}\left\{\frac{{\text{sinh}}2{\varsigma }_{0}+{\text{cos}}2\left(\alpha +\frac{\pi }{2}\right)-{e}^{2{\varsigma }_{0}}{\text{cos}}2\left(\alpha +\frac{\pi }{2}-\eta \right)}{{\text{cosh}}2{\varsigma }_{0}-{\text{cos}}2\eta }\right\}$$

(A.17)

1.1.1 Sub-problem-1.2

In this case, only the transformed in-situ in-plane stress ${\sigma }_{xy}$ is acting throughout the infinite material body. As shown in Fig. 25, the induced stress concentrations as a result of the action of the in-plane shear stress can be found by the superposition of tensile and compressive loadings, acting at infinity.

Similar potential functions given in Eq. (A.12) are also selected in this subproblem. And following the same procedure as shown in subproblem-1.1.1, the stress relations for this subproblem is

$$4\left({\sigma }_{\varsigma \varsigma }^{(\mathrm{1,2},1)^{\prime}}-i{\sigma }_{\varsigma \eta }^{\mathrm{1,2},1}\right)=\left[\begin{array}{l}{\sigma }_{xy}\left\{{e}^{2{\varsigma }_{0}}\mathit{cos}\left(\frac{\pi }{2}+2\alpha \right)+\left(1-{e}^{2{\varsigma }_{0}+i\left(\frac{\pi }{2}+2\alpha \right)}\right)\mathit{cot}h\xi \right\}\\ +{\sigma }_{xy}\left\{{e}^{2{\varsigma }_{0}}\mathit{cos}\left(\frac{\pi }{2}+2\alpha \right)+\left(1-{e}^{2{\varsigma }_{0}-i\left(\frac{\pi }{2}+2\alpha \right)}\right)\mathit{cot}h\left(2{\varsigma }_{0}-\xi \right)\right\}\\ +{\sigma }_{xy}\mathit{cot}h\left(2{\varsigma }_{0}-\xi \right)\left\{\left(1-{e}^{2{\varsigma }_{0}+i\left(\frac{\pi }{2}+2\alpha \right)}\right){\mathit{cosec}h}^{2}\xi \right\}\\ +{\sigma }_{xy}\mathit{cosec}h\left(2{\varsigma }_{0}-\xi \right)\left\{\begin{array}{l}-\left(\mathit{cos}h2{\varsigma }_{0}-\mathit{cos}\left(\frac{\pi }{2}+2\alpha \right)\right)\mathit{cot}h\xi \mathit{cosec}h\xi \\ +2{e}^{2{\varsigma }_{0}}\mathit{cos}h2\left(\xi -{\varsigma }_{0}-i\left(\frac{\pi }{4}+\alpha \right)\right)\mathit{cosec}h\xi \\ -{e}^{2{\varsigma }_{0}}\mathit{cot}h\xi \mathit{cosec}h\xi \mathit{sin}h2\left(\xi -{\varsigma }_{0}-i\left(\frac{\pi }{4}+\alpha \right)\right)\end{array}\right\}\end{array}\right]$$

(A.18)

And the hoop stress at the wellbore wall, as a result of this loading, is derived as

$${\left.{\sigma }_{\eta \eta }^{(\mathrm{1,2},1)^{\prime}}\right|}_{{\varsigma }_{0}}={\sigma }_{xy}\left\{\frac{{\text{sinh}}2{\varsigma }_{0}+{\text{cos}}\left(\pi /2+2\alpha \right)-{e}^{2{\varsigma }_{0}}{\text{sin}}2\eta }{{\text{cosh}}2{\varsigma }_{0}-{\text{cos}}2\eta }\right\}$$

(A.19)

1.1.1.1 Sub-problem-1.2.2

Similarly, when a tensile load, $-{\sigma }_{xy}$, is applied at infinity to the material body, at an angle of $3\frac{\pi }{4}$ from the major axis of the ellipse.

In the same vein, using the same form of potential functions in Eq. (A.12), the stress relation for Subproblem-1.2.2 is

$$\begin{array}{l}4\left({\sigma }_{\varsigma \varsigma }^{(\mathrm{1,2},2)^{\prime}}-i{\sigma }_{\varsigma \eta }^{\mathrm{1,2},2}\right)=-\left[\begin{array}{l}{\sigma }_{xy}\left\{{e}^{2{\varsigma }_{0}}{\text{cos}}\left(3\pi /2+2\alpha \right)+\left(1-{e}^{2{\varsigma }_{0}+i\left(3\pi /2+2\alpha \right)}\right){\text{coth}}\xi \right\}\\ +{\sigma }_{xy}\left\{{e}^{2{\varsigma }_{0}}{\text{cos}}\left(3\pi /2+2\alpha \right)+\left(1-{e}^{2{\varsigma }_{0}-i\left(3\pi /2+2\alpha \right)}\right){\text{coth}}\left(2{\varsigma }_{0}-\xi \right)\right\}\\ +{\sigma }_{xy}coth\left(2{\varsigma }_{0}-\xi \right)\left\{\left(1-{e}^{2{\varsigma }_{0}+i\left(3\pi /2+2\alpha \right)}\right){{\text{cosech}}}^{2}\xi \right\}\\ +{\sigma }_{xy}cosech\left(2{\varsigma }_{0}-\xi \right)\left\{\begin{array}{l}-\left({\text{cosh}}2{\varsigma }_{0}-{\text{cos}}\left(3\pi /2+2\alpha \right)\right)coth\xi cosech\xi \\ +2{e}^{2{\varsigma }_{0}}cosh2\left(\xi -{\varsigma }_{0}-i\left(3\pi /4+\alpha \right)\right)cosech\xi \\ -{e}^{2{\varsigma }_{0}}coth\xi cosech\xi sinh2\left(\xi -{\varsigma }_{0}-i\left(3\pi /4+\alpha \right)\right)\end{array}\right\}\end{array}\right]\\ \end{array}$$

(A.20)

And the hoop stress at the wellbore wall, as a result of this loading, is derived as

$${\left.{\sigma }_{\eta \eta }^{(\mathrm{1,2},2)^{\prime}}\right|}_{{\varsigma }_{0}}=-{\sigma }_{xy}\left\{\frac{{\text{sinh}}2{\varsigma }_{0}+{\text{cos}}\left(3\pi /2+2\alpha \right)+{e}^{2{\varsigma }_{0}}{\text{sin}}2\eta }{{\text{cosh}}2{\varsigma }_{0}-{\text{cos}}2\eta }\right\}$$

(A.21)

1.1.2 Sub-problem-1.3

Estimating the stress concentrations induced by the action of a uniform normal pressure on the boundary of a hole, with no remote loading on the infinite plate, has received interest from some authors, including Jeffery (1921), Lekhnitskii (1968), Pollard (1973), amongst others. A different solution method is presented in this paper, which does not violate the rule of an equivalent system. To determine the corresponding stress concentrations induced by the applied pressure at the cavity wall, an equivalent system is proposed. In Subproblem-1.3.1, a compressive hydrostatic pressure is applied throughout a fictitious material body, without the hole. While in Subproblem-1.3.2, a tensile hydrostatic stress, of the same magnitude, is applied at infinity throughout the material, but there is no traction at the boundary of the hole.

1.1.2.1 Sub-problem-1.3.1

Without the hole, the subproblem is exactly like an isotropic rock under isotropic compression. The associated boundary conditions are as follows

1.1.2.2 First boundary condition

At the fictitious hole wall, the effective stress is

$${\sigma }_{\zeta \zeta }^{(\mathrm{1,3},1)^{\prime}}\left({\varsigma }_{0},\eta \right)=\Delta {p}_{w} {\sigma }_{\zeta \eta }^{\mathrm{1,31}}\left({\varsigma }_{0},\eta \right)=0,$$

1.1.2.3 Second boundary condition

At infinity,

$${\sigma }_{\zeta \zeta }^{(\mathrm{1,3},1)^{\prime}}\left(\zeta \to \infty , \eta \right)=\Delta {p}_{w}, {\sigma }_{\zeta \eta }^{\mathrm{1,3},1}\left(\zeta \to \infty ,\eta \right)=0$$

This is a simple case of a uniformly loaded linearly elastic material body. Throughout the material, the effective stress magnitude is $\Delta {p}_{w}$. Hence, at the imaginary hole boundary, the effective hoop stress is $\Delta {p}_{w}.$

1.1.2.4 Sub-Problem-1.3.2

This is a similar problem to combined Subproblems 1.1.1 and 1.1.2 and the same potential functions, Eq. (A.12), are selected for this subproblem.

First Boundary Condition:

$${\sigma }_{\zeta \zeta }^{(\mathrm{1,3},2)^{\prime}}\left({\varsigma }_{0},\eta \right)=0, {\sigma }_{\zeta \eta }^{\mathrm{1,3},2}\left({\varsigma }_{0},\eta \right)=0,$$

Second Boundary Condition:

At infinity, the effective stresses are

$${\sigma }_{\zeta \zeta }^{(\mathrm{1,3},2)^{\prime}}\left(\zeta \to \infty , \eta \right)=-\Delta {p}_{w}, {\sigma }_{\zeta \eta }^{\mathrm{1,3},2}\left(\zeta \to \infty ,\eta \right)=0$$

In the same vein, using the same form of potential functions in Eq. (A.12), the stress relation for Subproblem-1.3.2 is derived thus

$$\begin{array}{l}4\left({\sigma }_{\varsigma \varsigma }^{(\mathrm{1,3},2)^{\prime}}-i{\sigma }_{\varsigma \eta }^{\mathrm{1,3},2}\right)=-\Delta {p}_{w}\left[\begin{array}{l}\left\{-{e}^{2{\varsigma }_{0}}{\text{sin}}2\alpha +\left(2-{e}^{2{\varsigma }_{0}+i2\alpha }\left({e}^{\pi }+1\right)\right){\text{coth}}\xi \right\}\\ +\left\{-{e}^{2{\varsigma }_{0}}{\text{sin}}2\alpha +\left(2-{e}^{2{\varsigma }_{0}-i2\alpha }\left({e}^{\pi }+1\right)\right){\text{coth}}\left(2{\varsigma }_{0}-\xi \right)\right\}\\ +coth\left(2{\varsigma }_{0}-\xi \right)\left\{\left(2-{e}^{2{\varsigma }_{0}+i2\alpha }\left({e}^{\pi }+1\right)\right){{\text{cosech}}}^{2}\xi \right\}\\ +cosech\left(2{\varsigma }_{0}-\xi \right)\left\{\begin{array}{l}-\left({\text{cosh}}2{\varsigma }_{0}+{\text{sin}}2\alpha \right)coth\xi cosech\xi \\ +2{e}^{2{\varsigma }_{0}}\left(\begin{array}{l}cosh2\left(\xi -{\varsigma }_{0}-i\alpha \right)\\ +cosh2\left(\xi -{\varsigma }_{0}-i\beta \right)\end{array}\right)cosech\xi \\ -{e}^{2{\varsigma }_{0}}coth\xi cosech\xi \left(\begin{array}{l}sinh2\left(\xi -{\varsigma }_{0}-i\beta \right)\\ +sinh2\left(\xi -{\varsigma }_{0}-i\alpha \right)\end{array}\right)\end{array}\right\}\\ \end{array}\right]\\ \end{array}$$

(A.22)

And the hoop stress at the wellbore wall, as a result of this loading is

$${\left.{\sigma }_{\eta \eta }^{(\mathrm{1,3},2)^{\prime}}\right|}_{{\varsigma }_{0}}=-{\Delta p}_{w}\left\{\frac{2{\text{sinh}}2{\varsigma }_{0}}{{\text{cosh}}2{\varsigma }_{0}-{\text{cos}}2\eta }\right\}$$

(A.23)

The internal pressure in the cavity causes tensile hoop stress that decays away from the wellbore wall, thus supporting Saint Venant’s principle. The mean normal stress and shear stress on the radial plane are zero everywhere.

The induced hoop stress around the borehole as it approaches a circular geometry becomes

$$\underset{{\varsigma }_{0}\to \infty }{{\text{lim}}}\left({\left.{\sigma }_{\eta \eta }^{(\mathrm{1,3},2)^{\prime}}\right|}_{{\varsigma }_{0}}+{\left.{\sigma }_{\eta \eta }^{(\mathrm{1,3},1)^{\prime}}\right|}_{{\varsigma }_{0}}\right)=-{\Delta p}_{w}$$

(A.24)

Equation (A.24) suggests that for a circular borehole, the wellbore pressure induces a constant tensile tangential stress, at the wellbore wall, which is independent of the wellbore orientation angle. On the other hand, for an elliptical wellbore geometry, the induced tensile tangential stress varies with the wellbore angle and wellbore ellipticity. This result is similar to what Aadnoy and Angell-Olsen (1995) observed in their investigation. As the complexity of the wellbore geometry deviates from a perfect circle, the complexity of the stress concentration becomes more glaring, and thus significantly impacts the stability analysis of the wellbore.

1.2 Sub-problem-2

In this subproblem, the stress concentrations around the elliptical wellbore under anti-plane shear loads are derived using the conformal mapping method. Induced stress concentrations around circular, elliptical, and arbitrary hole geometries under anti-plane shear loading have received the attention of many scientific investigators, especially in the mechanics of materials discipline. Some of the notable studies include the investigations by Luo and Wang (2009), Gong and Meguid (1992), Radaj and Zhang (1993), Guan and Li (2018), Lubarda (2015), and recently in the petroleum industry by Qi et al. (2018). Specific to this derivation is the arbitrariness of the elliptical hole orientation with respect to the borehole axis and the bi-directional loading of the shear stresses.

Sub-problem-2 is further decomposed into two subproblems—each of the anti-plane shear stresses is fictitiously applied at infinity (Fig. 

Fig. 28

Decomposing the subproblem-2 into two independent subproblems

28).

From Lubarda (2015), the combined hoop shear stress for the two subproblems is derived as

$${\sigma }_{\eta z}=\frac{\left(1+{\text{tanh}}{\varsigma }_{0}\right)}{\sqrt{{{\text{sin}}}^{2}\left(\eta \right)+{{\text{tanh}}}^{4}{\varsigma }_{0}{{\text{cos}}}^{2}\left(\eta \right)}}\left\{{\sigma }_{yz}{\text{cos}}\left(\eta +\alpha \right)-{\sigma }_{xz}{\text{sin}}\left(\eta +\alpha \right)\right\}$$

(A.25)

Equation (A.25) reduces to Kirsch’s solution for anti-plane shear stress when $k={\text{tanh}}{\zeta }_{0}=1.$

1.3 Sub-problem-3

Remember a plane strain assumption was made for subproblem 1. Therefore, the strain along the z-axis of the borehole is assumed to be zero. Hence, there is no axial displacement. From linear elastic constitutive relation between strain and stress

$${\upvarepsilon }_{ij}^{\prime}=\frac{1}{E}\left\{{\upsigma }_{ij}^{\prime}-v{\upsigma }_{kk}^{\prime}{\delta }_{ij}+v{\upsigma }_{ij}^{\prime}\right\}$$

(A.26)

By setting ${\varepsilon }_{zz}^{\prime}=0$, the resulting axial stress concentration becomes

$${\upsigma }_{zz}^{\prime}={{\text{S}}}_{zz}^{\prime}-v\left({\upsigma }_{xx}^{\prime}+{\upsigma }_{yy}^{\prime}\right)+v\left({\upsigma }_{\varsigma \varsigma }^{\prime}+{\upsigma }_{\eta \eta }^{\prime}\right)$$

(A.27)