1 Introduction

Shale gas, which refers to unconventional natural gas found within subsurface reservoirs dominated by organic-rich mudrocks (Zou et al. 2010), is widely distributed and holds significant development potential, positioning it as a suitable supplement and successor to conventional energy sources (Tang et al. 2011; Li et al. 2007). However, due to complex depositional environments and diagenesis, shale reservoirs typically exhibit low porosity (often below 10%), meager permeability (generally ranging from 0.1 to 0.00001 mD), and thus low gas production rates (Chen et al. 2011; Liang et al. 2011). Hydraulic fracturing is a key technique employed to enhance the effectiveness of gas recovery (Ciezobka et al. 2018; Long and Xu 2017; Xu et al. 2017). Principally, it involves injecting high-pressure fluids into the target reservoir to create numerous hydraulic fractures, thereby locally increasing reservoir porosity and thus permeability. This establishes a high-transmission seepage pathway for hydrocarbon recovery (Lecampion et al. 2018), ultimately increasing the production rate and cumulative mass of unconventional hydrocarbons. Shale gas reservoirs exhibit distinct lamellar characteristics in their structure and appearance—driven by their depositional mode. These laminations possess specific orientations, with limited cementation and low strength, making them the weakest feature within the shale matrix (Heng et al. 2021a). Consequently, hydraulic fractures may readily extend along these laminations, potentially redirecting their propagation relative to controls of the prevailing stress field and impacting the effectiveness of the hydraulic fracture (Hou et al. 2014; Al-Rbeawi 2017). Thus, comprehending the initiation, extension, and spatial distribution of hydraulic fractures in shale, especially in relation to the impact of laminations, forms a crucial scientific basis for optimizing hydraulic fracturing designs.

Laboratory investigations have made significant contributions in understanding hydraulic fracture penetration modes and key influencing factors in layered reservoirs. Large-scale shale true triaxial hydraulic fracturing tests (Li et al. 2018; Zou et al. 2017; Huang and Liu 2017) have defined the three primary modes of interaction between hydraulic fractures and bedding interfaces including: (i) penetration, in which the hydraulic fracture directly traverses the bedding interface; (ii) capture, where the hydraulic fracture terminates at the bedding interface or follows the course of the bedding interfaces; and (iii) offset steering, where the hydraulic fracture extends along the bedding interfaces for a certain distance before exiting the laminar structures into the matrix. Several factors influence the morphology of the hydraulic fracture network (Cai et al. 2023)—with the propagation direction of the fracture predominantly controlled by the initial stress orientation, with propagation oriented perpendicular to the direction of minimum principal stress. Larger stress differentials render hydraulic fractures less sensitive to the presence of fractures and bedding (Huang 1981; Gale et al. 2007; Xu et al. 2015). The strength of the weak surfaces comprising the laminations constitutes another pivotal factor affecting the resulting hydraulic fracturing network structure. Weaker interfaces, with lower resistance to crack propagation, facilitate the extension of hydraulic fractures into the laminar layers (Tan et al. 2017a; Fu et al. 2015). When the weak interface is oriented approximately 30° to 60° to the incoming hydraulic fracture, reactivation by shear-slip failure along the weak interface is likely, especially when the contrast between maximum and minimum principal stresses is substantial (Zhao et al. 2013; Wang et al. 2021). Furthermore, the effects of injection rate and fluid viscosity represent a further two fracturing-related variables that have garnered considerable attention in prior investigations. Lower flow rates and reduced viscosities contribute to increased fluid loss on discontinuous surfaces, impeding hydraulic fracture propagation and yielding smaller fracture heights (Zou et al. 2022; Hou et al. 2018; Llanos et al. 2017). Existing experimental studies concerning the propagation of hydraulic fractures in anisotropic shale primarily concentrate on the analysis of fluid injection rate and viscosity, with limited exploration of the geological conditions of the reservoir itself. This limitation arises from the challenges associated with regulating formation properties and monitoring hydraulic fracture extension processes in laboratory experiments (Wu et al. 2022). Therefore, complementary research using numerical simulation methods is imperative and warranted as an adjunct.

Numerous numerical methods have been employed to explore controls on hydraulic fracturing where layered interfaces are present. Various Finite Element Methods (FEM) enable the coupled analysis of crack propagation, stress distribution, and fluid flow (Adachi et al. 2007; Chen 2012; Carrier and Granet 2012). Similarly, Extended Finite Element Methods (XFEM) offer distinct advantages in solving for hydro-mechanical coupling associated with discontinuities. XFEM introduces local degrees of freedom into the conventional finite element theory framework (Saberhosseini et al. 2019). Results indicate that bedding surfaces influence propagation extent and extension patterns of hydraulic fractures, with lower inclinations of lamellae relative to the fracture orientation more likely to induce slip damage along the interface (Tan et al. 2021; Taleghani and Olson 2011). In contrast, Boundary Element Methods (BEM) reduce the dimensionality of the problem by one space dimension by meshing elements solely on the boundary of the defined domain. It is characterized by straightforward data input and high computational accuracy. BEM is utilized for hydraulic fracturing simulation studies in reservoirs containing interfaces, revealing four distinct modes of fracture evolution: penetration, termination at the interface, opening of the interface, and offset steering (Zhang et al. 2007). Furthermore, discrete element methods (DEM) divide continuous objects into discrete elements and simulate the motion, fracturing, and interactions of the entire system through iterative solution of Newton’s second law for velocity and displacement within each time step (Cundall 1971). Granular mechanics models are frequently employed to explore hydro-mechanical coupling in shale (Zhang et al. 2019, 2022; Dou and Wang 2022). Such models integrate smooth joint contact models to allow slip on bedding plans and effectively accommodate the impact of interface strength, dip, fracture density and other factors on hydraulic fracture extension. In summary, each numerical calculation method possesses inherent advantages and limitations. To overcome the constraints of traditional numerical methods, various hybrid methods have been developed and applied to problems related to rock hydro-mechanical coupling. Notably, the finite-discrete element method (FDEM) combines the strengths of FEM and DEM, proving useful in the investigation of fracturing in rock formations with discontinuous surfaces (Lisjak et al. 2017; AbuAisha et al. 2017; Yan and Jiao 2018). However, most of the existing numerical studies on shale hydraulic fracturing utilize simplified models that focus on a single discontinuity surface, indicating that the mechanism of interaction between hydraulic fractures and multilayer stratifications requires further investigation.

In the following, we explore controls on hydraulic fracturing in anisotropic shale utilizing a multi-physics fracture analysis FDEM-flow simulator (MultiFracS). This combines finite element and discrete element techniques while considering hydro-mechanical coupling (Yan et al. 2022; Yan and Zheng 2016). Our analysis systematically examines the impact of various factors, including the inclination of the bedding planes and the distribution of in-situ stresses, which influence the initiation and propagation of hydraulic fractures. These analyses potentially provide valuable insights into the evolving patterns of hydraulic fracturing in shale under the influence of weak interfaces and the complex interactions among multiple fractures.

2 FDEM governing equations

FDEM is a numerical simulation method that amalgamates the strengths of both the finite element method and the discrete element method, as first proposed by Munjiza (2004). The solution domain in 2D is divided into a mesh of triangular finite elements within the continuum with zero initial-thickness joint elements with adhesive properties defining the common edges of adjacent triangular elements. This approach enables regional modeling of discontinuous media, as depicted in Fig. 1.

Fig. 1
figure 1

Continuum characterization and element types in 2D FDEM (modified from Yan et al. 2016)

Full size image

2.1 Equation of motion

In the FDEM approach, the discretized components comprise triangular elements, joint elements, and nodes. The deformation response for each triangular element adheres to Newton’s second law, and the equations of motion are computed for each time step utilizing a second-order forward difference scheme. This process is employed to adjust the velocity and displacement of the nodes based on their respective masses and forces. Furthermore, the equations governing motion consider the impact of viscous damping:

$${\mathbf{M}}\ddot{x} + {\mathbf{C}}\dot{x} = {\mathbf{F}}$$
(1)

where \({\mathbf{M}}\) and \({\mathbf{C}}\) are the mass and damping matrices of the elements defined at nodal locations, \(\dot{x}\) and \(\ddot{x}\) are the first- and second-order derivatives of the nodal displacement vector and \({\mathbf{F}}\) is the nodal force vector. The damping matrix avoids the propagation of stress wave oscillations within the model, and is defined as:

$${\mathbf{C}} = \mu {\mathbf{I}}$$
(2)
$$\mu = 2h\sqrt {\rho E}$$
(3)

where \({\mathbf{I}}\) is the identity matrix, \(\mu\) is the damping coefficient, which is determined based on a single-degree-of-freedom mass-spring system. \(h\) is the element dimension, \(\rho\) is the material density, and \(E\) is the modulus of elasticity defined element by element.

2.2 Joint element constitutive model

An appropriate selection of fracture initiation criteria for the joint elements is crucial in following the initiation and propagation of hydraulic fractures in FDEM. Modes can be categorized among three types: mode I (tensile failure), mode II (shear failure), and mode I-II (mixed tensile-shear failure), as illustrated in Fig. 2.

Fig. 2
figure 2

Constitutive models for joint element fracture in FDEM: a Mode I, Mode II, and b Mode I-II

Full size image

A mode I fracture initiates when the normal stress \({\sigma }_{n}\) at the crack tip reaches the tensile strength \({f}_{t}\), and the opening of the joint element reaches a critical value \({o}_{p}\). Based on fracture dissipation energy \(G_{{{\rm I}f}}\), it is assumed that as the opening at the crack tip increases, the normal stress \({\sigma }_{n}\) gradually decreases until it reaches the residual opening value \({o}_{r}\), forming a traction-free surface. In mode II, the critical slip \({s}_{p}\) corresponds to the shear strength of the material \({f}_{s}\), and is defined as:

$$f_{s} = c + \sigma_{n} \tan \varphi_{i}$$
(4)

where \(c\) is the cohesion and \({\varphi }_{i}\) is the internal friction angle of the material. Once the tangential slip of the crack exceeds a critical value \({s}_{p}\), based on the fracture dissipation energy \(G_{{{\text{II}}f}}\), the shear stress will continue to decrease to a residual value \({f}_{r}\), which is pure frictional resistance:

$$f_{r} = \sigma_{n} \tan \varphi_{f}$$
(5)

where \({\varphi }_{f}\) is the internal friction angle of the fracture face. Mixed mode I-II occurs when the crack opening and slip satisfy certain conditions, with its failure envelope defined as:

$$\left( {\frac{{o - o_{p} }}{{o_{r} - o_{p} }}} \right)^{2} + \left( {\frac{{s - s_{p} }}{{s_{r} - s_{p} }}} \right)^{2} = 1$$
(6)

where \({o}_{r}\) and \({s}_{r}\) are the normal maximum opening and tangential slip of the crack, respectively.

3 Hydro-mechanical coupling

The FDEM-flow is an extension built upon the framework of the original FDEM chassis, accommodating hydro-mechanical coupling within rock fractures. The core concept of this approach is to enhance the finite-discrete element method by introducing a recursive search algorithm for interconnected joint fracture networks (Yan et al. 2023). This algorithm identifies which joint elements are involved in the fluid flow computation. Subsequently, following Darcy’s law, it computes the fluid pressure within each permeable fracture. The resulting fluid pressure distribution represents the forces acting on the surrounding rock that contributes to the equilibrium of that interface. The deformation and displacement within the rock mass, induced by these forces, results in changes in fracture aperture, which in turn influences fluid flow within the fractures (Fig. 3).

Fig. 3
figure 3

Hydro-mechanical coupling in a discontinuum (modified from Yan et al. 2016)

Full size image

The hydro-mechanical coupling equations within FDEM-flow are as follows (Yan et al. 2022, 2021):

$$F = p_{old} nL$$
(7)
$$Q = - \frac{1}{12\mu }a^{3} \frac{{\Delta p_{old} }}{L}$$
(8)
$$a_{new} = a_{old} + \Delta a$$
(9)
$$p_{new} = p_{old} + \frac{{K_{w} }}{V}\left( {\sum Q\Delta t - \Delta V} \right)$$
(10)
$$\Delta V = V_{new} - V_{old}$$
(11)

where \(F\) is the force of the fluid acting on the triangular element, \(n\) is the unit normal vector to the fracture face, \({p}_{old}\) and \({p}_{new}\) are the pressures of the fluid at the current and subsequent time steps, \(Q\) is the flow rate, \(\mu\) is the dynamic viscosity, \(a\) is the aperture of the joint element, \({a}_{old}\) and \({a}_{new}\) are the apertures at the current and subsequent time steps for the joint element, \(L\) is the length of the joint element, \({\Delta p}_{old}\) is the difference of the pressures at the two endpoints of the joint element, \({K}_{w}\) is the bulk modulus of the water, and \(\Delta t\) is the time step.

4 Numerical model

The effective establishment of a numerical model is paramount for conducting studies on hydraulic fracturing simulations. First, we describe the details of the model and assign values to the parameters it utilizes. Then, the key parameters are further calibrated by comparing the simulation results with published experimental results, and the rationality of the model is verified.

4.1 Model geometry

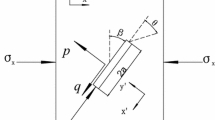
As shown in Fig. 4, we have established a two-dimensional model of shale matrix with multiple embedded bedding planes. This model is utilized to investigate the characteristics of hydraulic fracture propagation for various bedding plane orientations (angles) and stress conditions. The model is a 2D prismatic block \(300\mathrm{ mm}\times 300\mathrm{ mm}\), with a \(20\mathrm{ mm}\) diameter water injection hole. Discontinuous fractures were employed to represent the stratification, with a \(30\mathrm{ mm}\) layer spacing between parallel bedding surfaces. The angle between the bedding and the horizontal direction (namely the bedding plane angle) is denoted as \(\beta\). We define fixed displacement boundaries in the normal direction and impermeable fluid boundaries. The model is subjected to a vertical in-situ stress \({\sigma }_{1}\) and horizontal in-situ stress \({\sigma }_{3}\). Specifically, \({\sigma }_{1}\) is set at \(18\mathrm{ MPa}\), and \({\sigma }_{3}\) varies between \(6\mathrm{ MPa}\), \(9\mathrm{ MPa}\), \(12\mathrm{ MPa}\), \(15\mathrm{ MPa}\), and \(18\mathrm{ MPa}\), corresponding to lateral pressure coefficients (denoted as \(\lambda ={\sigma }_{3}/{\sigma }_{1}\)) of 0.33, 0.50, 0.67, 0.83, and 1.0, respectively.

Fig. 4
figure 4

Schematic 2D model of hydraulic fracturing in shale

Full size image

4.2 Model validation

To ensure the reliability of the model, parameters were determined based on experimental results (Tan et al. 2017b; Heng et al. 2020; Gehne et al. 2020), as summarized in Table 1. Subsequently, the simulation for horizontal bedding can be validated against the results of true triaxial hydraulic fracturing tests conducted on Longmaxi Formation shales (specimens 1#, 6#, 11#, 12#) (Tan et al. 2017b). This validation allowed for the further evaluation of aperture for the joint elements within our model. Ultimately, the relevant definitions of apertures for joint elements in the rock matrix were established at 10–7, 10–7, and 4 × 10–5 m, respectively. Meanwhile, the joint elements representing the stratification surfaces were assigned initial, minimum, and maximum apertures of 10–6, 10–6, and 4 × 10–5 m, respectively.

Table 1 Model parameters
Full size table

Figure 5 shows the validations against observed hydraulic fracture propagation patterns—comparison between experiments and simulations for various differential stress conditions. In the case of specimen 1#, with the highest differential stress of \(18-6\mathrm{ MPa}\), the primary crack is vertical, propagating along the direction of the maximum principal stress with marginal deviation, a trend replicated in the simulation with a single crack similarly propagating along the direction of the maximum principal stress. For specimen 6# at \(18-9\mathrm{ MPa}\) differential stress, the fracture pattern closely resembles that of specimen 1#, albeit with the emergence of secondary cracks in the simulation due to the reduced stress difference. Specimen 11# at \(18-12\mathrm{ MPa}\) differential stress displays a more branched pattern, with fractures occurring both vertically along the bedding planes and extending along the interface. The simulation also exhibits pronounced bifurcation and extension along the surface of the laminae. In contrast, the primary crack in specimen 12# struggles to penetrate the interface vertically to form a complete fracture. Instead, it extends along the bedding plane, with the simulation highlighting a significant tendency to initiate cracks along the directions of the minimum principal stresses. This facilitates the propagation of hydraulic fractures along the bedding. In summary, the agreement between the experimental and simulation results is striking and affirms the capacity of the model to reliably predict the topology of fracture propagation in laminated shales. The larger differential stress loading facilitates fracture propagation along the direction of the maximum principal stress, with little deviation and few secondary branching fractures.

Fig. 5
figure 5

Comparison between hydraulic fracturing experiment and simulation results (left are experimental results and right are simulation results)

Full size image

5 Results and analysis

In this section, the first subsection analyzes the possible fracture initiation modes of the wellbore in hydraulic fracturing; the second subsection provides a detailed exposition of hydraulic fracture propagation patterns under varying in-situ stress fields and laminar inclinations; and the third subsection further explores the factors influencing breakdown pressure—lateral pressure coefficient and bedding plane angle. The results are expected to contribute to a novel understanding of the hydraulic fracturing mechanism in shale reservoirs.

5.1 Mechanics of hydraulic fracture initiation

The initiation and propagation of hydraulic fractures play a pivotal role in shaping the morphology of the resulting fracture network and the subsequent fluid pressure response. The fluid pressure within the injection wellbore in the model steadily increases before reaching the critical threshold for fracture initiation—with fractures developing near the wellbore. These micro-fractures accumulate and nucleate, coalescing to form an initial macro-fracture. Subsequently, the elevated water pressure induces a stress concentration at the crack tip, facilitating the continuous extension of the hydraulic fracture from the crack tip.

Figure 6 shows the distribution of displacements in the horizontally laminated shale under two scenarios of stress loading during fracturing—these are for high (\({\sigma }_{1}/{\sigma }_{3}=18/6\mathrm{ MPa}\)) and low (\({\sigma }_{1}/{\sigma }_{3}=18/18\mathrm{ MPa}\)) stress obliquities. This allows the deformation stress response in the rock to be followed in different states. It is evident that the displacement fields within the rock mass exhibit marked disparities when subjected to high (\({\sigma }_{1}/{\sigma }_{3}=18/6\mathrm{ MPa}\)) and low (\({\sigma }_{1}/{\sigma }_{3}=18/18\mathrm{ MPa}\)) stress obliquities, giving rise to two distinctive hydraulic fracture initiation and expansion modes as modes I and II:

Fig. 6
figure 6

Distribution of contoured displacement magnitudes shown by streakline trajectories in the hydraulic fracturing model of horizontally bedded shale: a displacement contours in the critical state before hydraulic fracture initiation; b displacement contours during hydraulic fracture propagation; c enlarged view of the displacement field near the wellbore and around the fracture tip

Full size image

(1) Mode I: Tensile Initiation Fracturing. Under high differential stress, the rock elements are subjected to initial maximum compressive stress in the \({\sigma }_{1}\) direction and minimum compressive stress in the \({\sigma }_{3}\) direction. As fluid injection in the wellbore continues, the fluid pressure overcomes the influence of the minimum principal stress. Consequently, the rock elements are in a state of horizontal tension and vertical compression, resulting in a circumferential tensile stress concentration at the wall of the injection well, resulting in the initiation of tensile fracturing at the wellbore. During the fracture propagation process, a significant number of rock elements along the boundary in the direction of the maximum principal stress are displaced inward toward the wellbore center under the influence of \({\sigma }_{1}\). These elements intersect with elements driven outward by fluid pressure at the fracture tip. The relative motion of these two element components results in tensile stress at the fracture tip, leading to the formation of a series of hydraulic fractures characterized by tensile cracks (Type I) induced by the action of the maximum principal stress.

(2) Mode II: Shear Initiation Fracturing. When the magnitude of in-situ stress in both directions is nearly equal, the rock mass experiences hydrostatic loading. Before the hydraulic fracturing pressure reaches its critical state, the rock displaces outwards from the injection wellbore in the center. The heterogeneous perturbation of the perimeter stress field, caused by stratification within the shale, results in the possibility of both tensile and shear stress concentrations within the rock mass. In this scenario, the magnitude of the circumferential tensile stress is somewhat reduced, making it easier to develop shear cracks (Type II) or composite cracks (Type I-II) due to shear-initiation-fracturing. As the injected fluid continues to drive the propagating fracture, the displacement at the crack tip aligns with the direction of crack extension. This indicates that the in-situ stress field has a reduced influence on crack extension.

Based on this analysis, and combined with the simulation results presented in Fig. 7, stress difference exerts a decisive influence on the mechanism of hydraulic fracture initiation in shale. When the stress difference is large, hydraulic fractures are predominantly initiated through tension, initially manifested as tensile cracks within the weakened region of the wellbore wall. Conversely, as the stress difference decreases and approaches isoperimetric pressure conditions, shear initiation may take precedence near the wellbore wall, giving rise to shear or composite cracks. Moreover, it is worth noting that the resulting hydraulic fractures are predominantly tensile, despite variations in the form of the fractures initiating from the wellbore wall. This is consistent with previous observations based on extensive series of tests (Chong et al. 2017a). A detailed description of hydraulic fracture morphologies and extension patterns is provided in the subsequent section.

Fig. 7
figure 7

Topologies of hydraulic fractures propagating in the near-wellbore area

Full size image

5.2 Hydraulic fracture propagation patterns

During hydraulic fracturing, as fluids are continuously injected into a packed-off section, hydraulic fractures begin to initiate and propagate as the breakdown pressure is reached. In this study, a total of 20 sets of hydraulic fracturing simulations were conducted, considering the combined influence of different bedding plane angles and the in-situ stress field. Figure 8 gives the hydraulic pressure distribution and fracture morphology after fracturing for all of these models, representing the same bedding plane angles (stacked vertically) and the same in-situ stress states (arranged horizontally). The observations reveal that:

  1. 1.

    When the bedding orientation is set to 0° and 90°, under high stress obliquity and lower lateral pressure coefficients (\(\lambda\) is equal to 0.33 and 0.50), the point of initiation for the hydraulic fractures occurs near the upper and lower central wellbore walls. Fracture extension exhibits a distinct predominant direction, forming a single fracture that is parallel to the maximum principal stress. As the stress difference decreases, hydraulic fracture extension exhibits noticeable branching at \(\lambda\)=0.67. Furthermore, when \(\lambda\) is 0.83 and 1.00, the initiation of fractures becomes random, with the emergence of three initiation points, and hydraulic fractures are omni-directional, extending unpredictably in all directions.

  2. 2.

    When the bedding orientation is 30°, the hydraulic fractures exhibit “localized slip” along the bedding plane, displaying a “step-like” distribution, with their overall propagation towards the maximum principal stress direction in the case for \(\lambda =0.33\). This phenomenon may be attributed to the fact that, under higher stress difference, hydraulic fractures have a lower breakdown pressure, and the accumulated energy may be insufficient for them to penetrate all bedding planes continuously. Nonetheless, the higher stress difference still predominantly governs fracture extension, resulting in hydraulic fractures intermittently stepping in direction towards the maximum principal stress, particularly as they cross the bedding interfaces. When the lateral pressure coefficient is increased to \(\lambda\)=0.50, the fracture breakdown pressure increases with a decrease in stress difference, leading to a partial enhancement of hydraulic fracture penetration, with the “localized slip” phenomenon becoming relatively less pronounced. Subsequently, as the stress difference reduced to \(\lambda \ge 0.67\), multiple bifurcations of the hydraulic fractures occur, with the initiation and extension gradually deflecting in the direction of the minimum principal stress.

  3. 3.

    When the bedding is inclined at 60°, then for \(\lambda\)=0.33, the hydraulic fractures initially propagate along the direction of the maximum principal stress, before arresting and then propagating along the bedding plane. However, fractures predominantly propagate along the direction of the maximum principal stress at \(\lambda\)= 0.50 and 0.67, penetrating across the bedding planes, similar to the extension characteristics observed at \(\beta =30^\circ\). Nevertheless, the critical stress difference for fracture propagation changes in this scenario. In cases where the lateral pressure coefficient \(\lambda\)=0.83 and 1.00, the hydraulic fractures deviate towards the direction of the minimum principal stress, making them more prone to propagate along the bedding plane, eventually forming continuous planar fractures.

Fig. 8
figure 8

Hydraulic pressure distributions and fracture morphologies post-fracturing

Full size image

To further investigate the resulting fracture patterns for interaction between hydraulic fractures and bedding planes under different states, the main hydraulic fractures extending from the injection well outward will be denoted as HF1, HF2, and HF3, clockwise, as indicated by the yellow labels in Fig. 8. Additionally, the expansion of hydraulic fractures for different bedding inclinations and stress fields may be categorized into four distinct modes, as illustrated in Fig. 9. These are elaborated as follows:

  1. 1.

    Propagation Mode I: Penetration. In this mode, the main hydraulic fracture primarily extends through all the interfaces, and a few secondary cracks may be generated when it encounters the bedding plane due to fluid loss. However, its extension is significantly constrained, and it cannot connect with the bedding to form continuous branch fractures.

  2. 2.

    Propagation Mode II: Bifurcation. This mode is characterized by the appearance that when the hydraulic fracture encounters a weak interface during extension, a single main fracture may bifurcate into two fractures at the interface and then continue to expand. At this point, the bifurcated crack exhibits different morphologies which may extend through the bedding interface or form a macroscopic failure along the interface. The key discrepancy between this mode and Propagation Mode I is that the two fractures resulting from the bifurcation each grow almost simultaneously to the model boundary, without a clear distinction between primary and secondary cracks.

  3. 3.

    Propagation Mode III: Steering. This mode is manifest in the hydraulic fracture during extension when it deviates to propagate along a weak interface for a certain distance and then resumes propagation through the interface. The deviation is typically small and often follows a “step-like” distribution.

  4. 4.

    Propagation Mode IV: Capture. This mode of extension is distinguished by the hydraulic fracture either halting its growth when it confronts a weak interface or altering its course to follow the bedding until it reaches the boundary of the model, resulting in the formation of a macroscopic failure.

Fig. 9
figure 9

Schematic model of interactions between hydraulic fracture and bedding

Full size image

We define hydraulic fracture propagation mode classifications as shown in Fig. 9, for the various fracture types in different scenarios from Fig. 8 and tallied and presented in Table 2. Moreover, drawing from the aforementioned observations and analysis, it is evident that the distribution of in-situ stress and the inclination of the bedding are pivotal factors influencing the extension patterns of hydraulic fractures in bedded materials, viz. shales. Typically, hydraulic fractures tend to propagate in the direction of the maximum principal stress, and the greater the stress difference, the more pronounced the controlling effect of in-situ stress on fracture extension. Under these simulation conditions, the stress difference threshold value is approximately 3 MPa to 6 MPa corresponding to \(\lambda =0.83\) and 0.67. When it falls below this threshold, fracture initiation occurs randomly and the fracture network morphology during expansion becomes more intricate. The relative orientation of the bedding predominantly impacts the propagation mode of the hydraulic fractures. In the case of horizontal interfaces, primarily penetrating (Propagation Mode I) and bifurcated (Propagation Mode II) fractures result. However, a significant number of steering-type (Propagation Mode III) and capture-type (Propagation Mode IV) fractures begin to manifest during hydraulic fracturing, with a certain degree of bedding dip. Particularly, in instances of steeper bedding inclination (\(\beta =60^\circ\)), hydraulic fractures readily extend along the bedding surface, leading to the development of macro shear slip damage.

Table 2 Patterns and characteristics of main hydraulic fractures for different bedding plane angles and in-situ stress fields
Full size table

5.3 Factors influencing breakdown pressures

5.3.1 Hydraulic pressure and strain energy relations

Figure 10 shows the variation curves of hydraulic pressure and strain energy with time under different in-situ stresses and for bedding interface angles of 0°, 30°, 60°, and 90°, respectively. Correlating with classical pumping pressure curves, the fracturing process can be segmented into three distinct stages. The first stage is the pressure-building phase, characterized by the continuous injection of fracturing fluid. The fluid pressure inside the wellbore gradually increases until it reaches peak pressure, defining the (wellbore wall) breakdown pressure (\({P}_{b}\)). During this stage, the strain energy within the model experiences minimal change, essentially maintaining the initial strain energy induced by the initial stress loading. The second stage is the initiation then extension phase of the hydraulic fracture, marked by the formation of macroscopic cracks extending from the wellbore. Subsequently, the hydraulic pressure rapidly declines (the value of hydraulic pressure drop is \(\Delta {P}_{b}\)), while the strain energy rapidly accumulates, reaching its peak (the value of the strain energy increment is \(\Delta {E}_{s}\)). The third stage is the final equilibrium phase, where the fracturing fluid flows along the hydraulic fracture to the boundary of the specimen. Due to the minimal damping applied in the model, the strain energy exhibits some fluctuations and gradually approaches an equilibrium.

Fig. 10
figure 10

Pressure–time and strain energy-time curves for hydraulic fracturing at different inclinations of bedding relative to the in-situ stress field. Bedding at: a 0°; b 30°; c 60°; d 90° relative to the minimum principal stress \({\sigma }_{3}\)

Full size image

The results indicate that the state of the stress field is a critical factor influencing fracture initiation. For identical bedding interface angles, the breakdown pressure decreases with the increasing in-situ stress difference. This phenomenon is attributed to the heightened stress concentration at the wellbore due to an increasing stress difference, wherein the increased stress concentration typically results in a reduction in \({P}_{b}\). Consequently, an augmented stress difference corresponds to a diminished peak magnitude of strain energy, as the fracture reaches the sample edge. This indicates reduced deformation of the model under such fracturing conditions, potentially resulting in smaller opening of the hydraulic fracture aperture or reduced shear displacement. Furthermore, the inclination of the bedding interfaces can cause variations in the borehole-local stress state, which may lead to different fracture initiation modes and propagation patterns. Overall, the impact of layer inclination exerts a major influence in determining the strain energy. The peak strain energy of the model under each stress field at \(\beta =30^\circ\) and \(60^\circ\) is significantly lower than that at \(\beta =0^\circ\) and \(90^\circ\). Additionally, the time for hydraulic fracture extension (Stage II) is prolonged for bedding inclinations of 0° and 90°. This implies substantial differences in fracture propagation patterns at different inclinations of the bedding lamellae, suggesting a propensity for the formation of a complex fracture network in both horizontal and vertical laminations. The specific influence of each factor on breakdown pressure will be further discussed in the next subsection.

5.3.2 Influence of lateral pressure coefficient

Breakdown pressures during hydraulic fracturing can be expressed as (Hubbert and Willis 1957):

$$P_{b} = 3\sigma_{3} - \sigma_{1} + \sigma_{t}$$
(12)

where \({P}_{b}\) is the breakdown pressure, \({\sigma }_{t}\) is the tensile strength of the medium and \({\sigma }_{1}\) and \({\sigma }_{3}\) are the maximum and minimum principal stresses within the reservoir. Substituting \(\lambda ={\sigma }_{3}/{\sigma }_{1}\) and \({\sigma }_{1}=18\mathrm{ MPa}\) into Eq. (12), we have:

$$\begin{gathered} P_{b} = (3\lambda - 1)\sigma_{1} + \sigma_{t} \hfill \\ \, _{ \, } = 54\lambda + \sigma_{t} - 18 \hfill \\ \end{gathered}$$
(13)

Neglecting the effect of the inclined laminae on tensile strength \({\sigma }_{t}\), the breakdown pressure is a unique function of the lateral pressure coefficient, which is linearly and positively correlated.

Breakdown pressures under the varying lateral pressure coefficients of our simulations are summarized in Fig. 11. Breakdown pressure increases linearly with an increase in the lateral pressure coefficient. Specifically, the average breakdown pressure increases from 14.45 MPa at \(\lambda =0.33\) to 42.30 MPa at \(\lambda =1.00\). This linear fit is expressed as \({P}_{b}=1.49543+42.70956\lambda\), where \({P}_{b}\) represents the breakdown pressure, and \(\lambda\) signifies the lateral pressure coefficient. This linear equation illustrates the relationship between the breakdown pressure and the lateral pressure coefficient. The simulation results are congruent with predictions from Hubbert and Willis (1957) indicating the regional stress state governs the breakdown pressure (Ma et al. 2022). Weak bedding interface, that does not directly intersect the borehole, has a limited impact on the breakdown pressure. However, where the wellbore is directly intersected by a weak interface, the resulting breakdown pressure may be influenced significantly—although it is noted that the interface comes to within 0.5 borehole radii of the borehole wall, and even at that close proximity the effect on breakdown pressure is only a few megapascals.

Fig. 11
figure 11

Breakdown pressure under different lateral pressure coefficients

Full size image

5.3.3 Influence of bedding plane angle

The tensile strength of the reservoir and the distribution of in-situ stress are the key factors affecting the breakdown pressure in the fracturing process (Wang et al. 2024). Considering the bedding characteristics of shale, the relation proposed by Claesson and Bohloli (2002) is often used to calculate tensile strength as:

$$\sigma_{t} = \frac{2P}{{\pi Dt}}\left[ {\left( {\frac{E}{E^{\prime}}} \right)^{{\left( {{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0pt} 4}} \right)\cos 2\beta }} - \frac{\cos 4\beta }{4}\left( {b - 1} \right)} \right]$$
(14)

With

$$b = \frac{{\sqrt {EE^{\prime}} }}{2}\left( {\frac{1}{G^{\prime}} - \frac{2\nu^{\prime}}{{E^{\prime}}}} \right)$$
(15)

where \(P\) is the maximum vertical load of the shale specimen when splitting damage occurs, \(D\) is the diameter of the rock specimen, \(t\) is the thickness of the rock specimen, \(\beta\) is the angle between the loading direction and the normal to the lamellar surface (i.e., bedding plane angle) of the shale specimen, \(E\) is the modulus of elasticity of the shale transversely viewed on the isotropic plane, and \(E^{\prime}\) and \(G^{\prime}\) are the elasticity and shear moduli of the shale perpendicular to the isotropic plane, respectively, where the splitting test is conducted in the Brazilian configuration for diametral loading of a thin disc.

Substituting Eq. (14) and Eq. (15) into Eq. (13) gives:

$$P_{b} = \frac{2P}{{\pi Dt}}\left\{ {\left( {\frac{E}{E^{\prime}}} \right)^{{\left( {{1 \mathord{\left/ {\vphantom {1 4}} \right. \kern-0pt} 4}} \right)\cos 2\beta }} - \left[ {\frac{\cos 4\beta }{4}\left( {\frac{{\sqrt {EE^{\prime}} }}{2}\left( {\frac{1}{G^{\prime}} - \frac{2\nu^{\prime} }{{E^{\prime}}}} \right) - 1} \right)} \right]} \right\} + 54\lambda - 18$$
(16)

As shown in Fig. 12, the relationship between the tensile strength \({\sigma }_{t}\) and the bedding plane angle \(\beta\) was fitted by the experimental values of Brazilian splitting tests. Meanwhile, the analytical solutions for breakdown pressure under different ground stress conditions are plotted, as shown in Fig. 13. In this case, the five elastic constants \(E\), \(E^{\prime}\), \(\nu\), \(\nu^{\prime}\) and \(G^{\prime}\) of shale are used (Chong et al. 2017b), as 30.18 GPa, 17.84 GPa, 0.31, 0.33 and 6.66 GPa, respectively. It is noteworthy that variations in the lamination angle induce anisotropy in tensile strength (Wang et al. 2023), and the theoretical breakdown pressure follows a consistent pattern. The maximum value is attained when \(\beta\) equals 0°, while the minimum value is reached within the range \(\beta =60^\circ \sim 75^\circ\). In addition, as the lateral pressure coefficient increases, the analytical value of breakdown pressure also increases.

Fig. 12
figure 12

The curve of tensile strength vs bedding plane angle

Full size image
Fig. 13
figure 13

Theoretical curves of breakdown pressure as a function of bedding plane angle

Full size image

The influence of the inclination in bedding on breakdown pressure is further explored, as depicted in Fig. 14. The results indicate that when the stress difference is minimal (\(\lambda\)=0.83 and 1.00), the impact on breakdown pressure is minimal. However, for \(\lambda\)=0.33 and 0.50, there is a more pronounced trend, with the highest and lowest values occurring at the bedding plane angle of 0° and 30°, respectively. This observed trend aligns closely with observations on the anisotropic effect of shale bedding plane angle on its tensile strength (Chong et al. 2017b; Teng et al. 2018). Therefore, the tensile strength for different bedding inclinations is considered a key factor in determining breakdown pressure under conditions of high stress difference. This trend can be clearly observed in existing experimental studies (Shen 2021; He et al. 2018), as shown in Fig. 15. Additionally, at \(\lambda =0.67\), higher breakdown pressures are apparent for bedding plane angles of 30° and 60° compared to that at 0° and 90°. This divergence from the patterns observed at \(\lambda =0.33\) and \(\lambda =0.50\) is attributed to the presence of three crack initiation points and shear initiation at the wellbore when the bedding plane angle is set at 30° and 60°, as also supported by the analysis presented in Fig. 7. Upon comparing the simulation curve with the theoretical curve, it is observed that these two trends exhibit a strong degree of unity. However, some disparities emerge between the analytical and numerical values, notably when shear fracture at the wellbore wall initiates. This observation underscores the limited applicability of existing theoretical formulations, emphasizing the imperative need for employing numerical simulation techniques to enhance predictive accuracy and validation.

Fig. 14
figure 14

Influence of bedding plane angle on breakdown pressure in simulation results

Full size image
Fig. 15
figure 15

Tensile strength and breakdown pressure of shale at different bedding plane angles

Full size image

6 Discussion

We report numerical simulations of hydraulic fracturing in shale containing bedding lamellae that reveal that both the in-situ stress field and its orientation relative to bedding significantly influence the initiation and expansion of hydraulic fractures. In line with numerous previous studies (Heng et al. 2021b; Zhang et al. 2023), it is observed that a smaller in-situ stress difference results in higher breakdown pressure and a more intricate fracture extension pattern. Additionally, the initiation shear fractures at the wellbore wall may develop when the stress difference is minimal, deviating from the traditional theoretical analysis that primarily assumes that initiation at the wellbore wall is predominately in tension (Zeng et al. 2019). This discrepancy is mainly attributed to the common practice of neglecting the presence of non-uniform interference of bedding interfaces on the stress field at the borehole wall, emphasizing the importance of considering the effect of bedding proximity and orientation in the hydraulic fracturing of structured shales. The simulation results also indicate that orientation of the weak interfaces relative to the principal stress directions influences the mode of hydraulic fracture propagation, with smaller azimuthal obliquities between bedding and \({\sigma }_{1}\) favoring fracture extension along the interface, also leading to macroscopic shear-slip damage. Moreover, breakdown pressure exhibits greater sensitivity to bedding inclination under high stress differences. The impact of bedding plane angles on breakdown pressure follows a pattern similar to the influence of bedding plane angles on the tensile strength of shale, a conclusion similarly reached by Lin et al. (2017) in their experimental study.

In addition to the aforementioned analysis, two other issues necessitate further discussion and clarification in this study. One pertains to failure mechanisms along the bedding surface in hydraulic fracturing. To provide a clearer elucidation of this matter, the stress and displacement field distributions during the fracturing process are presented as an example, with the bedding plane angle at 60° and the in-situ stress distribution at \({\sigma }_{1}/{\sigma }_{3}=18/6\mathrm{ MPa}\), as illustrated in Fig. 16. It is apparent that when the hydraulic fracture propagates along the weak interface, the fracture tip consistently experiences tensile stress concentrations, leading to the initial accumulation of a series of tensile cracks. Concurrently, the displacement field reflects significant shear slip along the bedding plane as the hydraulic fracture grows. From this observation, we infer that failure along the weak interface during hydraulic fracturing may result from the formation of tensile cracks that dilate the bedding, followed by shear slip, ultimately culminating in macroscopic failure. This observation aligns with the crack types depicted in Fig. 7 and the observation of complex shear failure encountered during hydraulic fracturing in the presence of discontinuity surfaces, as noted in the literature (Heng et al. 2021b; Zhang et al. 2017). This sheds light on an alternative explanation for the relationship between microscopic damage and macroscopic failure in shale.

Fig. 16
figure 16

Distribution of stress and displacement fields in shale hydraulic fracturing (\(\beta =60^\circ\), \({\sigma }_{1}/{\sigma }_{3}=18/6 {\text{MPa}}\))

Full size image

The second issue concerns the impact of the bedding plane angle on strain energy evolution during fracturing. As fluid injection occurs, the energy input into the model increases, and the hydraulic fracture extends from the injection borehole to the model boundary. Using minimal damping, and fixing displacements on the exterior boundary, most of the work performed by the hydraulic pressure is converted into elastic strain energy between the model elements. Upon analyzing Fig. 10, it becomes evident that the peak strain energy of the model under each stress field is significantly smaller, when the bedding is inclined at 30° and 60° compared to when the inclination is 0° and 90°. This discrepancy can be attributed to the fact that at inclinations of 0° and 90°, the model primarily undergoes tensile failure, with the matrix in compression. In contrast, when the interfaces are inclined at 30° and 60°, the model experiences a substantial amount of irreversible shear-slip failure, resulting in a relatively lower elastic strain energy. This observation aligns with a phenomenon previously identified (Han et al. 2023) where ruptures along the bedding interface are characterized by narrow shear fractures, while cracks through the bedding surface tend to be wider tensile fractures.

7 Conclusions

In this paper, we investigate the influence of stress magnitude and orientation relative to bedding on the resulting morphology and topology of hydraulic fractures using a combined finite-discrete element method. The primary conclusions can be summarized as follows:

  1. 1.

    In-situ stress distribution is a crucial factor in hydraulic fracture initiation and expansion. When the lateral pressure coefficient (\(\lambda\)) is less than 0.67, hydraulic fractures primarily initiate as tensile fractures along the wellbore, aligning with the direction of the maximum principal stress. Conversely, for \(\lambda \ge 0.67\), shear cracks are favored to initiate for the minor stress difference, resulting in a less predictable initiation and extension direction.

  2. 2.

    The orientation of bedding planes mainly affects the mode and morphology of hydraulic fracture propagation. Beddings parallel to the direction of the minimum principal stress promote the formation of layer-penetrating and bifurcated fractures, while inclined beddings encourage the emergence of numerous steering-type and capture-type fractures. Particularly, at a steeper inclination, when \(\beta =60^\circ\), hydraulic fractures readily extend along the bedding surface, inducing macroscopic shear slip failure.

  3. 3.

    The state of in-situ stress plays a critical role in influencing breakdown pressure. Diminished stress differences correspond to elevated reservoir breakdown pressures, and there is a linear growth relationship between breakdown pressure and the lateral pressure coefficient.

  4. 4.

    The breakdown pressure exhibits greater sensitivity to bedding inclination under high stress disparities. Its influence pattern aligns with the variations in tensile strength, typically reaching maximum and minimum values at bedding inclination angles of 0° and 60°, respectively.