1 Introduction

The force on the soil is meaningful at 3D compression state. Meanwhile, the different mechanical properties in various directions are vital to distinguish the properties of soil from other materials, and the true-triaxial has particular advantages in determining these properties (Janssen and Verwijs 2007), especially in the study of anisotropy (Li et al. 2023). Anisotropy has a substantial influence on the soil stress history, stress path, intermediate principal stress, and the characteristics of plastic flow (Arthur and Phillips 1972; Yao et al. 2018). In particular, recent studies have found that the critical state line of sand is not unified, which is attributed to the effect of the intermediate principal stress coefficient and the anisotropy (Hight et al. 1984; Li and Dafalias 2011; Sadrekarimi and Olson 2013; Zhao and Guo 2013). The verification of these effects needs to be supported by the true-triaxial apparatus which can better show these results in the 3D space (Dong et al. 2019; Salimi and Lashkari 2020; Yasuo and Ishihara 1979). The existence of anisotropy increases the complexity of exploring the 3D mechanical of soil greatly. Although the variables in the stress tensor are needed to control six orientations independently to better study the generalized anisotropy, such an ideal apparatus is still within our expectations. True-triaxial apparatus is still the better equipment for studying orthotropic at present because the cuboid specimen corresponds to the three orthogonal principal stresses of the stress tensor and the loading direction of the three orthogonal directions can be converted freely, which is convenient for the study of soil anisotropy and has a clear physical significance (Rodriguez and Lade 2013; Shao et al. 2014; Zhang and Charkley 2017). The overall deformation of the cuboid specimen is uniform relatively and is the closest to the unit test, which is of great significance to the establishment of the constitutive model and the theoretical improvement of the soil in 3D space (Ko and Scott 1968; Nakai and Matsuoka 1983; Zhang et al. 2019). The orthogonal directions of the true-triaxial apparatus were controlled independently by more than two pairs of rigid loading plates, which also play an important role in the study of shear bands with complex stress paths, plane strain tests and their corresponding engineering backgrounds (Abelev and Lade 2003; Lo et al. 1996).

Although the true-triaxial apparatus is used to study various mechanical properties of soil, there are still some shortcomings that affect its application and promotion (Lade and Duncan 1973; Pearce 1971). First of all, the complex and changeable stress path in the orthogonal 3D space increases the difficulty of the software design and the equipment operation. In the stage of imperfect soil mechanics, the varied strength indicators in 3D have brought great challenges to the description of the constitutive model and the practical engineering application (Fan et al. 2017; Lade and Wang 2011). Secondly, to avoid the collision between the adjacent rigid loading plates of the true-triaxial apparatus before the soil failure, it is necessary to leave enough space for the deformation of the cuboid specimens, so that the uneven deformation will occur in the position of reserved space. This leads to boundary effects, however, if the reserved space is too small, the rigid loading plate will collide, and the soil specimen cannot reach the failure state normally (Calabresi and Callisto 1998; Li 1985; Shi and Li 2009; Shi et al. 2017). These shortcomings are exactly where the true-triaxial apparatus needs to be improved, and it is these shortcomings that greatly affect its application and promotion. Due to these shortcomings, the true-triaxial apparatus has a low usage rate in the world, which greatly hinders the exploration of the mechanical response of the soil in 3D space (Xu 2003). Furthermore, the true triaxial apparatus, although gaining in popularity, is still rather a rare device in geotechnical laboratories. It requires much more effort to properly carry out the experiments, specifically on no-cohesive soils, which is another reason why the existing research results on true triaxial experiments are not abundant. Therefore, it is necessary to address this issue from another perspective.

The work presented here proposes a novel method to achieve a three-dimensional stress path from a special perspective (Li and Ma 2023; Li et al. 2024). The proposed method herein is structured as follows. In the p–q space, the axisymmetric test path of the conventional triaxial and the stress path of the true-triaxial are kept consistent, by controlling the axial and radial loading ratio of the axisymmetric specimens to satisfy the stress path of the three orthogonal directions of the true-triaxial loading ratio in the generalized stress space, the true-triaxial stress path can be achieved. The rationality and feasibility of the proposed novel method are verified preliminarily through a series of undrained tests conducted by conventional triaxial apparatus on aeolian sand in the Tengger Desert. Once the software of conventional triaxial apparatus was developed by the novel method, the measuring range of stress paths could be expanded greatly. The expenditure could be further reduced for exploring the three-dimensional mechanical properties of soils.

2 Experimental design method

2.1 Loading characteristics of specimens

The conventional triaxial apparatus adopts a cylindrical specimen, as we all know, its advantages and disadvantages are obvious particularly. In the triaxial compression test, the axisymmetric directions of the cylindrical specimen are σ2 and σ3, it guarantees geometrically that σ2 is always equal to σ3, and the measured deformation of \(\varepsilon_{{2}} \equiv \varepsilon_{{3}}\) also reflects the average effect of the overall radial deformation. The specimen adopts the rigid loading in the axial direction and the flexible loading in the radial direction. The combination of flexible cylindrical surface and rigid loading perfectly guarantees that all stress path tests can reach the failure state, in addition, more stress paths can be completed only by controlling the forces in two independent directions. If the isotropic surface and the natural deposition surface of the soil are corresponding, the apparatus can measure its mechanical properties faultlessly, and the operation process is simple. These are the main advantages of conventional triaxial tests. However, the shortcomings of the apparatus are also obvious particularly. On the one hand, the apparatus can only measure the mechanical difference of the soil in a specific plane, and the difference in the axisymmetric plane cannot be measured. On the other hand, the apparatus cannot load the intermediate principal stress independently, so the apparatus is also called a pseudo-triaxial apparatus, which limits the test range of the apparatus greatly.

The true-triaxial apparatus adopts a cuboid specimen, which overcomes the defect of conventional triaxial apparatus perfectly in theory. The true-triaxial apparatus performs symmetric loading on the three pairs of orthogonal planes and can control the loading in the three orthogonal directions independently. If all rigid loading plates are used, the true-triaxial test is a perfect unit test. Not only can the mechanical differences of the three orthogonal surfaces be better measured, but also the load ratios in the three directions can be controlled, such as linear or nonlinear loading can be realized for any stress path in the 3D space, and the strength of other surfaces such as the π plane can be measured. This is the biggest advantage of true-triaxial apparatus. However, after the cuboid specimen is deformed by force, the rigid loading plate of the true-triaxial apparatus will collide. To avoid collisions, it is often necessary to increase the size of specimens. This results in a boundary effect at the end of the specimen of specimen deformation. If the specimen size is not controlled well, problems such as collisions will still occur, which increases the requirements for the control accuracy of the apparatus. The above problems are important factors that affect its application and promotion of true-triaxial apparatus. Based on the above analysis and the advantages of conventional triaxial, this paper controls the radial and axial loading ratios of the axisymmetric specimens to ensure that the stress path in the generalized stress space is consistent with the true-triaxial stress path. Finally, an equivalent solution is creatively proposed.

The true-triaxial apparatus can control the loading independently in three orthogonal directions. Most stress paths can be realized by changing the loading ratio in three loading directions, i. e. the true-triaxial apparatus can measure the yield strength characteristics of soil in 3D space and the mechanical response of anisotropy soil in three orthogonal directions. In the geotechnical experiment, we often pay attention to the yield, the flow and the failure characteristics of the invariant space of the stress tensor. For example, the spatial response of p–q–θσ, where p is the average principal stress, p = σkk; q is the generalized shear stress, \(q = \sqrt {3J_{2} }\), J2 = sijsij/2, sij = σij − δijp, δij is the Kronecker tensor (when i ≠ j, δij = 0, when i = j, δij = 1), and θσ is the stress Lode angle, \(\theta_{\sigma } = \sin^{ - 1} (3\sqrt 3 J_{3} /2J_{2}^{3} )/3\), \(J_{3} = s_{ij} s_{jk} s_{ki} /3\). The three orthogonal principal stress directions correspond to the three orthogonal surfaces of cuboid specimens, and the expression of p–q–θσ space can be obtained as follows:

$$\left. \begin{gathered} p = \frac{{\sigma_{1} + \sigma_{2} + \sigma_{3} }}{3} \hfill \\ q = \frac{{\sqrt {\left( {\sigma_{1} - \sigma_{2} } \right)^{2} + \left( {\sigma_{2} - \sigma_{3} } \right)^{2} + \left( {\sigma_{1} - \sigma_{3} } \right)^{2} } }}{\sqrt 2 } \hfill \\ \theta_{\sigma } = {\text{tg}}^{ - 1} (\frac{{2\sigma_{2} - \sigma_{1} - \sigma_{3} }}{{\sqrt 3 (\sigma_{1} - \sigma_{3} )}}){ = }{\text{tg}}^{ - 1} (\frac{2b - 1}{{\sqrt 3 }}) \hfill \\ b = \frac{{\sigma_{2} - \sigma_{3} }}{{\sigma_{1} - \sigma_{3} }} \Leftrightarrow \sigma_{2} { = }b\sigma_{1} + \left( {1 - b} \right)\sigma_{3} \hfill \\ \end{gathered} \right\}$$
(1)

where σ1 is the major principal stress; σ2 is the intermediate principal stress; σ3 is the minor principal stress. b is the intermediate principal stress coefficient, b ∈ (0,1), which describes the relationship of loading ratio between the σ2 and other principal stresses (σ1 andσ3). b and θσ have the same function, but b owns the advantage of a simple form which is used widely. In Eq. 1, p, q and θσ are the variables related to three invariants of the stress tensor, and the true-triaxial apparatus can realize independent control of these three variables. The equipotential line of q in 3D space is crucial to the test of yield surface, flow, and failure lows, which is also the critical parameter measured in the true-triaxial test.

Therefore, the stress path of the true-triaxial test is mainly designed in p–q–θσ space according to Eq. 1. After isotropic consolidation in p–q space, such as constant p, the different values of θσ are used to carry out tests, and the curves of all values of θσ can be obtained. At the same time, the loading direction of the specimen is changed, and the yield, the strength, and the failure curves on the π plane can be obtained. If θσ is a constant at different p-values are adopted, the critical state lines can be obtained. Thus, the complete mechanical response of p–q–θσ space can be obtained by integrating the results of different θσ and p. To better illustrate the proposed method in this paper, the stress paths under the conditions of constant p and varying b were designed according to Eq. 1 and the control equations using conventional triaxial apparatus are deduced.

2.2 The load method at the condition of constant b

In true-triaxial condition, when b is constant, the increment of the variable in Eq. 1 satisfies the following equation:

$$\left. \begin{gathered} {\text{d}}p = \frac{{{\text{d}}\sigma_{1} + {\text{d}}\sigma_{2} + {\text{d}}\sigma_{3} }}{3} \hfill \\ {\text{d}}q = \frac{{\left( {2{\mkern 1mu} \sigma_{1} - {\mkern 1mu} \sigma_{2} - \sigma_{3} } \right){\text{d}}\sigma_{1} - \left( {{\mkern 1mu} \sigma_{1} - 2{\mkern 1mu} \sigma_{2} + {\mkern 1mu} \sigma_{3} } \right){\text{d}}\sigma_{2} - {\mkern 1mu} \left( {\sigma_{1} + \sigma_{2} - 2{\mkern 1mu} \sigma_{3} {\mkern 1mu} } \right){\text{d}}\sigma_{3} }}{{\sqrt 2 \sqrt {\left( {\sigma_{1} - \sigma_{2} } \right)^{2} + \left( {\sigma_{2} - \sigma_{3} } \right)^{2} + \left( {\sigma_{1} - \sigma_{3} } \right)^{2} } }} \hfill \\ {\text{d}}\sigma_{2} { = }b{\text{d}}\sigma_{1} + \left( {1 - b} \right){\text{d}}\sigma_{3} \hfill \\ \end{gathered} \right\}$$
(2)

In the generalized stress space (p–q space), the slope of any stress path K1 at true-triaxial conditions is obtained according to Eq. 2:

$$K_{1} = \frac{{{\text{d}} q}}{{{\text{d}} p}} = \frac{{3\sqrt {\left( {b^{2} - b + 1} \right)} \left( {{\text{d}}\sigma_{1} - {\text{d}}\sigma_{3} } \right)}}{{\left( {b + 1} \right){\text{d}}\sigma_{1} - \left( {b - 2} \right){\text{d}}\sigma_{3} }}$$
(3)

where the slope K1 of the stress path in p–q space is determined by major principal increment dσ1, minor principal increment dσ3, and b. When b is a designated value, the loading mode of σ1 and σ3 of the true-triaxial apparatus is also uniquely determined.

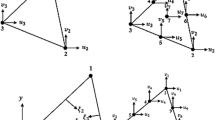
Under the conditions of conventional triaxial, as shown in Fig. 1a, when σ2 = σ3, then p = (σ1 + 2σ3)/3, q = σ1 − σ3, so the slope K2 of the stress path in generalized stress space can be expressed as follows.

$$K_{2} = \frac{{{\text{d}} q}}{{{\text{d}} p}} = \frac{{3\left( {{\text{d}}\sigma_{1} - {\text{d}}\sigma_{3} } \right)}}{{{\text{d}}\sigma_{1} {\text{ + 2d}}\sigma_{3} }}$$
(4)
Fig. 1
figure 1

Loading diagram of true-triaxial in p–q space

Full size image

In the generalized stress space, the stress path slope under conventional triaxial condition is consistent with that under true-triaxial condition, that is K1 = K2, the following equation is obtained.

$$\frac{{3\sqrt {\left( {b^{2} - b + 1} \right)} \left( {{\text{d}}\sigma_{1} - {\text{d}}\sigma_{3} } \right)}}{{\left( {b + 1} \right){\text{d}}\sigma_{1} - \left( {b - 2} \right){\text{d}}\sigma_{3} }}{ = }\frac{{3\left( {{\text{d}}\sigma_{1} - {\text{d}}\sigma_{3} } \right)}}{{{\text{d}}\sigma_{1} {\text{ + 2d}}\sigma_{3} }}$$
(5)

Calculate dσ1 from Eq. 5.

$${\text{d}}\sigma_{1} { = }\frac{{b - 2 + 2\sqrt {\left( {b^{2} - b + 1} \right)} }}{{b + 1 - \sqrt {\left( {b^{2} - b + 1} \right)} }}{\text{d}}\sigma_{3} \left( {0 < b < 1} \right)$$
(6)

Equation 6 is the governing equation to ensure that the stress paths for both types of devices in the p–q space are consistent. When the axial and radial stresses of the conventional triaxial are loaded according to Eq. 6, then in the p–q space, the conventional triaxial apparatus can ensure that the stress path is consistent with the true-triaxial apparatus strictly.

Therefore, the conventional triaxial apparatus can measure the mechanical response when 0 < b < 1. Using the same b-value and doing a series of tests at different confining pressures, as shown in Fig. 1a. The critical state line of the soil can be obtained, the true-triaxial stress path of different b at the same consolidated confining pressure 100 kPa as shown in Fig. 1b.

When the true-triaxial test determines the mechanical response on the π plane, then the true-triaxial test ensures that both p and b are constant during the shearing, and dp = 0 should be satisfied in Eq. 2. Then the loading paths of major and minor principal stresses can be obtained according to dp = 0 and dσ2 = bdσ1 + (1 − b) dσ3.

$${\text{d}}\sigma_{1} { = }\frac{b - 2}{{b + 1}}{\text{d}}\sigma_{3}$$
(7)

Equation 7 is the control equation for the loading path of σ1 and σ3 of the true-triaxial apparatus at different b-values. However, when the conventional triaxial is also loaded according to Eq. 7, and b is calculated by σ2 = bσ1 + (1 − b)σ3, then the stress path of the true-triaxial is obtained equivalently. As shown in Fig. 2a, in the principal stress space, the intermediate principal stress of the conventional triaxial is calculated by using σ2 = bσ1 + (1 − b)σ3 equivalent calculation, so that the same stress path as the true-triaxial is obtained. If this calculation method is also adopted for principal stress in p–q space, the same stress path as true-triaxial can also be obtained, as shown in Fig. 2b.

Fig. 2
figure 2

The stress paths in the π plane

Full size image

2.3 The loading method with b as a variable

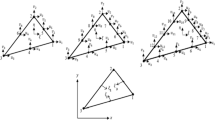
In the case of the deviatoric stress consolidation, when the generalized shear stress is small, i.e. the soil is in the state of plastic flow. If the loading path controlled by Eq. 7 is adopted, the 3D mechanical law of consolidated soil and over-consolidated soil can be studied experimentally, as shown in Fig. 3a. After the consolidation, if p and q are kept a constant and the value of b is changed continuously, the flow pattern of soil deformation is studied, as shown in Fig. 3b. The derivation process of the stress path is as follows.

Fig. 3
figure 3

The stress path under the deviatoric stress consolidation

Full size image

The expression that takes the variable b into p and q in Eq. 1 and reads:

$$\left. \begin{gathered} p = \frac{b + 1}{3}{\mkern 1mu} \sigma_{1} - \frac{b - 2}{3}{\mkern 1mu} \sigma_{3} {\mkern 1mu} \hfill \\ q = \sqrt {\left( {b^{2} - b + 1} \right)} \left( {\sigma_{1} - \sigma_{3} } \right) \hfill \\ \end{gathered} \right\}$$
(8)

In the true-triaxial test, when the deviatoric consolidation is used, the soil has both a generalized normal stress and a generalized shear stress, and then it is ensured that p and q are constant for loading, i.e. in Eq. 8, dp = 0, dq = 0.

$$\left. \begin{gathered} {\text{d}}p = \frac{b + 1}{3}{\mkern 1mu} {\text{d}}\sigma_{1} + \frac{2 - b}{3}{\text{d}}\sigma_{3} {\mkern 1mu} + \frac{{\sigma_{1} - \sigma_{3} }}{3}{\text{d}}b{ = }0{\mkern 1mu} \hfill \\ {\text{d}}q = \frac{{(2b - 1)(\sigma_{1} - \sigma_{3} )}}{{\sqrt {\left( {b^{2} - b + 1} \right)} }}{\text{d}}b + \sqrt {\left( {b^{2} - b + 1} \right)} ({\text{d}}\sigma_{1} - {\text{d}}\sigma_{3} ){ = }0 \hfill \\ \end{gathered} \right\}$$
(9)

According to Eq. 9, the loading equation with continuous change of b is obtained.

$$\left. \begin{gathered} {\text{d}}\sigma_{1} = - \frac{{b(\sigma_{1} - \sigma_{3} )}}{{2\left( {b^{2} - b + 1} \right)}}{\text{d}}b \hfill \\ {\text{d}}\sigma_{3} = \frac{{(b - 1)\sigma_{1} - (b - 1)\sigma_{3} }}{{2\left( {b^{2} - b + 1} \right)}}{\text{d}}b \hfill \\ \end{gathered} \right\}$$
(10)

Substituting \(b = \left( {\sqrt 3 \tan \theta + 1} \right)/{2}\) into Eq. 10, taking the Lode angle as a variable, the loading pattern of controlling the major principal stress and minor principal stress is as follows.

$$\left. \begin{gathered} {\text{d}}\sigma_{1} = - \frac{{(\sigma_{1} - \sigma_{3} )(\sqrt 3 \cos \theta_{\sigma } + 3\sin \theta_{\sigma } )}}{{6\cos \theta_{\sigma } }}{\text{d}}\theta_{\sigma } \hfill \\ {\text{d}}\sigma_{3} = - \frac{{(\sigma_{1} - \sigma_{3} )(\sqrt 3 \cos \theta_{\sigma } - 3\sin \theta_{\sigma } )}}{{6\cos \theta_{\sigma } }}{\text{d}}\theta_{\sigma } \hfill \\ \end{gathered} \right\}$$
(11)

Equations 10 and 11 can be simplified as follows.

$$\left. \begin{gathered} {\text{d}}\sigma_{1} = \frac{b}{b - 1}{\text{d}}\sigma_{3} = \frac{{\sqrt 3 \cos \theta_{\sigma } + 3\sin \theta_{\sigma } }}{{\sqrt 3 \cos \theta_{\sigma } - 3\sin \theta_{\sigma } }}{\text{d}}\sigma_{3} \hfill \\ 0 < b < 1, - \frac{\pi }{6} < \theta_{\sigma } < \frac{\pi }{6} \hfill \\ \end{gathered} \right\}$$
(12)

Equation 12 is the governing equation of nonlinear loading pattern with b or θσ as a control variable. The conventional triaxial apparatus can be loaded along the stress path according to Eqs. 11 or 12. Comparing the measured strain in ε1-ε2-ε3 space, the plastic flow pattern of the soil can be studied, as shown in Fig. 3b. Equations 10 and 11 require the conventional triaxial apparatus to adopt a nonlinear loading mode. However, the existing conventional triaxial apparatus only has a linear loading module, and the nonlinear loading module needs to be developed according to the formula suggested in this paper.

Sections 2.2 and 2.3 give the equations of the stress control method. According to the method presented in this paper, the strain control method can also be used to realize the strain path. Due to space limitations, this paper does not give specific formulas for the time being. However, the strain and stress control method brings greater convenience to the test as the most basic control module of the triaxial test. The strain and stress mixed control loading method was adopted in the true-triaxial plane strain test. Theoretically, the method proposed can also be equivalent to realize the stress path for plane strain test on the conventional triaxial apparatus, but it will increase the control difficulty of equipment greatly.

2.4 Strength criterion

To verify the rationality of the method proposed in this paper, two widely used strength criteria are selected for comparison and verification. The first is the Mohr–Coulomb criterion, in which a linear interpolation function is used in the p–q–θσ space (Bardet 1990), and its expression is as follows.

$$q - M_{f} g\left( {\theta_{\sigma } } \right)p = 0$$
(13)

where Mf is the peak stress ratio of conventional triaxial compression test (θσ = − 30°), Mf = 6sinφf/(3 − sinφf). φf is the triaxial compression peak internal friction angle measured experimentally. g1(θσ) is the shape function, and its expression is as follows.

$$g_{1} \left( {\theta_{\sigma } } \right){ = }\frac{\sqrt 3 \beta }{{\left( {\beta + 1} \right)\cos \theta_{\sigma } + \sqrt 3 \left( {\beta - 1} \right)\sin \theta_{\sigma } }}$$
(14)

where β is the peak stress ratio of θσ at 30° and − 30° respectively, \(\beta \, = \,\left( {M_{f} } \right)_{{\theta \sigma \, = { 3}0^\circ }} /\left( {M_{f} } \right)_{{\theta \sigma \, = \, - {3}0}}\), i.e. β is the peak stress ratio of triaxial compression test and triaxial elongation test.

The second one adopts the generalized Mohr–Coulomb criterion proposed by Willam and Warnke (1975), where g2(θσ) is the elliptic interpolation function, and its expression is as follows.

$$g_{2} \left( {\theta_{\sigma } } \right) = \frac{{2\left( {1 - \beta^{2} } \right)\cos \left( {\frac{\pi }{6} - \theta_{\sigma } } \right) + (2\beta - 1)\sqrt {4\left( {1 - \beta^{2} } \right)\cos^{2} \left( {\frac{\pi }{6} - \theta_{\sigma } } \right) + \beta (5\beta - 4)} }}{{4\left( {1 - \beta^{2} } \right)\cos^{2} \left( {\frac{\pi }{6} - \theta_{\sigma } } \right) + (2\beta - 1)^{2} }}$$
(15)

3 The verification by conventional triaxial test

3.1 Experimental description

The equipment adopts a triaxial apparatus developed by Ningxi Soil Instrument Co., Ltd in Nanjing, China, which is mainly composed of a host, a pressure controller, and a multi-channel communication digital acquisition instrument, as shown in Fig. 4. The specimen size is Φ39.1 mm × 80 mm, the axial load range is 0–30 kN, and the measurement accuracy is ± 1%FS (Full Scall). The range of the confining pressure controller is 0–1.99 MPa, the range of the back pressure controller is 0–0.99 MPa, and the control accuracy is ± 0.5%FS.

Fig. 4
figure 4

SLB-1 triaxial apparatus, Nanjing, China

Full size image

The sample is selected from the aeolian sand in the centre of the Tengger Desert. The constrained diameter d60 of the sand is 0.33, the medium particle diameter d30 is 0.30, the effective particle diameter d10 is 0.26, the unevenness coefficient Cu is 1.42, the curvature coefficient Cc is 0.97, and the fine particle content is less than 5%, which belongs to poorly graded sand. The moisture content of the dry sand of Tengger Desert aeolian sand is 0.14%, the maximum dry density is 1.68 g/cm3, and the minimum dry density is 1.40 g/cm3. In the experiment, a medium-density specimen with a density of 1.49 g/cm3 was prepared by controlling the relative compaction of Dr = 0.37, the initial void ratio is 0.79, and the specific gravity is 2.67. According to the size of specimens, weigh 143.2 g of the sand and divide it into 5 equal parts. Specimen preparation method using layered falling sand, the sand is dropped into the mould of specimen preparation to the specified height evenly. To reduce personal error in the specimen preparation process and ensure the stability of the specimen, it is necessary to control the specimen height error not to be higher than 1.5 mm, that is, less than 2% of the specimen height. For other test parameters of aeolian sand in the Tengger Desert, please refer to the study results of Ma and Li (2023).

The test is carried out for hydraulic head saturation first, and then for back pressure saturation. The vacuum state of the specimen was used to quickly inject water into the specimen to fill the void. The time of hydraulic head saturation is 30 min. When the discharged water volume is twice the specimen volume and there are no bubbles in the discharged water, the hydraulic head saturation is completed. After that, the graded back pressure saturation is carried out. When confining pressure, back pressure and pore pressure remain unchanged, and there is no liquid outflow from the back pressure controller, the next grade of back pressure saturation is carried out until the saturation reaches the test requirements. After the saturation test, isotropic consolidation is carried out on the specimen. When the volume of the water discharged from the specimen is less than 1% of the specimen within 30 min, the consolidation is regarded as completed.

3.2 The test scheme

To verify the correctness and rationality of the proposed method, we explore the strength characteristics, the deformation and the failure characteristics of the aeolian sand on the π plane, the undrained stress paths are carried out with a conventional triaxial apparatus when the effective average principal stress p is 100 kPa, 300 kPa, 600 kPa and the intermediate principal stress coefficient b is 0, 0.2, 0.4, 0.6, 0.8, 1 respectively. The scheme is shown in Table 1. Note the experimental results under drained conditions have been presented in the reference Ma and Li (2023).

Table 1 Test scheme at constant p and constant b
Full size table

In the test, it is necessary to control the increasing rate of σ1 and the decrease rate of σ3 to load according to the proportion set by Eq. 7, and the stress path loading scheme was achieved at different b and a constant p. Because there are many influencing factors in the actual operation of the test, to reflect the undrained characteristics of strength-deformation and failure under conditions of different stress paths accurately, it is necessary to keep the specimen preparation method, the density, the effective confining pressure, the consolidation conditions, the loading rate and other parameters consistent completely.

Figure 5 shows the stress path designed according to the conventional triaxial apparatus. The axial and radial stress increments are set according to Fig. 5a. The ratios of the axial and radial loading are different for different b values, as shown in Fig. 5b, which describes the true-triaxial stress path equivalently in the 3D space.

Fig. 5
figure 5

Schematic diagram of loading path

Full size image

Figure 6a is the equivalent stress path designed according to the characteristics of the conventional triaxial apparatus. In the figure: q = σ1 − σ3, p = (σ1 + σ2 + σ3)/3, σ2 = bσ1 + (1 − b)σ3, it can be concluded that the stress paths under the conditions of constant p and constant b are satisfied for the stress paths of the true-triaxial. Figure 6b is the actual stress path organized according to the traditional test method. In the Fig. 6b, p = (σ1 + 2σ3)/3, q = σ1 − σ3. In fact, the stress path itself can also reflect the difference in stress paths under different conditions.

Fig. 6
figure 6

The stress path of a conventional triaxial apparatus

Full size image

3.3 The results under undrained triaxial conditions

Figure 7 shows the effective stress path measured by conventional triaxial apparatus under undrained conditions when p is 100 kPa, 300 kPa, and 600 kPa, and b is 0, 0.2, 0.4, 0.6, 0.8, and 1, respectively. As shown in Fig. 7, under the condition of a constant b and different p, the specimen has obvious contraction at low confining pressure, and the specimen has obvious dilatation at high confining pressure. Finally, the specimen tends to the same critical state line at all p. In Fig. 7a–f all show the same law. As b increases, the slope of the critical state line decreases monotonically. For the phase transformation line, its evolution trend is consistent with the critical state line.

Fig. 7
figure 7

Test law under constant b and constant p

Full size image

When p is constant, the strength decreases monotonously with the increase of b, and the specimen changes continuously from contraction to dilatation continuously, and its phase transformation points also changes monotonously, as shown in Fig. 8a–c. The two crucial state lines are important for describing the mechanical behaviour of granular materials. Figure 8d summarizes these indexes and shows the overall variation pattern of effective stress paths. Combining all the test results, the triaxial test obtained the critical state line under the condition of a constant p and a constant b, the slope of which decreases monotonously. This is consistent with the trend of the results measured by the true triaxial apparatus, which is the result of the effect of the b-values. In addition, the laws under the three confining pressure conditions are the same, as shown in Fig. 8d.

Fig. 8
figure 8

Test law at the condition of constant p and different b

Full size image

Figure 9 shows the law of the peak stress on the π plane. In the figure, the failure curves of Mohr–Coulomb and nonlinear generalized Mohr–Coulomb are determined as parameters based on the peak stress ratio when b = 0 and b = 1. From the comparison of the test results under the three confining pressures, it can be concluded that the test results are close to the strength envelope of the generalized Mohr–Coulomb. In particular, the strength criterion parameters are determined according to the critical state line in Fig. 8d, and the results can better obtain the strength law of the aeolian sand on the π plane. The results reflect the determination purpose of the design scheme reasonably and prove the rationality and the practicability of the novel method presented in this paper preliminarily.

Fig. 9
figure 9

Test strength and criterion simulation on π plane

Full size image

4 Conclusions

This paper draws on the advantages of both conventional triaxial and true-triaxial tests to ensure that the stress paths of the both are the same in the generalized stress space. A novel method is presented to determine true-triaxial stress paths by the conventional triaxial test. The effectiveness and rationality of the method are verified by the conventional triaxial undrained test of aeolian sand in the Tengger Desert. The main conclusions are as follows:

Considering the loading characteristics of cylindrical specimens and cuboid specimens, it is ensuring that the stress paths of the conventional triaxial and true-triaxial are consistent in generalized stress invariant space, and the control formulas of conventional triaxial loading are deduced with b as a constant and a continuous variable respectively. When b is a constant and p is a variable, the derived equation can strictly ensure that the designed stress paths are consistent in the generalized stress space completely. All the stress paths of true-triaxial can be achieved by the conventional triaxial loading module. When b and p are constant, the derived equation controls the axial and radial loading of the conventional triaxial respectively, and the true-triaxial stress path can be achieved. Under the condition of a constant b and different p, the conventional triaxial test can determine the influence of the intermediate principal stress coefficient on the soil critical state line. Under the condition of a constant p and different b, the conventional triaxial test can determine the law of strength and deformation on the π plane. When p and q are constants, the control equation of the conventional triaxial apparatus is derived. The equation must adopt the nonlinear loading control method with b as the parameter, and it can be realized in case of adding a new module to the conventional triaxial apparatus. Using the proposed equation, the various stress paths of true-triaxial under the condition of deviatoric stress consolidation can be designed, and the deformation flow law of the soil in 3D space can be determined. It overcomes the shortcomings of the true-triaxial apparatus and its complicated operation.

The conventional triaxial test was carried out on Tengger Desert sand to verify the rationality and effectiveness of the novel method. According to the control equation with a constant of p and b, the stress path is designed when p is 100 kPa, 300 kPa and 600 kPa, and b is 0, 0.2, 0.4, 0.6, 0.8 and 1. Under the condition of a constant b and different p, the specimen has obvious contraction at low confining pressure, and the specimen has obvious dilatation at high confining pressure. Finally, the specimen tends to have the same critical state line at all p. As b increases, the slope of the critical state line decreases monotonically. The designed test can better obtain the strength law of the actual Tengger desert aeolian sand on the π-plane, and can better achieve the function of true triaxial apparatus. The results can reasonably reflect the measurement purpose of the design scheme, which preliminarily proves the rationality and practicability of the method proposed in this paper.