1 Introduction

Microwave is employed in industry as a source of thermal energy for several decades. Microwave heating is really popular in food industry (Satoshi et al. 2020). Recently, microwave heating was employed in construction industry (Wei et al. 2019, 2021a; Makul et al. 2014; Bai et al. 2021), microwave assisted aggregate recycling, microwave assisted concrete curing, microwave assisted rock drilling, etc. (Fan et al. 2020, 2017). Microwave is a form of electromagnetic radiation, in which frequencies varied between 300 MHz and 300 GHz. There are four frequencies designed for industrial and science applications: 915 MHz, 2450 MHz, 5800 MHz and 22,125 MHz. Microwave heating provide a volumetric heating process, the microwave absorption materials could be heated easily and volumetrically (Stuchly and Hamid 1972; Ahmadreza et al. 2021; Khashayar and Richard 2021). Microwave heating is based on the conversion of energy from electric and magnetic fields to joule heat. The heating process omitted the cavity warming-up period, the materials can be heated directly and simultaneously. Microwave heating represents the transformation process of electromagnetic to thermal energy. Microwave absorption ability depend on the heated materials’ dielectric properties. The microwave energy mechanism conversion is generally divided into dielectric loss and magnetic loss. Dielectric loss is the process in which microwave induced electromagnetic energy is converted into heat energy. Dielectric loss energy path is a way to convert energy from electromagnetic field to heat output. When the medium is heated by microwave, the electric field begins to oscillate polarity within the electromagnetic field. The microwave electric field causes the material molecule electric dipole to rotate instantaneously, lining up the molecules in the direction of the electric field (Samson et al. 2021). The molecule would rotate corresponding to the direction of the electric field to maintain alignment when the direction of the electric field changes. When the molecules spin, heat is efficiently generated (Walkiewicz et al. 1988). Since molecular clusters do not move precisely in response to electric fields, dielectric heating involves disorganized motion on a micro scale. Hysteresis is the main cause of magnetization. The heating process is actually the conversion of energy to molecular rotation, in the form of temperature changes. When a conductive material is subjected to microwave radiation, the electric field under the microwave radiation generates electric current and heat energy, which is defined as resistance loss. The magnetic field also causes heating under microwave irradiation, and the loss mode in this conversion process is called magnetic loss. Magnetic loss is the process by which a magnetic material is converted into heat after being magnetized (Wei et al. 2021b).

The microwave heating mechanism involves heat conduction, heat convection and electromagnetic heating (Wei et al. 2021c; Li et al. 1994). The anisotropic energy loss and electromagnetic field of heated materials during microwave irradiation result in the non-uniform temperature distribution within concrete. Owing to the imperfect analytical investigation, the microwave energy loss and heated temperature field subject to different materials were not explicit yet. The heating mechanism, the temperature and mechanical field variations were less investigated. During the electromagnetic heating, the concrete temperature variation significantly depends on the material’s dielectric loss, which relate to the microwave parameters and concrete properties. The heating mechanism determines the temperature and stress distribution within the concrete, which then influences the materials properties variation during the heating process. Many experimental and numerical investigations of microwave heating concrete have been conducted. However, few researchers have theoretically analyzed these problems. The analytical investigation is the basis to study the concrete heating response under microwave irradiation. The temperature distribution of different media under microwave heating, the temperature development and change process, and the corresponding changes in mechanical properties brought about by it should be investigated first. In terms of microwave heating concrete, the essence is to investigate the heating response of material with different wave absorption ability, the mortar and aggregate, respectively. Compared with most type of aggregate, mortar was low dielectric loss material, while the aggregate such as basalt and granite can be heated easily under microwave irradiation. During the heating process, one of these two materials can be regarded as microwave absorbing medium, and the other as microwave insensitive medium, to study the thermal–mechanical response mechanism of composite materials under microwave heating.

In this paper, the double-layer cylindrical concrete model is established, the electromagnetic field and energy absorption of concrete under microwave heating are analyzed. The energy absorption can be regarded as the internal heat source, and the transient heat conduction process between aggregate and mortar under microwave irradiation is studied by coupling the electromagnetic field with heat conduction equation. By employing the integral-transform method, solution for the time-dependent temperature is obtained. The variation of temperature in concrete and at the mortar-aggregate interface were discussed.

2 Microwave power formulation

Generally, there are two methods to calculate the energy generation in the heated materials, the Poynting theorem and Lambert law, respectively (Stratton 2007). Researches indicated that Poynting theorem was suitable for the materials with certain size, while for the large-size object, using Lambert law could obtain a more realizable results (Griffiths 1999; Liu et al. 2005). The Poynting theorem was employed to investigate the electric field and microwave power absorption in double-layer concrete in our research. Poynting theorem is a statement in electromagnetic theory: the transfer of energy by an electromagnetic wave is at right angles to both electric and magnetic components of the wave vibration and its rate is proportional to the vector product of their amplitudes.

2.1 Theoretical model

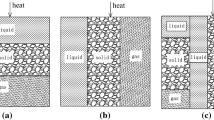
In this study, a double-layer concrete object was heated by microwave. The inner basalt aggregate is a kind of good microwave absorber and the outer mortar was relatively almost transparent to microwave. We assume microwave is transverse uniform plane electromagnetic waves, that is TEM wave. Although there will be a difference with the real case, the electric and temperature field formed in aggregate, mortar and the interface can be revealed clearly. Compared with mortar, basalt aggregate has much stronger microwave absorption ability. So we assume that microwave could only heated aggregate, which means that there was an internal heat source within aggregate when microwave treated the whole concrete sample. The mortar was heated through heat conduction from aggregate (Fig. 1).

Fig. 1
figure 1

Double-layer concrete model heated under microwave irradiation

Full size image

Other assumptions used to simplify the problem were:

  1. (1)

    Materials dielectric properties were not varied during heating process;

  2. (2)

    Materials properties were not varied during heating process, the thermal conductivity, specific heat, for example.

2.2 Solution of microwave power

Maxwell's Equations are a set of four equations that describe the world of electromagnetics. These equations describe how electric and magnetic fields propagate, interact, and how they are influenced by objects. When microwave heated concrete, the inner electromagnetic distribution can be given as:

$$\begin{aligned} \vec{\nabla } \times \vec{E} & = - \frac{{\partial \vec{B}}}{\partial t} \\ \vec{\nabla } \times \vec{H} & = \vec{J} + \frac{{\partial \vec{D}}}{\partial t} \\ \vec{\nabla } \cdot \vec{D} & = \rho_{V} \\ \vec{\nabla } \cdot \vec{B} & = 0 \\ \end{aligned}$$
(1)

where \(\vec{E}\) is the electric field, \(\vec{B}\) is the magnetic induction, \(\vec{H}\) is the magnetic field, \(\vec{J}\) is the current density, \(\vec{D}\) is the electric displacement, and \(\rho_{V}\) is the electric charge density.

Microwave heat generation can be calculated as Eq. (2):

$$\begin{aligned} \vec{q} & = \frac{1}{2}\vec{E} \times \vec{H}^{*} \\ Q(z) & = - {\text{Re}} (\vec{\nabla } \cdot \vec{q}) \\ \end{aligned}$$
(2)

where \(\vec{q}\) represent Poynting vector, \(\vec{H}^{*}\) is the complex conjugate of the magnetic field. During microwave heating process, inner heating temperature is governed by Eq. (3):

$$\rho C_{p} \frac{dT}{{dt}} = \vec{\nabla } \cdot (k\vec{\nabla }T) + Q$$
(3)

The governing Maxwell’s equation can be expressed as Eq. (4) based on the model and assumptions;

$$\begin{aligned} \vec{J} & = \sigma \vec{E} \\ \vec{D} & = \varepsilon \vec{E} \\ \vec{B} & = \mu \vec{H} \\ \end{aligned}$$
(4)

where σ is the electrical conductivity, ε is the dielectric constant, μis the magnetic permeability.

Calculated by curl, the Eq. (1) and (4) can be expresses as:

$$\left\{ {\begin{array}{*{20}l} {\nabla^{2} \vec{E} = \mu \varepsilon \frac{{\partial^{2} \vec{E}}}{\partial t}} \hfill \\ {\nabla^{2} \vec{H} = \mu \varepsilon \frac{{\partial^{2} \vec{H}}}{\partial t}} \hfill \\ \end{array} } \right.$$
(5)

If microwave incidents are propagating only within the axial direction, then there were:

$$\begin{aligned} & E_{z} = E_{\phi } = 0 \\ & \frac{{\partial E_{r} }}{\partial r} = \frac{{\partial E_{r} }}{\partial \phi } = 0 \\ \end{aligned}$$
(6)

For the TEM wave, when microwave propagated only in z direction, the only non-zero component of electric field was E = Er, the electric field equation can be expressed as Eq. (7) through the curl of Eq. (6):

$$\frac{{d^{2} E_{r} }}{{dz^{2} }} + \chi^{2} E_{r} = 0$$
(7)

where χ is the propagation constant, which can be give as \(\chi^{2} = \omega^{2} \mu_{0} \varepsilon_{0} (\kappa{\prime} + i\kappa^{^{\prime\prime}} )\).

The calculation in this part only involves the field vector that independent of time (Hossan et al. 2010), χ can be also expressed as \(\chi = \sigma + i\beta\),where the phase and attenuation factors were shown in Eq. (8).

$$\begin{aligned} \sigma & = \frac{2\pi f}{c}\sqrt {\frac{{\kappa^{\prime } \left( {\sqrt {1 + \tan^{2} \delta } + 1} \right)}}{2}} \\ \beta & = \frac{2\pi f}{c}\sqrt {\frac{{\kappa^{\prime } \left( {\sqrt {1 + \tan^{2} \delta } - 1} \right)}}{2}} \\ \tan \delta & = \frac{{\kappa^{\prime \prime } }}{{\kappa^{\prime } }} \\ \end{aligned}$$
(8)

where \(c = {1 \mathord{\left/ {\vphantom {1 {\sqrt {\mu_{0} \varepsilon_{0} } }}} \right. \kern-0pt} {\sqrt {\mu_{0} \varepsilon_{0} } }}\), \(\kappa^{\prime }\) is relative dielectric constant, \(\kappa^{\prime \prime }\) is relative dielectric loss.

Due to the microwave radiations directions (Ayappa et al. 1991; Hossan and Dutta 2012), the boundary conditions for TEM waves can be given as:

$$\begin{aligned} & E_{r,0} \left| {_{z = 0,L} } \right. = E_{r,l} \left| {_{z = 0,L} } \right. \\ & \frac{1}{{\mu_{0} \omega }}\frac{{dE_{r,0} }}{dz}\left| {_{z = 0} } \right. = \frac{1}{{\mu_{0} \omega }}\frac{{dE_{r,l} }}{dz}\left| {_{z = 0} } \right. \\ \end{aligned}$$
(9)

where 0 and 1 represent the aggregate and surrounding area, respectively.

The solution of Maxwell’s equation can be given as Eq. (10).

$$E_{r,l} = A_{l} e^{{i\chi_{l} z}} + B_{l} e^{{i\chi_{l} z}}$$
(10)

Substituting the boundary condition in Eq. (9), the coefficient of Ai and Bi can be represented as Eq. (11):

$$\begin{aligned} A_{l} & = \frac{{T_{01} E_{0} }}{{1 + R_{01} e^{{i\chi_{l} L}} }} \\ B_{l} & = \frac{{T_{01} E_{0} e^{{i\chi_{l} L}} }}{{1 + R_{01} e^{{i\chi_{l} L}} }} \\ \end{aligned}$$
(11)

where the transmission and reflection coefficient T01 and R01 can be expressed as Eq. (12):

$$T_{01} = \frac{{2\zeta_{1} }}{{\zeta_{1} + \zeta_{0} }},R_{01} = \frac{{\zeta_{1} - \zeta_{0} }}{{\zeta_{1} + \zeta_{0} }}$$
(12)

The intrinsic impedance can be calculated based on Eq. (13):

$$\zeta = \frac{\mu \omega }{\chi }$$
(13)

The microwave was TEM wave. Electric field propagated only along the z direction, which can be calculated as:

$$E = \frac{{T_{01} E_{0} }}{{1 + R_{01} e^{{i\chi_{1} L}} }}(e^{{i\chi_{1} z}} + e^{{i\chi_{1} (L - z)}} )$$
(14)

The magnetic field can be evaluated based on the governing equation and the solution of electric field, shown in Eq. (15):

$$\frac{{dE_{r,l} }}{dz} = i\mu_{l} \omega H_{\varphi ,l}$$
(15)

Based on the Poynting theorem, the microwave induced power generation can be obtained:

$$Q(z) = \frac{1}{2}\omega \varepsilon_{0} \kappa^{\prime \prime } \left| E \right|^{2} = \frac{1}{2}\omega \varepsilon_{0} \kappa^{\prime \prime } \left| {E_{0} } \right|^{2} \left| {T_{01} } \right|^{2} \times \frac{{e^{ - 2\beta z} + 2e^{ - \beta L} \cos (2\sigma z - \sigma L) + e^{ - 2\beta (L - z)} }}{{1 + 2\left| {R_{01} } \right|e^{ - \beta L} \cos (\delta_{01} + \sigma L) + \left| {R_{01} } \right|^{2} e^{ - \beta L} }}$$
(16)

where T01 and R01 represent the transmission and reflection coefficient, respectively.

$$\left| {T_{01} } \right| = \left| {\frac{2}{{1 + \sqrt {\kappa^{\prime } - i\kappa^{\prime \prime } } }}} \right|,\left| {R_{01} } \right| = \left| {\frac{{1 - \sqrt {\kappa^{\prime } - i\kappa^{\prime \prime } } }}{{1 + \sqrt {\kappa^{\prime } - i\kappa^{\prime \prime } } }}} \right|$$
(17)

2.3 Numerical simulation

The whole heating process was simulated in COMSOL Multiphysics 5.6. Based on the real dimensions of the test equipment and specimens, three-dimensional geometric model was established, as shown in Fig. 2 with detailed geometry. Microwave transparent porous alumina plate was placed in the center of cavity, and mortar-aggregate sample was placed above the center of the porous alumina plate. The resonator was filled with air, and microwave energy was transmitted to the resonant cavity through four rectangular waveguides. In order to compare with the theoretical analysis, only one waveguide was employed in the simulation process. In addition, for ensuring the accuracy of simulation results, the whole model was divided by triangle mesh, which results in 176,703 domain elements and 8660 boundary elements, and the average element quality of the geometry was 0.705. The three-dimensional finite element model combines electromagnetic field, heat transfer field, and mechanic field together.

Fig. 2
figure 2

Schematic diagram of microwave heating model

Full size image

2.4 Microwave electric field and power absorption

The investigation of microwave energy absorbed ability of materials was the basis for analyze the microwave heating effect. When concrete was heated under microwave irradiation, a portion of microwave energy can be absorbed by the heated materials, part of the microwave will be reflected or dissipated. We assumed that the incident electric field was 8000 V/m, the length of aggregate was 50 mm. Due to the TEM wave propagation properties, the electric field and microwave power absorption within r and ϕ direction were not changed. The theoretical results of electric field distribution along the center line in aggregates were shown in Fig. 3. It can be seen that the electric field presented the cosine distribution. The higher the frequency of microwave heating, the higher the frequency of electric field fluctuation. The value of electric field intensity was influenced by microwave heating frequency. For 50 mm aggregate, the maximum electric intensity occurred at the both ends of materials, which was only about one-tenth of incident electric field, majority of electric energy were reflected and dissipated.

Fig. 3
figure 3

Electric field in concrete aggregate (L = 0.05 m, E0 = 8000 V/m)

Full size image

As shown in Fig. 4, when microwave heating frequency changed, the power absorption varied apparently, in both values and fluctuated frequency. When the microwave heating frequency was 2450 MHz, the electric field fluctuation was more frequent than that at 915 MHz. It can be seen that the higher the frequency, the shorter the period, and the more frequent oscillation of high frequency wave.

Fig. 4
figure 4

Microwave power absorption in concrete aggregate (L = 0.05 m, E0 = 8000 V/m)

Full size image

When the intensity of incident electric field increased to 10000 V/m (Fig. 5), the aggregate absorbed electric intensity increased, while the distribution pattern was not changed. The maximum electric intensity was still at the both ends of materials, which increased to about 3000 V/m. It can be found that higher electric intensity lead to higher microwave energy loss.

Fig. 5
figure 5

Electric field in concrete aggregate (L = 0.05 m, E0 = 10000 V/m)

Full size image

When the incident electric intensity increased, the microwave power absorption increased accordingly, while the distributional pattern was unchanged, as shown in Fig. 6. The variation of power absorption will lead to the change of temperature field.

Fig. 6
figure 6

Microwave power absorption in concrete aggregate (L = 0.05 m, E0 = 10000 V/m)

Full size image

When the length of aggregate increased to 0.11 m, the cycle of electric intensity shortens, and the value was changed accordingly (Fig. 7). It was apparent that the size of heated sample could affect the electric field within the materials under the same input parameters.

Fig. 7
figure 7

Electric field in concrete aggregate (L = 0.11 m, E0 = 8000 V/m)

Full size image

The microwave power absorption was lower in 0.11 m aggregate compared with that in 0.05 m (Fig. 8), which may owning to the influence of microwave wave length, penetration depth and microwave incidence direction. For smaller size aggregate, the maximum power absorption formed at the center of cylinder, while for relatively larger aggregate, it occurred in the both ends of materials. The distribution of electric field and power absorption will influence the temperature field of concrete. Based on the solution of electrodynamics features, the temperature field can be obtained.

Fig. 8
figure 8

Microwave power absorption in concrete aggregate (L = 0.11 m, E0 = 8000 V/m)

Full size image

The numerical results were shown in Fig. 9 with incident electric field intensity = 10,000 V/m and the length of concrete was 0.05 m. Same with the theoretical results, the instantaneous value and amplitude of the electric field vary with depth. The value of electric intensity was close between numerical and theoretical results under the same electric incident. It can be seen that the electric field was waveform distributed within concrete, with the high and low electric region co-existed. When the microwave propagates through the waveguide to the cavity, due to the mismatch between the microwave and load, part of the energy will be reflected. In addition, the numerical simulation was obtained in a real heating cavity, while the theoretical results were reached in a more ideal situation. Under the circumstance, there were a difference between the electric field distribution between numerical and theoretical.

Fig. 9
figure 9

Simulated results of electric field distribution

Full size image

3 Solution of time-dependent temperature field

When the materials’ temperature is in a certain state during the heating process, it is called the steady-state temperature field (Kodur and Sultan 2003). The temperature of concrete under microwave irradiation was continuously changed. The original temperature balance of mortar will be broken when heat is transferred rapidly from aggregate to mortar phase. Due to the thermal inertia of concrete materials, heat transfer causes the uneven distribution of temperature, which changes with the heating time, forming the unsteady dynamic temperature field (Lienhard and John 2005). Microwave heating concrete is a typical dynamic heating conduction process with the internal volumetric heating source. The evolution of temperature distribution and interface temperature gradient is the basis to investigate the concrete heating response under microwave heating.

3.1 The unsteady-state heat conduction equation and equilibrium equations

As a quantity field, temperature field represents the transient temperature of each position in material. The temperature field is a time-dependent function for the unsteady state problem, which can be expressed as:

$$T = T(\varphi ,r,z,t)$$
(18)

In the double-layer cylinder concrete, the unsteady-state heat conduction equation can be expressed as:

$$\frac{1}{r}\frac{\partial }{\partial r}\left( {r\frac{{\partial T_{i} }}{\partial r}} \right) + \frac{{\partial^{2} T}}{{\partial z^{2} }} + \frac{1}{{k_{i} }}Q_{i} (r,z,t) = \frac{1}{{\partial_{i} }}\frac{{\partial T_{i} }}{\partial t},i = 1,2$$
(19)

where r is the radius, T is the heating temperature, k is heat conduction coefficients and 0 < z < L.

Within microwave absorber materials aggregate, the heat conduction equation was:

$$\frac{1}{r}\frac{\partial }{\partial r}\left( {r\frac{{\partial T_{1} }}{\partial r}} \right) + \frac{{\partial^{2} T_{1} }}{{\partial z^{2} }} + \frac{1}{{k_{1} }}Q_{1} (r,z,t) = \frac{1}{{\partial_{1} }}\frac{{\partial T_{1} }}{\partial t},0 < {\text{r < }}a$$
(20)

The heat conduction equation for microwave transparent materials mortar was shown in Eq. (21):

$$\frac{1}{r}\frac{\partial }{\partial r}\left( {r\frac{{\partial T_{2} }}{\partial r}} \right) + \frac{{\partial^{2} T_{2} }}{{\partial z^{2} }} = \frac{1}{{\partial_{2} }}\frac{{\partial T_{2} }}{\partial t},a < {\text{r < b}}$$
(21)

In the heating process, the boundary follows Newton's law of convective heat transfer. Through a given heat transfer coefficient between the object on the boundary and the surrounding environment, and assuming that the surrounding environment temperature remains constant, the boundary condition can be considered as the third type of boundary conditions, namely the Robin boundary (Landsberg and Tranter 1952).

The initial temperature boundary condition was:

$$r = 0,\frac{\partial T(0,z,t)}{{\partial r}} = 25$$
(22)

At the interface, the interface contact between mortar and aggregate was intact, temperature and heat flux were continuous:

$$r = a,T_{1} = T_{2}$$
(23)

Namely:

$$T_{1} (r_{a} ,z,t) = T_{2} (r_{a} ,z,t)$$
(24)
$$k_{1} \frac{{\partial T_{1} }}{\partial r} = k_{2} \frac{{\partial T_{2} }}{\partial r}$$
(25)

That is:

$$k_{1} \frac{{\partial T_{1} (r_{a} ,z,t)}}{\partial r} = k_{2} \frac{{\partial T_{2} (r_{a} ,z,t)}}{\partial r}$$
(26)
$$r = b,k_{2} \frac{{\partial T_{2} }}{\partial r} + h_{2} T_{2} = f_{2} (t)$$
(27)
$$k_{2} \frac{{\partial T_{2} (r_{b} ,z,t)}}{\partial r} + h_{2} T_{2} (r_{b} ,z,t) = f_{2} (t)$$
(28)
$$0 < {\text{r < a}},T_{1} = f_{1} (r)$$
(29)
$$z = L,k_{i} \frac{{\partial T_{i} (r_{i} ,z,t)}}{\partial z} = h_{i} \left( {T_{i} - T_{\infty } } \right),i = 1,2$$
(30)
$$z = 0, - k_{i} \frac{{\partial T_{i} (r_{i} ,z,t)}}{\partial z} = h_{i} \left( {T_{i} - T_{\infty } } \right),i = 1,2$$
(31)

The unsteady heat conduction equations and definite solution conditions for transient microwave heating process with internal heat source were obtained.

3.2 Theoretical analysis of time-dependent temperature field

When the heat conduction partial differential equation and the boundary condition are nonhomogeneous, it is complex to use the classical variables separation method to solve it. The integral transformation method can solve the nonhomogeneous unsteady heat conduction problem. In this method, the second partial derivative with respect to the spatial variable is usually removed from the heat conduction partial differential equation.

In the unsteady state problem, the partial derivative with respect to the spatial variable can be removed, and the partial differential equation was simplified to an ordinary differential equation. When solving an ordinary differential equation, the initial conditions after transformation should be satisfied, and the solution of the obtained solution should be inverted one by one, so as to obtain the solution of temperature.

In order to remove the partial derivative with respect to r from the Eq. (18), the forward and inverse transformations of the function T with respect to the variable r are:

$$T = \sum\limits_{m = 1}^{\infty } {\frac{{R_{0} (\beta_{m} ,r)}}{{N(\beta_{m} )}}} \overline{T} (\beta_{m} ,z,t)$$
(32)
$$\overline{T} (\beta_{m} ,z,t) = \int_{{r{\prime} = 0}}^{b} r ^{\prime}R_{0} (\beta_{m} ,r^{\prime})T(r^{\prime},z,t)$$
(33)

where \(R_{0} (\beta_{m} ,r)\),\(N(\beta_{m} )\) and \(\beta_{m}\) can be obtained through table look-up scheme. \(\overline{T}\) was the transformation of the variable r.

Through the integral transformation of Eq. (18) by employing Eq. (33):

$$- \beta_{m}^{2} \overline{T} (\beta_{m} ,z,t) + \frac{{\partial^{2} \overline{T} }}{{\partial z^{2} }} + \frac{{Q(\beta_{m} ,z,t)}}{k} = \frac{1}{\alpha }\frac{{\partial \overline{T} (\beta_{m} ,z,t)}}{\partial t}$$
(34)

The forward and inverse integral transformation of z were shown in Eqs. (35) and (36)

$$\overline{T} (\beta_{m} ,z,t) = \sum\limits_{p = 1}^{\infty } {\frac{{Z(\eta_{p} ,z)}}{{N(\eta_{p} )}}} \mathop {\overline{T} }\limits^{\sim } (\beta_{m} ,\eta_{p} ,t)$$
(35)
$$\mathop {\overline{T} }\limits^{\sim } (\beta_{m} ,\eta_{p} ,t) = \int_{z^{\prime} = 0}^{L} {Z(\eta_{p} ,z^{\prime})\overline{T} } (\beta_{m} ,z^{\prime},t)dz^{\prime}$$
(36)

where \(Z(\eta_{p} ,z)\), \(N(\eta_{p} )\) and \(\eta_{p}\) can be obtained through table look-up scheme. “ ~ ” represent the integral transformation of z.

Through the integral transformation of Eq. (34) by employing Eq. (36):

$$\frac{{d\mathop {\overline{T} }\limits^{\sim } }}{dt} + \alpha (\beta_{m}^{2} + \eta_{p}^{2} )\mathop {\overline{T} }\limits^{\sim } (\beta_{m} ,\eta_{p} ,t) = \frac{\alpha }{k}\mathop {\overline{g} }\limits^{\sim } (\beta_{m} ,\eta_{p} ,t)$$
(37)

The solution of \(\mathop {\overline{T} }\limits^{\sim } (\beta_{m} ,\eta_{p} ,t)\) can be obtained through Eq. (37). Through the inverse integral transformation of Eqs. (32) and (35), the solution of the heat conduction Eq. (18) can be expressed as Eq. (38):

$$T(r,z,t) = \sum\limits_{m = 1}^{\infty } {\sum\limits_{p = 1}^{\infty } {\frac{{R_{0} (\beta_{m} ,r)Z(\eta_{p} ,z)}}{{N(\beta_{m} )N(\eta_{p} )}}} } e^{{ - \alpha (\beta_{m}^{2} + \eta_{p}^{2} )t}} \cdot \left[ {\mathop {\overline{F} }\limits^{\sim } (\beta_{m} ,\eta_{p} ) + \frac{\alpha }{k}\int_{t^{\prime} = 0}^{t} {e^{{\alpha (\beta_{m}^{2} + \eta_{p}^{2} )t^{\prime}}} \mathop {\overline{g} }\limits^{\sim } (\beta_{m} ,\eta_{p} ,t^{\prime})dt^{\prime}} } \right]$$
(38)

The analytical solutions for time-dependent temperature of concrete under microwave irradiation was achieved. Due to the complexity of solving process, the Mathematica 12.1 Software was employed to solve these equations based on the NDSolveValue command.

3.3 Experimental verification

Experiment was carried out in an industrial multimode microwave heating system in the research. The microwave oven was manufactured by CHANGEMW Microwave Technology Development Co., Ltd., China (Fig. 10). The incident microwave power is tunable from 0 to 6 kW and the water-cooled magnetron operated at a frequency of 2450 MHz. The heating temperature, time and power input could be set before and during the heating process. The heating cavity is enclosed by the thermal insulation material. The temperatures were monitored by inserted thermocouple in microwave oven during the heating process and by infrared imaging devices after heating process.

Fig. 10
figure 10

Industrial microwave heating system

Full size image

Concrete specimens were designed as a cylinder, the high and radius of mortar were 50 and 40 mm, respectively, and the radius of aggregate was 15 mm. PO 42.5 grade ordinary Portland cement was used in the experiment. The samples can be used in microwave heating test after 28 days of standard water curing.

Based on poynting's theorem, the correlation of P and E can be expressed as:

$$P = \frac{1}{{2\eta_{z} }}\int {\left| E \right|}^{2} dS_{in} = \frac{{\left| E \right|^{2} S_{in} }}{{2\eta_{z} }}$$
(39)

where P is the microwave power input (W), \(\left| E \right|\) is mean square root of the incident electric field (V/m), Sin is the sectional area of microwave (m2), η is the system impedance.

Based on the Eq. (39), the microwave power can be related to the incident electric field. The theoretical results were verified through comparing with both microwave heating tests and simulation results, as shown in Fig. 11. The highest concrete surface temperature was selected for validation in experimental and numerical results. It can be seen that the regularity of experimental and theoretical results were same. It was obvious that the heating temperature of aggregate was much higher than that in mortar. Due to the waveform electric field within concrete, the temperature distribution on mortar surface was non uniform. The heating temperature of experimental results were relatively higher than the theoretical analysis, which may be due to the moisture effect of heating results (Fan et al. 2013, 2018). In addition, in experimental test, mortar was also reacted and heated timely under microwave irradiation, which was left out of consideration in theoretical calculation. A good agreement between them shows the effectiveness and reliability of analytical solutions.

Fig. 11
figure 11

Comparison of experimental, numerical and theoretical results

Full size image

3.4 Thermodynamic parameters of concrete

Before the analysis, the heat transfer coefficient between mortar and surroundings needs to be ascertained. The heat transfer coefficient was correlated with the wind velocity v. Based on the previous researches, the coefficient can be expressed as Eq. (40):

$$h_{c} = 6.02 + 3.46v$$
(40)

Under the natural wind, the heat transfer coefficient of concrete surface is about 5 ~ 11 W/m2K. Moreover, the heat transfer coefficient of concrete surface is affected by the environment temperature. The higher the temperature is, the greater the convective heat transfer coefficient will be. We assumed that the surface convective heat transfer coefficient of concrete was 8 W/(m2 K) under 200 °C, which increased to 20 W/(m2 K) when temperature varied from 200 to 400 °C.

As a kind of natural rock, aggregate has the properties of non-uniformity. Mortar is a composite material made of cement gel material and fine aggregate, which was also anisotropy and non-uniformity. To simplify the analysis, it is assumed that both mortar and aggregate are isotropic materials. Similarly, we assume that the physical properties of concrete do not change with heating temperature. The thermophysical properties such as thermal expansion coefficient, thermal conductivity coefficient and specific heat capacity were shown in Table 1.

Table 1 Materials properties
Full size table

4 Results and discussion

4.1 The time-dependent temperature fields

The results of the time-dependent temperature fields of concrete has been tabulated based on the above theoretical analysis. Figure 12 showed the temperature variation at different locations in the aggregate under different heating times, where the incident electric field E0 = 8000 V/m. According to the previous calculation of the microwave energy absorption of aggregate, we found that the microwave energy absorption of aggregate was the highest at z = 0.01 mm, so the cross section of z = 0.01 mm was selected to investigate the change of aggregate temperature along the r direction.

Fig. 12
figure 12

Temperature variation at different locations (E0 = 8000 V/m)

Full size image

It can be found that the internal temperature of the aggregate increases in a nonlinear transient state with the microwave heating time. At the beginning of heating process, owning to the effective absorption of microwave energy, the temperature of both aggregate and mortar increased rapidly. During the stage, the effect of heat conduction behaviour between aggregate and mortar were relatively weak compared with the microwave heating effect. When the microwave energy input and heating time reached a certain value, concrete temperature increases not obviously and gradually tends to be stable, part of the energy was used for insulation stage. During the period, the variation of concrete temperature were affected by both microwave heating and heat conduction process. At the center of aggregate, that is, where r = 0 mm, the temperature inside was the highest, which decreased along the axis outwards. After 2000s microwave heating, the maximum internal temperature of the aggregate has exceeded 240 °C, while the temperature at the interface was only 130 °C.

Figure 13 showed the temperature field distribution in concrete when the incident electric field increased to E0 = 10000 V/m. It can be seen that the distribution features of temperature field were similar under different electric field inputs, while the input intensity has a significant impact on the concrete temperature. When the intensity of microwave incident electric field increases to E0 = 10000 V/m, the peak temperature of the aggregate reached about 360 °C. The internal temperature of the aggregate increased by 50% when the electric field input increased by only 25%. Similarly, when the input electric field increased, the interface temperature also increased, which was about 240 °C at r = 15 mm. However, as a microwave transparency material, the internal temperature of mortar does not change significantly. When the microwave electric field input increases, the generated internal heat source Q increased. The increase of microwave heat source intensity will directly affect the heat generation and conduction process inside concrete and the final heating result.

Fig. 13
figure 13

Temperature variation at different locations (E0 = 10000 V/m)

Full size image

Figure 14 showed the temperature variation with the aggregate radius r, where the radius of mortar b = 50 mm. It can be seen that the aggregate temperature increased with the increment of r. The temperature distribution was approximately symmetric along the central axis. As a microwave absorption medium, when the radius of aggregate was relatively small, which means that the volume that can be heated directly by microwave was limited, leading to the relatively lower aggregate temperature. During the initial heating stage, temperature rise mainly depends on the rapid response of aggregate to microwave. When microwave input reached a certain level, the temperature rise of concrete was also depend on the heat conduction process between aggregate and mortar. The lower temperature and hysteretic conduction process caused the lower heating temperature of mortar. When the value of r increased, the effective heated area under microwave irradiation was increased, accelerating the heat conduction behaviour between aggregate and mortar, making the overall temperature of concrete increase significantly. It also can be found that maximum temperature difference does not increase linearly with aggregate radius. The maximum temperature difference between a = 5 and 10 mm was 70.1 °C, which was 109.6 °C between a = 15 and 20 mm. The results proved that the temperature increased nonlinearly with aggregate radius. In addition, for the larger aggregate radius, the inhomogeneous distribution of temperature was also more obvious.

Fig. 14
figure 14

Temperature variation with aggregate size

Full size image

4.2 Interfacial temperature variation

The ± 2.5 mm area near the mortar-aggregate interface was selected to analyze the variation of interface temperature. As can be seen from Fig. 15, the interface temperature gradient increased with the increase of heating time. Aggregate has strong wave-absorbing property under microwave heating, which lead to higher microwave energy absorption and caused a faster temperature rise compared with mortar, thus forming a temperature gradient between two materials. When the intensity of microwave incident electric field was 8000 V/m and heating time was 500 s, the temperature difference between aggregate and mortar interface was about 30 °C. When the heating time increased to 2000s, the interface temperature gradient increased to about 39 °C accordingly.

Fig. 15
figure 15

Interface temperature variation (E0 = 8000 V/m)

Full size image

When the intensity of microwave incident electric field increases to 10000 V/m, the interface temperature gradient of mortar and aggregate increased significantly, as shown in Fig. 16. After microwave heating 500 s, the temperature gradient reached about 51 °C. After heating 2000s by microwave, the interface temperature gradient reached 76 °C. Mortars’ temperatures under different microwave inputs were almost unchanged. The temperature gradient at aggregate-mortar interface was caused by microwave energy absorption ability and the inhomogeneity of the temperature field inside the aggregate. From the macro perspective, the generation of temperature gradient will lead to the stress gradient at the interface. The crack initiation, propagation and material failure in the heating process are largely dependent on the generated stress gradient, which eventually lead to the interface debonding between mortar and aggregate.

Fig. 16
figure 16

Interface temperature variation (E0 = 10000 V/m)

Full size image

In order to investigate the temperature field distribution characteristics of the concrete after microwave heating, the temperature uniformity was quantified by introducing the Coefficient of Variation (COV). Compared with standard deviation and other statistical parameters, temperature variation coefficient can effectively eliminate the influence of measurement scale and data dimension, which can objectively express the degree of data dispersion. The smaller the value was, the smaller the dispersion of data was. In this paper, smaller COV means that the temperature distribution was more uniform, which can be calculated based on Eq. (41):

$$COV = \frac{\sigma }{\mu } = \frac{1}{{\overline{T}}}\sqrt {\frac{1}{N}\sum\limits_{i = 1}^{N} {\left( {T_{i} - \overline{T}^{2} } \right)} }$$
(41)

where \(\sigma\) is standard deviation, \(\mu\) is the mean value.

Figure 17 showed the evolution law of COV subject to different incident electric field intensities. The intensity of incident electric field directly affects the microwave energy input. The greater the intensity of incident electric field, the higher microwave energy input. It can be seen from the figure that the greater the intensity of incident electric field, the greater the COV. The COV of concrete increased firstly and then decreases, and finally flattens out with the increment of heating time. The temperature change of the material under microwave heating was mainly determined by microwave absorption capacity and heat conduction. When the heating time was less than 250 s, the microwave medium with strong absorption, such as aggregate, can heat up rapidly, while the mortar with poor microwave absorption ability has a slower temperature variation. Due to the low heat conduction process in the sample, the COV raised rapidly, which indicates that the microwave irradiation in a relatively short time affects the uniformity of temperature distribution of the sample. With the further increase of heating time, the process of heat conduction inside the material became more rapidly. The sufficient internal heat conduction lead to the more uniform distribution of temperature inside concrete, resulting in the sharp fall of COV. The results indicate that the inhomogeneity of the temperature distribution of the sample will gradually increase with the growth of microwave energy. Such temperature distribution characteristics will promote in the separation behavior of mortar and aggregate.

Fig. 17
figure 17

COV variation in concrete under microwave irradiation

Full size image

5 Conclusion

In this paper, the coupling of electromagnetic and temperature field in concrete under microwave irradiation was studied theoretically. Based on the theory of electrodynamics, Poynting's theorem was employed to solve the electric field and absorbing energy in concrete under microwave heating. Based on the classical theory of thermoelasticity, the transient temperature field of concrete with internal heat source under microwave irradiation was solved, and the distribution of temperature field inside concrete was studied theoretically by integral transformation method. The main conclusions are as follows:

  1. (1)

    There were cosine-like fluctuations of electric intensity in aggregate. The electric field fluctuation was more frequent when the microwave heating frequency was 2450 MHz than that at 915 MHz. The higher the microwave heating frequency, the higher the electric intensity fluctuation frequency. When the microwave heating frequency changed, the change of microwave energy absorbed inside the aggregate was very obvious.

  2. (2)

    When the concrete aggregate length was different, its internal electric field and microwave absorption energy distribution were also different. For the shorter cylinder, the maximum microwave absorption energy was generally found in the middle part of the cylinder, and for the longer cylinder aggregate, the maximum aggregate absorption energy was found at both ends of the aggregate.

  3. (3)

    Under microwave heating, the internal temperature of aggregate was much higher than that in mortar. When the intensity of the incident electric field was 8000 V/m and the heating time was 2000s, the aggregate-mortar interface temperature gradient was about 39 °C, which increased to about 76 °C when the intensity of the incident electric field was 10000 V/m.

  4. (4)

    The greater the intensity of incident electric field, the more obvious nonuniformity of concrete inner temperature exhibited.