1 Introduction

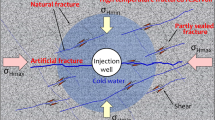
The production safety problems caused by hard roofs are very prominent in the mining of underground coal resources. Especially when the coal seam is overlain by thick igneous hard roof (Jiang et al. 2019; Zhang et al. 2020), which has become one of the major problems in the control of coal mine roof because of its high strength, large breaking span, wide influence range and strong ground pressure. Nowadays, the main treatment methods for hard roofs both domestically and internationally are blasting method (Chen et al. 2022a, b; Liu et al. 2021a, b; Zhang et al. 2022a, b) and hydraulic fracturing (Huang et al. 2018; Kang et al. 2022; Liu et al. 2020). While the blasting method achieved reasonable technical and economical results, many shortcomings still exist. Such as: The blasting method usually requires large amounts of explosives and engineering, which not only brings high costs, but also pollutes the air in the underground. In high gas mines or coal seams, the use of blasting methods to control hard roofs required measures to prevent gas or coal explosion. For the coal seams with shallow burial, the use of blasting method can constitute threat to the safety of the mining floor and the surrounding area. Hydraulic fracturing has been widely used in the oil and gas industry, geothermal resource development, storage of nuclear waste and hydroelectric engineering since it was proposed. However, the application of this technique is greatly influenced by the ground stress, and it is difficult to extend the cracks in the preset direction. To control the fracture extent more precisely, directional hydraulic fracturing technology was introduced from Poland (Lu and He 2020). The dominant idea of this technique is to cut grooves in the borehole and inject high pressure water to create directional fractures in the hard rock and destroy the integrity of the rock. With high ground stress in the deep part of the mine, however, the short cut channel usually makes it difficult for the hydraulic fractures to expand directionally along the cut channel direction. Hence, it is necessary to pre-produce directional fractures in the borehole to enable the hydraulic fractures to expand in the predetermined direction. Slitting equipment is usually bulky and is not suitable for small spaces. Moreover, the hard rocks cause more serious damage to the cutter, which makes it inconvenient to use the slitting equipment. Hence, to make hydraulic fracturing adaptable to more application scenarios, optimization of prefabricated fracture morphology and improvement of cutting equipment and methods are needed. In addition to mechanical cutting to create seams, the rock can also be fractured by high temperature.

Thermal fracture of rocks is known to be an extremely common natural and engineering phenomenon (Wen et al. 2023).The thermal expansion of minerals under high temperature causes the accumulation of thermal stress in the rock mass, which induces thermal fracture. The formation of thermal cracks modifies the physical and mechanical properties of the rock. For example, thermal fracture caused by high temperature can not only increase the porosity (Chaki et al. 2008; Reuschlé et al. 2003; Wen et al. 2023) and permeability (Aliyu et al. 2023; Yang et al. 2017a, b; Yang and Hu 2018) of rocks, but also reduce the uniaxial compressive strength (Peng et al. 2023; Yin et al. 2018) and elastic modulus (Fan et al. 2017; Nasseri et al. 2007; Yin et al. 2021) of rocks. Under the effect of high temperature, thermal stresses generated by the contact of single grain elements with other grains will accumulate. Thermal fracture will occur when the thermal stress reaches the tensile strength or shear strength of the rock (Browning et al. 2016; Peng et al. 2019). The mechanisms of thermal stress generation are mainly of two types: (1) The mismatch of thermal expansion generated with various mineral particles (Initiation of intergranular cracking). (2) Anisotropy of thermal expansion within individual mineral particles (Initiation of intracrystalline cracking) (Hale and Shakoor 2003; Yang et al. 2017a, b). However, when the rock is in non-constant temperature field, it can also fracture due to the rapid temperature change, which can cause the large temperature gradient inside the rock in a short period of time. Both mechanisms mentioned above cannot adequately explain the thermal fracture behavior of rocks triggered by large temperature gradients or thermal shock. The thermal shock fracture of rocks exists widely in various applications of high-temperature rock mechanics and engineering, such as deep geothermal energy development, thermal rock-breaking, tunnel fire prevention and rehabilitation, deep geological treatment of nuclear waste. Thermal shocks or large temperature gradients are usually caused by rapid temperature changes (Zhao et al. 2017), such as rapid cooling of high temperature rocks. In the deep geothermal energy development, water is usually used as the fracturing and heat-carrying medium (Shao et al. 2014). The temperature of deep hot dry rocks are usually high enough that when cold water is injected into the borehole, the rocks around the borehole will produce extremely high cooling rates, which lead to thermal shock fractures of the rocks. The thermal shock effects on the macroscopic physical and mechanical properties of granite have been extensively studied in (Kumari et al. 2019; Liu et al. 2019; Zhang et al. 2018; Zhao et al. 2018). Kumari et al. (2019) investigated the effect of different cooling treatments (constant high temperature, slow and rapid cooling) on the tensile strength of Australian granite. The results show that the effect of rapidly cooling on the tensile strength of the rock is much stronger than that of slowly cooling that caused by the strong thermal shock. Wu et al. (Wu et al. 2019) evaluated the effect of thermal shock on the tensile strength of granite. It was shown that granite cooled in water had the lowest tensile strength comparing with granite cooled in oven or air when the pre-heating temperature was greater than 600 °C. Shen et al. (2020) heated granite specimens to 150 °C, 350 °C, 550 °C and 750 °C, and then injected three refrigerants at 20, 0 and − 20 °C into granite boreholes to observe the effect of thermal shock on the granite fracture effect. As the results show, the high temperature granite at 550 °C and 750 °C are significantly affected by thermal shock, and the thermal shock will obviously enhance the rock fracture effects with the decrease of refrigerant temperature.

Similarly, when rocks are subjected to thermal shock by rapidly heating, large temperature gradients are produced inside the rock. On the one hand, high temperature thermal shock can deteriorate the physical and mechanical properties of the rock and reduce the strength of the rock. On the other hand, large temperature gradients can contribute to thermal shock fracture of rocks. Accordingly, the method of high temperature thermal shock directional pre-fracturing based on the theory of rock thermal shock fracture (Zhang et al. 2022a, b) was proposed as an alternative to the conventional slotting scheme. This technique is based on the main idea of installing directional heaters inside the rock for directional high temperature thermal shock to the borehole. This can cause high temperature gradients to be locally formed in the rock, accumulating high thermal stresses along the heating direction in the borehole and eventually leading to the formation of directional cracks in the borehole along the heating direction. Therefore, it can be seen that high temperature thermal shock directional fracturing is an extremely promising method for rock fracturing. Moreover, it is very important to accurately understand the typical characteristics of high temperature thermal shock fracturing and to clarify the mechanism of high temperature thermal shock fracturing. In this paper, high temperature thermal shock directional fracture tests were conducted by using the real triaxial loading system, homemade thermal shock system and acoustic emission test system with granite as material on the engineering background of the hard igneous roof overlying the coal seam. The temperature distribution regulation of granite during high temperature thermal shock directional fracturing and the typical AE characteristics of thermal shock fracture formation were investigated, and the quantitative relationship between the threshold temperature increment of rock hole wall and fracture was established. The research results will provide some experimental basis and theoretical guidance for the application of high temperature thermal shock directional fracture making technology.

2 Samples and methodology

2.1 Samples and test systems

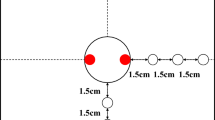
The granite specimens were taken from Ping Yi, Shandong Province, with the trade name of “Lu Grey Granite”. As shown in Fig. 1a, the specimens were machined uniformly into smooth cubes with the center hole. The specimen size is 200 mm × 200 mm × 200 mm, the side length error is controlled within 0.3 mm, and the parallelism error is controlled within 0.05 mm. The center hole has a diameter of 32 mm and a depth of 150 mm. Before the test, the surface of all specimens and the hole will be blown dry to ensure that the specimens are completely dry. Around the borehole of the specimen, temperature detection points 1–9 were marked at a certain spacing (20 mm, 40 mm, 60 mm) from the borehole, and the real-time temperature variation of the granite during the test was obtained by using the SMD thermocouple (Fig. 1b). For the convenience of the description, the y-direction is defined as along the heating direction, the x-direction as the vertical heating direction, and the 45°-direction as the oblique direction.

Fig. 1
figure 1

Granite specimen

Full size image

As shown in Figs. 2 and 3, the test system includes the loading system, the high temperature thermal shock system and the acoustic emission test system. The loading system used in the test is the large real three-axis pressure tester, which has the maximum loading capacity of 3000 KN. The high temperature thermal shock system is homemade in the laboratory. The system consists of a computer temperature control program, heaters, thermocouples, and temperature data collectors. The system provides the peak thermal shock temperature of 600 °C and the controllable thermal shock rate range of 0–114 °C/min. In the process of directional thermal shock, the heating rate of the thermal sources was controlled to be constant (110 °C/min), and the thermal shock temperatures were set to be 450 °C and 550 °C, respectively. The warming curves of the thermal sources are shown in Fig. 4, and it can be seen that the heating rate of the thermal sources is extremely rapid, which needs only about 150 s to increase from the room temperature to the pre-set temperature value. The acoustic emission test system is manufactured by PAC (Physical Acoustic Corporation), an American acoustic company. The system consists of twenty-four channels acquisition host, four preamplifiers and four acoustic emission sensors.

Fig. 2
figure 2

Schematic diagram of high temperature thermal shock directional fracturing test system

Full size image
Fig. 3
figure 3

High temperature thermal shock directional fracturing test system

Full size image
Fig. 4
figure 4

Warming curves of thermal sources

Full size image

2.2 Experimental procedure

2.2.1 Mounting the specimen in the loading system

The specimens were assembled in the true triaxial pressure tester as shown in Fig. 3. Using the true triaxial pressure tester to put bidirectional horizontal load on the specimen. Where the maximum horizontal principal stress is σH and the minimum horizontal principal stress is σh. In this way, it simulates the stress state of the hard roof in the underground coal mine. At room temperature, the minimum horizontal principal stress is set to 2 MPa and the maximum horizontal principal stress is set to range from 4 to 8 MPa. After installing the specimen, stabilize the pressure by using the real three-axis pressure tester accumulator to ensure continuous and stable pressure output during the test.

2.2.2 Installation of directional heaters

Install the directional heaters in the center hole, ensure that the heaters are close to the inner wall of the center hole. Filling the center hole with the ceramic thermal insulation cotton to fix the heater position and prevent the dissipation of heat. Ensure that the plane consisting of the two heaters is parallel (or perpendicular) to the end face of the specimen. The direction of thermal shock is guaranteed to be perpendicular to the direction of maximum horizontal principal stress. Connect the thermal shock system after installation.

2.2.3 Connect the AE system

The AE sensors were connected to the specimen in the position shown in Fig. 2, and the sensors were fixed using rubber bands. Between the sample and the sensors, we applied the thin layer of petroleum jelly to provide good acoustic coupling.

2.2.4 Test start

After the test system finished assembling, the loading system was started first, and the bi-directional horizontal main stress was adjusted to reach the preset value. After that, the high temperature thermal shock system and the AE test system were activated simultaneously. The heating rate was set to 110 °C/min, and the heating temperature were 450 °C and 550 °C, respectively. Setting the sampling rate of the AE test system to 1 MSPS and the threshold value of 45 dB. All tests were conducted for 90 min.

2.2.5 Test completion

At the end of the test, the high temperature thermal shock system and the AE test system were turned off at the same time. The location of the cracks formation were outlined by using a red ink pen and photographed and recorded.

The above steps were repeated for high temperature thermal shock directional fracturing tests at different bi-directional pressures and different heating temperatures, respectively. The experimental groupings are shown in Table 1.

Table 1 Test groups
Full size table

3 Results

3.1 Temperature distribution regulation of the surrounding rock of the center hole

The temperature data of specimen #1 and specimen #4 were used to study the temperature distribution pattern of the surrounding rock in the center hole of the specimens under the effect of different heating temperatures. Figures 5 and 6 show the thermal distribution cloud maps of borehole surrounding rock temperature at thermal shock temperatures of 450 °C and 550 °C, respectively. The cloud maps were obtained using the real-time temperature data recorded from measurement points 1–9 in the experiment and interpolating them. The four moments of heating time of 300 s, 1200 s, 3000 s and 5400 s were selected to plot the temperature field clouds. As can be seen from the figure, the isotherm during the thermal shock process is basically centered on the central hole and extends in an elliptical direction toward the edge of the specimen. The major axis of the elliptical temperature field is parallel to the y-direction (thermal shock direction) and the short axis is vertical to the y-direction. This indicates that the specimen transfers more heat in the y-direction in a short period of time which enables the formation of higher thermal stresses. For specimens heated at 450 °C, the central hole temperature evolves as follows: 60 °C, 105 °C, 135 °C and 150 °C (from 300 to 5400 s). And for the specimens heated at 550 °C, the center hole temperature evolves as follows: 60 °C, 120 °C, 150 °C and 155 °C (from 300 to 5400 s). It is obvious that for specimens with different heating temperatures, the higher the thermal shock temperature, the faster the rate of temperature change around the central hole in a short period of time. Meanwhile, it can be observed that the longer the thermal shock time, the smaller the ratio of the major axis to the short axis of the elliptical temperature field, which forms an approximately circular temperature field. It showed that the heat transfer from the heater is directional at the beginning of the thermal shock, but eventually the temperature distribution will tend to be uniform distribution throughout the specimen. The results show that the thermal shock direction gained much more heat at the beginning of the thermal shock, which created higher temperatures. However, the temperature of the granite specimen surface eventually tended to be uniformly distributed.

Fig. 5
figure 5

Temperature distribution of specimen #1(450 °C)

Full size image
Fig. 6
figure 6

Temperature distribution of specimen #4(550 °C)

Full size image

Figure 7 shows the trends of heating rate with time for temperature measurement points 1–9. According to the results, for the specimens with different heating temperatures, the heating rate variation rules of each temperature measurement point are essentially the same and can be divided into three stages: (1) Rapidly rising stage (heating rate is greater than 0.05 °C/s), (2) Rapid decline stage (heating rate is at 0.02–0.05 °C/s) and (3) Slowly declining stage (heating rate is less than 0.02 °C/s). Meanwhile, the heating rates of temperature measurement points 1, 4 and 7 were found to be the maximum values in the y-direction, x-direction and 45°-direction, respectively. It means that the closer to the central hole, the greater the rate of heating and the faster the rate of change. The peak heating rate at monitoring point 1 for specimen #1 and specimen #4 is 0.062 °C/s and 0.075 °C/s, respectively, and the arrival time of the peak is 204 s and 237 s, respectively. This indicated that the higher the heating temperature, the higher the peak of the heating rate. The heating rate peak of specimen #4 is higher owing to the same heating rate of the test setup, and it would take longer time for specimen #4 to reach the peak of heating rate.

Fig. 7
figure 7

Evolution of heating rate with heating time

Full size image

The temperature data of specimen #1 and specimen #4 were used to simulate the temperature in y-direction, x-direction and 45°-direction at different heating temperature, and the temperature evolution rules in all directions were obtained, as shown in Fig. 8, and the fitting equations are shown in Tables 2 and 3. The results show that the temperature variation of the rock in the same direction basically follows the logarithmic distribution, and the distribution trend decreases with increasing distance from the central hole. The fitting formulas can be used to calculate the real-time temperature at various locations of the specimens. The quantitative calculations were performed in Section four of this paper by using the fitting formula.

Fig. 8
figure 8

Temperature fitting curves

Full size image
Table 2 Fitting results at heating temperature of 450 °C
Full size table
Table 3 Fitting results at heating temperature of 550 °C
Full size table

In our previous study, we set one point “A” at the location “a” mm from the borehole in order to calculate the temperature of the borehole wall and used the temperature of point “A” to substitute the temperature of the borehole wall (Zhang et al. 2023). In this study, we used the same method (a = 0.005) to obtain the borehole wall temperature–time curves at different thermal shock temperatures, which are shown in Fig. 9. As can be seen from the figure, the hole wall temperature increased gradually with the increasing of thermal shock time. The borehole wall temperature of specimen #4 was always higher than that of specimen #1, which was attributed to more heat being available for the same amount of time at 550 °C.

Fig. 9
figure 9

Borehole wall temperature–time curve

Full size image

3.2 AE characteristics of granite high temperature thermal shock directional fracturing

3.2.1 Evolutionary characteristics of AE count

AE count refer to the number of oscillations of ringing pulses crossing the set threshold signal per unit time, reflecting the strength of the signal during rock damage, which can reveal the characteristics of rock damage patterns caused by microscopic defect extension development (Liu et al. 2021a, b). The evolution characteristics of AE count of granite specimens from specimen #1 to specimen #6 are shown in Fig. 10. Figure 10 shows the sum of the AE counts collected by the four sensors during the directional thermal shock damage of the granite specimens.

Fig. 10
figure 10

Characteristics of AE count evolution of granite specimen #1 ~ specimen #6

Full size image

As shown in Fig. 10, all six time-AE count plots formed dramatic peaks. The reasons are as follows: Before the test, the granite specimens were subjected to bi-directional horizontal stress with the real triaxial pressure tester. Hence, the original defects of the specimens have been compacted to some extent. This made the internal defects of the specimen closed, and the rock tended to be intact as a whole, which did not have the conditions for significant AE activities to occur. At the initial stage of thermal shock, the center hole of the specimen was subjected to localized rapidly heating causing uneven internal temperature distribution. Causing thermal stress to form at the center hole entrance, which changed the original stress distribution of the center hole surrounding rock. At this stage, the specimens were subjected to the combination of transverse horizontal stress and thermal stress until the thermal stress accumulated and increased to reach the rock strength limitation, resulting in micro cracks or macro cracks. Before the thermal stress reached the rock strength limitation, the specimens were in nearly integrity inside. However, microcracks were formed locally by thermal stress and horizontal stress, which caused the acoustic signals to be enhanced in the short term and the AE count and cumulative AE counts to fluctuate. Once the thermal stress reached the strength limitation, macro cracks were generated in the specimen. This resulted in the generation of large amounts of AE signals, and the AE ringing counts formed a peak with the accumulated AE ringing counts increasing steeply. When the specimens were broken, the accumulated strain energy of the specimens was released and the AE count returned to calm. Hence, it is possible to consider the moment of AE ringing counts peak formation to be the moment of macroscopic cracking of the specimen. All figures show only one peak, except Fig. 10c, which shows multiple peaks. This is because the cracks in specimen #3 (Fig. 10c) germinated at the boundary of the specimen due to boundary stresses, and the cracks were more in number. Hence, there were multiple AE count peaks. The cracks of the remaining specimens were subjected to thermal stresses and germinated and expanded simultaneously at the borehole boundaries. Hence, they produced only one AE count peak. According to the time of macro cracks formation, we divided the granite AE count evolution curves into calm stage, sharply increasing stage and slowly increasing stage.

3.2.1.1 Calm stage

In this stage, AE count and cumulative AE counts are both at low levels. Before the experiment, the rock was subjected to bi-directional horizontal loading, which caused some degree of closure of the original defects and fissures, and the intensity of AE activities was reduced. The AE count fluctuations that appeared at this stage came from the microcracks produced in the rock by the thermal shock effects. The acoustic emission ringing count fluctuations that appeared at this stage came from the microcracks produced in the rock by the thermal shock effects. However, the number of microcracks is small at this time and they are mostly formed in isolation, so that the acoustic signals were weak. The results showed that the AE count are basically below 5 × 102 in the calm stage of specimen #1 and specimen #2. Most of the AE count in the calm stage of specimen #4 ~ specimen #6 were situated below 10 × 102, which were slightly higher than those of specimen #1 and specimen #2. This was caused by raising the thermal shock temperature.

3.2.1.2 Sharply increasing stage

The reason for the sharp increasing of AE count and cumulative AE counts at this stage is that the internal microcracks intersect and penetrate, which form macro cracks. Moreover, there is an obvious silent period of AE signals before the granite high temperature thermal shock damage, i.e., there is no large AE activities generated in short term, which can be used as a precursor criterion to predict rock damage. The specific reason is: the acoustic signals are generated as the result of energy dissipation. To fracture the rock, it requires to lose its load carrying capacity completely. Therefore, it is essential to accumulate a large amount of elastic energy to break through the obstruction created by the dislocation and frictional effect among the particles. Further, it showed diminished AE activities. The experimental results show that there is abrupt variability in the AE signals, corresponding to the macroscopic fracture with sharp increases in AE ringing counts. At this time, the development of internal defects in the rock increased and the rock deterioration became more and more advanced.

3.2.1.3 Slowly increasing stage

This stage happened after the peak of the AE count, the AE count dropped abruptly and the AE activities returned to calm, but the AE activities did not stop. The reason is that the accumulated elastic energy was released after the formation of macroscopic cracks and the intensity of AE activities decreased. However, the continuous thermal shock continued to cause deterioration within the rock, which caused microcracks to develop. While the intensity of the AE signal released during macroscopic cracks formation were much stronger than that of the AE signals released during microcracks formation.

In addition, the cumulative AE counts characteristics of granite high temperature thermal shock under different horizontal pressure differ greatly. The differences are reflected in the sharply increasing stage and the slowly increasing stage. There was only one sharp increase in the cumulative AE ringing counts for the granite specimens (specimen #1, specimen #2, specimen #4, specimen #5) with stress conditions of 2–4 MPa and 2–6 MPa, corresponding to the generation of one macro crack. For the granite specimens with stress conditions of 2–8 MPa (specimen #3, specimen #6), the acoustic emission activities were frequently and distributed over a wide time range, and the accumulated AE count all showed several sudden increasing, indicating that macro cracks were produced many times and the specimen deteriorated more seriously.

3.2.2 Characteristics of b value

The concept of b value originated from seismological studies, in which B. Gutenberg and C. F. Richter (Frequency-of-Earthquakes-in-California-1945 n.d.) were the first to propose that the relationship between earthquake frequency and magnitude satisfies the equation:

$$ \begin{array}{*{20}c} {\lg N = a - bM} \\ \end{array} $$
(1)

where M is the earthquake magnitude, N is the corresponding earthquake number, and a is the constant. It was found that the characteristics of the distribution of AE events of rocks during damage have some similarity with the mechanism of earthquake evolution, and the AE b-value parameter was induced from it, which is calculated as follows:

$$ \begin{array}{*{20}c} {\lg N = a - b\left( {A_{{{\text{d}}B}} /20} \right)} \\ \end{array} $$
(2)

where \(A_{{{\text{d}}B}}\) is the maximum amplitude of the AE events. It has been shown that the increase of b value indicate the occurrence of more microcracks within the specimen. While, the decreasing of b value indicate that large scale cracks germinate in the specimen (Ma et al. 2018; Peng et al. 2019). In this study, we calculated the b value by using the maximum likelihood estimation method with the frequency of calculation fixed at 1000 (Chen et al. 2022a, b).The calculation formula used is the following.

$$ \begin{array}{*{20}c} {b = \frac{20lge}{{\overline{A} - A_{min} }}} \\ \end{array} $$
(3)

As shown in Fig. 11 is the b value-AE count-time curves. As shown in Fig. 11, the b value of AE of thermal shock granite under different thermal–mechanical conditions basically corresponds to the AE count peaks during the damage. When the thermal shock temperature was 450 °C, the b value of specimen #1 dropped sharply around 2000s, and the AE count formed one peak around 2000s. It is caused by the development of macro cracks within the specimen. Specimen #2 showed the similar phenomenon of Specimen #1, but the increased and decreased b value after failure were more frequently interspersed. It showed that even though failure had occurred, the defects within the specimen continued to propagate. Specimen #3 showed multiple sharp decreases in b value and multiple peaks in the AE count curve, which was caused by the repeated occurrence of macroscopic defects or cracks in the specimen. When the thermal shock temperature was 550 °C, the AE count curves of specimen #4, specimen #5, specimen #6 all formed only one peak. Significantly, even though two or more macro cracks formed in specimen #1, specimen #3, specimen #4, specimen #6, only specimen #3 developed multiple peaks in the AE count curve. The reason was that specimen #3 germinated cracks several times during the test, with multiple bursts of AE and the formation of multiple cracks. For specimen #1, specimen #4, specimen #6, on the other hand, although two or more macro cracks were initiated in the specimens, they germinated almost simultaneously. Hence, the AE experienced only one burst and formed only one peak. This indicated that the formation of peaks in the AE count was unrelated to the crack strips, but related to the number of times the cracks were germinated. Also, it indicated that the thermal shock cracks within the same specimen were generated at the same time, while specimen #3 was possibly more affected by the boundary stress disturbance, which resulted in the generation of multiple cracks at the specimen boundary, and these cracks were not generated simultaneously. As can be seen by comparing Fig. 11a, b, d, e, when the horizontal stress difference was the same, the peak formation time of AE count was shorter for the 550 °C heating condition compared to 450 °C, indicating that increasing the thermal shock temperature could shorten the time of thermal shock failure of granite.

Fig. 11
figure 11

AE b value and AE count of specimens under different conditions

Full size image

3.3 Morphology of thermal shock cracks

Figure 12 illustrates the damage results of granite specimens from Specimen #1 to Specimen #6. As shown in the figure, the crack morphology on the surface of the rock specimen changed with the increase of the horizontal stress difference when the thermal shock temperature was 450 °C. When the horizontal stress difference is 2–4 MPa, cracks germinate at the boundary of the borehole, and the direction of crack extension is consistent with the direction of thermal shock. When the horizontal stress difference is 2–6 MPa, cracks germinate at the boundary of the borehole, and the direction of crack extension is vertical to the direction of thermal shock, which is consistent with the direction of high stress. The reason is that horizontal stress difference is the dominant influence on the direction of crack extension, and the thermal stress generated by 450 °C is relatively small and is not enough to release the crack extension from the control of the geological stress. When the horizontal stress difference is 2–8 MPa, crack germinate at the specimen boundary, which is caused by the specimen boundary stress. Moreover, the cracks still extend in the direction of high stress because of the influence of the horizontal stress difference. For granite specimens with thermal shock temperature of 550 °C, it can be obtained the similar laws. When the horizontal stress difference is 2–4 MPa and 2–6 MPa, the cracks expand directionally along the thermal shock direction. When the horizontal stress difference is 2–8 MPa, the crack extension direction loses directionality, i.e., the crack expands along the direction of thermal shock and the vertical thermal shock direction. It is noticed by comparing specimen #2 and specimen #5 that when the horizontal stress difference is 2–6 MPa, the cracks in the two specimens expand in different directions. This shows that 550 °C provided higher thermal stresses comparing to 450 °C, which made the crack expansion released from the control of geological stresses, i.e., the crack expanded directionally along the direction of thermal shock.

Fig. 12
figure 12figure 12

Fracture results for specimen #1 to specimen #6

Full size image

Notably, the thermal shock cracks formed in Fig. 12 are single wing cracks located at both sides of the borehole, with two cracks distributed symmetrically (specimen #1, specimen #4, and specimen #6). Influenced by the heterogeneity of the rock, thermal shock cracks formed in specimen #2, specimen #5 and specimen #6, which were located only at one side of the borehole. To observe the morphology of the thermal shock cracks inside the rock specimen, CT scan observations were made by drilling \(\emptyset\) 25 mm × 200 mm core in the specimen, which was positioned above the thermal shock crack. Since the cracks formed within the rock by the directional thermal shock were of the same morphology, we only show the CT scan results of specimen #1. The results of the CT scan of specimen #1 were sliced and the images were numbered No.0–No.2200 from the upper part to the bottom part of the rock core, as shown in Fig. 13. As can be seen in Fig. 13a, the specimen formed a single primary crack on the upper surface, which was accompanied by secondary cracks next to the primary crack, which were fewer in number and lighter in color. As can be seen in Fig. 13b, c, the primary crack gradually becomes lighter in color and produces little angular deflection with increasing depth. At the bottom of the specimen (Fig. 13d), the primary crack continued to lighten in color, although it was still clearly observable. This indicated that the thermal shock cracks penetrated through the top and bottom of the specimen, while the reason for the lighter color of the cracks at the bottom could be related to the hole-bottom stresses.

Fig. 13
figure 13

CT scan results

Full size image

4 Theoretical analysis of granite high temperature thermal shock directional fracturing under bi-directional horizontal stress

Generally speaking, thermal expansion will take place in materials which are subjected to heat. Thermal stress exists when the thermal expansion is hindered. The temperature gradient in the material is one of the presentations of this hindrance (Feng et al. 2021). The thermal stress can be expressed by the following equation:

$$ \begin{array}{*{20}c} {\sigma = E\alpha_{m} \Delta T} \\ \end{array} $$
(4)

where E is the modulus of elasticity, \(\alpha_{m}\) is the coefficient of thermal expansion, and \({\Delta }T\) is the temperature variation. Meanwhile, high temperature will cause the physical and mechanical properties of granite materials to deteriorate, which are mainly manifested as follows: (1) The uniaxial compressive strength decreases with the increase of temperature. The reason is that, on the one hand, granite is a crystalline rock, and the thermal movement of the grains in the rock will improve with the increase of temperature, which causes the bond between the grains to weaken, thereby causing the strength of the rock to decrease (Meigooni et al. 1994). On the other hand, it is composed of different mineral grains, and the coefficient of thermal expansion of different mineral grains is different. It causes uncoordinated thermal expansion of the mineral particles upon heating, which induces structural thermal stresses and leads to micro cracks within the rock, thereby reducing its strength (Liu and Xu 2015). (2) The elastic modulus decreases with the increase of temperature, but there is no order of magnitude transition. (3) The coefficient of thermal expansion usually increases with the increase of temperature, but the difference is small at different temperatures. The reason is that at high temperature, the water inside the rock evaporates and the minerals do not fully expand (Liu and Xu 2015). Simultaneously, because of the expansion of the mineral particles, the rock has been compressed, which resulted in a very small measured coefficient of thermal expansion.

From the elasticity mechanics, it can be seen that the directional fracture of the wellbore along the y-direction is due to the formation of stress concentration in the y-direction of the borehole wall, and the thermal stress formed by the thermal shock is an influential factor. As can be seen from Eq. 4, if we would like to calculate the thermal stress at the borehole wall, we should firstly obtain the temperature value at the borehole wall, and then obtain the variation laws of the elastic modulus and the thermal expansion coefficient with the temperature. In this study, the borehole wall temperature can be calculated according to the fitting formulas which were given in Tables 2 and 3 respectively, and the results of the calculations were shown in Tables 4 and 5. For the thermal expansion coefficient, which values are usually small and varies little with temperature, thus it has little effect on the results of the calculations. Hence, the thermal expansion coefficient was considered to be fixed in the calculations (2 × 10−5/℃). While the elastic module is a function of temperature, E(T). One of our group's researchers has already tested granite specimens originating from the same batch, and obtained the elastic modulus with different temperature (Zhao et al. 2019). We have fitted the data by using the “Lorentz” model to obtain the function E(T), which is shown in Fig. 14.

Table 4 Temperature of borehole wall of Specimen #1 (450 °C)
Full size table
Table 5 Temperature of borehole wall of Specimen #4 (550 °C)
Full size table
Fig. 14
figure 14

Elastic modulus-temperature curve

Full size image

With the above data, we calculated the thermal stresses of the borehole wall at different thermal shock temperatures respectively, and the results were shown in Fig. 15. As can be seen from the figure, the thermal stress of the hole wall increased gradually with the increasing of the thermal shock time. Meanwhile, both thermal stress curves gradually flatten after rapidly increasing, which is caused by the temperature distribution inside the specimen gradually becoming homogeneous. Moreover, it was found that the thermal stress was much higher at 550 °C by comparing the thermal stress curves at different temperatures. The thermal stress value at the time of failure of specimen #1 was 56.86 MPa, which was higher than the thermal stress value at the time of failure of specimen #4 (52.33 MPa), which might be caused by the more significant affects of 550 °C on the physical and mechanical properties of the rocks.

Fig. 15
figure 15

Borehole wall thermal stress-time curve

Full size image

These results show that the thermal stress formed in the borehole wall of the wellbore was varied for different thermal shock temperatures. With increasing horizontal stress difference, the fractures within the rock gradually lost their directionality, which indicated that the ability of directional thermal shock to modify the stress field of the surrounding rock was limited. We established a new model to theoretically explain the effects of directional thermal shock on the stress field of the surrounding rock.

As shown in Fig. 16, we assumed that infinite rock contained one blind hole, only considering the open hole portion and ignoring the influence of boundary stress. According to thermoelastic mechanics, there will be extra additional thermal stress around the borehole caused by temperature changed, which would be calculated by the following formula:

$$ \begin{array}{*{20}c} {\sigma_{rT} = \frac{{E\alpha_{m} }}{{3\left( {1 - v} \right)}}\frac{1}{{r^{2} }}\mathop \smallint \limits_{{r_{B} }}^{r} T^{f} \left( {r,t} \right)r{\text{d}}r} \\ \end{array} $$
(5)
$$ \begin{array}{*{20}c} {\sigma_{\theta T} = \frac{{E\alpha_{m} }}{{3\left( {1 - v} \right)}}\left[ {T^{f} \left( {r,t} \right) - \frac{1}{{r^{2} }}\mathop \smallint \limits_{{r_{B} }}^{r} T^{f} \left( {r,t} \right)r{\text{d}}r} \right]} \\ \end{array} $$
(6)
$$ \begin{array}{*{20}c} {\sigma_{zT} = \frac{{E\alpha_{m} }}{{3\left( {1 - v} \right)}}T^{f} \left( {r,t} \right)} \\ \end{array} $$
(7)

where \(\sigma_{rT}\), \(\sigma_{\theta T}\), and \(\sigma_{zT}\) are additional radial stresses, additional tangential stresses, and additional axial stresses caused by thermal effects around the borehole, respectively; \(T^{f} \left( {r,t} \right)\) = \(T\left( {r,t} \right)\)-\(T\)0 is the temperature change around the borehole; \(r_{B}\) is the radius of the borehole. The additional thermal stresses caused by high temperature thermal shock in physical tests were calculated by using Eqs. (5, 6, 7), and the results are shown in Fig. 15. The calculated parameters are as follows: E = 13GPa, \(v\) = 0.3, \(\alpha_{m} \) = 2.0 × 10−5/°C, the initial temperature T0 of the inner wall of the central hole is 20 °C, and the duration of thermal shock is 600 s. The temperature data in Sect. 3.1 were used to fit the temperature variation patterns in the x-direction and y-direction, respectively, and the temperature of each monitoring point in the specimen at different points in time was calculated by using the fitting formula.

Fig. 16
figure 16

Borehole stress model in rock

Full size image

When the temperature of the inner wall of the central hole increased, the inner wall was subjected to compressive stress, as shown in Fig. 17. The triaxial principal stresses around the borehole all increased, however, the additional radial stresses increased the least. The additional tangential stress and additional axial stress have increased substantially. It is worth noting that the maximum value of additional radial stress appeared in the range of 20–40 mm from the borehole, while the maximum value of additional tangential stress and additional axial stress appeared in the borehole wall. Thermal shock fracturing of the rock occurred at the borehole wall, so the stresses in the axial and tangential directions around the borehole are most likely the main factors initiating the fracture of the borehole. Meanwhile, it can be found that the additional tangential stress and additional axial stress in the y-direction is about twice as much as that in the x-direction by comparing the triaxial stress values in different directions at the same temperature. While the additional radial stresses in the two directions differed little.

Fig. 17
figure 17

Additional stress caused by high temperature thermal shock

Full size image

Typically, triaxial stresses are used to simulate ground stresses in the deep strata. The calculation of the stress in the borehole surrounding rock under the coupling of ground stress and hydrostatic pressure of drilling fluid have been provided in the literatures (Al-Ajmi and Zimmerman 2006). On this basis, we obtained the stress distribution around the borehole under the action of high temperature thermal shock:

$$ \begin{aligned} \sigma_{r} & = \frac{{r_{B}^{2} }}{{r^{2} }}E\alpha_{m} T^{f} \left( {r,t} \right) + \frac{{\sigma_{H} + \sigma_{h} }}{2}\left( {1 - \frac{{r_{B}^{2} }}{{r^{2} }}} \right) + \frac{{\sigma_{H} - \sigma_{h} }}{2}\left( {1 + 3\frac{{r_{B}^{4} }}{{r^{4} }} - 4\frac{{r_{B}^{2} }}{{r^{2} }}} \right)\cos 2\theta \\ & \quad + \frac{{E\alpha_{m} }}{{3\left( {1 - v} \right)}}\frac{1}{{r^{2} }}\mathop \smallint \limits_{{r_{w} }}^{r} T^{f} \left( {r,t} \right)r{\text{d}}r \\ \end{aligned} $$
(8)
$$ \begin{aligned} \sigma_{\theta } & = - \frac{{r_{B}^{2} }}{{r^{2} }}E\alpha_{m} T^{f} \left( {r,t} \right) + \frac{{\sigma_{H} + \sigma_{h} }}{2}\left( {1 + \frac{{r_{B}^{2} }}{{r^{2} }}} \right) - \frac{{\sigma_{H} - \sigma_{h} }}{2}\left( {1 + 3\frac{{r_{B}^{4} }}{{r^{4} }}} \right)\cos 2\theta \\ & \quad + \frac{{E\alpha_{m} }}{{3\left( {1 - v} \right)}}\left[ {\frac{1}{{r^{2} }}\mathop \smallint \limits_{{r_{B} }}^{r} T^{f} \left( {r,t} \right)r{\text{d}}r - T^{f} \left( {r,t} \right)} \right] \\ \end{aligned} $$
(9)
$$ \begin{array}{*{20}c} {\sigma_{z} = - v\left[ {2\left( {\sigma_{H} - \sigma_{h} } \right)\frac{{r_{B}^{2} }}{{r^{2} }}\cos 2\theta } \right] + \frac{{E\alpha_{m} }}{{3\left( {1 - v} \right)}}T^{f} \left( {r,t} \right)} \\ \end{array} $$
(10)

where \(\sigma_{r}\), \(\sigma_{\theta }\), \(\sigma_{z}\) are the radial stress, tangential stress and axial stress around the borehole, respectively; \(\sigma_{H}\), \(\sigma_{h}\), \(\sigma_{z}\) are the maximum horizontal principal stress, minimum horizontal principal stress and axial stress, respectively; \(\theta\) is the angle from \(\sigma_{H}\) to the radius of the hole. The stress distributions in the surrounding rock of the borehole caused by the heating temperature of 550 °C under the bi-directional horizontal stress were calculated. The calculation parameters are shown in Table 6, and the calculation results are shown in Fig. 18.

Table 6 Calculated parameters of stress distribution
Full size table
Fig. 18
figure 18

Stress distribution around the borehole

Full size image

According to the calculation results, the maximum values of radial stress, tangential stress and axial stress all appeared on the wall of the borehole. As the distance from the borehole increased, the stress value gradually decreased. Cracks are usually generated at high stress concentrations, i.e.at the wall of the borehole. This is consistent with the research findings of Holditch (Holditch 1979). The stress distribution in the central hole wall of the specimen under the action of high temperature thermal shock is:

$$ \begin{array}{*{20}c} {\sigma_{r} = E\alpha_{m} T^{f} \left( {r,t} \right) + \frac{{E\alpha_{m} }}{{3\left( {1 - v} \right)}}\frac{1}{{r^{2} }}\mathop \smallint \limits_{{r_{w} }}^{r} T^{f} \left( {r,t} \right)r{\text{d}}r} \\ \end{array} $$
(11)
$$ \begin{aligned} \sigma_{\theta } & = - E\alpha_{m} T^{f} \left( {r,t} \right) + \sigma_{H} + \sigma_{h} - 2\left( {\sigma_{H} - \sigma_{h} } \right)\cos 2\theta \\ & \quad + \frac{{E\alpha_{m} }}{{3\left( {1 - v} \right)}}\left[ {\frac{1}{{r^{2} }}\mathop \smallint \limits_{{r_{B} }}^{r} T^{f} \left( {r,t} \right)r{\text{d}}r - T^{f} \left( {r,t} \right)} \right] \\ \end{aligned} $$
(12)
$$ \begin{array}{*{20}c} {\sigma_{z} = - v\left[ {2\left( {\sigma_{H} - \sigma_{h} } \right)cos2\theta } \right] + \frac{{E\alpha_{m} }}{{3\left( {1 - v} \right)}}T^{f} \left( {r,t} \right)} \\ \end{array} $$
(13)

In the process of high temperature thermal shock, the axial and radial stresses on the borehole wall are always compressive stresses, while the tangential stresses show a tendency to change from compressive to tensile stresses. In the y-direction (Fig. 18a), the triaxial principal stresses in the borehole wall showed maximum values and exhibited compressive stresses when the heating time was 300 s. When the heating time is 1800s, the radial and axial stresses gradually increased and were always compressive stresses. However, the tangential stresses exhibit tensile stresses at the central hole wall and gradually exhibit compressive stresses as the distance from the borehole increases. This indicated that there was a transition from compressive to tensile stresses in the central hole wall tangential stresses in the time range of 300–1800s. In the x-direction (Fig. 18b), the radial and axial stresses always exhibit compressive stresses and decrease with increasing distance from the hole wall. The tangential stresses were almost always tensile stresses and only presented small compressive stress for limited time at the beginning of the thermal shock. As can be seen, high temperature thermal shock can change the stress distributions around the borehole, and the hole wall tangential stress is the most sensitive to thermal shock. Therefore, tangential stress is an essential influencing factor for the fracture of the central hole. In rock mechanics, shear damage follows the Mohr–Coulomb criterion (Eq. 15).

$$ \begin{array}{*{20}c} {\left\{ {\begin{array}{*{20}c} {\sigma_{1} \left[ {\sqrt {\left( {t^{2} + 1} \right)} - t} \right] - \sigma_{3} \left[ {\sqrt {\left( {t^{2} + 1} \right)} + t} \right] = 2C \sigma_{1} \ge \frac{1}{2}s_{t} } \\ {\sigma_{3} = - s_{t} \sigma_{3} \le \frac{1}{2}s_{t} } \\ \end{array} } \right.} \\ \end{array} $$
(14)

where \(\sigma_{1}\) is the maximum principal stress, \(\sigma_{3}\) is the minimum principal stress, \(\varphi\) is the rock internal friction angle, \(C\) is the rock cohesion, \(t = \tan \varphi\), and \(s_{t}\) is the rock tensile strength. The critical pressure at the borehole wall during the directional fracturing of granite by high temperature thermal shock is:

$$ \begin{gathered} - v\left[ {2\left( {\sigma_{H} - \sigma_{h} } \right)\cos 2\theta } \right] + \frac{{E\alpha_{m} }}{{3\left( {1 - v} \right)}}T^{f} \left( {r,t} \right)\left[ {\sqrt {\left( {t^{2} + 1} \right)} - t} \right] + E\alpha_{m} T^{f} \left( {r,t} \right) \hfill \\ + 2\cos 2\theta \left( {\sigma_{H} - \sigma_{h} } \right) - \left( {\sigma_{H} + \sigma_{h} } \right) + \frac{{E\alpha_{m} }}{{3\left( {1 - v} \right)}}T^{f} \left( {r,t} \right)\left[ {\sqrt {\left( {t^{2} + 1} \right)} + t} \right] = 2C \hfill \\ \end{gathered} $$
(15)

5 Engineering application scenarios

Schematic of application of the directional thermal shock pre-fracture technique is shown in Fig. 19. Before mining the coal seam, several fracture holes are arranged as shown in Fig. 18a, and the fracture holes reach inside the main roof through the immediate roof. Then the directional thermal shock system will be installed in the fracture holes. It is worth noting that to avoid the effect of high temperature on the coal seam, it is necessary to ensure that the directional thermal shock device installed to the above of the coal seam, and the holes are sealed by insulation at the location of the coal seam. Directional thermal shock creates directional cracks or directional weakened zones within the roof rock strata, and after connecting the cracks between the fracture holes, a macroscopic crack will be formed above the hard roof, which disconnects the transverse connection between the roof rock strata and the surrounding rocks, distributing the stresses to the deeper rocks, thus achieving the purpose of releasing the stress. The crucial point of this technique is to solve the issue of connecting fractures between fractured holes, and we have proposed two solutions. (1) Arranging more intensive fracture holes or arranging guide holes between fracture holes. (2) Using hydraulic fracturing to extend thermal shock cracks. These are also priorities in our subsequent research work.

Fig. 19
figure 19

Schematics of thermal shock directional fracture technology

Full size image

6 Conclusion

In this paper, the experimental study of high temperature thermal shock directional fracture of rocks under bi-directional horizontal loading was carried out with granite as the material. During the test, the typical characteristics of acoustic emission and fracturing mechanism of high temperature thermal shock directional fracture of granite under thermo-mechanical coupling were researched by using AE test system for real-time tracking, and some interesting conclusions were obtained.

  1. (1)

    The temperature rising rate inside the granite specimen through three stages: rapidly rising stage (temperature rising rate is greater than 0.05 °C/s), rapidly falling stage (temperature rising rate is at 0.02–0.05 °C/s), slowly falling stage (temperature rising rate is less than 0.02 °C/s).

  2. (2)

    During the high temperature thermal shock, the AE ringing counts of granite specimens are monitored by AE and observed to experience the calm stage, the sharply increasing stage and the slowly increasing stage. With the increase of the horizontal stress difference, the cumulative AE ringing counts of the specimen increases steeply gradually from 1 to multiple times, and the AE activities of the specimen become more frequently and the degradation degree becomes stronger. When the macroscopic fracture of the specimen appears, the b value shows an obvious characteristic of sudden drop.

  3. (3)

    A computational model of the dynamic changes of stress distribution around the borehole in the center of the specimen during high temperature thermal shock directional fracturing is established. The calculation results show that the highest stress is formed in the inner wall of the borehole during the high temperature thermal shock. At the initial stage of thermal shock, all the triaxial stresses in the y-direction of the inner wall of the borehole show compressive stresses. However, the tangential stress in the y-direction of the inner wall of the borehole changes from compressive stress to tensile stress in the mid stage of thermal shock.

  4. (4)

    Directed thermal shock modifies the state of stress distribution in the borehole surrounding rock. We have established a model for stress distribution and given a formula for calculating the initiation stress of rocks, which provides essential theoretical support for the industrial application of directional thermal shock fracturing technology.