1 Introduction

The engineering rock mass is subjected to long-term crustal movement, engineering excavation, and various types of load disturbances. Its interior contains numerous joints, cracks, and structural surfaces. These flaws are primarily developed due to external loads, causing them to nucleate in localized areas of failure. Subsequently, the flaws further localize and eventually lead to the propagation of macroscopic crack coalescence. This phenomenon gives rise to common disasters such as tunnel collapse, mine subsidence, rock slope instability, landslides, and poses a significant threat to human life and property (Chang et al. 2018; Zhang and Zhou 2020; Lei et al. 2020; Han et al. 2020). Therefore, conducting research on the effect of crack parameters on the crack propagation and failure patterns of rock materials under uniaxial compression conditions is crucial for evaluating the extent of rock failure and holds great engineering significance.

In recent years, there have been numerous experimental studies conducted by scholars on rock materials with prefabricated flaws using indoor testing methods. The mechanical properties and failure patterns of cracked rocks have been studied in two main ways: firstly, by creating different geometrical arrangements of flaws on intact rock specimens, and secondly, by creating different geometrical arrangements of flaws on specimens of rock-like materials. For instance, Yang et al. (2022) conducted triaxial compression tests on cracked granite specimens to examine the effects of rock bridge angle and circumferential pressure on the mechanical properties and damage modes of granite specimens. They also analyzed the internal microscopic damage characteristics of granite specimens using CT scanning technology. Similarly, Li et al. (2005a) created flaws on rock specimens through the drilling and cutting method and studied the process of crack propagation, identifying two types of nascent cracks. Huang et al. (2022) proposed five crack propagation paths and corresponding damage modes based on their study of rock crack propagation rules. Reisi et al. (2015) conducted experimental studies on cracked sandstone specimens and identified and proposed nine crack types to study crack propagation and damage patterns. Zhou et al. (2014) described the characteristics of five crack types using specimens containing double and multiple cracks. Similar studies have also been conducted by Zhou et al. (2019a), Liu et al. (2021), Wang et al. (2023), and Alneasan and Behnia (2022), Alneasan et al. (2022, 2023). These research findings provide a theoretical basis for understanding the fracture mechanism of engineering rock masses.

Due to the challenges and expenses associated with obtaining and fabricating flawed rock specimens, researchers have conducted numerous studies to investigate crack propagation patterns and specimen damage by using different types of rock-like materials to fabricate flawed specimens. Initially, some studies explored the crack propagation pattern under compressive loading using glass specimens (Hoek and Bieniawski 1965). Bobet and Einstein (1998) used gypsum materials to fabricate double-flaw specimens for experimental studies, aiming to observe crack misalignment, secondary crack sprouting, and coalescence patterns, and analyze the relationship between specimen failure patterns and the distribution of prefabricated flaws. Zhao et al. (2018) examined the crack propagation process of gypsum samples containing two parallel flaws through uniaxial compression tests. While compression tests using glass or gypsum materials effectively describe the compression damage characteristics of crystalline connection type rock materials, they still have limitations in explaining the compression damage characteristics of cemented connection type rock materials. Therefore, some studies have proposed the use of cement mortar materials to simulate the deformation failure characteristics of cracked rock. Yang et al. (2021) investigated the correspondence between crack propagation and stress‒strain curves by creating flawed specimens with cement mortar. Cao et al. (2015) utilized cement mortar specimens to simulate the crack initiation and agglomeration behavior of brittle rock materials. The combination of coarse and fine aggregates in the cement mortar better aligns with the characteristics of engineered rock masses. Similar studies have also been conducted by Meysam et al. (Lak et al. 2019a, 2019b; Mohebbi et al. 2017; Abdollahipour and Marji 2020; Fu et al. 2022; Abdollahipour et al. 2016).

With the advancement of technology, auxiliary monitoring means in the laboratory can be utilized to study the failure characteristics and processes of cracked rocks in more detail from a microscopic perspective. Currently, the commonly used methods for this purpose are acoustic emission monitoring techniques (AE) (Modiriasari et al. 2017; Morgan and Einstein 2017; Zhang et al. 2019) and digital image correlation techniques (DIC) (Ji et al. 2016; Munoz and Taheri 2017; Liu et al. 2015). Eberhardt et al. (Eberhardt et al. 1998) employed acoustic emission techniques to investigate the damage process of granite and found that significant acoustic emission events or a sudden increase in acoustic emission characteristic parameters often correspond to the initiation of microcracks. Lin et al. (2013) analyzed the damage process of the specimen by examining the changing law of the strain field on the specimen surface. Moreover, the rapid development of modern computer technology has made numerical simulation methods a popular approach for studying rock mechanics problems. Some commonly used software for this purpose includes RFPA (Wong and Lin 2015; Wang et al. 2014), PFC (Sarfarazi et al. 2014; Huang et al. 2019), and UDEC (Debecker and Vervoort 2013).

Intermittent joints are a prevalent type of discontinuous structural surfaces in engineering rock masses. The inclination angle and number of joints play a crucial role in the stability of these rock masses. However, there is a lack of systematic discussion on how the angle and number of intermittent joints affect rock mass failure. To address this gap, this paper focuses on fine sandstone, a commonly used rock in engineering. The study involves creating artificial flaws with varying inclinations and numbers in sandstone specimens, which are then subjected to uniaxial compression testing. The rupture process of these flawed specimens is analyzed using acoustic emission technology and digital imaging. By doing so, the study aims to explore the influence of flaw inclination angle and number on the cracking evolution and failure mode of sandstone. The findings of this research can serve as a theoretical reference and provide insights into the failure mechanisms of cracked rock and the development of effective disaster control methods in rock engineering. The research conclusion can be used for blasting, hydraulic fracturing, and rock slopes.

2 Overview of the test

2.1 Test specimen preparation and program

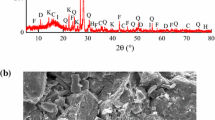
This study focuses on investigating the impact of crack angles and numbers on the failure mode and mechanical properties of rock masses. The research object is intermittent cracks found in engineering rock masses, which are known to contain various types of cracks. The test material used is sandstone, specifically taken from the rock group of hard and relatively hard layered gravel and mudstone interbedded rocks in Zigong City, Sichuan Province. This type of rock is commonly encountered in rock mass engineering and aligns with the engineering background of the analysis and study of destabilization failure in this field. Please refer to Fig. 1 for a visual representation.

Fig. 1
figure 1

Sampling location for sandstone samples

Full size image

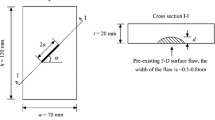
The original rock samples were processed into rectangular specimens of thickness × width × height of 20 mm × 50 mm × 100 mm according to the requirements of the test specification of the International Society of Rock Mechanics (ISRM), with different through-flaws prefabricated in the center of the specimens using the center drilling method, as shown in Fig. 2. The prefabricated flaw consists of four parameters: flaw length a, flaw width d, number of flaws and flaw inclination α. The flaw length and flaw width were kept constant at a = 20 mm and d = 1 mm, respectively. Three flaw inclination types (the angle between the flaw and the horizontal direction) were set up, with inclination angles of 30°, 45°, and 60°, and the corresponding specimen numbers were J-30°, J-45°, and J-60°, respectively. Four different types of flaws were set up, the numbers of which were 2, 3, 4 and 5, and the corresponding specimen numbers were M-2, M-3, M-4 and M-5, respectively; the specific dimensions are shown in Fig. 2. The mechanical parameters of the intact sandstone specimen are average peak strength 89.07Mpa, elastic modulus 8.5GPa Poisson's ratio 0.26, tensile strength 6.8 MPa, density 2.52 × 103 kg/m3, wave speed velocity 3624 m/s, and porosity 17%.

Fig. 2
figure 2

Prefabricated flaw size of the test specimen (unit: mm)

Full size image

2.2 Test system and loading conditions

To ensure controlled variables and minimize experimental errors, the rock specimens were dried at a temperature of 105 °C for 12 h. Before conducting the test, the surface of each specimen was coated with white paint, which was followed by random spraying of black paint after the white paint had completely dried. This spraying process ensured that the paint covered the specimens uniformly and created random scattering spots, which facilitated effective identification during the test. The high-speed camera used for the test had a frame rate of 60 fps. For the uniaxial compression tests on the rock specimens, a microcontrolled electronic universal testing machine (Changchun Kexin Testing Instrument Co., Ltd., TAW-2000 type) was employed as the loading system. The specimens were loaded based on displacement, with a loading rate of 0.05 mm/min. During compression, the acoustic emission signals from the rock samples were monitored using an acoustic emission monitoring system (Acoustic Physics Corporation PAC, Model PCI-II, USA). To ensure accurate crack observation and minimize the impact of probe arrangement, two probes were positioned on the left and right surfaces of each specimen. The test system and acoustic emission probe arrangement are illustrated in Fig. 3.

Fig. 3
figure 3

Principle diagram of the rock mechanics and acoustic emission parameter test system

Full size image

3 Influence of the flaw inclination angle on the mechanical properties and failure pattern of specimens

3.1 Stress‒strain curves and strength characteristics

Figure 4 presents the load–displacement curves of rock specimens with different flaw inclination angles. The specimens underwent a similar process during loading, which can be roughly divided into four stages: the compaction stage, the elastic stage, the plastic stage, and the failure stage. The compaction stage occurs at the beginning of loading, where the load–displacement curve is typically concave, and the primary cracks within the rock specimen close under the applied load. In the elastic stage, the load–displacement curves exhibit a linear variation. The load–displacement curves in the plastic stage show an upward concave pattern, indicating the propagation of cracks within the rock specimen without any macroscopic fracture. Finally, the load displacement curve experiences a vertical drop during the failure stage.

Fig. 4
figure 4

Load‒displacement curves of specimens with different crack angles

Full size image

The peak load of the specimen increases as the flaw inclination angle increases. This is because as the flaw inclination angle increases, the rock undergoes a transition from tensile to compressive-shear damage, which gradually strengthens its ability to resist external loads. The load‒displacement curves (Fig. 4) show that rock specimens with flaw inclination angles of 45° and 60° experienced significant deformation before final failure, while specimens with a crack inclination angle of 30° experienced minimal deformation before brittle failure. When the flaw inclination angle is greater than 45°, the ductile damage characteristics of the flaw specimen in general with the increase of flaw inclination tends to weaken, which may be due to the fact that when the flaw inclination angle is greater than 45°, the rock structural effect with the increase of flaw inclination is gradually strengthened, which effectively reduces the role of the flaw on the stress concentration of the rock. These findings align with the uniaxial compressive strength law of single crack specimens in rock mechanics (Cai et al. 2002). When the flaw inclination angle reaches 90°, the strength of the rock mass becomes independent of the flaw, and the strength of the rock mass is solely determined by the rock itself. On the other hand, when the flaw inclination angle is 0°, the rock mass will be destroyed due to lateral propagation of the crack.

3.2 Analysis of the failure characteristics of sandstone specimens

The rock gradually accumulates energy under load and releases it by creating new cracks when it reaches its critical value. The final failure pattern of a rock specimen often depends on the type of crack it produces. Essentially, there are two main types of cracks that occur during the compression failure of rock specimens: tensile or wing cracks and shear or secondary cracks (Bobet 2000). In general, wing cracks appear earlier and are tensile in nature, while secondary cracks appear later and are shear in nature. Literature (Zhou et al. 2019b) categorizes the types of crack propagation under uniaxial compression into nine types, as shown in Fig. 5. A total of seven crack types were observed in this test: tensile wing cracks ④, tensile cracks ⑤, anti-tensile cracks ①, tensile wing cracks ⑥, tensile cracks ⑦, far-field cracks ⑧, and surface spalling ⑨.

Fig. 5
figure 5

Nine crack types observed in flawed specimens under uniaxial compression

Full size image

Figure 6 illustrates the development of cracks in the rock specimen influenced by the flaw inclination angle. The cracks are represented by numbers ① ~ ⑨. The analysis of Fig. 6 reveals that the failure of rock specimens is typically a result of multiple crack types occurring simultaneously. For instance, in the case of the J-60° rock specimen, failure characteristics include anti-tensile cracks, tensile wing cracks, and tensile cracks. The failure pattern exhibits clear tensile characteristics. The following summarizes the characteristics of the aforementioned crack types: Among all rock specimens with different flaw inclination angles, tensile cracks are generally the initial crack to appear, with winged tensile cracks being the predominant macroscopic manifestation. However, it is important to note that tensile cracks are often not the ultimate cause of the final failure of the rock specimen. Using the J-30° rock specimen as an example, it can be observed that as stress increases, the development process of the tensile wing crack and anti-tensile crack gradually transforms into secondary shear cracks. This transformation ultimately leads to the failure of the rock specimen through a combination of tensile and shear forces. Additionally, when the inclination angle of the crack increases, the rock specimen experiences compressive shear failure. This is evident in specimens with an inclination angle of J-60°.

Fig. 6
figure 6figure 6

Damage process of specimens with different crack angles. a J-30° sandstone specimen, b J-45° sandstone specimen, c J-60° sandstone specimen

Full size image

To analyze the crack propagation evolution law of the specimen under different flaw inclination angles in a more detailed manner, the major principal strain field change diagram of the specimen during the loading process is utilized. This analysis provides a fine-grained perspective on the failure process of the specimen, as depicted in Fig. 6. In the case of the J-45° rock specimen, for instance, strain localization initially occurs at the tip of the specimen's prefabricated flaw 2, propagating downwards at an angle. As the stress increases, strain localization becomes more pronounced, leading to visible cracks in the specimen. Although penetration occurs between these cracks, the specimen does not fail. With further loading, the strain concentration band penetrates through the bottom of the specimen, resulting in significant failure. Subsequently, new strain concentration bands emerge in the specimen, indicated by the appearance of new cracks at a macroscopic level. In essence, the final failure of the specimen is attributed to the continuous accumulation of preexisting damage, with microfractures originating from the tip of the specimen's prefabricated flaws leading to the occurrence of preexisting damage.

3.3 Test results of acoustic emission

The damage of rock is a dynamic process involving internal crack initiation, propagation, and coalescence. The acoustic emission characteristics of rocks are closely related to their internal damage. In order to further investigate the relationship between crack evolution and damage in rock specimens, this section utilizes acoustic emission and photographic monitoring to analyze the damage process in cracked sandstone specimens. Due to the length of the article, only specimen J-30° is analyzed. Figure 7 illustrates the relationship between load, AE counts, and cumulative AE counts over time during loading of the specimen. Figure 6 (No. J-30°) displays the evolution of macroscopic cracks on the surface of the specimen. In Fig. 7, the black line represents the load, the red line represents the AE counts, the blue line represents the cumulative AE counts, and points 1 to 5 correspond to characteristic points selected based on the load‒displacement curves of the specimens, which align with the characteristics of the specimen crack evolution shown in Fig. 6 (No. J-30°).

Fig. 7
figure 7

Acoustic emission test results of specimens with different crack angles. a J-30° sandstone specimen, b J-45° sandstone specimen, c J-60° sandstone specimen

Full size image

As illustrated in Fig. 7, the specimen underwent the crack compaction stage and the elastic deformation stage during loading. There were no significant acoustic emission (AE) counts observed between 0 and 270 s, and no visible cracks were observed on the surface of the rock specimens, as shown in Fig. 6 (No. J-30°). The trend of AE cumulative counts in Fig. 7a indicates a gradual increase, suggesting a slow increase in the damage level of the rock specimens. It is important to note that even though no visible cracks formed on the surface of the specimen at this stage, it does not imply that damage failure did not occur internally. Furthermore, Fig. 6 reveals a regular distribution of the strain field and clearly shows areas of stress concentration, indicating the potential for crack initiation and propagation.

With the extension of loading time, the stress–strain curve of the specimen gradually exhibited nonlinear characteristics. Simultaneously, the count value of the AE (acoustic emission) showed an increasing trend, rising from 9 to 367. When the load reached 24.32 MPa (3 points), the rock specimen exhibited its first peak value of AE counts (2487), as depicted in Fig. 7a. At this point, macroscopic cracks formed on the surface of the specimen, and anti-tensile cracks were generated at the tip of the prefabricated flaws, as shown in Fig. 6 (J-30°-3). Subsequently, the AE counts of the specimen entered an 'intense period', with cumulative counts rapidly increasing. This indicated that the damage process of the specimen was accelerated during this stage. The cracks on the surface of the specimen propagated rapidly, generating new cracks, and new anti-tensile cracks formed at the tip of the prefabricated flaws when the stresses reached the 4 points, as shown in Fig. 6 (J-30°-4). When the stress reached point 5, the energy stored in the rock sample reached its critical value, resulting in a sudden drop in stress. This led to the generation of two new shear cracks, as shown in point (J-30°-5) of Fig. 6, ultimately leading to shear failure.

4 Influence of the number of flaws on the mechanical properties and failure pattern of specimens

4.1 Stress‒strain curves and strength characteristics

Figure 8a presents the load‒displacement curves of specimens with varying numbers of flaws. The loading stages of the specimens are similar and can be categorized into four stages: compression-tightening, elasticity, plasticity, and failure. As shown in Fig. 8a, rock specimens with 4 and 5 flaws exhibited minimal deformations prior to failure, while the rock specimen with 2 flaws underwent significant deformations before failure. The number of cracks in the specimen increased from 2 to 5, leading to a decrease in vertical displacement of the rock from 1.05 to 0.4 mm. Consequently, the rock's ability to withstand external loads gradually diminished.

Fig. 8
figure 8

a Load‒displacement curves of specimens with different crack numbers, b relationship between specimen strength and number of cracks

Full size image

Figure 8b illustrates that the peak load of the rock mass decreases as the number of flaws in the specimen increases. Specifically, the peak load decreased by 34.5% when the number of flaws changed from 2 to 4. However, as the number of flaws continued to increase, the rate of reduction of the peak load slowed down. For instance, the peak strength was reduced by 10.4% when the number of flaws changed from 4 to 5. The number of cracks had a lesser impact on the initiation load compared to the peak load. When the number of flaws changed from 2 to 5, there was a 15.7% reduction in the initiation load. The trend of the curve for the initiation load is similar to that of the peak load, indicating that the effect of an increasing number of flaws on the initiation load becomes less significant over time, ultimately leading to a stabilization of the initiation load of the flaws in the specimen.

Literature (Zhu et al. 2002) applied fracture mechanics to derive the propagation length of the wing crack under uniaxial stress. Considering the interaction between the crack and introducing the interaction factor F1, the extension length l of the secondary crack is:

$$ l = \frac{{6.073T^{2} }}{{\pi K_{{{\text{IC}}}}^{2} }}F_{1}^{2} $$
(1)

where F1 is the interaction factor between the cracks, KIC is the critical stress intensity factor, and T is the force on the open (Type I) crack.

$$ T = aF_{n} \sin \theta $$
(2)
$$ F_{n} = \left| {\sigma_{1} \sin \beta \cos \beta } \right| - f_{{\text{j}}} \sigma_{{\text{n}}} - C_{{\text{j}}} $$
(3)

where \(\sigma_{{\text{n}}} = \sigma_{1} \sin^{2} {\upbeta }\), the compressive stress is specified to be positive and the tensile stress is negative, Fn is the crack surface force, σn is the crack normal force, and fj and Cj are the friction coefficient and cohesion of the crack surface, respectively.

The increase in the number of cracks is actually a decrease in the crack spacing h, while the limiting length of crack propagation is:

$$ l_{{\text{m}}} \le \frac{h}{{\sin {\upbeta }}} $$
(4)

From Eq. (4), it can be seen that the increase in the number of cracks is actually a decrease in the ultimate propagation length of the winged cracks under the condition of a constant crack inclination angle, so the cracked rock mass can produce through damage under lower compressive stress, resulting in the reduction of bearing capacity.

4.2 Analysis of the failure characteristics of sandstone specimens

As depicted in Fig. 9, when the number of flaws is small (e.g., D-2), the flaws primarily propagate through tensile wing cracks. These cracks form on both ends of the prefabricated flaws and initially propagate at an angle of approximately 0° to 20° to the compressive stress. Subsequently, the branch cracks bend and align parallel to the direction of the compressive stress. During this stage, as the tensile stress field dominates, the cracks mainly propagate under the influence of tensile stress, following a tensile mode of propagation. Due to the relatively wide spacing between the flaws, the tensile wing crack resulting from the propagation of the two cracks continues along the direction of the compressive stress until it penetrates through the entire specimen, causing penetration damage between the prefabricated flaw and the tensile wing crack.

Fig. 9
figure 9figure 9

Damage process of specimens with different crack numbers. a D-2 sandstone specimen, b D-3 sandstone specimen, c D-4 sandstone specimen, d D-5 sandstone specimen

Full size image

As the number of cracks increases, the outer two prefabricated flaws generate tensile wing cracks when subjected to tensile stress and propagate in the direction of compressive stress. The stress field of the rock bridge section between the two outer prefabricated flaws gradually transitions from a tensile stress field to a compressive stress field due to the interaction between the prefabricated flaws. This means that the inner prefabricated flaws experience high pressure stress and undergo pressure-shear damage, causing the propagation of their cracks to be suppressed by the compressive stress field. The damage is manifested as the absence of tip cracks in the inner prefabricated flaw. The destruction of the entire specimen occurs along the direction of tensile wing crack of the outer prefabricated flaw and the inner prefabricated flaw. Moreover, as the number of prefabricated flaws increases, the angle at which fracture propagation begins gradually increases, transitioning from a direction roughly parallel to the compressive stress to a direction perpendicular to the prefabricated flaws. When the density of the prefabricated flaws is increased, the specimens exhibit resistance to tensile crack propagation, as observed in D-4 and D-5.

4.3 Test results of acoustic emission

According to Fig. 10, the rock initially exhibited weak AE counts and low cumulative AE counts before the specimen failed. However, a sudden increase in AE counts occurred, which accounted for a significant portion of the total AE energy. Subsequently, the specimen failed rapidly after the appearance of the AE event with the highest energy, exhibiting a typical brittle collapsing failure. As the number of prefabricated flaws in the specimen increased, more energy accumulated in the damage, resulting in slightly fluctuating peaks of acoustic emission events recorded by the AE equipment. Overall, there was an increasing trend in these peaks. The cumulative AE counts showed a significant increase with the number of prefabricated flaws in the specimen. The peak value of AE counts under uniaxial compression did not increase linearly with the number of prefabricated flaws, as it was influenced by crack development and microfracture generation. However, the cumulative value of AE counts increased with an increase in the number of prefabricated flaws. This relationship can serve as a theoretical basis for future assessments of crack propagation during rock mass failure and the relative sizes of prefabricated flaws in specimens.

Fig. 10
figure 10

Acoustic emission test results of specimens with different crack numbers. a D-2 sandstone specimen, b D-3 sandstone specimen, c D-4 sandstone specimen, d D-5 sandstone specimen

Full size image

5 Discussion

To further investigate the mechanical process of crack propagation, the theory of fracture mechanics is employed to examine the pattern of crack initiation. A mechanical model of crack propagation was created using the uniaxial force diagram of the specimen depicted in Fig. 11. The fracture penetration mode of the sandstone specimen was analyzed. In this model, the axial stress is denoted as σ1, and the angle between the inclined cleavage and the maximum principal plane is α. The axial stress σ1 is divided into the tangential stress τn and the normal stress σn at the inclined crack surface, which can be expressed as follows:

$$ \left\{ \begin{gathered} \sigma_{n} = \sigma_{1} \cos^{2} \alpha \hfill \\ \tau_{n} = \frac{{\sigma_{1} }}{2}\sin 2\alpha \hfill \\ \end{gathered} \right. $$
(5)
Fig. 11
figure 11

Mechanical model of crack propagation

Full size image

In Eq. (5), σn > 0, the force acting on the inclined crack surface behaves as a tensile stress; σn < 0, as a compressive stress. A two-dimensional fracture mechanics analysis of the cracks in the specimen is performed by considering the specimen profile as an infinite-body planar problem containing cracks of length 2a. The specimen is unidirectionally pressurized and is more significantly affected by the boundary, and the stress intensity factor at the tip of the crack is approximated as (Li et al. 2005b):

$$ \left\{ \begin{gathered} K_{{\text{I}}} = \sigma_{1} \sqrt {\pi a} \cos^{2} \alpha \hfill \\ K_{{{\text{II}}}} = \sigma_{1} \sqrt {\pi a} \cos \alpha \sin \alpha \hfill \\ \end{gathered} \right. $$
(6)

where KI is the type I fracture stress intensity factor and KII is the type II fracture stress intensity factor.

The stress component in polar coordinates for a type I and II composite crack, as shown in Fig. 11, can be expressed as:

$$ \left\{ \begin{gathered} \sigma_{r} = \frac{1}{{2\sqrt {2\pi r} }}\left[ {K_{{\text{I}}} (3 - \cos \theta )\cos \frac{\theta }{2} + K_{{{\text{II}}}} (3\cos \theta - 1)\sin \frac{\theta }{2}} \right] \hfill \\ \sigma_{\theta } = \frac{1}{{2\sqrt {2\pi r} }}\cos \frac{\theta }{2}\left[ {K_{{\text{I}}} (1 + \cos \theta ) - 3K_{{{\text{II}}}} \sin \theta } \right] \hfill \\ \tau_{r\theta } = \frac{1}{{2\sqrt {2\pi r} }}\cos \frac{\theta }{2}\left[ {K_{{\text{I}}} \sin \theta + K_{{{\text{II}}}} \left( {3\cos \theta - 1} \right)} \right] \hfill \\ \end{gathered} \right. $$
(7)

According to the maximum circumferential tensile stress criterion, the crack initiates and propagates along the direction where the circumferential stress σθ is maximum, and the direction of initiation satisfies the following condition:

$$ \frac{{\partial \sigma_{\theta } }}{{\sigma_{\theta } }} = 0\quad \frac{{\partial^{2} \sigma_{\theta } }}{{\partial \sigma_{\theta }^{2} }} = 0 $$
(8)

Substituting Eq. (3) into Eq. (4) and setting \(\partial \sigma_{\theta } /\sigma_{\theta } =0\), the calculation result can be expressed as:

$$ K_{{\text{I}}} \sin \theta_{0} + 3K_{{{\text{II}}}} (3\cos \theta_{0} - 1) = 0 $$
(9)

When σθmax = σθc, the crack starts to initiate and propagate. σθc is the maximum circumferential stress critical value, and σθc can be determined by the fracture toughness KΙc of the type I crack to be \( \sigma_{{\theta {\text{c}}}} =K_{IC} /\sqrt {2{\uppi }r}\). Combined with Eq. (3), it can be further determined that the fracture criterion of the composite crack of type I, II is:

$$ \cos \frac{{\theta_{0} }}{2}\left[ {K_{{\text{I}}} \cos^{2} \frac{{\theta_{0} }}{2} - \frac{3}{2}K_{{{\text{II}}}} \sin \theta_{0} } \right] = K_{{{\text{IC}}}} $$
(10)

The approximate values of KI and KII are:

$$ \left\{ \begin{gathered} K_{{\text{I}}} = \frac{1}{2}\sigma_{1} \sqrt {\pi a} \sin \alpha \hfill \\ K_{{{\text{II}}}} = \frac{1}{2}\sigma_{1} \sqrt {\pi a} \cos \alpha \hfill \\ \end{gathered} \right. $$
(11)

As shown in the model in Fig. 11, the crack initiation angle at the tip of an inclined crack can be calculated from the crack tip stress intensity factor and combined with the maximum circumferential stress criterion. KI and KII are calculated by bringing α into Eq. (11), following which the angle of initiation of the crack, θ0, can be calculated by bringing α into Eq. (9). As shown in Table 1 for the theoretical value of the crack initiation angle and the test value comparison results, the theoretical calculation results and test results are in the error base allowable range, which further verifies the feasibility and reasonableness of the theoretical calculation results in this paper.

Table 1 Theoretical value and test comparison of the crack initiation angle
Full size table

This study reveals that the destruction of the rock mass occurs due to the movement and opening of the original crack surface, leading to the formation of wing-type cracks. These wing-type cracks intersect with primary cracks, creating a network of interconnected cracks in the surrounding rock. This results in significant deformation of the rock mass. If the wing crack does not propagate up to its maximum length, it indicates the absence of a perimeter rock fracture zone. Therefore, the boundary of intermittent fracture penetration failure can be defined as the boundary of the perimeter rock rupture zone. In this zone, primary cracks and wing cracks intersect, and the rock mass is weakened due to the penetration of these cracks. If the winged cracks of adjacent cracks are not penetrated, it suggests that the rock mass still possesses high strength but has reached its limit state and will quickly undergo destruction, although it can still withstand high loads. Since the majority of the rock formation in the roadway area is characterized by intermittent cracks, the boundary of intermittent crack penetration failure can be considered as a universal and general definition.

6 Conclusions

Fractured rock mass is a highly intricate medium characterized by strong non-uniformity and nonlinearity. It contains intersecting crack defects of various scales that significantly influence its physical and mechanical properties. Additionally, in engineering applications, rocks are subject to dynamic disturbances like earthquakes, blasting vibrations, and excavation activities, which can lead to the formation of interconnected cracks and trigger geological disasters. This study focuses on the fabrication of sandstone into diverse fractured rock samples for subsequent uniaxial compression and acoustic emission experiments. By analyzing fracture mechanics and acoustic emission characteristics, the research delves into the crack initiation mechanisms of fractured rock masses. The conclusion is as follows:

  1. 1.

    The displacement and peak load of the specimens decreased as the number of cracks increased. The increase in the number of flaws reduces the ultimate propagation length of the wing crack, leading to through failure and a reduced load carrying capacity of the specimen at lower compressive stresses.

  2. 2.

    As the inclination angle of the flaw increases, the failure mode of the specimen transitions from shear to compressive failure. During the initial stage of loading, a high-strain region emerges around the flaw. As loading continues, a localized high-strain region develops on the surface of the specimen, indicating the path along which a macroscopic crack may form.

  3. 3.

    When there are only a few flaws, the flaws primarily spread through tensile wing cracks. As the number of flaws increases, the inner flaw does not generate tip cracks. Instead, the failure of the entire specimen occurs along the direction of the tensile wing crack of the outer prefabricated flaw, with the inner flaw extending through the specimen, resulting in an anti-tensile crack.

  4. 4.

    Among the rock specimens with all flaw inclination angles, the winged tensile crack was the first crack to appear. Based on the principle of fracture mechanics, the expression of the stress intensity factor at the tip of the crack under uniaxial compression conditions without considering the closure effect was given, the crack initiation angle was calculated, and the theoretical calculation of the initiation angle was basically consistent with the test results.