1 Introduction

The accurate identification and evaluation of litho-facies in oil and gas exploration are crucial for determining reservoir properties, identifying potential drilling targets, and optimizing production. Well log data analysis provides high-resolution information on subsurface geological formations and is a valuable tool in this regard. However, the interpretation of well logs can be challenging due to their complexity and variability. To overcome these challenges, various machine learning methods have been applied to well log data analysis to enhance the accuracy of facies classification. In this study, we employ five supervised machine learning algorithms (Random Forest, Support Vector Machine, Artificial Neural Network, Extreme Gradient Boosting, and Multilayer Perceptron) to accurately estimate different litho-facies in Lower Indus Basin.

Understanding reservoir structure and determining reservoir-scale geobodies require the use of reservoir facies modeling. According to Gaafar et al. (2016). integrated techniques constrained by 3D seismic and facies logs may be used to produce exact facies models as stated by Stien and Kolbjørnsen (2011). The spatial resolution of facies is crucial since it controls fluid flow in reservoir models according to Shi et al. (2019) and AlHakeem (2018). By integrating geophysical, geological, and engineering data about the reservoir, reservoir facies modeling aims to construct a prediction model for the accumulation of hydrocarbons. Several authors including (Ullah et al 2023), (Liu et al. 2019), and (Radwan and Sen 2021) and others have highlighted the importance of combination investigation for depicting reservoir geobodies applying integrated 3D seismic, well-log, and geology data. The concepts of facies, lithofacies, environmental facies, and biofacies exhibit interdependencies, as certain facets can be deduced from others. For instance, both environmental and paleogeographic facies encompass the depositional context. Lithofacies and petrographic facies similarly pertain to the lithological attributes and the initial lithic states (Moradi et al. 2019).

Machine learning (ML) techniques have been integrated with petrophysical and geophysical data in recent years to accurately identify different lithologies. However, obtaining reliable lithological models from well data remains a challenging task in reservoir studies. In addition to being utilized in reservoir characterisation for petroleum exploration, statistical techniques and supervised and unsupervised ML algorithms have been used effectively to identify litho-facies on geophysical logs. Despite this advancement, very little study has been done on utilizing geophysical data to identify different litho-facies and reservoir attributes (Al-Mudhafar et al. 2022; Alaudah et al. 2019; Asedegbega et al. 2021; Lee et al. 2022; Radwan and Sen 2021).

A recent study utilized supervised machine learning algorithms to classify litho-facies in the Sawan field of the Southern Indus Basin. The study employed five popular classification algorithms, namely Random Forest, Artificial Neural Network, Extreme Gradient Boosting, Support Vector Machine, and Multilayer Perceptron. These methods utilize forward and backward propagation using input, hidden, and output layers to reduce the difference between expected and actual values. To prevent bias, all input data were randomized and standardized before being fed into the algorithms. The algorithms were trained on 77% of total data samples, with the remaining 23% reserved for validation purposes. The litho-facies were classified into five categories: fine sand (1), medium sand (2), coarse sand (3), shale (4), and siltstone (5). The study employed a confusion matrix (accuracy and misclass) and an evaluation matrix (precision, recall, and F1-score) to assess classifier accuracy. By utilizing these methods, the study successfully predicted litho-facies in the Sawan field and provided insight into the classification performance of each algorithm.

C-N modelling is an advanced technique for spotting anomalous zones (Ullah et al. 2022). C-N is based on an inverse association between the cumulative frequency of critical concentrations and the number of core samples (Hassanpour and Afzal 2013). C-N fractal methods are frequently used to illustrate geology interpretation utilizing geochemical data and classical statistics techniques (Ahmadfaraj et al. 2019), permeability attributes and fractal dimension analysis (Shuyun et al. 2008), fractal and multiracial modelling (Somayeh Rezaei et al. 2015), and singularity modelling (Liang et al. 2023; Hao et al. 2021). We created a C-N model in its basic form using well log data to help illustrate the problem of facies classification on the basis of radiogenic characteristics include gamma ray (GR), heat production (HP), thermal conductivity (TC), and heat transfer (HT).

This multidisciplinary approach combines expertise in geology, machine learning, and statistics to provide a comprehensive analysis of the well log data. The results demonstrate the effectiveness of machine learning techniques in accurately identifying litho-facies, with Random Forest and Extreme Gradient Boosting performing particularly well (Amarullah Bekti 2020; Shi et al. 2019).

Regarding the novelty of this topic, the integration of machine learning techniques and statistical analysis in facies evaluation represents a promising approach that is gaining popularity in the field. To determine the effectiveness of these methods in a specific geological context, this study uses well log data from the Sawan-8 well to identify the litho-facies present. By combining various analytical approaches, the research aims to deliver an inclusive considerate of the facies in the well. The results demonstrate the potential application of this approach in enhancing accuracy and aiding decision-making during oil and gas exploration.

2 Geology and depositional environment of study area

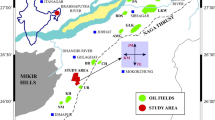
The Sawan gas field is located in the southern area of Pakistan, specifically in Sindh province. Its discovery dates back to 1989 and it is under the operation of the Oil and Gas Development Company Limited (OGDCL), which is a state-run enterprise. The geology of Sawan gas field has intricate structures with numerous anticlinal and synclinal features. The reservoirs, which primarily comprise sandstone and shale formations of Eocene and Paleocene age, are found at depths between 2500 and 3000 m. The primary producing zones include the Lower Goru and Upper Sands formations (Ali et al. 2023; Hussain et al. 2022).

The Sawan field's creation is impacted by the geological conditions of the region, which are a consequence of the convergence of the Indian and Eurasian plates. This convergence has resulted in the emergence of the Himalayan Mountain range and several fault systems across the region, such as the Khirthar and Kirthar Fold belts, which have significantly contributed to the evolution of the Sawan field. The Indus Basin, where the field is located, is one of the largest sedimentary basins globally, formed due to the same collision between the two plates (Yasin et al. 2021).

During the sediment deposition in the Lower Indus Basin, the climate was warm and humid with substantial rainfall. The sediments consist of mudstones, sandstones, and conglomerates that were deposited about 20–25 million years ago, during the early Miocene period. These sediments were carried by rivers and then settled in channels, floodplains, and levees. In the Sawan Field, the sandstones are typically well-sorted and coarse-grained, indicating a high-energy transportation and deposition process (Naeem et al. 2016).

The mudstones are often interbedded with the sandstones and represent periods of lower-energy deposition in floodplain or lacustrine environments. Overall, the depositional environment of the Lower Indus Basin Sawan Field is indicative of a dynamic river system that underwent fluctuating conditions of high and low-energy sediment transport and deposition (Ali et al. 2020) (Fig. 1a, b and c).

Fig. 1
figure 1

a The geological map of Pakistan displays the country's various sedimentary basins, tectonic features, and structural settings It is worth noting that the Sawan gas field is in close proximity to the JKH at the intersection of the Middle and Lower Indus Basin, which is marked with blue squares b Additionally, the map highlights the study wells and clearly shows the position of the SGF. In particular, c the reservoir interval for the Lower Indus Basin is highlighted by a red rectangle on the map, as emphasized in a study conducted by (Ashraf et al. 2021)

Full size image

3 Material and method

The seismic data for the Sawan gas field in the Lower Indus Basin, Pakistan were acquired from the Directorate General Concession Petroleum (DGPC) located in Islamabad. Our research incorporated log data from the Sawan-08 well, A range of geophysical measurements, such as gamma-ray (GR) readings in API units, spontaneous potential (SP) measured in millivolts (mV), neutron porosity (ΦN),expressed as a volume fraction (v/v), bulk density (ρb) measured in grams per cubic centimetre (g/cc), sonic (DT) measured in microseconds per foot (us/ft), thorium (Th) measured in parts per million (ppm), potassium (K) indicated as a percentage (%), and deep resistivity (LLD) measured in ohm-meters were included in the data analysis for accurately analysing the subsurface structure of the reservoir. The authenticity of the data was ensured, and measures were taken to eliminate any errors.

The methodology for the multidisciplinary approach to facies evaluation of Lower Indus Basin using well log analysis, machine learning, and statistical methods is as follows:

  1. 1.

    Well log data preparation The well log data was collected from the SAWAN-8 well and prepared for analysis. This included cleaning, formatting, and standardizing the data.

  2. 2.

    Facies identification Based on gamma-ray log shapes, facies analysis using electro-facies was concluded to mark several environmental interpretations.

Feature extraction Features were extracted from the well log data using standard techniques such as gamma ray log shape and cross-plot analysis. These features captured important information about the lithology, porosity, and fluid content in the subsurface. In this research, we evaluated the effectiveness of five machine learning algorithms for predicting litho-facies labels in the SAWAN-8 well. In our investigation, we used Multilayer Perceptron, Adaptive Boosting, Extreme Gradient Boosting, Support Vector Machine, Random Forest, and Artificial Neural Network. To train these models, we used a portion of the well log data and ensured that they were capable of accurately predicting litho-facies labels for unseen data by validating them on a separate set of logs. The performance of each model was compared using standard metrics like accuracy, precision, recall, and F1 score, and the best-performing model was selected for litho-facies prediction. Utilizing the chosen model, we predicted litho-facies for the entire well log dataset and compared the results to the actual labels to assess the accuracy of the model. To analyse the outcomes, we applied statistical methods such as Concentration-Number (C-N) model, which involved calculating descriptive statistics, generating histograms and box plots, and conducting regression analysis. This helped us identify potential correlations between geothermal parameters such as heat production (HP) and thermal conductivity (TC) based on their radiogenic activity.

In summary, this multidisciplinary approach involved preparing the well log data, identifying litho-facies, extracting features, training and validating machine learning models, predicting litho-facies labels for the entire well log dataset, and conducting statistical analysis of the results (Fig. 2).

Fig. 2
figure 2

Represents the work flow adopted for facies classification

Full size image

4 Interpretation

4.1 Facies analysis via well-log data

A study conducted by Ghazi and Mountney (2011), along with Martinius et al. (2002), classified five different litho-facies and their corresponding depositional processes and environments based on an analysis of the shape of a gamma-ray curve. These facies are referred to as Cfs, and they provide valuable insights into the geological history of the area under study.

The following are descriptions of different types of rock formations based on their characteristics as observed through well-log data:

  • Cf-1: This type of rock is a sandstone with a very coarse-grained texture and moderate sorting.

  • Cf-2: Sandstone, with a range of grain sizes from coarse to extremely fine, makes up the majority of these rocks. Cavities between them are filled with fine-grained limestone. Sorting ranges from fair to subpar.

  • Cf-3: Medium-grained sandy lime mudstone with inadequate sorting makes up this rock formation. In calcitic veins, it also has sub-angular quartz, silt, and limestone particles.

  • Cf-4: This type of rock is a combination of mud, lime, shale, and silt beds with extremely fine-grained and thinly laminated layers.

  • Cf-5: These rocks are typically small, black shale particles rich in organic material that have been deposited along a transgression shelf in a low in oxygen environment.

4.2 Different ML algorithms

4.2.1 Random forest (RF)

Random forest is an effective supervised machine learning algorithm that can be used for both classification and regression tasks. By building many decision trees during training, this technique uses an ensemble learning approach, and the final output is decided by the mean prediction (regression) or mode of the classes (classification) from the individual trees (Di et al. 2019). Compared to single decision trees, random forests tend to have better accuracy because they reduce overfitting and handle noisy data more effectively. During training, random forests use a random selection of features, which helps increase diversity among the trees and improves overall performance. These features of random forest make it a popular choice in many applications (Horrocks et al. 2015).

4.2.2 Artificial neural network (ANN)

An artificial neural network (ANN) is a computational model that mimics the structure and function of the biological nervous system. ANN consist of interconnected processing nodes, similar to neurons in the brain, which collaborate to process information (Lot et al. 2020). Each neuron receives inputs from other neurons, performs a simple operation on those inputs, and sends an output to other neurons in the network. The architecture of an ANN can differ widely depending on the task it aims to solve, but most ANNs are composed of several layers of nodes. The input layer accepts data from the outside world, while subsequent hidden layers analyse that data to extract meaningful features. Finally, the output layer produces a prediction or classification based on the input. ANNs are powerful tools that have been successfully used for a wide range of tasks, such as image recognition, natural language processing, and speech recognition. They are particularly useful for problems that are too complex for traditional rule-based programming approaches (Rydell 2022; Sak and Suchodolska 2021).

To train an artificial neural network, researchers generally follow these four steps. Firstly, random values are assigned to the connection weights as initial values. Next, each input pattern is propagated through the network to calculate the ANN's output using forward propagation. The third step is computing the error by comparing the actual output with the planned output. Finally, the error is propagated backward through the network to adjust the connection weights using backpropagation. The Mean Square Error (MSE) between the desired output (\(t_{i}\)) and the actual output (\(a_{i}\)) produced by the ANN is then calculated using Eq. 1 (Cios & Shields 1997):

$$E_{k} = \mathop \sum \limits_{i = 1}^{n} \left( {t_{i} - a_{i} } \right)^{2}$$
(1)

In the next step, Eq. 2 is used to adjust the connection weights in order to minimize the error. Here, \(W_{t}\) represents the weight, \(\frac{{dE_{k} }}{d\omega }\) is the gradient, and η is the learning rate.

$$W_{t + 1} = W_{t} + - \eta \frac{{dE_{k} }}{d\omega }$$
(2)

The process of training artificial neural networks involves adjusting the weights until the desired level of accuracy is achieved. This iterative process is crucial for complex tasks such as image and speech recognition, and natural language processing. Neural networks have demonstrated remarkable effectiveness in these domains. It's important to note that this training process relies on a series of steps, which involve modifying the weights based on the errors produced by the network. By repeating this process, the network can learn from its mistakes and improve its performance over time.

4.2.3 Extreme gradient boost (XGB)

Extreme Gradient Boosting (XGB) is a powerful machine learning algorithm that has gained popularity for its ability to handle both classification and regression problems. What sets XGB apart from other algorithms is its robustness in handling missing values and outliers. This is achieved through a unique approach of splitting the data based on feature values, rather than random split points as seen in traditional decision trees (Alaudah et al. 2019). Moreover, XGB is known for its speed and scalability, making it a popular choice for real-world applications. It has been optimized for efficiency, allowing it to handle large datasets with millions of rows and thousands of columns. A regularisation term is added to the loss function to further boost performance (Rencher and William 2012),

$$l\left( \varphi \right) = \mathop \sum \limits_{i} (y_{i} - y_{i} ) + \mathop \sum \limits_{k}^{n} f\Omega \left( k \right)$$
(3)

Additionally, XGB includes regularization techniques such as L1 and L2 to prevent overfitting and improve generalization performance. These techniques help ensure that the model doesn't memorize the training data and performs well on new data. Overall, XGB can be applied to various machine learning tasks and is a valuable tool in a data scientist's toolbox.

$$f\Omega \left( k \right) = yT + \frac{1}{2}\lambda \omega^{2}$$
(4)

The above equation represents the regularization parameters for a decision tree model. The variables used in the equation are as follows: k represents the leaf number, \(\omega\) is a constant, \(T\) represents the number of leaves in the tree, \(\lambda\) is a constant, and w represents the leaf node's value. The equation helps to regulate the values of the leaf nodes and control overfitting in the model.

4.2.4 Support vector machine (SVM)

Supervised machine learning classifiers that utilize well-organized characteristic learning samples can yield highly accurate results in lithology classification. In order to achieve optimal results, statistical learning theory and the structural risk minimization principle suggest that Support Vector Machines (SVMs) are the most appropriate method for identifying the ideal separating hyperplane for classification which explain the linear data as \(\left( {x_{i , } y_{i } } \right)\) with \(x_{i } \in R^{m} , y_{i } \in \left\{ {1, - 1} \right\}, i = 1, \ldots ,n\). The SVM find out tow hyperplanes with equation elaborated as \(\left| {\upomega x_{i } + b} \right|\)= 1. \(\frac{2}{{\left\|\upomega \right\|^{2} }}\), the boundary in between those two planes, should be maximized, which indicates a minimum of \(\left\|\upomega \right\|^{2}\). This problem also defined as follow.

$$\min r\left(\upomega \right) = \frac{1}{2}\left\|\upomega \right\|^{2}$$
(5)
$${\text{Subjected to}}:\;\;y_{i} \left( {\upomega \cdot x} \right) + b \ge 1,\quad i = 1, \ldots .,n$$
(6)

To permit misclassification, the SVM presents slack variables \(\xi_{i}\) and penalty parameter C. the problem elaborated as follow

$${\text{Subjected to}}:y_{i} \left( {\upomega \cdot x} \right) + b \ge 1 - \xi_{i} , \quad i = 1, \ldots .,n$$
(7)
$${\text{Subjected to}}:\;\;\mathop \sum \limits_{i = 1}^{n} y_{i} \alpha_{i} = 0, \alpha_{i} \ge 0, y_{i} = 1, \ldots .,n$$
(8)

where \(0 \le \alpha_{i} \le C\).

To overcome the problem of nonlinear learning data, a kernel function is selected to project data into higher dimensional feature spaces. So, we select the Gaussian radial basis function \(K \left( {x_{i} , x_{j} } \right) = {\text{exp}}( - \gamma \left\| {x_{i} - x_{j} } \right\|^{2} ), \quad \gamma > 0\) and resultant solution has the form

$$x\left( y \right) = sgn\left[ {\mathop \sum \limits_{i = 1}^{n} \alpha_{i} y_{i} K\left( {x, x_{i} } \right) + b} \right]$$
(9)

In our study, as the lithology distribution is non-binary, the SVM binary classifier was extended to a multi-class classification using the one-against-one method (Hsu et al. 2002). The performance of the SVM model is heavily dependent on the penalty parameter C (Rencher and William 2012). However, the same penalty parameter C is applied to both majority and minority class samples in SVM, which can lead to misclassification of minority class samples. Additionally, due to the optimal separating hyperplane, there are often more samples belonging to the majority class than the minority class. Consequently, misclassification of the minority class sample has less negative impact on overall accuracy. Therefore, the optimal separating hyperplane tends to be inclined towards the minority class to maximize the margin and minimize the empirical hazard of misclassification, at the cost of higher testing error.

4.2.5 Multilayer perceptron (MLP)

A MLP, also known as a multilayer perceptron, is a form of artificial neural network that is made up of several interconnected layers of nodes, or neurons. Typically, the MLP will consist of an input layer, one or more hidden layers, and an output layer (Juna et al. 2022). Each neuron in the MLP gets input from the previous layer's neurons and performs a weighted sum of those inputs. This sum is then fed through an activation function to create an output. During training, backpropagation is used to adjust the weights on these connections to minimize the difference between predicted and actual outputs (Murtagh 1991).

$$y = \mathop \sum \limits_{i = 1}^{n} \omega_{i} x_{i} + bias$$
(10)

MLPs are a potent tool for tasks such as prediction, classification and pattern recognition because they can understand complicated relationships between inputs and outputs due to the use of multiple hidden layers. However, if MLPs are not correctly regularized or if the training data does not represent the underlying distribution, they can suffer from overfitting (Chen et al. 2021). It is critical to keep in mind that overfitting can lead to an MLP model that performs well on the training dataset but poorly on new data (Fig. 3).

Fig. 3
figure 3

Represents the work flow adopted for machine learning algorithms to classify the facies of Sawan-8 well

Full size image

4.3 Concentration number (C-N) modeling

The C-N fractal model has been utilized in the past to characterize anomalous zones in geophysical data. Based on the inverse relationship between the cumulative frequency of core samples and their critical concentration, this approach is highly appreciated (Hassanpour and Afzal 2013). Traditional statistical methods used for geophysical data analysis often have limitations as they do not consider the data's solitary recurrent cycle (Afzal et al. 2016; Mueller et al. 2016). Additionally, these methods fail to account for spatial variance due to the lack of geographic relationship data accessibility. Other approaches that assume log-normality also have their limitations as they overlook factors such as range, size, geophysical zone conditions, and data distribution (Asfahani 2019). However, the C-N model is not constrained by the limitations of traditional statistical approaches and can effectively separate geophysical abnormalities from their context. Since anomalies may be recognized as threshold values in such plots, the log–log plots and C-N fractal model are often used to characterize and categorize geology for mineralogical data processing (Hosseini et al. 2015). In order to identify minerals along any fault zone according to their radiogenic activity, geothermal variables like GR, HP, TC, and HF are required. We first calculated the HP and TC, and then used them in the C-N modeling to categorize minerals into different population ranges based on their radiogenic activity. Moreover, HF can be used to detect friction heating during sliding or shearing along faults.

4.4 Calculation of geothermal parameters (HP, TC, and HF)

The brief introduction and calculation of the utilized geothermal parameters required for the C-N Modeling are as follows;

4.4.1 Heat production (HP)

HP is often measured in the laboratory utilizing core samples and GR spectrometry (Fernández-Ponce et al. 2011). The HP parameter is calculated using the GR log. The HP was estimated by applying formula (Bücker and Rybach 1996);

$${\text{HP }}\left( {\upmu {\text{W}}/{\text{m}}^{{3}} } \right) = 0.0{158}\left( {{\text{GR }}\left( {{\text{API}}} \right) - \, 0.{8}} \right)$$
(11)

4.4.2 Thermal conductivity (TC)

TC is often measured in the lab using cores or drill cuttings drilled through boreholes. The core samples were collected from Sawan-8 well. The TC was calculated using 115 core samples that were 25 cm long and 22 cm wide. In the SAWAN-8, core samples were taken at depths ranging from 3260 m to around 3410 m. After every 7 m interval, samples were taken. As indicated in Table 1 and Fig. 4, we used these 120 core samples and presented the corrections to analyse the TC for submerged conditions.

Table 1 Represents thermal conductivity (TC) measurements from core samples. aThe provided data displays TC measurements obtained from core samples of sandstone, shale and siltstone. bMean TC value and Model Fit are taken from Li et al. (2015). cModel Fit γ indicates the value derived from the highest TC value assessed for each mineral, with γ representing rock samples possessing low-porosity values. This makes it closer to the in-situ TC values. Therefore, it is near to in-situ TC values dis determined using the average laboratory γ and the Model Fit γ values
Full size table
Fig. 4
figure 4

Represents the GR, HP and TC curves measured from well log data

Full size image

5 Results and discussion

5.1 Electro-facies analysis

Geophysical log analyses were conducted on Sawan-8 to evaluate the thickness of the C-sand interval in the study area using petrophysical parameters. The results showed that the C-sand reservoir has a high matrix content, low volume of shale, and favourable porosity (Fig. 5). However, significant amounts of shale were present above and below the C-sand layer. The Lower Goru sand exhibited four distinct log-curve shapes, including cylindrical, funnel-shaped, bell-shaped, and irregular-shaped patterns. The irregular pattern was attributed to the presence of carbonaceous materials with poorly sorted sub-angular grains, as explained by Rider and Munn (1967). Furthermore, the Lower Goru formation's chlorite cement, calcite, and fracture-filling veins all had an impact on the uneven or serrated shapes of cylindrical, funnel, and bell-shaped patterns seen in our study.

Fig. 5
figure 5

Gamma-ray log correlation of depositional environments and electro-facies classification in the C-sand interval of Lower Goru Formation of Sawan gas field

Full size image

After a careful analysis of the research conducted by Pendrel and Schouten (2017). The funnel-shaped sequence, which is mostly seen in extremely coarse sandstone (Cf-1), was found to show an upward coarsening tendency, which denotes an increase in grain size. This type of sequence typically implies the presence of delta-front settings where mouth bars tend to accumulate and deposit thick clastic sediments (Fig. 6). These formations are distinctive in their coarser grain trend in the upward direction of the funnel-shaped sequence. Therefore, it can be concluded that such formations are typical of delta-front settings, particularly mouth bars.

Fig. 6
figure 6

a The log interpretation at the well Sawan-8 in the Lower Indus basin b The cross-plot, which is color-coded with gamma ray, as indicated by the density versus neutron porosity relationship c Volumetric representation of the “shaly sands” petrophysical model adopted for the quantitative interpretation of well logs

Full size image

Upon reviewing the research findings of Martinius et al. (2002), Wood (2022), it has been observed that the bell-shaped sequence follows a fining-upward trend, indicating a decrease in grain size, especially in coarse- to very fine-grained sandstone (Cf-2). These types of sequences are indicative of the presence of fluvial deltaic channels where sediments ranging from coarse- to very fine-grained tend to accumulate. The gradual decrease in grain size upwards, which is typically observed in bell-shaped sequences, is a distinguishing feature of fluvial deltaic channels.

After analysing the data provided by Zhang and Zhang (2021). It is evident that there is a pattern of coarsening in the sequence, indicating an upward trend in the grain size. This type of sequence is typically characterized by the presence of very coarse sandstone (Cf-1), which suggests the accumulation of thick clastic sediments in the delta-front settings. This deposition process usually occurs in mouth bars, as noted by Cant's research conducted in 1992.

According to Wood (2021), the sequence with a bell-like shape exhibits a trend of fining upward. This implies that the grain size is getting smaller, especially in the coarse- to very-fine-grained sandstone (Cf-2). Bell-shaped sequences are frequently seen in fluvial deltaic channels, where sediments with this range of particle sizes prefer to collect. Cant's research from 1992 supports this finding.

The regularity in grain size observed in cylindrical-shaped sequences, specifically the medium-grained sandy lime mudstone (Cf-3), indicates a consistent trend. This type of pattern is usually associated with medium clastic sediments resulting from prograding delta distributaries, which was reported by Imamverdiyev and Sukhostat (2019). In addition, the existence of fine-grained black shales (Cf-5) is indicated by high gamma-ray values in sand-shale baselines with erratic patterns. According to Jiang et al. (2021) these organic-rich shales are typically found in rapid transgressive environments with shallow-water deposition.

Porosity, texture, diagenesis, provenance, and paleo-environments of the Lower Goru Formation were deciphered using petrophysical logs and facies analyses, as well as well-log and seismic data. This information was gathered from several literature sources and included in a petrographic investigation in order to establish the formation's mineral composition. The petrographic data was analysed, and then it was coupled with petrophysical logs and facies analysis utilizing seismic and well-log data. This aided in precisely determining the Lower Goru Formation's mineral composition.

5.2 Integrating logs and cross plot for facies characterization

A neutron density cross-plot is a type of analysis used to study the properties of subsurface formations. It involves plotting two measurements, the Neutron porosity (ΦN) and Bulk density (ρb), on a graph. The neutron porosity measurement provides information about the amount of hydrogen in the formation, while the bulk density measurement gives an estimate of the formation density (Li et al. 2021). Using this analysis, different types of rocks and minerals can be identified based on their characteristic positions on the cross-plot. For example, limestone typically falls in the high-density, low-porosity region of the plot, while sandstones with high porosity fall in the low-density, high-porosity region (Fig. 6).

In addition to identifying rock types, the neutron density cross-plot can also be used to estimate other important formation parameters, such as water saturation and lithology. Water saturation can be determined by comparing the measured neutron porosity with a calculated shale baseline. Lithology can be estimated using various techniques, including the use of cross-plot templates or statistical analysis methods (Avseth and Mukerji 2002).

Overall, the neutron density cross-plot is a valuable tool for understanding the properties and characteristics of subsurface formations, which can help guide oil and gas exploration and production activities.

5.3 Evaluating machine learning techniques for predicting litho-facies

This study utilized five different machine learning classification models to predict litho-facies, including Random Forest, Artificial Neural Network, XGB, Support Vector Machine, and Multilayer Perceptron. The models were trained on 77% of the available dataset and validated on the remaining 23%. Precision, Recall, and F1-score evaluation metrics were calculated for each predictive method and presented in Fig. 7 and Table 2. Additionally, a normalized confusion matrix was generated to assess accuracy and misclassification for each ML technique as illustrated in Figs. 8 and 9 and Table 3.

Fig. 7
figure 7

The results of each prediction model's assessment metrics, computed for each litho-facies, are A precision, B recall, and C F1 score

Full size image
Table 2 Statistics, including Precision, Recall, and F1-score, calculated using several machine learning classifier methods to classify shale sand and carbonate facies
Full size table
Fig. 8
figure 8

In part figure labels (A–D) are associated with various machine learning classifiers used in the study,including Random Forest (RF), Artificial Neural Network (ANN), Extreme Gradient Boosting (XGB), and Support Vector Machine (SVM). The normalized confusion matrix for these classifiers is displayed, with lithology codes 1 and 2 representing shale and sand/carbonate facies, respectively. The color variations in the matrix indicate different levels of normalization, with the color scale representing the degree of normalization and nonnormalization

Full size image
Fig. 9
figure 9

Represents each litho-facies and overall, the predictive models' confusion matrix outp uts were computed to determine their accuracy (A) and misclassification rate (B)

Full size image
Table 3 The statistics for the classification of shale sand and carbonate facies using various machine learning classifier algorithms
Full size table

A crucial statistic called precision evaluates the precision of expected litho-facies for all litho-facies found in the log data. The precision values differ for different litho-facies, with sand facies (fine, medium, and coarse) demonstrating precision values ranging from 0.84 to 0.92, shale facies ranging from 0.65 to 0.78, and carbonate facies ranging from 0.82 to 0.87%. Table 3 shows that, in the categorization of shale facies, MLP, RF, ANN, and XGB algorithms demonstrate significantly higher precision than SVM, as illustrated in Fig. 6A. MLP, RF, and ANN algorithms outperform XGB and SVM models for classifying sand facies. In contrast, MLP, SVM, and XGB algorithms outperform ANN and RF models in the categorization of carbonate facies. For classifying all three litho-facies, the MLP technique performs the best in terms of precision, followed by the RF, ANN, XGB, and SVM algorithms.

Recall is a crucial metric that measures the accuracy of a model to identify actual litho-facies present in log data. The recall value for sand facies ranges from 0.87 to 0.93, while for shale facies, it ranges from 0.78 to 0.89, and for siltstone facies, it ranges from 0.65 to 0.79 (Table 2). For classifying sand facies, the RF, MLP, ANN, and SVM algorithms often have greater recall values than the XGB technique. MLP, RF, ANN, and XGB algorithms show greater recall values than SVM for classifying shale facies. Lastly, for siltstone facies classification, MLP, ANN, XGB, and RF algorithms show greater recall than SVM. For classifying all three litho-facies, the MLP technique is thought to be the best-performing approach based on recall, followed by the ANN, XGB, RF, and SVM techniques.

The F1-score is a metric that measures the harmonic mean of precision and recall values. A higher F1-score indicates better performance of the model in litho-facies classification, with scores varying across all models between 0.86 and 0.93 for fine sand facies, 0.66–0.79 for medium sand facies, 0.70–0.92 for shale facies, and 0.68–0.73 for siltstone facies. The MLP, RF, and ANN methods exhibit better performance than the XGB and SVM methods for sand (fine, medium, and coarse) facies classification based on F1-score. Similarly, in shale facies classification, the MLP algorithm outperforms the XGB, ANN, SVM, and RF methods based on F1-score. For determining all three litho-facies, the MLP strategy emerges as the most effective model overall, followed by the RF, ANN, XGB, and SVM approaches, according to F1-score.

The confusion matrix is an essential tool in machine learning that allows for the comparison of actual and predicted results based on true positives, true negatives, false positives, and false negatives. The real positives for each litho-facies are shown by the diagonal values of the confusion matrix. Important criteria used to assess categorization issues include accuracy and misclassification. The ratio of accurately predicted records to all records is known as accuracy, and misclassification may be computed as one minus accuracy (Xu et al. 2020).

The present study compared the accuracy of RF, MLP ANN, SVM, and XGB algorithms for classifying shale, sand, and carbonate facies. Shale facies classification display greater accuracy values for the RF, MLP, ANN, and SVM algorithms, whereas sand facies classification showed higher accuracy for the MLP, RF, ANN, and XGB methods. In contrast, the MLP algorithm demonstrated noticeably high accuracy in the categorization of carbonate facies when compared to other approaches. Overall, the MLP approach was shown to be the best-performing model based on accuracy values, followed by the RF, ANN, XGB, and SVM methods. The MLP approach had the lowest misclassification values, and it was followed by the RF, ANN, XGB, and SVM approaches. The MLP technique was determined to be the best method based on accuracy and misclassification values, compared to the RF, ANN, XGB, and SVM models.

5.4 Concentration-number modelling

Determining the appropriate threshold value to describe and visualize the fluctuations in geothermal parameters, like GR (API), TC (W/mK), and HP (μW/m3), are essential after computing the geothermal characteristics of the Lower Indus Basin (Fig. 4) (Shahed Rezaei et al. 2018). To differentiate between different intensities of discrete breakpoints using the C-N model, we applied it to the whole SAWAN-8 well, which contained a total of 1520 GR, HP, and TC data points. A log–log plot was generated for geothermal characteristics such as GR, HP, and TC, with slope differences and fractures observed in the fitted straight lines reflecting different population variances (Fig. 10a2, b2, c2). Various coloured lines represent various slope lines, with the colours indicating the population of each formation. Breakpoints parallel to x-axis, like B1, B2, B3, B4, and B5, indicate the intersection of each slope line, providing GR, HP, and TC values parallel to x-axis. The corresponding intensity maps and histogram plots are shown in Fig. 10a1, b1, and c1, and a3, b3, and c3 show the various degrees of intensity along the fault zone. These results describe the various intensity levels along the fault zone based on the greatest values of GR and HP populations in the C-N model log–log plot with high intensities at fault sites (Table 6).

Fig. 10
figure 10

a2, b2, and c2 Five cut-off point may be found in the fractal C-N log log plot to each geothermal parameter (GR, HP, and TC). Straight-line segments were fitted with least squares (GR, HP and TC) holds six cut-off breakpoints. Least squares fixed straight-line sections. a1, b1 and c1 The C-N fractal model in the South Indus Basin highlights the recognised maps for the geothermal properties. a3, b3, and c3 indicates the histograms of GR, HP, and TC

Full size image

In distinction, TC is associated with the lowermost values at the point where HP and GR are at higher values. On the log–log plot of the C-N model, the population parameters for TC are linked to much smaller values. The intensity of GR varies widely, ranging from a high of 150 API to a low of 10.2 API. The SAWAN-8 well reports an average intensity of 178.4 API for GR, with a standard deviation of 46.8 API. The highest intensity of HP is approximately 5.3 μW/m3, while the lowest intensity is around 0.1 μW/m3. The average intensity of HP in the SAWAN-8 well is 1.7 μW/m3, with a standard deviation of 0.5 μW/m3. The higher value for TC power is 4.41 W/mK, while the lower value is 0.18 W/mK. In the SAWAN-8 well, TC intensity values typically range between 2.3 and 2.8 W/mK, with a standard variation of 0.7 W/mK (Table 5).

Five population zones were found using the C-N model log–log plot on geothermal variables based on their radiogenic intensities (Fig. 10). When using ML techniques to RF, SVM, ANN, XGB and MLP, we discovered that the total C-N model agrees with previous statistical research after combining the results obtain from ML techniques. In addition, the C-N model is utilized to determine the facies of the borehole, which confirms the earlier research conducted at SAWAN-8 (Tables 4, 5).

Table 4 The GR (API), HP (μW/m3), and TC (W/mk) statistical characteristics in the studied region. Log–log plots of N (≥ μ) against μ (GR, HP, and TC) log–log plots reveal a direct association and suggest straight-line sections via a number of slopes that agree to various concentration forms
Full size table
Table 5 The lineament factor (LF) map's range of values as calculated using C-N fractal modeling (Fig. 10)
Full size table

5.5 Comparative evaluation of ML techniques for litho-facies classification

Various machine learning (ML) classification techniques have been evaluated to determine their accuracy in distinguishing between different litho-facies, including shale, sand, and carbonate facies. To accomplish this, wireline logs obtained from wells were analysed to predict litho-facies. This study aimed to examine the performance of six distinct ML approaches (RF, ANN, XGB, SVM, and MLP), as well as a statistical analysis known as the C-N model. In past research, machine learning techniques were utilized to examine the distribution of lithology in petroleum and coal deposits. The efficacy of each model was assessed by considering all relevant factors, such as evaluation and confusion matrices, with accuracy being among the metrics employed to evaluate performance.

5.6 Limitations

Overall, the findings of this research article highlight the importance of utilizing a multidisciplinary approach to improve the accuracy and reliability of facies evaluation in oil and gas exploration.

Overfitting One of the significant limitations of machine learning algorithms is overfitting, where the algorithm becomes too complex and fails to generalize well on new or unseen data.

Data quality The accuracy and reliability of machine learning algorithms are heavily dependent on the quality of the training data. If the data is incomplete or contains errors, it can lead to inaccurate predictions.

Interpretability Machine learning algorithms, especially neural networks, are often considered as black boxes because they lack interpretability. It can be challenging to understand how the algorithm arrived at a particular decision or conclusion.

Computational resources Some machine learning algorithms require significant computational resources, such as memory and processing power, which may not be available in all environments.

Concentration Number Modeling as a Statistical Analysis: Concentration Number Modeling is a powerful statistical analysis tool that can be used to evaluate the facies of a well log based on the number of times a particular set of values occur within a specified range. This method can provide useful insights into the sedimentary characteristics of the formation.

Based on our findings, MLP is the best and superior approach since it just requires adjusting one variable, which is the number of inputs, to get optimal performance. MLP is very flexible and efficient, and it needs no previous information about the network to function. It's a tried-and-true method with a high success rate. Table 6 shows that it also performs well in the case of geologically complicated areas.

Table 6 The accumulation of facies according to GR, HP, and TC intensities measured by using fractal C-N model
Full size table

6 Conclusions

The multidisciplinary approach combining well log analysis, machine learning, and statistical methods has proven to be a successful strategy for evaluating the facies of the SAWAN-8 well. Among the machine learning techniques employed in this study, Random Forest (RF), Support Vector Machine (SVM), Artificial Neural Network (ANN), Extreme Gradient Boosting (XGB), and Multilayer Perceptron (ML) showed promising results (Table 7).

Table 7 displays the statistics of the employed algorithms
Full size table

This study shows how different machine learning methods, including RF, ANN, XGB, SVM, and MLP, are successful in correctly classifying shale, sand, and carbonate facies in the South Indus Basin Sawan field. Using interpreted litho-facies data from wells for training and validation, the models' performance was evaluated on test data using a confusion matrix and evaluation matrix. The classification of shale facies, followed by sand and carbonate facies, fared well across all models, according to the results, with accuracy scores ranging from 85 to 93%, 65 to 79%, and 61 to 77%, respectively. MLP was found to be the top-performing model for all three litho-facies classifications. Interestingly, the estimated distribution of different litho-facies aligned well with prior geological knowledge and the eustatic curve from the Jurassic to Cretaceous period in the region. This study emphasizes the significance of taking a multidisciplinary approach to enhance the accuracy and dependability of facies evaluation in oil and gas exploration.