1 Introduction

The geodynamic disasters induced by human beings during the construction of deep underground space utilization and deep mineral resource mining have been the focus of global research for nearly a hundred years (Borisov et al. 2019). Coal bursts and mining-induced seismicity are typical geodynamic disasters, often causing severe damage to shafts and roadways and heavy casualties (Cao et al. 2023; Cheng et al. 2023). Coal bursts have occurred in coal mines in over 20 large coal mining countries, including South Africa, Germany, Canada, Russia, and Australia (Wu et al. 2022). On May 12, 2014, a coal burst accident occurred at a coal mine in Boone County, West Virginia, USA, killing two miners (Newman and Newman 2021). Coincidentally, on May 24, 2020, a coal burst accident happened at the Mengcun coal mine in Shaanxi Province, China, injuring six miners. The assessment of coal burst risk (CBR) is the premise of coal burst disaster prevention and the implementation criterion to guide various coal burst prevention and control measures (Dou et al. 2018; Dai et al. 2022). Accurate coal burst prediction is critical for high-efficiency mine production and ensures the life safety of underground workers.

Research on CBR assessment methods in coal mines mainly focuses on dynamic monitoring and early warning (DMEW) as well as static prediction and evaluation of CBR (Dou et al. 2022). The DMEW method largely uses practices such as drilling cuttings, mine-pressure measurements, microseismic, ground sound, and electromagnetic radiation monitoring (Jiang et al. 2016; Cai et al. 2020; Duan et al. 2021). These methods are affected by the scope of underground mining activities and are suitable for real-time dynamic early warning of coal burst hazards in the production stage. The static evaluation of coal burst risk is widely used in the mine design and development preparation stage.

Numerous studies have been completed on the static prediction and evaluation of CBR in recent years. Dou and He (2002) statistically analyzed the cases of coal burst mines in China. They proposed a comprehensive index method for the prediction of CBR by using mining and geological factors such as Coal seam thickness (CST), Mining depth (MD), Elastic energy index, the Ratio of stress increment caused by the structure to the standard stress value (RIS), and rock-layer thickness characteristic parameter (RTP). Bukowska (2006) studied the Upper Silesia Coal Basin and proposed an assessment system of the CBR based on seven natural conditions of mining operations. Peng et al. (2010) analyzed the mechanism of coal bursts and, taking the bursting liability and stress state of coal as the influencing factors of the CBR, proposed a simple CBR assessment method. Zhang et al. (2016a, b) used the geodynamic zoning method to analyze active regional faults, dividing the fault block structure of active faults at all levels. They proposed an evaluation method for CBR based on fault structure and coal-rock characteristics. Konicek and Schreiber (2018) analyzed typical examples of coal bursts recorded in the Czech part of the Silesian Coal Basin in rock mass protection pillars, using microseismic activity recorded during longwall mining to roughly assess the CBR in coal mines. Zhu et al. (2018) analyzed the relationship between coal burst and five factors: MD, tectonic stress, vertical crustal movement, active fault, and roof hard rock ratio. They established an assessment model for the CBR using AHP (Analytic Hierarchy Process) and a fuzzy comprehensive evaluation method. Zhang et al. (2022) used the LS-FAHP-CRITIC method to evaluate the CBR in mining areas by combining five indicators: CST and MD, initial in-situ stress, geological structure, and sedimentation. Du et al. (2022) selected microseismic monitoring signals as critical indicators, establishing a normal distribution function of microseismic daily frequency, and proposed a quantitative evaluation method for CBR.

Although the above studies have promoted the development of CBR assessment, there are still several issues. First, many factors affect coal bursts, and there is a deep coupling between each factor Qi et al. (2019). Based only on the geological and mining information before mining, the qualitative classification and evaluation of CBR in mines and local areas are highly subjective and unreliable. Second, the existing static prediction methods with dynamic monitoring and early warning methods are independent. Some data are ignored, and there are still significant errors in the actual comparison to prediction results. Applying the results of dynamic monitoring to the static prediction and evaluation of CBR is critical research.

This study proposes a method for quantifying mining-induced seismicity information based on the fractal theory. A deep learning framework of coal burst risk (DLFR) based on the fractal dimension of dynamic monitoring information is constructed using the deep learning method. Using the Gaojiappu Coal Mine as an example, a prediction of CBR is carried out based on the DLFR. During the modelling process, the gray relational analysis (GRA), information gain ratio (IGR), and Pearson correlation coefficient are used to screen the model factors to gain more representative samples and improve the model accuracy. Finally, the model performance is evaluated using statistical evaluation indicators such as macro-F1 (macro-F1), accuracy rate (ACC), and fitness curve. Conduct a comparative analysis between the predicted results of a study area and the actual field results through a specific case study to validate the reliability of research findings. The performances of deep learning models are discussed, such as BP, SVM, PSO-BP, and PSO-SVM, under this framework, aiming to establish a stable and high-quality CBR identification model and provide some inspiration for the research on CBR assessment methods. According to the results of CBR identification, a "graded" precise pressure relief design can be performed, providing the basis and guidance for the design of coal mine coal burst prevention and control.

1.1 Geological setting

The Gaojiapu coal mine is located in the plateau area in the southwest Ordos Basin, primarily a beam and gully landform. The length and width of the coal mine are 25.7km and 16.6km, respectively, and the minefield area is 219.16 km2 (Fig. 1a). The mine uses the vertical shaft development method, and the underground coal mining method consists of longwall coal mining of mainly the No.4 coal seam of the Jurassic Yan'an Formation. Currently, the research area is divided into three panels for mining. Due to the coal burst disaster impact, the first-panel subsequent working face is not mined. The second-panel has been fully extracted, and the third-panel area is designated as the continuous production area. The research area has installed a new 'SOS' microseismic monitoring system designed and manufactured by the Polish Institute of Mine Research. The system is capable of Real-time dynamic monitoring of microseismic signals with energy greater than 100J in the study area. It can accurately calculate the energy, time, and location of mining-induced microseismicity (Kan et al. 2022). The sensor installation position of this monitoring system is shown in Fig. 1b. By collecting all the microseismic monitoring data in the study area since installing the 'SOS' microseismic monitoring system. Due to the complex geological conditions of the study area, the geodynamic hazards are highly active. Because of coal extraction, numerous coal burst accidents have occurred, seriously affecting the safety of mine production (Fig. 2).

Fig. 1
figure 1

Location of the study area and layout of microseismic monitoring sensors

Full size image
Fig. 2
figure 2

Photos showing severe coal burst in the study area

Full size image

1.2 Coal burst affecting factors

Based on an extensive literature survey, field survey analysis, and previous work, the previous coal burst prediction included the following factors (Dou and He 2002; Sun et al. 2021; Zhu et al. 2018): CST, coal seam dip angle, MD, roof lithology, elastic energy (W), structural conditions, maximum tangential stress, uniaxial compressive strength (Uc), ratio of stress increment caused by the structure to the standard stress value (RIS), and rock-layer thickness parameter (RTP). In this study, 11 factors, both qualitative and quantitative, were selected, namely coal seam thickness (CST), mining depth (MD), rock-layer thickness parameter (RTP), thickness of overburden hard rock-layer and its spacing with the coal seam, sedimentary characteristics of roof strata, rock mass quality evaluation score (RQS), geological structural capacity dimension (GSD), RIS, lateral pressure coefficient (LPC), and elastic energy (W). Table 1 shows the source of each factor selection and its significance.

Table 1 Influencing factors of coal burst and its significance
Full size table

In China's coal burst prevention and control standards, RTP within 100 m of the roof is used as an evaluation indicator. However, due to the development of the Jurassic Coalfield and the change in coal mining technology, the range of the mining deformation and damage disturbance zone is more extensive than that of the previous mining projects (Han et al. 2023). Therefore, this study selected an RTP within 200 m of the roof as the evaluation factor. According to the geological data of the Gaojiapu coal mine, there are three widely distributed hard sandstone strata on the roof layer (Fig. 1c). Therefore, a total of 6 groups of information on the thickness of overburden hard rock-layer and its spacing with the coal seam were used to reflect the impact of the roof hard rock layer on coal explosion (Fig. 3d–i). Besides, based on the tectonic evolution history, the overburden sedimentary microfacies of the study area were divided into three levels by the sedimentary discontinuity as the dividing line, namely the Yan'an Formation sedimentary microfacies (YS) (Fig. 3j), the Zhiluo and Anding Formations sedimentary microfacies (ZAS) (Fig. 3k), and the Luohe Formation sedimentary microfacies (LS) (Fig. 3l). Finally, 17 pieces of information out of 11 factors were selected in this Study (Fig. 3).

Fig. 3
figure 3

Spatial distribution of each factor in the study area (a-q). a Coal seam thickness. b Mining depth. c Roof-layer thickness parameter. d Thickness of the fine sandstone in the Yan'an Formation. e Thickness of the coarse sandstone in the Anding Formation. f Thickness of the middle sandstone in the Luohe Formation. g Distance between the fine sandstone in the Yan'an Formation and coal seam. h Distance between the coarse sandstone in the Anding Formation and coa seam. i Diatance between the middle sandstone in the Luohe Formation and coal seam. j Sedimentary microfacies of Yan'an Formation. k Sedimentary microfacies of Zhiluo and Anding Formation. l Sedimentary microfacies of Luohe Formation. m Rockmass quality evaluation score. n Geological structure capacity dimension. o Ratio of stress increment caused by the structure to the standard stress value. p Lateral pressure coefficient. q Elastic energy.

Full size image

2 Methodology

2.1 Deep learning framework of coal burst risk (DLFR)

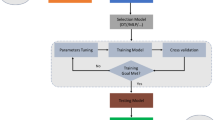
With the rapid development of computational simulation and deep learning technology, deep learning-assisted geoscience mining has shown good application prospects (Ma and Mei 2021). Many studies use deep learning technology to provide effective paths and solutions for solving geological problems (Polson and Sokolov 2020). This study constructed a deep learning framework of coal burst risk (DLFR) based on the fractal dimension of microseismic information. The risk identification of coal bursts was performed as shown in Fig. 4. First, based on the fractal theory, the mining-induced seismicity information data of underground monitoring were quantified. A CBR database was established for the study area through statistical analysis of mine geological data. Then, the collinearity diagnosis and screening of factors were performed through the GRA, Pearson correlation coefficient, and IGR. This enables more representative samples and improved model accuracy. Statistical evaluation metrics such as macro-F1, ACC, and fitness curve were used to evaluate model performance, and the performances of deep learning models such as BP, SVM, PSO-BP, and PSO-SVM under the DLFR were discussed. Finally, conduct a comparative analysis between the predicted results of a study area and the actual field results through a specific case study to validate the reliability of research findings.

Fig. 4
figure 4

Flowchart of this study

Full size image

2.2 Fractal quantification method of mining-induced seismicity

Fractal geometry was first proposed in the 1960s to describe complex natural shapes (King 1983). The fractal theory is widely used in various disciplines such as mathematics, physics, biology, economics, and geology (Turcotte 1986). The location and area where microseismic events occur have a self-similarity system, which is the same as the geological structures and has statistical similarity in geometry. The microseismic monitoring signal can be used as a parameter to comprehensively reflect the risk of coal burst (Si et al. 2020; Wang et al. 2022). In this paper, fractal research on the distribution characteristics of microseismic events was performed through the fractal dimension to obtain the fractal quantitative evaluation of coal burst risk.

Assuming that the plane distribution of microseismic events is a fixed point set A contained in a rectangle, it can be divided into several grids with side length a (Velandia and Bermúdez 2018). The distribution points of microseismic events are covered with grids with side length a, and the number of grids containing microseismic events N(a) is recorded. The grid size ai is continuously reduced to obtain the corresponding grid number N(ai). A curve can be obtained in the lna-ln N(a) coordinate system, and the slope of the straight line segment is the capacity dimension Dms of the distribution of microseismic events in the rectangle (Fig. 5), reflecting the complexity of the distribution of microseismic events in the rectangular area. Dms is calculated as follows:

$$D_{ms} \left( A \right){ = }\mathop {{\text{lim}}}\limits_{a \to 0} \frac{{{\text{ln}}N\left( a \right)}}{{{\text{ln}}\left( {a^{ - 1} } \right)}} = - \mathop {\lim }\limits_{a \to 0} \frac{{{\text{ln}}N\left( a \right)}}{\ln a}$$
(1)
Fig. 5
figure 5

Flowchart of mining-induced seismicity fractal quantification method

Full size image

2.3 Deep learning method

2.3.1 SVM

SVM is a deep learning method suitable for small, non-linear samples with high-dimensional numbers. It was studied and proposed by Vapnik et al. in the 1970s (Cherkassky and Ma 2004). It is widely used in imaging, biological information, and other information recognition, classification, and regression technologies (Dou et al. 2020). For two-dimensional linear binary classification problems, the optimal classification line becomes the optimal classification surface after being extended to high-dimensional space (Wu et al. 2013). Assuming that the sample set \(D = \left\{ {(x_{i} ,y_{i} ),\quad i = 1,2, \ldots n} \right\},\;y_{i} = \left\{ { - 1,1} \right\}\) is linearly separable, its classification surface equation is:

$$\left[ {(w \cdot x_{i} ) + b} \right] - 1 \ge 0,\quad i = 1,2, \ldots ,n$$
(2)
$$w \cdot x + b = 0$$
(3)

where yi is the category label.

Using the Lagrangian function \(L(w,\alpha_{i} ,b) = \frac{1}{2}\left\| w \right\|^{2} - \sum\limits_{i = 1}^{n} {\alpha_{i} } \left\{ {y_{i} \left[ {(w \cdot x_{i} ) + b} \right] - 1} \right\}\) to transform the above formula into a dual problem is as follows:

$$\max \sum\limits_{i = 1}^{n} {\alpha_{i} - \frac{1}{2}} \sum\limits_{i,j = 1}^{n} {\alpha_{i} \alpha_{j} } y_{i} y_{j} (x_{i} \cdot x_{j} )$$
(4)
$${\text{s.t.}}\sum\limits_{i = 1}^{n} {\alpha_{i} y_{i} } = 0,\alpha_{i} \ge 0,i = 1,2, \ldots ,n$$
(5)

The kernel function can replace the transformation of the high-dimensional space, and the inner product operation between the sample set data can be processed to determine the optimal classification surface in the high-dimensional space (Liu et al. 2011). The Gaussian Radial Basis Function (RBF) is the most commonly used kernel function and can analyze non-linear data. The optimal classification function is as follows:

$$f(x) = sgn\left( {\sum\limits_{i = 1}^{n} {\alpha_{i} y_{i} K(x_{i} \cdot x) + b} } \right)$$
(6)

2.3.2 BP

Artificial neural networks (ANN) are divided into two types of network structures: feed-forward neural networks and feedback neural networks (Sun et al. 2015). The backpropagation (BP) method is the core part of the feed-forward neural network, solving non-linear optimization problems through the input and output of a set of samples. Any non-linear function can be approximated with arbitrary precision by adjusting the BP connection weights and network size (including n, m, and the number of hidden layer neurons) (Liu et al. 2021). The non-linear relationship between the coal burst risk being inverted and a set of neural networks describes the impact factors \((n,h_{1} , \ldots ,h_{p} ,m)\) as follows:

$$\left\{ {\begin{array}{*{20}l} {NN(n,h_{1} , \ldots ,h_{p} ,\;m):R_{n} \to R_{m} } \hfill \\ {D = NN(n,h_{1} , \ldots ,h_{p} ,\;m)(P)} \hfill \\ {\begin{array}{*{20}c} {P = (p_{1} ,p_{2} , \ldots ,p_{n} )} & {D = (d_{1} ,d_{2} , \ldots ,d_{n} )} \\ \end{array} } \hfill \\ \end{array} } \right.$$
(7)

where \(P = \left( {p_{{\mathbf{1}}} ,p_{{\mathbf{2}}} ,...,p_{n} } \right)\) is the input node expression of the neural network, \(D = \left( {d_{{\mathbf{1}}} ,d_{{\mathbf{2}}} , \ldots ,d_{n} } \right)\) is the output node expression of the neural network, NN(n, h1,…, hp, m) is the established multi-layer neural network structure, and n, h1,…, hp, m are the node's number of neural networks.

2.4 Particle swarm optimization (PSO)

PSO is a method to solve optimization problems by simulating the process of bird foraging. In particle swarm optimization, birds are abstracted as a group of random particles, and the optimal solution is found through iteration (Zhao et al. 2015). A particle can find the optimal position \(P_{b}\) by itself and identify the optimal position \(P_{b,g}\) found by other particles in the entire population. Particles update their position by tracking two optimal solutions (i.e., \(P_{b}\), \(P_{b,g}\)) calculated according to the following (Li and Wei 2021):

$$\left\{ {\begin{array}{*{20}l} {V_{i} \left( {t + 1} \right) = wV_{i} \left( t \right) + c_{1} r_{1} \left[ {P_{b,i} \left( t \right) - x_{i} \left( t \right)} \right] + c_{2} r_{2} \left[ {P_{b,gi} \left( t \right) - x_{i} \left( t \right)} \right]} \hfill \\ {x_{i} \left( {t + 1} \right) = x_{i} \left( t \right){ + }V_{i} \left( {t + 1} \right)} \hfill \\ \end{array} } \right.$$
(8)

where \(V_{i} \left( t \right)\) and \(x_{i} \left( t \right)\) are the time \(t\)'s speed and positions of particle \(i\), respectively. \(c_{i}\) is the learning factors and \(w\) is the inertia factor. \(r_{1}\) and \(r_{2}\) are random numbers in \(\left[ {0,1} \right]\).

2.5 Factor screening metrics

2.5.1 GRA

GRA is a method for quantitatively describing and comparing the development and changes of an overall system. According to the geometric similarity of the time series curves of each relevant factor, the relationship between the factors is close, reflecting the degree of correlation between the indicators (Yan and Li 2013). To eliminate the impact of the non-uniform dimensions of each factor on the results, range transformation is used to perform dimensionless processing on the characterization sequence Y and the impact sequence X. The correlation degree between each component of each sequence is calculated as follows (Wu et al. 2005):

$$\xi \left( {x_{0} \left( k \right),x_{i} \left( k \right)} \right) = \frac{{\mathop i\limits^{\min } \mathop k\limits^{\min } |x_{0} \left( k \right) - x_{i} \left( k \right)| + \rho \mathop i\limits^{\max } \mathop k\limits^{\max } |x_{0} \left( k \right) - x_{i} \left( k \right)|}}{{|x_{0} \left( k \right) - x_{i} \left( k \right)| + \rho \mathop i\limits^{\max } \mathop k\limits^{\max } |x_{0} \left( k \right) - x_{i} \left( k \right)|}}$$
(9)
$$r\left( {X_{0} ,X_{i} } \right) = \frac{1}{n}\sum\limits_{k = 1}^{n} {\xi \left( {x_{0} \left( k \right),x_{i} \left( k \right)} \right)}$$
(10)
$$Y = X_{0} = (x_{0} (1),x_{0} (2),...,x_{0} (k))$$
(11)
$$X = \left[ {\begin{array}{*{20}c} {x_{1} (1)} & \cdots & {x_{1} (k)} \\ \vdots & \ddots & \vdots \\ {x_{n} (1)} & \cdots & {x_{n} (k)} \\ \end{array} } \right]$$
(12)

where x0(m) is the m-th feature index of Y, xi(k) is the k-th factor of the i-th component in X, i = 1, 2, …, n, k = 1, 2, …, m. X', Y' are X, Y dimensionless series, respectively. \(r\) is the degree of correlation, \(\xi\) is the correlation coefficient, n is the number of samples, i is the number of sub-factors, k is the k-th group of samples, \(|x_{0} \left( k \right) - x_{i} \left( k \right)|\) is the absolute value of the sequence \(X_{0}\) and \(X_{i}\) at the point \(k\), \(\rho\) is the resolution coefficient, and the value range is (0, 1).

2.5.2 IGR

Information gain (IG) represents the uncertainty-reduced value of categorical feature M by knowing the information of feature N. It is used to measure the ability of feature N to distinguish datasets (Shen et al. 2022). If there are more feature values, IG is greater. Therefore, only using IG to evaluate the composition of a sample set is not objective enough (Yao et al. 2022). The IGR only offsets the complexity of the feature variables and avoids the existence of over-fitting. IGR is calculated as follows:

$$IGR(\left. M \right|N) = \frac{g(\left. M \right|N)}{{H_{x} (M)}}$$
(13)

where \(H(Y|X)\) is the IG of M by given N condition, \(g(Y|X)\) is the information gain entropy corresponding to feature N, and \(H_{x} (Y)\) is the information entropy of M about feature N.

2.6 Model performance evaluation metrics

Model performance evaluation is key to predictive models (Yang et al. 2023). In binary classification model evaluation, several commonly used statistical parameters are precision (P), recall (R), and accuracy(ACC). By comparing actual markers with predicted markers, true negatives (TN), true positives (TP), false negatives (FN), and false positives (FP) are determined (Dao et al. 2020). For multi-classification problems, the P and R of different categories are different. Here, evaluation parameters such as macro precision (macro-P), macro recall (macro-R), and macro F1 (macro-F1) are introduced to determine the performance of the entire model. The formulas for calculating the above evaluation parameters are as follows (Sharma and Kaur 2021):

$$P = \frac{TP}{{TP + FP}}$$
(14)
$$R = \frac{TP}{{TP + FN}}$$
(15)
$$macro - P = \frac{1}{n}\sum\limits_{i = 1}^{n} {P_{i} }$$
(16)
$$macro - R = \frac{1}{n}\sum\limits_{i = 1}^{n} {R_{i} }$$
(17)
$$macro - F_{1} = \frac{2 \cdot macro - P \cdot macro - R}{{macro - P + macro - R}}$$
(18)
$$ACC = \frac{TP + TN}{{TP + FP + TN + FN}}$$
(19)

Furthermore, in the PSO optimization model, the fitness function is one of the main concepts used to evaluate the quality or fitness of each particle's solution. The fitness function evaluates the solution quality and judges the model's optimal solution or a solution close to the optimal solution.

3 Results

3.1 Influencing factor screening

First, the correlation between each influencing factor is compared with CBR, and the GRA is used to calculate the correlation degree. The results show that the correlation degree between each influencing factor with CBR is above 0.65, which has a good correlation and can fully indicate the risk of coal burst. Secondly, Pearson correlation analysis was used to determine the correlation among the various factors. When the absolute value of the correlation coefficient of the two factors is greater than 0.7, the relationship is very close (Arndt et al. 1999; Yao et al. 2022). The results of Pearson correlation analysis are shown in Fig. 6. The distance between the medium sandstone strata of the Luohe Formation and coal seam (DLSC) and CST, as well as the LPC and RIS, all show a high correlation (R values are 0.78 and 1, respectively). Finally, the IGR is used to compare the sensitivity of each influencing factor to the CBR and rank the importance of each factor (Fig. 7). The greater the IGR, the greater the information content of the index. Each factor positively contributes to varying degrees (IGR > 002). Among them, compared with DLSC, the IGR of CST is relatively small. Hereby, factor removal is performed to reduce data redundancy, and CTS was chosen to be eliminated. In this study, since we inverted the in-situ stress field (Cheng et al. 2023), RIS is essentially the value obtained by subtracting LPC to 1. Therefore, deleting RIS or LPC has no practical significance because RIS has the same IGR as LPC, and the information they contain is the same. In addition, since LPC is frequently used in most research, we retain LPC in this article. After eliminating factors that cause data redundancy, the filtered influencing factors are used to predict CBR.

Fig. 6
figure 6

Pearson correlation coefficient heat map

Full size image
Fig. 7
figure 7

Analysis results of gray relational degree and information gain ratio

Full size image

3.2 Model performance evaluation

Based on the microseismic monitoring results of the mined areas of the first-panel and the second-panel, the fractal and fractal dimension calculations are carried out. Considering that the horizontal positioning error of the 'SOS' microseismic monitoring system is about 20m (Zhou et al. 2020), we select 20m × 20m as the grid size for microseismic fractal quantification. The Jenks natural breaks method divides the monitoring results into four categories: safe area, relatively safe area, dangerous area, and highly dangerous area. The classification results of training samples' risk of coal burst are obtained. Combined with the screened high-purity influencing factor data, a better sample database is obtained for subsequent training and prediction. Seventy percent of the sample data are then randomly selected for model training, and the remaining 30% are for testing the model. The parameters of the deep learning model are set through past experience and trial and error. The calculation results of model testing indicators are shown in Tables 2, 3, and Fig. 8.

Table 2 Comparison of model training set metrics
Full size table
Table 3 Comparison of model testing set metrics
Full size table
Fig. 8
figure 8

Time series distribution plot of training and testing samples

Full size image

It is worth noting that after the 39th iteration of PSO-SVM, the fitness tends to stabilize, indicating that the model training is the optimal solution. Comparing the results of PSO-SVM and SVM models shows that ACC and Macro-F1 increased by 21.26% and 20.46%, respectively, indicating that the model after PSO optimization has higher accuracy and lower error.

After training the BP neural network model for comparison, the model evaluation index shows that when the SVM model (ACC = 65.35%) is used for the discrimination and classification of this problem, the accuracy is higher than that of the BP neural network model (ACC = 65.03%). The PSO-SVM and PSO-BP model accuracies are 86.61% and 82.21%, respectively, indicating that CBR can be effectively identified under the DLFR in this dataset (Figs. 9, 10).

Fig. 9
figure 9

The fitness curve of the PSO optimization model

Full size image
Fig. 10
figure 10

Prediction results of coal burst risk for each model. a BP model. b SVM model. c PSO-BP model. d PSO-SVM model

Full size image

Although the precision and accuracy of each model after PSO optimization have been significantly improved, the PSO-BP model tends to stabilize after the 48th iteration. The fitness value is also greater than that of the PSO-SVM model. In addition, the ACC and Macro-F1 of the PSO-SVM model are still greater than those of the PSO-BP model, indicating that the PSO-BP model needs a longer time and process to solve the problem. Furthermore, the accuracy of the PSO-BP model is not high than that of the PSO-SVM model, indicating that the PSO-SVM model is more significant for solving this problem.

3.3 Model results validation

To further verify the reliability of the research results and methods, a comparative analysis by comparing the high-energy microseismic records and shock manifestations of the 3rd-panel coalfaces. During the mining of the 301 coalface and the 302 coalface, more than 100 high-energy microseismic events of more than 103 J occurred. Among them, there are 39 microseismic events greater than 104 J and 17 microseismic events greater than 105 J, as shown in Fig. 11. In addition, the coal burst phenomena occurred in two areas in the middle of the 301 coalface and near the stop production line, resulting in the sinking of the roof and the drop of the shotcrete layer. From the results of the PSO-BP model and PSO-SVM model in Fig. 11, it can be seen that the microseismic high-energy events during the 3rd-panel mining period are mostly located in the predicted dangerous area and high dangerous area, and the microseismic events greater than 103 J are less distributed in the safe area and relatively safe area. In addition, high-energy microseismics greater than 105 J are mostly located in high dangerous area. Especially the area where the coal burst phenomena occurred are also found in high dangerous area. The results show that the prediction results of the model in this study are basically consistent with the actual results, the model and method are reliable and effective, and can be used for coal burst risk prediction and further guidance for field production work.

Fig. 11
figure 11

Comparison of forecasted results and actual results of 3rd-panel working face. a PSO-BP model. b PSO-SVM model

Full size image

It is worth noting that the energy of microseismic events in high dangerous area and dangerous area is high. In contrast, the energy of microseismic events in safe area and relatively safe area is low. This also means that strong pressure relief measures need to be developed in high dangerous area and dangerous area to avoid coal bursts. The CBR warning and prevention are complementary. With this, reasonable and effective pressure relief measures are formulated for different CBR levels based on the results of the deep learning predictions to achieve "graded" precise prevention and control. Taking the study area as an example, the "graded" pressure relief suggestions and measures are shown in Table 4.

Table 4 “Graded” stress relief suggestions and measures of the study area
Full size table

4 Discussion

4.1 Analysis of influencing factors of coal burst

Like other geological disasters, the occurrence of coal bursts is a complex non-linear process affected by numerous factors. This study uses the weighted frequency ratio (FR) in the statistical analysis method to determine the importance of each factor to the highly dangerous area, as shown in Fig. 12. Coal burst high dangerous areas mainly occur in areas with large MD, high W, large LPC, and high GSD. This area's geological environment and tectonic stress are complex and have a high static load. When interacting with small dynamic load disturbances, the critical stress load may be exceeded to induce a coal burst.

Fig. 12
figure 12

FR of coal burst influencing factors

Full size image

Except for depth, GSD and W are positively correlated with the coal burst risk, and the thickness of fine-grained Yan'an Formation sandstone (YST), DLSC, and the distance between the fine-grained Yan'an Formation sandstone and coal seam (DYSC) also have a positive correlation with the coal burst risk to a certain extent. This indicates that the overburden hard rock-layer has a specific influence on the coal burst. Among them, the greater YST and DYSC are, the easier it is to induce coal bursts. On the contrary, the thinner the sandstone strata in the Luohe Formation (LST) and DLSC, the easier it is to induce coal bursts. This indicates that the thickness and spacing of the hard rock formations of the roof must be in the appropriate range to cause a coal burst. This is also confirmed by the Anding Formation coarse-grained sandstone (AST) thickness results and its distance to the coal seam (DASC). This result is also helpful in studying the target layer identification of underground roof fracturing pressure relief technology.

It is worth mentioning that RTP and RQS did not show a linear relationship with coal burst hazard. This seems to be inconsistent with previous studies. The smaller the RTP, the easier it is for the roof rock to break under mining conditions. Furthermore, it is easier to generate dynamic loads to induce coal bursts. The results of RQS show that the extremes of roof strata quality adversely affect coal bursts. Because the better the quality of the roof strata, the overburden is difficult to break under mining conditions. However, a poor-quality roof typically has more broken strata, and it is not easy to accumulate a large amount of elastic energy. The sedimentary microfacies of each group of formations show a certain degree of consistency; that is, the depositional environment with strong hydrodynamic conditions is more likely to induce coal burst than the depositional environment with weak hydrodynamic conditions. Finally, when the LPC is high, FR is high, indicating that the CBR is small when the difference in the stress environment is small.

4.2 Performance of deep learning for the CBR prediction

The traditional static prediction method of coal bursts can only be evaluated by fusing qualitative and quantitative multivariate information. Also, its prediction results lack reliability. In this study, the fractal and fractal dimension calculation of the microseismic monitoring results in the mining area is converted into the classification results of CBR. This solves the problem of insufficient coal burst training samples to a certain extent.

This study chose PSO-SVM as the basic model to solve the problem of the CBR's non-linear judgment, improving the model accuracy and reducing data redundancy through factor selection and screening. The effect of the deep learning structure optimized by the PSO algorithm is significantly better than ordinary deep learning. One of the fundamental reasons is that the combined deep learning algorithm can ensure the convergence and accuracy of deep learning and improve the convergence speed of problem-solving. By combining deep learning technology, this study provides a new method for studying coal mine coal burst risk assessment.

5 Conclusions

Based on the fractal theory, this study quantified the mining-induced seismicity information. High-reliability samples were screened out through factor analysis, a deep learning risk identification framework based on microseismic information fractal dimensions was constructed, and the performances of deep learning models such as BP, SVM, PSO-SVM and PSO-BP under this framework were compared. Through a specific case study, the prediction results in the study area are compared with the actual results, and the reliability of the research results was verified. The following conclusions can be drawn:

  1. 1.

    The microseismic monitoring results in the mined area were calculated by the fractal dimensions method and converted into the classification results of CBR. This method can solve the problem of insufficient training samples in coal burst scenarios. Under the DLFR, the accuracy of the PSO-SVM and PSO-BP models reached 86.61% and 82.21%, respectively. The CBR can be effectively identified using the DLFR proposed in this paper.

  2. 2.

    In the deep learning model, the effect of the deep learning structure optimized by the PSO algorithm is significantly better than that of the ordinary deep learning structure. The PSO method ensures the convergence and accuracy of deep learning and improves the convergence speed.

  3. 3.

    Coal burst phenomenon areas and high-energy microseismic events mostly occur in high dangerous area, with this, different pressure relief measures can be formulated for different CBR levels based on the results of the deep learning predictions to achieve "graded" precise prevention and control.

  4. 4.

    Based on the PSO-SVM model, the results show that the highly dangerous areas of coal bursts mainly occur in areas with large MD, high W, large LPC, and high GSD.