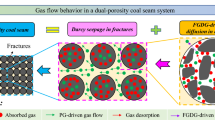
Abstract
The viscosity and density of different gases (CO2 and N2) vary with the gas species, composition and temperature, which may raise variant results of gas injection enhanced coalbed methane (ECBM) extraction. The fluid–structure interaction within the coal seam was established to study the evolution of coal strain in the process of ECBM extraction by injecting CO2 or N2. After verifying the equations governing the interaction via experimental tests, the ECBM extraction by injecting different gases was simulated. The characteristics of coal strain induced by gas sorption was comprehensively analyzed. Results show that N2 has strong fluidity in coal fractures, leading to wider influencing range of injected N2 than that of injected CO2. Due to the greater affinity of CO2 to coal, the effect of gas displacement and competitive sorption is more obvious, manifesting in more likely to migrate towards the coal matrix. Compared with regular extraction, the CH4 content at 180d in CO2-ECBM and N2-ECBM extraction has decreased by 24.3% and 13.8%, respectively. The effect of gas extraction is CO2-ECBM > N2-ECBM > regular extraction. The coal strain induced by gas sorption mainly depends on the proportion of adsorbed gas in the coal matrix. The permeability evolution is opposite to the coal strain induced by gas sorption. For CO2-ECBM, the proportion of CH4 decreases gradually caused by the competitive sorption with CO2 in matrix, and the coal strain increases. The influencing factors on the coal strain are injection pressure, initial permeability, water saturation and extraction pressure in order. While for N2-ECBM, the influencing factors on the coal strain are initial permeability, injection pressure, water saturation and extraction pressure in order.
Article Highlights
-
We have established the fluid-structure interaction within the coal seam system to study the evolution of coal strain in the process of enhanced CBM extraction (ECBM) by injecting different gases of CO2 and N2.
-
After verifying the equations governing the interaction via experimental tests, we simulated the enhanced CBM extraction with different injected gas species, and comprehensively analyzed the characteristics of coal strain induced by gas sorption.
-
The coal strain induced by gas sorption mainly depends on the proportion of adsorbed gas in the coal matrix. For CO2-ECBM, the proportion of CH4 decreases gradually caused by the competitive sorption with CO2 in matrix, and the coal strain increases. For N2-ECBM, the proportion of CH4 in the coal matrix is high, and the coal strain decreases with the time.
-
For CO2-ECBM, the influencing factors on the coal strain are injection pressure, initial permeability, water saturation and extraction pressure in order. For N2-ECBM, the influencing factors on the coal strain are initial permeability, injection pressure, water saturation and extraction pressure in order.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
With the increase of coal mining depth, the permeability of coal seam decreases gradually. Improving coalbed methane (CBM) extraction efficiency is significantly important for the safe and efficient production of coal mines (Lu et al. 2021). Gas injection in coal seam can effectively improve the efficiency of CBM extraction by flooding free gas and replacing adsorbed gas (Liang et al. 2021). At the same time, the injection of CO2 or flue gas into coal seams can increase the sequestration of CO2 and slow down the greenhouse effect (Wang et al. 2022). In the process of gas injection enhanced coalbed methane (ECBM) extraction, the permeability determines the speed of gas seepage in coal seam, and is an important parameter affecting the efficiency of gas injection and extraction (Bai et al. 2022). Generally, the coal deforms after adsorbing gases (CH4, CO2, N2), which will directly affect the permeability (Long et al. 2021). Therefore, it is great significance to carry out research on the coal strain characteristics after exposed to different injected gas species, as well as its influence on permeability.
Coal is a typical complex natural porous medium containing fractures and coal matrix (Huang et al. 2020; Wang et al. 2019a; Xu et al. 2020). Many scholars have researched the law of gas migration within coal seam. Fick's law is generally used to describe the gas migration in the coal matrix including the processes of gas adsorption and desorption (Huang et al. 2021), while Darcy's law is applied to express gas migration in fractures (Wang et al. 2019b, 2020). Therefore, the fluid–structure interactions becomes the focus to reveal the process of gas extraction from coal seam. Injection of external gas (CO2, N2, flue gas) (Wu et al. 2019; Merey and Sinayuc 2016) can be used to enhance gas extraction efficiency. According to the pioneering experiments on gas displacement, when there are different gases in the adsorption system of coal seam, the adsorption amount of each component will change with the adsorption capacity and properties (Yu et al. 2019; Fan et al. 2019a; Yi et al. 2013). Multiple groups of mixed gases exist at the same time that they will compete with each other in the coal. In recent decades, scholars have conducted adsorption experiments on coals with different gases under different temperatures, pressures, coal metamorphism and gas types, and found that the adsorption capacity of CO2 is significantly stronger than that of CH4 and N2 (Clarkson and Bustin 2000; Silva and Ranjith 2014; Zhang et al. 2016). Injecting CO2 or N2 will reduce the partial pressure of free CH4, and change the pressure gradient in coal fractures to displace CH4 (Lin et al. 2018). More than N2, the stronger adsorption capacity of CO2 will replace CH4 on the adsorption site by competitive sorption (Zhou et al. 2021; Fang et al. 2019). The gas sorption on coal matrix will produce coal strain, which causes swelling or shrinkage of coal matrix, thus alter the fracture porosity and coal permeability. During gas extraction, the sorption induced strain under different injected gases in coal matrix varies. For the original CH4-saturated coal seam, the coal matrix will expand after CO2 injection, but will shrink after N2 injection (Wei et al. 2019a; Fang 2009). Hence, the effects of CO2-ECBM and N2-ECBM extraction are quite different. The injection pressure, water saturation and initial permeability in coal seam are the main factors (Wei et al. 2019b; Shiqi et al. 2019). These research have promoted the theoretical research and technical application of gas injection enhanced CBM extraction. However, the systematic and detailed study on the sorption induced coal strain after injection of different gases has not been carried out.
In this paper, the equations of fluid–structure interaction of gas injection enhanced CBM extraction are proposed, and are verified by conducting N2 seepage experiments in laboratory. Taking Zhangcun Coal Mine as the research background, a series of numerical simulations on CO2-ECBM, N2-ECBM and regular extraction are comparatively carried out. The sorption induced strain of coal seam in these three extraction methods was detailed discussed, as well as the influencing factors—injection pressure, water saturation, extraction pressure and initial permeability, on enhanced CBM extraction. This study provides a theoretical reference for optimizing the gas injection enhanced CBM extraction and obtaining an increased efficiency.
2 Fluid–structure interactions in gas injection enhanced CBM extraction
2.1 Basic assumptions
To simplify the study, assumptions are made on the physical properties of coal and gas (Fan et al. 2021; Luo et al. 2022): (1) Coal seam is a poroelastic medium including pores and fractures; (2) Gas migration in the matrix is driven by concentration gradients satisfying the Fick's diffusion law, while gas migration in fractures is driven by pressure gradient satisfying the Darcy's law; (3) CH4, N2 and CO2 are regarded as ideal gas; (4) Gas gravity is ignored, and gas slippage effect is considered; (5) Water in coal seam only exists and migrates in fractures; (6) The adsorption and desorption of CH4, N2 and CO2 is in the state of constant temperature.
Coal seam is simplified as a regularly-arranged cuboid with equal coal matrix intervals, namely representing element volume (REV). a0 is the width of equivalent matrix, and b0 is the width of equivalent fracture. The values of a0 and b0 are calculated from the initial fracture porosity φf0 and the initial permeability k0 in the free state:
2.2 Evolution equations of coal seam porosity and permeability
Coal matrix porosity is mainly controlled by matrix strain and initial matrix porosity, and its mathematical model can be expressed as Fan et al. (2016):
where φm0 is initial matrix porosity; αm is Biot’s coefficient of matrix pores; ΔS = S − S0 is variation of matrix pore strain; S0 is initial matrix pore strain; S is matrix pore strain. αm, S and S0 are calculated as follows:
where K is the bulk modulus, GPa; Ks is the skeleton bulk modulus, GPa; εν is the volum strain in the coal; εa is the skeleton adsorption gas strain, GPa; Es is the skeleton elastic modulus, GPa; ν is Poisson ratio; D is the elastic modulus, GPa; Kn is fracture stiffness, GPa/m; the subscript ‘0’ represents the initial value of the parameter.
The gas sorption induced coal deformation is expressed as Fan et al. (2019b):
where n is the number of considered gas species; εai is the Langmuir volume constant of gas component i; bi is the absorption equilibrium constant of gas component i, MPa−1; Pmgi is pressure of gas component i in the matrix, Pa; i is gas component, i = 1 represents CH4; i = 2 represents CO2 or N2.
The fracture porosity is affected by the stress field and the seepage field, and its mathematical model can be expressed as:
where φf0 is the initial fracture porosity; Kf = b0·Kn is the equivalent fracture stiffness, GPa; b0 is the initial fracture width, m.
According to the cubic law, the relationship between porosity and permeability is:
where k0 is the initial permeability of coal seam, m2.
Substituting Eq. (5) into Eq. (6) can obtain the dynamic evolution equation of permeability:
Considering the effect of water on gas migration in fractures, the relative permeability models of gas and water phases are Xu et al. (2014):
where krg0 is the endpoint relative permeability of gas phase, m2; sw is the water saturation; swr is the irreducible water saturation; sgr is the residual gas saturation fraction; krw0 is the endpoint relative permeability of water phase, m2.
2.3 Governing equations of fluid transport field
According to the ideal gas state equation, the density of each component gas under standard conditions is:
where Mgi is the molar mass of gas component i, g/mol; pa is standard atmospheric pressure, 101.325 kPa; R is gas molar constant, 8.3143 J/(mol K); T is the temperature in coal seam, K.
Generalized Langmuir equation for binary gas adsorption is:
where cpi is the content of gas component i in coal, kg/m3; ρc is the density of coal seam, kg/m3; pmgi is the pressure of gas component i in coal matrix, MPa; ρgi is the density of gas component i under standard conditions, kg/m3; ai is the limit adsorption capacity of gas component i, m3/kg.
The gas content in coal matrix per unit volume equals the sum of the free and adsorbed gas content, which is obtained from the generalized Langmuir equation and the ideal gas state equation:
Under the action of gas injection and extraction, the original equilibrium state of gas adsorption–desorption in coal seam is broken. Forced by the concentration gradient, the gas in the coal matrix migrates into the fractures by diffusion. According to Fick’s law, the conservation of gas mass in the matrix can be derived as Ren et al. (2017a):
where pfgi is the pressure of gas component i in the fracture, MPa; τi is the desorption time of gas component i, d.
Combining Eqs. (9)–(12), the gas transport equation in the matrix can be obtained as:
Considering the gas slippage effect and the generalized Darcy law of gas–water two-phase flow, the transport flows of gas and water are gained respectively (Fan et al. 2019c):
where b is the Klinkenberg factor, Pa; μgi is the dynamic viscosity of gas component i, Pa·s; μw is the dynamic viscosity of water, Pa·s.
The change of free gas in the fracture is equal to the sum of the gas seeping out (into) the fracture and the gas diffusing into (out) the fracture. The CH4 first desorbs from the matrix pore surface into the pore space, then diffuses from the pore space to the fracture space, and finally seeps from the fracture space to the drainage borehole. While, the injected CO2 or N2 transports in the reverse direction of CH4. According to the mass conservation law, the governing equation of gas transport in the fracture is:
where sg is the gas saturation in fracture, sg + sw = 1.
The governing equation for water transport is:
where ρw is the density of water, kg/m3.
2.4 Governing equations of coal structure deformation field
The total strain of the coal mass is the sum of the strain caused by the stress, the fluid pressure in the matrix and the fractures on the coal mass, and the gas adsorption or desorption. According to the Navier equation—stress–strain relationship, the governing equation for the coal structure deformation field in CO2 or N2-ECBM is obtained as (Li et al. 2016):
where G is the shear modulus of coal, GPa; ei,ij are in tensor form (e can be displacement u, pressure p, or strain ε). The first subscript represents the i-direction component of variable e. The second subscript represents the partial derivative of ei in the i-direction. The third subscript represents the partial derivative of ei,ij in the j direction. αf is the Biot coefficient; Fi is the volume force, GPa; pm is pressure of gases in the matrix, Pa; pf is pressure of gases in the fracture, Pa. The calculation formulas are:
3 Model validation
3.1 Geometric model and parameter setting
In this paper, the evolution of coal permeability with N2 injection under stress loading and unloading were tested experimentally to verify the equations of fluid–structure interactions. In CO2 or N2-ECBM extraction, we simulated the gas interactions in the coal by setting the relevant parameters required by the gas in the equation. The coal samples were taken from the 3# coal seam of Zhangcun Coal Mine in Shanxi Province, China, and were processed to be standard cylindrical specimens with diameter of 50 mm and height of 100 mm. The triaxial stress coal and rock seepage experimental device in Liaoning Technical University was adopted. The device is composed of five parts: the hydraulic servo loading system, the clamping system, the constant temperature system, the gas pressure control system, and the data acquisition & analysis system. The schematic diagram of the adopted device is shown in Fig. 1.
The coal sample with natural moisture content preserved in a seal is placed in the holder. The axial pressure of 5 MPa was first applied, and then the confining pressure of 4 MPa was applied, followed that N2 with constant pressure of 2 MPa was injected into the coal core from the air inlet. The gas pressure at the air outlet kept at the atmospheric pressure. After that, the axial pressure and confining pressure were increased at the rates of 2.5 MPa/step in axial and 2 MPa/step in confining. The increasing operation was suspend when the axial pressure and confining pressure reached 20 MPa and 16 MPa respectively. The axial pressure kept unchanged until the end of the test. The confining pressure was unloaded at a rate of 0.5 MPa/step. The gas flow was monitored to calculate the change of coal permeability in the whole process.
The equations of fluid–structure interaction in above was embedded in COMSOL Mutiphysics software for simulation of CO2- or N2-ECBM extraction. The geometric model is shown in Fig. 2. The top surface was loaded with vertical stress, and the surrounding surface was loaded with confining stress, and the bottom surface was set as a fixed boundary. Gas was injected from the top surface, and the surrounding surface was set as impermeable boundary. The mathematical equations were verified by comparing the results of gas flow in experiments and numerical simulations. Basic parameters used in this section are shown in Table 1.
3.2 Results of verification
The comparison of N2 flow rate at outlet between the results of experimental tests and numerical simulations is made, as shown in Fig. 3. The change of N2 rate at outlet in the simulation is similar to that of the N2 rate measured in the laboratory, despite a slight deviation is observed. The simulated results are generally higher than those measured in the laboratory. The error at the beginning of gas injection is 19%, which is higher than that of other stages, remaining ~ 10%. The mathematic equation only considers the elastic deformation of coal sample, rather ignores the plastic deformation. The simulated result of N2 rate at outlet is higher than that of tested result, but the changing trend is basically similar. Therefore, the proposed equations can be adopted to simulate gas injection enhanced CBM extraction, as well as the evolution of key variables in this process, e.g. sorption induced coal deformation, coal permeability and gas pressure.
4 Simulation of enhanced CBM extraction with different gases
4.1 Physical model and solution conditions
The feasibility of CBM extraction enhanced by CO2 or N2 injection in Zhangcun Coal Mine was studied. The buried depth of coal seam is 537 m, the temperature is 298.15 K, the gas content is 8.5–10.0 m3/t, and the initial gas pressure is 0.8 MPa. As shown in Fig. 4, coal seam was simplified to be a 2D rectangle geometric model with size of 6 m × 12 m, and 3 boreholes were arranged in the coal seam, with two for extraction and one for injection. The drilling spacing was set as 3 m. Line AB and points C, D, E and F were referred to observe the simulated result. The upper boundary of the geometry model was subjected to an overburden load of 14.85 MPa, the two sides were roller supports, the lower boundary was fixed. The surrounding was impermeable boundary. The sucking pressure for CBM extraction was set as 20 kPa, while the injection pressure of CO2 or N2 was set as 1.0 MPa. The parameters for numerical simulation are listed in Table 2.
4.2 Results of simulation
4.2.1 Variation of gases pressure in fracture
Figure 5 shows the variation of gas pressure in fracture of regular extraction, CO2-ECBM and N2-ECBM at 10d, 60d, 120d and 180d, respectively. From Fig. 5a, CH4 pressure in coal seam continues to decrease with the time for regular extraction. The extraction effect is more obvious as the distance from the extraction borehole is closer.
In Fig. 5b, the fracture gas pressure of CO2-ECBM is the sum pressure of CH4 and CO2 mixed gases. At the beginning, the gas pressure in fracture continues to decrease around the extraction borehole, while continues to increase around the injection borehole. Due to the CO2 injection, the influence range around the extraction borehole is larger than that around the injection borehole. With the increase of time, the gas pressure in fracture shows a downward trend overall. The pressure around the injection borehole also gradually decreases, but is slower than that near the extraction borehole. The decreasing rate in the vertical direction is slower than that in the horizontal direction. Affected by CO2 injection, CH4 pressure decreases, while CO2 pressure increases. The CH4 pressure in fracture decreases slowly.
In Fig. 5c, gas pressure in fractures of N2-ECBM is the sum pressure of CH4 and N2 mixture. At the beginning, the rising rate of CH4 pressure is faster than that of CO2 pressure. Because of the weaker competitive adsorption of N2 compared to CH4, the amount of N2 retained in fracture is more than that of CO2. In CO2-ECBM, gas pressure generally decreases with time, except for it around the injection borehole. The decrease rate around the extraction borehole is higher than that around the injection borehole.
Comparing with the results of regular extraction, CO2-ECBM and N2-ECBM, the gas pressure in fracture of enhanced CBM extraction is higher than that of regular extraction, especially for the N2-ECBM extraction.
4.2.2 Evolution of CH4 content
Figure 6 shows the variation of CH4 content in different extraction methods at 10 d, 60 d, 120 d and 180 d, respectively. For regular extraction, the reduction range of CH4 content is mainly dominated by the extraction. While for enhanced CBM extraction, this range is dominated by both injection and extraction. For enhanced extraction (CO2- or N2-ECBM), the reduction of CH4 content is larger than that of regular extraction. Compared Fig. 6b and c, the gas extraction effect of CO2-ECBM is better than that of N2-ECBM.
Under the same gas injection and extraction conditions, the effect difference caused by the change of gas injection concentration gradient can be ignored. Due to the greater affinity of CO2 to coal, the reduction range of CH4 content is more obvious.
Figure 7 shows the CH4 content change curves of regular extraction, CO2-ECBM and N2-ECBM, respectively. CH4 content decreases rapidly during 10d to 60d, meanwhile the decreasing rate reduces. At the beginning, CH4 content is relative high, and the pressure gradient around the extraction borehole is large, leading to fast gas migration in coal seam. As CH4 content decreases, the pressure gradient around the extraction borehole decreases, resulting in slow speed of gas migration.
At 180 d, the peak CH4 contents for regular extraction, CO2-ECBM, and N2-ECBM are 5.07 m3/t, 3.84 m3/t, and 4.37 m3/t, respectively. Compared with regular extraction, the peak CH4 content of CO2- or N2-ECBM extraction has decreased by 24.3% and 13.8% at 180d, respectively. The effect of gas extraction is CO2-ECBM > N2-ECBM > regular extraction in order.
4.2.3 Gas sorption induced coal strain
Figure 8 illustrates the change of the proportion of CH4 in the adsorbed gas at observation points in coal seam for CO2- and N2-ECBM. Comparing the points C and E closed to the injection borehole, the adsorbed CH4 ratio of CO2-ECBM decreases faster than that of N2-ECBM. It indicates that the gas displacement effect and competitive sorption effect of CO2 is more obvious, CH4 is more likely to migrate towards the matrix in CO2-ECBM. The effect of CO2 injection to displace CH4 is better than that of N2 injection. For CO2- and N2-ECBM, the proportion of CH4 on point D at 180d is 73.81% and 76.75%, respectively. At this time, the adsorbed gas is mainly CH4, which proves that gas injection has little influence on point D.
Figure 9a shows the variation of sorption induced coal strain on observation points during regular extraction. As time prolongs, the sorption strain on all points in coal seam decreases. The curves of sorption strain on points C, D and F are coincident, because the points are equidistant to the extraction borehole. At the beginning, point E is weakly affected by the extraction, showing a slow decrease rate of strain. As time prolongs, the influence of extraction on point E gradually increases. The sorption induced coal strain on points C, D and F is determined by the amount of adsorbed CH4. As CH4 continues to be desorbed and extracted out, the CH4 pressure around the extraction borehole gradually decreases, causing a smaller decreasing rate of the sorption induced strain. As the location of point E is far from the extraction borehole, the amount of adsorbed CH4 is higher than that on points C, D, and F. As a result, the sorption induced strain on point E is higher than that on the other points.
In Fig. 9b the sorption induced strain on points C and E shows a short-term decrease and then continues to increase during CO2-ECBM. This may be caused by the influence of injected CO2 gas. At point D, the sorption induced strain shows a decreasing trend, which is greatly affected by the extraction effect. At point F, the sorption induced strain is affected by both extraction and injection, showing a trend of first decreasing and then increasing. The decreasing trend is dominated by the reduction of proportion of adsorbed CH4, as shown in Fig. 9a. After a period of time, the injected CO2 arrives at point C and the amount of adsorbed CO2 increases. The sorption induced strain is dominated by the CO2 adsorption, and the sorption induced strain increases gradually. In the later stage, the CO2 adsorption reaches an equilibrium state that the variation of the sorption induced strain on point C also shrinks. The position of point E determines that the sorption induced strain on this point is dominated by the injected CO2, showing an increasing trend. The distance of Point D from the injection borehole is the farthest among the observation points, which leads to a continuous decreasing trend of sorption induced strain. The change of the sorption induced strain on point F is similar to that at point D at the initial stage, and then the decreasing rate is reduced compared to that on point D, and finally the sorption induced strain rebounds at ~ 90 d. The sorption induced strain on point F shows a trend of first decreasing dominated by gas extraction, and then increasing dominated by the reached CO2.
Figure 9c shows the variation curves of sorption induced strain on the observation points in coal seam during N2-ECBM. The sorption induced strain on point D continues to decrease. From Fig. 9b, the N2 adsorption will rise the coal strain, which neutralizes parts of the reducing of coal strain induced by CH4 desorption. The pressure gradient between the matrix and the fracture becomes small. The strain reduction rate decreases as the CH4 desorption rate decreases. After a while, the decreasing rate of sorption induced strain tends Affected by earlier arrive of injected N2, the sorption induced strain on Point F reduces with a decreasing amplitude. The change of the sorption induced strain on point C is dominated by both extraction and injection, manifested by a steady decreasing trend. At the beginning, the strain on point E does not change significantly due to the slight influence of extraction. As time prolongs, the strain on point E is more and more affected by extraction, as a result, the strain at point E increases until finally tends to be stable. The overall change of the sorption induced strain of N2-ECBM is similar to that of regular extraction, except for a higher magnitude. This may be resulted from the increasing adsorption of injected N2 and the decreasing adsorption of CH4 on coal matrix.
In the coal matrix, the sorption induced strain caused by the adsorption of CO2 is higher than that of CH4 and N2. The sorption induced strain caused by the adsorption of CO2 and nitrogen in coal is different, resulting in different effects of the two gases on the sorption induced coal strain. In CO2-and N2-ECBM, the sorption induced strain of coal matrix increases with CO2 displace CH4, while decreases with N2 displace CH4.
4.2.4 Variation of coal permeability
In Fig. 10, the variation of coal permeability is opposite to that of sorption induced strain, e.g. the sorption induced strain decreases and coal permeability increases. The larger the sorption induced strain in coal seam, the greater swelling of coal matrix, which will occupy the fracture space, and reduce the fracture porosity, as a result, the permeability of coal seam is reduced. For regular extraction and N2-ECBM, the coal permeability continues to increase. While for CO2-ECBM, the coal permeability on points C and E decreases due to the increase in sorption induced strain, but the coal permeability on points D and F increases compared to the initial permeability.
5 Influencing factors on sorption induced coal strain
The single variable controlling method was adopted to analyze the influence of four factors, i.e. injection pressure, initial water saturation, extraction pressure, and initial coal permeability, on the sorption induced strain of coal seam in N2-ECBM and CO2-ECBM. The average strain caused by the unit change of the factor is used as the judgment index of influence degree. The designed scheme of numerical simulations is shown in Table 3.
Taking point C as a reference, the influence of different factors on the sorption induced strain of coal seam is analyzed. Figure 11a shows the variation curves of sorption induced strain of coal seam of N2-ECBM and CO2-ECBM under different injection pressures. The sorption induced strain of CO2-ECBM increases with the injection pressure with a larger change compared to N2-ECBM. For N2-ECBM, the higher the injection pressure, the lower the amount of sorption induced strain decreases. The sorption induced strain of CO2-ECBM is mainly affected by the amount of CO2 adsorption. Higher injection pressure corresponds to more CO2 adsorbed on coal, and larger sorption induced strain. While, N2 caused coal strain is finite that the sorption induced strain is mainly dominated by the amount of absorbed CH4, although the increased adsorbed N2 will offset part of the CH4 desorption caused decrease in coal strain. As a result, the sorption induced strain will increase with the increase of injection pressure during N2-ECBM.
The sorption induced strain of CO2-ECBM increases with the initial permeability, as shown in Fig. 11b. The higher the initial permeability, the shorter the time that the coal strain affected by the CH4 adsorption. For N2-ECBM, higher initial permeability will lead to faster migration of injected gas, as well as larger decrease in sorption induced strain in coal seam.
Figure 11c shows the variation of sorption induced strain under different initial water saturations. For CO2-ECBM, smaller water saturation will lead to earlier rising and larger value of sorption induced strain in coal seam. As time prolongs, the disparity of sorption induced strain under varying water saturation narrows. For N2-ECBM, the larger the water saturation, the slighter the decrease of sorption induced strain and the slower gas migration n the fracture will be. When the water saturation is high, and the sorption induced strain will be dominated by the CH4 adsorption for a long duration. For N2-ECBM, high water saturation will result in high gas pressure in the fractures and the low desorption degree of CH4, as well as small decrease of sorption induced strain.
Figure 11d shows the variation of sorption induced strain under different extraction pressures. For both CO2 -ECBM and N2 -ECBM, the curves of sorption induced strain overlap, indicating that the coal strain is less affected by the extraction pressure.
Table 4 illustrates the average variation of sorption induced strain of coal seam under different factors of both CO2 and N2-ECBM. The influencing degree of different factors varies obviously. For CO2-ECBM, the influencing degree is in the order of injection pressure, initial permeability, water saturation, and extraction pressure. For N2-ECBM, the order is initial permeability, injection pressure, water saturation, extraction pressure.
6 Conclusions
-
(1)
Based on the dual porosity (fracture-pore) structure of coal seam, the mathematical equations of fluid–structure interactions involving gas (CH4, CO2 or N2) migration, coal deformation, and two-phase flow are derived for gas injection enhanced CBM extraction. The rationality of the governing equations is verified by the experimental tests.
-
(2)
The CH4 content gradually decreases with time, especially fastest at the initial stage. Compared with regular extraction, the CH4 content at 180d of CO2-ECBM and N2-ECBM has decreased by 24.3% and 13.8%, respectively. The extraction effect is CO2-ECBM > N2-ECBM > regular extraction in order.
-
(3)
The evolution of coal strain mainly depends on the integrated result of gas de/adsorption caused shrinkage and swelling with different injected gases. The adsorption affinity of N2 on coal is lower than that of CH4, leading to a decreasing of the sorption induced strain in N2-ECBM. The adsorption affinity of CH4 is lower than that of CO2, as a result the sorption induced strain continues to increase in CO2-ECBM. The change of coal permeability is opposite to the sorption induced strain.
-
(4)
For CO2-ECBM, the influencing factors on the coal strain are injection pressure, initial permeability, water saturation and extraction pressure in order. While for N2-ECBM, the factors are initial permeability, injection pressure, water saturation and extraction pressure in order.
References
Bai G, Su J, Zhang Z et al (2022) Effect of CO2 injection on CH4 desorption rate in poor permeability coal seams: an experimental study. Energy 238:121674
Clarkson CR, Bustin RM (2000) Binary gas adsorption/desorption isotherms: effect of moisture and coal composition upon carbon dioxide selectivity over methane. Int J Coal Geol 42(4):241–271
De Silva PNK, Ranjith PG (2014) Understanding and application of CO2 adsorption capacity estimation models for coal types. Fuel 121:250–259
Fan C, Li S, Luo M et al (2016) Numerical simulation of deep coalbed methane extraction based on fluid-solid-thermal coupling. Journal of China Coal Society 41(12):3076–3085
Fan C, Elsworth D, Li S, Zhou L, Yang Z, Song Y (2019) Thermo-hydro-mechanical-chemical couplings controlling CH4 production and CO2 sequestration in enhanced coalbed methane recovery. Energy 173:1054–1077
Fan C, Elsworth D, Li S et al (2019b) Thermo-hydro-mechanical-chemical couplings controlling CH4 production and CO2 sequestration in enhanced coalbed methane recovery. Energy 173:1054–1077
Fan C, Li S, Luo M et al (2019c) Numerical simulation of hydraulic fracturing in coal seam for enhancing underground gas drainage. Energy Explor Exploit 37(1):166–193
Fan CJ, Yang L, Wang G, Huang QM, Fu X, Wen HO (2021) Investigation on coal skeleton deformation in CO2 injection enhanced CH4 drainage from underground coal seam. Front Earth Sci 9:766011
Fang Z (2009) Mechanisms and experimental study of gas mixture enhanced coalbed methane recovery technology. Chinese Academy of Sciences, Wuhan
Fang H, Sang S, Liu S (2019) The coupling mechanism of the thermal-hydraulic-mechanical fields in CH4-bearing coal and its application in the CO2-enhanced coalbed methane recovery. J Petrol Sci Eng 181:106177
Huang Q, Liu S, Cheng W et al (2020) Fracture permeability damage and recovery behaviors with fracturing fluid treatment of coal: an experimental study. Fuel 282:118809
Huang Q, Liu S, Wang G et al (2021) Evaluating the changes of sorption and diffusion behaviors of Illinois coal with various water-based fracturing fluid treatments. Fuel 283:118884
Li S, Fan C, Han J et al (2016) A fully coupled thermal-hydraulic-mechanical model with two-phase flow for coalbed methane extraction. J Nat Gas Sci Eng 33:324–336
Liang W, Yan J, Zhang B et al (2021) Review on coal bed methane recovery theory and technology: recent progress and perspectives. Energy Fuels 35(6):4633–4643
Lin J, Ren T, Wang G et al (2018) Experimental investigation of N2 injection to enhance gas drainage in CO2-rich low permeable seam. Fuel 215:665–674
Long H, Lin H, Yan M et al (2021) Molecular simulation of the competitive adsorption characteristics of CH4, CO2, N2, and multicomponent gases in coal. Powder Technol 385:348–356
Lu YY, Zhang HD, Zhou Z et al (2021) Current status and effective suggestions for efficient exploitation of coalbed methane in China: a review. Energy Fuels 35(11):9102–9123
Luo M, Yang L, Wen H et al (2022) Numerical optimization of drilling parameters for gas predrainage and excavating-drainage collaboration on roadway head. Geofluids 2022:1–10
Merey S, Sinayuc C (2016) Analysis of carbon dioxide sequestration in shale gas reservoirs by using experimental adsorption data and adsorption models. J Nat Gas Sci Eng 36:1087–1105
Ren T, Wang G, Cheng Y, Qi Q (2017a) Model development and simulation study of the feasibility of enhancing gas drainage efficiency through nitrogen injection. Fuel 194:406–422
Ren T, Wang G, Cheng Y et al (2017b) Model development and simulation study of the feasibility of enhancing gas drainage efficiency through nitrogen injection. Fuel 194:406–422
Shiqi L, Huihuang F, Shuxun S et al (2019) Numerical sinulation study on coal seam CO2-ECBM based on multi-physics fields coupling solution. Coal Sci Technol 47(9):51–59
Wang G, Shen J, Liu S et al (2019a) Three-dimensional modeling and analysis of macro-pore structure of coal using combined X-ray CT imaging and fractal theory. Int J Rock Mech Min Sci 123:104082
Wang G, Qin X, Shen J et al (2019b) Quantitative analysis of microscopic structure and gas seepage characteristics of low-rank coal based on CT three-dimensional reconstruction of CT images and fractal theory. Fuel 256:115900
Wang G, Han D, Qin X et al (2020) A comprehensive method for studying pore structure and seepage characteristics of coal mass based on 3D CT reconstruction and NMR. Fuel 281:118735
Wang Z, Sang S, Zhou X et al (2022) Numerical study on CO2 sequestration in low-permeability coal reservoirs to enhance CH4 recovery: gas driving water and staged inhibition on CH4 output. J Petrol Sci Eng 214:110478
Wei M, Liu J, Elsworth D et al (2019a) Influence of gas adsorption induced non-uniform deformation on the evolution of coal permeability. Int J Rock Mech Min Sci 114:71–78
Wei Z, Kang X, Liu Y et al (2019b) A fully coupled fluid flow and geomechanics model for coalbed methane reservoir. Lithol Reserv 31(2):151–158. https://doi.org/10.12108/yxyqc.20190217
Wu S, Deng C, Wang X (2019) Molecular simulation of flue gas and CH4 competitive adsorption in dry and wet coal. J Nat Gas Sci Eng 71:102980
Xu H, Tang DZ, Tang SH et al (2014) A dynamic prediction model for gas–water effective permeability based on coalbed methane production data. Int J Coal Geol 121:44–52
Xu H, Qin Y, Wang G et al (2020) Discrete element study on mesomechanical behavior of crack propagation in coal samples with two prefabricated fissures under biaxial compression. Powder Technol 375:42–59
Yi H, Li F, Ning P et al (2013) Adsorption separation of CO2, CH4, and N2 on microwave activated carbon. Chem Eng J 215–216:635–642
Yu S, Bo J, Fengjuan L (2019) Competitive adsorption of CO2/N2/CH4 onto coal vitrinite macromolecular: effects of electrostatic interactions and oxygen functionalities. Fuel 235:23–38
Zhang XG, Ranjith PG, Perera MSA et al (2016) Gas transportation and enhanced coalbed methane recovery processes in deep coal seams: a review. Energy Fuels 30(11):8832–8849
Zhou F, Hussain F, Cinar Y (2013) Injecting pure N2 and CO2 to coal for enhanced coalbed methane: experimental observations and numerical simulation. Int J Coal Geol 116:53–62
Zhou X, Han M, Bai G et al (2021) Experimental study on the influence of CO2 gas injection pressure on gas diffusion coefficient. Coal Geol Prospect 49(01):81–86
Engineering Toolbox (2001). https://www.engineeringtoolbox.com/
Acknowledgements
The author(s) would like to thank all editors and anonymous reviewers for their comments and suggestion. This research was financially supported by the National Natural Science Foundation of China (Grant Nos. 52004117 and 52174117), the Postdoctoral Science Foundation of China (Grant Nos. 2021T140290 and 2020M680975), and the discipline innovation team of Liaoning Technical University (Grant Nos. LNTU20TD-03 and LNTU20TD-30).
Author information
Authors and Affiliations
Contributions
All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests with this submission.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Fan, C., Sun, H., Zhu, Z. et al. Strain evolution in coal seam exposed to injected gas with different species for enhanced CBM extraction: a numerical observation. Geomech. Geophys. Geo-energ. Geo-resour. 9, 69 (2023). https://doi.org/10.1007/s40948-023-00614-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s40948-023-00614-3