1 Introduction

Efficient evaluation of tunnel boring machine (TBM) performance is a dominant target for successful implementation in the tunneling construction stage (Maryam et al. 2021; Adoko and Yagiz 2019; Yazdani-Chamzini et al. 2013). Suitable indicators should originate from tool–rock interaction analysis and also consider the effects of TBM parameters, rock mass properties, and operational factors (Zhao et al. 2019; Yagiz et al. 2009). In the last few decades, several reasonable indicators, such as the rate of penetration (ROP), advance rate, and field penetration index (FPI), have been implemented to evaluate TBM performance (Hassanpour et al. 2011; Armaghani et al. 2019; Ma et al. 2020). Among them, FPI, defined as the ratio of individual cutter force to the rate of penetration for each complete revolution of TBM head, was able to effectively represent geological conditions with no impact on TBM parameters such as thrust, torque, and machine specifications (Maryam et al. 2021; Lee et al. 2017; Yagiz and Karahan 2015). Therefore, FPI is regarded as a significant indicator of TBM performance prediction in real tunnel projects. Distinct categories of FPI models have been proposed based on in situ cutting tests and field performance databases (Nelson et al. 1983; Feng et al. 2021; Delisio and Zhao 2014). These FPI models have been reviewed as follows.

1.1 Empirical models

Most studies reviewed field TBM performance databases and linked FPI with geological conditions such as rock strength, joints, and discontinuities through regression analysis (Table 1) (Delisio and Zhao 2014; Hassanpour et al. 2010; Salimi et al. 2018a, b; Armetti et al. 2018; Liu et al. 2017; Hamidi et al. 2010; Farrokh et al. 2012). Tunnels with similar geological conditions and TBM specifications will thus adjust tunnel schedules and machine operating parameters on the basis of empirical FPI models. Uniaxial compressive strength (UCS), joint spacing and number, rock quality designation (RQD), and joint plane angle are frequently employed in empirical models (Hassanpour et al. 2010, 2011; Salimi et al. 2018a, b). Alternatively, the above rock mass properties are integrated into rock mass classification systems, such as rock mass rate (RMR), tunneling quality index (Q) system, basic quality (BQ), and HC, establishing empirical equations between rock mass classification ratings and FPI (Armetti et al. 2018; Liu et al. 2017; Hamidi et al. 2010). For instance, Armetti et al. (2018) and Hamidi et al. (2010) proposed similar empirical FPI models to estimate TBM performance using the RMR system. Although empirical models have merit in easy applications because of the few rock parameters used, they can only be applied limitedly and may even result in substantial errors because the rock parameters are challenging to collect in the geological exploration stage. Moreover, geological conditions and TBM specifications differ depending on the case historical data (Farrokh et al. 2012). Before empirical models are used, thus, their background and input rock parameters should be clarified first. Additionally, input rock parameters in empirical models are typically the average values of each tunnel section, resulting in the inability to predict and adjust machine parameters in real time, especially for faults.

Table 1 Review of some FPI models
Full size table

1.2 Computational models

To overcome the shortcomings of empirical models, computer-aided methods such as non-linear regression analysis and machine learning (ML) techniques, have been utilized for enough prediction capacities or model influencing factors adjustment (Maryam et al. 2021; Salimi et al. 2016). However, there are only few studies aiming at FPI evaluation using computational models (Table 1), including fuzzy inference system (FIS), support vector machines (SVMS), deep belief network (DBN) (Feng et al. 2021; Salimi et al. 2018a, b). Compared to empirical models, computational models used more specific filed TBMs performance data and employed computer-aided methods with higher optimization capabilities. For example, Maryam et al. proposed an evolutionary adaptive neuro-fuzzy inference system (ANFIS) for estimating FPI in TBMs; the hyper parameters of the ANFIS were optimized through the use of ABC algorithm (Maryam et al. 2021). In another similar study, Adoko et al. implemented fuzzy inference system (FIS) to predict FPI by various rock mass properties from the Queens Water Tunnel underneath Brooklyn and Queens (Adoko and Yagiz 2019). However, those computational models still need acquire adequate rock mass properties in the geological exploration stage to preform those computer-aided methods, which significantly limited the application of computational models in actual tunnel projects. For real-time prediction purpose, Feng et al. (2021). conducted the preceding k number observations of FPI1, FPI2 …, FPIk to forecast FPIk + 1 by DBN algorithm; preceding historical TBMs data would be available to predict next performance data because of the continuity of geological conditions and tool-rock interaction mechanism.

Despite several decades of evolution and practical tunnel engineering validation in FPI models, some fundamental knowledge is still lacking on how FPI could be related to rock mass characteristics with no impact on TBM parameters. Nevertheless, some researchers conducted laboratory cutting tests and numerical simulations to demonstrate rock breakage mechanisms, such as fracture propagation, chip formation, and force equilibrium equations (Innaurato and Oreste 2011; Mishnaevsky 1995). However, only a few studies have addressed the fundamental mechanism of FPI in TBMs. Since the rock-breaking process of a TBM cutter is similar to that of a polycrystalline diamond compact (PDC) bit in indentation and chipping processes, we could follow the mechanism analysis method of the PDC bit to address that of the disc cutter.

This study deals with the theoretical FPI model of the TBM disc cutter from a theoretical viewpoint to provide a basis for understanding the relationship between FPI and rock mass properties. The tool–rock interaction of disc cutters and PDC bit are first reviewed and compared for analyzing the cutter force equilibrium. A series of laboratory cutting tests are conducted using a new laboratory drilling monitoring equipment to analyze the torque change and its influencing factors. Theoretical FPI models for the disc cutter and PDC bit are proposed respectively. Field FPI performance data in the literature are subsequently used to validate those theoretical models and analysis the influence of rock mass parameters on FPI. Finally, some theoretical suggestions for applying FPI in TBM performance prediction, such as semiempirical model updating are discussed.

2 Tool-rock interaction of disc cutters and PDC bit

Two ways exist for excavating tunnels in hard rock: conventional drill and blast methods and mechanical excavation techniques. As a cutting or boring tool at the end of the drilling head, rotary drilling bits in mechanical excavation techniques can be classified into rolling cutters (such as disc cutters in TBMs) and drag bits (such as PDC bits). To better understand the rock-breaking mechanism and impact on the FPI, the tool–rock interactions of disc cutter and PDC bit are reviewed and compared in Table 2 (Li et al. 2012; Pan et al. 2019; Che and Ehmann 2014; Liu et al. 2018; Doshvarpassand et al. 2017).

Table 2 Comparison of tool-rock interaction of disc cutter and PDC bit
Full size table

According to the literature and Table 2, both disc cutter and PDC bit in tool–rock interaction would first perform indentation by thrust and then cutting by shear force from the machine. In rock indentation, crushed zone and cracks are created beneath the bit and controlled by the bit shape, thrust magnitude (Fn), and rock mass properties (Mishnaevsky 1995). Further, the cracks extend toward the free surface and form cutting chips via a horizontal cutting force (also called the rolling cutting force, Fr). Although the tool–rock interaction of the disc cutter is slightly different from that of the PDC bit because of the shape of the bit, their rock-breaking mechanism is similar in principle and caused by a combination of thrust and rolling cutting forces (Table 2: Force equalization diagram). The penetration depth for each complete revolution is, therefore, controlled by thrust and related to the rolling cutting force. Additionally, this rolling cutting force originates from the excavation machine’s rotary torque. Hence, rotary torque analysis in tool–rock interaction could contribute to a sound understanding of FPI.

3 Laboratory cutting test for relationship between thrust and rotary torque

3.1 Test apparatus and material

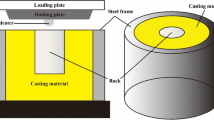
To address rotary torque analysis in tool–rock interaction, a serial of rock cutting tests with different thrusts (0.7–2.6 kN) and rotary speeds (30 rev/min, 50 rev/min) using a PDC bit were conducted on granite, marble, and limestone using a new laboratory drilling monitoring equipment. The drilling monitoring equipment consists of a magnetic drilling machine (Model #: BSD-MAB-1300), a loading frame, and a data acquisition system for real-time cutting parameters measurement (Fig. 1).

Fig. 1
figure 1

Schematic diagram of rock cutting tests

Full size image

This loading frame is comprised of a pressure sensor, torque sensor, and a cylindrical specimen box. The magnetic core drilling machine, which can move back and forth along the vertical direction, applies different thrusts and rotation speeds on the cylindrical specimens by a typical T-shaped PDC bit with the drilling angle of 180°. The drilling performance parameters (e.g., thrust, rotation speed, and torque) could be monitored and collected in real-time by these sensors and the data acquisition system, respectively. The data analysis software installed in the computer is connected directly to the data acquisition system to output and analyses the drilling performance data.

Brief laboratory rock tests, such as rock triaxial compression test, cerchar abrasivity test, and Brazilian tests, were first performed on cylindrical specimens (Φ50 × 100 mm) to determine their conventional properties, including UCS, tensile strength, and the Cerchar abrasivity index (CAI). There were five specimens for each conventional mechanical parameter, and Table 3 summarizes the average values of rock test results. Core specimens were then placed in the rock load frame with lateral confinement across the specimen. Cutting test was subsequently conducted by applying different thrusts (0.72, 1.33, 1.95, and 2.56 kN) at constant rotary speeds of 30 and 50 rev/min. There were three cylindrical specimens for each cutting conditions. Torque variations of various rock types along different thrusts were recorded using the data acquisition system to discuss the relationship between torque and thrust. Figure 2 shows the test results.

Table 3 Physical properties of rocks used for cutting tests
Full size table
Fig. 2
figure 2

Torque variations of different rocks during the cutting tests

Full size image

3.2 Test results

As shown in Fig. 2, during the rock cutting, a positive linear relationship occurred between torque and applied thrust with good correlations (R2 > 0.9). While the slope of this linear relationship is controlled by the rock mass properties in Table 3 but is independent of the rotation speed. According to Detournay et al. and Kaba, the simultaneous action of cutting and frictional contact causes rock fragmentation in the PDC bit, where rock strength parameters (UCS and tensile strength) and friction coefficient under the same thrust determine the cutting and frictional processes (Detournay and Defourny 1992; Kaba 2018). Thus, larger UCS, tensile strength, and CAI could result in a higher slope. Additionally, rotation speed contributes to rock-breaking efficiency without affecting the tool–rock interaction mechanism. When the applied thrust reaches a critical value, the PDC bit will become stuck in the borehole because of the rock’s high intrinsic specific energy and frictional resistance. For example, in Fig. 2, this critical value is around 1.5 kN in granite, whereas the bit continues to move in marble and limestone because of lower rock strength parameters and abrasiveness. However, it stays linear between torque and thrust in the stuck phase.

Based on PDC drilling and field TBM performance data obtained from water conveyance projects in China, the relationships between thrust and torque in real projects were demonstrated to validate the relationship in Fig. 3 (Feng et al. 2020; Luo et al. 2018). Figure 3 shows the relationship thrust and torque for PDC bit and TBM disc cutter, respectively. According to the literature, PDC bit data in Fig. 3a were measured in a 50-m cement grouting borehole with a constant rock UCS (15 MPa); while TBM disc cutter data were collected from different rock mass class (determined by BQ) in the Yingsong water conveyance tunnel (Feng et al. 2020; Luo et al. 2018). As shown in Fig. 3, in both PDC bit and TBM disc cutter, the relationship between thrust and torque remains linear, even under different rotation speeds and geological conditions.

Fig. 3
figure 3

Relationship between applied thrust and rotary torque: a PDC bit; b TBMs disc cutter

Full size image

Consequently, this linear equation can be introduced as

$$T = \left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {k_{1} \times F_{n} } & {\left( {F_{n} \le F_{c} } \right)} \\ \end{array} } \\ {\begin{array}{*{20}c} {k_{1} \times F_{c} + k_{2} \times \left( {F_{n} - F_{c} } \right)} & {\left( {F_{n} > F_{c} } \right)} \\ \end{array} } \\ \end{array} } \right.$$
(1)

where T is the torque (N m), k1 and k2 are the slopes of this linear relationship, depending on rock mass properties, cutter shape, and cutter size. According to Fig. 2, the magnitude of k1 is larger than k2. Fc is the critical value of thrust (N).

4 Establishment of the theoretical FPI models

In this section, the theoretical FPI model of a disc cutter is introduced. The model is based on the PDC bit cutting theory because of their similar tool–rock interaction mechanisms and cutter force equilibrium (Fig. 4). For simplicity, disc cutters and PDC bits were assumed to be rigid bodies without wear and would not be in the stuck phase.

Fig. 4
figure 4

Rock breakage mechanism by a TBMs disc cutter; and b PDC bit

Full size image

In the indentation process of PDC cutting and disc rolling, an exponential relationship existed between thrust and penetration depth (d), as shown in Eq. (2) (Chiaia et al. 2013; Liu et al. 2016),

$$F_{n} = Kd^{a}$$
(2)

where K is an indentation coefficient, depending on rock strength properties and the cutter shape and size. a is a material constant and is calculated by the rock tensile behavior law (Hernot et al. 2006). According to Liu, a = 1 because this exponential relationship shows a positive linear relationship in the first indentation process (Liu et al. 2016).

Following the suggestion for the coexistence of cutting and frictional contact, component Fr of a single cutter could be expressed as

$$F_{r} = \varepsilon dw + \mu F_{n}$$
(3)

where ε is the intrinsic specific energy for the breakage of the unit volume of the rock (J/m3), w is the width of a single cutter (m), and μ is the friction coefficient. According to Fig. 4, number cutters were mounted together on the bit’s bottom surface and formed a circle of radius R. There are m rows of cutters, each row has n cutters, and the radius of each cutter is equal to r. For example, in Fig. 4b, m is simplified to 3 and n is 5. The cutting torque of the individual cutter in the first cutting process is provided by

$$T_{r} = F_{n} \left( {\frac{\varepsilon w}{K} + \mu } \right)r$$
(4)

Eq. (4) also represents a linear relationship between torque and thrust, verifying the laboratory test’s reliability. After a complete revolution of the PDC bit, the penetration depth is denoted as δ (m). The penetration depth of each cutter is assumed to be constant; therefore, it would be δ/m. Based on Eq. (4) and Fig. 3, the cutting torque of the PDC bit can be defined as

$$T = m\sum\limits_{i = 0}^{n} {\left[ {\int_{0}^{2\pi } {\left( {\varepsilon \frac{\delta }{m}w + \mu \frac{{F_{n} }}{m}} \right)r_{i} {\text{d}}} \theta } \right]}$$
(5)

Eq. (5) could be rewritten as:

$$T = 2\pi \left( {\varepsilon \delta w + \mu F_{n} } \right)\sum\limits_{i = 0}^{n} {r_{i} }$$
(6)

Combining Eq. (1) with Eq. (6), the FPI of the PDC bit could be expressed as

$$FPI = \frac{bw \times \varepsilon }{{k - b\mu }}$$
(7)

With

$$FPI = \frac{{F_{n} }}{\delta }$$
(8)
$$b = 2\pi \sum\limits_{i = 0}^{n} {r_{i} }$$
(9)
$$k = \sum\limits_{i = 0}^{n} {k_{i} }$$
(10)

Consequently, Eq. (7) demonstrates the theoretical FPI model of the PDC bit associated with rock mass properties (intrinsic specific energy and friction coefficient) and bit specifications (bit angle and layout). As shown in Eqs. (7), (8), and (9), this FPI model was able to effectively represent geological conditions because the bit specifications could be identified before tunneling. Thus, the theoretical FPI model of TBMs could be similarly introduced as follows.

According to CSM hard rock TBM performance prediction models and Fig. 4 (Rostami et al. 1996), it is assumed that load distribution in the contact zone is homogeneously distributed. The rolling cutting force is defined as

$$F_{r} = \int_{0}^{\phi } {\sin \theta } dF_{t} + \mu F_{n}$$
(11)

With

$$dF_{t} = wRPd\theta$$
(12)
$$P = c\sqrt[3]{{\frac{{\sigma_{c}^{2} \sigma_{t} }}{\phi }}}$$
(13)
$$\phi = \cos^{ - 1} \left( {\frac{d}{R - d}} \right)$$
(14)

where Ft is the resultant force of the cutter (N), R is the diameter of the TBM head (m), P is the load distribution in the contact zone (MPa), and σc and σt are the UCS and the Brazilian tensile strength of the rock (MPa), respectively. C is an integrated constant, depending on TBM specifications. During cutting, the penetration depth is small as compared to the disc cutter radius; therefore, P is an indicator similar to ε, relating to rock properties and TBM specifications. The rolling cutting force is rewritten as

$$F_{r} = P\left( \theta \right)wd + \mu F_{n}$$
(15)

After a complete revolution of the disc cutter, following the above assumptions of PDC, the theoretical FPI model of the disc cutter is similarly introduced. The cutting torque of the disc cutter can be defined as

$$T = m\sum\limits_{i = 0}^{n} {\left[ {\int_{0}^{2\pi } {\left( {P\frac{\delta }{m}w + \mu \frac{{F_{n} }}{m}} \right)r_{i} {\text{d}}} \theta } \right]}$$
(16)

Combining Eqs. (1), (8), (9), and (10) with Eq. (16), the FPI of the disc cutter can be expressed as

$$FPI = \frac{bw \times P}{{k - b\mu }}$$
(17)

As shown in Eqs. (7) and (17), in the theoretical FPI model, the TBM and PDC bits have similar model structures and influencing factors. Based on tool–rock interaction studies, the magnitude of interaction parameters, such as k and P are essentially influenced by the rock mechanical parameters and dimensions of the cutter of TBM during the rock cutting process. Therefore, in addition to the machine specifications, rock properties, including UCS, tensile strength, and rock abrasiveness, control the magnitude of FPI in homogeneous rock. Equation (17) could be expressed as

$$FPI = f({\text{D}} ,UCS)$$
(18)

where D is the TBM specification, especially dimensions of the cutter (m).

To validate the potential of FPI in TBM performance prediction, it should demonstrate that FPI is an independent indicator without influence of mechanical parameters (such as rotation speed) and only related to rock properties in practical engineering.

Based on field TBM data obtained from water conveyance projects in China, the relationships between Fn and δ were discussed in Fig. 5 (Feng et al. 2020; Luo et al. 2018). The slope of this linear relationship between Fn and δ is the magnitude of FPI.

Fig. 5
figure 5

Relationship between thrust and penetration depth per rotation of TBMs disc cutter at: a different rotation speeds with same UCS; b different UCSs with similar rotation speeds (Luo et al. 2018)

Full size image

Figure 5a shows the relationship between Fn and δ for TBMs disc cutter at different rotation speeds in different sections of the Yingsong water conveyance tunnel with a same UCS. Figure 5b demonstrates the relationship between Fn and δ for the TBM disc cutter in a section of the Yingsong water conveyance tunnel with different UCSs at similar rotation speeds. As shown in Fig. 5, in the TBM disc cutter, the relationship between Fn and δ remains linear, even under different geological conditions. Specifically, FPI (the reciprocal of linear slope in Fig. 5) can be maintained when drilling the same formation using different rotation speeds and stays linear with the UCS value at a constant rotation speed (the rotation speed is nearly constant in TBM boring). A higher FPI means larger rock properties at the same rotation speed. In particular, FPI could represent the geological conditions along the tunnel under complex machine operating parameters. Additionally, Fig. 6 reviews several relationships between UCS and actual FPI data in real tunneling projects (e.g., Karaj Water Conveyance Tunnel and Nowsood water conveyance tunnels) to show the potential of FPI in geological formation evaluations (Hassanpour et al. 2009, 2010, 2011; Salimi et al. 2018; Wu et al. 2020). As shown in Fig. 6, FPI shows a better linear correlation with UCS in different tunnel projects (R2 > 0.60), sharing a similar linear slope. Therefore, it should emphasize the identification of FPI as a universal and reliable predictor of TBM performance prediction in real tunnel projects because of its high capacity and theoretical basis in rock mass property determination.

Fig. 6
figure 6

FPI-UCS relationship curves of some hard rock tunnel projects

Full size image

5 Discussion

5.1 Influence of rock mass parameters on FPI from a theoretical view

The theoretical FPI model of TBM in this study is derived for homogeneous rock without considering other rock mass properties such as joints, ground stress, and rock integrity. Although the relationships between FPI and above parameters have been studied using TBM field performance databases (Hassanpour et al. 2009; Yagiz et al. 2009; Wu et al. 2020), it is still unclear how they affect the application of FPI in TBM performance prediction from a theoretical view. Based on tool–rock interaction studies, the abovementioned parameters could affect the magnitude of interaction parameters, such as k and P during the rock cutting process. For example, high ground stress significantly affects the load distribution, yielding lower penetration depth and higher intrinsic specific energy, resulting in lower FPI or jamming. As shown in Fig. 7, there is an inconspicuous linear correlation between FPI and Kv (rock integrity), mainly because the effect of uniaxial compressive strength on FPI is not excluded. Comparing Figs. 6 and 7, it can can see that UCS has more influence on FPI than Kv. According to Fig. 4 and Eq. (13), the interaction parameters of k and P are completely influenced by the compressive and tensile strength of the rock, while rock integrity can only the strength magnitude of the rock for part of its length.

Fig. 7
figure 7

FPI-Kv relationship curves of some hard rock tunnel projects

Full size image

To further clarify the influence of rock mass parameters on FPI, the relationship between FPI and uniaxial compressive strength at different rock integrity are shown in Fig. 8. As can be seen, rock integrity does not alter the linear relationship between FPI and UCS but decreases the magnitude of the linear slope and the correlation. The FPI of highly fractured rock mass is lower than that of continuous rock mass. According to the theoretical FPI model, poor quality rocks could affect the load distribution, crack spreading, and weaken jointed rock mass strength, resulting in a lower FPI. Additionally, FPI vibrate more in tunnel with higher KV values. The linear slope of FPI versus rock strength and the intensity of FPI dispersion are the basis for identifying the geological conditions. Therefore, it is more appropriate to establish relationships between FPI and geological conditions using multiparameter rock classification system values, such as RMR, Q, and RSR, e.g., Armetti et al. (2018).

Fig. 8
figure 8

FPI-UCS relationship curves at different Kv in the Yingsong water conveyance tunnel

Full size image

Although this theoretical FPI model have not quantitatively determine the magnitude of interaction parameters, they lay the theoretical basis for explaining why the FPI could effectively predict TBM performance in real projects, also show the basic form of the empirical FPI model from a theoretical view.

During the tunnel construction period, the relationships between FPI and geological conditions are used for project scheduling, boring efficiency adjustment, and disc cutter wear determination because the interaction between rocks and worn disc cutters could affect the tool–rock interaction mechanism. Another significant purpose is optimizing the TBM boring efficiency using advanced borehole drilling datasets and identifying rock mass properties from PDC bits equipped in the TBM head because of similar tool–rock interaction mechanisms.

6 Conclusions

To strengthen the theoretical basis of FPI in TBM performance prediction, this study revealed the tool–rock interaction of TBM disc cutter by comparing a PDC bit’s rock-breaking mechanism and rock cutting tests. The theoretical FPI model for TBM was then proposed and validated by field TBM performance datasets form Yingsong water conveyance project. The main conclusions are summarized below:

  1. 1.

    Rotary torque shows a positive linear correlation with applied thrust during the cutting but is independent of rotation speed on basis of the laboratory PDC bit cutting tests and field TBM performance datasets.

  2. 2.

    The proposed theoretical models of TBMs proved that the relationship between Fn and δ remains linear, even under different drilling conditions (thrusts and rotation speeds) and different geological conditions (UCS and rock integrity),

  3. 3.

    Using multiparameter rock classification system values is more appropriate than individual factors, such as UCS or rock integrity, to build the relationships between FPI and geological conditions, because tool–rock interaction is essentially influenced by multiple rock mass properties.

This study confirms that fully understand the tool–rock interaction mechanism is a powerful way to identify the relationships between FPI, rock mass properties, and TBM parameters for TBM performance estimation. Thus, more work should be conducted to fully understand the tool–rock interaction mechanism to allow for further development of the relationships between FPI and various rock mass properties and updating theoretical or semiempirical FPI models. Since it is challenging to update geological conditions along the tunnel in real time for FPI estimation, using advanced borehole drilling datasets from PDC bits is recommended to optimize the TBM’s boring efficiency.