1 Introduction

A considerable amount of structural planes such as joints, faults and bedding planes, which vary in size and shape, are generated in rock masses due to the complex geological processes (Chai et al. 2017). These discontinuities not only govern the mechanical behavior of rock masses, but also definitely cause pronounced effects on the stress wave propagation in rock masses (Jiao et al. 2005; Li et al. 2019, 2016; Zhu et al. 2021; Huang et al. 2018).

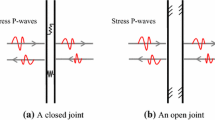
Generally, there are two kinds of joints in rock masses, i.e., persistent joints and non-persistent joints, as shown in Fig. 1. The existence of rock bridges between joint segments results in non-persistent attributes of joints and fundamental difference (Kim et al. 2007; Wasantha et al. 2014). When stress wave propagates through non-persistent joints, complicated wave diffraction can be observed besides the wave reflection and transmission (Zhu et al. 2020). And it is worth noting that the previous studies about wave propagation in jointed rock masses were substantially related to persistent joints (Cai and Zhao 2000; Zhao et al. 2006a; Li 2013; Li et al. 2014). However, few studies have been reported on wave propagation across non-persistent joints. It is essential to conduct the research on wave propagation through non-persistent joints, which is of great interest to mining engineers, seismologists and geoscientists for determining the safety and stability of underground structures.

Fig. 1
figure 1

Persistent joints and non-persistent joints in rock masses

Full size image

Existing studies have applied theoretical analysis, numerical simulations and experimental tests to investigate the stress wave propagation across persistent joints. Regarding theoretical methods, the displacement discontinuity model (DDM) and equivalent medium model (EMM) are frequently used by researchers. In DDM, when waves propagate through a joint, the stresses on both sides of the joint are regarded to be continuous, whereas the displacement across the joint is discontinuous. Cook (1992) and Pyrak-Nolte et al. (1990b) adopted DDM to study the P-wave, SV-wave and SH-wave transmission across a single joint at arbitrary angles and derived the analytical expressions of transmission and reflection coefficient in closed form. Cai and Zhao (2000) and Zhao et al. (2006a, b) combined DDM with the method of characteristics to study the interaction between stress wave and multiple parallel joints with linear and non-linear deformational behavior. Later, Fan et al. (2018) and Wang et al. (2022a) investigated the wave transmission in complex rock masses where the wave impedances on each side of the joint are different. Prompted by the demand for theoretical methods with respect to oblique wave incidence across a set of parallel joints, a time domain recursive method was proposed by Li et al. (2012) and Li (2013). The equivalent medium model is another essential theoretical method. However, the idea of treating jointed rock masses as elastic continuous medium in traditional EMM cannot account for the phenomena of frequency dependence and multiple wave reflection between joints (Schoenberg and Muir 1989; Pyrak-Nolte et al. 1990a). To tackle this problem, Li et al. (2010) introduced a linear equivalent viscoelastic model for the rock mass containing several parallel joints. Fan et al. (2012) further extended the equivalent viscoelastic model to a non-linear one. In addition to the above methods, the plane wave propagation across several sorts of imperfect interfaces in the piezothermoelastic media and piezothermoelastic fiber-reinforced composite half-spaces were studied in detail by Guha et al. (2019) and Guha and Singh (2021), respectively. Singh et al. (2022) analyzed the effects of incident angle, initial stresses and rotation on energy ratios for the case of plane wave propagation in two piezomagnetic fiber-reinforced composite half-spaces.

Experimental approaches are also commonly used to study wave propagation across rock joints. Based on the modified Split Hopkinson Pressure Bar (SHPB) apparatus, Li and Ma (2009) studied the effects of filled rock joints on wave propagation. The research carried out by Kurtulus et al. (2012) revealed the characteristics of ultrasonic wave attenuation in specimens arranged with different numbers and orientations of joints. Zou et al. (2019) conducted a study on P-wave transmission across artificial joint and obtained the variation of reflected and transmitted coefficients with incident angles by designing a new experimental setup.

In comparison to theoretical analysis and experimental methods, numerical simulation can be regarded as an economic and efficient technique. Zhao et al. (2008) presented the UDEC modeling on P-wave propagation through both single and multiple parallel joints and indicated that the numerical results were in good agreement with theoretical ones. Huang et al. (2015) employed the PFC2D to simulate the dominant effects of natural joints filled with granular material on stress wave propagation. In addition, the numerical manifold method was applied to simulate the coupling effects between wave propagation and cracking behavior by Fan et al. (2019), and the transient stress field in fractured rock masses was obtained.

When it comes to the stress wave propagation across non-persistent joints, there exists great difficulties in evaluating wave propagation due to the scattering effects generated at the rock bridge ends and joint segment ends. Therefore, there is still a lack of research on wave propagation across non-persistent joints. The researchers paid more attention to the strength, deformational behavior, failure mechanism and failure mode of rock specimens with different crack and rock bridge parameters (Wasantha et al. 2014; Haeri et al. 2016; Huang et al. 2019; Zhang et al. 2020). Bi et al. (2009) carried out a study of ultrasonic tests to investigate the wave propagation in rock-like material with cracks of different lengths, thickness, orientations, densities, and forms. Zhu et al. (2020) carried out a theoretical analysis of wave propagation across a single non-persistent joint for the case of normal incidence by combining DDM with the angular spectrum theory, and utilized the RFPA numerical model to study the P-wave transmission across multiple non-persistent joints. By combining SHPB apparatus with the photoelasticity technique, Wang et al. (2022b) found that the characteristics of wave propagation are obviously affected by contact area ratios and distribution patterns of the joint. The indirect boundary element method (IBEM) was used by Han et al. (2005) to simulate the stress wave induced by a point explosive source propagating through one circular dry/water-filled crack. Pointer et al. (1998) also applied IBEM to model seismic waves scattered by hydrofractures.

Because of a lack of studies on wave propagation through non-persistent joints, the boundary integral equation method and displacement discontinuity boundary model are adopted to investigate the wave propagation across a single non-persistent joint with three joint segments in this paper. And the effects of rock bridge length, joint segment length, wave frequencies, and incident angles on the displacement field behind the joint plane are subsequently analyzed.

2 Methodology

Numerical methods can be categorized into domain-type methods, boundary-type methods, and hybrid methods (Liang et al. 2019; Li et al. 2022). The boundary integral equation method, which is a boundary-type method, is used in this paper to investigate the wave propagation. Compared with domain-type methods, only the boundary of the model needs to be divided into elements in boundary element method (BEM). Therefore, the BEM can reduce the calculation dimension (Li et al. 2021a). In addition, the BEM can automatically satisfy the infinite radiation condition due to the use of Green’s functions. Therefore, in terms of problems in infinite or semi-infinite domain, the BEM has significant advantages over the domain-type methods such as the finite element method and the finite difference method (Li et al. 2021a).

2.1 Analysis model

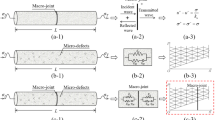
Considering a single non-persistent joint with three joint segments in an infinite domain, as shown in Fig. 2, the rock around the joint segments is assumed to be homogeneous, elastic and isotropic, and the joint lies in the x–y plane and extends to infinity in the z direction. The lengths of the joint segment and rock bridge are Lj and Lr respectively, as denoted in the figure. And the midpoint o on the intermediate joint segment is set as the origin of the orthogonal coordinate system. A plane incident wave with an angle of θ impinges on the non-persistent joint, as shown in Fig. 2. The problem can be simplified as a plane strain case. The monitoring points 1 to 4 and points 5 to 8 in Fig. 2 are set on the perpendicular bisector lines of intermediate joint segment and rock bridge, respectively. And the symbol d denotes the vertical distance from each monitoring point to the joint plane.

Fig. 2
figure 2

Schematic view for wave propagation across a non-persistent joint in a rock mass

Full size image

As shown in Fig. 3, according to the idea of domain division and conjunction (Liu et al. 2019), the whole region of the model could be divided into four subregions, i.e., the infinite domain Ω1 and the finite domains Ω2, Ω3 and Ω4. The infinite domain Ω1 consists of the joint interfaces Г2, Г4 and Г6 and three auxiliary virtual semicircular boundaries Г1, Г3 and Г5. The finite domains Ω2, Ω3 and Ω4 consist of Г1 and Г2, Г3 and Г4, and Г5 and Г6, respectively. Г2, Г4 and Г6 represent the interfaces of the joint segments. The diameter of the semicircular boundary is Lj.

Fig. 3
figure 3

Domain partition of the calculation model

Full size image

2.2 Analysis method

The scattered wave field in the infinite domain and three semicircular finite domains can be generated by the virtual wave sources distributed on the boundaries. Both of the free wave field and the scattered wave field contribute to the dynamic response of rock in the infinite domain Ω1. But only the scattered wave field exists in the semicircular domains Ω2, Ω3 and Ω4.

2.2.1 Free wave field

For the free wave field, there is no reflected wave in the unbounded space. The potential function of incident P wave can be expressed as (Li et al. 2021b)

$$\varphi = \exp [ - ik(x\sin \theta - y\cos \theta )]e^{i\omega t}$$
(1)

where the symbol i denotes imaginary unit; \(\theta\) is the incident angle, i.e., the angle between the propagation direction of incident P wave and y axis; k is the P wave number, with k = ω/cp and cp denotes the velocity of P wave; ω is the circular frequency of incident wave. The time-related term \(e^{i\omega t}\) can be dropped for the steady-state wave field.

According to the potential function of incident wave and theories in elastic mechanics, the displacement, stress, and traction in the rock can be written as

$$u_{i}^{ff} = \varphi_{{,{\kern 1pt} i}}$$
(2)
$$\sigma_{ij}^{ff} = \lambda u_{i,i}^{ff} \delta_{ij} + \mu (u_{i,j}^{ff} + u_{j,i}^{ff} )$$
(3)
$$t_{i}^{ff} = \sigma_{ji}^{ff} n_{j}$$
(4)

where \(\varphi_{,i}\) denotes the first-order partial derivative of \(\varphi\) with respect to the variable i; λ and μ are Lame’s constants; δij denotes Kronecker delta; the subscripts i and j take the value of x or y; \(n_{j}\) denotes the cosine of angle between the outward normal n and the direction j over the boundary; the superscript ff denotes the free field; \(u_{i}^{ff}\) and \(t_{i}^{ff}\) represent the displacement component and traction component in the direction i, respectively; \(\sigma_{ij}^{ff}\) denotes the components of stress tensor.

2.2.2 Scattered wave field

According to the single layer potential theory (Sanchez-Sesma and Campillo 1991), the displacement and traction of scattered wave field can be expressed as follows when the body forces are omitted:

$$u_{i}^{s} (x) = \int_{\Gamma } {G_{ij} (x,\eta )\psi_{j} } (\eta )dS_{\eta }$$
(5)
$$t_{i}^{s} (x) = \frac{1}{2}\delta_{ij} \psi_{j} (x) + \int_{\Gamma } {T_{ij} } (x,\eta )\psi_{j} (\eta )dS_{\eta }$$
(6)

where Г is the boundary of the region; the superscript s represents the scattered wave field; the subscripts i and j take the value of x or y; \(\psi_{j} (\eta )\) represents the virtual load density in the direction j at point \(\eta\) on the boundary; \(\delta_{ij}\) denotes Kronecker delta; \(G_{ij} (x,\eta )\) is the displacement Green’s function, which means the displacement along the direction i at a point x due to the unit concentrated force along the direction j at a point \(\eta\); and \(T_{ij} (x,\eta )\) is called traction Green’s function, i.e., the traction in the direction i at the point x due to the unit concentrated force in the direction j at the point \(\eta\); \(\eta\) and x can also be called the source point and the field point, respectively. The first term on the right-hand side in Eq. (6) will disappear when the point x represents the inner point of the domain. The Green’s functions can be calculated based on the following equations (Sanchez-Sesma and Campillo 1991):

$$G_{ij} \left( {x,\eta } \right) = \frac{1}{i8\rho }\left[ {\delta_{ij} A - \left( {2\gamma_{i} \gamma_{j} - \delta_{ij} } \right)B} \right]$$
(7)
$$\begin{gathered} T_{ij} \left( {x,\eta } \right) = \frac{i\mu }{{2\rho r}}\left\{ {\left[ {B + \frac{{\lambda D\left( {k_{{\text{p}}} r} \right)}}{{2\mu c_{{\text{p}}}^{2} }}} \right]\gamma_{j} n_{i} { + }\left[ {B + \frac{{D\left( {k_{{\text{s}}} r} \right)}}{{2c_{{\text{s}}}^{2} }}} \right]} \right. \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left. {\begin{array}{*{20}c} {} \\ {} \\ \end{array} \times \left( {\gamma_{i} n_{j} + \gamma_{k} n_{k} \delta_{ij} } \right){ + }\left( {C - 4B} \right)\gamma_{i} \gamma_{j} \gamma_{k} n_{k} } \right\} \hfill \\ \end{gathered}$$
(8)
$$A = \frac{{H_{0}^{\left( 2 \right)} \left( {k_{{\text{p}}} r} \right)}}{{c_{{\text{p}}}^{2} }} + \frac{{H_{0}^{\left( 2 \right)} \left( {k_{{\text{s}}} r} \right)}}{{c_{{\text{s}}}^{2} }}$$
(9)
$$B = \frac{{H_{2}^{\left( 2 \right)} \left( {k_{{\text{p}}} r} \right)}}{{c_{{\text{p}}}^{2} }} - \frac{{H_{2}^{\left( 2 \right)} \left( {k_{{\text{s}}} r} \right)}}{{c_{{\text{s}}}^{2} }}$$
(10)
$$C = \frac{{D\left( {k_{{\text{p}}} r} \right)}}{{c_{{\text{p}}}^{2} }} - \frac{{D\left( {k_{{\text{s}}} r} \right)}}{{c_{{\text{s}}}^{2} }}$$
(11)
$$D\left( p \right) = pH_{1}^{\left( 2 \right)} \left( p \right)$$
(12)

where ρ represents the material density; \(k_{{\text{p}}}\) and \(k_{{\text{s}}}\) denote the P wave number and S wave number, respectively; \(c_{p}\) and \(c_{s}\) are the wave propagation velocities of P and S waves, respectively; \(\gamma_{i} = \left( {x_{i} - \eta_{i} } \right)/r\); \(r = \sqrt {\left( {x_{1} - \zeta_{1} } \right)^{2} + \left( {x_{2} - \zeta_{2} } \right)^{2} }\); \(H_{m}^{\left( n \right)}\) is Hankel function of the nth kind and order m.

2.2.3 Boundary conditions and solution of linear equations

The continuity conditions of stress and displacement are adopted for the semicircular fictitious boundaries, i.e., \(\Gamma_{1}\), \(\Gamma_{3}\) and \(\Gamma_{5}\). The displacement discontinuity condition is utilized on the joint interfaces \(\Gamma_{2}\), \(\Gamma_{4}\) and \(\Gamma_{6}\), whereas stresses on these interfaces are continuous.

The stresses on the boundaries \(\Gamma_{1}\), \(\Gamma_{2}\), \(\Gamma_{3}\), \(\Gamma_{4}\), \(\Gamma_{5}\) and \(\Gamma_{6}\) are continuous, that is

$$t_{i}^{{\left( {s,\Omega_{1} } \right)}} (x) + t_{i}^{{\left( {ff,\Omega_{1} } \right)}} (x) = - t_{i}^{{\left( {s,\Omega_{p} } \right)}} (x)$$
(13)

The displacements on boundaries \(\Gamma_{1}\), \(\Gamma_{3}\) and \(\Gamma_{5}\) are also continuous,

$$u_{i}^{{\left( {s,\Omega_{1} } \right)}} (x) + u_{i}^{{\left( {ff,\Omega_{1} } \right)}} (x) = u_{i}^{{\left( {s,\Omega_{p} } \right)}} (x)$$
(14)

While the displacements on boundaries \(\Gamma_{2}\), \(\Gamma_{4}\) and \(\Gamma_{6}\) are discontinuous,

$$u_{i}^{{\left( {s,\Omega_{1} } \right)}} (x) + u_{i}^{{\left( {ff,\Omega_{1} } \right)}} (x) - u_{i}^{{\left( {s,\Omega_{p} } \right)}} (x) = t_{i}^{{\left( {s,\Omega_{p} } \right)}} \left( x \right)/K$$
(15)

where the symbol K denotes joint stiffness; the superscript s in \(u_{i}^{{\left( {s,\Omega } \right)}}\) and \(t_{i}^{{\left( {s,\Omega } \right)}}\) represents the scattered wave field; \(\Omega\) denotes the corresponding region; the subscript p in \(\Omega_{p}\) can take the value of 2, 3 or 4, i.e., the symbol p will be set to 2 if the point x is located on the boundary \(\Gamma_{1}\) and \(\Gamma_{2}\), p equals to 3 if the point x is located on the boundary \(\Gamma_{3}\) and \(\Gamma_{4}\), p equals to 4 if the point x is located on the boundary \(\Gamma_{5}\) and \(\Gamma_{6}\). We assume that the normal stiffness and shear stiffness of the joint in this study are both equal to K.

The boundary \(\Gamma_{i}\) consists of \(NE_{i}\) elements. And the length of each element is \(\Delta L\). Constant elements are adopted in this study, where the nodes are located in the middle of the element. The virtual load density \(\psi_{j}\) on each element is constant and equals to the value at the node. Therefore, the term of virtual load density \(\psi_{j}\) in Eq. (5) and Eq. (6) can be placed outside the integrals. Then, after the discretization of Eq. (5), Eq. (6), and above boundary conditions, the system of linear equations can be derived and expressed in the following form:

$$\begin{gathered} \sum\limits_{m = 1}^{sum1} {\psi_{j}^{{\left( {\Omega_{1} } \right)}} \left( {\eta_{m} } \right)t_{ij} \left( {x_{n} ,\eta_{m} } \right) + } \sum\limits_{m = 1}^{sum2} {\psi_{j}^{{\left( {\Omega_{p} } \right)}} \left( {\eta_{m} } \right)t_{ij} \left( {x_{n} ,\eta_{m} } \right)} = - t_{i}^{{\left( {ff,\Omega_{1} } \right)}} \left( {x_{n} } \right){\kern 1pt} \hfill \\ {\text{for}}\;x_{n} \in \Gamma_{1} ,\;\Gamma_{2} {\kern 1pt} ,\;\Gamma_{3} ,\;\Gamma_{4} ,\;\Gamma_{5} ,\;{\kern 1pt} \Gamma_{6} {\kern 1pt} \hfill \\ \end{gathered}$$
(16)
$$\begin{gathered} \sum\limits_{m = 1}^{sum1} {\psi_{j}^{{\left( {\Omega_{1} } \right)}} \left( {\eta_{m} } \right)g_{ij} \left( {x_{n} ,\eta_{m} } \right) - } \sum\limits_{m = 1}^{sum2} {\psi_{j}^{{\left( {\Omega_{p} } \right)}} \left( {\eta_{m} } \right)g_{ij} \left( {x_{n} ,\eta_{m} } \right)} = - u_{i}^{{\left( {ff,\Omega_{1} } \right)}} \left( {x_{n} } \right){\kern 1pt} \hfill \\ {\text{for}}\;x_{n} \in \Gamma_{1} ,\;\Gamma_{3} ,\;\Gamma_{5} {\kern 1pt} \hfill \\ \end{gathered}$$
(17)
$$\begin{gathered} \sum\limits_{m = 1}^{sum1} {\psi_{j}^{{\left( {\Omega_{1} } \right)}} \left( {\eta_{m} } \right)g_{ij} \left( {x_{n} ,\eta_{m} } \right) - } \sum\limits_{m = 1}^{sum2} {\psi_{j}^{{\left( {\Omega_{p} } \right)}} \left( {\eta_{m} } \right)g_{ij} \left( {x_{n} ,\eta_{m} } \right)} - \frac{1}{K}\sum\limits_{m = 1}^{sum2} {\psi_{j}^{{\left( {\Omega_{p} } \right)}} \left( {\eta_{m} } \right)t_{ij} \left( {x_{n} ,\eta_{m} } \right)} = - u_{i}^{{\left( {ff,\Omega_{1} } \right)}} \left( {x_{n} } \right) \hfill \\ {\text{for}}\;x_{n} \in \Gamma_{2} ,\;\Gamma_{4} ,\;\Gamma_{6} {\kern 1pt} \hfill \\ \end{gathered}$$
(18)

where

$$t_{ij} \left( {x_{n} ,\eta_{m} } \right) = \frac{1}{2}\delta_{ij} \delta_{mn} + \int_{{\eta_{m} - \Delta L/2}}^{{\eta_{m} + \Delta L/2}} {T_{ij} \left( {x_{n} ,\eta } \right)} dS_{\eta }$$
(19)
$$g_{ij} \left( {x_{n} ,\eta_{m} } \right) = \int_{{\eta_{m} - \Delta L/2}}^{{\eta_{m} + \Delta L/2}} {G_{ij} \left( {x_{n} ,\eta } \right)} dS_{\eta }$$
(20)

The subscript p in \(\Omega_{p}\) has the same meaning as that in Eqs. (13)–(15); the symbol sum1 is the sum of \(NE_{1}\), \(NE_{2}\), \(NE_{3}\), \(NE_{4}\), \(NE_{5}\) and \(NE_{6}\); the symbol sum2 is equal to \(NE_{1} + NE_{2}\), \(NE_{3} + NE_{4}\), and \(NE_{5} + NE_{6}\), when the subscript p in \(\Omega_{p}\) takes the value of 2, 3 and 4, respectively.

The integrals in \(t_{ij} \left( {x_{n} ,\eta_{m} } \right)\) and \(g_{ij} \left( {x_{n} ,\eta_{m} } \right)\) can be solved according to the Gaussian quadrature formula. The virtual load density Ψj is obtained from the system of linear equations by adopting the Gaussian elimination method. The displacement and stress in scattered wave field are then expressed by the virtual load density and single layer potential theory.

3 Verification of the presented boundary integral equation method

In this section, a single non-persistent joint with only one joint segment will be utilized to study the P-wave propagation for the case of normal incidence. The analysis model can be obtained by retaining only the intermediate joint segment and monitoring points 1 and 2 in Fig. 2. Then, the results based on the presented boundary integral equation method are compared with those from UDEC, a numerical software based on the discrete element method, and those from the analytical equation to verify the effectiveness of the presented boundary integral equation method. The incident wave is assumed to be in the harmonic waveform with a frequency of f. The transmission coefficient T is defined as the ratio of the amplitude of transmitted wave \(u_{t}\) behind the joint to the amplitude of incident wave \(u_{i}\), that is,

$$T(f) = \frac{{u_{t} (f)}}{{u_{i} (f)}}$$
(21)

An incident P wave is applied on the bottom boundary of the model to propagate upwards. In UDEC simulations, it is essential to take the effects of artificial boundaries into consideration. The horizontal velocities along the lateral boundaries are fixed. The artificial viscous boundaries, also called the absorbing boundaries, are adopted on the upper and lower boundaries. Meanwhile, the dimension of the model should be large enough to minimize the influence of reflected waves generated at the left and right artificial boundaries. It is worth noting that the viscous boundaries can also be applied on all boundaries of the model, which could efficiently reduce the influence of the reflected waves from the sides of the model. But in this case, the incident wave near the lateral boundaries will become non-planar due to the existence of model boundaries. Therefore, when viscous boundaries are applied on all the boundaries, it is necessary to increase the model dimension so that the incident wave remains as a plane wave before arriving at the joint.

By referring to Zhu et al. (2020), the relevant parameters are set as follows. The elastic modulus E of the rock is \(30.0\;{\text{GPa}}\), the density \(\rho\) is \(2500.0\;{\text{kg}}\;{\text{m}}^{ - 3}\), the Poisson’s ratio \(\nu\) is \(0.3\), and the shear and normal stiffness of the joint are equal to \(2.0\;{\text{GPa}}\,{\text{m}}^{ - 1}\). Monitoring points 1 and 2 are set with a distance of 2.0 m and 4.0 m away from the joint plane, respectively. The length of joint is set to 15.0 m.

Figure 4 illustrates the variation of the transmission coefficients at points 1 and 2 with the frequency of the incident wave. It can be observed that the calculation results based on the presented boundary integral equation method agree well with those from UDEC. The differences between the two numerical methods mainly come from the following aspects. Firstly, although the model size is enlarged properly, the reflected waves produced at the left and right artificial boundaries still have minor impacts on the dynamic responses of the region. Secondly, there exists imperfect energy absorption at the viscous boundaries, especially for the waves striking the boundaries at angles lower than 30°. Thirdly, the calculation errors are primarily due to the gridding of the computational domains in UDEC. If the monitoring points 1 and 2 are close to but not on the exact gridpoints, the difference happens. Since the computational domain need not to be meshed in the presented boundary integral equation method, the results for the given monitoring points can be exactly obtained.

Fig. 4
figure 4

Variation of transmission coefficients for the normal incidence of harmonic P waves with different frequencies, a point 1 and b point 2

Full size image

The analytical solution for wave propagation across a persistent joint is expressed as (Pyrak-Nolte et al. 1990b),

$$T\;{ = }\;\frac{{2\left( {\frac{{\text{k}}}{z\omega }} \right)}}{{ - i\; + \;2\left( {\frac{{\text{k}}}{z\omega }} \right)}}\;,\;\;|T|\; = \;\sqrt {\frac{{4\left( {\frac{{\text{k}}}{z\omega }} \right)^{2} }}{{4\left( {\frac{{\text{k}}}{z\omega }} \right)^{2} \; + \;1}}}$$
(22)

Figure 5 shows the comparison between the transmission coefficients obtained from the above analytical equation for a persistent joint and those obtained from the boundary integral equation method for a joint segment with varying lengths. The monitoring point 1 is close to the joint interface, and point 2 is set with a distance of 2 m away from the joint plane. The normalized joint-segment length is defined as the ratio of the joint segment length to the incident wavelength. The incident wave frequency is set to 100 Hz. It can be observed from Fig. 5 that as the joint segment length increases, the transmission coefficients of non-persistent joint become close to those of persistent joint. In addition, due to the smaller distance between point 1 and joint plane, the transmission coefficient of point 1 converges faster to the theoretical value of persistent joint.

Fig. 5
figure 5

Comparison of transmission coefficients between calculation results obtained from the boundary integral equation method and analytical solution with respect to persistent joint for different lengths of joint segment, a point 1 and b point 2

Full size image

4 Parametric study

In this section, a single non-persistent joint with three joint segments is utilized to perform parametric studies using the boundary integral equation method. The calculation model is shown in Fig. 2. Two groups of monitoring points are chosen behind the rock bridge and joint segment, respectively. Each group has 4 points. And those four monitoring points in each group are set with a distance of 0.5 m, 1.0 m, 2.0 m, and 4.0 m away from the joint plane, respectively. The rock surrounding the joint segments is assumed to be homogeneous, elastic and isotropic. The parameters of the rock and the joint in this section, i.e., the elastic modulus, density, Poisson’s ratio of the rock, and the shear and normal stiffness of the joint, are the same as those mentioned in Sect. 3. During a realistic engineering blasting, the principal frequency of the stress wave can reach several thousand Hertz at the wall of the charge chamber, whereas the wave frequency will reduce sharply at a short distance due to the existence of joints which can filter out the high-frequency components (Jiao et al. 2005). Therefore, a frequency of 100 Hz is adopted for the incident wave, which has a wavelength of 40.2 m, as the reference case.

4.1 Effects of joint segment length

Figure 6a, b illustrate the variation of transmission coefficient T with the normalized joint segment length \(L_{{\text{j}}}\) for rear points of joint segment and rock bridge, respectively, when the incident wave with a frequency of 100 Hz normally impinges on the non-persistent joint. The rock bridge length is set to be 0.5 m. The transmission coefficient contour maps for different joint segment lengths are shown in Fig. 7. The red lines on the coordinate axis represent the joint segments. And the symbols DJE and DWP stand for the direction of joint extension and the direction in which the incident wave propagates, respectively.

Fig. 6
figure 6

Variation of transmission coefficient with joint segment length, a monitoring points behind the joint segment and b monitoring points behind the rock bridge

Full size image
Fig. 7
figure 7

The transmission coefficient contour maps for different joint segment lengths

Full size image

It can be observed from Figs. 6 and 7 that the transmission coefficients vary with the position of the points behind the joint segment and the rock bridge, although the points have the same distance from the joint plane. This indicates that the transmitted wave field behind a non-persistent joint is complex and non-uniform, which is different to the case of persistent joint causing regularly transmitted wave field. The complex wave field is caused by the scatted waves from the non-persistent joint. In addition, the maximum displacement for the points behind the rock bridge decreases with the increase of joint segment length, as shown in Fig. 6b, while the transmission coefficients for the points behind the joint segment fluctuate with the joint segment length, as shown in Fig. 6a. The transmission coefficients remain around 1.0 for all the monitoring points when the normalized joint segment length is less than 0.07, as shown in Fig. 6. It can also be found from Fig. 7 that the transmitted wave field almost has no attenuation if the length of joint segment is apparently smaller than the wavelength, e.g., 0.5 m. On the contrary, the obvious wave attenuation and enhancement will happen if the joint segment length increases to a certain value which is comparable to the wavelength, e.g., 5.0 m, 9.0 m and 15.0 m.

Wave propagation across a non-persistent joint is also calculated when the length of joint segment is much longer than the wavelength. The normalized length of joint segment is assumed to be 4.98 and 6.22. According to the method shown in Sect. 2.2, the transmission coefficient at point 1 reaches 0.55 and 0.48, respectively. If the incident P wave propagates across a persistent joint with the same joint stiffness as the non-persistent joint, the transmission coefficient, according to Eq. (22), is 0.54. Therefore, if the length of joint segment is much larger than the wavelength, the non-persistent joint can be approximately considered as a persistent one.

4.2 Effects of rock bridge length

This section investigates the effects of rock bridge length on wave propagation across a single non-persistent joint. The length of the joint segment is set as 0.5 m, and the frequency of the incident wave is 100 Hz. The wavelength of incident P wave is 40.2 m. The normalized rock bridge length \(L_{{\text{r}}}\) is defined as the ratio of the rock bridge length to the incident wavelength. The transmission coefficient contour maps in the transmitted field for different rock-bridge lengths are shown in Fig. 8.

Fig. 8
figure 8

The transmission coefficient contour maps for different rock bridge lengths

Full size image

It can be observed that the transmission coefficients for all points are approximately equal to 1.0 when the rock bridge length varies from 0.5 to 8 m. This indicates that the effect of the non-persistent joint on stress waves is quite weak due to the small length of joint segment compared to the wavelength.

When the length of joint segment is 5 m and the normalized rock bridge length changes from 0.0025 to 0.373, the corresponding transmission coefficients are also calculated and shown in Fig. 9. It can be seen from the figure that the transmission coefficients of all monitoring points behind the joint segment and the rock bridge increase with the rise of normalized rock-bridge length. When \(L_{r}\) is equal to 0.0025, the joint segments are almost connected, and the transmission coefficients are about 0.75. We found from Fig. 9b that the point 5, which is closest to the rock bridge, has the largest displacement amplitude. In addition, for a given \(L_{r}\), the monitoring point closer to the rock bridge has a larger transmission coefficient, but the maximum value for all monitoring points behind the rock bridge eventually approaches 1.0 with the increase of the normalized rock bridge length. For the points behind the joint segment, the transmission coefficients are close to each other and exceed 1.0 when the rock bridge length is approximately equal to the joint segment length. Comparison between Fig. 9a and Fig. 9b shows that the scattered wave has a greater impact on the movement of the points behind the joint segment.

Fig. 9
figure 9

Variation of transmission coefficient with normalized rock bridge length, (\(L_{{\text{j}}} \;{ = }\;{5}{\text{.0}}\;{\text{m}}\)) a monitoring points behind the joint segment and b monitoring points behind the rock bridge

Full size image

4.3 Effects of wave frequency

Previous studies have indicated that the joints in rock masses act as low-pass filters which only allow the lower frequency components to pass through and filter out the high frequency components (Cai and Zhao 2000; Zhao et al. 2006a, b). Similarly, the feature of frequency dependence still exists in the case of wave propagation across non-persistent joints. Here, the rock-bridge length and joint-segment length are both selected as 0.5 m. The transmission coefficient contour maps for different wave frequencies are shown in Fig. 10.

Fig. 10
figure 10

The transmission coefficient contour maps for different incident wave frequencies

Full size image

The relation between the transmission coefficient and the frequency of incident wave is shown in Fig. 11a, b for points behind the joint segment and the rock bridge, respectively. The figure shows that the transmission coefficients remain constant around 1.0 for wave frequencies lower than 500 Hz, whereas change rapidly as the wave frequency increases. In terms of low-frequency waves, the existence of joint has little impact on transmitted wave field since the joint segment length is far less than the wavelength. To characterize the relation between the transmission coefficient of non-persistent joint and the incident wave frequency, a new parameter should be introduced here, i.e., the critical frequency \(f_{cr}\). When the incident wave frequency is lower than the critical frequency \(f_{cr}\), which is 500 Hz in this section, the transmission coefficients behind the joint plane remains approximately constant around 1.0. In other words, there is almost no wave attenuation across the joint and the effect of joint segment on wave propagation can be ignored. Figure 11a, b indicate a strong dependence of transmission coefficient on wave frequency. Additionally, the scattering effect and interference of stress wave also contribute to the fluctuation characteristics of transmission coefficient.

Fig. 11
figure 11

Variation of transmission coefficient with incident wave frequency, a monitoring points behind the joint segment and b monitoring points behind the rock bridge

Full size image

4.4 Effects of incident angle

Wave coupling will be observed when a P wave obliquely impinges on the persistent joints, i.e., the reflected P wave, SV wave and transmitted P wave, SV wave will be generated simultaneously. For non-persistent joints, it would be more complex due to the generation of scattered waves. The effects of incident angles ranging from \(0^{^\circ }\) to \(85^{^\circ }\) on wave propagation through a non-persistent joint will be analyzed in this section. The contour maps of transmission coefficient for different incident angles are shown in Fig. 12.

Fig. 12
figure 12

The contour maps of transmission coefficient for different incident angles (\(L_{{\text{r}}} { = }\;{1}{\text{.0}}\;{\text{m}}\;{,}\;L_{{\text{j}}} { = }\;{1}{\text{.0}}\;{\text{m}}\;{,}\;f\;{ = }\;{600}\;{\text{Hz}}\))

Full size image

As has been discussed above, non-persistent joints will have minor effects on transmitted wave field for the case of low-frequency incident wave and small joint segment length. For example, the transmission coefficients are approximately equal to 1.0 for all monitoring points when the joint segment length and wave frequency are 0.5 m and 300 Hz, respectively. Hence, the P-wave frequency in this section is set to 600 Hz. And both the joint segment length and rock bridge length are selected as 1.0 m.

It can be observed from Fig. 12 that the contour maps of transmission coefficient are asymmetrical and complex, which is different from the case of normal incidence of stress wave. When P waves obliquely impinge on the non-persistent joint, the transmitted P waves, SV waves and scattered waves will simultaneously generate, which causes the complexity of the displacement field. It can also be seen from Fig. 13 that the preference direction of particle vibration will change. For example, the x-component of the displacement amplitude at an incident angle of \(85^{^\circ }\) is larger than that at an incident angle of \(5^{^\circ }\), whereas the opposite trend can be seen for the y-component of the displacement amplitude. However, it can be found from Fig. 12 that the maximum and minimum values of total displacement amplitude in the transmitted wave field will not change significantly as the incident angle increases. In addition, the obvious displacement amplification and depression effect will be mainly concentrated in the region which is closer to the joint plane for the case of larger incident angles, e.g., \(85^{^\circ }\).

Fig. 13
figure 13

The contour maps of transmission coefficient in the direction x and y for two kinds of different incident angles

Full size image

5 Discussion

The present study indicates that the joint-segment length, rock-bridge length, wave frequency and incident angle produce salient effects on transmitted wave field.

The existence of rock bridges causes the wave diffraction and makes the transmitted waves become non-plane during wave propagation across non-persistent joint. Meanwhile, the transmitted wave field is no longer regular. In other words, the transmission coefficient varies with the location of monitoring point, which is significantly different from that in wave propagation across persistent joints. According to the Huygens-Fresnel principle (Pao and Mow 1973), each point on the surface where the wave arrives can be considered as a secondary wavelet source, and each wavelet source emits secondary waves to its surroundings. Since these wavelet sources are definitely coherent, the perturbation of any point in the transmitted wave field is the result of the interference of all these wavelets. And the envelope surface of these wavelets forms a new wavefront.

As shown in Fig. 14a, the persistent joint will produce the same attenuation effects on the energy or amplitude of each wavelet source of the harmonic plane wave. Thus, the transmitted wave with a decrease in its amplitude is still the harmonic plane wave. Those black circles represent the wavelets having higher amplitude whereas those gray circles represent wavelets having lower amplitude. Figure 14b shows the schematic diagram of plane wave propagation across a single non-persistent joint. When plane wave propagates through a non-persistent joint, the wavelets at the rock bridge will not be weakened. However, the wavelets at the joint segment will be attenuated to a certain extent, which causes the variation of the transmission coefficient in transmitted field.

Fig. 14
figure 14

Schematic diagram of stress wave propagation across a joint, a single persistent joint and b a single non-persistent joint

Full size image

The scattering effect becomes dominant if the joint segment is comparable in length to the wavelength. When discussing the effects of joint segment length and rock bridge length on transmitted wave field in Sect. 4, the wavelength is about 40 m. If the joint segment length is 0.5 m, 1.0 m or 2 m, which are far less than the wavelength, the transmission coefficients on monitoring points behind the joint plane roughly equal to 1.0, which can be found from Fig. 6 and Fig. 8. However, when the length of joint segment increases, the effect of scattered waves on transmitted wave field becomes more significant. Additionally, the longer joint segment indicates that the propagation of stress waves will be hindered in a larger range. Then, the secondary wavelet sources located at the joint segment and rock bridge will emit secondary waves with different amplitude. And the variation of particle vibration amplitude with the location of monitoring points in the transmitted wave field could be attributed to the interference and superposition of these secondary waves having various amplitude. It is noteworthy that when the joint segment length is much larger than the wavelength, the scattered waves generated at the joint-segment tips and rock-bridge tips will have negligible effects on the transmission coefficient in the middle regions behind the joint segment. In other words, the wave field in those regions will be mainly controlled by transmitted waves, not the scattered waves. This phenomenon can also be observed from Fig. 5. When the normalized joint segment length approximately increases to 5.5, the value of T nearly equals to the transmission coefficient obtained from the case of wave propagation across persistent joints.

The contour maps of transmission coefficient indicate that the non-persistent joint will have remarkable effects on the dynamic response of the region behind the joint plane. For the case of high-frequency waves whose wavelengths are close to the length of natural joints, the amplitude of the particle located in some regions near to the joint segment will be significantly amplified. Constructive interference and destructive interference of different wavelets forms the wave crests and wave troughs. Moreover, the maximum and minimum values of displacement amplitude differ greatly for the incident wave with high frequencies. Much attention should be paid to these regions with large vibration amplitude in the process of structural design and protection.

6 Conclusions

This paper presents a study on harmonic wave propagation through a single non-persistent joint arranged with three joint segments by means of boundary integral equation method. In the section of method verification, for the case of wave propagation across a single non-persistent joint with only one joint segment, the calculation results based on boundary integral equation method are compared with those based on the UDEC software and those calculated by theoretical formula with respect to persistent joint. Thus, the accuracy and effectiveness of the boundary integral equation method to study wave propagation across non-persistent joints are verified.

The parametric studies are then carried out to investigate the effects of joint-segment length, rock-bridge length, wave frequency and incident angles on the spatial distribution of transmission coefficient. Compared with dynamic responses of rock masses only containing the persistent joints, there exists a noticeable difference for wave propagation through non-persistent joints. For the case of non-persistent joints, the scattered waves cannot be neglected because of the existence of rock bridges and the wave front of the transmitted wave is not planar any more. Additionally, the amplitude of transmitted waves will be depressed in some regions and amplified in other regions, which is different from the features of amplitude attenuation in the case of wave propagation across a persistent joint.

The ratio between wavelength and joint segment length, rock bridge length can significantly affect the scattered wave field. Especially when the joint segment is comparable in length to the wavelength, the obvious scattering effects will be observed. If the joint segment has a length more than 5.5 times the wavelength, the transmission coefficient at the rear monitoring points of the joint segment is mainly controlled by the process of wave transmission, while the influences of scattered waves correspondingly become weak.

It should be noted that the harmonic wave is used as the incident wave in this research. The dynamic responses of the rock masses under arbitrary time-domain signals can be obtained according to the transmission coefficient, also called transfer function obtained in frequency-domain analysis and inverse Fourier transform technique. In addition, the effects of material damping and multiple non-persistent joints on wave propagation need to be further investigated.