1 Introduction

Underground rock strata have numerous discontinuous structures, including cavities formed by structural discontinuities and inclusions formed by medium discontinuities. These cavities include roadways, chambers, and cracks. After being filled with other media, the cavities became inclusions. Therefore, the concrete plug structure of a diversion tunnel, mining backfill body, underground construction, and even the ore body in the rock stratum can be characterized as inclusions. Disturbances caused by earthquakes and blasting propagate in the form of stress waves in the rock strata, and scattering and dynamic stress concentrations occur in discontinuous structures, which lead to structural failure (Zhang et al. 2011; Sheikhhassani and Dravinski 2016; Liu et al. 2017; Li et al. 2019).

The dynamic stress concentration caused by stress-wave scattering has been extensively investigated, and their study methods have been improved and developed. (Tao et al. 2017, 2019b, 2020a; Zhou et al. 2018; Jiang et al. 2019; Zhao et al. 2020). Pao and Mow (1973) systematically summarized the research status of dynamic stress concentration in 1973 and solved the scattering of the circular and elliptical cavity model. The dynamic stress concentration factors (DSCF) around these models were determined based on the wave function expansion method, and the influencing factors of DSCF were analyzed. Liu et al. (1980) utilized the complex function method to determine the spatial distribution of DSCF near arbitrary shaped cavity, which extended the complex function to solve the process of scattering problem. Ghafarollahi and Shodja (2018) investigated the scattering around arbitrarily oriented elliptic cavity/crack using the multipole expansion method, and the numerical results revealed that the angle and wave number of the incident wave had a significant influence on the DSCF value for the medium. Lu et al. (2019) considered the blasting waves as cylindrical P-waves and determined the DSCF for underground tunnels based on the wave function expansion method in multi-polar coordinates. The numerical results indicated that the main influence factors of DSCF were the blasting wave frequency and the scaled distance. Li et al. (2020) determined the analytical formula of DSCF for an underground circular cavity subjected to the transient P wave based on the complex function method, and the transient response obtained by using the Butterworth filter to eliminate singularities. Leng et al. (2022) evaluated the DSCF around two circular cavities subjected to SH-wave in a plate by using the mirror method with the wave function expansion method and the influence of the band thickness, difference of two cavities sizes, and wave number on DSCF was analyzed.

The scattering process of stress wave around inclusions has been a focus of research for many years, but the boundary conditions of inclusions are more complex than cavities (Yang et al. 2002; Xu et al. 2011; Tao et al. 2022). Lee et al. (2013) utilized a volume integral equation method to solve the scattering of multiple elliptical inclusions in infinite space and presented the displacement of inclusions under various wave numbers. The advantage of this approach was that only the inclusions need to be discretized, not the entire region. Qi et al. (2019) investigated the dynamic response of the elliptical inclusion in half-space, which partially debonded with the medium. The displacement and stress fields were determined by the Green's function method and conformal mapping and the influence factors for the spatial distribution of DSCF were analyzed. Jiang et al. (2020) employed the complex function method to obtain the DSCF around an elliptical inclusion in the anisotropic half-space. The numerical results indicated that the wave number, incidence angle, and anisotropic parameters significantly influenced the spatial distribution of DSCF. Jang et al. (2020) studied the scattering of SH waves by a three-layer inclusion near the bi-material interface and obtained the displacement fields resulting from the forces using the Green’s function method. Yang et al. (2021) established a mathematical model for an inhomogeneous half-space and investigated the dynamic stress around a circular inclusion in an inhomogeneous medium. In addition, the effects of inhomogeneous parameters, reference wave number, and burial location on the DSCF around a circular inclusion were analyzed. Zhang and Qi (2021) calculated the dynamic response of an elliptic inclusion in an infinite strip region under a plane SH wave by using the conformal mapping method.

In previous studies, the interface between the inclusion and surrounding rock was considered a perfect bond, which revealed that the stress and displacement at the interface were continuous. In fact, owing to the existence of micro-cracks and interstitial media, the interface between the inclusion and surrounding rock is not always perfect, which influences the propagation of stress waves. In addition, previous research has primarily concentrated on the dynamic response of inclusions under steady-state incidence, which cannot directly guide the protection of underground structures under transient disturbances caused by blasting and earthquakes. Therefore, in this study, the spring model and Ricker wavelet were adopted to represent the imperfect interface and transient seismic wave. The analytical formula of the DSCF for an elliptic inclusion with imperfect interfaces subjected to plane SH-wave was derived based on the wave function expansion method and Fourier transform. The theoretical solution was verified by numerical simulation using the LS-DYNA software, and the effects of wave number (k), radial coordinate (ξ), stiffness parameter (β), and difference in material properties on the dynamic response were analyzed.

2 Formulation in the elliptical coordinate system

2.1 Governing equations

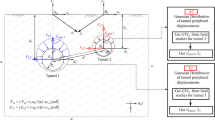
The simplified mathematical-physical model is shown in Fig. 1. The inclusion and medium are assumed to be elastic materials. The l, h and θ depicted the major and minor axes of inclusion and incident angle, respectively. The μ and k denote the shear modulus and wave number. In addition, subscripts 1 and 2 denote the parameters related to the medium and inclusion, respectively.

Fig. 1
figure 1

The geometry model

Full size image

In the elliptical coordinate system, the dynamic response for inclusion can be determined by the wave function expansion method, and the elliptical coordinate system is illustrated in Fig. 2.

Fig. 2
figure 2

Elliptical coordinate system

Full size image

The transformation relation between the rectangular coordinate system and the elliptical coordinate system and the scale factor is defined as follows:

$$ \left\{ {\begin{array}{l} {x = a\cosh \xi \cos \eta ,\quad 0 < \xi < \infty } \\ y = a\sinh \xi \sin \eta ,\quad 0 < \eta < 2\pi \hfill \\ h_{\xi }^{2} = h_{\eta }^{2} = a^{2} J \hfill \\ J^{2} = \cosh^{2} \xi - \cos^{2} \eta \hfill \\ \end{array} } \right. $$
(1)

where ξ and η are the radial and angular coordinates, respectively.

The elliptical major axis l, elliptical minor axis h, and axis ratio ε can be expressed as

$$ \left\{ \begin{array}{l} l = {2}a\cosh \xi \hfill \\ h = {2}a\sinh \xi \hfill \\ \varepsilon = coth\xi \hfill \\ \end{array} \right. $$
(2)

In the elliptical coordinate system, the Helmholtz equation and the analytic expression of the incident wave can be written as (Pao and Mow 1973)

$$ \nabla^{2} \varphi + k^{2} \varphi = \frac{1}{{a^{2} J^{2} }}\left( {\frac{{\partial^{2} \varphi }}{{\partial \xi^{2} }} + \frac{{\partial^{2} \varphi }}{{\partial \eta^{2} }}} \right) + k^{2} \varphi = 0 $$
(3)
$$ u_{z1}^{i} = u_{{_{0} }} e^{{i\left[ {k\left( {x\cos \theta + y\sin \theta } \right) - \omega t} \right]}} $$
(4)

where k and ω denote the wave number and circular frequency, respectively, and k = ω/cs.

Assuming that the maximum displacement u0 of uzi is one and omitting the time-dependent term e−iωt for simplifying the calculation, the incident wave can be expressed by Mathieu functions as follows:

$$ \begin{aligned} u_{z1}^{i} & = 2\sum\limits_{m = 0}^{\infty } {i^{m} } ce_{m} \left( {\theta ,q_{1} } \right)Mc_{m}^{1} \left( {\xi ,q_{1} } \right)ce_{m} \left( {\eta ,q_{1} } \right) \\ & \quad + 2\sum\limits_{m = 1}^{\infty } {i^{m} } se_{m} \left( {\theta ,q_{1} } \right)Ms_{m}^{1} \left( {\xi ,q_{1} } \right)se_{m} \left( {\eta ,q_{1} } \right) \\ \end{aligned} $$
(5)

where cem, sem and Mcm, and Msm are the radial and angular Mathieu functions, respectively, and q = (ak)2/4.

The radial and angular Mathieu functions can be represented as follows (Abramowitz et al. 1965):

$$ \left\{ {\begin{array}{*{20}l} {ce_{2m} \left( {\eta ,q} \right) = \sum\limits_{r = 0}^{\infty } {A_{2r}^{2m} } \left( q \right)\cos 2r\eta } \hfill & {b = a_{2m} } \hfill \\ {se_{2m + 2} \left( {\eta ,q} \right) = \sum\limits_{r = 0}^{\infty } {B_{2r + 2}^{2m + 2} } \left( q \right)\sin \left( {2r + 2} \right)\eta } \hfill & {b = b_{{2m + 2}} } \hfill \\ {ce_{2m + 1} \left( {\eta ,q} \right) = \sum\limits_{r = 0}^{\infty } {A_{2r + 1}^{2m + 1} } \left( q \right)\cos \left( {2r + 1} \right)\eta } \hfill & {b = a_{{2m + 1}} } \hfill \\ {se_{2m + 1} \left( {\eta ,q} \right) = \sum\limits_{r = 0}^{\infty } {B_{2r + 1}^{2m + 1} } \left( q \right)\sin \left( {2r + 1} \right)\eta } \hfill & {b = b_{{2m + 1}} } \hfill \\ \end{array} } \right. $$
(6)
$$ \left\{ \begin{aligned} & b = a_{m} ,p = 0,1 \\ & Mc_{2m + p}^{j} \left( {\xi ,q} \right) = \left[ {ce_{2m + p} (0,q)} \right]^{ - 1} \sum\limits_{r = 0}^{\infty } {\left( { - 1} \right)}^{r + m} A_{2r + p}^{2m + p} Z_{2r + p}^{j} \left( {2\sqrt q \cosh \xi } \right) \\ & b = b_{m} ,p = 1,2 \\ & Ms_{2m + p}^{j} \left( {\xi ,q} \right) = \left[ {se_{2m + p}^{\prime } (0,q)} \right]^{ - 1} \tanh \xi \sum\limits_{r = 0}^{\infty } {\left( { - 1} \right)}^{r + m} \left( {2r + p} \right)B_{2r + p}^{2m + p} Z_{2r + p}^{j} \left( {2\sqrt q \cosh \xi } \right) \\ \end{aligned} \right. $$
(7)

The scattering wave around the inclusion uz1s can be expressed as

$$ \begin{aligned} u_{z1}^{s} = \sum\limits_{m = 0}^{\infty } {B_{m} Mc_{m}^{3} \left( {\xi ,q_{1} } \right)ce_{m} \left( {\eta ,q_{1} } \right)} \hfill \\ \quad + \sum\limits_{m = 1}^{\infty } {C_{m} Ms_{m}^{3} \left( {\xi ,q_{1} } \right)se_{m} \left( {\eta ,q_{1} } \right)} \hfill \\ \end{aligned} $$
(8)

Therefore, the full-wave expression in the medium can be determined as

$$ u_{z1} = u_{z1}^{i} \left( {\xi ,\eta ,q_{1} } \right) + u_{z1}^{s} \left( {\xi ,\eta ,q_{1} } \right) $$
(9)

The standing wave uz2 inside the inclusion can be given by the following formulas (Pao and Mow 1973):

$$ \begin{aligned} u_{z2} & = \sum\limits_{m = 0}^{\infty } { - D_{m} Mc_{m}^{1} \left( {\xi ,q_{2} } \right)ce_{m} \left( {\eta ,q_{2} } \right)} \\ & \quad + \sum\limits_{m = 1}^{\infty } { - E_{m} Ms_{m}^{1} \left( {\xi ,q_{2} } \right)se_{m} \left( {\eta ,q_{2} } \right)} \\ \end{aligned} $$
(10)

In Eqs. (8), (10), Bm, Cm, Dm and Em denote the undetermined coefficients.

In addition, the stress component in the elliptical coordinate can be represented as (Liang and Jia 2011):

$$ \left\{ {\begin{array}{*{20}c} {\sigma_{\xi } = \frac{\mu }{aJ}\frac{{\partial u_{z} }}{\partial \xi }} \\ {\sigma_{\eta } = \frac{\mu }{aJ}\frac{{\partial u_{z} }}{\partial \eta }} \\ \end{array} } \right. $$
(11)

2.2 Boundary conditions

In fact, the interface between the inclusion and the surrounding rock is not always perfect owing to the existence of micro-cracks and interstitial media. The stress and displacement behavior of inclusion is very dependent on the surface status (Son and Cording 2007). For the imperfect interface, much fundamental research has been conducted to develop different kinds of models (Gurtin and Murdoch 1975; Chen et al. 2006; Benveniste 2006). The spring model is one of the most widely used models, and its validity has been verified in previous literature (Yi et al. 2014, 2016; Fang et al. 2015; Fang and Jin 2017; Zhang et al. 2019). Therefore, the spring model is adopted to model the imperfect interface, which assumes the stress is continuous but displacement is discontinuous at the interface. Moreover, the stress is proportional to the discontinuity of displacement through a stiffness parameter β. The boundary condition can be described as

$$ \left\{ {\begin{array}{l} {u_{z1} (\xi_{0} ,\eta ,q_{1} ) - u_{z2} (\xi_{0} ,\eta ,q_{2} ) = \frac{{\sigma_{\xi z1} }}{\beta }} \\ {\sigma_{\xi z1} (\xi_{0} ,\eta ,q_{1} ) = \sigma_{\xi z2} (\xi_{0} ,\eta ,q_{2} )} \\ \end{array} } \right. $$
(12)

The extent of contact between inclusion and surrounding rock can be defined through β. For β → ∞, which indicates that displacement and stress of inclusion and medium are continuous at the interface. Therefore, the imperfect interface approaches the perfect interface. For β → 0, we obtain σξz → 0, which means that no waves are transmitted from the medium to the inclusion, and the inclusion model becomes the cavity model.

3 Steady-state response

3.1 Dynamic stress concentration factor (DSCF)

The wave function has four undetermined coefficients, but boundary conditions only have two equations which result in the equation set cannot be solved directly. The incident angle θ is set as 0, which means that the incident wave is parallel to the x-axis, resulting in sem(θ,q) = 0 and Cm, Em does not affect the solution of the equation set. Therefore, Eqs. (5), (8), and (10) can be written as

$$ u_{z1}^{i} = 2\sum\limits_{m = 0}^{\infty } {i^{m} } ce_{m} \left( {0,q_{1} } \right)Mc_{m}^{1} \left( {\xi ,q_{1} } \right)ce_{m} \left( {\eta ,q_{1} } \right) $$
(13)
$$ u_{z1}^{s} = \sum\limits_{m = 0}^{\infty } {B_{m} Mc_{m}^{3} \left( {\xi ,q_{1} } \right)ce_{m} \left( {\eta ,q_{1} } \right)} $$
(14)
$$ u_{z2} = \sum\limits_{m = 0}^{\infty } { - D_{m} Mc_{m}^{1} \left( {\xi ,q_{2} } \right)ce_{m} \left( {\eta ,q_{2} } \right)} $$
(15)

Substituting Eqs. (13), (14), and (15) into Eq. (12) gives the following two equations:

$$ \left\{ \begin{aligned} & \sum\limits_{m = 0}^{\infty } {\left[ \begin{aligned} 2i^{m} ce_{m} \left( {0,q_{1} } \right)Mc_{m}^{1} \left( {\xi_{0} ,q_{1} } \right)ce_{m} \left( {\eta ,q_{1} } \right) + B_{m} Mc_{m}^{3} \left( {\xi_{0} ,q_{1} } \right)ce_{m} \left( {\eta ,q_{1} } \right) \hfill \\ + D_{m} Mc_{m}^{1} \left( {\xi_{0} ,q_{2} } \right)ce_{m} \left( {\eta ,q_{2} } \right) \hfill \\ \end{aligned} \right]} \\ & \quad = \frac{{\mu_{1} }}{\beta aJ}\sum\limits_{m = 0}^{\infty } {\left[ {2i^{m} ce_{m} \left( {0,q_{1} } \right)Mc_{m}^{1\prime}\left( {\xi_{0} ,q_{1} } \right)ce_{m} \left( {\eta ,q_{1} } \right) + B_{m} Mc_{m}^{3\prime}\left( {\xi_{0} ,q_{1} } \right)ce_{m} \left( {\eta ,q_{1} } \right)} \right]} \\ & \sum\limits_{m = 0}^{\infty } {\left[ {B_{m} Mc_{m}^{3\prime}\left( {\xi_{0} ,q_{1} } \right)ce_{m} \left( {\eta ,q_{1} } \right) + \frac{{\mu_{2} }}{{\mu_{1} }}D_{m} Mc_{m}^{1\prime}\left( {\xi_{0} ,q_{2} } \right)ce_{m} \left( {\eta ,q_{2} } \right)} \right]} \\ & \quad = - 2\sum\limits_{m = 0}^{\infty } {i^{m} } ce_{m} \left( {0,q_{1} } \right)Mc_{m}^{1\prime}\left( {\xi_{0} ,q_{1} } \right)ce_{m} \left( {\eta ,q_{1} } \right) \\ \end{aligned} \right. $$
(16)

Due to the characteristics of the Mathieu function, cem(η, q1) and cem(η, q2) are not orthogonal. Consequently, solving the equation set requires the orthogonal formula of the Mathieu function. The orthogonal formula is given as follows:

$$ \int\limits_{0}^{2\pi } {ce_{m}^{2} } \left( {\eta ,q} \right)d\eta = \int\limits_{0}^{2\pi } {se_{m}^{2} } \left( {\eta ,q} \right)d\eta = \pi $$
(17)

Substituting Eq. (17) into Eq. (16) gives the following two equations:

$$ \left\{ \begin{aligned} & 2i^{n} ce_{n} \left( {0,q_{1} } \right)Mc_{n}^{1} \left( {\xi_{0} ,q_{1} } \right) + B_{n} Mc_{n}^{3} \left( {\xi_{0} ,q_{1} } \right) + \sum\limits_{m = 0}^{\infty } {D_{m} } Mc_{m}^{1} \left( {\xi_{0} ,q_{2} } \right)p_{mn} \\ & \quad = \frac{{\mu_{1} }}{\beta aJ}\left[ {2i^{n} ce_{n} \left( {0,q_{1} } \right)Mc_{n}^{1\prime}\left( {\xi_{0} ,q_{1} } \right) + B_{n} Mc_{n}^{3\prime}\left( {\xi_{0} ,q_{1} } \right)} \right] \\ & B_{n} Mc_{n}^{3\prime}\left( {\xi_{0} ,q_{1} } \right) + \frac{{\mu_{2} }}{{\mu_{1} }}\sum\limits_{m = 0}^{\infty } {D_{m} } Mc_{m}^{1\prime}\left( {\xi_{0} ,q_{2} } \right)p_{mn} \\ & \quad = - 2i^{n} ce_{n} \left( {0,q_{1} } \right)Mc_{n}^{1\prime}\left( {\xi_{0} ,q_{1} } \right) \\ \end{aligned} \right. $$
(18)

where

$$ p_{mn} = \frac{1}{\pi }\int\limits_{0}^{2\pi } {ce_{n} (\eta ,q_{1} )} ce_{m} (\eta ,q_{2} )d\eta $$
(19)

Eliminating Bm from the two equations in Eq. (18) enables an algebraic equation system to be derived for Dm:

$$ \sum\limits_{m = 0}^{\infty } {D_{m} } d_{mn} = b_{n} \quad n = 0,1,2 \ldots $$
(20)

where

$$ \left\{ {\begin{array}{*{20}c} {d_{mn} = p_{mn} \left[ {\frac{{Mc_{m}^{(1)} (\xi_{0} ,q_{2} )}}{{Mc_{n}^{(3)} (\xi_{0} ,q_{1} )}} - \frac{{\mu_{2} }}{{\mu_{1} }}\frac{{Mc_{m}^{(1)\prime}(\xi_{0} ,q_{2} )}}{{Mc_{n}^{(3){\prime}}(\xi_{0} ,q_{1} )}} + \frac{{\mu_{2} }}{\beta aJ}\frac{{Mc_{m}^{(1){\prime}}(\xi_{0} ,q_{2} )}}{{Mc_{n}^{(3)} (\xi_{0} ,q_{1} )}}} \right]} \\ {b_{n} = - 2i^{n} ce_{n} (0,q_{1} )\left[ {\frac{{Mc_{n}^{(1)} (\xi_{0} ,q_{1} )}}{{Mc_{n}^{(3)} (\xi_{0} ,q_{1} )}} - \frac{{Mc_{n}^{(1){\prime}}(\xi_{0} ,q_{1} )}}{{Mc_{n}^{(3){\prime}}(\xi_{0} ,q_{1} )}}} \right]} \\ \end{array} } \right. $$
(21)

The numerical solution of the Mathieu function is obtained by truncating the N-th term. For the accuracy of the numerical solution, the value of N needs to be determined by comparing the error of the Mathieu function between the sum of N and N + 1 terms. N is set to 12 in this study. After computing Dm, we returned to Eq. (18) to determine Bn, the expression for which is as follows:

$$ B_{n} = \frac{{ - 2i^{n} ce_{n} \left( {0,q_{1} } \right)Mc_{n}^{1\prime}\left( {\xi_{0} ,q_{1} } \right) - \frac{{\mu_{2} }}{{\mu_{1} }}\sum\limits_{m = 0}^{\infty } {D_{m} } Mc_{m}^{1\prime}\left( {\xi_{0} ,q_{2} } \right)p_{mn} }}{{Mc_{n}^{3\prime}\left( {\xi_{0} ,q_{1} } \right)}} $$
(22)

Therefore, the full-wave expression in the medium can be determined as

$$ \begin{aligned} u_{z1}^{i} & = 2\sum\limits_{m = 0}^{\infty } {i^{m} } ce_{m} \left( {0,q_{1} } \right)Mc_{m}^{1} \left( {\xi ,q_{1} } \right)ce_{m} \left( {\eta ,q_{1} } \right) \\ & \quad + \sum\limits_{m = 0}^{\infty } {B_{m} Mc_{m}^{3} \left( {\xi ,q_{1} } \right)ce_{m} \left( {\eta ,q_{1} } \right)} \\ \end{aligned} $$
(23)

The DSCF value is defined as the ratio of ση and σ0. The σ0 is the stress generated by the incident wave. Thus, the DSCF and σ0 can be expressed as (Pao and Mow 1973)

$$ \left\{ \begin{aligned} & DSCF = \left| {\frac{{\sigma_{\eta } }}{{\sigma_{0} }}} \right| \\ & \sigma_{0} = \mu ku_{0} \\ \end{aligned} \right. $$
(24)

Substituting Eq. (23) into Eq. (24) gives the steady-state DSCF, which is represented as follows:

$$ DSCF = \left| {\frac{1}{aJk}\left[ \begin{aligned} 2\sum\limits_{m = 0}^{\infty } {i^{m} } ce_{m} \left( {0,q_{1} } \right)Mc_{m}^{1} \left( {\xi_{0} ,q_{1} } \right)ce_{m}^{\prime } \left( {\eta ,q_{1} } \right) \hfill \\ + \sum\limits_{m = 0}^{\infty } {B_{m} Mc_{m}^{3} \left( {\xi_{0} ,q_{1} } \right)ce_{m}^{\prime } \left( {\eta ,q_{1} } \right)} \hfill \\ \end{aligned} \right]} \right| $$
(25)

Both real and imaginary parts of numerical results represent the steady-state DSCF, but at different moments. The real part and imaginary parts represent the moment of T = 0 and T/4, respectively (where T is the period of incident waves).

3.2 Case study and verification

In this study, the semi-focal length a was set to 1 m for simplifying calculations. The radial coordinate ξ was set to 0.2 and 1.5, which controlled the shape of the ellipse and the corresponding axis ratios were 5 and 1.1, respectively. The wave velocity of the SH wave was in the range of 2000–3000 m/s at the project site. Thus, the wave velocity cs was predetermined to be 2200 m/s. In addition, the incident wavenumber k was set to 0.2 and 1, with the wavenumber range covering earthquakes, engineering blasts, and most impacts (Tao et al. 2020b). The difference in the material properties of the medium and elliptical inclusions also affects scattering around the elliptical inclusions (Yi et al. 2016). In this study, we set up two cases for the calculation. For case 1, k2/k1 = 0.5 and μ1/μ2 = 0.25, indicating that the inclusion was stiffer than the medium. For case 2, k2/k1 = 2 and μ1/μ2 = 4, indicating that the inclusion was softer than the medium. In addition, three sets of dimensionless spring stiffnesses were considered: β = 0.1µ2/J, 1.0µ2/J, and 10µ2/J.

Subsequently, to verify the derivation, we set the inclusion and medium to the same material property parameters. For β → 0 and ξ = 1.5, the elliptical inclusion degenerated into a circular cavity, and the numerical result was two from Pao and Mow (1973). For β → ∞, the imperfect interface approaches the perfect interface, which means that the stress waves propagate through the rock without a discontinuous structure and scattering. According to the definition of the DSCF, its maximum value of DSCF is one. The verification results are shown in Fig. 3.

Fig. 3
figure 3

Verification of theoretical results

Full size image

As shown in Fig. 3, the DSCF approaches two for β → 0, and it becomes one for β → ∞. The maximum value of the DSCF appeared at an angle perpendicular to the incident direction, and its minimum value occurred in the incident direction. The DSCF value gradually increased with an increasing angle in the range of 0° to 90°, and the spatial distribution of DSCF was symmetrical about the elliptical major and minor axes. Its maximum value and spatial distribution of DSCF were in excellent agreement with the available literature.

3.3 Numerical results

The numerical results for the steady-state DSCF are shown in Figs. 4, 5, 6, 7, 8, 9, 10 and 11. Figures 4, 5, 6 and 7 present the distribution of the steady-state DSCF around the elliptical inclusion in the two cases. Figures 8, 9, 10 and 11 depict the variation in the DSCF with the wave number (k), radial coordinate (ξ), and stiffness parameter (β) at η = π/2 (3π/2) in the two cases. In this study, an area with a DSCF greater than one was defined as the stress concentration area, and an area with a DSCF less than one was defined as the stress reduction area. As shown in Figs. 4, 5, 6, 7, the distribution of the DSCF was highly dependent on the wave number (k), radial coordinate (ξ), stiffness parameter (β), and differences in material properties. Figure 4 shows that, for β = 0.1µ2/J, the DSCF achieved a minimum value of zero in the incident direction, gradually increased with increasing angle, and reached the maximum value at an angle perpendicular to the incident direction. The spatial distribution of DSCF is symmetrical along η = 0 (π) and η = π/2 (3/2π). This phenomenon demonstrates that the DSCF achieved minimum and maximum values at both ends of the major and minor axes and that values were symmetrically distributed along the major and minor axes. For k = 0.2 and 1, the maximum DSCF values were 0.944 and 0.918, respectively. For β = 1.0µ2/J and 10µ2/J, the maximum DSCF values were 0.7156, 0.6742 and 0.6679, 0.6115, respectively, indicating that the DSCF decreased with the increase in β, but the difference range was only about 0.3. In addition, all the values of the DSCF were < 1, and the entire elliptical inclusion was in the stress reduction area. Figure 5 reveals that the DSCF distribution changed significantly. For k = 0.2, the spatial distribution of the DSCF was the same as that shown in Fig. 4, but its maximum value changed. For β = 0.1µ2/J, the maximum value of the DSCF reached 1.410. The stress concentration area was mainly distributed in the ranges of η = π/4–3π/4 and 5π/4–7π/4, and other areas were stress reduction areas. In the case of β = 1.0µ2/J and 10µ2/J, the maximum DSCF value was only about 0.5. Therefore, the entire elliptical inclusion was in the stress reduction area. At k = 1.0, the DSCF had six stress peak areas, and the stress concentration area was only present when β = 0.1µ2/J, being mainly distributed near η = π/2 and 3π/2 with a maximum of 1.325. The other four stress peak areas occurred near η = π/6, 5π/6, 7π/6, and 11π/6, and the DSCF values were 0.7595, 0.5344, 0.5344 and, 0.7595, respectively. The phenomenon of multiple stress peak areas at a high-wave-number incidence is consistent with the available literature (Zhang et al. 2021). The reason for the stress peaks appearing at other angles was that multiple stress wave crests existed in the elliptical inclusion under a high-wave-number incidence and the location of the wave crests was prone to dynamic stress concentration. In addition, the distribution of the DSCF is symmetrical along the elliptical major axis. For β = 1.0µ2/J, the DSCF exhibited six stress peak areas, and the distribution range was identical to that for distribution at β = 0.1µ2/J. However, for β = 10µ2/J, the DSCF had only four stress peak areas, appearing near η = π/2, 5π/6, 7π/6, and 3π/2, respectively. In addition, all peaks of the DSCF < 1 in the cases of β = 1.0µ2/J and 10µ2/J, indicating that the whole elliptical inclusion was in the stress reduction area.

Fig. 4
figure 4

The distribution of steady-state DSCF with ξ = 0.2 in case 1

Full size image
Fig. 5
figure 5

The distribution of the steady-state DSCF with ξ = 1.5 in case 1

Full size image
Fig. 6
figure 6

The distribution of the steady-state DSCF with ξ = 0.2 in case 2

Full size image
Fig. 7
figure 7

The distribution of the steady-state DSCF with ξ = 1.5 in case 2

Full size image
Fig. 8
figure 8

The variation in the DSCF with wave number (k) in case 1

Full size image
Fig. 9
figure 9

The variation in the DSCF with wave number (k) in case 2

Full size image
Fig. 10
figure 10

The variation in the DSCF with radial coordinate (ξ) in two cases

Full size image
Fig. 11
figure 11

The variation of the DSCF with stiffness parameter (β) in two cases

Full size image

The spatial distribution of the DSCF as shown in Fig. 6, was approximately equal to that in Fig. 4, and minimum and maximum values appeared at both ends of the major and minor axes. However, β had no significant influence on the DSCF value. For k = 0.2 and 1.0, the maximum values of the DSCF for the three values of β were approximately 1.1817 and 1.1999, but the distributions of the stress concentration areas were different. For k = 0.2, the stress concentration area was mainly distributed in the ranges of η = π/6–5π/6 and 7π/6–11π/6. Whereas, for k = 1.0, the stress concentration area was mainly distributed in the ranges of η = π/3–2π/3 and 4π/3–5π/3. The spatial distribution of the DSCF in Fig. 7 is similar to that in Fig. 5. For k = 0.2, the DSCF exhibited only two stress concentration areas, which were mainly distributed in the ranges of η = π/6–5π/6 and 7π/6–11π/6. Meanwhile, the DSCF reached maximum values at both ends of the minor axis, being 1.9124, 1.7633, and 1.6638, respectively. In the case of k = 1.0, the DSCF had six stress peak areas for the three values of β, mostly appearing near η = π/6, π/2, 5π/6, 7π/6,3π/2, and 11π/6. The stress concentration and stress reduction areas were mainly distributed around π/2, 3π/2 and 5π/6, 11π/6. The DSCF values of stress peak areas near η = π/6, 11π/6 were around 1. The maximum values of DSCF at both ends of the minor axis were 1.5197, 1.6977, and 1.421, respectively.

These analyses reveal that changes in k and ξ led to variations in the DSCF value and spatial distribution, but changes in β resulted only in variations in the DSCF value. This is because k and ξ directly affected the number of stress peaks in the elliptical inclusion, which led to the appearance of multiple extreme values at different angles, and then affected the spatial distribution and values of the DSCF. However, β only affected the propagation of stress waves and did not alter the number of stress peaks in the elliptical inclusion, which resulted in β not affecting the DSCF spatial distribution but only the DSCF value. According to previous studies, the spatial distribution of the DSCF should exhibit multiple stress peak areas under high-wave-number incidence. However, the numerical results showed that this phenomenon only occurred when the ellipse approached becoming a circle. This is because, at 0° incidence, the effective incident area of the elliptical inclusion was directly proportional to the elliptical minor axis, and the reduction in the effective incident area weakened the scattering. Therefore, the distribution of the DSCF with a shorter elliptical minor axis did not exhibit multiple stress peak areas.

Figures 8 and 9 present the variation in the DSCF with wave number (k) in two cases. As shown in these figures, for β = 0.1µ2/J, the DSCF first decreased and then increased with the increase in wave number and finally approached a constant value being 1.04 and 1.32 for ξ = 0.2 and 1.5, respectively. For β = 1.0µ2/J and 10µ2/J, the DSCF decreased gradually with increasing wave number, and their maximum value did not exceed one. In addition, with the variation in wave number, the DSCF with a small β was always greater than that with a large β value. Figure 9 indicates that the variation in material property parameters had a significant influence on the variation in the DSCF with wave number. At ξ = 0.2, the DSCF first increased with increasing wave number, decreased sharply at greater wave number, and then increased gradually. In the case of ξ = 1.5, the DSCF first increased with increasing wave number, reached a maximum value for k = 0.2, and then gradually decreased to a constant value. The DSCF values approached were different for different β values being 1.4143, 1.3682, and 0.8920 for β = 0.1µ2/J, 1.0µ2/J, and 10µ2/J, respectively. However, the DSCF with larger β changed dramatically in the process of approaching the constant value, exhibiting an oscillation. This behavior can likely be attributed to resonance scattering, as observed by Rajabi and Hasheminejad (2009). In addition, under the same conditions, the DSCF with a low wave number was greater than that with a high wave number, which was consistent with the conclusions of available studies (Hei et al. 2015; Yi et al. 2016; Tao et al. 2019a).

Figure 10 shows the variation in the DSCF value with the radial coordinate (ξ) in two cases. For β = 0.1µ2/J, the DSCF gradually increased with the increase of radial coordinate, finally becoming greater than one. For β = 1.0µ2/J and β = 10µ2/J, the DSCF decreased gradually with the increase in radial coordinate, always being less than one. The variation characteristics of the DSCF with radial coordinates seen in Fig. 10(b) are remarkably different from those in Fig. 10(a). For k = 0.2, the DSCF increased gradually with the increase of radial coordinate, reached a maximum value in the range of ξ = 1.5–1.6, and then decreased with increasing radial coordinate. In the case of k = 1.0, the DSCF exhibited an oscillation with the increase in radial coordinate, which was likely ascribed to the existence of multiple stress peak areas in the elliptical inclusion with high wave number, and the distribution of stress peak areas and the value of DSCF changed dramatically. Figure 10a and b reveal that the difference in the material properties of the surrounding rock and inclusion significantly affected the variation in the DSCF with the radial coordinate. When the elliptical inclusion was stiffer than the surrounding rock, the variation characteristics of the DSCF mainly depended on β, but when the elliptical inclusion was softer than the surrounding rock, the variation characteristics of the DSCF mainly depended on k.

Figure 11 presents the variation in the DSCF with stiffness parameter (β) in two cases. Figure 11(a) shows that the DSCF decreases rapidly in the range of β = 0–5µ2/J, then gradually decreases in the range of β = 5µ2/J–100µ2/J before approaching a constant value. This behavior demonstrates that the DSCF exhibited high sensitivity to the variation in β in the range of 0–5µ2/J and that the imperfect interface approached the perfect interface for β > 100µ2/J. The final constant DSCF values differed from those for different ξ and k values being 0.6621, 0.6031, 0.3846 and 0.2954, respectively. The variation characteristics of the DSCF with β in case 2 were approximately the same as those in case 1, and its final constant values were 1.1470, 1.2024, 1.6458, and 1.3468. However, a rapid oscillation occurred for k = 1.0. Computing the distribution of the DSCF near the oscillation, showed that this phenomenon was not caused by a singular value. It was likely attributed to the drastic variation in the distribution of the stress peak area and the value of the DSCF in the elliptical inclusion with the high wave number. Moreover, the maximum DSCF value did not appear at both ends of the elliptical minor axis.

4 Transient response

The steady-state incident wave is a simple harmonic wave in the infinite time domain, but the dynamic disturbance of the project site is an incident wave with a complex waveform in the finite time domain. Therefore, it is significant for practical engineering to determine the dynamic response for inclusion under transient disturbance. The transient response can be obtained by using the Fourier transform based on the steady-state response. The transient DSCF of elliptical inclusion can be expressed as

$$ u_{t} = \frac{1}{{\sqrt {2\pi } }}\int_{ - \infty }^{\infty } {F\left( \omega \right)} \chi \left( \omega \right)e^{ - i\omega t} d\omega $$
(26)

where χ(ω) and F(ω) denote the steady-state response and frequency distribution function, respectively.

The Ricker wavelet is a zero-phase seismic wavelet that is widely used in theoretical calculations and engineering simulation (Assimaki et al. 2005; Wang et al. 2012). Therefore, the Ricker wavelet was adopted to represent the transient disturbance generated by earthquakes. The Ricker wavelet can be written as (Wang 2015; Zhang et al. 2017):

$$ f(x) = \left( {1 - \frac{1}{2}\omega_{p}^{2} t^{2} } \right)e^{{ - \frac{1}{4}\omega_{p}^{2} t^{2} }} $$
(27)
$$ F\left( \omega \right) = \frac{{4\omega^{2} \sqrt \pi }}{{\omega_{{_{p} }}^{3} }}e^{{\left( { - \frac{{\omega^{2} }}{{\omega_{{_{p}^{2} }} }}} \right)}} $$
(28)

where ωp denotes the dominant frequency.

In the time domains, the Ricker wavelet has one wave crest and two wave troughs in a short duration, the ratio of the wave crest and trough amplitude is 0.5e1.5, which is ≈ 2.241 (Ricker 1940). In the frequency domains, the Ricker wavelet achieves the maximum value at the dominant frequency. In this study, the dominant frequency ωp was set to 100, 800, and 2500, which corresponds to low, medium and high frequencies for the Ricker wavelet, respectively.

Substituting Eqs. (25) and (28) into Eq. (26), the transient response of inclusion with the time-dependent term was determined. The transient DSCF is even more significant for engineering projects at the moment of the Ricker wavelet crest. Therefore, that moment was chosen for numerical calculation and analysis in this study.

The numerical results for the transient DSCF are shown in Figs. 12, 13, 14, 15. Notice that, under the same conditions, the distribution of the transient DSCF was approximately equal to that of the steady-state DSCF, with minimum and maximum DSCF values occurring at both ends of the major and minor axes. The distribution of the transient DSCF always appeared in the stress concentration areas, which was mainly in the ranges of η = π/8–7π/8 and 9π/8–15π/8. This phenomenon was the most significant difference between the transient and steady-state responses. At ξ = 0.2, only the DSCF with ωp = 2500 is symmetrically distributed along the elliptical major axis. In the case of ξ = 1.5, only the DSCF with ωp = 800 and 2500 were symmetrically distributed along the elliptical major axis. The DSCF was not symmetrically distributed along the elliptical minor axis, which indicates that the spatial distribution of the DSCF between the front and back-wave surfaces was different. In addition, only for the high-frequency incident wave and when the shape of the inclusion approached that of a circle did the distribution of the DSCF exhibit six peak stress areas, which is consistent with the steady-state response. However, as the distribution and properties of the stress peak areas changed, all stress peak areas under transient incidence were stress concentration areas, mainly occurring near η = π/4, π/2, 3π/4, 5π/4, 3π/2, and 7π/4. Under the same parameter conditions, lower values of ωp and β led to a larger DSCF value, and the value of the transient DSCF was greater than that of the steady-state DSCF, and it was generally greater by a factor of 2–3. For ωp = 100 and β = 0.1µ2/J in the two cases, the maximum DSCF values were 2.3711, 3.5281, 2.9536, and 4.726, respectively. This phenomenon demonstrates that a transient low-frequency incidence and weak interface connections are more likely to result in structural failure. Figure 16 reveals that the distributions of the DSCF in the two cases were approximately the same under the same parameter conditions. However, the value of the DSCF in case 2 was greater than that in case 1, which indicates that, for the inclusion that was softer than the surrounding rock, the dynamic stress concentration was more significant, and structural failure was more likely to occur.

Fig. 12
figure 12

The distribution of the transient DSCF with ξ = 0.2 in case 1

Full size image
Fig. 13
figure 13

The distribution of the transient DSCF with ξ = 1.5 in case 1

Full size image
Fig. 14
figure 14

The distribution of the transient DSCF with ξ = 0.2 in case 2

Full size image
Fig. 15
figure 15

The distribution of the transient DSCF with ξ = 1.5 in case 2

Full size image
Fig. 16
figure 16

The distribution of the transient DSCF in different cases

Full size image

5 Simulation verification results

The numerical simulation is an effective verification method for the scattering process in the rock. In this study, we validate the numerical results by simulation using LS-DYNA software. The model was initially constructed as a 27 × 8 × 10 m cube. The elliptical major and minor axes were constructed to be 2 and 0.4 m, and some planar areas in the model were selected and loaded with transient disturbances along the z-axis. Through this loading mode, an SH-wave propagating along the x-axis direction was generated, simulating the scattering process around the elliptical inclusion subjected to the transient SH wave. The keyword of “CONTACT_AUTOMATIC_SURFACE_TO_SURFACE” defined the boundary between the elliptical inclusion and the surrounding rock, which indicated continuous stress and discontinuous displacement at the interface. The loading waveform was a Ricker wavelet with ωp = 2500, and the peak stress was 60 MPa.

The numerical model and transient loading curves are shown in Fig. 17. To ensure that the propagation waveform was consistent with the Ricker wavelet, the displacements in the x- and y- directions of the elements from the unloaded part were constrained. Subsequently, a non-reflecting boundary was set on the surface of the model, excluding the plane where the loading face was located, thereby avoiding the influence of the reflected wave on the scattering process. The surrounding rock and elliptical inclusion were defined as linear elastic materials. By using the relationship between the wave velocity (cs) and basic mechanical parameters according to the parameter setting of case 2, the following material parameters were determined: ρ1 = ρ2 = 2700 kg/cm3, υ1 = υ2 = 0.25, E1 = 32.67GPa, and E2 = 8.1675GPa.

Fig. 17
figure 17

Numerical model and transient loading curve

Full size image

Figure 18 shows the verification of the theoretical results and numerical simulations. The simulation results demonstrate that the DSCF always exhibited minimum and maximum values at both ends of the elliptical major and minor axes under a transient disturbance and that the stress concentration area was mainly distributed in the ranges of η = π/8–7π/8 and 9π/8–15π/8, which is consistent with the results of theoretical calculations. Consequently, the simulation results verified the accuracy of the theoretical calculation, which revealed that the theoretical derivation of this study was effective. The size of the numerical model elements has a significant influence on the numerical simulation results. The greater the number of elements, the closer the numerical simulation results are to the theoretical calculation results, and the computation of the numerical simulation is correspondingly larger. In this study, the number of elements on a plane was 3832 and their size was 0.25 × 0.25; the calculation results were almost the same as those for an element size of 0.125 × 0.125. Therefore, elements with a size of 0.25 × 0.25 were selected for numerical simulation to minimize the computational time as much as possible under the condition of ensuring the accuracy of the numerical simulation results. In addition, the shape of the element affects the results of the numerical simulation. The elliptical boundary of the inclusion caused the shape of the elements not to be all quadrilateral with equal area, therefore, even if the appropriate element size was chosen, the numerical simulation results and the theoretical calculation results deviated from each other.

Fig. 18
figure 18

The verification of the theoretical results and numerical simulations

Full size image

6 Discussion

In this study, a model of an underground elliptical inclusion with imperfect interfaces subjected to transient loads was investigated in detail. The distribution of the transient DSCF near the elliptical inclusion was determined, and the influence of the wave number (k), radial coordinate (ξ), stiffness parameter (β), and difference in material properties between the medium and inclusion on DSCF was analyzed.

There were two important features of the model in this study: transient wave incidence and imperfect interfaces. In practical engineering, a dynamic disturbance is a non-periodic transient incidence, having a limited action time. Previous studies have mainly focused on steady-state responses. Our numerical results demonstrate that the steady-state and transient responses of elliptical inclusions differ and that the dynamic stress concentration caused by transient disturbance is more obvious and the structural failure likelihood of the surrounding rock is greater. Moreover, the interface between the inclusion and surrounding rock is not always perfect, which influences the propagation of the stress wave and boundary conditions. Consequently, the imperfect interface was represented by the spring model. This study serves as a foundation for the development and design of mining backfill bodies, underground construction, and other underground space projects and thus will prove valuable in the field of practical engineering.

Compared with the complex function method based on conformal transformation (Liu et al. 1982; Zhang et al. 2016; Yang et al. 2020; Sun et al. 2021), the Mathieu function is more convenient for handling elliptic boundary problems, which prevents errors from conformal transformations and difficult boundary mapping. Additionally, the mathematical form is simpler. The semi-analytical solution determined by truncating Eq. (20) is more precise than the numerical solution obtained using the complex function method. In this study, to ensure the correctness of the derivation, the numerical results were verified in terms of theory and numerical simulation. The elliptical inclusion model with imperfect interfaces approached the circular cavity model and the same continuum model by controlling the parameters, and the theoretical results were consistent with those from previous studies. The spatial distribution and maximum value of DSCF from the numerical simulation were in good agreement with the theoretical results, which was significant for the preservation of the underground structure.

However, only the dynamic response of the incidence angle θ = 0 can be determined, because the number of boundary conditions is less than that of undetermined coefficients when incidence angles θ is not equal to 0. Due to the Mathieu function having no primitive function, the transient response was difficult to calculate by definite integrals. Therefore, the trapezoidal integral was used for the Fourier transform, which significantly increased the computation. The truncation term number N of the Mathieu function affects the accuracy of the numerical solution. The error range of the Mathieu function was within 0.01% by comparing the sum of 12 and 16 terms. Thus, the value of N is set to 12 for numerical calculations in this study. In addition, the β in the numerical simulation cannot be set directly, which is determined by the basic parameters of the elliptical inclusion and surrounding rock. It can only be obtained using stress and displacement calculation after numerical simulation.

7 Conclusions

In this study, the theoretical solutions of an elliptical inclusion with imperfect interfaces under plane SH-wave incidence were determined by using the wave function expansion method and Fourier transform. The theoretical solution was verified by numerical simulation using LS-DYNA software, and the calculation results were provided. The wave number, radial coordinate, stiffness parameter, and difference in material properties, all of which influenced the spatial distribution and value of DSCF for the elliptical inclusion were analyzed. The following conclusions were drawn reached:

  1. 1.

    The maximum DSCF always appeared at both ends of the elliptical minor axis, and the transient DSCF was generally a factor of 2–3 greater than the steady-state DSCF. Under the same parameter conditions, lower ωp and β led to a larger DSCF. Therefore, strengthening the interface between the upper and lower parts of underground construction can effectively prevent structural failure caused by low-frequency seismic waves.

  2. 2.

    Changes in k and ξ led to the variation in the DSCF value and spatial distribution, but changes in β resulted only in a variation in the DSCF value. Because k and ξ directly affect the number of stress peaks in the elliptical inclusion and β only affects the propagation of the stress wave, the latter did not affect the number of stress peaks in the elliptical inclusion.

  3. 3.

    The DSCF exhibited high sensitivity to variations in β in the range of 0–5µ2/J. The sensitivity of the DSCF to the variation in β diminished when β was in the range of 5µ2/J –100µ2/J. For β > 100µ2/J, the imperfect interface approached the perfect interface.

  4. 4.

    The difference in the material properties between the medium and inclusion significantly affected the variation characteristics of the DSCF with k and ξ, and under the same parameter conditions, the value of the DSCF in case 2 was greater than that in case 1. The surrounding rock is more likely to experience structural failure when the inclusion is softer than the surrounding rock.

  5. 5.

    Because the reduction in the effective incident area led to the weakening of the scattering, the spatial distribution of the DSCF exhibited multiple stress peak areas under high-wave-number incidence only when the ellipse approached a circle.