1 Introduction

Rock discontinuities are a key factor in controlling rock mass stability (Du et al. 2022b; Hao et al. 2022; Wang et al. 2020a, b). The dominant properties of discontinuities play an important role in the analysis of the deformations and strengths of rock masses (Du et al. 2022a; Hu et al. 2022). The distribution of discontinuities is complex and random after long-term and uncertain geological activity (Wang and Goh 2021a, b; Yang et al. 2022). Clustering analysis can group random discontinuities into several dominant sets in a specific geological range. The dominant properties of discontinuities are determined to further evaluate the rock mass stability. Therefore, the clustering analysis of rock discontinuities is fundamental for stability evaluation in rock engineering.

Rock discontinuities in the same set have similar properties because they have almost identical tectonic periods and formation. Generally, two methods are considered to identify discontinuity sets in previous studies: clustering discontinuities according to the orientation and considering several discontinuity properties, including the orientation. In geotechnical investigations of dam foundations, tunnels, and slopes, the discontinuity orientation (dip direction and dip) is not the only factor that affects stability. For example, open and closed discontinuities with similar orientations have very different effects on seepage rates and stability. Therefore, a clustering method considering multiple properties of rock discontinuities is essential to identify discontinuity sets, and it is more applicable in engineering practice.

Conventional methods to group rock discontinuities are graphic methods, including stereographic plot projections of poles, rose diagrams, and equal-density graphs (Cui and Yan 2020a; Xu et al. 2013a, b). Although these methods are intuitive and concise, the grouping results are highly subjective due to researcher bias and experience differences. When the discontinuities are dispersed, the graphic methods cannot be used specifically to group them. To solve these problems, clustering methods have been developed to automatically identify rock discontinuity sets. Clustering analysis is a statistical method to study classification problems that aims to obtain sets, so that objects in the same set have significant similarities and objects in different sets have great dissimilarity. Clustering analysis plays a vital role in data mining, pattern recognition, information retrieval, microbiology analysis, and machine learning (Ye 2016). Shanley and Mahtab (1976) first applied the clustering method to group rock discontinuities. Afterwards, several different clustering methods were developed, including the K-means clustering method (Tokhmechi et al. 2011; Zhou and Maerz 2002), fuzzy C-means (FCM) clustering method (Hammah and Curran 1998, 1999, 2000), spectral clustering method (Jimenez 2008; Jimenez and Sitar 2006), affinity propagation (AP) method (Liu et al. 2017), and netting method (Hou et al. 2020). Among them, the K-means clustering method and FCM are sensitive to the selection of the initial clustering centers and easily trapped in local optima. To solve this problem, many researchers have continuously explored and proposed corresponding solutions to find the optimal initial clustering center (Cui and Yan 2020a, 2020b; Li et al. 2014; Ma et al. 2014; Song et al. 2017; Xu et al. 2013a, b). Furthermore, for the spectral clustering method, determining a proper similarity matrix and reasonable scale parameters is complex, and this method requires a large amount of calculation. For the affinity propagation algorithm, the initial parameters require a trial calculation to find the ideal clustering number.

The above methods take only the orientation as a clustering factor and ignore the importance of other discontinuity properties. Several studies (Sirat and Talbot 2001; Tokhmechi et al. 2011; Wang et al. 2020a, b; Zhou and Maerz 2002) have highlighted the shortcomings of these methods and the necessity of considering multiple properties. To cluster rock discontinuities with multiple properties, Zhou and Maerz (2002) used four methods to obtain discontinuity sets based on orientation, spacing, and roughness: the nearest neighbor method, K-means method, FCM, and vector quantization method. Tokhmechi et al. (2009; 2008; 2011) considered orientation, infilling material, and infilling percentage as clustering factors to repeatedly perform clustering analysis; these studies investigated the shortcomings of several clustering methods and obtained different results considering various discontinuity properties. Song et al. (2015a, b), Xu et al. (2013a, b), and Ding et al. (2018) considered the same properties (orientation, trace length, aperture, and surface morphology) to cluster discontinuities; the artificial bee colony algorithm, mutative scale chaos optimization algorithm, and improved iterative self-organizational data analysis algorithm were used as clustering methods. Moreover, Song et al. (2015a, b) added a property of the infilling materials as a factor to cluster discontinuities based on a quantum particle swarm optimization algorithm. These studies performed beneficial explorations to cluster discontinuities with multiple properties. However, the influences of property weights are ignored in these methods; i.e., they determine similarity measures without considering the weights. This shortcoming is seriously neglected because different properties affect rock mass stability differently. For example, the dip direction and dip determine the failure direction of the rock mass; the trace length, spacing and aperture affect the completeness of the rock mass; the roughness, rock strength, water permeability, and infilling affect the shear strength of discontinuities. Furthermore, the discontinuity development in different geological environments is random, which results in various differences in discontinuity properties. These differences in the data structure are neglected when the property weights are not considered. Therefore, reasonable property weights should be required to obtain similar clustering results to those in engineering practice.

This paper is organized as follows. The next section proposes the improved netting algorithm, where the data representation, methodology, and general steps are described in detail. Section 3 develops a comparative analysis and a case study to show the reliability and excellent performance of the new method. In Sect. 4, the selection of the confidence level and minimum number of samples in a dominant set are discussed, and suggestions are made. Finally, the conclusions are drawn in Sect. 5.

2 The improved netting algorithm

The netting algorithm is an unsupervised clustering algorithm based on similarity. The similarity matrix is obtained by calculating the similarity among all data points. In the matrix network, each data point is considered a node, and the nodes are connected through longitude and latitude lines to perform clustering. This method has performed well in clustering discontinuity orientations (Hou et al. 2020). However, the clustering analysis of multiple discontinuity properties has not been developed. Therefore, this paper develops an improved netting algorithm to cluster discontinuities with multiple properties and obtain dominant discontinuity sets.

2.1 Data representation

Up to 10 properties can be recorded to describe the rock discontinuity characteristics on site (Tokhmechi et al. 2011). The stability evaluation of rock masses is more realistic when more data from sites are considered (Wang and Goh 2021a, b). This study selected 10 discontinuity parameters that can be easily measured on site for the clustering analysis (see Table 1), which has great convenience in engineering applications. Meanwhile, these properties have been used in previous studies and are highly representative (Ding et al. 2018; Song et al. 2015a, b; Tokhmechi et al. 2009, 2008, 2011; Xu et al. 2013a, b; Zhou and Maerz 2002). Based on these properties, the spatial distribution, geometric shape, and physical and mechanical properties of rock discontinuities were comprehensively considered.

Table 1 Ten rock discontinuity properties
Full size table

The sizes of discontinuities play a crucial role in determining the damage degree of the rock mass. Large-scale discontinuities, which range in size from hundreds to thousands of meters, significantly influence the rock mass stability. These discontinuities are not required for clustering analysis because they are uncommon, and they can be directly observed on site. Therefore, only a statistical analysis is conducted for rock discontinuities, such as rock joints, cleavages, minor faults, and minor stratifications, which range from a few millimeters to tens of meters. The discontinuities have random distributions and complex geometric and mechanical characteristics; i.e., there are inherent uncertainties in these calculations. Therefore, clustering analysis should be performed with these discontinuities to determine the dominant discontinuity sets.

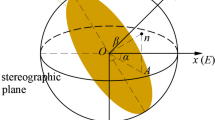
When a discontinuity orientation is mathematically analyzed, it is usually assumed to be a pole using the equal-angle lower hemisphere projection method (Lisle and Leyshon 1996). As shown in Fig. 1, pole A' is the point where the downward unit vector normal to the discontinuity plane intersects with a reference sphere of unit radius. The positive x1-axis and positive x2-axis represent due north (N) and due east (E), respectively. The positive x3-axis is vertically downward. Furthermore, the dip direction α is the angle of clockwise rotation from the due north direction to the projection of the unit normal vector on the horizontal plane (0° ≤ α ≤ 360°). The dip β is the angle between the unit normal vector and the x3-axis (0° ≤ β ≤ 90°). The unit normal vector of a discontinuity can be expressed as V = {x1, x2, x3}. Therefore, the discontinuity orientation is expressed in spherical space, and each point on the hemispherical surface corresponds to an orientation.

$$\left. \begin{gathered} x_{{1}} = \cos \alpha \cdot \sin \beta \hfill \\ x_{{2}} = \sin \alpha \cdot \sin \beta \hfill \\ x_{{3}} = \cos \beta \hfill \\ \end{gathered} \right\}$$
(1)
Fig. 1
figure 1

Representation of a discontinuity orientation (modified from Liu (2017))

Full size image

The quantitative values of orientations, trace length t, spacing s, aperture a, infilling percentage p, roughness r, and rock strength h of rock discontinuity can be measured at the engineering site. Table 2 uses semiquantitative coding to describe the properties of the infilling material f and water permeability w. In summary, a rock discontinuity can be expressed as A = {α, β, t, s, a, f, p, r, w, h}.

Table 2 Semiquantitative coding to describe the properties of infilling material and water permeability
Full size table

2.2 Methodology

Similarity measures (distance metrics) can calculate the distance between two discontinuities according to specific metric criteria. The selection of similarity measures is crucial for clustering rock discontinuities. In fuzzy mathematics, the index to measure the similarity between classified objects is called rij, where i = 1, 2,…, n; j = 1, 2, …, n; and n is the total number of classified objects. This index indicates that there is less similarity between data points if the distance between them is smaller. Common similarity measures include the Euclidean distance, maximum-minimum method, correlation coefficient method, and included angle cosine method (Liang and Cao 2007).

A particular issue has been noted for similarity measures of the orientation. When a pair of discontinuities have steeply inclined angles and the dip directions differ by approximately 180°, the two discontinuities should be classified into the same group. For example, in Fig. 2, if the Euclidean distance or spherical distance between the discontinuity unit normal vectors is adopted as the similarity measure, the distance A1A2 is much larger, and the two discontinuities may be mistaken as belonging to two different sets (Liu et al. 2017). To address this problem, the sine-squared value of the acute angle between discontinuity unit normal vectors is chosen as the similarity measure (Hammah and Curran 1999). For any two unit normal vectors Vi = {xi1, xi2, xi3} and Vj = {xj1, xj2, xj3}, the similarity measure can be computed as

$$r_{ij}^{{\text{o}}} = \sin^{2} \theta = 1 - ({\varvec{V}}_{i} \cdot {\varvec{V}}_{j} )^{2}$$
(2)

where \(r_{ij}^{{\text{o}}}\) is the similarity of orientation; Vi…Vj is the dot product of the two vectors; θ is the acute angle between two unit normal vectors Vi and Vj, as follows:

$$\theta = \arccos \left| {{\varvec{V}}_{i} \cdot {\varvec{V}}_{j} } \right|$$
(3)
Fig. 2
figure 2

Spherical projection of two rock discontinuities with steeply inclined angles and dip directions differing by approximately 180°

Full size image

In this study, the rock discontinuity properties other than orientation are scalars. The value ranges and units of these properties are also different. Therefore, these properties must be normalized before clustering analysis to eliminate the influences of each dimension and adjust the property values to fit within a range. This step is very convenient for subsequent calculations. Normalization formulas can be divided into beneficial and nonbeneficial types (Ai et al. 2019). Beneficial means that a greater property value is better, while nonbeneficial means that a smaller the property value is better.

In the case of a beneficial property, the following formula applies:

$$y_{ik} = \frac{{x_{ik} - x_{\min }^{k} }}{{x_{\max }^{k} - x_{\min }^{k} }},\;k = \, 1, \, 2, \ldots ,m$$
(4)

In the case of a nonbeneficial property, the following formula applies:

$$y_{ik} = \frac{{x_{\max }^{k} - x_{ik} }}{{x_{\max }^{k} - x_{\min }^{k} }},\;k = 1, \, 2, \ldots ,m$$
(5)

where xik is the kth property value of the ith discontinuity; yik is the kth property value of the ith discontinuity after normalization; m is the total number of discontinuity properties; \(x_{{{\text{min}}}}^{k}\) and \(x_{{{\text{max}}}}^{k}\) are the minimum and maximum values of the kth property, respectively.

Assuming the same importance for each discontinuity property in the similarity measures is unreasonable. Table 1 shows different effects of various properties on the rock mass stability. Meanwhile, the preprocessing step of normalization may weaken the differences among various properties. Therefore, a weighted Euclidean distance (Hammah and Curran 1999) is introduced to calculate the similarity for the discontinuity properties other than orientation, including the trace length, spacing, aperture, infilling material, infilling percentage, roughness, water permeability, and rock strength. The equation is expressed as

$$d^{2} \left( {y_{ik} ,y_{jk} } \right) = \omega_{k} \cdot \left( {y_{ik} - y_{jk} } \right)^{{\text{T}}} \left( {y_{ik} - y_{{_{jk} }} } \right) = \omega_{k} \cdot \left\| {y_{ik} - y_{{_{jk} }} } \right\|^{2} = \omega_{k} \cdot \left( {y_{ik} - y_{jk} } \right)^{2}$$
(6)

where yjk is the kth property value of the jth discontinuity after normalization and ωk is the weight coefficient of the kth property.

The object weights are the relative importance of each influencing factor in the evaluation process. The rationality of the weights directly affects the accuracy and effectiveness of the clustering results. Various methods have been developed to determine the weighting coefficients of objects in multiple-attribute decision making (MADM), and these methods are mainly divided into subjective and objective weighting methods. Subjective weighting methods are qualitative methods that directly yield weights according to the experience of the decision makers. These mainly include the expert survey method (Shands and Levary 1986), binomial coefficient method (Liu and Wu 2017), analytic hierarchy process (AHP) (Ataei et al. 2012), and order relationship analysis (G1) (Xie et al. 2010; Zhang et al. 2020). Objective weighting methods calculate the weights based on an established mathematical model. These methods mainly include the principal component analysis method (PCA) (Liu et al. 2020), entropy weights method (EWM) (Kumar et al. 2021), linear programming method (Li and Yu 1996), factor analysis method (Gaskin and Happell 2014), and technique for order preference by similarity to the ideal solution (TOPSIS) (Rao 2008). These two weighting methods have advantages and disadvantages in the clustering analysis of rock discontinuities. Subjective weighting methods can determine the relative importance of properties according to the experience of decision makers, which will be consistent with common understanding. However, these methods have great subjectivity, and their accuracy and reliability are somewhat poor. Objective weighting methods are advantageous because the property weights are obtained based on mathematical models. However, these methods are greatly affected by data characteristics and neglect understanding of the actual situation, which results in deviations between the weight values and the actual situation. To reflect the intuitive understanding of discontinuity properties and the regularity of objective survey data, the G1 method (a subjective weighting method) and EWM (an objective weighting method) are used to obtain the subjective weights and objective weights, respectively. Then, a combined weighting model is established to determine the weights of the discontinuity properties based on the additive synthesis method (Ai et al. 2019; Kumar et al. 2021).

The G1 method addresses the shortcomings of the AHP, such as massive and complex calculations and the need for consistency tests. This method obtains weights by determining the importance order of each property and relative importance of adjacent properties. The main steps are as follows.

  1. (1)

    The relative importance and order of each property are determined as follows:

    $$K_{1} > K_{2} > \ldots > K_{k}$$
    (7)

    where Kk is the kth discontinuity property and “ > ” implies that the property on the left is more important than that on the right Table 3.

    Table 3 Quantitative table to evaluate the relative importance of rock discontinuity properties
    Full size table
  2. (2)

    The relative importance of the sorted properties is assigned a quantitative value according to Table 3. The relative importance ratio is computed as

    $$I_{c} = \frac{{\omega_{c - 1}^{{\text{s}}} }}{{\omega_{c}^{{\text{s}}} }},\;c = 2, \, 3,,m$$
    (8)

    where Ic is the relative importance ratio of the (c-1)th property to the cth property and ωsc-1 and ωsc are the subjective weights of the (c − 1)th property and cth property based on the G1 method, respectively.

  3. (3)

    The subjective weights of the discontinuity properties based on the G1 method are calculated as

    $$\omega_{c}^{{\text{s}}} = \left( {1 + \sum\limits_{c = 2}^{m} {\prod\limits_{k = c}^{m} {I_{k} } } } \right)^{ - 1}$$
    (9)
    $$\omega_{c - 1}^{{\text{s}}} = I_{c} \cdot \omega_{c}^{{\text{s}}}$$
    (10)

The EWM is an objective weighting method that does not include any preferences of decision makers. Probability theory is used to compute uncertain information (entropy). In addition, this method can enhance or weaken the roles of properties in decision making according to the diversity of data, and the index information with a higher weight is more valuable than that with a lower weight. The main steps are as follows.

  1. (1)

    Decision matrix X is constructed by Eq. (11). Each row in the matrix represents a rock discontinuity, and each column represents a property of rock discontinuity.

    $${\mathbf{X}} = \left[ {\begin{array}{*{20}l} {x_{{11}} } \hfill & {x_{{12}} } \hfill & \cdots \hfill & {x_{{1k}} } \hfill & \cdots \hfill & {x_{{1m}} } \hfill \\ {x_{{21}} } \hfill & {x_{{22}} } \hfill & \cdots \hfill & {x_{{2k}} } \hfill & \cdots \hfill & {x_{{2m}} } \hfill \\ \vdots \hfill & \vdots \hfill & \vdots \hfill & \vdots \hfill & \vdots \hfill & \vdots \hfill \\ {x_{{i1}} } \hfill & {x_{{i2}} } \hfill & \cdots \hfill & {x_{{ik}} } \hfill & \cdots \hfill & {x_{{im}} } \hfill \\ \vdots \hfill & \vdots \hfill & \vdots \hfill & \vdots \hfill & \ddots \hfill & \vdots \hfill \\ {x_{{n1}} } \hfill & {x_{{n2}} } \hfill & \cdots \hfill & {x_{{nk}} } \hfill & \cdots \hfill & {{\text{ }}x_{{nm}} } \hfill \\ \end{array} } \right]$$
    (11)
  2. (2)

    Normalization is performed by Eqs. (4) and (5) to obtain matrix Y.

    $${\mathbf{Y}} = \left[ {\begin{array}{*{20}l} {y_{{11}} } \hfill & {y_{{12}} } \hfill & \cdots \hfill & {y_{{1k}} } \hfill & \cdots \hfill & {y_{{1m}} } \hfill \\ {y_{{21}} } \hfill & {y_{{22}} } \hfill & \cdots \hfill & {y_{{2k}} } \hfill & \cdots \hfill & {y_{{2m}} } \hfill \\ \vdots \hfill & \vdots \hfill & \vdots \hfill & \vdots \hfill & \vdots \hfill & \vdots \hfill \\ {y_{{i1}} } \hfill & {y_{{i2}} } \hfill & \cdots \hfill & {y_{{ik}} } \hfill & \cdots \hfill & {y_{{im}} } \hfill \\ \vdots \hfill & \vdots \hfill & \vdots \hfill & \vdots \hfill & \ddots \hfill & \vdots \hfill \\ {y_{{n1}} } \hfill & {{\text{ }}y_{{n2}} } \hfill & \cdots \hfill & {y_{{nk}} } \hfill & \cdots \hfill & {y_{{nm}} } \hfill \\ \end{array} } \right]$$
    (12)
  3. (3)

    The entropy of the kth discontinuity property is calculated as

    $$E_{k} = - \frac{1}{\ln n}\sum\limits_{i = 1}^{n} {\left( {p_{ik} \ln p_{ik} } \right)}$$
    (13)
    $$p_{ik} = \frac{{1 + y_{ik} }}{{\sum\limits_{i = 1}^{n} {\left( {1 + y_{ik} } \right)} }}$$
    (14)

where Ek is the entropy of the kth discontinuity property and pik is the probability of yik in the kth discontinuity property.

  1. (4)

    Based on the entropy of the kth discontinuity property, the entropy weight of the kth discontinuity property is calculated as

    $$\omega_{k}^{{\text{o}}} = \frac{{\left| {1 - E_{k} } \right|}}{{\sum\limits_{k = 1}^{m} {\left| {1 - E_{k} } \right|} }}$$
    (15)

    where \(\omega_{k}^{{\text{o}}}\) is the objective weight of the kth property based on the EWM.

The additive synthesis method is adopted to combine the subjective weights and objective weights. The equation can be expressed as

$$\left. \begin{gathered} \omega_{k} = b \cdot \omega_{k}^{{\text{s}}} + d \cdot \omega_{k}^{{\text{o}}} \hfill \\ b + d = 1 \hfill \\ \end{gathered} \right\}$$
(16)

where b is the subjective weight preference coefficient and d is the objective weight preference coefficient.

Determination of the preference coefficients is difficult because of the complexity and uncertainty of the decision objects. An optimization model of the combination weighting method was introduced to obtain the optimal solutions for preference coefficients (Ai et al. 2019). This model is evaluated based on the minimum sum of the squared deviations between subjective and objective weights and the maximum comprehensive evaluation value of the decision scheme. The optimization model is synthesized as follows.

$$\begin{aligned} & \max Q = \frac{1}{n} \cdot \sum\limits_{i = 1}^{n} {\sum\limits_{k = 1}^{m} {y_{ik} \cdot \left( {b \cdot \omega_{k}^{{\text{s}}} + d \cdot \omega_{k}^{{\text{o}}} } \right)} } - \sum\limits_{k = 1}^{m} {\left( {b \cdot \omega_{k}^{{\text{s}}} - d \cdot \omega_{k}^{{\text{o}}} } \right)^{2} } \\ & S.t.\quad b + d = 1;\;b \ge 0;\;d \ge 0 \\ \end{aligned}$$
(17)

In the new method, similarity matrix R is established by Eqs. (2) and (6) and expressed as

$${\mathbf{R}} = \left[ {\begin{array}{*{20}c} {r_{11} } & {r_{12} } & \cdots & {r_{1n} } \\ {r_{21} } & { \, r_{22} } & \cdots & { \, r_{2n} } \\ \vdots & \vdots & \ddots & \vdots \\ {r_{n1} } & {r_{n2} } & \cdots & { \, r_{nn} } \\ \end{array} } \right]$$
(18)

The similarity matrix R has self-reflexivity (rii = 1) and symmetry (rij = rji), but it does not have transferability (R2 ∈ R). Traditional fuzzy clustering methods require fuzzy similarity matrices R to obey a fuzzy equivalence relation, i.e., self-reflexivity, symmetry, and transferability. Therefore, matrix self-multiplication is usually employed to obtain a fuzzy equivalence relation based on the transitive closure method. However, this method has some shortcomings, such as a large workload, complex computation, and multiple matrix self-multiplication.

To solve the above problems, the netting method was proposed and first applied to the fuzzy clustering analysis (Zhao 1980). Wang et al. (2011) proposed a netting method to cluster data in an intuitionistic fuzzy environment. Ye et al. (2016) proposed a netting method for clustering-simplified neutrosophic information. Hou et al. (2020) first clustered orientation data of rock discontinuities based on a netting algorithm. These studies have some applications and extensions to the netting method, but clustering multiple properties of rock discontinuities has not been developed.

The netting method is a clustering analysis method developed from fuzzy mathematics. Similarity matrix R can adequately represent the distance relationship among multiple properties of rock discontinuities. In addition, this method has remarkable advantages that make it straightforward and convenient to use. Therefore, the netting method is adopted to identify rock discontinuities with multiple properties automatically. The core idea of the method is described as follows.

First, similarity matrix R is restructured. All elements above the diagonal line are deleted because of symmetry. The elements on the diagonal line are replaced with the classified object numbers Oi. Then, by choosing different confidence levels λ, a λ-cutting matrix Rλ is constructed as

$${\mathbf{R}}_{\lambda } = \left[ {\begin{array}{*{20}c} {O_{{1}} } & {} & {} & {} \\ {r^{\lambda }_{{{21}}} } & {O_{{2}} } & {} & {} \\ { \vdots \, } & { \, \vdots } & \ddots & {} \\ {r^{\lambda }_{{n{1}}} \, } & {r^{\lambda }_{{n{2}}} } & { \, \cdots } & {O_{n} } \\ \end{array} } \right]$$
(19)

where

$$r^{\lambda }_{ij} = \left\{ \begin{gathered} 1 \, (r_{ij} \le \lambda ) \hfill \\ 0 (r_{ij} > \lambda ) \hfill \\ \end{gathered} \right.$$
(20)

Furthermore, λ-cutting matrix Rλ is restructured. Below the diagonal, all “1” entries are replaced by the node number “*”, and all “0” entries in Rλ are ignored.

Finally, the node “*” determines the longitude and latitude lines on the diagonal line, and the samples connected by the same node become a group. The clustering process is shown in Fig. 3.

Fig. 3
figure 3

Clustering process based on the netting algorithm

Full size image

The clustering algorithm is an evaluation process that does not require prior experience. Its key issues lie in determining reasonable sets and evaluating the clustering result validity. The ideal number of sets is generally determined to be 2 to 8 because the use of too many sets is not convenient for engineering applications. The clustering validity index is required to evaluate the grouping result. Many scholars have proposed different clustering validity indices (Capitaine and Frelicot 2011; Kim et al. 2004; Rezaee et al. 1998; Wu and Yang 2005; Xie and Beni 1991; Zhang et al. 2008). Among them, the VXB index proposed by Xie and Beni (1991) can well evaluate the quality of clustering results and determine a reasonable number of sets. The index combines the geometric characteristics of data and fuzzy membership degree. Based on the VXB index, compactness is the sum of the distances from all sample data to the cluster centers, and separation is the minimum distance between any pair of cluster centers. Suppose that n discontinuity samples are clustered into g sets; this is expressed as

$$V_{{X{\text{B}}}} { = }\frac{{\sum\limits_{o = 1}^{g} {\sum\limits_{j = 1}^{n} {u_{oj}^{e} \left\| {x_{j} - v_{o} } \right\|^{{2}} } } }}{{n\;\min_{z,o} \left\| {v_{z} - v_{o} } \right\|^{{2}} }}$$
(21)
$$u_{oj} = \frac{{\left\| {x_{j} - v_{o} } \right\|^{{ - \frac{2}{e - 1}}} }}{{\sum\limits_{o = 1}^{g} {\left\| {x_{j} - v_{o} } \right\|^{{ - \frac{2}{e - 1}}} } }}$$
(22)

where 1 ≤ o ≤ g, 1 ≤ z ≤ g, g is the total number of sets, and \(\left\| \cdot \right\|^{{2}}\) is the criterion to measure the distance in the classification space. For the orientation, the sine-squared measurement is adopted to calculate the similarity. For properties other than the orientation, the Euclidean distance is used to calculate the similarity. uoj is the fuzzy membership degree, which denotes the degree to which xj belongs to the cluster center vo. e is the fuzzy weighted index. The range of e is obtained from the clustering effectiveness test of Capitaine and Frelicot (2011); the range is [1.5, 2.5]; generally, e = 2.

For a series of sets, a smaller VXB index indicates a better clustering effect. The ideal clustering number is determined by the minimum value of the VXB index.

2.3 General steps

To quickly and accurately cluster rock discontinuities with multiple properties, a clustering method based on an improved netting algorithm is proposed, and its main steps are as follows.

  1. (1)

    To obtain sufficient rock discontinuity data, as many systematic measurements as possible should be taken in the field.

  2. (2)

    The orientation is transformed into polar coordinates by Eq. (1), and the unit normal vector is expressed in three-dimensional Cartesian coordinates. The properties of rock discontinuities, including the trace length, spacing, aperture, infilling material, infilling percentage, roughness, water permeability, and rock strength, are normalized by Eqs. (4) and (5) to eliminate the influence of the dimensions on subsequent calculations.

  3. (3)

    The subjective weights are calculated based on the G1 method, and the objective weights are calculated based on EWM. The subjective and objective preference coefficients are obtained based on the optimization model of Eq. (17). Then, the combined weights of the discontinuity properties are determined using the additive synthesis method.

  4. (4)

    The similarities between rock discontinuities are calculated by Eqs. (2) and (6), and a similarity matrix R is established based on the calculation results.

  5. (5)

    Similarity matrix R is restructured. All elements above the diagonal line are deleted because of symmetry. The elements on the diagonal line are replaced with the classified object numbers Oi.

  6. (6)

    Based on Eq. (19), the λ-cutting matrix Rλ is constructed by choosing a confidence level λ.

  7. (7)

    The λ-cutting matrix Rλ is restructured. All “1” entries are replaced by the node number “*”, and all “0” entries in Rλ are ignored.

  8. (8)

    Clustering grouping is performed in Rλ. The node “*” determines the longitude line and latitude line on the diagonal line, and the samples connected by the same node become a group.

  9. (9)

    According to the clustering results, the effectiveness evaluation index VXB is calculated. When the rationality of the results is not appropriate, steps (6)-(9) are repeated by choosing different confidence levels λ.

  10. (10)

    The dominant discontinuity sets are determined based on the clustering results.

The flowchart of the main steps for the improved netting algorithm is shown in Fig. 4.

Fig. 4
figure 4

Flowchart of the main steps for the improved netting algorithm

Full size image

3 Results

3.1 Comparison and validation

To investigate the validity of the new method, the artificial data obtained based on the Monte Carlo method (James 1980) and in situ data from the relevant literature were used. The Monte Carlo method is a conventional method to generate data that conform to a specific probability distribution, and it is widely used (Cui and Yan 2020a, 2020b; Ding et al. 2018; Gao et al. 2019; Liu et al. 2017, 2021; Wang et al. 2020a, b; Zheng et al. 2014, 2015). In this study, a data set of 268 discontinuities was obtained from an underground oil storage facility, containing only orientation data (Liu et al. 2017). Therefore, the data of the other discontinuity properties, including the trace length, spacing, aperture, infilling material, infilling percentage, roughness, water permeability, and rock strength, were generated based on the Monte Carlo method.

Although the discontinuity characteristics in a rock mass are complex and random, many statistical engineering data show that each property of rock discontinuities conforms to a specific probability distribution. The Monte Carlo method can be considered the inverse process of sampling statistics based on probability theory and statistical theory. Its basic process is as follows. (1) A domain of possible inputs is defined. (2) The data are randomly generated based on a probability distribution. (3) The results are outputted. This method can obtain the data of different discontinuity properties in a specific depth range.

Based on the Monte Carlo method, six discontinuity sets with different numbers of samples and different distributions are generated according to different probability distribution models. Among them, the orientation is measured data. The trace length, spacing, and aperture are set to a negative exponential distribution. The roughness and rock strength are set to a normal distribution. The infilling material, filling percentage, and water permeability are uniformly distributed. The numbers of data points in artificial data sets 1–5 are 73, 75, 44, 8, and 6, respectively. Additionally, 62 noisy data points are generated. To show the excellent performance of the proposed method, the property parameters of the rock discontinuities are staggered among different sets. The parameter distributions of the artificial data based on the Monte Carlo method are shown in Table 4. The pole isodensity map of the rock discontinuities is shown in Fig. 5.

Table 4 Parameter distributions of the artificial data based on the Monte Carlo method
Full size table
Fig. 5
figure 5

Pole isodensity map of the rock discontinuities

Full size image

The subjective and objective weights of the 10 discontinuity properties are determined based on the G1 method and EWM. Then, the subjective and objective preference coefficients are calculated by Eq. (17). The results show that the subjective preference coefficient b is 0.47, and the objective preference coefficient d is 0.53. Furthermore, the combined weights of the 10 discontinuity properties are calculated by Eq. (16), and the results are shown in Table 5. Based on the obtained data, the clustering results of the new method are shown in Table 6.

Table 5 Importance ranking of the rock discontinuity properties and the subjective and objective weights
Full size table
Table 6 Clustering results based on the new method (λ = 0.024)
Full size table

Table 6 shows that the clustering results are consistent with the predefined data set, which verifies the performance of the new method. Furthermore, the results are compared with those of the modified affinity propagation algorithm (Liu et al. 2017), Shanley and Mahtab method (1976), FCM, spectral clustering method (Jimenez and Sitar 2006), and K-means method based on particle swarm optimization (KPSO) (Li et al. 2014). The results of the six clustering methods are shown in Table 7 and Fig. 6.

Table 7 Clustering results of different methods for the test data
Full size table
Fig. 6
figure 6

Comparison of the clustering results for the test data: a new method; b modified affinity propagation algorithm; c Shanley and Mahtab method; d FCM; e spectral clustering method; f KPSO

Full size image

As shown in Table 7 and Fig. 6, the new method has very similar results to the other five clustering methods, which illustrates the applicability and effectiveness. Meanwhile, the initial groups and initial clustering centers do not need to be set in advance, and all data are simultaneously considered potential clustering centers. This reduces the subjectivity of human intervention and achieves global optimization. Furthermore, each dominant set obtained by the new method has fewer data points than the other clustering methods. The advantage of filtering noise data is the main reason to support this result. Although the discontinuity data measured at the site are practical, the noise data may be secondary discontinuities caused by human factors, such as vehicle vibration load and artificial blasting. These data significantly deviate from the set centers, and their dispersion is high. Therefore, the filtering of noise data does not affect the originality and integrity of the data, and they should be eliminated to improve the accuracy of the clustering results.

The VXB indices of the six clustering methods were calculated based on Eq. (21), and the results are shown in Table 8. When there are 5 clusters, the VXB indices are 0.06 for the new method, 0.10 for the Shanley and Mahtab method, and 0.09 for the modified affinity propagation algorithm, FCM, spectral clustering method, and KPSO method. The new method has a smaller VXB than the other five clustering methods. According to the validity criterion of the VXB index, a smaller index indicates better quality, and the reliability of the new method is confirmed.

Table 8 VXB index of different clustering methods
Full size table

In terms of computational efficiency, the new method has significantly lower computational complexity than the other five clustering methods because the new method has a straightforward principle and a concise clustering process. Meanwhile, the method does not need a complicated and repeated iterative process. With the increase in amount of data, the calculation times of the other five clustering methods significantly increase. The clustering results of the Shanley and Mahtab method, fuzzy FCM, and KPSO are not unique after each clustering analysis, and the ideal clustering results are obtained based on several repeated operations. In contrast, the new method has unique and repeatable results. The modified affinity propagation algorithm and spectral clustering method must set multiple parameters before running these methods. In contrast, the new method can effectively reduce the calculation quantity and save time. Therefore, the new method lays a foundation for extensive sample data clustering analysis.

In the new method, the determination of property weights significantly affects the clustering results. To investigate the effects of weights on the clustering analysis, the new method was performed without considering the weights. The results are shown in Fig. 7 and Table 9.

Fig. 7
figure 7

Spherical projection of the clustering results based on the new method without the considering weights

Full size image
Table 9 Clustering results based on the new method without considering the weights (λ = 0.18)
Full size table

Comparing Table 6 and Table 9, the dominant discontinuity sets without considering weights are similar to the results considering the weights. However, compared to Fig. 6(a), the clustering results without considering weights are confused in certain regions, such as the enlarged areas (a) and (b) in Fig. 7. These notable samples in set 3 are found in Fig. 7(b), including the following:

  • A1 = {26.20, 244.23, 16.66, 20.47, 9.79, 0.20, 65.05, 13.23, 0.41, 38.37}

  • A2 = {23.51, 239.81, 8.74, 16.20, 4.26, 0.25, 63.34, 9.80, 0.55, 39.79}

  • A3 = {27.76, 230.95, 5.53, 1.39, 5.12, 0.34, 44.75, 3.80, 0.53, 58.37}

  • A4 = {28.37, 250.18, 41.73, 10.79, 3.54, 0.31, 39.69, 13.27, 0.49, 43.27}

  • A5 = {23.78, 254.87, 31.46, 14.84, 1.19, 0.53, 20.17, 9.51, 0.42, 47.82}

Table 9 compares the property parameters of these notable samples and dominant set 3, and the orientations are similar. Other property values, such as the trace length, spacing, infilling percentage, and rock strength, have significant differences from those of dominant set 3. Among them, the largest difference is 31.84 m for the trace length, 17.26 m for the spacing, 28.23% for the infilling percentage, and 13.40 MPa for the rock strength. When the weights are not considered, these notable sample properties produce major effects, which lead to larger differences in distance measures and ultimately affect the clustering results. When the weights are considered, the importance of each discontinuity property is evaluated and the differences between different properties are neutralized, which results in more scientific clustering results. Therefore, a reasonable weight assignment to each discontinuity property is critical in the clustering analysis, and it can optimize the clustering process and make the results more reliable.

3.2 Case study

The Jingxi open-pit mine slope is located in Xinjiang Province, China, with geographical coordinates of 81° 31′ 8.58ʺ E and 44° 20′ 3.47ʺ N. Figure 8 shows the basic information of this slope. Moreover, the slope height is 115 m with 11 steps, and tuff is developed on the slope. In this paper, the data of 120 discontinuities were obtained from the field. The new method was used to identify the discontinuity sets using these data; then, the slope stability was further evaluated. The property of water permeability was not considered because no water was found on the overall slope. Figure 9 shows the statistical distribution of the field discontinuity properties, including the pole isodensity map generated by the orientation and the histogram generated by the trace length, spacing, aperture, infilling material, infilling percentage, roughness, and rock strength. Among them, the distributions of the trace length, spacing, aperture, infilling material, and infilling percentage are consistent with a negative exponential distribution; the distributions of roughness and rock strength are consistent with the normal distribution.

Fig. 8
figure 8

Basic information of the Jingxi slope, including the a location, b regional stereoscopic restructuring model, and c actual situation

Full size image
Fig. 9
figure 9

Statistical distribution of field discontinuities, including the a pole isodensity map, b histogram of trace length, c histogram of spacing, d histogram of aperture, e histogram of infilling material, f histogram of infilling percentage, g histogram of roughness, and h histogram of rock strength

Full size image

The subjective weights, objective weights, and combined weights of the field discontinuity properties are determined based on the new method, as shown in Table 10. Among them, the subjective preference coefficient b is 0.47, and the objective preference coefficient d is 0.53. Furthermore, based on the combined weights, the new method obtains the dominant discontinuity sets by selecting different confidence levels. The clustering results are shown in Fig. 10 and Table 11.

Table 10 Importance ranking of the field discontinuity properties and the subjective and objective weights
Full size table
Fig. 10
figure 10

Clustering results of field discontinuities, including the results of a 2 sets taking λ as 0.067, b 3 sets taking λ as 0.048, and c 4 sets taking λ as 0.041

Full size image
Table 11 Clustering results of the field discontinuities
Full size table

Table 12 shows the clustering validity indices of different sets for the field discontinuities. We can see that the VXB index is 0.36 for two sets, 0.26 for three sets, and 0.29 for four sets. The ideal number of discontinuity sets is 3, for which the index is minimal. Therefore, the optimal clustering result of the Jingxi open-pit mine slope is three sets, with dominant orientations of 228.40° ∠44.66°, 349.87° ∠76.12°, and 72.11° ∠67.93°. The results show that 31 noise data points are eliminated, and the rejection rate is approximately 26%.

Table 12 Clustering validity index for field discontinuities
Full size table

4 Discussion

The confidence level λ is an essential parameter in the proposed method, and its selection directly affects the clustering results. When λ gradually increases, the number of sets shows a pattern of change from more sets to fewer until they merge into a single set. Finding a λ value that can obtain optimal clustering results is a crucial and challenging issue. The determination of λ is related to the discontinuity properties and data characteristics. However, due to the complexity of engineering data, we cannot know in advance which λ value can generate the optimal cluster number. To address these issues, we give suggested ranges and selection criteria of λ. For the clustering analysis of orientation, the optimal clustering result is most likely obtained in the range 0.01–0.03. For the clustering analysis of multiple properties, the optimal clustering result is most likely obtained in the range 0.01–0.05. In addition, a technique is recommended to adaptively scan the λ value based on different engineering applications. The technique is as follows. (a) A smaller value of λ is specified to execute the algorithm, and its initial value can be set to 0.01. (b) λ is dynamically increased to obtain different clustering results, and the step increment is set to 0.005. (c) The optimal clustering number is determined according to the VXB index. When the clustering results are better represented in a specific λ interval, the results can be further improved according to the actual engineering situation or the increase in trial calculation accuracy. Furthermore, with the continuous increase in engineers’ experience, the time costs of this technique will be continuously shortened.

A distinctive advantage of the proposed method over other clustering methods is that the clustering results can effectively filter the noise data. However, the number of samples in a set should be required to satisfy the statistical requirements of a minimum number to fully characterize the nature of the dominant sets. If there are too few samples in a set, the set is not representative, and the validity of the clustering results will be questionable. Therefore, when the number of samples in a set is less than 5% of the total number of samples, these data should be eliminated to ensure the validity and rationality of the dominant set. Moreover, these suggestions should be flexibly applied in combination with engineering practice, which makes the clustering results better aligned with objective reality.

5 Conclusions

Identifying discontinuity sets and determining dominant discontinuity properties are fundamental to evaluate the rock mass stability. Clustering analysis with multiple discontinuity properties has a stronger significance than considering only orientation, which better reflects the comprehensive contributions of discontinuity properties to the deformations and strengths of rock masses. Therefore, this paper proposes a new method to cluster discontinuities with multiple properties based on an improved netting algorithm.

In the new method, ten discontinuity properties are considered clustering factors. Meanwhile, a novel weighting method is used to weigh each property, combining the advantages of subjective and objective weighting methods. The proposed method obtains unique and repeatable results. The initial number of sets and initial clustering centers are not needed in advance; all data are simultaneously considered potential clustering centers, which reduces the subjectivity of human intervention and achieves global optimization. In addition, a distinctive advantage is that the proposed method can effectively filter the noise data to improve the accuracy of the clustering results, and the rejection rate was approximately 26%.

The performance of the new method was validated using artificial data and in situ data. Compared with five conventional clustering methods, the proposed method provided consistent results with the predefined data set and the results of the other methods, which exhibits good clustering capability. Furthermore, this method was applied to cluster discontinuity data from an open-pit mine slope in Xinjiang Province, China. The ideal number of sets was determined to be 3, and the utility of the method was demonstrated. Finally, two parameters were discussed and recommended: 0.01–0.05 for the confidence level and 5% of the total samples for the minimum number of samples in a dominant set. Moreover, the proposed method is believed to be a potentially useful tool to rapidly obtain dominant discontinuity sets in rock engineering.