Modelling underground excavations in rock masses with anisotropic time-dependent behaviour

Abstract

When modelling rock masses that behave anisotropically and in addition present a time dependent behaviour, it is relevant to select a constitutive model able to represent their actual behaviour realistically. This article presents an alternative anisotropic time-dependent constitutive model able to predict the coupling between anisotropic behaviour and time-dependent (or viscous) behaviour. The viscous behaviour is simulated with the Burgers model and all elastic springs and viscous dashpots are considered to exhibit transversely isotropic properties. The proposed constitutive model has been implemented in the finite element method software CODE_BRIGHT. To verify the basic anisotropic elastic solution, it has been compared with that of PLAXIS results. And to verify the isotropic viscoelastic solution, it has been compared with analytical solutions. Furthermore, the proposed constitutive model has been used to predict the behaviour of samples from laboratory tests. Finally, parametric analyses have been carried out to investigate the influence of different factors on tunnelling responses, including the selection of different constitutive models, anisotropy of initial stresses and anisotropy of material properties. The proposed model provides an alternative method for the preliminary design of geotechnical engineering works involving geomaterials that exhibit anisotropic time-dependent behaviour.

Article highlights

• • An anisotropic time-dependent model has been implemented in CODE_BRIGHT and validated.

• • The model can predict the coupled anisotropic time-dependent behaviour of geomaterials.

• • Parametric analyses have been performed to study the influence of different factors in ground response.

1 Introduction

Underground excavation is in high demand due to the increasing demands of nuclear waste disposal, geothermal projects or deep underground structures (Alonso et al. 2003, 2021a, b; Cui et al. 2015a, b, 2020, 2022; Guan et al. 2018, 2020a, b; Zhang et al. 2020; Guo et al. 2021; Mánica et al. 2021; Xue et al. 2021; Tarifard et al. 2022). However, it is not easy to analyse the tunnelling response due to the use of inadequate geomaterial models or due to the limited numerical approaches (Lade 1993; Rodriguez-Dono 2011; Paraskevopoulou 2016; Dong et al. 2021; Song 2021; Song et al. 2021a; Fan et al. 2022). Many different types of geomaterials are prone to exhibit time-dependent behaviour as well as anisotropy (Kolymbas et al. 2006; Mánica 2018). To address this problem, an alternative constitutive model is theoretically developed in this article, which can be used to simulate the coupled behaviour between the anisotropy and the time-dependency of geomaterials.

Laboratory tests show that many types of geomaterials exhibit a time-dependent behaviour (Sulem et al. 1987; Malan 2002; Paraskevopoulou 2016; Paraskevopoulou and Diederichs 2018; Chu et al. 2019), e.g., in creep tests, the deformations of samples increase with time under a constant applied load (see Fig. 1a). When considering underground excavations, the viscous behaviour of geomaterials may result in a gradual convergence of the tunnel wall (Eberhardt et al. 1999; Damjanac and Fairhurst 2010). Not accounting for the time-dependent behaviour of geomaterials may result in inadequate designs that might produce safety issues for the working projects (Paraskevopoulou 2016; Wang et al. 2020a; Song 2021). Typically, mechanical models simulating the time-dependent behaviour of geomaterials are based on viscoelastic rheological models (Weng et al. 2010; Wang et al. 2014a; Song 2021), and these models generally consist of elastic springs and viscous dashpots in parallel or/and in series (Paraskevopoulou 2016; Song 2021). Based on the viscoelastic models, including Maxwell, Kelvin, Generalized Kelvin and Burgers models, some researchers developed theoretical solutions to analyse underground structures, such as circular openings (Brady and Brown 1986; Wang and Nie 2010; Wang et al. 2020b), or supported tunnels (Lo and Yuen 1981; Sulem et al. 1987; Pan and Dong 1991; El Naggar et al. 2008; Mason and Abelman 2009; Fahimifar et al. 2010; Nomikos et al. 2011; Song et al. 2018a, b; Chu et al. 2021) excavated in time-dependent rocks. On the other hand, some researchers developed numerical approaches for modelling the excavation of tunnels in time-dependent geomaterials (Paraskevopoulou 2016; Paraskevopoulou and Diederichs 2018; Song et al. 2020; Song 2021). However, none of these researches considered the anisotropy of geomaterials.

Fig. 1

Creep test: a conceptual model; b stress–strain curves of slate rock samples. Based on the work of Song (2021) and Alejano et al. (2021)

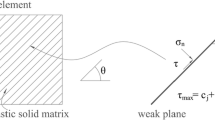
On the other hand, it has long been recognised that geomaterials may exhibit anisotropic behaviour, i.e. materials may have different properties in different directions (Barla 1976; Wittke 1990; Wu 1998; Mánica 2018; Setiawan and Zimmerman 2018; Alejano et al. 2021), as shown in Figs. 1(b), 2(a) and 2(b). It would introduce significant errors in the mechanical analyses if the anisotropy of geomaterials is incorrectly considered as isotropy (Barla 1972; Kanfar et al. 2015). Based on the cross-anisotropic constitutive model, some researchers have developed solutions to analyse the effect of anisotropy on tunnelling works, such as deeply circular tunnels (Hefny and Lo 1999; Vitali et al. 2020), shallow circular tunnels (Zymnis et al. 2013), triangular holes (Daoust and Hoa 1991), arbitrary cross-section tunnels (Tran Manh et al. 2015a; Lu et al. 2017), or twin circular tunnels (Tran-Manh et al. 2015). Considering three-dimensional (3D) problems, some researchers (Tonon and Amadei 2002; Franzius et al. 2005) investigated the effect of anisotropy on the ground settlement. Furthermore, Vu et al. (2013) developed semi-analytical solutions of stresses and displacements for tunnelling in cross-anisotropic rocks. Nevertheless, the mentioned anisotropic solutions did not consider the time-dependent behaviour of geomaterials.

Fig. 2

Solignano’s tunnel: a Excavation face at km 436; b Excavation face at km 432; c Displacements versus time (at km 417.5); d Longitudinal deformation profile (at km 417.5)

Experimental tests show that the time-dependency of geomaterials may exhibit an anisotropic response which may be similar to the elastic anisotropic response (Sone and Zoback 2013a, b, 2014; Li et al. 2019). In some cases, both factors, -anisotropy and time-dependency-, must be taken into account, to estimate properly the actual behaviour of geomaterials, or even more properly represent the response of underground excavations (Dubey and Gairola 2008; Lee et al. 2019; Li et al. 2019). To simulate the excavation of tunnels in anisotropic time-dependent geomaterials, Manh et al. (2015b) and Lee et al. (2019) developed an alternative model through coupling the Burgers-creep viscoplastic (CVISC) and the ubiquitous-joint (UBI) models, and implemented this alternative model in FLAC. Moreover, Weng et al. (2010) proposed a shear-induced anisotropic degradation model involving time-dependent behaviour, and their conceptual model is extended based on the Burgers viscoelastic model.

In this study, we attempt to theoretically develop an alternative anisotropic time-dependent model to provide a simple approach to predicting the mechanical responses of the geomaterials, considering the coupled behaviour between time-dependency and anisotropy. The anisotropic time-dependent model is first introduced and implemented into the finite element method software CODE_BRIGHT (Olivella et al. 2021). The proposed constitutive model incorporates the elastic, Maxwell, Kelvin, Generalized Kelvin and Burgers viscoelastic models, both in isotropic and anisotropic forms. A rather simple approach to calibrate the input parameters is presented. As a verification step, CODE_BRIGHT results are compared with PLAXIS results and analytical solutions. Additionally, numerical simulations of uniaxial tests are carried out, and numerical results have been validated by comparison with experimental data. Finally, comprehensive parametric analyses are presented to illustrate the sensitivity of tunnelling response to anisotropic properties of geomaterials and the selection of different constitutive models. Note that further improvements might be introduced in the anisotropic time-dependent model. For example, introducing a degradation model or introducing heterogeneity in the model.

2 Theoretical background

2.1 The time-dependent behaviour of geomaterials

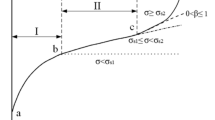
The time-dependent behaviour has been widely observed in laboratory tests for different types of rocks, such as rock salt (Sulem et al. 1987; Wang et al. 2013; Paraskevopoulou 2016; Chu et al. 2019; Song et al. 2020; Song 2021). Figure 1(a) shows a typical creep curve of rock samples, which can be usually characterised by four stages (Sterpi and Gioda 2009; Paraskevopoulou 2016): the instantaneous elastic response, the primary, the secondary and the accelerated creep stages. Note that the current study focuses on the viscoelastic response of rocks, i.e., the response of the accelerated creep stage is not considered, which might be reasonable for some cases, such as rock salt (Olivella and Gens 2002).

Figure 2 presents different aspects of Solignano’s tunnel in Italy, excavated in flysch, a rock known to present viscous behaviour. Figure 2(a) and (b) show photographs of different tunnel sections in which we can observe the bedding planes. Therefore, anisotropy should be considered when analysing the ground response. Figures 2(c) shows the measurements corresponding to the convergence of the tunnel crown at different days and it can be observed that the displacements of the tunnel wall increase with time. This might be due to the tunnelling advancement and/or the creep behaviour of geomaterials (Wang and Nie 2010; Wang et al. 2020a; Song 2021). However, representing the longitudinal deformation profile in Fig. 2(d), i.e. the measured displacements versus the distance to the tunnel face, it can be observed that deformations increase with time even when there is no tunnelling advancement (e.g. at 15 m from the tunnel face). This type of incremental deformation may mainly cause by a creep response. Therefore, both anisotropy and time-dependency are critical aspects to consider when analysing the response of such geomaterials.

The elastic springs and the viscous dashpot are usually coupled in series or/and parallel to model the time-dependency of geomaterials, in the framework of rock mechanics (Weng et al. 2010; Wang et al. 2013; Paraskevopoulou 2016; Song 2021). Figure 3 presents five typical mechanical models for geomaterials, including an elastic model and four linear viscoelastic models (Maxwell, Kelvin, Generalized Kelvin and Burgers models). Figure 4 presents the creep response considering the aforementioned four different mechanical models. The elastic model, the Maxwell model, the Kelvin model and the Generalized Kelvin model can be considered as particular cases of the Burgers model, as shown in Fig. 3. The material parameters E_ij and η_ij (i = M, K; j = e, v) in Fig. 3, can be experimentally determined. i = M (or K) represents the Maxwell (or the Kelvin) model; j = e (or v) represents the elastic spring (or the viscous dashpot).

Fig. 3

Comparison between five different mechanical constitutive models

Fig. 4

Creep responses considering four different mechanical models: Maxwell, Kelvin, Generalized Kelvin and Burgers models. Based on the work of Wang et al. (2014b) and Song (2021)

2.2 Anisotropic behaviour of geomaterials

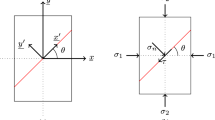
Another property of interest in rock mechanics is anisotropy, which can be observed in many different types of rocks, such as metamorphic, sedimentary, rock salt or slate (Dubey and Gairola 2008; Mánica 2018; Vitali et al. 2020; Alejano et al. 2021). Regarding the cross-anisotropy, two main directions of anisotropy (parallel and orthogonal to the bedding plane) are generally identified. Figure 5 shows the conceptual model of cross-anisotropic geomaterials (Wittke 1990; Mánica 2018).

Fig. 5

a Global coordinate system (x, y, z), b local coordinate system (1, 2, 3), c rotation angles (α and β) between the global and local coordinate systems. The global coordinate system (x, y, z) first rotates α deg around the z-axis, and then β deg around the y-axis, to obtain the local coordinate system (1, 2, 3). Based on the work of Mánica (2018) and Alejano et al. (2021)

For cases of the global coordinate system (x, y, z) does not coincide with the local one (1, 2, 3), transformation matrices are needed, which are shown in Eqs. (1) and (2) (Wittke 1990).

$${\text{D}} = \left[ {T_{C}^{{}} } \right]_{{}}^{T} {\text{D}}_{{}}^{local} \left[ {T_{C}^{{}} } \right]$$

(1)

$${\text{C}} = \left[ {T_{D}^{{}} } \right]_{{}}^{T} {\text{C}}_{{}}^{local} \left[ {T_{D}^{{}} } \right]$$

(2)

where D (or D^local) is the global (or local) stiffness matrix; C (or C^local) is the global (or local) compliance matrix; T_C (or T_D) is the strain (or stress) transformation matrix. “Appendix” section shows the expression of these transformation matrices, which are adapted from Mánica (2018) and Wittke (1990). The reader is referred to the source for a detailed description of the transformation matrices.

3 Anisotropic time-dependent constitutive model

3.1 The proposed anisotropic time-dependent constitutive model

The Burgers model does not consider the effect of the bedding plane on creep behaviour, although this model has been investigated as it is applied to many geomaterials (Wu et al. 2018). In this study, to incorporate the anisotropic time-dependent behaviour of geomaterials, a cross-anisotropic time-dependent model is theoretically developed based on the Burgers model.

The total strain rate tensor of the Burgers viscoelastic model ($\frac{{d{\upvarepsilon }_{B}^{{}} }}{dt}$) can be decomposed into the Maxwell ($\frac{{d{\upvarepsilon }_{M}^{{}} }}{dt}$) and the Kelvin ($\frac{{d{\upvarepsilon }_{K}^{{}} }}{dt}$) parts, as shown in Eq. (3). The strain rate tensor of the Maxwell model ($\frac{{d{\upvarepsilon }_{M}^{{}} }}{dt}$) consists of two components: strain rate tensor of the elastic spring ($\frac{{d{\upvarepsilon }_{Me}^{{}} }}{dt}$) and strain rate tensor of the viscous dashpot ($\frac{{d{\upvarepsilon }_{Mv}^{{}} }}{dt}$).

$$\frac{{d{\upvarepsilon }_{B}^{{}} }}{dt} = \frac{{d{\upvarepsilon }_{M}^{{}} }}{dt} + \frac{{d{\upvarepsilon }_{K}^{{}} }}{dt} = \frac{{d{\upvarepsilon }_{Me}^{{}} }}{dt} + \frac{{d{\upvarepsilon }_{Mv}^{{}} }}{dt} + \frac{{d{\upvarepsilon }_{K}^{{}} }}{dt}$$

(3)

${\upvarepsilon }_{Me}^{{}}$ represents the instantaneously elastic strain; ${\upvarepsilon }_{Mv}^{{}}$ represents the delayed time-dependent strain of viscous dashpot in the Maxwell model; ${\upvarepsilon }_{K}^{{}}$ is the delayed time-dependent strain of the Kelvin model.

In the proposed constitutive model, the elastic springs and the viscous dashpots are assumed to exhibit cross-anisotropic behaviour. For the elastic spring with the cross-anisotropic response, in the most general cases, stiffness anisotropy is incorporated in the elastic framework utilising the generalised Hooke’s law, and the cross-anisotropic elastic spring expresses the elastic stiffness matrix as a function of five independent elastic constants: two elastic moduli, two Poisson's ratios and one shear modulus (Wittke 1990). This anisotropic stiffness is utilised to represent the cross-anisotropic behaviour of elastic springs, in the proposed anisotropic viscoelastic model. Similarly, in this study, five independent viscous constants are adopted to exhibit the cross-anisotropic behaviour of a viscous dashpot. This theoretical development for viscous dashpot is reasonable because experiment results indicate that the tendencies of time-dependent creep deformations are similar to the instantaneous elastic responses (Weng et al. 2010).

The anisotropic Burgers viscoelastic model consists of two elastic springs and two viscous dashpots (see Fig. 3) and, therefore a total of twenty input parameters are needed in the proposed anisotropic Burgers viscoelastic model. However, it might be sufficient to consider that the Poisson’s ratios of rheological models exhibit similar properties, i.e. the Poisson’s ratio of viscous dashpot in the Maxwell model and the Poisson’s ratio of the Kelvin model are the same. Finally, the total number of constitutive parameters of the cross-anisotropic Burgers viscoelastic model is sixteen, as shown in Table 1. Note that the anisotropic model can be simplified to be the isotropic model, through assigning X_ij1 = X_ij2 (X = E, η; i = M, K; j = e, v), ν_j1 = ν_j2 (j = e, v) and G_ij = $\frac{{X_{ij}^{{}} }}{{2\left( {1 + \nu_{j}^{{}} } \right)}}$. Specifically, if only the deviatoric viscosity and no volumetric viscosity is considered, the Poisson’s ratio of the viscous dashpot and the Kelvin model, i.e. ν_v1, ν_v2, should be assumed as 0.5.

Table 1 Constitutive parameters of the cross-anisotropic Burgers model

3.2 Parameters calibrations

In this section, based on creep tests, a rather simple approach is proposed to identify all the input parameters in Table 1. Under a constant applied stress σ, a typical creep response in a uniaxial laboratory test could be that shown in Fig. 6:

Fig. 6

Conceptual model of typical creep response in a creep test

(a) The instantaneous elastic strain ε₁ occurs at time t = t_1, and ε₁ is caused by the elastic spring of the Maxwell model. Therefore, the parameters of elastic spring in the Maxwell model can be determined through Eqs. (5), (8) and (11).

(b) The secondary creep stage from t = t₂ onwards, the incremental strain in this stage is only caused by the viscous dashpot in the Maxwell model. Thus, the parameters of the dashpot in the Maxwell model can be calibrated by using Eqs. (6), (9) and (12).

and, (c) The primary creep stage, from time t = t₁ to time t = t₂. The incremental strains in the primary creep stage ($\varepsilon^{2}$—$\varepsilon^{1}$) are contributed by two parts: the viscous dashpot part of the Maxwell model and the Kelvin model. In addition, the total incremental strain in the primary creep stage caused by the Kelvin model can be expressed as ε_{K, max} = $\varepsilon^{2}$—$\varepsilon^{1}$—ε$_{{\text{M}}}^{{}} \left( {t_{2}^{{}} } \right)$—ε$_{{\text{M}}}^{{}} \left( {t_{1}^{{}} } \right)$. Note that ε_{K, max} only depends on the values of elastic spring in the Kelvin model and is independent of the properties of the viscous dashpot in the Kelvin model. Therefore, the parameters of the elastic spring in the Kelvin model can be determined through Eqs. (7), (10) and (13).

In addition, T_K = η_K /G_K denotes the retardation time, which is the delayed response to applied stress and can be described as ‘delay of the elasticity’ (Song et al. 2021b). As the value of T_K decreases, less time is needed for the Kelvin model to achieve a very low strain rate, i.e., the response of the rock mass to applied stress will be faster (Song et al. 2021b). In this study, η_K is recommended to be determined through back-analysis based on the creep curves.

In addition, some researchers (Worotnicki 1993; Amadei 1996; Alejano et al. 2021) found that some experimental data for several types of rock samples support the validity of the Saint–Venant approach (Worotnicki 1993), with some exceptions. Therefore, as an alternative, the shear parameters (G_ij) can be recommended through the Saint–Venant solution (Worotnicki 1993), as shown in Eq. (4). X = E with j = e, while X = η with j = v. i = M (or K) represents the Maxwell (or Kelvin) model, and j = e (or v) represents the elastic spring (or viscous dashpot).

$${\text{G}}_{ij}^{{}} = {1 \mathord{\left/ {\vphantom {1 X}} \right. \kern-\nulldelimiterspace} X}_{ij1}^{{}} + {1 \mathord{\left/ {\vphantom {1 X}} \right. \kern-\nulldelimiterspace} X}_{ij2}^{{}} + 2{{\nu_{j2}^{{}} } \mathord{\left/ {\vphantom {{\nu_{j2}^{{}} } X}} \right. \kern-\nulldelimiterspace} X}_{ij2}^{{}}$$

(4)

Furthermore, it is generally assumed that the time-dependent behaviour depends mainly on the deviatoric strain, while the effect of the volumetric strain is less significant (Sulem et al. 1987; Song et al. 2020; Song 2021). Therefore, to simplify, the Poisson’s ratio of the time-dependent parts (ν_v1, ν_v2) –i.e. the viscous dashpots of Maxwell and Kelvin is assumed to be 0.5.

	$\frac{{\varepsilon_{z}^{1} }}{\sigma } = \frac{1}{{E_{Me2}^{{}} }}; \, \frac{{\varepsilon_{x}^{1} }}{\sigma } = \frac{{\varepsilon_{y}^{1} }}{\sigma } = - \frac{{\nu_{e2}^{{}} }}{{E_{Me2}^{{}} }}$	(5)
	$\frac{{\varepsilon_{z}^{3} - \varepsilon_{z}^{2} }}{{\left( {t_{3}^{{}} - t_{2}^{{}} } \right)\sigma }} = \frac{1}{{\eta_{Mv2}^{{}} }}; \, \frac{{\varepsilon_{\text{x}}^{3} - \varepsilon_{x}^{2} }}{{\left( {t_{3}^{{}} - t_{2}^{{}} } \right)\sigma }} = \frac{{\varepsilon_{y}^{3} - \varepsilon_{y}^{2} }}{{\left( {t_{3}^{{}} - t_{2}^{{}} } \right)\sigma }} = - \frac{{\nu_{v2}^{{}} }}{{\eta_{Mv2}^{{}} }}$	(6)
	$\left\{ \begin{gathered} \frac{{\varepsilon_{z}^{2} - \varepsilon_{z}^{1} - \frac{\sigma }{{\eta_{{{\text{Mv}} 2}}^{{}} }}\left( {t_{2}^{{}} - t_{1}^{{}} } \right)}}{\sigma } = \frac{1}{{E_{{{\text{K}} {\text{e}} 2}}^{{}} }} \hfill \\ \frac{{\varepsilon_{x}^{2} - \varepsilon_{x}^{1} + \frac{{\sigma \nu_{v2}^{{}} }}{{\eta_{Mv2}^{{}} }}\left( {t_{2}^{{}} - t_{1}^{{}} } \right)}}{\sigma } = \frac{{\varepsilon_{y}^{2} - \varepsilon_{y}^{1} + \frac{{\sigma \nu_{v2}^{{}} }}{{\eta_{Mv2}^{{}} }}\left( {t_{2}^{{}} - t_{1}^{{}} } \right)}}{\sigma } = - \frac{{\nu_{{{\text{v}} 2}}^{{}} }}{{E_{Ke2}^{{}} }} \hfill \\ \end{gathered} \right.$	(7)
	$\frac{{\varepsilon_{z}^{1} }}{\sigma } = \frac{1}{{E_{Me1}^{{}} }}; \, \frac{{\varepsilon_{y}^{1} }}{\sigma } = - \frac{{\nu_{e1}^{{}} }}{{E_{Me1}^{{}} }}; \, \frac{{\varepsilon_{\text{x}}^{1} }}{\sigma } = - \frac{{\nu_{e2}^{{}} }}{{E_{Me2}^{{}} }}$	(8)
	$\frac{{\varepsilon_{z}^{3} - \varepsilon_{z}^{2} }}{{\left( {t_{3}^{{}} - t_{2}^{{}} } \right)\sigma }} = \frac{1}{{\eta_{{{\text{Mv}} 1}}^{{}} }}; \, \frac{{\varepsilon_{y}^{3} - \varepsilon_{y}^{2} }}{{\left( {t_{3}^{{}} - t_{2}^{{}} } \right)\sigma }} = - \frac{{\nu_{{{\text{v}} 1}}^{{}} }}{{\eta_{Mv1}^{{}} }}; \, \frac{{\varepsilon_{x}^{3} - \varepsilon_{x}^{2} }}{{\left( {t_{3}^{{}} - t_{2}^{{}} } \right)\sigma }} = - \frac{{\nu_{v2}^{{}} }}{{\eta_{Mv2}^{{}} }}$	(9)
	$\left\{ \begin{gathered} \frac{{\varepsilon_{z}^{2} - \varepsilon_{z}^{1} - \frac{\sigma }{{\eta_{{{\text{Mv}} 1}}^{{}} }}\left( {t_{2}^{{}} - t_{1}^{{}} } \right)}}{\sigma } = \frac{1}{{E_{{{\text{K}} {\text{e}} 1}}^{{}} }} \hfill \\ \frac{{\varepsilon_{y}^{2} - \varepsilon_{y}^{1} + \frac{{\sigma \nu_{v1}^{{}} }}{{\eta_{Mv1}^{{}} }}\left( {t_{2}^{{}} - t_{1}^{{}} } \right)}}{\sigma } = - \frac{{\nu_{{{\text{v}} 1}}^{{}} }}{{E_{Ke1}^{{}} }} \hfill \\ \frac{{\varepsilon_{x}^{2} - \varepsilon_{x}^{1} + \frac{{\sigma \nu_{v2}^{{}} }}{{\eta_{Mv2}^{{}} }}\left( {t_{2}^{{}} - t_{1}^{{}} } \right)}}{\sigma } = - \frac{{\nu_{{{\text{v}} 2}}^{{}} }}{{E_{Ke2}^{{}} }} \hfill \\ \end{gathered} \right.$	(10)
	$\left\{ \begin{gathered} \frac{{\varepsilon_{x}^{1} }}{\sigma } = \frac{{\sin_{{}}^{2} 2\beta }}{4}\left( {\frac{1}{{E_{{{\text{Me}} 1}}^{{}} }} + \frac{1}{{E_{{{\text{Me}} 2}}^{{}} }} - \frac{1}{{G_{{\text{Me}}}^{{}} }}} \right) - \frac{{\nu_{e2}^{{}} }}{{E_{{{\text{Me}} 2}}^{{}} }}\left( {\cos_{{}}^{4} \beta + \sin_{{}}^{4} \beta } \right) \hfill \\ \frac{{\varepsilon_{z}^{1} }}{\sigma } = \frac{{\sin_{{}}^{4} \beta }}{{E_{{{\text{Me}} 1}}^{{}} }} + \frac{{\cos_{{}}^{4} \beta }}{{E_{{{\text{Me}} 2}}^{{}} }} + \frac{{\sin_{{}}^{2} 2\beta }}{4}\left( { - \frac{{2\nu_{e2}^{{}} }}{{E_{{{\text{Me}} 2}}^{{}} }} + \frac{1}{{G_{{\text{Me}}}^{{}} }}} \right) \hfill \\ \frac{{\varepsilon_{y}^{1} }}{\sigma } = - \sin_{{}}^{2} \beta \frac{{\nu_{e1}^{{}} }}{{E_{{{\text{Me}} 1}}^{{}} }} - \cos_{{}}^{2} \beta \frac{{\nu_{e2}^{{}} }}{{E_{{{\text{Me}} 2}}^{{}} }} \hfill \\ \end{gathered} \right.$	(11)
	$\left\{ \begin{gathered} \frac{{\varepsilon_{x}^{3} - \varepsilon_{x}^{2} }}{{\left( {t_{3}^{{}} - t_{2}^{{}} } \right)\sigma }} = \frac{{\sin_{{}}^{2} 2\beta }}{4}\left( {\frac{1}{{\eta_{{{\text{Mv}} 1}}^{{}} }} + \frac{1}{{\eta_{{{\text{Mv}} 2}}^{{}} }} - \frac{1}{{G_{{\text{Mv}}}^{{}} }}} \right) - \frac{{\nu_{v2}^{{}} }}{{\eta_{{{\text{Mv}} 2}}^{{}} }}\left( {\cos_{{}}^{4} \beta + \sin_{{}}^{4} \beta } \right) \hfill \\ \frac{{\varepsilon_{z}^{3} - \varepsilon_{z}^{2} }}{{\left( {t_{3}^{{}} - t_{2}^{{}} } \right)\sigma }} = \frac{{\sin_{{}}^{4} \beta }}{{\eta_{{{\text{Mv}} 1}}^{{}} }} + \frac{{\cos_{{}}^{4} \beta }}{{\eta_{{{\text{Mv}} 2}}^{{}} }} + \frac{{\sin_{{}}^{2} 2\beta }}{4}\left( { - \frac{{2\nu_{v2}^{{}} }}{{\eta_{{{\text{Mv}} 2}}^{{}} }} + \frac{1}{{G_{{\text{Mv}}}^{{}} }}} \right) \hfill \\ \frac{{\varepsilon_{y}^{3} - \varepsilon_{y}^{2} }}{{\left( {t_{3}^{{}} - t_{2}^{{}} } \right)\sigma }} = - \sin_{{}}^{2} \beta \frac{{\nu_{v1}^{{}} }}{{\eta_{{{\text{Me}} 1}}^{{}} }} - \cos_{{}}^{2} \beta \frac{{\nu_{v2}^{{}} }}{{\eta_{{{\text{Mv}} 2}}^{{}} }} \hfill \\ \end{gathered} \right.$	(12)
	$\left\{ \begin{gathered} \varepsilon_{x}^{2} - \varepsilon_{x}^{1} - \sigma \left( {t_{2}^{{}} - t_{1}^{{}} } \right)\left[ {\frac{{\sin_{{}}^{2} 2\beta }}{4}\left( {\frac{1}{{\eta_{{{\text{Mv}} 1}}^{{}} }} + \frac{1}{{\eta_{{{\text{Mv}} 2}}^{{}} }} - \frac{1}{{G_{{\text{Mv}}}^{{}} }}} \right) - \frac{{\nu_{v2}^{{}} }}{{\eta_{{{\text{Mv}} 2}}^{{}} }}\left( {\cos_{{}}^{4} \beta + \sin_{{}}^{4} \beta } \right)} \right] \hfill \\ \, = \sigma \left[ {\frac{{\sin_{{}}^{2} 2\beta }}{4}\left( {\frac{1}{{E_{Ke1}^{{}} }} + \frac{1}{{E_{Ke2}^{{}} }} - \frac{1}{{G_{{\text{Me}}}^{{}} }}} \right) - \frac{{\nu_{v2}^{{}} }}{{E_{Ke2}^{{}} }}\left( {\cos_{{}}^{4} \beta + \sin_{{}}^{4} \beta } \right)} \right] \hfill \\ \varepsilon_{z}^{2} - \varepsilon_{z}^{1} - \sigma \left( {t_{2}^{{}} - t_{1}^{{}} } \right)\left[ {\frac{{\sin_{{}}^{4} \beta }}{{\eta_{{{\text{Mv}} 1}}^{{}} }} + \frac{{\cos_{{}}^{4} \beta }}{{\eta_{{{\text{Mv}} 2}}^{{}} }} + \frac{{\sin_{{}}^{2} 2\beta }}{4}\left( { - \frac{{2\nu_{v2}^{{}} }}{{\eta_{{{\text{Mv}} 2}}^{{}} }} + \frac{1}{{G_{{\text{Mv}}}^{{}} }}} \right)} \right] \hfill \\ \, = \sigma \left[ {\frac{{\sin_{{}}^{4} \beta }}{{E_{Ke1}^{{}} }} + \frac{{\cos_{{}}^{4} \beta }}{{E_{Ke2}^{{}} }} + \frac{{\sin_{{}}^{2} 2\beta }}{4}\left( { - \frac{{2\nu_{v2}^{{}} }}{{E_{Ke2}^{{}} }} + \frac{1}{{G_{Ke}^{{}} }}} \right)} \right] \hfill \\ \varepsilon_{y}^{2} - \varepsilon_{y}^{1} - \sigma \left( {t_{2}^{{}} - t_{1}^{{}} } \right)\left[ { - \sin_{{}}^{2} \beta \frac{{\nu_{v1}^{{}} }}{{\eta_{{{\text{Me}} 1}}^{{}} }} - \cos_{{}}^{2} \beta \frac{{\nu_{v2}^{{}} }}{{\eta_{{{\text{Mv}} 2}}^{{}} }}} \right] \hfill \\ = \sigma \left[ { - \sin_{{}}^{2} \beta \frac{{\nu_{v1}^{{}} }}{{E_{Ke1}^{{}} }} - \cos_{{}}^{2} \beta \frac{{\nu_{v2}^{{}} }}{{E_{Ke2}^{{}} }}} \right] \hfill \\ \end{gathered} \right.$	(13)

3.3 Numerical implementation

The proposed anisotropic Burgers model has been implemented into the Finite Element Method software CODE_BRIGHT (Olivella et al. 2021). Based on the presented theory in Sect. 3.1, in the local coordinate system (1-2-3), the stiffness matrix of the cross-anisotropic elastic spring (X = E) or the cross-anisotropic viscous dashpot (X = η) can expressed as in Eq. (14). $\overline{m}$ _ij = 1-ν_j1-2 $\overline{n}$ _ij ν_j2ν_j2; $\overline{n}$ _ij = X_ij1/X_ij2 (X = E with j = e, while X = η with j = v). The compliance matrix in the local coordinate system can be obtained by inversing the stiffness matrix of Eq. (14), i.e. ${\text{C}}_{ij}^{local}$ = [${\text{D}}_{ij}^{local}$]⁻¹.

$${\text{D}}_{ij}^{local} = \left[ \begin{gathered} M_{ij}^{local} ,0 \hfill \\ 0, N_{ij}^{local} \hfill \\ \end{gathered} \right]$$

(14)

where ${\text{M}}_{ij}^{local} = \left[ \begin{gathered} X_{ij1}^{{}} \frac{{1 - \overline{n}_{ij}^{{}} \nu_{j2}^{2} }}{{\left( {1 + \nu_{j1}^{{}} } \right)\overline{m}_{ij}^{{}} }},X_{ij1}^{{}} \frac{{\nu_{ij1}^{{}} + \overline{n}_{ij}^{{}} \nu_{j2}^{2} }}{{\left( {1 + v_{j1}^{{}} } \right)\overline{m}_{ij}^{{}} }},X_{ij1}^{{}} \frac{{\nu_{j2}^{{}} }}{{\overline{m}_{ij}^{{}} }} \hfill \\ X_{ij1}^{{}} \frac{{1 + \overline{n}_{ij}^{{}} \nu_{j2}^{2} }}{{\left( {1 + \nu_{j1}^{{}} } \right)\overline{m}_{ij}^{{}} }},X_{ij1}^{{}} \frac{{1 - \overline{n}_{ij}^{{}} \nu_{j2}^{2} }}{{\left( {1 + \nu_{j1}^{{}} } \right)\overline{m}_{ij}^{{}} }},X_{ij1}^{{}} \frac{{\nu_{j2}^{{}} }}{{\overline{m}_{ij}^{{}} }} \hfill \\ X_{ij1}^{{}} \frac{{\nu_{j2}^{{}} }}{{\overline{m}_{ij}^{{}} }},X_{ij1}^{{}} \frac{{\nu_{j2}^{{}} }}{{\overline{m}_{ij}^{{}} }},X_{ij2}^{{}} \frac{{1 - \nu_{j1}^{{}} }}{{\overline{m}_{ij}^{{}} }} \hfill \\ \end{gathered} \right]$ and ${\text{N}}_{ij}^{local} = \left[ \begin{gathered} \frac{{X_{ij1}^{{}} }}{{2\left( {1 + \nu_{j1}^{{}} } \right)}} ,0,0 \hfill \\ 0,G_{ij}^{{}} ,0 \hfill \\ 0,0,G_{ij}^{{}} \hfill \\ \end{gathered} \right]$.

For the Kelvin model, the equivalent stiffness matrix (D $_{K}^{local}$), and the equivalent compliance matrix (C $_{K}^{local}$) in the local coordinate system, can be determined in Eqs. (15) and (16), respectively.

$${\text{D}}_{K}^{local} = D_{Ke}^{local} + {{D_{Kv}^{local} } \mathord{\left/ {\vphantom {{D_{Kv}^{local} } {\Delta t}}} \right. \kern-\nulldelimiterspace} {\Delta t}}$$

(15)

$${\text{C}}_{K}^{local} = \left[ {D_{K}^{local} } \right]_{{}}^{ - 1} = \left[ {D_{Ke}^{local} + {{D_{Kv}^{local} } \mathord{\left/ {\vphantom {{D_{Kv}^{local} } {\Delta t}}} \right. \kern-\nulldelimiterspace} {\Delta t}}} \right]_{{}}^{ - 1}$$

(16)

where ${\text{D}}_{Ke}^{local}$ (or ${\text{D}}_{Kv}^{local}$) represents the local cross-anisotropic stiffness matrix of the elastic spring (or the viscous dashpot) in the Kelvin model.

Following “Appendix” section, the stiffness (or compliance) matrix D (or C) in the global coordinate system (x, y, z) can be determined by combining the transformation matrices [T_C] (or [T_D]) and the local stiffness (or local compliance) matrix D^local (or C^local). Furthermore, the accumulated strain tensor of the Kelvin model is chosen as the history variable (Olivella et al. 2021). For the Kelvin model, ε_K = ε_Ke = ε_Kv and σ_K = σ_Ke + σ_Kv and, therefore the strain rate of the Kelvin model at time t = t_k can be expressed as in Eq. (17). Finally, the strain rate of the Burgers model at time t = t_k can be expressed as in Eq. (18).

$$\left. {\frac{{d{\upvarepsilon }_{K}^{{}} }}{dt}} \right|_{{t = t_{k}^{{}} }}^{{}} = {\text{C}}_{Kv}^{{}} \left( {\left. {\upsigma } \right|_{{t = t_{k}^{{}} }}^{{}} - {\text{D}}_{Ke}^{{}} \left. {{\upvarepsilon }_{\text{K}}^{{}} } \right|_{{t = t_{k}^{{}} }}^{{}} } \right)$$

(17)

$$\left. {\frac{{d{\upvarepsilon }_{B}^{{}} }}{dt}} \right|_{{t = t_{k}^{{}} }}^{{}} = {\text{C}}_{Me}^{{}} \left. {\frac{{d{\upsigma }}}{dt}} \right|_{{t = t_{k}^{{}} }}^{{}} + {\text{C}}_{Mv}^{{}} \left. {\upsigma } \right|_{{t = t_{k}^{{}} }}^{{}} + {\text{C}}_{Kv}^{{}} \left( {\left. {\upsigma } \right|_{{t = t_{k}^{{}} }}^{{}} - {\text{D}}_{Ke}^{{}} \left. {{\upvarepsilon }_{\text{K}}^{{}} } \right|_{{t = t_{k}^{{}} }}^{{}} } \right)$$

(18)

where C_Me (or C_Mv) represents the cross-anisotropic compliance matrix of the elastic spring (or the viscous dashpot) in the Maxwell model; C_Kv represents the cross-anisotropic compliance matrix of the viscous dashpot in the Kelvin model; $\left. {{\upvarepsilon }_{\text{K}}^{{}} } \right|_{{t = t_{k}^{{}} }}^{{}}$ is the accumulated strain of the Kelvin model at time t = t_k.

4 Numerical verification and validation

To verify the numerical implementation and to validate the applications of the proposed constitutive model, the anisotropic elastic results and isotropic viscoelastic results from CODE_BRIGHT simulations are verified separately by comparison with PLAXIS (Brinkgreve et al. 2016) results and analytical solutions in Sects. 4.1 and 4.2, respectively. Furthermore, numerical simulations of uniaxial tests are carried out in Sect. 4.3, and the obtained numerical results are compared with experimental data.

4.1 Comparison with anisotropic elastic solutions under anisotropic initial stresses

As shown in Fig. 3, the presented constitutive model can be simplified to an anisotropic elastic model. To verify the obtained anisotropic elastic results, an example of a circular tunnel excavated in an anisotropic elastic ground is carried out in CODE_BRIGHT. The numerical results of the displacements obtained from CODE_BRIGHT are compared with PLAXIS results.

Both numerical models are calculated under plane-strain conditions with small deformations. As shown in Fig. 7, the normal displacements along all boundaries are restrained, and the discretised area is 100 m × 100 m. The radius of tunnel R₁ is 6.5 m. The initial stresses are p_x and p_y, respectively, in the x and y directions. Three different cases are adopted in the comparison (see Table 2). Figure 8(a) presents the mesh of the CODE_BRIGHT model, consisting of 3850 quadratic triangle elements, whereas Fig. 8(b) shows the mesh in the PLAXIS model, which consists of 19,804 15-noded elements. In both models, finer elements near the excavation zone are generated.

Fig. 7

Basic features of the numerical model. (r, θ) represents the adopted polar coordinates

Table 2 Input parameters of the initial stresses and anisotropic elastic models

Fig. 8

Meshes used in the plane-strain excavation model: a CODE_BRIGHT (3850 quadratic triangle elements); b PLAXIS (19,804 15-noded elements)

In the numerical simulations, the initial stresses are applied in the numerical models before excavation, to simulate the initial field stresses. A comparison of the incremental displacements along the tunnel wall (r = R₁) that occurred after the excavation predicted by CODE_BRIGHT and by PLAXIS is shown in Fig. 9. A good agreement between the CODE_BRIGHT and the PLAXIS results is observed, verifying the adopted theory and the implementation of the anisotropic model (elastic part), as well as the transformation matrices in CODE_BRIGHT.

Fig. 9

Comparison between CODE_BRIGHT (C_B) and PLAXIS results of the incremental displacements at the tunnel wall (r = R₁) versus angle for the cases shown in Table 2. (r, θ) represent the adopted polar coordinates

4.2 Comparison with isotropic viscoelastic solutions under anisotropic initial stresses

The cross-anisotropic mechanical model can be simplified to the isotropic constitutive model, as described in Sect. 3. In this section, the obtained viscoelastic results from CODE_BRIGHT are compared with the analytical solutions from Wang et al. (2015), in terms of the incremental deformations of tunnels excavated in isotropic viscoelastic rocks. The Generalized Kelvin viscoelastic model is adopted in the comparison. By using the complex potential theory, the Laplace transformation and the time inversion, Wang et al. (2015) presented the extension of the corresponding principle to solid media subjected to anisotropic initial stresses.

Both numerical and analytical solutions are calculated under plane-strain conditions with small deformations. Neumann boundary conditions are adopted in the numerical model and a big enough zone is considered for the calculation, to eliminate the effect of boundaries, as shown in Fig. 10. Anisotropic initial stresses (p_x, p_y) are considered. Table 3 shows the input parameters of the anisotropic viscoelastic model and information of the initial stresses.

Fig. 10

Numerical model: a Basic features; b mesh size

Table 3 Input parameters of the constitutive model and initial stresses

First, initial stresses are applied on the plane without holes for a sufficiently long time (500 days in this numerical example) to account for the displacement and stress fields before excavation. Then, the tunnel cross-section is instantaneously excavated at time t = 0. The calculation is completed at time t = 60 days. A comparison of the time-dependent incremental displacements for Points A (r = 6 m, θ = 0 deg), B (r = 6 m, θ = 45 deg) and C (r = 6 m, θ = 90 deg) predicted by the analytical solutions and by CODE_BRIGHT is shown in Fig. 11. (r, θ) represents the adopted polar coordinates. It can be observed a good agreement between CODE_BRIGHT results and analytical solutions, verifying the theory and implementation of the viscoelastic model in CODE_BRIGHT.

Fig. 11

Comparison between analytical solutions (Wang et al. 2015) and CODE_BRIGHT (C_B) results for time-dependent incremental displacements of Points A (r = 6 m, θ = 0 deg), B (r = 6 m, θ = 45 deg) and C (r = 6 m, θ = 90 deg): a for Case 1 (in Table 3), and b for Case 2 (in Table 3)

4.3 Comparison with experimental data from laboratory tests

In this section, a rather simple numerical validation is carried out, to demonstrate that the proposed anisotropic time-dependent constitutive model can be used to predict the coupled time-dependent anisotropic behaviour of geomaterials. To do that, numerical simulations of uniaxial tests are performed and compared with experimental data found in Dubey and Gairola (2008). Dubey and Gairola (2008) made laboratory tests to analyse the anisotropic time-dependent behaviour of rock salt, and the rock samples were obtained from Shali Formation (Precambrian), Himachal Pradesh, India. The experiments were performed on cubic specimens 0.05 × 0.05 × 0.05 m³ cut from large rock salt samples collected from the field.

In this section, for simplicity, only two groups of data are analysed: (1) specimens are orthogonal compressed perpendicular to the bedding plane (SPR with β = 0 deg), and (2) specimens are axially compressed parallel to the bedding plane (SPL with β = 90 deg), and therefore, only Eqs. (5)–(10) were used in the parametric calibration. The compressive strength of SPR and SPL specimens are 29.33 MPa and 28.08 MPa, respectively. A more detailed description of the laboratory tests can be found in Dubey and Gairola (2008).

To simplify, the values of compressive strength for SPR and SPL specimens are approximately assumed as the average of both specimens. The adopted Poisson’s ratio of the elastic spring in the Maxwell model is 0.3, and others Poisson’s ratios related to time-dependency are assumed to be 0.5. The shear moduli were determined through the Saint–Venant solution (see Eq. (4)). Table 4 contains the input parameters of the anisotropic Burgers model for different applied constant stresses. All other parameters can be determined through the back-analysis approach. Due to the mechanical properties depending on the applied stress level for these samples (Dubey and Gairola 2008), the input parameters in Table 4 are different for different applied stresses.

Table 4 Input parameters of the anisotropic Burgers model

In the numerical simulations, a three-dimensional (3D) numerical model with a domain of 0.05 × 0.05 × 0.05 m³ is used, consistent with the laboratory tests. Figure 12 shows the basic features and boundary conditions of the numerical model in CODE_BRIGHT. The normal displacements along the z = 0 surface is restrained. Constant stresses were applied along the top surface (z = 0.05 m). Figure 13 presents the mesh of the numerical model, with 2058 quadratic tetrahedral elements. Figure 14 presents the strain of the point at the centre of the top surface (x = y = 0.025 m, z = 0.05 m). It can be observed that the strain increases with time, i.e., time-dependent response; meanwhile, results obtained from β = 0 deg and β = 90 deg samples are different even under the same applied stress level, i.e., anisotropy response. A good agreement between numerical and experimental results is observed, which may validate the potential application of the proposed anisotropic time-dependent constitutive model in engineering works. Note that these parameters in Table 4 are estimated with the intent of matching experimental data from the scientific literature of Dubey and Gairola (2008). Although some simplifications were made in this sub-section, however, if the input parameters are properly chosen, it may validate that the proposed constitutive model might be meaningful in predicting the engineering data.

Fig. 12

Basic features and boundary conditions for a uniaxial creep test: a in the x–y-z domain (real scale), and b in the x-o-z plane or y–o-z plane (not real scale)

Fig. 13

Mesh (real scale)

Fig. 14

Comparison of strains in the z-direction for point (x = y = 0.025 m, z = 0.05 m), between CODE_BRIGHT results and the experimental data found in Dubey and Gairola (2008)

5 Application to underground excavation problems

The Generalized Kelvin viscoelastic model is commonly employed for rocks with good mechanical properties or subjected to low stresses, since the exhibited mechanical behaviour shows limited viscosity (Wang et al. 2013; Song et al. 2018a, b). Regarding this type of creep behaviour commonly encountered in rock engineering, comprehensive parametric analyses for the influence of different factors on tunnelling responses are carried out, including the selection of constitutive models, anisotropy of initial stresses and anisotropy of material properties.

A circular tunnel with radius R₁ being 6 m is excavated in time-dependent anisotropic rocks. In the numerical simulation, the boundary conditions and the model size are the same as those described in Sect. 4.2. The constitutive parameters of anisotropic Generalized Kelvin viscoelastic model are: E_Me1 = 2000 MPa, E_Ke1 = 1000 MPa, η_Kv1 = 8.64 × 10⁸ MPa.s, ν_e1 = 0.3. The anisotropy degree is defined as λ = $\frac{{E_{ij1}^{{}} }}{{E_{ij2} }}$ = $\frac{{\eta_{ij1}^{{}} }}{{\eta_{{{\text{ij}} 2}} }}$ = $\frac{{\nu_{e1}^{{}} }}{{\nu_{e2} }}$ (i = M, K; j = e, v), and λ = 1 represents the isotropic mechanical model. The shear moduli were determined through Eq. (4). The applied initial stresses are p_x = K₀ p_y in the x-direction and p_y = 20 MPa in the y-direction.

5.1 Influence of the selection of the constitutive models

The tunnelling response of four different cases is investigated: (1) isotropic elastic model (λ = 1), (2) anisotropic elastic model (λ = 1.25), (3) isotropic Generalized Kelvin model (λ = 1), (4) anisotropic Generalized Kelvin model (λ = 1.25). Isotropic initial stresses are applied in this section, i.e. K₀ = 1. The rotation angle α is adopted as 0.

In some applications, the displacements of the tunnel wall increase with time and achive a stable value (the maximum one) when the time is big enough. The final stable displacements are presented in Fig. 15. For cases of K₀ = 1, i.e. isotropic initial stresses, it is well known that the assumption of isotropy will lead to uniform stresses and displacements. It can be also found that the distribution of deformations for isotropic elastic and isotropic viscoelastic models are uniform under isotropic initial stresses, however, the distribution of deformations for anisotropic models is non-uniform. This type of non-uniform distribution of tunnelling response results from the anisotropic properties of geomaterials. As shown in Fig. 15(a), in these examples of anisotropic models, the displacements first increase to the peak value at θ = 90 deg and then decrease to the minimum value at θ = 180 deg.

Fig. 15

Displacements along the tunnel wall (in absolute value) a Final stable total displacements versus angle θ; b Displacements versus time at θ = 90 deg. The definition of ‘Angle’ can be found in Fig. 10

The displacements versus time for the above aforementioned four mechanical models are plotted in Fig. 15(b), where the quantities are at the gallery with θ = 90 deg. The elastic responses are time-independent. The viscoelastic displacements increase with time and finally reach stable values, while the increasing rate is decreased versus time. The difference between stable displacements of the isotropic elastic model (or anisotropic elastic model, isotropic viscoelastic model) and final displacements of the anisotropic viscoelastic model, approximately accounts for 73.8% (or 66.7%, 21.4%) of the anisotropic viscoelastic results. Therefore, the mechanical response of tunnels heavily depends on the time-dependent behaviour as well as anisotropic properties. At this point, the proposed time-dependent anisotropic model may be useful to reproduce the actual behaviour of geomaterials.

5.2 Effect of the anisotropy of geomaterials

In this section, the influence of anisotropy degree (λ) on the resulting displacements are analysed with α = 0 and K₀ = 1 in all cases. Three different anisotropy degree are adopted, λ = 0.65, 1.0 and 1.35. According to the symmetry of the problem, only the quantities between θ = 0–180 deg are discussed herein.

As shown in Fig. 16, for cases of λ bigger than 1.0, the displacements first increase to the peak value around θ = 90 deg and then decrease. However, the variations of the displacements against the polar angle θ are opposite to those with λ less than 1.0. The bigger values of λ, the smaller values of displacements, because the bigger values of λ would result in the smaller stiffness of geomaterials.

Fig. 16

Total displacements (in absolute value) along the tunnel wall versus the angle θ

In Fig. 17, the difference of displacements under different values of λ depend on locations. The maximum difference in these cases of final stable displacements due to λ accounts for 20.4% and 54.4% of the largest displacements for θ = 0 and θ = 90 deg, respectively.

Fig. 17

Total displacements along the tunnel wall (in absolute value) versus time for: a θ = 0 deg; and b θ = 90 deg

5.3 Influence of the lateral pressure ratio and the bedding plane directions

In geotechnical engineering, the initial stress in the vertical direction is normally different from the stress in the horizontal direction. The lateral pressure ratio K₀ is defined as the horizontal initial stress over the vertical stress. To analyse the effect of the lateral pressure ratios on boreholes deformations, three options are considered: (1) K₀ = 0.65, (2) K₀ = 1.0, (3) K₀ = 1.35. Note that λ is adopted as 1.35 in all cases of this section.

Because the isotropic initial stresses state is assumed for cases of K₀ = 1.0, the results for the case of α = 90 deg are the same as the results of α = 0 deg by simply rotating the coordinate by 90 deg. Moreover, the maximum value of displacements is the same for above both cases, although the maximum values are achieved at different locations, as shown in Figs. 18, 19 and 20.

Fig. 18

The distributions of the final stable displacements at time t = 60 days

Fig. 19

Time evolution of the geometry and total displacements (in absolute value) for different lateral pressure ratios. The factor of deformed mesh is adopted as 10.0. α = 0 deg

Fig. 20

Time evolution of the geometry and total displacements (in absolute value) for different lateral pressure ratios. The factor of deformed mesh is adopted as 10.0. α = 90 deg

In Figs. 18, 19 and 20, it can be found that the deformation patterns and the values of displacements are affected by the lateral pressure ratio coupled with the bedding plane directions α. Under anisotropic initial stresses, different bedding plane directions will result in different maximum displacements, which are critical to underground structures safety analysis. Moreover, in Figs. 19, 20, it can be found that in all cases the displacements progressively increase over time and, the deformation patterns are similar at different times.

6 Conclusions

This article provides an alternative anisotropic time-dependent constitutive model for geomaterials. In the proposed constitutive model, anisotropic properties are incorporated in the elastic springs and viscous dashpots of the viscoelastic models and, thus the proposed model can simulate the coupled behaviour between time-dependency and anisotropy.

The proposed constitutive model has been implemented into the finite element method (FEM) software CODE_BRIGHT. The numerical implementation has been verified by a comparison between the CODE_BRIGHT results and other numerical or analytical results. After that, numerical validations are carried out through the comparison between CODE_BRIGHT results and experimental data. Finally, the effects of different factors are investigated, including the selection of different constitutive models, anisotropy of initial stresses and anisotropic properties of geomaterials. The proposed approach can be utilized in the preliminary design of underground excavation in anisotropic time-dependent geomaterials. Some conclusions may be drawn from the parametric analyses:

• (1) The mechanical response of the considered underground excavation heavily depends on the time-dependent behaviour and on anisotropy. Therefore, the proposed anisotropic time-dependent model might be useful to reproduce the actual behaviour of some geomaterials.

• (2) For underground excavation problems, the deformations progressively increase over time and, exhibit an anisotropic response in the whole excavation and operation period. The deformation patterns heavily depend on the anisotropy of initial stresses and the anisotropic properties of geomaterials.

Although the proposed model can reproduce the behaviour of many different rock masses, there are still some limitations. For example, the response of the accelerated creep stage has not been incorporated, the numerical analyses are carried out through homogeneous material models and the viscous properties are considered to be independent from the stress state. In future research, viscous properties could be considered stress dependent, and a degradation viscoelastic model or an anisotropic viscoelastic-viscoplastic model could be proposed to consider the influence of accelerated creep behaviour, thus improving the applicability of the numerical approach to real engineering works.

Appendix: The expressions of transformation matrices

In this article, global coordinate system (x, y, z) first rotate around z-axis for α deg, and then around x-axis for β deg, to obtain the local coordinate system (1, 2, 3), as shown in Fig. 5. Thus, the transformation matrices can expressed in Eqs. (19) and (20).

$${\text{T}}_{\text{D}}^{{}} = \left[ \begin{gathered} l_{1}^{2} ,m_{1}^{2} ,0,2l_{1}^{{}} m_{1}^{{}} ,0,0 \hfill \\ l_{2}^{2} ,m_{2}^{2} ,n_{2}^{2} ,2l_{2}^{{}} m_{2}^{{}} ,2m_{2}^{{}} n_{2}^{{}} ,2n_{2}^{{}} l_{2}^{{}} \hfill \\ l_{3}^{2} ,m_{3}^{2} ,n_{3}^{2} ,2l_{3}^{{}} m_{3}^{{}} ,2m_{3}^{{}} n_{3}^{{}} ,2n_{3}^{{}} l_{3}^{{}} \hfill \\ l_{1}^{{}} l_{2}^{{}} ,m_{1}^{{}} m_{2}^{{}} ,0,l_{1}^{{}} m_{2}^{{}} + l_{2}^{{}} m_{1}^{{}} ,m_{1}^{{}} n_{2}^{{}} ,n_{2}^{{}} l_{1}^{{}} \hfill \\ l_{2}^{{}} l_{3}^{{}} ,m_{2}^{{}} m_{3}^{{}} ,n_{2}^{{}} n_{3}^{{}} ,l_{2}^{{}} m_{3}^{{}} + l_{3}^{{}} m_{2}^{{}} ,m_{2}^{{}} n_{3}^{{}} + m_{3}^{{}} n_{2}^{{}} ,n_{2}^{{}} l_{3}^{{}} + n_{3}^{{}} l_{2}^{{}} \hfill \\ l_{3}^{{}} l_{1}^{{}} ,m_{3}^{{}} m_{1}^{{}} ,0,l_{1}^{{}} m_{3}^{{}} + l_{3}^{{}} m_{1}^{{}} ,m_{1}^{{}} n_{3}^{{}} ,n_{3}^{{}} l_{1}^{{}} \hfill \\ \end{gathered} \right]$$

(19)

$${\text{T}}_{C}^{{}} = \left[ \begin{gathered} l_{1}^{2} ,m_{1}^{2} ,0,l_{1}^{{}} m_{1}^{{}} ,0,0 \hfill \\ l_{2}^{2} ,m_{2}^{2} ,n_{2}^{2} ,l_{2}^{{}} m_{2}^{{}} ,m_{2}^{{}} n_{2}^{{}} ,n_{2}^{{}} l_{2}^{{}} \hfill \\ l_{3}^{2} ,m_{3}^{2} ,n_{3}^{2} ,l_{3}^{{}} m_{3}^{{}} ,m_{3}^{{}} n_{3}^{{}} ,n_{3}^{{}} l_{3}^{{}} \hfill \\ 2l_{1}^{{}} l_{2}^{{}} ,2m_{1}^{{}} m_{2}^{{}} ,0,l_{1}^{{}} m_{2}^{{}} + l_{2}^{{}} m_{1}^{{}} ,m_{1}^{{}} n_{2}^{{}} ,n_{2}^{{}} l_{1}^{{}} \hfill \\ 2l_{2}^{{}} l_{3}^{{}} ,2m_{2}^{{}} m_{3}^{{}} ,2n_{2}^{{}} n_{3}^{{}} ,l_{2}^{{}} m_{3}^{{}} + l_{3}^{{}} m_{2}^{{}} ,m_{2}^{{}} n_{3}^{{}} + m_{3}^{{}} n_{2}^{{}} ,n_{2}^{{}} l_{3}^{{}} + n_{3}^{{}} l_{2}^{{}} \hfill \\ 2l_{3}^{{}} l_{1}^{{}} ,2m_{3}^{{}} m_{1}^{{}} ,0,l_{1}^{{}} m_{3}^{{}} + l_{3}^{{}} m_{1}^{{}} ,m_{1}^{{}} n_{3}^{{}} ,n_{3}^{{}} l_{1}^{{}} \hfill \\ \end{gathered} \right]$$

(20)

where l₁ = cos α, l₂ =—sin α cos β, l₃ = sin α sin β, m₁ = sin α, m₂ = cos α cos β, m₃ =—cos α sin β, n₂ = sin β, n₃ = cos β. In this study, for 2D problems, only α is needed to define the orientation of the isotropic plane and β = 0 deg.

$$\left[ {{\text{T}}_{D}^{{}} } \right]{\upsigma } = D_{{}}^{local} \left[ {T_{C}^{{}} } \right]{\upvarepsilon }$$

(21)

$$\left[ {T_{C}^{{}} } \right]{\upvarepsilon } = C_{{}}^{local} \left[ {T_{D}^{{}} } \right]{\upsigma }$$

(22)

Combining with $\left[ {T_{C}^{{}} } \right]_{{}}^{T} = \left[ {T_{D}^{{}} } \right]_{{}}^{ - 1}$ and $\left[ {T_{D}^{{}} } \right]_{{}}^{T} = \left[ {T_{C}^{{}} } \right]_{{}}^{ - 1}$, Eqs. (21) and (22) can be determined to Eqs. (23) and (24).

$${\upsigma } = \left[ {T_{C}^{{}} } \right]_{{}}^{T} D_{{}}^{local} \left[ {T_{C}^{{}} } \right]{\upvarepsilon }$$

(23)

$${\upvarepsilon } = \left[ {T_{D}^{{}} } \right]_{{}}^{T} C_{{}}^{local} \left[ {T_{D}^{{}} } \right]{\upsigma }$$

(24)

Thus, the compliance matrix C (or the stiffness matrix D) can be expressed in Eqs. (25) and (26).

$${\text{C}} = \left[ {T_{D}^{{}} } \right]_{{}}^{T} C_{{}}^{local} \left[ {T_{D}^{{}} } \right]$$

(25)

$${\text{D}} = \left[ {T_{C}^{{}} } \right]_{{}}^{T} D_{{}}^{local} \left[ {T_{C}^{{}} } \right]$$

(26)