Impact of injection rate ramp-up on nucleation and arrest of dynamic fault slip

Abstract

Fluid injection into underground formations reactivates preexisting geological discontinuities such as faults or fractures. In this work, we investigate the impact of injection rate ramp-up present in many standard injection protocols on the nucleation and potential arrest of dynamic slip along a planar pressurized fault. We assume a linear increasing function of injection rate with time, up to a given time $t_c$ after which a maximum value $Q_m$ is achieved. Under the assumption of negligible shear-induced dilatancy and impermeable host medium, we solve numerically the coupled hydro-mechanical model and explore the different slip regimes identified via scaling analysis. We show that in the limit when fluid diffusion time scale $t_w$ is much larger than the ramp-up time scale $t_c$, slip on an ultimately stable fault is essentially driven by pressurization at constant rate. Vice versa, in the limit when $t_c/t_w \gg 1$, the pressurization rate, quantified by the dimensionless ratio $\dfrac{Q_m t_w}{t_c Q^*}$ with $Q^*$ being a characteristic injection rate scale, does impact both nucleation time and arrest distance of dynamic slip. Indeed, for a given initial fault loading condition and frictional weakening property, lower pressurization rates delay the nucleation of a finite-sized dynamic event and increase the corresponding run-out distance approximately proportional to $\propto \left( \dfrac{Q_m t_w}{t_c Q^*}\right) ^{-0.472}$. On critically stressed faults, instead, the ramp-up of injection rate activates quasi-static slip which quickly turn into a run-away dynamic rupture. Its nucleation time decreases non-linearly with increasing value of $\dfrac{Q_m t_w}{t_c Q^*}$ and it may precede (or not) the one associated with fault pressurization at constant rate only.

1 Introduction

Anthropogenic fluid injection into underground formations is a common operation in many industrial applications. In the context of deep geothermal energy extraction, for instance, fluid is injected into targeted deep fault/fracture zones in order to enhance reservoir permeability and hence fluid circulation between injection and production wells (Giardini 2009; Deichmann and Giardini 2009). Among other applications that involve injection of fluid into subsurface there are hydraulic fracturing for oil and gas extraction from hydrocarbon reservoirs and wastewater disposal using deep wells (Warpinski and Teufel 1987; Horton 2012).

Although these engineering techniques are widely used, the injection of fluids into underground formations alters the local equilibrium of the Earth’s crust, inducing micro-seismicity and, in some cases, large earthquakes (Horton 2012; Ellsworth 2013; Kim 2013; Keranen et al. 2014; Weingarten et al. 2015). Significant earthquakes have been directly correlated with the injection activities, among these the Pohang earthquake of 2017 in South Korea with $M_w = 5.5$ (Kim et al. 2018; Grigoli et al. 2018; Yeo et al. 2020), the four $M_w = 3$ events in Basel, Switzerland, between 2006 and 2007 (Deichmann and Giardini 2009; Goertz-Allmann et al. 2011), an event of $M_w=3.5$ in the city of St. Gallen, Switzerland, back in 2013 (Diehl et al. 2014; Edwards et al. 2015; Diehl et al. 2017) and the $M_w =5.7$ earthquake near Prague, Oklahoma, in 2011 (Keranen et al. 2013; Sumy et al. 2014).

Many numerical and theoretical models have been developed in order to investigate the impact of operational design parameters, such as injection pressure or injection rate, on fault slip activation and earthquakes nucleation upon fluid injection. Most of them are based on a Rate- and State-dependent friction model and, therefore, are well suited to explain features of earthquake cycles and seismicity rates. For example, Dempsey and Riffault (2019) used a pressure diffusion model coupled to R&S friction model to show that a reduction in injection rate may lead to a decrease in the seismicity rate in Oklahoma (USA). A similar result has been obtained by Lagenbruch and Zoback (2016) using instead a statistical model calibrated over many injection induced-earthquakes in Oklahoma. Using a poroelastic model incorporating R&S friction, Barbour et al. (2017) observed that in Oklahoma a variable injection rate may lead to a larger seismicity rate increases compared to the one under constant injection rate (for an equivalent injected volume). Chang et al. (2018), instead, studied the effect of injection rate variation on seismicity rate post shut-in and they showed that a gradual reduction of injection rate minimises the post-injection seismicity rate. Using a Dietrich-Ruina heterogeneous 2D fault, Almakari et al. (2019) investigated the effect of injection scenario not only in terms of seismicity rate, but also in terms of magnitude content. They showed that the total seismic moment increases with both maximum pressure and pressure rate and that the total number of induced seismic events is controlled by the maximum pressure. A recent study of Rudnicki and Zhan (2020) on a spring-block model shows that larger pressurization rates stabilize fault slip events due to rate and state friction.

The role of injection design parameters on fault slip behaviour has been extensively investigated also in many laboratory experiments. Among others, Wang et al. (2020) showed that fault slip propagation is manly governed by fluid pressurization rate rather than injection pressure. French et al. (2016), instead, observed that fluid pressurization is less effective than mechanical changes in the fault normal stress at initiating accelerated slip events. The effect of fluid pressure oscillations on fault slip stability has been investigated by Noël et al. (2019) via a triaxial laboratory experiment. They showed that perturbations caused by pore fluid oscillations promote seismic slip and that seismic activity along a fault increases for increasing oscillation’s amplitudes.

Despite the numerous studies on the effects of injection parameters on earthquakes nucleation and occurrence along faults, the impact of pressurization rate on the onset of dynamic fault slip remains still elusive. Garagash and Germanovich (2012) investigated extensively the conditions of nucleation and arrest of dynamic fault slip on a frictional weakening pressurized 2D fault. This work was then extended by Galis et al. (2017) to planar 3D faults subjected to point source injection and axisymmetric diffusion. Their generic findings, however, are valid only for two types of fault pressurizations, constant over-pressure and constant injection rate, which are over-simplification of many injection protocols commonly used in industrial applications. In numerous fault reactivation experiments, for instance related to deep geothermal energy exploitation, the injection protocol consists of one (or more) stimulation cycle, where the controlled injection rate or injection pressure increases in time (typically with stair-like increments), up to reach a steady state regime, followed then by a shut-in phase (Hofmann et al. 2018). In the hydraulic stimulation experiments conducted in Grimsel Test Site, Switzerland, back in 2017 for example, the injection protocol consisted of 4 injection cycles in which either injection pressure or injection flow rate was increased in a stepwise manner, before reaching a plateau and shut-in phase (Villiger et al. 2020). A similar trend of injection rate was also used during the hydraulic stimulation of Enhanced Geothermal System in the city of Basel, Switzerland (2006) (Häring et al. 2008) and in the more recent EGS project in Pohang, South Korea (Hofmann et al. 2018), to cite a few examples.

In this contribution, we extend the model of Garagash and Germanovich (2012) to account for an initial ramp-up of injection rate in time and investigate its effect on dynamic fault slip nucleation and arrest. We approximate the step-wise increase of injection rate adopted in standard injection protocols using a simple linear increasing function with time, followed by a maximum plateau (the shut-in phase is out of context and thus is not considered in this work). This choice represents a good approximation when the time scale of each increment is much larger that the corresponding one of each step (and thus a linear increasing function is a reasonable approximation). We solve the two-dimensional hydro-mechanical problem numerically and verify the results with theoretical predictions. The goal of this study is to evaluate the effects of the pressurization rate, quantified by the injection rate ramp-up variation, on the nucleation and arrest of a seismic rupture on a frictional weakening planar fault.

2 Fault model

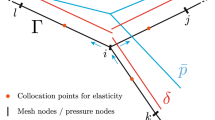
We consider a planar fault embedded in an isotropic, homogeneous and unbounded elastic medium under plane-strain conditions (see Fig. 1). The fault is subjected to an ambient pore-pressure $p_o$ and a uniform far-field stress state that resolved on the fault plane result in an effective normal $\sigma ^\prime _o = \sigma _n - p_o$ and shear $\tau ^o$ stress component. Such a uniform ambient stress state, typical of a limited fault extent compared to the background in-situ gradient, is perturbed via a point source injection of volumetric flow rate Q(t) $\left[ L^2/T\right]$ directly in the middle of the fault (specifically at $x=0$). In order to investigate the effect of injection rate ramp-up on fault slip stability, we consider a linear increase of injection flow rate in time, followed by a plateau after a given time $t_c$ (the shut-in phase is out of scope here, hence it will not be considered—see Fig. 1). This parametrisation represents an approximation of many standard fault injection protocols used in hydro-shearing stimulation of fractured reservoirs, in which the design (constant) value of injection rate is reached upon stair-like increments.

Prior fluid injection, we assume that the fault is in static equilibrium with the uniform in-situ stress state (locked status). This tacitly assumes that there is no effect of remote plates loading that would cause steady movements with slow energy release (creep) (Chen and Bürgmann 2017). The ambient equilibrium is violated throughout pressurization, during which pore-pressure perturbation diffuses along the fault plane and activates a symmetric shear crack of length 2a. This scenario of mechanically weak, fault unit accommodating slip and pore fluid flow may be representative of a highly permeable thick unit in a damage zone of a fault zone, whose hydraulic conductivity is much larger than the one of the host rock around it (and thus impermeable host medium is a reasonable assumption).

Fig. 1

Plane-strain fault model subjected to a far-field stress state and fluid injection. The conductive planar fault is embedded into an homogeneous, isotropic and linear-elastic medium characterized by a negligible hydraulic diffusivity. The thin fault gouge unit, therefore, accommodates accelerating slip due to friction weakening condition and pore-pressure diffusion

Before presenting the governing equations, it must be noted that we assume normal stresses positive in compression and shear stresses positive for clockwise rotation. Furthermore, thermal effects, dilatancy/compaction during shear deformations and poroelastic stress changes in the surrounding medium are neglected.

2.1 Governing equations for quasi-static slip development driven by pore-pressure diffusion

2.1.1 Static equilibrium and constitutive law for frictional slip

We consider the activation and propagation of a symmetric shear crack of length 2a driven by pore fluid flow inside the conductive fault plane. The shear stress $\tau$ at a given time t and position x on the slip surface is linearly related to slip $\delta$ (or shear displacement discontinuity) within the slipping region via the following quasi-static elastic equilibrium equation

$$\begin{aligned} \tau (x,t) = \tau ^o - \frac{E_p}{4 \pi } \int _{a_{-}(t)}^{a_{+}(t)} \frac{\partial \delta (\zeta ,t)/ \partial \zeta }{\zeta - x} \text {d}\zeta , \end{aligned}$$

(1)

where $a_+$ and $a_-$ are respectively the positive and negative positions of the crack tips, $\tau ^o$ is the uniform background shear stress, $E_p = \dfrac{2 G}{1-\nu }$ is the plane-strain Young’s modulus (with G and $\nu$ being shear modulus and Poisson’s ratio, respectively), $\partial \delta (\zeta ,t)/\partial \zeta$ is the shear dislocation density along the crack that must satisfy the following condition

$$\begin{aligned} \lim _{\zeta \rightarrow a_{\pm }(t)} \frac{\partial \delta (\zeta ,t)}{\partial \zeta } \sqrt{a \mp \zeta } = 0 \end{aligned}$$

(2)

in order to remove stress singularity at crack tips (Uenishi and Rice 2003), and $\dfrac{1}{\zeta - x}$ is the non-local elastic kernel. For merely planar frictional problems that do not account for dilatancy or compaction during crack propagation, the elastic kernel affects only the shear stress distribution along the fault plane, while the uniform total normal stress $\sigma _n$ remains constant.

Inside the sliding region, the force balance requires that the shear stresses must equal the available frictional resistance which we assume here to obey the Mohr-Coulomb yielding criterion (without cohesion), accounting for a slip weakening of friction coefficient

$$\begin{aligned} \tau (x,t) = f(\delta ) \left( \sigma _n - p(x,t)\right) , \qquad \left| x\right| \le a(t) \end{aligned}$$

(3)

where $(\sigma _n - p(x,t)) = \sigma _n^\prime (x,t)$ is the local effective normal stress, strictly function of pore-pressure evolution p(x, t) inside the fault, and $f(\delta )$ is the slip weakening friction coefficient

$$\begin{aligned} f(\delta ) = {\left\{ \begin{array}{ll} f_p - \frac{(f_p - f_r)}{\delta _r} \cdot \delta \quad &{} \delta \le \delta _r\\ f_r \quad &{}\delta > \delta _r \end{array}\right. } \end{aligned}$$

(4)

The frictional resistance, therefore, weakens linearly with shear deformations $\delta$, from a peak value associated with peak friction coefficient $f_p$, to a residual value, after sufficiently large slip $\delta _r$ (such that the friction coefficient drops to its residual value $f_r$). Although more complicated frictional laws can be considered in (3), we use here the simple piece-wise linear weakening of friction coefficient with slip, which can be shown to be a good approximation of the phenomenological rate- and state- friction law at large slip rates and for small values of a/b (Uenishi and Rice 2003; Rubin and Ampuero 2005), or when $\varDelta f_p/b \gg 1$, with $\varDelta f_p$ being the peak change of friction coefficient from the steady-state value (Garagash 2021). Since the total weakening $\varDelta f_p$ on rate- and state- faults depends on the slip front speed, the condition $\varDelta f_p/b \gg 1$ holds when the front speed varies appreciably (see Fig. 4a in (Garagash 2021)) and thus the linear slip weakening friction law can realistically approximate the rate- and state- friction law.

2.1.2 Pore-pressure diffusion

Under the assumption of negligible fluid leak-off in the surrounding elastic medium, fluid flow is confined within the fault gouge unit characterised by a constant hydraulic aperture $w_h$. Upon injection of volumetric flow rate Q(t) at $x=0$, the diffusion of pore fluid over-pressure ${\bar{p}}(x,t) = p(x,t) - p_o$ is governed by the width-averaged fluid mass conservation equation

$$\begin{aligned} w_h c_f \frac{\partial {\bar{p}}}{\partial t} + \frac{\partial w_h v}{\partial x} = 0, \end{aligned}$$

(5)

where $c_f$ $\left[ M^{-1} T L^2\right]$ is a parameter that combines pore fluid compressibility and pore space expansivity and v is the gap-averaged fluid flow velocity given by the Poiseuille’s law

$$\begin{aligned} v = - \frac{k_f}{\mu } \frac{\partial {\bar{p}}}{\partial x}, \end{aligned}$$

(6)

where $k_f$ $\left[ L^2\right]$ is the longitudinal fault permeability and $\mu = 12 \mu ^\prime$ $\left[ M T^{-1} L^{-1}\right]$ is a viscosity parameter (with $\mu ^\prime$ as dynamic viscosity of the fluid).

The point injection boundary condition requires that

$$\begin{aligned} w_h v = \pm \frac{Q(t)}{2}, \qquad \text {at} \quad x=0^{\pm } \end{aligned}$$

(7)

where the volumetric flow rate Q(t) $\left[ L^2 T^{-1}\right]$ increases linearly with time t, up to reach a plateau after a given time $t_c$, i.e.

$$\begin{aligned} Q(t) = {\left\{ \begin{array}{ll} \frac{Q_m}{t_c} \cdot t \qquad &{}t\le t_c \\ Q_m \qquad &{}t > t_c\\ \end{array}\right. } \end{aligned}$$

(8)

Since we neglect dilatation/compaction of fault gouge unit during shear crack propagation, fault permeability $k_f$ and hydraulic aperture $w_h$ remain constant throughout pressurization. Equations (5) and (6), therefore, reduce to the well-known parabolic diffusion equation

$$\begin{aligned} \frac{\partial {\bar{p}}}{\partial t} - \alpha \frac{\partial ^2 {\bar{p}}}{\partial x^2} = 0 \end{aligned}$$

(9)

that govern over-pressure diffusion inside the fault conduit characterized by a constant hydraulic diffusivity $\alpha = \frac{k_f}{c_f \cdot \mu }$ $\left[ L^2 T^{-1}\right]$. Using specific boundary and initial conditions representative of the particular injection scenario and its time history, equation (9) can be solved analytically for the spatial and temporal evolution of pore-fluid over-pressure along the fault plane ${\bar{p}}(x,t)$ (see “Appendix” A for full details). During the ramp-up phase of injection rate, i.e. for $t\le t_c$, the over-pressure evolution in function of time t and the normalized coordinate $\xi = \dfrac{x}{\sqrt{4 \alpha t}}$ is given by

$$\begin{aligned} {\bar{p}}(\xi ,t\le t_c) = \underbrace{\left( \frac{2 Q_m \mu \sqrt{\alpha } t^{3/2}}{3 k_f \sqrt{\pi } t_c w_h}\right) }_{\varDelta P(t)} \cdot \underbrace{\left( \text {e}^{-\xi ^2} \left( 1+ \xi ^2\right) - \sqrt{\pi } \left| \xi \right| \left( \frac{3}{2} + \xi ^2\right) \text {Erfc}(\left| \xi \right| ) \right) }_{\varPsi (\xi )}, \end{aligned}$$

(10)

where $\text {Erfc}$ is the complementary error function. Notice that the analytical solution (10) is expressed as a product two independent functions, $\varDelta P(t)$ and $\varPsi (\xi )$, which identify respectively the maximum over-pressure evolution at injection point and its instantaneous spatial distribution.

The pore-fluid evolution after the ramp-up phase, instead, is governed by the following equation (Cole et al. 2011)

$$\begin{aligned} {\bar{p}}(x, t> t_c)= & {} \int _{-\infty }^{\infty }G(x-x^\prime , t - t_c) \cdot {\bar{p}}\left( \frac{x^\prime }{\sqrt{4 \alpha t_c}}, t_c \right) \text {d}x^\prime \nonumber \\&+ \frac{\alpha Q_m \mu }{w_k k_f} \int _{t^\prime =t_c}^{t} G(x, t - t^\prime ) \text {d}t^\prime \end{aligned}$$

(11)

where ${\bar{p}}\left( \dfrac{x^\prime }{\sqrt{4 \alpha t_c}}, t_c \right)$ denotes the over-pressure distribution at time $t_c$ and $G(x-x^\prime , t-t^\prime )$ is the fundamental heat conduction solution valid for an infinite one-dimensional body subjected to an instantaneous point source (also called Green’s function) (Carslaw and Jaeger 1959). We revert the reader to “Appendix” A for its analytical expression. It is worth mentioning that the solution (11) is valid for $t>t_c$ and it takes into account the whole injection history during the ramp-up phase. If $t_c$ vanishes, then we recover the analytical solution of pressurization at constant injection rate (see “Appendix” A).

In this contribution, we assume that maximum over-pressure occurring at injection point $x=0$ remains always below the ambient effective normal stress $\sigma ^\prime _o = \sigma _n - p_o$ applied on the fault plane, i.e.

$$\begin{aligned} \frac{{\bar{p}}(0,t)}{\sigma ^\prime _o} < 1, \quad \forall t \end{aligned}$$

(12)

implying that the minimum principal effective stresses $\sigma ^\prime _n(x,t)$ remain always compressive (positive) throughout pressurization and hydraulic fracturing type of failure never occurs (which would require the full coupling between flow and elastic deformations).

The along-fault pore-pressure diffusion changes the local effective normal stresses and hence drives the symmetric slip propagation when the Mohr-Coulomb criterion (3) is locally violated. Shear deformations, instead, do not affect pore-pressure evolution since shear-induced dilatancy or compaction is neglected and so fault permeability / porosity changes too. Although this assumption is debatable, since such inelastic deformations do affect slip stability on a planar fault with frictional weakening properties (Garagash and Rudnicki 2003; Zhang et al. 2005; Ciardo and Lecampion 2019), we want to minimise the complexities in the model and focus solely on the effect of injection rate ramp-up on the potential nucleation and arrest of dynamic slip. The hydro-mechanical model, therefore, is only one-way coupled and it is equivalent to the one proposed by Garagash and Germanovich (2012), with the difference that the point injection volumetric rate is not constant in time but changes according to (8).

We have introduced in the model an additional parameter $t_c$, therefore we expect another dimensionless parameter governing the hydro-mechanical fault’s response (on top of the ones introduced by Garagash and Germanovich (2012)). For sake of completeness we present and discuss in the next section all the dimensionless governing parameters resulting from scaling analysis (see “Appendix” B for more details), as well realistic values that are then used in the numerical simulations.

2.2 Dimensionless governing parameters

Upon normalization of all the governing equations (1-8) following Uenishi and Rice (2003); Garagash and Germanovich (2012) (see “Appendix” B), the hydro-mechanical fault response depends only on four dimensionless parameters:

• Stress criticality $\dfrac{\tau ^o}{\tau _p}$, which represents the closeness of the ambient fault stress state to failure (and thus to the peak shear strength $\tau _p = f_p \sigma _o^\prime$). Levandowski et al. (2018) claims that stress criticality is the most important factor for induced earthquakes hazard. Favourably oriented frictional weakening faults with respect to the in-situ stress field, typically characterised by a large stress criticality ($\dfrac{\tau ^o}{\tau _p}\lesssim 1$), are very susceptible to host run-away seismic ruptures. Indeed, a little stress perturbation is sufficient to re-activate slip and its velocity propagation tends to diverge rapidly due to friction weakening and possibly other weakening mechanisms, such us flash-heating and thermal pressurization (Viesca and Garagash 2015). Garagash and Germanovich (2012) have shown via a stability analysis that critically stressed pressurized faults, for which the relation $\tau ^o > \tau _r = f_r \sigma _o^\prime$ is strictly satisfied, host always the nucleation of an unabated dynamic event. Such a run-away rupture, however, can be suppressed when shear-induced dilatancy kicks-off and dilatant hardening stabilises slip propagation (Lockner and Byerlee 1994; Segall et al. 2008; Ciardo and Lecampion 2019). Critically stressed faults in seismogenic zones have been observed in Oklahoma and Southern Kansas (Qin et al. 2019), in the German continental deep drillhole (KTB) (Ito and Zoback 2000) and in central California along the San Andreas fault system (Zoback et al. 1987; Rice 1992) to cite a few examples.

  On the other hand, fault zones not favourably oriented to the local in-situ stress field are characterised by low stress criticality ($\dfrac{\tau ^o}{\tau _p} \gtrsim 0$), which implies that larger over-pressures are required to activate slip. By making the analogy with critically stressed pressurized faults exhibiting linear slip-weakening behaviour, low stress criticality and $\tau ^o<\tau _r$ implies a quasi-static, stable slip propagation with eventually a nucleation and arrest of a dynamic event at large pressurization time (Garagash and Germanovich 2012).

  The role of the initial effective stress state on the nature of seismicity has been also investigated in fault lab experiments by Passelègue et al. (2020), where they show that faults with similar frictional properties can rupture at both slow and fast rupture velocity depending on their initial stress criticality, in agreement with theoretical predictions based on linear elastic fracture mechanics (LEFM).

• Friction weakening ratio $\dfrac{f_r}{f_p} = 1 - \dfrac{\delta _r}{\delta _w}$ that governs the shear stress drop within the crack tips (with $\delta _w = \dfrac{f_p}{(f_p - f_r)}\delta _r$ being the amount of slip at which the friction coefficient goes to zero if an unlimited linear slip-weakening friction law is considered). According to slip laboratory experiments of granite intact specimens, the slip weakening distance $\delta _r$ is approximately half a millimetre (Rice 1980), but it can drop even below 0.1 mm (Wong 1986). Similarly, $\delta _w$ is on the order of fault’s asperities and thus ranges between 0.1 and 10mm. The friction weakening ratio, therefore, can assume any values within the interval $\left( 0,1\right)$.

• Normalized maximum injection rate $\dfrac{Q_m}{Q^*}$, where $Q^* = \dfrac{2 \sigma ^\prime _o w_h k_f}{a_w \mu }$ is the characteristic injection rate scale and $a_w = \dfrac{E_p}{2 \tau _p}\delta _w$ is the slipping patch length-scale. Its value is typically in the order of a meter, but roughly one order of magnitude of variation is plausible due to the variation of $\delta _w$ with fault’s roughness and $\sigma _o^\prime$ with hydrogeological conditions. In normally pressurized formations, typically located in the Earth’s upper crust and characterised by lithostatic gradient and hydro-static pore-pressure conditions (Brace and Kohlstedt 1980; Grawinkel and Stockhert 1997), $\sigma _o^\prime$ may be a fraction of megapascals, while a boost to hundred of megapascals may be obtained in over-pressurized formations located below the fluid retention depth (Suppe 2014). Assuming a fluid viscosity parameter $\mu \sim 10^{-3} \text {Pa}\cdot \text {s}$ (water), a fault gouge permeability $k_f$ in the order of $\sim 10^{-16} \text {m}^2$ (Wibberley et al. 2008) and hydraulic width $w_h$ in the order of meters (representative of a relatively-high permeable thick unit typically present in a damage zone of a fault zone—see Sect. 4.2 for a more in-depth discussion), the injection rate characteristic scale $Q^*$ ranges between $\sim 10^{-6}\text {m}^2/\text {s}$ and $10^{-3} \text {m}^2/\text {s}$. If we assume that the out-of-plane fault length is $\sim 1$ km, then the volumetric injection rate scale would range between few to hundreds litres per second.

  The maximum injection rate $Q_m$ is a design parameter that can vary considerably from tens or hundreds litres per second in hydraulic-fracturing operations (see (Holland 2013) for one example where $> 160$ l/s were injected in south-central Oklahoma), to few or fractions of litres per second for hydro-shearing stimulations (see for instance hydro-shearing experiments in Grimsel Test Site, Switzerland, where the maximum injection rate never exceeded 0.5 l/s (Villiger et al. 2020)).

  The dimensionless parameter $\dfrac{Q_m}{Q^*}$, therefore, can assume relatively low or large values depending on the specific problem configuration. Since hydraulic fracturing type of failure is not considered in our model, all the numerical results that will be presented later are characterised by a relatively low/moderate value of $\dfrac{Q_m}{Q^*}$.

• $\dfrac{t_c}{t_w} \rightarrow$ ratio between the ramp-up time scale and along-fault diffusion time-scale $t_w = \dfrac{a_w^2}{4 \alpha }$. This ratio may vary considerably due to the variation of slipping patch length-scale $a_w$ previously discussed, the specific fault hydraulic properties considered as well as the choice of the parameter $t_c$. Assuming a compressibility parameter $c_f\sim 0.5$ $\text {GPa}^{-1}$ (Wibberley 2002) and the hydraulic parameters previously defined (albeit the fault longitudinal permeability may range within the interval $10^{-19}-10^{-15}$ $\text {m}^2$), we estimate an hydraulic diffusivity of $\alpha \sim 2\cdot 10^{-4}$ $\text {m}^2/\text {s}$, which leads to a diffusion time scale of $t_w \sim 21$ $\text {min}$ for $a_w = 1$ $\text {m}$.

  The parameter $t_c$ may be in the order of several minutes for relatively fast fault pressurizations (see for instance one cycle of the injection protocol used for one hydro-shearing stimulation in Grimsel, Switzerland (Amann et al. 2018)), but it may get up to several hours or few days for relatively slow pressurizations (see for instance the injection protocol used for hydraulic stimulation of Pohang Enhanced Geothermal System, 2017 (Yeo et al. 2020; Hofmann et al. 2018)). The ratio $t_c/t_w$, therefore, may be very large, in the order 1 or possibly very small.

In the following we explore the parameter space identified by these dimensionless ratios via numerical simulations. We vary them systematically in order to investigate their impact on the nucleation and arrest (if occur) of dynamic fault slip.

3 Numerical results

Fig. 2

Map of slip regimes for a frictional weakening pressurized fault (adapted from Garagash and Germanovich (2012)), as function of stress criticality $\tau ^o/\tau _p$, friction weakening ratio $f_r/f_p$ and normalized (constant) injection rate $Q_m/Q^*$. Region (1) corresponds to the scenario of an ultimately stable fault in which pressurization leads always to quasi-static (stable) slip propagation. Region (2) corresponds to the case of quasi-static slip propagation, followed by a nucleation and arrest of dynamic slip. Regions (4b) and (4a), instead, represent the scenarios of an unstable fault exhibiting quick quasi-static crack propagation followed by an unabated dynamic rupture, whose nucleation is affected or not by residual friction coefficient $f_r$, respectively. Finally, in region (3) the nucleation of a run-away rupture on an unstable fault is preceded by a finite-sized seismic event

We use a fast boundary element based solver in order to solve numerically the one-way coupled hydro-mechanical problem (1-11) (see details in (Ciardo et al. 2020)). It is suited for 2D non-linear geo-mechanical problems involving localized inelastic deformations along pre-existing structural discontinuities, such as faults or fractures. The elasto-static balance of momentum (1) is discretized using displacement discontinuity method that, together with the discretized form of shear weakening Mohr-Coulomb criterion (3), lead to a non-linear system of equations for the unknowns inelastic deformations (or displacement discontinuities) and effective tractions. For a given pore-pressure history calculated using (10) and (11) (with the latter evaluated numerically using a trapezoidal quadrature rule), such a resulting system is solved iteratively using fixed point iterations combined with under-relaxation (Quarteroni et al. 2000), and adopting a fully implicit integration scheme in time. A speed up of computations is obtained via hierarchical approximation of the fully populated elasticity matrix (on top of memory reduction), together with the use of an adequate block pre-conditioner that improves spectral properties of the resulting matrix of coefficients (see full details in (Ciardo et al. 2020)).

All the numerical results that will be presented in the following are obtained by considering a sufficiently long planar fault such that $L_o/a_w = 40$, with $L_o$ being its half-length. The planar fault is then uniformly discretized with $2\cdot 10^3$ equal-sized straight elements, resulting in having 50 elements inside the slip weakening region near crack tips (sufficient to accurately capture the model non-linearity).

3.1 Ultimately stable fault ($\tau ^o < \tau _r$)

Firstly, we present the case of fluid injection into an ultimately stable fault characterised by $\tau ^o/\tau _r < 1$, where $\tau _r = f_r \sigma ^\prime _o$ is the residual frictional strength prior pressurization. This condition automatically implies that the fault is far from being critically stressed, and thus the ratio $\tau ^o/\tau _p$ is kept relatively low. By fixing the frictional weakening ratio to $f_r/f_p = 0.6$, we investigate the fault’s hydro-mechanical response for different values of normalized maximum injection rate $Q_m/Q^*$, in the two plausible limiting scenarios of $t_c/t_w \ll 1$ and $t_c/t_w \gg 1$.

3.1.1 Fast ramp-up: the limit when $t_c/t_w \ll 1$

If the diffusion time-scale $t_w$ is much larger than the ramp-up time $t_c$ of injection rate, slip activation and propagation occurs when the injection rate has already reached its maximum value $Q_m/Q^*$. The quick ramp-up of injection rate has a negligible effect on pore-pressure evolution and the hydro-mechanical fault response is essentially driven by injection at constant volumetric rate. Garagash and Germanovich (2012) studied extensively the effect of such a type of fault pressurization on the nucleation and potential arrest of a dynamic event. They came up with a slip regimes diagram reported in Fig. 2, in which a frictional weakening planar fault may experience a finite-sized dynamic event (region (2)), a run-away rupture (affected or not by the residual friction coefficient $f_r$, region (4b) and (4a) respectively), a finite-sized dynamic event followed by an unabated seismic rupture (region (3)), or only aseismic slip (region (1)). This depends on the particular set of dimensionless parameters that identifies a specific initial fault loading condition, pressurization and frictional property. Their theoretical and semi-analytical results, therefore, provide benchmark solutions for our numerical results.

Under ultimately stable conditions (i.e. $\tau ^o < \tau _r$, left side of Fig. 2), Garagash and Germanovich (2012) proved via a stability analysis that a fault experiences a stable, quasi-static growth of slipping patch throughout sustained pressurization (i.e. aseismic slip). However, for sufficiently low injection rates $Q_m/Q^*$, the fault exhibits a finite-sized dynamic event, whose nucleation time $t_n$ is considerably larger than fluid diffusion time-scale $t_w$ (and thus $t_c \ll t_w \ll t_n$).

Fig. 3

Time evolution of normalized half-crack length $a/a_w$ (black solid lines) as function of various stress criticality values $\tau ^o/\tau _p$, for two values of maximum injection rates $Q_m/Q^* = 0.05, 0.5$ and $t_c/t_w = 0.01\ll 1$. The friction weakening ratio is set to $f_r/f_p = 0.6$, resulting in ultimately stable conditions, i.e. $\tau ^o < \tau _r$ for each value of ambient fault loading condition. Grey dashed lines represent the small scale yielding (s.s.y.) solutions (see “Appendix” C) associated with constant injection rate type of pressurization, which represents a good approximation of the hydro-mechanical fault response when $t_c/t_w \ll 1$. In this particular example, indeed, the normalized ramp-up time is $\sqrt{4 \alpha t_c}/a_w = 0.1$ and thus shear crack activation and propagation is essentially driven at constant injection rate. Red dots, instead, denote the nucleation and arrest of dynamic slip

Fig. 4

Normalized slip $\delta /\delta _w$, shear stress $\tau /\tau _p$ and friction coefficient $f/f_p$ profiles at different normalized time snapshots, for the case of maximum injection rate $\dfrac{Q_m}{Q^*} = 0.05$, ramp-up time scale $t_c/t_w = 0.01\ll 1$ and two stress criticality values, i.e. $\tau ^o/\tau _p = 0.4$ and 0.6 (ultimately stable faults as $f_r/f_p = 0.6$). Dashed blue and black lines correspond to the numerical solutions at nucleation time $t_n$ (or in normalized form $\dfrac{\sqrt{4 \alpha t_n}}{a_w}$), while dashed vertical red lines denote the asymptotic solution (13) provided by Garagash and Germanovich (2012)

These considerations are also confirmed with our numerical results reported in Fig. 3, where the normalized time evolution of half crack length $a/a_w$ is displayed for two different values of $Q_m/Q^* = 0.05, 0.5$ and different values of low/moderate stress criticality $\tau ^o/\tau _p$ (with the ratio $t_c/t_w$ equal to 0.01 and $\tau ^o$ always below or equal $\tau _r$).

For the case of low injection rate $Q_m/Q^* = 0.05$, a nucleation of dynamic event followed by an arrest always occurs for each value of stress criticality considered, with larger dynamic run-out distances for increasing values of $\tau ^o/\tau _p$ (see Fig. 3-left). Since the ambient effective stress states applied on the fault plane are far from failure, resulting in a stable quasi-static slipping patch propagation before reaching the nucleation time $t_n$ (or in normalized form $\sqrt{4 \alpha t_n}/a_w$), the shear crack tips are located well within the pressurized region. At nucleation time, the rupture is not affected by the residual friction coefficient $f_r$ (due to the low slip accumulation during quasi-static slip propagation phase) and its half-length assumes the asymptotic expression (Garagash and Germanovich 2012)

$$\begin{aligned} \frac{a_n}{ a_w} \simeq 0.579 \cdot \frac{\tau _p}{\tau ^o} \end{aligned}$$

(13)

A careful investigation of Fig. 4 that displays the corresponding slip, shear stress and friction coefficient profiles at different time snapshots (with dashed lines corresponding to the ones at nucleation time) and for two stress criticality values $\tau ^o/\tau _p = 0.4, 0.6$ confirms these theoretical predictions. It is worth noting at the arrest of the dynamic slip propagation, the friction coefficient has reached its residual value over almost the entire crack. The subsequent shear crack propagation, therefore, remains always stable in time as depicted in Fig. 3-left. In addition to this, Garagash and Germanovich (2012) proposed an asymptotic solution for the nucleation time $t_n$ that is valid for an ultimately stable fault that exhibits a dynamic event right after slip activation (similarly to the scenarios reported in Fig. 3-left). Under this condition, indeed, the shear crack at nucleation time is confined near injection point and is subjected to a uniform over-pressure equal to the minimum value required to activate slip, i.e. ${\bar{p}}(x\simeq 0,t_n) = (\tau _p - \tau ^o)/f_p$. This asymptotic solution reads (Garagash and Germanovich 2012)

$$\begin{aligned} \frac{\sqrt{4 \alpha t_n}}{a_w} \simeq \frac{\tau _p - \tau ^o}{f_p \varDelta P_w}, \end{aligned}$$

(14)

where $\varDelta P_w = \dfrac{Q_m a_w \mu }{2 k_f \sqrt{\pi }w_h}$ is the characteristic pore-pressure drop over the distance $a_w$. In order to guarantee that crack instability follows shortly after slip activation, $\varDelta P_w$ must be very small compared to ${\bar{p}}(x\simeq 0,t_n)$, resulting in the following necessary condition

$$\begin{aligned} \frac{Q_m}{Q^*} \ll \sqrt{\pi } \left( 1 - \frac{\tau ^o}{\tau _p}\right) \end{aligned}$$

(15)

The comparison between the nucleation times associated with numerical simulations reported in Fig. 3-left (for which $Q_m/Q^* = 0.05$ strictly satisfies the condition (15) for each value of stress criticality considered) and the asymptotic solution (14) is displayed in Fig. 5. A good agreement is obtained, specially for larger values of $\tau ^o/\tau _p$ for which the assumption of nucleation after activation is truly valid (see Fig. 3-left). Obviously, lower values of $Q_m/Q^*$ would lead to an earlier nucleation and thus a closer match between numerical and asymptotic solution.

Fig. 5

Comparison between the asymptotic solution (14) for ultimately stable faults valid for $t_c/t_w \ll 1$ and numerical solutions corresponding to the case of $t_c/t_w = 0.01$ and $Q_m/Q^* = 0.05$ (for which the necessary condition (15) is strictly satisfied for all values of $\tau ^o/\tau _p$ considered)

For a larger value of injection rate $Q_m/Q^* = 0.5$ (such to fall into region (1) of Fig. 2 for $\tau ^o/\tau _p < 0.6$), instead, the slipping patch propagates always quasi-statically for all values of $\tau ^o/\tau _p$, before reaching the maximum pressurization time $\sqrt{4 \alpha t_{max}}/a_w$ at which the condition (12) is violated (and at which all the simulations were stopped). One exception is a very small seismic event corresponding to the boundary case of $\tau ^o/\tau _p=0.6$—see Fig. 3-right. For values of normalized time larger than $\sqrt{4 \alpha t_{max}}/a_w$, a mixed mode fracture would propagate symmetrically from injection point, with a slipping patch located ahead of the tips of an opening (frictionless) patch. This problem has been studied by Azad et al. (2017) whose findings reveal that: i) the critical shear crack length $a_n/a_w$ and slip at the hydraulic fracture tips increase rapidly with decreasing value of stress criticality $\tau ^o/\tau _p$ (with $\tau ^o>\tau _r$), ii) the slip instability weakly depends on the injection rate applied and iii) fault slip development remains stable for $\tau ^o\le \tau _r$. From these considerations we can infer that after $\sqrt{4 \alpha t_{max}}/a_w$ the propagation of the slipping patch ahead of the hydraulic fracture tips will always be stable, with an increasing yet quasi-static slip rate for values of stress criticality approaching the boundary value $\tau ^o/\tau _p=0.6$.

These numerical results confirm that in case the maximum flow rate $Q_m$ is reached before pore fluid can actually diffuse into the fault, the hydro-mechanical fault response is essentially driven by pressurization at constant volumetric rate and a good match with theoretical results of Garagash and Germanovich (2012) is obtained. This is further strengthened by looking at the comparison between the numerical results reported in Fig. 3 (black lines) and the small-scale yielding (s.s.y.) asymptotic solutions (dashed grey lines) associated with pressurization at constant injection rate only (see “Appendix” C). For $a/a_w \gtrsim 2$, indeed, a perfect match is obtained, suggesting that the effect of the quick ramp-up phase on slip propagation is negligible.

3.1.2 Slow ramp-up: the limit when $t_c/t_w \gg 1$

We present here the opposite scenario in which injection rate increases linearly in time but the maximum value is reached after the pore fluid substantially diffuses along the fault plane (i.e. $t_c \gg t_w$). Under this condition, pore-pressure perturbation activates a shear crack (slip) during the ramp-up of injection rate, and the potential nucleation of a dynamic event would occur when pressurization is approaching the changing time $t_c$. In other words, $t_c \gg t_w$ and $t_n \lesssim t_c$.

Fig. 6

Time evolution of normalized half-crack length $a/a_w$ (black solid lines) as function of stress criticality $\tau ^o/\tau _p$, for two values of maximum injection rates $Q_m/Q^* = 0.05, 1$ and $t_c/t_w = 2\cdot 10^3\gg 1$. The friction weakening ratio is set to $f_r/f_p = 0.6$, resulting in ultimately stable conditions, i.e. $\tau ^o < \tau _r$ for each value of ambient fault loading condition. Grey dashed lines represent the small scale yielding (s.s.y.) solution associated with linear ramp-up of injection rate (see “Appendix” C), whose normalized ending time in this example is $\sqrt{4 \alpha t_c}/a_w = 44.72$. Red dots, instead, denote the nucleation and arrest of dynamic slip

Scaling analysis reported in “Appendix” B suggests that the pressurization rate, i.e. how quick is the ramp-up of injection rate before time $t_c$, does play a role in the hydro-mechanical fault response. In order to investigate its effect on the potential nucleation and arrest of dynamic slip on ultimately stable faults, we run several simulations keeping the ratio $t_c/t_w$ constant (and much larger than 1) and varying the maximum injection rate $Q_m/Q^*$. This is equivalent to keeping the normalized injection rate constant and varying the (large) ratio $t_c/t_w$, resulting in relatively low or large pressurization rates.

Fig. 6 displays the time evolution of half-crack length for different values of stress criticality, a ratio $t_c/t_w = 2\cdot 10^3$ and two maximum injection rates $Q_m/Q^* = 0.05, 1,$ representative of low and moderate fault pressurization rates, respectively. Notice that the maximum injection rates considered are similar to the ones used in the previous case of $t_c/t_w \ll 1$ (see Fig. 3), although the pressurization rates are considerably different. From a comparison of Figs. 6-right and 3-right, we clearly observe that, in the case of $t_c/t_w \gg 1$, a moderate maximum injection rate is not sufficient to quench the finite-sized dynamic slip event for each value of stress criticality (unlike the case previously discussed). This is certainly due to the different type of fault pressurization that drives the slipping patch expansion. In this case, indeed, slip is driven by linear increase branch of injection rate and pore-pressure at injection point evolves proportional to $\sim t^{3/2}$ (see Eq. (10)). A further comparison of Figs. 3-left and 6-left for the exact same value of $Q_m/Q^*=0.05$ reveals that the dynamic run-out distances are rather similar for each corresponding value of stress criticality, while the nucleation times differ considerably. With the similar approach of Garagash and Germanovich (2012), we derive an asymptotic expression for the nucleation time that is valid when nucleation of dynamic slip follows shortly shear crack activation. By setting ${\bar{p}}(\xi \simeq 0, t_n)$ from equation (10) equal to $(\tau _p-\tau ^o)/f_p$, i.e. equal to the minimum over-pressure required to activate slip, we get the following asymptotic expression for the normalized nucleation time

$$\begin{aligned} \frac{\sqrt{4 \alpha t_n}}{a_w}&\simeq \left( \frac{3}{2} \cdot \frac{\tau _p - \tau ^o}{f_p \varDelta P_w} \cdot \frac{t_c}{t_w} \right) ^{1/3} \iff \frac{Q_m}{Q^*} \nonumber \\&\ll \sqrt{\pi } \left( 1 - \frac{\tau ^o}{\tau _p}\right) , \end{aligned}$$

(16)

where $\varDelta P_w$ is the same characteristic pore-pressure drop reported in Eq. (14). Unlike the asymptotic solution (14) valid for $t_c/t_w \ll 1$, in this case the normalized nucleation time varies non-linearly with stress criticality $\tau ^o/\tau _p$, with a power law exponent equal to 1/3. Furthermore, it appears the dependency on the dimensionless ratio $t_c/t_w$ with the same power law exponent (as expected from scaling analysis), revealing that the nucleation time of dynamic slip does depend on how quick the injection rate ramp-up occurs in time, and thus on how large is the ratio $\dfrac{Q_m \cdot t_w}{Q^* \cdot t_c}$. The comparison between the numerical results corresponding to the case of $Q_m/Q^* = 0.05$, for which the condition $\dfrac{Q_m}{Q^*} \ll \sqrt{\pi } \left( 1 - \dfrac{\tau ^o}{\tau _p}\right)$ is strictly satisfied for all the values of $\tau ^o/\tau _p$, and the asymptotic solution (16) is displayed in Fig. 7. A good agreement is obtained, with a closer match for larger values of $\tau ^o/\tau _p$ due to the earlier nucleations after slip activations (see Fig. 6-left).

Fig. 7

Comparison between the asymptotic analytical solution (16) for ultimately stable faults valid for $t_c/t_w \gg 1$ and numerical solutions corresponding to the case of $t_c/t_w = 2\cdot 10^3$ and $Q_m/Q^* = 0.05$ (for which the necessary condition (15) is strictly satisfied for all values of $\tau ^o/\tau _p$ considered)

The asymptotic solution (16) gives also an estimation of the normalized position of the fluid front at nucleation time. A careful inspection of Fig. 6-left reveals that, at the onset of dynamic slip, the slipping patch front lags well within the pressurized region, and their relative distance decreases dramatically after the arrest of dynamic event (with fluid front always located ahead the slip front). Furthermore, we can observe that our numerical results (black lines) match perfectly with the small-scale yielding (s.s.y.) asymptotic solutions associated with linear increase of injection rate (dashed grey lines—see “Appendix” C for more details) for each value of stress criticality. Since the extent of the arrested dynamic crack is always much larger than the slipping patch length scale $a_w$ (thus s.s.y. condition is truly valid) and the corresponding nucleation time is known analytically from (16), we can calculate analytically the dynamic run-out distances $a_{arr}$ directly from the small-scale yielding solution resolved at nucleation time. By simply replacing the nucleation time $t_n$ obtained from Eq. (16) into the increment of stress intensity factor associated with ramp-up of injection rate (43), we can solve the resulting implicit equation obtained from propagation criterion (46) for the unknown arrested crack lengths. Obviously, this analytical equation is only valid in the case of early dynamic crack nucleation after activation, but it allows to investigate systematically the effect of the other dimensionless parameters on the arrest of dynamic rupture.

Fig. 8

Normalized dynamic run-out distances $a_{arr}/\sqrt{4 \alpha t_n}$ in function of stress criticality $\tau ^o/\tau _p$ and friction weakening ratio $f_r/f_p$, for different ramp-up scenarios of injection rate, i.e. different values of $\dfrac{Q_m t_w}{t_c Q^*}$. These latter are obtained by fixing the maximum injection rate at $Q_m/Q^* = 0.05$ and varying the (large) ratio $t_c/t_w$ (notably $t_c/t_w = 2\cdot 10^3, 2\cdot 10^4 , 2\cdot 10^5 \gg 1$ ). In all the cases nucleation occurs prior reaching time $t_c$, even for low values of $f_r/f_p$

We examine the effect of pressurization rate by fixing the maximum injection rate to $Q_m/Q^* = 0.05$ (such to satisfy the necessary condition in Eq. (16) for the whole range of stress criticality $\tau ^o/\tau _p$) and varying the large ratio $t_c/t_w$, obtaining thus a relatively quick or slow ramp-up of injection rate. In Fig. 8, we display the normalized dynamic run-out distances $a_{arr}/\sqrt{4 \alpha t_n}$ in function of stress criticality and friction weakening ratio $f_r/f_p$. We can observe that, for a given ramp-up of injection rate, the nucleation of a dynamic event is expected on a wider range of stress criticality for intermediate values of friction weakening ratio (compared to the cases of $f_r/f_p \rightarrow 0$ or $f_r/f_p \rightarrow 1$). Moreover, for a given value of $f_r/f_p$, the range of stress criticality in which a dynamic event is expected increases for increasing values of $t_c/t_w$ (i.e. for decreasing values of $\dfrac{Q_m t_w}{t_c Q^*}$), revealing that low pressurization rates promote the nucleation of a finite-sized dynamic rupture on ultimately stable faults. It is also interesting to note that the arrest of the dynamic rupture always occurs within the pressurized region, i.e. $\dfrac{a_{arr}}{\sqrt{4 \alpha t_n}}\lesssim 1$, regardless of i) how quick the injection rate increase in time, ii) friction weakening ratio considered and iii) stress criticality value. Furthermore, for a given value of $f_r/f_p$ and $\tau ^o/\tau _p$, the dynamic run-out distance increases for decreasing values of $\dfrac{Q_m t_w}{t_c Q^*}$, i.e. for slower ramp-up of injection rate. This can be grasped clearly from Fig. 9 where the normalized ramp-up rate $\dfrac{Q_m t_w}{t_c Q^*}$ is plotted against the normalized dynamic run-out distance $a_{arr}/a_w$ in a log-log plot. As one can see, the arrest of the dynamic slipping patch decreases non-linearly with increasing values of ramp-up rates, approximately proportional to an inverse power-law with exponent equal to -0.472 (see red line in Fig. 9).

3.2 Unstable fault ($\tau ^o > \tau _r$)

Finally, we present the case of injection into an unstable fault characterised by $\tau ^o/\tau _r >1$ at ambient conditions. In this particular scenario the fault is critically stressed and thus prompt to fail. A small strength perturbation, due to for instance a small pore-pressure increment ${\bar{p}}$, always leads to a quick quasi-static shear crack propagation followed by a run-away dynamic rupture (albeit in some circumstances a finite-sized dynamic event may precede the run-away rupture—see region (3) of Fig. 2 valid for the injection scenario at constant volumetric rate). Assuming a shear crack activation during the early ramp-up of injection rate (valid when $t_c$ is not much smaller than $t_w$ and thus pore fluid can diffuse within the fault plane), the slipping patch outpaces rapidly the pore fluid front and, at nucleation time $t_n$, the following condition hold

$$\begin{aligned} \frac{a_n}{a_w} \gg \frac{\sqrt{4 \alpha t_n}}{a_w}, \end{aligned}$$

(17)

Fig. 9

Normalized dynamic run-out distances $a_{arr}/a_w$ (black dots) in function of pressurization rate $\dfrac{Q_m t_w}{t_c Q^*}$ (with $t_c/t_w \gg 1$), for an ultimately stable fault characterised by $\tau ^o/\tau _p = 0.55$ and friction weakening ratio of $f_r/f_p = 0.6$. The red solid line represents a linear fit of the numerical results (black dots) in the log-log plot

with $t_n$ much smaller than both fluid diffusion time-scale $t_w$ and ramp-up time scale $t_c$. The pressurized region at nucleation time, therefore, is always confined near injection point and the corresponding pore-pressure distribution can be approximated using an equivalent point force distribution ${\bar{p}}(x,t) \simeq \varDelta P(t) \delta _{dirac}(x)$, with $\varDelta P(t)$ defined in (10).

Based on the previous work of Uenishi and Rice (2003), Garagash and Germanovich (2012) showed that there exist an asymptotic solution in terms of critical shear crack length that is universal (i.e. independent of the particular type of injection scenario) and it reads

$$\begin{aligned} \frac{a_n}{a_w} \simeq 0.579 \end{aligned}$$

(18)

In addition to this, they developed semi-analytically an outer and inner asymptotic solutions that are valid at different fault position with respect to fluid front location (see “Appendix” D). The outer solution is so called because is valid outside the pressurization region, i.e. for $\left| x\right| \gg \sqrt{4\alpha t}$. The inner asymptotic solution, instead, is valid for $\left| x\right| \lesssim \sqrt{4\alpha t}$, i.e. near injection point due to the limited extension of pressurization region on unstable faults before instability.

Since the outer asymptotic solution is universal, i.e. it is valid for any type of peak pore-pressure distribution (see “Appendix” D), we can make use of such a solution to derive an asymptotic expression for the nucleation time $t_n$ in function of the ramp-up of injection rate (and compare it with the solution of Garagash and Germanovich (2012) valid for pressurization at constant flow rate that can actually be retrieved here in the limit of $t_c \rightarrow 0$). Based on the outer solution, indeed, the integrated net over-pressure along the fault at crack instability is approximately given by (Garagash and Germanovich 2012)

$$\begin{aligned} \varDelta P(t_n) = \int _{- \infty }^{+ \infty } {\bar{p}}(x, t_n) \text {d}x \simeq {\mathcal {P}} \frac{\tau _p - \tau ^o}{f_p} a_w, \end{aligned}$$

(19)

where ${\mathcal {P}} \simeq 0.8369$ is the scaled magnitude of the point force, independent of the type of fault pressurization. By replacing Eq. (10) into Eq. (19), after some algebra, we obtain

$$\begin{aligned} \frac{\sqrt{4 \alpha t_n}}{a_w} \simeq \left( \frac{2^2 \cdot 0.8369}{\sqrt{\pi }} \cdot \frac{\tau _p - \tau ^o}{f_p \varDelta P_w} \cdot \frac{t_c}{t_w}\right) ^{1/4}, \end{aligned}$$

(20)

where $\varDelta P_w$ is the same characteristic pore-pressure drop of Eq. (14). It is interesting to note that the normalized nucleation time in the case of an unstable fault subjected to a ramp-up of injection rate varies non-linearly with both stress criticality $\tau ^o/\tau _p$ and pressurization rate $\dfrac{Q_m \cdot t_w}{Q^* \cdot t_c}$ (with a power law exponent equal to 1/4). A comparison with the normalized nucleation time associated with constant injection rate type of pressurization (Garagash and Germanovich 2012)

$$\begin{aligned} \frac{\sqrt{4 \alpha t_n}}{a_w} \simeq \left( \frac{2 \cdot 0.8369}{\sqrt{\pi }} \frac{\tau _p - \tau ^o}{f_p \varDelta P_w}\right) ^{1/2} \end{aligned}$$

(21)

suggests that the ramp-up of injection rate prior the maximum plateau may promote an earlier or later nucleation of a run-away dynamic event, with respect to the injection scenario at constant volumetric rate. Indeed, by taking the ratio between equation (20) and equation (21), we obtain $1.20636 \cdot \left( \dfrac{f_p \varDelta P_w}{\tau _p - \tau ^o} \dfrac{t_c}{t_w}\right) ^{1/4}$, implying that an earlier nucleation is expected when

$$\begin{aligned} \frac{t_c}{t_w} < \frac{1}{1.20636^4} \frac{\tau _p - \tau ^o}{f_p \varDelta P_w}, \end{aligned}$$

(22)

for a given maximum value of injection rate $Q_m$.

Fig. 10

Left: time evolution of normalized half-crack length $a/a_w$ for different values of (large) stress criticality $\tau ^o/\tau _p = 0.95, 0.9, 0.85$. Since the friction weakening ratio is $f_r/f_p=0.6$, all the scenarios correspond to very unstable faults. The maximum injection rate is set to $Q_m/Q^* = 100.$, while the normalized ramp-up time is $t_c/t_w =0.5$ (or in terms of normalized square root of time $\sqrt{4 \alpha t_c}/a_w \simeq 0.71$). Right: comparison between the asymptotic analytical solution (20) and the numerical results in terms of normalized nucleation time $\sqrt{4 \alpha t_n}/a_w$, for each value of $\tau ^o/\tau _p$ considered (see left plot)

In order to verify all these theoretical predictions, we run several numerical simulations with different stress criticality values, such to obtain highly critically stressed fault conditions for which condition (17) is strictly satisfied. We fixed the maximum injection rate at $Q_m/Q^* = 100$, the friction weakening ratio at $f_r/f_p = 0.6$ and the normalized changing time at $t_c/t_w = 0.5$. As we can observe from Fig. 10, the quick quasi-static shear crack propagation is always followed by a run-away dynamic rupture, whose nucleation time is in good agreement with theoretical prediction of Eq. (20) (with a better accuracy for larger values of $\tau ^o/\tau _p$ due to a more strict validity of condition (17)). At the instability, the normalized crack length $a/a_w$ is approximately $\sim 0.579$ for each value of stress criticality considered (as expected) and the corresponding scaled slip distributions match very well the outer and inner asymptotic solutions at $\left| x\right| \gg \sqrt{4\alpha t}$ and $\left| x\right| \lesssim \sqrt{4\alpha t}$, respectively (see Figs. 12 and 13 in “Appendix” D).

4 Discussions

In this section, we first discuss the limitations of our modelling approach and their effects on nucleation and arrest of dynamic fault slip. We then talk about the fault zone permeability structure and its relation to the parametrization of the model. Finally, we present the implications of our results on injection-induced seismicity, a topic that has raised the attention of scientific community and public opinion since second half of $20^{th}$ century (Simpson 1986).

4.1 Model limitations

The most severe approximation in our model is the neglect of dilatancy during fluid-driven shear crack propagation. Strong dilatant behavoir associated with sliding over fault’s asperities has been observed in laboratory experiments (Lockner and Byerlee 1994; Samuelson et al. 2009) as well as during field experiments in the context of geothermal energy exploitation (Batchelor 1985). Under the assumption of no fluid leak-off in the relative undamaged rock around the fault, shear-induced dilatancy does affect pore-pressure evolution, which in turn leads to a feedback on slip propagation (due to full coupling between flow and elastic deformations). Under undrained conditions, indeed, shear-induced dilatancy leads to a pore-pressure drop and thus to a local increase of effective normal stress (dilatant hardening) (Rudnicki 1979; Segall and Rice 1995). Ciardo and Lecampion (2019) have shown that such a dilatant hardening effect, quantified by a scaled undrained pore-pressure drop $\dfrac{\varDelta w_h}{w_h c_f \sigma ^\prime _o}$ with $\varDelta w_h$ being the increment of fault opening, does impact the transition between aseismic and seismic slip on frictional weakening immature faults. They showed, in fact, that a large dilatant behaviour suppresses the nucleation of run-away seismic rupture on otherwise unstable faults, even for sustained increases of fault permeability with slip. On ultimately stable faults, instead, dilatant hardening effect delays the nucleation of finite-sized seismic event and increases its dynamic run-out distance. We can certainly say, however, that the findings obtained in this work are valid for a fault whose dilatant compliance is relatively small, i.e. for $\dfrac{\varDelta w_h}{w_h c_f \sigma ^\prime _o} \ll 0.1$ which would result in an undrained pore-pressure drop of fractions of MPa.

In this contribution we also neglect other weakening mechanisms that can kick in during the onset of dynamic crack propagation, such as thermal pressurization and flash heating (Rice 2006).

Thermal pressurization of pore-fluid by rapid shear heating of fault gouge unit has been showed to be a prominent process of fault weakening (Viesca and Garagash 2015). This mechanism depends on fluid thermodynamics properties and drives the shear strength loss at low fluid pressure conditions (Acosta et al. 2018). Garagash and Germanovich (2012) showed that dynamic weakening due to thermal pressurization increases the dynamic run-out slip distances on ultimately stable faults. However, they also stated that such an effect is relatively small, due to the fact the most of dynamic weakening is expected to occur at slip scale $\delta _{w,dyna}$ that is likely larger than $\delta _w$. Without loss of generality, we can claim that the results presented in this contribution in terms of dynamic run-out distances on ultimately stable faults are valid for sufficiently low values $\delta _w$ compared to the characteristic dynamic slip-weakening distance $\delta _{w,dyna}$ (which depends on heat properties of both fault gouge unit and injected fluid).

Flash heating on fault’s asperities, instead, kicks in when the slip velocity exceeds $\sim 0.1 \text {m/s}$, a scenario that is very plausible during dynamic crack propagation, which characteristic slip rate at the rupture tip typically exceeds $\sim 10 \text {m/s}$ (Garagash 2011). Laboratory experiments on various types of rocks have shown a drop of friction coefficient of up to one order of magnitude due to flash heating on asperities contacts (Di Toro et al. 2011). These considerations suggest that this weakening mechanism would impact the dynamic run-out distances presented in this contribution. However, this is outside the scope of this work and it is left for future investigations.

Finally, we adopted a simple linear slip-weakening friction law compared to a more elaborate Rate- and State- friction model (Dieterich 1979). Although a number of studies have demonstrated that the linear slip-weakening friction model is a good approximation of the velocity weakening R&S friction law (Uenishi and Rice 2003; Rubin and Ampuero 2005; Garagash 2021) even at slip instability (Viesca 2016b, a), it does not allow to investigate scenarios in which fault frictional properties evolve during pressurization, for instance from velocity weakening to velocity strengthening depending on current slip velocity (as observed in laboratory experiments by Cappa et al. (2019)). Indeed, this can only be captured by using R&S friction law with heterogeneous distribution of a and b parameters. Future works with incorporation of R&S friction model will follow.

4.2 Fault zone permeability structure

Fault zones are complex lithological zones that typically contain a fault core with possibly branching subsidiary faults and a damage zone (Faulkner et al. 2010). Their geological structures are highly heterogeneous, anisotropic and discontinuous, and thus characterised by highly variable permeability structures (Lockner et al. 2009). A common description of a fault zone is a central core surrounded by a damage zone. Exhumed fault zones typically reveal the presence of several relatively higher permeability units compared to the host rock, with values around $k_f \sim 10^{-16} - 10^{-15} \text {m}^2$ (Wibberley 2002)). In case of an injection in or near the damage zone, the pore pressure would distribute in a relatively large region, as the damage zone itself would plausibly serve as main fluid conduit. Generally, the permeable units in the damage zone (fractures/faults) are relatively thick, in the order of meters, and cover a wide range of length scales. On the other hand, the fault core is typically thinner (centimetres/millimetres) and composed of gouge, cataclasite and/or ultracataclasite. Its permeability is relatively low, in the range of $k_f \sim 10^{-19} - 10^{-18} \text {m}^2$ (Wibberley 2002), and therefore it acts as an impermeable barrier for pore-fluid diffusion, at least at the time scale of injection. However, the core is the part of the fault zone that accommodates most of the slip (Faulkner et al. 2010).

The model presented in this contribution is a simplification of such a complex fault zone structure. We assume that fluid is injected into or near a highly permeable thick unit that accommodates both pore fluid diffusion and slip propagation. This assumption has an important consequence on the hydro-mechanical response since the permeability of the conductive unit $k_f$ and its thickness $w_h$ enter in the fluid diffusion time scale $t_w$ (only the former) as well as in the characteristic injection rate scale $Q^*$. These two scales, indeed, are used to normalised the two operational parameters in the model, i.e. the ramp-up time scale $t_c$ and the maximum injection rate $Q_m$, respectively.

4.3 Implications on injection-induced seismicity

The results above may indicate that injection-induced seismicity can be mitigated by controlling operational parameters, in particular the injection volumetric rate or, more specifically to the problem addressed in this contribution, the pressurization rate $\dfrac{Q_m t_w}{t_c Q^*}$.

Upon fluid injection into a specific fracture zone, possibly indicating of a well-developed (mature) fault zone, pore-pressure perturbation is likely to activate slip on favourably oriented (and critically stressed) conductive fractures within the damage zone. The initial stable slip propagation could be quickly followed by run-away seismic ruptures that in turn could trigger events on other fractures and propagate over the entire fault zone. Our results show that the onset of the contained micro-seismicity, however, may be delayed in time for slow increases of injection rate prior reaching a steady-state phase. If a specific stable principal fault plane is targeted for fluid injection, instead, a larger pore-fluid perturbation is required to activate slip. A ramp-up of the injection rate, in this case, strongly affects the slip propagation, in particular when the ramp-up time scale is much larger than the along-fault diffusion time scale. Although counter-intuitive, a fast ramp-up of injection rate on stable fault planes would reduce the possibility of triggering a larger finite-sized seismic event (with respect to the one that could be triggered if fault pressurization occurs at constant injection rate), which can potentially turn into an unabated rupture due to the activation of other dynamic weakening mechanisms (as discussed in Sect. 4.1).

The results are essentially in line with previous laboratory and numerical observations. Indeed, previous results highlighted how the initial state of effective stress (Gischig 2015; Passelègue et al. 2018) and essentially its relationship to the frictional behaviour (Larochelle et al. 2021) control whether a fault slip is confined to the pressurized region or runaways. Similarly, the numerical analysis by Alghannam and Juanes (2020) reports how the pressurization rate may influence the seismic reactivation of a fault zone. Here we generalize both approaches by showing that the ruptures and its final behaviour (confined or runaway) are linked to both the initial state of stress as well as the initial ramp-up of the injection, which is then closely linked to the pressurization rate.

Fig. 11

Map of slip regimes for a frictional weakening pressurized fault in which injection rate increases linearly in time, up to reach a maximum plateau after time $t_c$. This parametric diagram is function of stress criticality $\tau ^o/\tau _p$, friction weakening ratio $f_r/f_p$, normalized maximum injection rate $Q_m/Q^*$ and normalized ramp-up time scale $t_c/t_w$. For a given value of $Q_m/Q^*$, the larger is the ratio $t_c/t_w$, i.e. the lower is the pressurization rate $\dfrac{Q_m t_w}{t_cQ^*}$, the more wide are region (2) and (3). All the slip regimes of this Figure are the same of those reported and described in Fig. 2

The effects of the controlling operational parameters on risk of induced-seismicity associated with the specific physic-based model presented in this contribution are summarized in Fig. 11. It displays the effects of the initial ramp-up of injection rate on the different slip regimes (the same of Fig. 2), as function of all the other governing dimensionless parameters. From the characteristics of fault zone permeability structures discussed in the previous section, we deduce that the characteristic injection rate scale $Q^*$ might be realistically in the order of tens or even hundreds of litres per seconds due to the presence of highly permeable thick units that serve as fluid conduits. This leads to values of $Q_m/Q^*$ relatively low for hydro-shearing type of stimulations, implying that the risk of triggering a seismic event is also plausible in the case of injection into ultimately stable fault zones. This scenario is even more plausible for very large values of normalized ramp-up time scale $t_c/t_w$, which mean lower pressurization rates $\dfrac{Q_m t_w}{t_c Q^*}$ and thus a larger region (2) in Fig. 11. For slightly unstable faults ($\tau ^o \gtrsim \tau _r$), instead, a lower pressurization rate would lead to a larger slip accumulation during the quick quasi-static phase of crack propagation. The friction coefficient, therefore, would drop quicker to its residual value and the probability of triggering a run-away dynamic rupture preceded by a finite-sized event is higher, resulting in a larger region (3). This also implies that the nucleation time of such a run-away rupture increases for lower pressurization rates, as more and more part of the shear crack has reached the residual shear strength during its quasi-static stable propagation.

5 Conclusions

In this study, we have extended the model of Garagash and Germanovich (2012) to account for an initial ramp-up of injection rate in time before the maximum plateau and investigated its effect on nucleation and arrest of dynamic fault slip. Despite the simplicity of the homogeneous model (planar bidimensional fault, uniform stress conditions and rock properties, linear weakening of friction, no dilatancy), it allows to get insight into the mechanisms that govern the transition between aseismic and seismic slip on a pressurized planar fault.

We have approximated standard injection protocols that consist of an initial step-wise ramp-up of injection rate in time with a linear increasing function, followed by a maximum plateau after a given time $t_c$. We have solved numerically the coupled hydro-mechanical problem and explored the different slip regimes identified via scaling analysis. Our results show that the initial ramp-up of injection rate affects the slip propagation on ultimately stable faults ($\tau ^o<\tau _r$) if and only if the ramp-up time scale $t_c$ is much larger than fluid diffusion time scale $t_w$. Notably, we have shown that slip stability is governed by the pressurization rate (quantified by the dimensionless parameter $\dfrac{Q_m t_w}{Q^* t_c}$) and thus by how quickly the injection rate increases before reaching time $t_c$. From our results we can conclude that low pressurization rates applied on ultimately stable faults with frictional weakening properties and $t_c\gg t_w$ promote the nucleation of a finite-sized dynamic event. Moreover, the lower is the pressurization rate, the larger is the dynamic runt-out slip distance and hence the larger is the magnitude of the induced seismic event. We have also developed an asymptotic solution in terms of nucleation time that is valid when slip instability follows shortly crack activation and verified it with numerical simulations.

When $t_c\ll t_w$, instead, the initial ramp-up of injection rate can be neglected on ultimately stable faults and slip are driven by pressurization at constant volumetric rate. A good agreement with theoretical predictions of Garagash and Germanovich (2012) valid for that particular injection condition has been obtained.

Finally, we have demonstrated that the ramp-up of injection rate does affect the quick slip propagation on critically stressed faults prior the nucleation of a run-away dynamic rupture. By using the universal outer asymptotic solution of Garagash and Germanovich (2012), we developed a new analytical solution for the nucleation time and verified it with numerical simulations. This solution reveals that the initial ramp-up of injection rate may lead to an earlier or later nucleation of unabated dynamic event, compared to the case of fault pressurization at constant volumetric rate.

Appendices

Appendix A: Along-fault pore-pressure diffusion—analytical solution

Equation (5) or equivalently equation (9) is a parabolic, linear second-order partial differential equation with constant coefficients. It governs the one-dimensional over-pressure diffusion ${\bar{p}}(x,t) = p(x,t)-p_o$ inside the fault gouge unit with constant hydraulic diffusivity $\alpha$ $\left[ L^2/T\right]$. Together with the boundary conditions

$$\begin{aligned} {\bar{p}}(\pm \infty ,t) = 0, \qquad - \frac{w_h k_f}{\mu } \left. \frac{\partial {\bar{p}}}{\partial x} \right| _{x=0^{\pm }} = \pm {\left\{ \begin{array}{ll} \frac{Q_m}{2 t_c} \cdot t \quad &{}t\le t_c \\ \frac{Q_m}{2} \quad &{}t > t_c\\ \end{array}\right. }, \end{aligned}$$

(23)

and the specific initial conditions, it represents a well-posed diffusion problem that can be solved analytically (Carslaw and Jaeger 1959).

Firstly, we solve the diffusion problem for the case of linear ramp-up of injection rate valid for $t\le t_c$, for which the initial condition reads

$$\begin{aligned} {\bar{p}}(x, 0) = 0 \end{aligned}$$

(24)

We use Laplace transform in time (with Laplace parameter s) in order to turn equation (9) into an ordinary differential equation (with transformed variables denoted with an hat $\hat{}$ ). With the initial condition (24), such a subsidiary equation reads

$$\begin{aligned} \frac{\partial ^2 {\hat{p}}(x,s)}{\partial x^2} - k^2 {\hat{p}}(x,s) = 0 \quad \text {with} \qquad k^2 = \frac{s}{\alpha }, \end{aligned}$$

(25)

whose analytical solution is

$$\begin{aligned} {\hat{p}}(x,s) = c_1(s) \cdot \text {e}^{k x} + c_2(s) \cdot \text {e}^{-k x} \end{aligned}$$

(26)

$c_1(s)$ and $c_2(s)$ are two constants that can be obtained in closed form using the boundary conditions (23) associated only with linear ramp-up of injection rate:

$$\begin{aligned} c_1(s) = 0, \quad c_2(s) = - \frac{\mu Q_m}{2 t_c k_f s^2 w_h k} \end{aligned}$$

(27)

By taking the inverse Laplace transform of equation (26) with the constants defined in equation (27), we get the analytical expression for along-fault over-pressure diffusion reported in Eq. (10) and valid for $t\le t_c$, i.e.

$$\begin{aligned} {\bar{p}}(\xi ,t\le t_c)= & {} \left( \frac{2 Q_m \mu \sqrt{\alpha } t^{3/2}}{3 k_f \sqrt{\pi } t_c w_h}\right) \cdot \left( \text {e}^{-\xi ^2} \left( 1+ \xi ^2\right) \right. \nonumber \\&\left. - \sqrt{\pi } \left| \xi \right| \left( \frac{3}{2} + \xi ^2\right) \text {Erfc}(\left| \xi \right| ) \right) , \end{aligned}$$

(28)

where $\xi = \dfrac{x}{\sqrt{4 \alpha t}}$ is the along-fault normalized coordinate and $\text {Erfc}$ is the complementary error function.

We then solve the pore-fluid diffusion problem for time $t> t_c$, taking into account the injection history during the ramp-up phase.

In view of problem linearity, the analytical expression for the over-pressure evolution valid for time $t> t_c$ can be obtained by solving the diffusion equation (9) using as initial condition the over-pressure distribution evaluated at time $t_c$ (using Eq. (28)), and as boundary conditions the relations (23) associated only with constant injection rate. By using the fundamental heat conduction solution valid for an infinite one-dimensional body subjected to an instantaneous point source (also called Green’s function) (Carslaw and Jaeger 1959)

$$\begin{aligned} G(x-x^\prime , t-t^\prime ) = \frac{1}{\sqrt{4 \pi \alpha (t-t^\prime )}} \text {e}^{- \frac{(x-x^\prime )^2}{4 \alpha (t-t^\prime )}} \quad \text {for} \quad t-t^\prime \ge 0 \end{aligned}$$

(29)

and the superimposition principle, we can express the over-pressure evolution valid for time $t > t_c$ via the following analytical formula (Cole et al. 2011):

$$\begin{aligned} {\bar{p}}(x, t> t_c)= & {} \int _{-\infty }^{\infty }G(x-x^\prime , t - t_c) \cdot {\bar{p}}\left( \frac{x^\prime }{\sqrt{4 \alpha t_c}}, t_c \right) \text {d}x^\prime \nonumber \\&+ \frac{\alpha Q_m \mu }{w_k k_f} \int _{t^\prime =t_c}^{t} G(x, t - t^\prime ) \text {d}t^\prime \end{aligned}$$

(30)

Notice that the first term of Eq. (30) is the convolution with respect to the variable x of the fundamental solution (29) and the over-pressure distribution at time $t_c$ (obtained from (28)), while the second term is the contribution due to the constant flux boundary condition at fault centre. If the ramp-up time $t_c$ vanishes (i.e. $t_c = 0$), then fault pressurization would occur at constant injection rate. The first member of equation (30) would vanish (due to the initial condition (24)) and the analytical solution for the over-pressure evolution along the fault plane upon integration would read as

$$\begin{aligned} {\bar{p}}(x,t) = \frac{\alpha Q_m \mu }{w_k k_f} \cdot \frac{t \cdot E_{\frac{3}{2}}\left( \frac{x^2}{4 t \alpha }\right) }{2 \sqrt{\pi } \sqrt{\alpha t}}, \end{aligned}$$

(31)

where $E_{n} \left( z \right)$ is the Exponential integral function, or expressed in a similar form of (28) as

$$\begin{aligned} {\bar{p}}(\xi ,t) = \left( \frac{Q_m \mu \sqrt{\alpha t}}{\sqrt{\pi } k_f w_h}\right) \cdot \left( \text {e}^{-\xi ^2}- \sqrt{\pi } \left| \xi \right| \text {Erfc}(\left| \xi \right| )\right) \end{aligned}$$

(32)

with $\xi = \dfrac{x}{\sqrt{4 \alpha t}}$.

Appendix B: Scaling analysis

Scaling analysis applied on physics-based models represents a powerful technique that can help a systematic investigation of all the physical processes occurring. For sake of completeness, we report here the dimensionless solution structure as well as the normalised set of governing equations.

Based on previous work of Garagash and Germanovich (2012), we introduce the following characteristic scales in order to normalize elasticity equation (1) and shear stress evolution within the crack tips (3):

$$\begin{aligned} \tau (x,t) = \tau _p \cdot {\mathcal {T}}\left( x, t \right) , \qquad \delta (x, t) = \delta _w \cdot \varDelta \left( x,t \right) , \qquad {\bar{p}}(x,t) = \sigma _o^\prime \cdot \varPi \left( x, t\right) \qquad x = a \cdot {\mathcal {X}} \end{aligned}$$

(33)

where $\delta _w$ is the slip weakening length-scale (see Fig. 1), $\tau _p = f_p \sigma _o^\prime$ is the peak shear strength at ambient conditions and a is half-length of the shear crack. The corresponding governing equations upon introduction of (33) read:

$$\begin{aligned} {\mathcal {T}}\left( a{\mathcal {X}},t\right)= & {} \frac{\tau ^o}{\tau _p} - \frac{1}{2\pi }\frac{a_w}{a} \int _{-1}^{1} \frac{\partial \varDelta (a {\mathcal {X}},t)}{\partial \zeta } \frac{\text {d}\zeta }{\left( \zeta /a - {\mathcal {X}}\right) } , \end{aligned}$$

(34)

$$\begin{aligned} {\mathcal {T}}\left( a{\mathcal {X}},t\right)= & {} \frac{f(\delta )}{f_p} \left( 1- \varPi (a{\mathcal {X}},t)\right) , \end{aligned}$$

(35)

where $a_w = \dfrac{E_p}{2 \tau _p} \delta _w$ is a characteristic length-scale of the slipping patch and the normalized friction coefficient evolution is defined as

$$\begin{aligned} \frac{f(\delta )}{f_p} = {\left\{ \begin{array}{ll} 1- \varDelta \left( a{\mathcal {X}},t\right) \qquad &{}\varDelta \left( a{\mathcal {X}},t\right) \le 1- \frac{f_r}{f_p} \\ \frac{f_r}{f_p} \qquad &{} \varDelta \left( a{\mathcal {X}},t\right) > 1- \frac{f_r}{f_p} \end{array}\right. } \end{aligned}$$

(36)

In order to normalize the fluid diffusion problem (5-8), we use the same characteristic scales introduced in (33), with the exception that now we scale the spatial coordinate x with the length-scale $a_w$ previously obtained. Time t, instead, is normalized with the diffusion time-scale $t_w=\dfrac{a_w^2}{4 \alpha }$ such that

$$\begin{aligned} t = t_w \cdot \mathrm {T} \end{aligned}$$

(37)

Equations (5-8), therefore, reduce to

$$\begin{aligned}&\frac{\partial \varPi }{\partial \text {T}} - \frac{1}{4} \frac{\partial ^2 \varPi }{\partial {\mathcal {X}}^2} = 0, \end{aligned}$$

(38)

$$\begin{aligned}&\left. \frac{\partial \varPi }{\partial {\mathcal {X}}} \right| _{{\mathcal {X}}=0^{\pm }} = {\left\{ \begin{array}{ll} \pm \frac{Q_m}{Q^*} \frac{t_w}{t_c} \cdot \text {T} \qquad &{}\mathrm {T} \le \frac{t_c}{t_w} \\ \pm \frac{Q_m}{Q^*}\qquad &{}\mathrm {T} > \frac{t_c}{t_w} \end{array}\right. } \end{aligned}$$

(39)

where $Q^*$ is the characteristic scale of maximum injection rate and is defined as

$$\begin{aligned} Q^* = \frac{2 \sigma _o^\prime w_h k_f}{a_w \mu } \end{aligned}$$

(40)

Inspecting equations (34-36) and (38-39) we can readily observe that the dimensionless solution is function of only four dimensionless parameters:

• $\dfrac{\tau ^o}{\tau _p}\rightarrow$ fault stress criticality

• $\dfrac{f_r}{f_p}\rightarrow$ friction weakening ratio

• $\dfrac{Q_m}{Q^*}\rightarrow$ normalized maximum injection rate

• $\dfrac{t_c}{t_w}\rightarrow$ normalized ramp-up time scale

Appendix C: Small-scale yielding asymptotics

When half-length of slipping patch a is sufficiently larger than the characteristic length-scale $a_w$, the model non-linearity (i.e. slip weakening of friction coefficient) is localized only over a region that is small compared to geometrical dimensions of the rupture zone. A clear example of such a condition, typically named as small-scale yielding, is depicted in Fig. 4-bottom where, after the arrest of dynamic slip, the friction coefficient has not reached its residual value $f_r$ only over a small region near crack tips. The elastic stress-intensity factor, therefore, controls the local deformation field when $a\gg a_w$ (Rice 1968), and its analytical expression can be obtained in closed form by superimposing the effects of net loading applied on the shear crack (i.e. far-field stress $\tau ^o$ minus residual shear tractions $\tau _r$) and of fluid pressurization as (Tada et al. 2000)

$$\begin{aligned} K_{II} = \left( \tau ^o - \tau _r \right) \sqrt{\pi a} + \varDelta K_{II}, \end{aligned}$$

(41)

where

$$\begin{aligned} \varDelta K_{II} = f_r \sqrt{\frac{a}{\pi }} \int _{-a}^{+a} \frac{{\bar{p}}\left( x,t\right) }{\sqrt{a^2 - x^2}} \text {d}x \end{aligned}$$

(42)

By replacing the analytical expression for over-pressure evolution during the ramp-up phase (10) into (42), we find that the increment of stress-intensity factor due to pressurization at time $t\le t_c$ is

$$\begin{aligned} \!\begin{aligned} \varDelta K_{II}&= -\frac{f_r \sqrt{a} \mu Q_m t e^{-\frac{a^2}{8 \alpha t}}}{36 \sqrt{\pi } k_f t_c w_h (\alpha t)^{3/2}} \left( 4 a^3 \sqrt{\alpha t} e^{\frac{a^2}{8 \alpha t}} \right. \\&\left. \quad + 36 a (\alpha t)^{3/2} e^{\frac{a^2}{8 \alpha t}} - \sqrt{\pi } a^4 I_0\left( \frac{a^2}{8 t \alpha }\right) - \right. \\&\quad - \left. 9 \sqrt{\pi } a^2 \alpha t I_0\left( \frac{a^2}{8 t \alpha }\right) - \sqrt{\pi } a^4 I_1\left( \frac{a^2}{8 t \alpha }\right) \right. \\&\left. \quad - 11 \sqrt{\pi } a^2 \alpha t I_1\left( \frac{a^2}{8 t \alpha }\right) - \right. \\&\quad - \left. 3 \sqrt{\pi } a^2 \alpha t e^{\frac{a^2}{8 \alpha t}} \cosh \left( \frac{a^2}{8 | \alpha | | t| }\right) I_0\left( \frac{a^2}{8 | t| | \alpha | }\right) - \right. \\&\quad - \left. 24 \sqrt{\pi } \alpha ^2 t^2 e^{\frac{a^2}{8 \alpha t}} \cosh \left( \frac{a^2}{8 | \alpha | | t| }\right) I_0\left( \frac{a^2}{8 | t| | \alpha | }\right) + \right. \\&\quad + \left. 3 \sqrt{\pi } a^2 | \alpha | | t| e^{\frac{a^2}{8 \alpha t}} \cosh \left( \frac{a^2}{8 | \alpha | | t| }\right) I_1\left( \frac{a^2}{8 | t| | \alpha | }\right) + \right. \\&\quad + \left. 3 \sqrt{\pi } a^2 | \alpha | | t| e^{\frac{a^2}{8 \alpha t}} \sinh \left( \frac{a^2}{8 | \alpha | | t| }\right) I_0\left( \frac{a^2}{8 | t| | \alpha | }\right) + \right. \\&\quad + \left. 24 \sqrt{\pi } \alpha t | \alpha | | t| e^{\frac{a^2}{8 \alpha t}} \sinh \left( \frac{a^2}{8 | \alpha | | t| }\right) I_0\left( \frac{a^2}{8 | t| | \alpha | }\right) - \right. \\&\quad - \left. 3 \sqrt{\pi } a^2 \alpha t e^{\frac{a^2}{8 \alpha t}} \sinh \left( \frac{a^2}{8 | \alpha | | t| }\right) I_1\left( \frac{a^2}{8 | t| | \alpha | }\right) \right) \end{aligned} \end{aligned}$$

(43)

where $I_n(z)$ is the modified Bessel function of the first kind.

If pressurization consists of injection at constant flow rate only, then the increment of stress-intensity factor would be obtained by replacing equation (32) into (42), leading to the following expression

$$\begin{aligned} \varDelta K_{II}= & {} -\frac{e^{-\frac{a^2}{8 \alpha t}} \sqrt{a} f_r \mu Q_m}{4 \sqrt{\pi } k_f w_h \sqrt{\alpha t}} \left( 4 a e^{\frac{a^2}{8 \alpha t}} \sqrt{\alpha t}\right. \nonumber \\&\left. -\sqrt{\pi } a^2 I_0\left( \frac{a^2}{8 t \alpha }\right) -\sqrt{\pi } a^2 I_1\left( \frac{a^2}{8 t \alpha }\right) \right. \nonumber \\&\left. -4 \sqrt{\pi } \alpha t I_0\left( \frac{a^2}{8 t \alpha }\right) \right) \end{aligned}$$

(44)

During the slipping patch propagation driven by pore-fluid diffusion, the energy release rate $G = \dfrac{K_{II}^2}{E_p}$ must be equal to the fracture energy $G_c$, whose analytical expression under the assumption of small-scale yielding and constant effective normal stress near crack tips is (Palmer and Rice 1973)

$$\begin{aligned} G_c \simeq (f_p - f_r) \sigma ^\prime (a) \frac{\delta _r}{2} \end{aligned}$$

(45)

The quasi-static propagation criterion

$$\begin{aligned} G = G_c \end{aligned}$$

(46)

therefore provides an asymptotic solution for the slipping patch length a as function of pressurization time t.

Following the previous work of Dempsey et al. (2010), however, Garagash and Germanovich (2012) have shown that by replacing the slipping patch length a in (41-42) by an effective (reduced) length $a_{eff}$, a more accurate expression of the stress-intensity factor in the limit of $a\gg a_w$ is obtained. Such an effective crack length $a_{eff}$ is function of a process zone size d that Dempsey et al. (2010) determined numerically for the case of cohesive crack with linear softening traction separation law and propagating under uniform far-field tractions (which share the same mathematical formulation), i.e.

$$\begin{aligned} a_{eff} \simeq a - 0.466\cdot d, \end{aligned}$$

(47)

where d is defined as

$$\begin{aligned} d \simeq 0.466 \cdot \lambda \end{aligned}$$

(48)

and $\lambda = \left( \dfrac{\pi }{2} \right) \cdot \left( \dfrac{K_{II}}{(\tau _p - \tau _r)}\right) ^2$ is a characteristic length-scale.

In this contribution, the implicit equation (46) incorporates the reduced crack length (47) and it is solved numerically for time t (thus imposing the variable crack length a) by minimizing the residual function using a random search method. When the slipping patch is driven essentially by pressurization at constant injection rate (for instance in the case of an ultimately stable fault in the limit when $t_c/t_w \ll 1$), equation (46) is solved using the stress-intensity factor obtained in (44). Instead, when the shear crack is driven up to the nucleation of a dynamic event by the ramp-up of injection rate (for instance in the case of an ultimately stable fault with $t_c/t_w \gg 1$), then equation (46) is solved using (43) (obviously up to the maximum value $t_c$).

The comparison between the numerical results (black lines) and small-scale asymptotic solutions (dashed grey lines) in Figs. 3 and 6 shows a good match for slipping patches a larger than $\sim 2 a_w$.

Appendix D: Outer and inner asymptotic solutions at instability for an unstable fault

Here we briefly report the outer and inner asymptotic solutions at instability for an unstable fault $\tau ^o/\tau _r >0$ developed by Garagash and Germanovich (2012). The former is universal, which means it is independent of a particular pore-pressure profile, while the latter does depend on the particular pore-pressure distribution. Since dynamic instability for an unstable fault occurs quickly after fluid injection and crack activation (and thus during the ramp-up of injection rate for values of $t_c$ comparable to or greater than $t_w$), the inner asymptotic solution is solved only for the particular distribution (10).

1.1 Outer solution

At instability, the slipping patch extent is much larger than the pressurized region, due to the rapid propagation of the shear crack after its activation. Under this condition, the pore pressure distribution can be replaced by an equivalent point-force distribution

$$\begin{aligned} {\bar{p}}(x,t) \simeq \varDelta P(t) \delta _{dirac}(x) \end{aligned}$$

(49)

where $\delta _{dirac}$ is the delta Dirac function and $\varDelta P(t) = \int _{-\infty }^{\infty } {\bar{p}}(x,t) \text {d}x$. This equivalent distribution, however, approximates well ${\bar{p}}(x,t)$ only for distances much larger than fluid front position, i.e. for $x\gg \sqrt{4\alpha t}$ (outside pressurization region).

Garagash and Germanovich (2012) solved semi-analytically the hydro-mechanical problem with the equivalent pore-pressure distribution (49) and proved that the normalized slip profile at instability is given by

$$\begin{aligned} \frac{\delta (x)}{\epsilon \delta _w} = {\mathcal {P}} \left( \bar{\delta _1}(X) - \frac{a}{a_w} \bar{\delta _2}(X) \right) + {\bar{\delta }}(X), \end{aligned}$$

(50)

where ${\mathcal {P}} \simeq 0.8369$ is the scaled magnitude of the point force, $\epsilon = 1 - \tau ^o/\tau _p$ is the understress parameter, $X = x/a$ is the normalized fault coordinate, and $\bar{\delta _1}(X)$, $\bar{\delta _2}(X)$, and ${\bar{\delta }}(X)$ are three functions that are defined as

$$\begin{aligned} \begin{aligned} \bar{\delta _1}(X)&= \frac{2}{\pi } \cdot \text {ln}\left( \frac{1+ \sqrt{1-X^2}}{\left| X\right| }\right) ,\\ {\bar{\delta }}(X)&\simeq -1.1732 \cdot \text {sin}( \text {arcos}(X)) - 0.0608\cdot \text {sin}(3\cdot \text {arcos}(X)) \\&\quad + 0.0235\cdot \text {sin}(5\cdot \text {arcos}(X))\\ \bar{\delta _2}(X)&= \frac{2}{\pi } \int _{-1}^{1} \text {ln} \left| \frac{X-s}{1-sX + \sqrt{1-s^2}\sqrt{1-X^2}} \right| {\bar{\delta }}_1(s) \text {d}s \end{aligned} \end{aligned}$$

(51)

In Eq. (51), ${\bar{\delta }}(X)$ is a continuous and differentiable function whose analytical expression has been obtained numerically using Gauss-Chebyshev polynomial quadrature (with truncation at third term - see (Garagash and Germanovich 2012) for more details), while ${\bar{\delta }}_2(X)$ is the inverse of the Cauchy integral in terms of ${\bar{\delta }}(X)$ (solved numerically in this contribution).

Equation (50) represents a good approximation of slip distribution only for $\left| \dfrac{x}{a}\right| \gg \dfrac{\sqrt{4\alpha t}}{a}$. A near-field asymptotic expansion of (50), however, is proved to be a good approximation of the critical distribution of normalized slip $\delta /(\epsilon \delta _w)$ for $X \ll 1$ and $a=a_n$ (Garagash and Germanovich 2012). Such an expansion is given as

$$\begin{aligned} \frac{\delta (x)}{\epsilon \delta _w} = -\frac{2}{\pi } {\mathcal {P}} \text {ln} \frac{\left| X\right| }{2} - \frac{a}{a_w} {\mathcal {P}} {\bar{\delta }}_2 (0) + {\bar{\delta }}(0) + {\mathcal {O}}(X), \end{aligned}$$

(52)

where the ratio $a_n/a_w$ is defined in (18).

Fig. 12

Corresponding normalized slip distributions $\delta _n/(\epsilon \delta _w)$ (black solid lines) at nucleation time $t_{n}$ of the numerical simulations reported in Fig. 10. The red solid line denotes the outer asymptotic solution valid outside the pressurization regions (whose extents at instability are identified by blue dashed lines), i.e. for $\left| \dfrac{x}{a_n}\right| \gg \dfrac{\sqrt{4\alpha t_n}}{a_n}$, while the grey solid line represents the near-field expansion of the outer asymptotic solution that is valid for $x/a_n \ll 1$

In order to check the accuracy of these theoretical predictions, we display in Fig. 12 the corresponding slip profiles at nucleation time $t_n$ of the numerical simulations reported in Fig. 10. As we can observe, the scaled slip distributions $\delta _n/(\epsilon \delta _w)$, which collapse into nearly one black line due to the scaling adopted, match the outer asymptotic solution (50) (denoted by a red solid line) for $\left| x/a_n \right| \gg \sqrt{4 \alpha t_n}/a_n$, i.e. outside the pressurization regions whose extents are identified by blue dashed lines (for a given value of stress criticality $\tau ^o/\tau _p$). For $x/a_n \ll 1$, instead, the scaled slip distributions tend to converge to the near-field asymptotic expansion of the outer solution (52) (as expected).

1.2 Inner solution

Fig. 13

Linear-log plot showing the corresponding normalized slip distributions $\delta _n/\delta _w$ (black solid lines) at nucleation time $t_{n}$ of the numerical simulations reported in Fig. 10. The green solid lines denote the inner asymptotic solutions valid within the pressurization regions, i.e. for $\left| \dfrac{x}{ \sqrt{4 \alpha t_{n}}}\right| \lesssim 1$

Within the small pressurization region, i.e. for $x\lesssim \sqrt{4 \alpha t}$, the normalized pore-pressure distribution is approximately ${\bar{p}}(x)/\sigma ^\prime _o \sim 1$, which means that the stress perturbation can be written as (Garagash and Germanovich 2012)

$$\begin{aligned} \frac{\tau (x) -\tau ^o}{\tau _p} \simeq - \frac{{\bar{p}}(x)}{\sigma ^\prime _o} + {\mathcal {O}}(\epsilon ) \end{aligned}$$

(53)

for $\epsilon \ll 1$. Using this condition, Garagash and Germanovich (2012) showed that the normalized slip distribution at instability $\delta _n/\delta _w$ for a particular pore-pressure profile $\varPsi (s)$ is given as

$$\begin{aligned} \frac{\delta _n(\xi )}{\delta _w} = \frac{\delta _n(0)}{\delta _w} -\frac{2}{\pi } \epsilon {\mathcal {P}} \frac{\int _{-\infty }^{\infty } \varPsi (s)\text {ln}\left| 1- \xi /s \right| \text {d}s}{\int _{-\infty }^{\infty } \varPsi (s) \text {d}s} \end{aligned}$$

(54)

where $\delta _n(0)$ is the critical slip at $\xi = \dfrac{x}{4 \alpha t}=0$, which can be obtained by matching the outer ($x\gg \sqrt{4\alpha t}$) and inner ($x\lesssim \sqrt{4\alpha t}$) asymptotic solutions at intermediate distances (Garagash and Germanovich 2012)

$$\begin{aligned} \frac{\delta _n(0)}{\delta _w} = 0.533 \epsilon \left( - \text {ln} \frac{{\hat{\epsilon }}}{C} + 1.003 \right) , \end{aligned}$$

(55)

where ${\hat{\epsilon }} = (\tau _p - \tau ^o)/f_p \varDelta {\bar{p}}(t_n)$ and the constant C is defined as

$$\begin{aligned} C = \left( \int _{-\infty }^{\infty } \varPsi (s)\text {d}s\right) \cdot \text {Exp} \left( -\frac{\int _{-\infty }^{\infty } \varPsi (s)\text {ln}\left| s \right| \text {d}s}{\int _{-\infty }^{\infty } \varPsi (s) \text {d}s} \right) \end{aligned}$$

(56)

Unlike the outer asymptotic solution, the inner solution does depend on the particular pore-pressure profile $\varPsi (s)$. By replacing the instantaneous spatial distribution (10) associated with ramp-up of injection rate, we obtain $C = 3.75576$, allowing us to calculate the normalized slip distribution using (55) and (54) (with numerical evaluation of the integral $\int _{-\infty }^{\infty } \varPsi (s)\text {ln}\left| 1- \xi /s \right| \text {d}s$). For the same injection condition, friction weakening ratio and initial loading conditions of the simulations reported in Fig. 10, we show in Fig. 13 the corresponding normalized slip distributions $\delta _n/\delta _w$ at nucleation time $t_n$ on a linear-log plot. We can observe that, for each value of (large) stress criticality $\tau ^o/\tau _p$, the corresponding inner asymptotic solution matches well the numerical results (back solid lines) for $\left| x\right| /\sqrt{4\alpha t_n} \lesssim 1$ (as expected).