A 3D model of hydraulic fracturing and microseismicity in anisotropic stress fields

Abstract

We present a 3D numerical model for hydraulic fracturing and damage of low permeable rock in an anisotropic stress field. The model computes the intermittent damage propagation, microseismic event-locations, microseismic event-distribution, damaged rock volume and injection pressure. The model builds on concepts from invasion percolation theory, where cells in a regular grid are connected by transmissibilities, also called bonds. An intact bond breaks when the fluid pressure exceeds the least compressive stress and random uniformly distributed bond strength. Analytical expressions are obtained for the fractions of the weakest bonds in the x-, y- and z-directions as a function of the stress anisotropy and the rock strength anisotropy. A strategy is suggested for a fast solution of the pressure equation when the fluid pressure is restricted to the damaged rock volume. An expression for the volume of damaged rock is obtained in the cases where it has a high permeability. The model is demonstrated on a published case from the Barnett Shale and it reproduces the observed main features, such as the spatial and temporal distribution of the events, the magnitude–frequency distribution and the injection pressure. The microseismic event-distribution and the b-value depend on the permeability of the damaged rock volume. The b-value increases with decreasing permeability from a little < 0.6 to a value above 2 for the maximum possible permeabilities. The damaged rock volume is non-compact and similar to a percolation cluster for “high” damaged rock permeabilities, and it becomes increasingly compact with decreasing permeabilities. The resulting loop-less fracture network is found to have similar characteristics for different damaged rock permeabilities.

1 Introduction

Hydraulic fracturing is the basis for US shale gas and shale oil production. The year 2016 had an average production of 4.25 million barrels daily of crude oil from tight shales (EIA 2017). The oil- and gas-rich shales are practically impermeable, and oil and gas production would have been nearly impossible unless large volumes of rock had its bulk permeability greatly enhanced by stimulation. How the hydraulic fracturing process creates a dense and pervasive fracture network is being debated, but it seems linked to the geohistory of the shales (Turcotte et al. 2014). Shale units, which are petroleum source rocks, are rich in organic matter. Burial brings the source rocks down to depths where hydrocarbon generation is active (Allen and Allen 2013). The conversion of solid organic matter to less dense oil and gas leads to a volume increase and thereby an internal pressure build-up. The pressure build-up produces fracturing of the tight shales and hydrocarbon expulsion through a pervasive fracture network. Hydrocarbon expulsion may fill a conventional reservoir if the source rock is adjacent to porous and permeable sandstone (Allen and Allen 2013).

The naturally generated fracture network created by hydrocarbon generation seems to be important for hydraulic fracturing to efficiently enhance petroleum production. It appears that hydraulic fracturing is less effective in shales where hydrocarbon generation and expulsion are active processes and where the fracture network is open. On the other hand, hydraulic fracturing is effective in shales which has been uplifted and where generation and expulsion have stopped. In these shales, the naturally generated fracture network may have been cemented by quartz, calcite or other minerals. The injection of large volumes of water under high pressure reopens the sealed fracture network and mobilizes the hydrocarbons that are trapped in the source rock (Turcotte et al. 2014).

There are few means to directly observe the hydraulic fracturing process in the field and to detect how the injected fluid makes its way through nearly impermeable shales. One of the few means to observe the process is indirectly by microseismic monitoring. Microseismicity provides data about how the fracturing process spreads out away from the injection point. Microseismicity, like large-scale seismicity, has a magnitude–frequency distribution, which indicates that hydraulic fracturing is not a smooth process. Instead, fracture propagation takes place in discrete steps of different sizes. Additional information about the hydraulic fracturing process comes from the well-pressure response.

We present a 3D numerical model for hydraulic fracturing and the damage of low permeable rocks, which aims at producing realistic results in terms of injection pressure and microseismicity. The suggested modelling approach builds on a 2D invasion percolation model for microseismicity developed by Norris et al. (2015a, b, 2016). Their invasion percolation model has burst dynamics similar to microseismicity. Wangen (2017) added a fluid pressure equation to a 2D model similar to the one presented by Norris et al. (2015a, b, 2016), where a dynamic fluid pressure was used to trigger the propagation of fracturing and damage.

The term damage is used to describe the fracturing of intact rocks. It implies that a pervasive fracture network has developed, which allows the injected fluid to reach a large part of the pore space of the damaged rock. It also implies that the hydrocarbons that once were sealed in the rock are mobilized and can be produced.

A number of different simulation approaches have been suggested for the modelling of intermittent fracturing triggered by fluid pressure. Examples are the beam model (Tzschichholz et al. 1994; Tzschichholz and Herrmann 1995; Tzschichholz and Wangen 1998; Wangen 2011, 2013), discrete element models (Bruel 2007; Bruel and Charlety 2007; Riahi and Damjanac 2013; Itasca International 2016), models populated with discrete fractures that may be activated (Izadi and Elsworth 2014; Verdon et al. 2015). These models have in common that each fracture is represented explicitly. Another approach is taken here because the fracture network in a damaged rock volume is too fine to be represented explicitly. Instead, the effect of a pervasive fracture network is represented by means of a damage permeability. The intact cells in the grid have their permeability changed from impermeable to damage permeability when they fracture.

This paper is organized as follows: A short review of percolation models is given before the proposed model is presented. The paper then accounts for how an anisotropic stress state is implemented and how the pressure is obtained in the damaged rock volume. Then, the model is demonstrated by a case study from the Barnett Shale. How the frequency–magnitude distribution depends on the permeability of the damaged rock is studied before some properties of the loop-less fracture network are discussed.

2 Percolation models

Percolation theory is the study of the connectivity of clusters, normally by use of regular numerical grids (Stauffer and Aharony 1992; Feder 1989; Sahimi 1994). The ideas of the invasion percolation theory were developed by Wilkinson and Willemsen (1983) as a model for the slow displacement of immiscible fluids in a porous medium, for instance the displacement of oil by water. When the displacement is slow, capillary forces completely dominate viscous forces, and the process is determined on the pore level by the capillary thresholds of the pore throats. The porous rock may be represented by a regular grid, where the cells are pores, and the pore throats are bonds connecting neighbour cells. The invading fluid is represented by occupied cells on the grid. The displacement proceeds by searching for the bond with the least capillary threshold, which connects a vacant cell with the invaded cluster. This vacant cell becomes the next cell to be invaded, and the process repeats itself by searching a vacant cell to invade.

The invasion percolation model of Wilkinson and Willemsen (1983) addressed the final cluster of invaded cells that connects the two opposite sides of a regular grid (Feder 1989). The dynamics of the invasion process were subsequently studied by Furuberg et al. (1988). The displacement of water in a porous medium by injection of air at a constant rate leads to burst dynamics. These kinds of bursts have been extensively studied both experimentally and numerically using invasion percolation models by Måløy et al. (1992), Furuberg et al. (1996).

A wide range of phenomena with intermittent behaviour have event-sizes with a power-law distribution Turcotte (1997). Examples of models for such phenomena are the sand pile model of Bak et al. (1987), earthquake models (Crampin and Gao 2015), natural hydraulic fracturing (Miller and Nur 2000), pore throat models for immiscible displacement in porous media (Furuberg et al. 1988; Aker et al. 1998) and acoustic emissions by the triaxial testing of rocks (Amitrano 2003, 2012). The modelling of bursts with a regular grid has in common that when one cell becomes critical it shares mass, energy or stress with is neighbours cells, which in turn can become critical and thereby trigger an avalanche of critical cells.

3 A model based on concepts from invasion percolation

The proposed model of hydraulic fracturing is an extension of a 2D model (Wangen 2017) to a 3D rock volume in an anisotropic stress field. Both the 2D model (Wangen 2017) and the suggested 3D model are in turn based on a 2D invasion percolation model for hydraulic fracturing developed by Norris et al. (2014, 2015a, 2016), which is able to produce realistic microseismic event-distributions. The invasion percolation model of Norris et al. (2014, 2015a, 2016) grows a cluster of bonds by always invading the “weakest” bond on the perimeter. The bonds are assigned random strength, which is uniformly distributed at an interval from 0 to 1. Burst dynamics are introduced by a “water-level”. A burst of broken bonds begins when a bond strength falls below the water-level, and it continues until there are no other bonds that are weaker than the water-level. Norris et al. (2014) show that choosing the water-level right below the strongest failed bond in a cluster gives a power-law distribution of the burst sizes. The busts are the microseismic events, where the number of bonds in the burst is the event-size. The total number of the broken bonds is termed the cluster mass, and it corresponds to the total volume of injected fluid.

The 2D model (Wangen 2017) and the suggested 3D model have in common with percolation models that they are based on a regular grid of cells, where the cells are of two types: intact rock and damaged rock. The nearest neighbour cells are connected by transmissibilities (bonds), and the fracture condition is assigned to these bonds. Fluid injection builds up the pressure in the near-well area, which can lead to fracturing. A bond fractures when the fluid pressure exceeds the sum of the least compressive stress on the bond and a random rock strength. When an intact bond and the associated intact cell become damaged, the fluid will invade the newly damaged cell, and the fluid pressure decreases slightly. Just like an invasion percolation model, fracturing an intact cell can lead to a burst of fractured cells, where the bursts are responsible for the microseismicity. The proposed model in 3D defines the event-size in terms of a cluster of connected cells rather than connected bonds. The event-size is the number of broken and connected cells in a cluster formed during a time step. The magnitude of the event is the $\log _{10}$ of the event-size.

The fractured cells form a loop-less network as in the model of Norris et al. (2014, 2015a, 2016). A loop-less network means that the different branches of fractured cells are never connected by a fractured bond. This also implies that the number of fractured cells in the grid is always one more than the number of fractured bonds.

4 Classical models of hydraulic fracturing

The suggested modelling approach is different from the classical models of hydraulic fracturing, such as the PKN-model. The PKN-model was first introduced by Perkins and Kern (1961), where a vertical fracture with an elliptical cross-section propagates by fluid injected at a constant rate. The approach of Perkins and Kern was considerably improved by Nordgren (1972) who added fluid loss to the model, and obtained analytical and numerical results for the fracture width, length and volume as a function of time (Charlez 1997). A particular feature of the single fracture models, such as the PKN-model and a number of other analytical models for hydraulic fracturing (Savitski and Detournay 2002; Wangen 2017), is that fracture propagation is assumed to take place in a homogeneous rock and that the fracture is planar. The PKN-model has a well-defined fracture in terms of length, height and width, and it can be used for benchmarking numerical models where the fractures are explicitly represented. Examples from nature of planar hydraulic fractures are magmatic intrusions such as sills and dikes (Spence and Turcotte 1985). Since the intruding magma solidifies, it allows these hydraulic fractures to be mapped out.

The model suggested here is for hydraulic fracturing of low-permeable oil- and gas-shales, where a dense network of a large number of fractures are produced. The assumption of a dense fracture network is built into the model, where the fracture network is characterized by fine fractures. The number of fractures is assumed so large that it is practically impossible to represent them even at a marcroscopic scale. The macroscopic to megascopic properties of a fracture network are represented by a fracture porosity and a fracture permeability, instead of detailed fluid flow in explicit fractures. Since this model does not have an explicit fracture representation, it cannot deal with a single fracture. Therefore, it is difficult to compare the suggested modelling approach with the results of single fracture models, such as the PKN-model.

Nevertheless, parts of the model can be tested separately. For example, it is verified that the numerical pressure solution approaches the correct stationary solution for long time spans. The horizontal 2D version of this 3D model becomes the 2D model of Wangen (2017), and it produces events with a radius that is proportional to square root of time (Shapiro and Dinske 2009) using the same input data.

5 Stress anisotropy

It is assumed that the principal stress increases with depth. Therefore, the background stress field in the principal system is taken to be

$$\begin{aligned} \sigma _z=\varrho _b g z, \quad \sigma _x=f_x\sigma _z \quad \text{ and }\quad \sigma _y=f_y\sigma _z, \end{aligned}$$

(1)

where the $\sigma _x$, $\sigma _y$ and $\sigma _z$ are the principal stresses in the x-, y- and z-directions, respectively, $\varrho _b$ is the bulk rock density, z is the depth and g is gravitational acceleration. The factors $f_x$ and $f_y$ give the size of the principal stress in the x- and y-directions relative to the vertical stress. An alternative way to specify the stress anisotropy is to introduce the similar coefficients $f'_x$ and $f'_y$ for the effective stress

$$\begin{aligned} \sigma '_z=\sigma _z - p_h, \quad \sigma '_x=f'_x\sigma '_z \quad \text{ and }\quad \sigma '_y=f'_y\sigma '_z, \end{aligned}$$

(2)

where $\sigma '_x$, $\sigma '_x$ and $\sigma '_x$ are the principal effective stress in the x-, y- and z-directions, respectively, where $p_h=\varrho _f g z$ is the hydrostatic pressure and where $\varrho _f$ is the pore fluid density. The two pairs of coefficients are related by

$$\begin{aligned} f_x = f'_x + (1-f'_x)(\varrho _f/\varrho _b) \qquad \text{ and } \qquad f_y = f'_y + (1-f'_y)(\varrho _f/\varrho _b), \end{aligned}$$

(3)

which follows from the definitions (1) and (2).

6 Anisotropic bond strength

Fig. 1

a A bond (or a transmissibility) is a hydraulic connection between two nearest neighbour cells. b The bonds are oriented orthogonally to the directions of the principal stress

Norris et al. (2015b) introduce an anisotropic stress field in 2D by assigning uniformly distributed random numbers in the interval [0, 1) for the x-direction and uniformly distributed random numbers in the interval [0, a) for the y-direction, where $a>1$. For instance, the case $a=2$ makes it twice as likely that the weakest bond is in the x-direction rather than in the y-direction.

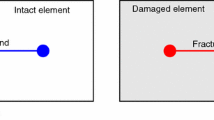
We introduce anisotropy in a slightly different way. The algorithm is still based on bonds that break. The bonds are transmissibilities that connect nearest neighbours cells, as shown in Fig. 1a. The condition for breaking an intact bond is that fluid pressure in the broken element exceeds the bond strength plus the least compressive stress acting normal to the bond. This rule makes it more likely for bonds to break that are oriented normally to the least compressive stress than the bonds with a larger compressive stress. Figure 1b illustrates how the compressive stress acts on the bonds in 3D, where it is assumed that the grid is aligned with the direction of the principal stress.

The stress anisotropy suggested by Norris et al. (2015b) is represented by random bond strength. The breaking condition suggested here is different by having the stress anisotropy and the random bond strength as separate quantities. The fracture pressure for a bond in direction $i=x,y,z$ is expressed as

$$\begin{aligned} p_{i,\max }=s_i + m_i u_i, \end{aligned}$$

(4)

where $s_i$ is the least compressive stress normal to the bond, $m_i$ is a constant characterisitic bond strength for direction i and $u_i$ is a uniformly distributed random number in the interval [0, 1). The least compressive bond stresses are

$$\begin{aligned} s_x= & {} \min (\sigma _H,\sigma _v)=\sigma _H \nonumber \\ s_y= & {} \min (\sigma _h,\sigma _v)=\sigma _h \nonumber \\ s_z= & {} \min (\sigma _h,\sigma _H)=\sigma _h \end{aligned}$$

(5)

since it is assumed that

$$\begin{aligned} (\sigma _x=\sigma _h) \,\,<\,\, (\sigma _y=\sigma _H) \,\,<\,\, (\sigma _z=\sigma _v), \end{aligned}$$

(6)

where $\sigma _h$ and $\sigma _H$ are the minimum and the maximum principal stresses in the xy-plane, respectively. In the following, we will assume that compressive stress in the xy-plane is less than the vertical compressive stress, such that $f_x<f_y<1$. Furthermore, we assume that the $m_y=m_x$ and that $m_z\ge m_x$. The layered texture of shales is the reason for introducing an isotropic random strength in the xy-plane ($m_x=m_y$), with the possibility of a different strength in the vertical direction. The critical pressures for bonds in the x-, y- and z-directions can now be written

$$\begin{aligned} p_{x,\max }= & {} \sigma _H + m_x u_x \nonumber \\ p_{y,\max }= & {} \sigma _h + m_x u_y \nonumber \\ p_{z,\max }= & {} \sigma _h + m_z u_z \end{aligned}$$

(7)

The largest compressive stress is on the x-bonds, which means that it is more likely that y-bond or a z-bond will break in the case of anisotropic bond strength. The critical bond pressure can also be written in terms of effective pressure by subtracting the hydrostatic pressure $p_h$ on both sides in Eq. (7), and we get

$$\begin{aligned} p'_{x,\max }= & {} \sigma '_H + m_x u_x \nonumber \\ p'_{y,\max }= & {} \sigma '_h + m_x u_y \nonumber \\ p'_{z,\max }= & {} \sigma '_h + m_z u_z \end{aligned}$$

(8)

where $p'_{i,\max }=p-p_h$ is the critical effective pressure and where $\sigma '_h$ and $\sigma '_H$ are the effective principal stresses in the xy-plane, respectively.

7 Fraction of weakest bonds

Fig. 2

The distribution of weakest bonds given by the normalized volume fractions (9)

When the random critical pressures $p_{i,\max }$ are generated, it is of interest to know how large the fraction of the bonds in a given direction i that have the least critical pressure, $p_{i,\max }$. For example, the fraction of the bonds in the x-direction that have the least critical pressure are the bonds where $p_{x,\max }<p_{y,\max }$ and $p_{x,\max }<p_{z,\max }$. The fraction of the bonds in the y-direction with least critical pressure have $p_{y,\max }<p_{x,\max }$ and $p_{y,\max }<p_{z,\max }$ and similarly, for the z-direction, where the condition is $p_{z,\max }<p_{x,\max }$ and $p_{z,\max }<p_{y,\max }$. The answer to these questions is given as volume fractions of the rectangular cuboid with sides $m_x$, $m_y$ and $m_z$, because the uniformly distributed random variables $u_x$, $u_y$ and $u_z$ span this cuboid by Eq. (7). The fraction of the i-bonds with least critical pressure is denoted $v_i$, and we have that

$$\begin{aligned} v_x(a,s)= & {} \frac{(1-a)^2s}{2(1+s)} + \frac{(1-a)^3}{3(1+s)} \nonumber \\ v_y(a,s)= & {} \frac{1}{2(1+s)} - \frac{(1-a)^3}{6(1+s)} + \frac{s}{(1+s)} - \frac{(1-a)^2 s}{2(1+s)} \nonumber \\ v_z(a,s)= & {} \frac{1}{2(1+s)} - \frac{(1-a)^3}{6(1+s)} \end{aligned}$$

(9)

when it is assumed that $m_x=m_y$ and $m_z>m_x$, and where

$$\begin{aligned} a= & {} (\sigma _H - \sigma _h)/m_x = (f_y-f_x)\sigma _v/m_x \end{aligned}$$

(10)

$$\begin{aligned} s= & {} (m_z-m_x)/m_x. \end{aligned}$$

(11)

The parameter $a$ is a dimensionless expression for the stress anisotropy, and parameter $s$ is a dimensionless measure of strength anisotropy. The sum of the volume fractions $v_i$ ($i=x,y,z$) is 1, as expected. The volume fractions (9) show that parameter $a$ is limited to the interval 0 to 1. It means that the maximum random strength $m_x$ has to be larger than the difference in the stress anisotropy, $m_x > \sigma _H - \sigma _h$. If not, $p_{y,\max }$ can never be larger than $p_{x,\max }$, even when the random variable $u_y$ reaches its upper limit $u_y=1$.

Figure 2a shows the volume fraction of the weakest bonds for increasing anisotropy ($a$-parameter), when the rock strength is isotropic ($s=0$). For an isotropic stress state ($a=0$) the distribution is equal, and therefore 1/3 for each of the three directions. With increasing anisotropy, the fraction of x-bonds goes to zero and the since the strength is isotropic, the fraction of the y-bonds and z-bonds are the same and therefore approach 1/2.

The distribution of weak bonds between the y- and z-directions becomes different when the strength increases in the vertical direction. With increasing anisotropy, the fraction of weakest y-bonds increases at the expense of the x-bonds, while the fraction of weakest z-bonds increases slowly at the expense of the x-bonds. A doubling of the rock strength in the z-direction gives a similar distribution, where the x-bonds go to zero, while the fraction of the weakest y-bonds and z-bonds are approximately 0.2 and 0.8, respectively.

Notice that principal stress increases with depth, which implies that the dimensionless anisotropy $a$ also increases with depth because the rock strength $m_x$ and $m_y$ are taken as constant. If these rock strength parameters were proportional to depth z, as the principal stress, the distribution of the weakest bonds would have been depth independent.

8 The fluid pressure and rock damage

During each time step $\Delta t$, a fixed volume $\Delta V=Q_0\Delta t$ is injected into the center cell of the grid, where $Q_0$ is the injection rate. The resulting fluid pressure in the cells is obtained by solving a discrete parabolic pressure equation. A derivation of the pressure equation and its numerical representation are given in Appendix 1.

Injection of a fluid volume leads to a pressure increase in the damaged rock volume and intact cells may become critical. The breaking of a bond and the associated intact cell changes the permeability field of the model. The damaged bond allows the fluid to enter the damaged cell, and the pressure decreases in the damaged rock volume outside the cell. In order to model the pressure decrease, it is, therefore, necessary to recompute the fluid pressure each time a bond and a cell is fractured. A new and reduced fluid pressure may still be large enough to fracture new intact bonds and cells, and the damage process may continue further into the rock. The process of breaking cells and recomputing the fluid pressure does not stop until there are no more critical cells.

Resolving the fluid pressure for all cells in a grid with fine resolution may be a time-consuming task. In the case of a nearly impermeable rock, there will be no changes in the fluid pressure in the intact cells. These cells keep their initial pressure. Therefore, it is only necessary to resolve the pressure in the fractured and damaged cells—the cells that allow for fluid flow. The implementation of such an approach saves a considerable amount of computer time. The only overhead is the allocation of a new mass matrix at each time step, which corresponds to the currently connected network of damaged cells.

Models can also be rapidly tested using stationary pressure (25), which does not require any solution of a large linear equation system (see Appendix 1). The stationary solution becomes a good approximation in the case of a high permeability of the damaged rock volume.

The stationary solution can also be used to estimate the damaged rock volume during a time step (Wangen 2017). The overpressure has to be larger than the least compressive effective stress $\sigma '_h$ for a bond and a cell to fracture. The least compressive effective stress $\sigma '_h$ is therefore a lower limit for the fracture pressure. The stationary solution (25) allows for an estimate of the maximum bulk volume of damaged rock during a time step, which is

$$\begin{aligned} \Delta V_D = \frac{Q_0\,\Delta t}{\phi _D\alpha _D\,\sigma '_h} \end{aligned}$$

(12)

because $\sigma '_x$ is a lower limit for the fluid pressure during fracturing. The porosity of the damaged rock is denoted by $\phi_D$ and $\alpha_D$ is the effective compressibility of damaged rock. How many cells there are in bulk volume $\Delta V_D$ is found by division with the cell size

$$\begin{aligned} {V}_{\mathrm {cell}}=\frac{l^2\,h}{n_0^2 n_1}, \end{aligned}$$

(13)

where l is length in the x- and y-directions, h is the layer thickness, $n_0$ is the number of cells in the x- and y-directions and $n_1$ is the number of cells in the z direction. Therefore, an estimate for the maximum event-size is

$$\begin{aligned} {S}_{\mathrm {max}}=\frac{\Delta V_D}{{V}_{\mathrm {cell}}} =\frac{Q_0\,\Delta t\,n_0^2 n_1}{\phi _D\alpha _D\,\sigma '_h l^2\,h}, \end{aligned}$$

(14)

and the corresponding estimate for the maximum magnitude is

$$\begin{aligned} {M}_{\mathrm {max}}=\log _{10}({S}_{\mathrm {max}}). \end{aligned}$$

(15)

These estimates are useful for the interpretation of simulation results.

9 A case study of Barnett Shale

Table 1 The parameters used in the Barnett case study

Fig. 3

a The injection overpressure as a function of time. b A zoom-in on the pressure in (a)

Fig. 4

The fractured and damaged elements in Barnett case example. The colour scale shows the time of fracture in seconds. The white vertical line at the center is the injection well. (The axes have the unit meter)

Fig. 5

The event-locations and the event-sizes. (The axes have the unit meter)

Fig. 6

The event-size distribution

The 3D model is demonstrated with data similar to a case from the Barnett shale in Texas presented by Shapiro and Dinske (2009), which builds on data from Fisher et al. (2002, 2004), Maxwell et al. (2009). In the Barnett case, hydraulic fracturing took place in a 60 m thick shale layer at a depth interval from 2340 to 2400 m, where 2916 $\hbox {m}^3$ of fluid was injected in 5.4 h, which gives an injection rate of 150 $\hbox {l}\,\hbox {s}^{-1}$. The parameters for the case are shown in Table 1. The hydraulic fracturing process was observed by monitoring microseismic events that spread out laterally to a distance of about 300 m away from the injection point in two opposite directions. These directions are the main directions. The spreading of the microseismic cloud normal to the main directions is roughly 75 m on each side. The different sizes of the microseismic cloud in the two orthogonal directions indicate an anisotropic stress field. The bottomhole injection pressure increases slowly from 40 MPa at the beginning of injection to 43 MPa at the end. Therefore, the least compressive stress appears to be larger than 40 MPa.

The Barnett case is constructed within a box sized 990 m $\times$ 990 m  $\times$  60 m, which is oriented parallel to the principal stress directions. The box is discretized with cells sized 10 m $\times$ 10 m $\times$ 10 m, which gives a grid of 99 $\times$ 99 $\times$ 6 cells. The layers above and below the shale unit are assumed to be much stronger than the shale in the middle and are therefore not included in the simulation.

The vertical stress at the center of the shale unit, at the injection depth of 2370 m, is taken to be $\sigma _v=51.1$ MPa. This corresponds to an average bulk density of $\varrho =2200$ $\hbox {kg}\,\hbox {m}^{-3}$ when the constant of gravity is 9.8 $\hbox {m}^{2}\,\hbox {s}^{-1}$. The effective vertical stress becomes $\sigma '_v=27.9$ MPa when it is assumed an initially hydrostatic fluid pressure, $p_h=23.2$ MPa. To simulate an anisotropy similar to the one reported by Shapiro and Dinske (2009), the factors $f_x=0.836$ and $f_y=0.918$ are used. In terms of effective stress, the companion factors are $f'_x=0.70$ and $f'_y=0.85$. The factors $f_x$ and $f'_x$ give the least compressive stress, and the least effective compressive stress is $\sigma _x=42.7$ MPa, or alternatively $\sigma '_x=f'_x\sigma '_z=19.5$ MPa.

The porosity of intact samples from the Barnett shale is measured with an average of 5.7% by Kale et al. (2010), an average around 7% by (Morsy and Sheng 2014) and an average of 9.9% by Fu et al. (2015). These porosity measurements cover a range from below 4% to more than 10%. There are little data on what the damage porosity could be, but it depends on how much the fracture network is opened by the fluid pressure. The porosity of the damaged rock is taken to be $\phi =0.15$, and effective compressibility (see Eq. (18) in Appendix 1) is taken to be $\alpha _D={5}\times 10^{-10}$ $\hbox {Pa}^{-1}$. The parameters used in the solution of the pressure equation are listed in Table 1.

Figure 3 shows the transient injection overpressure as a function of time, and it is close to the stationary overpressure. The stationary overpressure is derived in Appendix 1. This is because of the large damage permeability, $k_D={1}\times 10^{-8}$, which implies that pressure transients decay fast. The time for the decay of pressure transients can be estimated by the characteristic time (26). Case data from Table 1 and the length of 300 m give that $t_0=0.7$ s, which is a short time compared to the time step $\Delta t=389$ s. The injection overpressure is seen from Fig. 3 to be approximately 5 MPa above $\sigma '_x$, which is due to the random bond strength of 10 MPa.

The fractured cells at the end of the simulation are plotted in Fig. 4, where the injection well is the vertical line. The cell colours give the time of damage, and they show that the damaging of the rock is not symmetric in time around the injection well, which is due to random bond strength. It begins at the left (blue cells), then it takes place mainly at the right (green cells) before it ends at the red clusters. Another feature of the damage region is that it is not compact. Due to the random rock strength, there are a number of intact cells in between the broken ones (Fig. 4).

The isotopic rock strength $m_x=m_y=m_z=m_0=10$ MPa and the vertical stress $\sigma _z=51.1$ MPa give the $a$- and $s$-parameters $a=0.42$ and $s=0$. From the distribution of bond strength shown in Fig. 2, we have that only 6% of the bonds are in the x-direction, and remaining bonds are split equally with 47% in the y- and z-directions. The simulation (one realization) gave the distribution of broken bonds in the x-, y- and z-directions of 6%, 50%  44%, respectively.

The event-locations and the event-sizes are plotted in Fig. 5, where the colours show the time of the events. There are events from the entire time span in the near-well region. The event-locations show that the hydraulic fracturing process is not expanding away from the injection point as a well-defined front: The events spread out from the injection point, but at the same time there are events everywhere inside the damaged area. The event-locations from the Barnett shale presented by Shapiro and Dinske (2009), show that there are also a few events that appear too far away from the main cloud to be directly related to the fluid-driven fracturing process. Such events, sometimes called “dry” events, are not generated by the present algorithm.

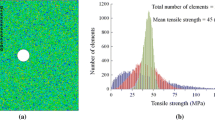
Figure 6 shows the magnitude-size distribution of the events generated during the simulation for the cell size $\Delta s=10$ m and for two finer cell sizes of $\Delta s=5$ m and $\Delta s=2.5$ m, respectively. The x-axis is the event magnitude M, and the y-axis is $\log _{10}$ of the number N of events larger than the magnitude M. The slope of the curve is the b-value, and for large-scale seismicity it is $b\approx 1$ (Baan et al. 2013). Figure 6 shows that there are two segments in the magnitude-size distribution, with a cross-over between the parts. The segment for small events has a b-value of $b\approx 0.5$, and the other segment for larger events has a b-value of $b\approx 3.2$. The slope of the frequency–magnitude distribution changes smoothly between these two end-values for the b-value.

Microseismicity is frequently observed with a $b\approx 2$ (Eaton et al. 2014; Eaton and Maghsoudi 2015; Eaton 2018), although Sil et al. (2012) reports b-values in the range from 1 to 3 for the Barnett Shale, where they also report a b-value above 3. The observed b-values are often based on just one decade along the magnitude axis, and the frequency–magnitude distribution may be curved (Urbancic et al. 2010; Sil et al. 2012; Zorn et al. 2014; Verkhovtseva et al. 2015; Dohmen et al. 2017; Calvez et al. 2016). The variability could correspond to slopes in the cross-over part of the frequency–magnitude distribution. Norris et al. (2014) obtained a b-value $b\approx 0.46$ with their 2D loop-less percolation model. They commented that an extension of the model from 2D to 3D might give a different b-value. Urban et al. (2016) observed a b-value as low as 0.75 during the filling of the Song Thranh dam in Vietnam.

The frequency–magnitude distribution in Fig. 5 can be adjusted with an offset $M_0$ in order to match the real scale of magnitudes,

$$\begin{aligned} {M}_{\mathrm {real}}= M - M_0. \end{aligned}$$

(16)

Figure 6 shows that such an offset is resolution dependent. The number of events is also resolution dependent. A finer resolution gives more events than a coarse resolution, and the cross-over interval gets wider in the frequency–magnitude distribution.

It should be noted that the randomness in the model makes it impossible to reproduce exactly the same events as observed. The aim of the above example is to demonstrate that the proposed modelling approach can reproduce the main features of the Barnett case.

10 Event-magnitude distribution and permeability of the damaged rock

Fig. 7

a The injection overpressure and the b frequency–magnitude distribution for three different damage permeabilities

Fig. 8

The overpressure in the damaged rock in case of damaged rock permeability $k_D={1}\times 10^{-12}$ ${\text {m}}^{2}. {\text{(The axes have the unit meter)}}$

Fig. 9

The fractured elements for the three different cases of damaged rock permeability. (The axes have the unit meter)

Fig. 10

The event-locations and the magnitude sizes for the three cases of the damaged rock permeability. (The axes have the unit meter)

The 2D model of hydraulic fracturing and damage (Wangen 2017) has the property that the b-value increases by decreasing permeability of the damaged rock, when the total injected volume and injection time are kept constant. The same behaviour is observed with this 3D model in an anisotropic stress field. This behaviour is demonstrated using nearly the same case as in the previous paragraph, except that the resolution is increased from a cell size of 10 m $\times$ 10 m $\times$ 10 m to 5 m  $\times$ 5 m $\times$ 5 m. Three versions of the case are studied with damage permeability decreasing in steps from ${1}\times 10^{-8}$ to ${1}\times 10^{-10}$ $\hbox {m}^{2}$ and ${1}\times 10^{-12}$ $\hbox {m}^{2}$. Figure 7 shows the resulting injection pressures and the corresponding frequency–magnitude distributions. The highest damage permeability, ${10}\times 10^{-8}$ $\hbox {m}^{2}$, gives an injection pressure that is nearly the same as the stationary injection pressure. Any larger damage permeability gives almost the same result, using the same injection rate and injection time. An injection pressure close to the stationary pressure implies that there are negligible pressure gradients inside the damage zone (see Fig. 8).

Decreasing the damage permeability by two orders of magnitude to ${1}\times 10^{-10}$ $\hbox {m}^{2}$ makes a difference. The injection pressure is slightly higher, and the slope of the frequency–magnitude distribution is steeper. A further decrease in the damage permeability to ${1}\times 10^{-12}$ $\hbox {m}^{2}$ results in a considerably higher injection pressure, and the slope of the frequency–magnitude distribution is even steeper. This case provides a lower limit for a constant damage permeability because of the high injection pressure. The pressure distribution inside the damage rock volume is characterized by a pressure gradient from the injection cell towards the rim of the damage zone.

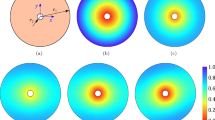
Figure 9 shows the damaged rock volume for the three different cases of permeability. The case of high damage permeability, $k_D={1}\times 10^{-8}$ $\hbox {m}^{2}$, gives a percolation type of damaged volume. The damaged volume is fragmented and, therefore, not compact. The colours in Fig. 9a give the time when the cell fractured. The colours show that the damaging process was not symmetric in time around the injection point. The low permeability case ($k_D={1}\times 10^{-12}$ $\hbox {m}^{2}$), shown in Fig. 9c, gives a damaged volume that is nearly compact. The colours show that the structure is formed by a uniform expansion outward from the injection well. The case of the intermediate permeability $k_D={1}\times 10^{-10}$ $\hbox {m}^{2}$, shown in Fig. 9b, is an intermediate structure between the non-compact structure (Fig. 9a) and the compact structure (Fig. 9c).

How the damage volume grows outwards from the injection well is also seen in Fig. 10, which shows the event-locations and the event-sizes for the three cases. The case of high damage permeability, $k_D={1}\times 10^{-8}$ $\hbox {m}^{2}$, has fewer events than two cases with a lower permeability. In addition, the event-sizes are spanning a larger range of magnitudes. The low damage permeability case, $k_D={1}\times 10^{-12}$ $\hbox {m}^{2}$, has the largest number of events of the three cases, and the magnitude of the events are generally smaller. This case of low damage permeability gives a substantial pressure increase in the damaged rock volume, which leads to the fracturing of all cells in the near-well region. The result is the compact structure as can be seen in Figs. 8 and 10. The large number of the smaller events relative to the two other cases, created by the increase in fluid pressure, explains the steeper frequency–magnitude distribution in Fig. 7.

11 Comparison of loop-less fracture networks

Fig. 11

The fracture network for the case $k={1}\times 10^{-8}$ $\hbox {m}^{2}$. The bond colour indicates the time when the bond was created

Fig. 12

a The Strahler number and b the Shreve number

The fracture network is made loop-less by the damage-algorithm. A loop-less network is also the result of the invasion percolation approach taken by Norris et al. (2015a, b, 2016). If a new fractured cell becomes the nearest neighbour of a previously fractured cell, it will not be connected to the previously fractured cell, which assures that the network remains loop-less. The reason for not connecting these nearest neighbours is the assumption that nearly all the fluid flow follows the branches and that there will be little fluid flow across the bridge that connects two branches. This assumption has been tested by allowing fracture branches to connect, and the end result is that very little is changed. The number of connections increases, but these extra connections barely change the well-pressure, the number of damaged cells or the distribution of damaged cells.

When the fracture network has no loops it becomes a tree with the injection cell as the root. Figure 11 shows the network tree in the case where damage permeability is $k={1}\times 10^{-8}$ $\hbox {m}^{2}$. One way to compare the fracture networks of the 3 cases of damage permeability is to compare the Strahler numbers and Shreve numbers, of the respective trees. These two numbers were introduced to measure the branching complexity and stream size of river networks, (Strahler 1952; Shreve 1966). Both the Strahler number and Shreve number are resolution dependent but we are comparing cases with the same resolution. River networks normally have only two streams that join, but the fracture network in Fig. 11 may have 2–5 streams that join.

The Strahler number is assigned to each segment in the network, beginning at the perimeter, where all segments have number 1. When two streams of the same order meet, the resulting stream gets a number that is one higher. If meeting streams have different orders then the resulting stream gets the highest order of the merging streams. See Fig. 12a for how the Strahler numbers are assigned the fracture branches. The Strahler number at the root of the tree measures the degree to which the network is dominated by one main or a few main streams. If one stream dominates, the Strahler number is low. The Strahler numbers of the three cases of damage permeability are 8, 8 and 7, respectively. These Strahler numbers indicate that the three cases have similar branching characteristics in terms of main channels in the network.

The Shreve stream number is a measure of the total flow in the network, (Shreve 1966). The Shreve number is also obtained by assigning 1 to the segments at the perimeter. Whenever two streams meet, the order of the resulting stream is the sum of the orders of the merging streams; see Fig. 12b. Therefore, the root of the tree gets the number of branches starting from the perimeter. The Shreve numbers for the three cases of damage permeability are 3897, 3869 and 3529, respectively, which are seen to decrease slightly with decreasing permeability. The considerably higher injection pressure in third and low permeability case leads to more compressed fluid in the damaged volume. The number of damaged cells are therefore less, with a slightly lower Shreve number.

12 Conclusion

A 3D numerical model is suggested for hydraulic fracturing and damage of low permeable rocks in an anisotropic stress field. The model builds on concepts from invasion percolation theory, which is a framework for modelling cluster formation with burst dynamics. The simulation grid is regular, and all nearest neighbour cells are connected by transmissibilities, also called bonds. The grid is aligned with the anisotropic stress field, where the bonds are orthogonal to two principal stress directions. An intact bond breaks when the fluid pressure exceeds the least compressive stress and a random bond strength. The anisotropy of the local stress field implies that the fractions of the weakest bonds in the spatial directions are uneven. Expressions for these fractions are obtained as a function of the stress anisotropy and the rock strength anisotropy when the bond strength is uniformly distributed.

Breaking a bond implies that the fluid flow invades the associated broken cell, and the fluid pressure decreases. The damaging process continues during a time step until the fluid pressure is sufficiently low for no more bonds to be critical. The number of connected broken cells during a time step is the event-size, and the $\log _{10}$ of the event-size is the event-magnitude. The new fluid pressure, after a bond breaks, is obtained by solving a transient pressure equation. A strategy for a fast solution of the pressure equation is demonstrated when the numerical domain is restricted to the damaged cells.

The model computes the intermittent damage propagation, microseismic event-locations, microseismic event-distributions, damaged rock volume and injection pressure. The model is demonstrated on a published case from the Barnett Shale, and it reproduces the observed main features, such as the spatial and temporal distribution of the events, the magnitude–frequency distribution and the injection pressure. The microseismic event-distribution and the b-value depend on the permeability in the damaged rock volume. The b-value increases with decreasing permeability from little less than 0.6 to a value above 3 when the injection rate and injection volume are kept constant. An expression for the volume of damaged rock is obtained in the case where the volume has high permeability. The model produces a loop-less fracture network. The branching properties of the network for different permeabilities of the same case are compared in terms of the Strahler number and the Shreve number, and the networks have similar characteristics.

Appendix 1: The pressure equation

Conservation of fluid mass is expressed as

$$\begin{aligned} \frac{\partial {(\phi \varrho _f)}}{\partial {t}} + \nabla \cdot (\varrho _f\,{\mathbf v}) = q({\mathbf x}), \end{aligned}$$

(17)

where $\phi$ is the porosity, $\varrho _f$ is the fluid density, ${\mathbf v}$ is the Darcy flux and $q({\mathbf x})$ is the source term for fluid injection. The source term is zero, except inside the cell where injection takes place. The expression of mass conservation (17) can be turned into a pressure equation by introducing the effective compressibility

$$\begin{aligned} \alpha _D= \frac{1}{\phi \varrho _f}\frac{d{(\phi \varrho _f)}}{d{p_f}}, \end{aligned}$$

(18)

where $p_f$ is the fluid pressure and Darcy’s law is

$$\begin{aligned} {\mathbf v}=\frac{k}{\mu }\Big (\nabla p_f- \varrho _fg {\mathbf n}_z\Big ). \end{aligned}$$

(19)

An alternative to the fluid pressure as an unknown is the overpressure, which is the part of the fluid pressure that exceeds the hydrostatic pressure,

$$\begin{aligned} p=p_f- p_h\qquad \text{ and } \qquad p_h=\int _0^z \varrho _fg\,dz, \end{aligned}$$

(20)

where $p_h$ is the hydrostatic pressure. Assuming a constant fluid density in the divergence-term gives the pressure equation

$$\begin{aligned} \phi \alpha _D\frac{\partial {p}}{\partial {t}}-\nabla \cdot \Big (\frac{k({\mathbf x})}{\mu }\nabla p\Big ) = q({\mathbf x}), \end{aligned}$$

(21)

where gravity disappears from the Darcy-term. The permeability is dependent on whether the rock is intact or damaged and therefore dependent on position ${\text{x}}$.

A finite volume formulation of the pressure equation is obtained by volume integration over the cell i and by using the Gauss theorem to replace the volume integral over the divergence-term in cell i by a surface integral. The pressure equation for cell i is then

$$\begin{aligned} \phi _i\alpha _i\frac{(p^{n+1}_i - p^n_i)}{\Delta t} V_i -\sum _{j\in <Emphasis Type="Italic">}A_{ij}\frac{k_{ij}}{\mu } \frac{(p^{n+1}_j - p^{n+1}_i)}{l_{ij}} = Q_0\delta _{i0} \end{aligned}$$

(22)

where the subscript i denotes a property of cell i, such as the porosity $\phi _i$, the compressibility $\alpha _i$ and the cell volume $V_i$. The subscript ij denotes the property of the connection between nearest neighbour cells i and j, such as the interface area $A_{ij}$, the distance between cell centers $l_{ij}$ and the permeability between cells $k_{ij}$. The injection cell is given cell number 0 in the source term on the right-hand side of Eq. (22).

The average pressure inside the total damaged rock volume $V_D$ can be obtained the by volume integration of pressure Eq. (21) over $V_D$, which gives

$$\begin{aligned} \phi _D\alpha _D\int _{V_D}\frac{\partial {p}}{\partial {t}}\,dV + \int _{V_D}\!\!{\mathbf v}\,dV = Q_0 V_D. \end{aligned}$$

(23)

The Gauss theorem gives that the volume integral over the flow term is zero

$$\begin{aligned} \int _{V_D}\!\!{\mathbf v}\,dV=\int _{\partial V_D}\!\!{\mathbf n}\cdot {\mathbf v}\,dS = 0 \end{aligned}$$

(24)

because there is now flow into the intact rock through the boundary $\partial V_D$ of the damaged rock volume $V_D$. The average pressure inside the damaged rock volume becomes

$$\begin{aligned} {p}_{\mathrm {av}}= \frac{1}{V_D}\int _{V_D}\!p\,dV = \frac{Q_0 t}{\phi _D\alpha _DV_D} \end{aligned}$$

(25)

when it is assumed that the damaged rock volume $V_D$ is constant. The stationary pressure inside the damaged rock volume becomes exactly the same as average pressure ${p}_{\mathrm {st}}={p}_{\mathrm {av}}$ because there are no pressure gradients inside the damaged volume in the stationary state. The stationary pressure ${p}_{\mathrm {st}}$ is therefore constant inside $V_D$, which is also the average.

The condition for being close to a stationary state can be given in terms of the time constant for the decay of the pressure transients, which is

$$\begin{aligned} t_0=\frac{1}{k_D}\mu \phi _D\alpha _D l_{\max }^2 \end{aligned}$$

(26)

where $k_D$ is the permeability, $\mu$ is the fluid viscosity, $\phi _D$ is the porosity, $\alpha _D$ is the effective compressibility and $l_{\max }$ is the maximum distance from the injection point to a point on the perimeter. The subscript D indicates that the property is of damaged rock. The fluid pressure becomes nearly stationary for time steps that are much smaller the time constant $t_0$.