Introduction

Groundwater reservoirs play a crucial role in both the environment and the development of our 21st-century society. The preservation of these reservoirs is increasingly challenging due to a range of factors such as natural ones like dry seasons combined with low precipitation ranges and non-natural ones such as over-exploitation, contamination, and climate change. This preservation dilemma has become a prominent global concern. According to the latest report by the Intergovernmental Panel on Climate Change (IPCC), southern European countries are at high risk of extreme drought and with the potential for flooding, with a temperature increase equal to or greater than 1.5 °C, defined as a target value not to be exceeded (Pörtner et al. 2022). With these temperature increases, the hydrological cycle will be affected, and consequently, the aquifer systems will be too.

In order to find a solution, the initial step involves researching the evolution of groundwater systems throughout time and identifying factors that can either enhance or hinder their effective management.

Analysis of GDL evolution through time is a crucial key-issue for the understanding of the dynamics and the evolutionary conditions of groundwater systems. The GDL consist of the difference between the elevation of the top of the well and the groundwater level. If GDL increases, it means that the groundwater level decreases. If GDL decreases, the groundwater level increases. This gives us direct information of the health of the groundwater system, compared to de precipitation and temperature information.

When considering the application of GDL, it is crucial to take into consideration two assumptions. Firstly, the GDL time series are influenced by both local and regional conditions and so GDL time-series result in non-stationary behaviour. Therefore, it is necessary to explore alternative options for its trend analysis. Traditional trend identification and significance tests are restrictive and make assumptions that may not be applicable for monitoring hydrodynamic parameters such as GDL. Understanding and determining the factors that influence the spatial and temporal variation of groundwater levels and hydrochemical parameters is essential to outline action and monitoring measures, allowing the preservation of this resource.

As a reference many publications reflect the use of multivariate statistical analysis in the evolution of salinization conditions in coastal areas (Ferchichi et al. 2018; Soltani and Mellah 2023), in the study of water quality (Kantiranis et al. 2017; Wang et al. 2018; De Andrade Costa et al. 2020; Varol 2020; Ghashghaie et al. 2022;Ghaemi and Noshadi 2022; Wali et al. 2022), and in the variation of piezometric levels (Machiwal, and Singh 2015; Adamovic et al. 2016; Rabiei et al. 2022). These techniques thus allow the analysis of relationships between variables in a comprehensive way and their quantification (Shiker 2012; Javadinejad et al. 2019a).

Factorial Analysis (FA) is a set of multivariate statistical analysis techniques that helps understand the relationship between variables. By transforming data and simplifying the relationships between variables it is possible to highlight a smaller number of intrinsic characteristics, designated as factors (Pagès 2004). It is, therefore, also known as Common Factor Analysis (CFA) (Seth 2022).

Factors capture much of the information of a set of variables in the dataset by providing an understanding of the underlying concepts of its interrelations. The FA can be applied to group the samples in a dataset based on their similarity for a certain characteristic. It can explore deeper factors that may not be evident in the dataset, reducing its multidimensionality. This technique can be handy for exploring relationships in a particular dataset category. The explored concepts or causes may not be immediately evident but may represent peculiarities or certain tendencies that may be difficult to identify or measure in a simpler way. The FA is beneficial for the interpretation of groundwater-quality data and for understanding specific hydrogeochemical processes, many distinct studies regarding multivariate statistics and FA applied in distinct contexts of groundwater study can be found in the related literature (Ruiz et al. 1990; Cerón et al. 2000; Love et al. 2004; Celestino et al. 2018; Krishnan et al. 2019; Panda et al. 2019; Fatahi et al. 2021).

The most widely used FA technique is Principal Component Analysis (PCA), which enables the relationships between quantitative variables to be assessed. There is another technique that simply assesses the relationship between qualitative variables, which is the Multiple Correspondence Analysis (MCA). There are several examples in the literature where factors identified with FA are considered in subsequent analyses, such as regression or unsupervised classification (cluster analysis). K-means Cluster Analysis and Hierarchical Classification Analysis (HCA) are the most common methods considered in this context (Celestino et al. 2018; Oh et al. 2020; Barbosa et al. 2021). However, in the presence of variables that contain both quantitative and qualitative information, it is not possible to use PCA or MCA.

Since this case study falls into this situation, FAMD technique and its potentialities were experimented. FAMD is an extension of the Factor Analysis (FA) method (Abdi 2003; Adamovic et al. 2016),. it is a multivariate statistical analysis method that is used to analyse datasets with both continuous and categorical variables. It is, in practical terms, a combination of FA and MCA techniques, FAMD is a multivariate statistical technique that is used to identify underlying dimensions or factors that explain the observed variation in a set of quantitative and qualitative variables.

In groundwater studies, the Hierarchical Classification Analysis (HCA) method, can be combined or not with FA, PCA or FAMD factors, allowing a clearer grouping of data (Wang et al. 2015; Jiang et al. 2015; Bayo and Lopez-Castellano 2016; Al Naeem et al. 2019; Rao and Chaudhary 2019; Subba et al. 2019; Visbal-Cadavid et al. 2020; Rahbar et al. 2020; Batdelger et al. 2023).

The other assumption is that GDL trends may change significantly through time due to the dependence on distinct factors that cause variations in hydrodynamic conditions, some of these causes may act independently in time or could be a part of complex combined trending effects. In these cases, verification of positive or negative slope tendencies may be difficult or even impossible using simple linear approaches. In geosciences, parametric methods are widely used, although often that the data under analysis does not meet the necessary normality criteria.

In hydrological studies it is wrong to assume that the data is stationary and independent of the time series, as this does not correspond to reality (Helsel 1987; Anderson 2008; Mumby 2002; Riaz et al. 2016; Mirabbasi et al. 2020). Furthermore parametric methods are hypersensitive in to the presence of outliers in the data series, unlike non-parametric methods (Mirabbasi et al. 2020). Thus, it is natural to resort to non-parametric methods, like, Mann–Kendall Analysis (MKA) and Şen's T Analysis, also known as Innovative Trend Analysis (ITA). According to Şen (2012, 2014) ITA is proposed as an improved technique of the classical MKA, there are some differences between these two techniques.

In MK analysis it is assumed that time series are independent and have no serial correlation. In ITA it is considered the opposite situation, in this technique it is considered that serial correlations in small series are usually significant in the interpretations of the phenomena as an all (Şen 2017).

ITA allows the identification of monotonous and holistic trends, as is the case with MK, however, ITA is a graphical method that allows trend patterns to have low, medium, and high values in the data, therefore applying to non-stationary datasets (Şen 2012, 2014, 2017). This method was originally developed for hydro-climatological time series and has been increasingly used due to problems of non-stationary, high magnitude and variability which are increasingly more often detected in distinct type of climate and environmental data time series. Examples of its applicability can be found in recent works (Caloiero 2019; Javadinejad et al. 2019b; Alifujiang et al. 2020; Güçlü 2020; Minea et al. 2020; Achite et al. 2021; Zakwan 2021; Buri et al. 2022; Swain et al. 2022; Umar et al. 2022). Nevertheless, Şen et al. (2019) proposed another innovative method, defined was Innovative Polygon Trend Analysis (IPTA), which has been used in several studies and investigations in Hydrogeology (Caloiero et al. 2018; Sanikhani et al. 2018; Kuriqi et al. 2020; Harkat and Kisi 2021; Ahmed et al. 2022),in this method, polygon patterns are obtained using information such as the mean, minimum, maximum, standard deviation or skewness parameters of the data at different time scales (daily, monthly, etc.) (Akçay et al. 2022). When compared to the ITA this method allows for the information associated to one year to be symbolized and can retain the trend, the magnitude and slope of trend transitions between successive segments (e.g., days, months) (Akçay et al. 2022).

In the present study, due the two characteristics of GDL trends, FAMD was applied first to identify the temporary evolution of each well and to verify existence of effects of depletion or rising in the groundwater levels and their spatial distributions along the basin. After that, the results were combined with HCA to group wells by the results. Lastly, ITA, IPTA and MK algorithm were applied with the aim of having a synthesis of positive and negative trends of GDL dataset which are a direct consequence of distinct hydrodynamic conditions. Examples of application of ITA to groundwater levels data series can be found in the references Minea et al. (2020), and Zakwan (2021).

Materials and methods

Geological and hydrogeological characteristics of study area

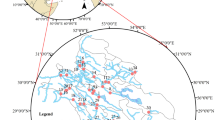
The area of study integrates the Central and Southern sectors of the aquifer systems of the Left Bank of the Tagus-Sado Basin (Portugal, Iberian Peninsula, Fig. 1). The Tagus-Sado Basin is a wide sedimentary basin, formed by Cenozoic and Quaternary sediments, it consists of a long depression with NE-SW diretion, limited in the W and N by Mesozoic formations, and NE, E and SE by Paleozoic subtract (Almeida et al. 2000).

Fig. 1
figure 1

Study area, located in the Central and Southern sectors of the aquifer systems of the Left Bank of the Tagus-Sado Basin (Portugal)

Full size image

The studied wells reach groundwaters from the Upper Miocene, which includes various types of aquifers (semi-confined and confined systems). It is a complex multilayer aquifer system (Costa 1994) mainly composed by alternating sedimentary sequences of continental and marine facies, resulting from transgressions and regression phenomenons, controled by the reactivation of graben and horst structures during the Alpine orogeny, promoting different hydrogeological behaviours and high spatial variability, thus allowing the creation of free, semi-confined and confined aquifer systems (Costa 1994; Fernandes and Silva 1998; Simões 1998; Simões and Legoinha 2014). This system is connected vertically with the free aquifer of Quartenary Pliocene–Pleistocene age (Zbyszewski et al. 1976; Antunes 1983; Manuppella et al. 1999; Pais et al. 2006), which is mainly constituted by fluvial deposits from deltaic systems associated to last regression of the basin, these allow some parts of the basin have a length of 800 m deeper. Most of the fault structures in the basin area are associated with the tectonic inversion of the Lusitanian Basin (Mesozoic) and the Paleozoic punch, as a result of the convergence of the African continent, relatively, to the Iberian continental block (Kullberg et al. 2000).

In the North sector, the basin was controlled by structures with NE-SW diretion (Carvalho et al. 1983–85; Cunha 1992). However, one the most important struteres, Pinhal Novo fault presents a general orientation NNW-SSE and covers a wide zone of deformation (about 1.5 km) (Correia 2017), in which it presents a pattern of branching and anastomosing faults.

In the South sector, the basin was controlled by te reactivation of the late-Hercynian faults of the Iberian Pyrite Belt, which have a general NW–SE orientation, showing cleavage and folding planes compatible with a strong vergence to SW (Matos 2021). During this time the fragmentation of the Paleozoic background happened due to alpine and/or late-variscan faults with NNE-SSW orientation NE-SW, NW–SE and E-W, creating stratigraphic variations between the North and South sector of the basin, as well as the diffraction from other aquifers systems associated to Tagus-Sado Basin (Oliveira et al. 1998, 2001).

The main method of drainage of the basin occurs extensively in depth and the recharge of the aquifer system depends mostly in precipitation in which the infiltration of water flows into the soil, with descending and lateral flows, which then communicate with the water lines. The flow is conditioned by the two main water lines (the Tagus River to the North and the Sado River to the South), where the discharge of the system occurs. In the coastal sectors, the flow goes towards the Atlantic Ocean (Almeida et al. 2000). There are other types of flow, like local flows, whose discharge areas are the adjacent water lines and the recharge areas are the interfluves. These are flows where descending and lateral flow directions predominate. Also, there could occur intermediate groundwater flows, associated with one or more basins of the main tributaries (Almeida et al. 2000).

Data set information

The selected statistical techniques were applied to understand common characteristics underlying the GDL trends of a set of wells that are used for public monitoring purposes by the Portuguese National Water Resources Information System Entity, SNIRH (“Sistema Nacional de Informação de Recursos Hídricos”, Fig. 2).

Fig. 2
figure 2

GDL Monitoring wells considered for the study, located in the Central and Southern sectors of the aquifer systems of the Left Bank of the Tagus-Sado Basin (Portugal)

Full size image

The considered wells were selected following a previous rigorous work, the wells that were considered for the study are those that represent undoubtedly the chronostratigraphic units selected for the case study and presented data series with sufficient representativeness for the chosen period of study, that is, from 1999 to 2021, which are define in the Table 1.

Table 1 Characteristics of the wells for the representatives analysis
Full size table

It can be said that the high increases in GDL found in some monitoring wells, particularly in the South sector of the basin, were the initial motivation for this study (Fig. 3). To gain a comprehensive understanding of the results, the climatological evaluation of the area between 2000 and 2020 was also analyzed, which are represented in the Fig. 4.

Fig. 3
figure 3

Total GDL variations in distinct monitoring wells of the Left Bank of the Tagus-Sado Basin

Full size image
Fig. 4
figure 4

Evolution of climatological parameters – total annual precipitation (P) and annual mean of temperature (T) of each hydrogeological year, in distinct monitoring weather wells, from 1999 to 2021

Full size image

The data was collected from the Comporta, Moinhola, and Monte de Caparica weather stations (SNIRH). For the initial understanding of the climatological evolution of data between years, data was analyzed every five years since the hydrological year 2000. From that data there is some evidence of a decrease of precipitation, in the South area according to weather station of Comporta.

In Monte and Moinhola stations, the rate of precipitation is decreasing but it has some flutuation. However, the average tempeturate has a erratic tendency, and doesn’t have correlation with the precipitation rate. Therefore, this suggests the influence of other factors that promote this decrease in the last 20 years.

To understand how these tendencies manifest over time, for each technique, the selections of wells were considered according to the relevance of the information and the quantity of data.

Multivariate analysis – factorial analysis of mixed data

FAMD consists of a multivariate factorial analysis technique in which it is assumed that there is no dependency between the variables (independent variables), focusing simply on the relationship between the data.

The method combines the principles of Factorial Analysis (FA) with Multiple Correspondence Analysis (MCA), data is first transformed using MCA to create a set of synthetic variables that capture the underlying structure of the categorical variables then, FA is applied to the synthetic and continuous variables to extract the common factors that explain the variance in the dataset.

Quantitative variables are scaled to unit variance, while qualitative variables are transformed into a disjunctive data table (Husson et al. 2017, 2020). Thus, this technique allows data to be analysed and the balance and influence of the two types of variables to be assessed (Abdi 2003; Pagès 2004; Adamovic et al. 2016).

This method provides a comprehensive analysis of the dataset by uncovering the relationship among the variables and identifying the most important factors that drive the variation.

According to Abdi (2003), Pagès (2004) and Adamovic et al. (2016), FAMD can be applied: (a) to data with few qualitative variables compared to quantitative variables, (b) when the number of individuals in the population under study is generally low.

In the analysis of results, the representation of individuals in the data population is performed directly from factors, as a projection on the first two dimensions, where quantitative variables are represented through the circle of correlations associated with the PCA analysis and qualitative variables are represented in the same way as in MCA, in which the categorical variable is represented at the centroid of the individual who has it (Adamovic et al. 2016).

By performing this procedure, indicators “cos2” are obtained, these determine the representativeness of a variable and consist of the measure between the square of the cosine and the vector issued from the position of the variable and its projection on the axis (Husson et al. 2017, 2020; Lê et al. 2008). For indicator “cos2” values are close to 1 when a variable is well represented in the projection. According to Adamovic et al. (2016), usually, after performing this technique, it is advisable to proceed with HCA to complete the classification of individuals into groups that represent distinct well trend patterns.

As the mathematical concept, according to Audigier et al. (2016), the first step of FAMD consists of coding the categorical variables using the indicator matrix of dummy variables. For that, we have to initially define the information to the respective parameter, where \(I\) is the number of individuals, \({K}_{1}\) is the number of continuous variables, \({K}_{2}\) is the number of categorical variables, and \({K=K}_{1}+{K}_{2}\) is the total number of variables. Each continuous variable is a constructed matrix, where \({X}_{i\times j}\) is the matrix where \({{(x}_{j})}_{1\le \mathrm{ j}\le {K}_{1}}\) are continuous variables \({{(x}_{j})}_{1\le \mathrm{ j}\le {K}_{1}}\) and are dummy variables. The total number of columns is \({J=K}_{1}+{\sum }_{k={K}_{1}+1}^{K}qk\) where L is the number of categories of the variable k.

The PCA in the FAMD can be represented as \((\left(X-M\right){D}_{\Sigma }^{-\frac{1}{2}}),\) where \({M}_{I\times J}\) is the matrix with each row being the vector of the means of each column of \(X\) and \({D}_{\Sigma }\) is the diagonal matrix \(diag({\sigma }_{x1}^{2},.\dots , {\sigma }_{x{K}_{1}}^{2}, \dots ., {p}_{{K}_{1}+1},\dots ., {p}_{j}, \dots ., {p}_{J})\), being the standard deviation of the continuous variable \({x}_{j}\) and \({p}_{j}\) being the proportion of individuals in the category \(j(j={K}_{1}+1, \dots , 1,\dots , J)\). The matrix \({D}_{\Sigma }\) is the metric used to compute distances between rows. The loss function (known as the reconstruction error), which in the PCA is minimized in matrix \(X\) is:

$$\left\| {X - U\Lambda^{1/2} V^{\prime}} \right\|^{2}$$
(1)

Thus, FAMD can be defined as minimizing:

$$\left\| {\left( {X - M} \right)D_{\Sigma }^{{ - \frac{1}{2}}} - U\Lambda^{1/2} V^{\prime}} \right\|^{2}$$
(2)

FAMD provides the best low-rank \((S<\left(J-{K}_{2}\right))\) approximation of the matrix \(\left(X-M\right){D}_{\Sigma }^{-\frac{1}{2}}\) in the least square sense. The solution is given by the singular value decomposition (SVD) of the matrix \(\left(X-M\right){D}_{\Sigma }^{-\frac{1}{2}}\), with \({\hat{U} }_{I\times S}\) the left singular vectors and \({\widehat{{\varvec{V}}}}_{{\varvec{J}}\times {\varvec{S}}}\) the right-singular vectors associated with the S largest singular values gathered in the matrix \({({\widehat{\boldsymbol{\Lambda }}}_{{\varvec{S}}\times {\varvec{S}}})}^{1/2}=diag\left(\sqrt{{\widehat{{\varvec{\lambda}}}}_{1}},\dots ,\sqrt{{\widehat{{\varvec{\lambda}}}}_{{\varvec{S}}}}\right)\). Notice that the maximum number of non-null eigen values is \(\left(J-{K}_{2}\right)\) because of the linear restrictions on the columns for the categorical variables (the row sum for each variable equals 1).

The specific weighting implies that the distances between two individuals in the initial space, \(i\) and \(i^{\prime}\) (before approximating the distances by keeping the first \(S\) dimensions obtained from the SVD), is:

$$d^{2} \left( {i,i{^{\prime} } } \right) = \sum\limits_{{k = 1}}^{{K_{1} }} {\frac{{\left( {x_{{ik}} - x_{{i{^{\prime}} k}} } \right)^{2} }}{{\hat{\sigma }_{{x_{k} }}^{2} }}} + \sum\limits_{{j = K_{1} + 1}}^{J} {\frac{1}{{p_{j} }}} \left( {x_{{ij}} - x_{{i{^{\prime }} j}} } \right)^{2} ,$$
(3)

Weighting by \(\frac{1}{{\widehat{{\varvec{\sigma}}}}_{{{\varvec{x}}}_{{\varvec{k}}}}^{2}}\) ensures that units of continuous variables do not influence the (square) distance between individuals. Weighting by \(\frac{1}{{p}_{j}}\) unequivocally establishes that two individuals who belong to different categories for the same variable are significantly more distant from each other when one of them is in a rare category compared to when both of them belong to frequent categories. The marginal frequencies of the categorical variables play a crucial role in this method. Categories with a small frequency have a greater inertia than the others, and consequently, rare categories have a greater influence on the construction of the principal components. The specific weighting also implies that, in FAMD, the principal components maximize the associations with both continuous and categorical variables. More precisely, the first principal component \({f}_{1}\), maximizes:

$$\sum_{k=1}^{K}{R}^{2}\left({x}_{k},{f}_{1}\right)+\sum_{k={K}_{1}+1}^{K}{\eta }^{2}\left({z}_{k},{f}_{1}\right),$$
(4)

With \({\left({z}_{k}\right)}_{k}=K+1, \dots , K\) the categorical variables. The first principal component is the synthetic variable, which has the highest correlation with both the continuous variables (measured by the coefficient of determination, (\({R}^{2}\))) and the categorical variables (measured by the squared correlation ratio (\({\eta }^{2}\))). The second principal component is the synthetic variable, which maximizes the criterion among variables orthogonal to the first principal component and to the rest of the other principal component.

Multivariate analysis – hierarchical classification analysis

In support of FAMD results, HCA was executed, it is a method of clustering data based on the similarity of the variables or cases.

In the case of FA, HCA can be used to identify groups of variables or cases that share similar factor scores. This can be particularly useful in identifying patterns or subgroups within a dataset that might not be immediately apparent from the initial FA.

Unsupervised classification is a technique used to determine homogeneous groups, defined as clusters, whose data presents similarities among themselves in a population. For this purpose, it includes techniques that use successive iterative processes, which process all objects in a set through divisive or agglomerative methods.

Agglomerative methods start with each case or variable as its own cluster and then merges clusters together based on their similarity, while divisive methods start with all cases or variables in one cluster and then split them into smaller clusters based on their dissimilarity. This process ends when all objects are processed (Almeida et al. 2007).

The choice of method will depend on the characteristics of the dataset and the research question being addressed. The HCA results are often presented in a dendrogram, where each linking step in the clustering process is represented by a connecting line (Smoliski et al. 2002; Granato et al. 2018). One common approach to conducting HCA in the context of Factorial Analysis is to use Ward's method, as in our case-study, which aims to minimize the sum of squared distances between the cases or variables within each cluster.

Other methods, such as single linkage or complete linkage, can also be used, depending on the research question and the characteristics of the dataset.

According to Nielsen (2016), this method groups all potential groups in pairs, in which the differences between the sum of the square of the differences of each object to the centroid is the smallest when comparing before and after the junction. The Ward linkage function is characterized as: To merge \({{\varvec{X}}}_{{\varvec{i}}}({{\varvec{n}}}_{{\varvec{i}}}=\left|{{\varvec{X}}}_{{\varvec{i}}}\right|)\) with, \({{\varvec{X}}}_{{\varvec{j}}}({{\varvec{n}}}_{{\varvec{j}}}=\left|{{\varvec{X}}}_{{\varvec{j}}}\right|)\) where consider the following Ward criteria:

$$\Delta \left({{\varvec{X}}}_{{\varvec{i}}},{{\varvec{X}}}_{{\varvec{j}}}\right)=\boldsymbol{ }\frac{{{\varvec{n}}}_{{\varvec{i}}}{{\varvec{n}}}_{{\varvec{j}}}}{{{\varvec{n}}}_{{\varvec{i}}}+{{\varvec{n}}}_{{\varvec{j}}}}{\Vert {\varvec{c}}\left({{\varvec{X}}}_{{\varvec{i}}}\right)-{\varvec{c}}\left({{\varvec{X}}}_{{\varvec{j}}}\right)\Vert }^{2},$$
(5)

where \({\varvec{c}}\left({{\varvec{X}}}^{\boldsymbol{^{\prime}}}\right)\) denotes the centroid of the subset \({{\varvec{X}}}^{\boldsymbol{^{\prime}}}\subseteq \boldsymbol{ }{\varvec{X}}:{\varvec{c}}\left({{\varvec{X}}}^{\boldsymbol{^{\prime}}}\right)=\frac{1}{\left|{{\varvec{X}}}^{\boldsymbol{^{\prime}}}\right|}{\sum }_{{\varvec{x}}\in {{\varvec{X}}}^{\boldsymbol{^{\prime}}}}{\varvec{x}}\). Observe that the distance between two elements induced from the sub-set distance \(\Delta\) is merely half of the squared Euclidean distance:

$$\Delta \left(\left\{{{\varvec{x}}}_{{\varvec{i}}}\right\},\left\{{{\varvec{x}}}_{{\varvec{j}}}\right\}\right)={\varvec{D}}\left({{\varvec{x}}}_{{\varvec{i}}},{{\varvec{x}}}_{{\varvec{j}}}\right)=\frac{1}{2}{\Vert {{\varvec{x}}}_{{\varvec{i}}}-{{\varvec{x}}}_{{\varvec{j}}}\Vert }^{2},$$
(6)

According to the equation in each iteration, the centroid of each group is calculated, and the sum of squared error (SSE) is calculated as the Euclidean distance between each object and the centroid of the group. Then, for all possible pairwise groupings, the hypothetical centroid resulting from the merger of the two groups is calculated, along with the sum of the Euclidean distances from each object to the hypothetical centroid. For each evaluated group merger, the value resulting from the sum of the two distances calculated separately is compared with the distance calculated already as a group (it is always an increment), and the similarity matrix is updated with these increments. Once the matrix is fully populated, the pair of groups leading to the smallest increment is merged. At the beginning of the process, each object is a group with zero dispersion, so the sum of dispersions for all groups is zero. In the end, only one group will remain, so the total dispersion is the sum of the squares of the differences between each value and the mean of the respective variable. The distance recorded in the dendrogram is the sum of the dispersions of the involved groups.

Innovative trend analysis and innovative polygon trend analysis

ITA (Jiang et al. 2015) divides the time series into two equal subseries based on the average of its values, which are consequently classified separately in ascending order. Each subseries is subsequently distributed along two axes, the \({X}_{i}\) subseries on the \(X\) axis, and the \({X}_{j}\) subseries on the Y axis. With the subseries defined, the arithmetic means of each subseries are obtained, allowing for the determination of the slope value, according to Eq. (1) where n is the number of total time series data.

$$E\left({S}_{a}\right)=\frac{2}{n}\left[E(\overline{{X }_{2}})-E(\overline{{X }_{1})}\right],$$
(7)

If \(E\)(\(\overline{{X }_{1}}\)) = \(E\)(\(\overline{{X }_{2}}\)), then \(E\left(s\right)=0\), and the centroid of the trend line falls on the 1:1 line, indicating that there is no trend. This corresponds with the null hypothesis, \({H}_{0}\), where it is assumed that there is no trend if the calculated slope value, \({S}_{a}\), remains below a critical value, \({S}_{cr}\). Otherwise, an alternative hypothesis is applied, \({H}_{a}\), in which \({S}_{a}\)>\({S}_{cr}\) (Şen 2017). In this case, if \({X}_{1}\)>\({X}_{2}\), there is a negative trend, that is, there is a decrease, and if \({X}_{1}\)<\({X}_{2}\) there is a positive trend, that is, there is an increase (Şen 2017).

This can also be verified by the variance \({V(S}_{a}\)), in which,

$$V\left({S}_{a}\right)=E\left({S}_{a}^{2}\right)-{E}^{2}\left({S}_{a}\right),$$
(8)

In this situation the null hypothesis H_0 assumes that \({V(S}_{a})=E\left({S}_{a}^{2}\right)\) according to Eq. (3).

$$E\left({S}_{a}^{2}\right)=\frac{\left[E\left({\overline{{X }_{2}}}^{2}\right)-2E\left(\overline{{X }_{2}}\overline{{X }_{1}}\right)+E\left({\overline{{X }_{1}}}^{2}\right)\right]}{{n}^{2}/4},$$
(9)

In the situation that \(E\left({\overline{{X }_{2}}}^{2}\right)= E\left({\overline{{X }_{1}}}^{2}\right)\), variance mean is equal to:

$$E\left({S}_{a}^{2}\right)=\frac{\left[E\left({\overline{{X }_{2}}}^{2}\right)-E\left(\overline{{X }_{2}}\overline{{X }_{1}}\right)\right]}{{n}^{2}/8},$$
(10)

The correlation coefficient between two values is given according to its autocorrelation which is equal to:

$${\rho }_{{\overline{X} }_{1}{\overline{X} }_{2}}=\frac{E\left(\overline{{X }_{2}}\overline{{X }_{1}}\right)-E(\overline{{X }_{2}})E(\overline{{X }_{1})}}{{S}_{{\overline{X} }_{1}}{S}_{{\overline{X} }_{2}}},$$
(11)

where \({S}_{{\overline{X} }_{1}}={S}_{{\overline{X} }_{2}}=S/\sqrt{n}\). Hence, the equation can be written according as:

$$E\left({S}_{a}^{2}\right)=\frac{(1-{\rho }_{{\overline{X} }_{1}{\overline{X} }_{2}})}{{n}^{2}/8}*\frac{{S}_{a}^{2}}{n},$$
(12)

where the correlation coefficient corresponds to the arithmetic means between the two subseries. Thus, the standard deviation of the sampling slope value can be obtained from Eq. (7).

$$\sqrt{E\left({S}_{a}^{2}\right)}=\frac{2\sqrt{2}}{n\sqrt{n}}S\sqrt{1-{\rho }_{{\overline{X} }_{1}{\overline{X} }_{2}}},$$
(13)

Under these circumstances, the third-order moment of the slope variable is also equal to zero, and the same is true for all odd-order moments. For this reason, the slope respects the normal (Gaussian) Probability Distribution Functions (PDF) with zero mean and standard deviation, thus being the basic criterion of this method (Almazroui and Şen 2020). As previously mentioned, this technique makes it possible to distinguish between series values in “low”, “medium” and “high”. Individualization and characterization of data is possible to be considered into 9 subareas, according to Fig. 5, with the next following interpretative means (Almazroui and Şen 2020):

  1. 1.

    Trendlines running parallel to the 1:1 line (45º) implies an increase or decrease, which is constant (B and C), while partial lines (D, E, I and L), encompass ratings below ("low", "medium" or "high"). If the centroid is on the 1:1 straight line (45º), then there is a trend;

  2. 2.

    Non-parallel trend lines (F, G, H, J, K or M) to the 1:1 (45º) straight line implies a change in the deviation pattern over time;

  3. 3.

    Straight lines F and G have trends in standard deviation but not in arithmetic mean;

  4. 4.

    Trend lines, H (K) and J (M) imply an increasing (decreasing) standard deviation trend.

Fig. 5
figure 5

Different partial trends considered by ITA technique (adapted from Almazroui and Şen 2020)

Full size image

According to Şan et al. (2021), Şen et al. (2019) proposed the IPTA graphic method and revealed that it has certain advantages compared to other traditional trend methods in specific areas, such as the agricultural field and in hydrological studies. The ability to identify trends in a sequence is one of its significant characteristics that provides a highly productive basis for better linguistic and numerical interpretation and deduction.

If IPTA is applied to monthly data, according to Şen et al. (2019) and Şan et al. (2021), five processing steps are required. Step (1): monthly (e.g. Jan., Feb., Mar…) time series is divided into two equal periods. Step (2): basic statistics (e.g. mean, max) or desired criteria (e.g. uncertainty) for each month are calculated in both periods. Step (3): the first (second) period is placed on the horizontal (vertical) axis in the scatter chart, and 12 points are marked for 12 months. Step (4): the points of consecutive months are connected by straight lines forming a polygon (Fig. 2). Step (5): the slope and size of the line between consecutive points are calculated.

$$\left|{\varvec{A}}{\varvec{B}}\right|=\sqrt{{\left({{\varvec{x}}}_{2}-{{\varvec{x}}}_{1}\right)}^{2}+{\left({{\varvec{y}}}_{2}-{\varvec{y}}\right)}^{2}}$$
(14)
$${\varvec{s}}=\frac{{{{\varvec{y}}}_{2}-{\varvec{x}}}_{2}}{{{{\varvec{y}}}_{1}-{\varvec{x}}}_{1}}$$
(15)

where \({\varvec{s}}\) is the trend slope, \(\left|{\varvec{A}}{\varvec{B}}\right|\) is the trend length,\({{\varvec{x}}}_{1}\) and \({{\varvec{x}}}_{2}\) are two consecutive points in the first part in horizontal, \({{\varvec{y}}}_{1}\) and \({{\varvec{y}}}_{2}\) are two consecutive points in the second part. In the Cartesian coordinate system, a 1:1 (45°) line is drawn, where the points are below (above) the line representing a decreasing (increasing) trend (Şen 2012). Straight lines connecting the points provide information about the changes between the successive months. If the slopes of the lines between consecutive months are far from each other, the contribution of the changes between months to the average change in the hydrometeorological series is significant and vice versa (Şan et al. 2021).

Mann–Kendall analysis

According to diverse authors (Hamed 2008; Güçlü 2020; Mirabbasi et al. 2020) the MKA developed by Mann (1945) and revised by Kendall in 1948 (NLJ 1948), assumes that the trend value to be obtained is calculated according to the Eq. (8), and (9).

$$sgn\left({x}_{j}-{x}_{i}\right)=\left\{\begin{array}{c}1; \,If\, {x}_{j}>{x}_{i}\\ 0;\, If \,{x}_{j}={x}_{i}\\ -1;\, If \,{x}_{j}<{x}_{i}\end{array}\right.,$$
(16)
$$S=\sum_{i=1}^{n-1}\sum_{j=i+1}^{n}sgn({x}_{j}-{x}_{i})$$
(17)

Each pairwise of a data series is classified in one of the three subsets (-1, 0, 1) according to their differences (Eq. (8)). In Eq. (9) \({x}_{i}\) and \({x}_{j}\) are the data values for time \(i\) and \(j\), and \(n\) is the dataset length. When the S value is positive, it indicates an increasing trend, otherwise, it verifies a decreasing trend. When a data length of a series is higher than n > 10, the data distributions approach a normal distribution law, with a mean equal to zero, where the variance [\(Var\left(S\right)]\) assumes the following expression (Eq. (10)):

$$Var\left(S\right)=\frac{n-\left(n-1\right)\left(2n+5\right)-C}{18},$$
(18)

where \(C\) is a factor for modified variation and \(n\) represents the number of defined groups. In the presence of data series with the occurrence of successive data, the parameter \(C\) is calculated by the following formula:

$$C=\sum_{i=1}^{m}{t}_{i}\left({t}_{i}-1\right)\left(2{t}_{i}-5\right),$$
(19)

where \({t}_{i}\) defines the number of linked data in the group. If there are no groups, it automatically skips this process. After calculating the variance of the series data, the standard Z value is calculated according to the following equation:

$$Z=\left\{\begin{array}{c}\frac{S-1}{\sqrt{Var (S)}}; If S>0\\ 0; If S=0\\ \frac{S+1}{\sqrt{Var (S)}}; If S<0\end{array}\right. ,$$
(20)

In the MK analysis, the null hypothesis \({H}_{0}\) represents “no significant trend in the time series”, and it is accepted if the confidence level, \(\alpha\), is:

$${-Z}_{\left(1-\frac{\alpha }{2}\right)}\le Z \le {-Z}_{\left(1+\frac{\alpha }{2}\right),}$$
(21)

If this hypothesis is not verified, \({H}_{0}\) is rejected, and the alternative hypothesis (that is, existence of a significant trend in terms of importance) is accepted (Dinpashoh et al. 2014).

In the graphical results of MKA information is divided into two different lines: the prograde and the retrograde line. The prograde line corresponds to Z(S) values, and the retrograde line represents Z^* (S). When these two lines touch each other, we are under an event that represents an inversion of the tendency. With this, it is possible to determine at which point the transition occurs. The arrangement of lines gives us information about the type of tendency and the confidence level interval value (CL). If the line prograde is above the other line, that indicates a positive tendency, which means an increase in GDL and if the opposite situation manifests, that indicates a decrease in GDL. However, for the analysis to be correct, it is necessary for the two lines to be inside the CL value of 95%. In the case where just one of the lines is inside that interval, the tendency is represented by the line inside the CL if 95% prior to the inversion. For the null hypothesis to occur, the two lines must touch each other constantly with a minimal gap in between.

Results

FAMD and HCA

Information was analysed between 2006 and 2021 for the monitoring wells defined in Table 2.

Table 2 Average value of water level depth (m) from 2006 to 2021 in distinct monitoring well
Full size table

In this study, the years represent the quantitative variables, and the wells represent the qualitative variables. Figure 6 presents the distribution of the qualitative variables (that is, the monitoring wells) in Dimension 1 (Dim 1), and Dimension 2 (Dim2) axes, it is possible to observe the projection of the contribution of each qualitative variable for dimensions 1 and 2 (axes values) and its classification for the indicator “cos2” simultaneously (colour gradient scale).

Fig. 6
figure 6

Projection of the contribution scores of qualitative variables in Dim1 and Dim2 without the consideration of monitoring well “476/20”

Full size image

For a better understanding of the projection results and on the meaning of each dimension, the well “476/20” was not considered in the initial analysis, due to is behaviour, this well shows a very marked downward trend with a difference of GDL close to 24 m between 2006 and 2021 (Table 2) having a behaviour of extreme outlier.

In the performed analysis, Dim 1 and Dim 2 represents about 72% of the variance. The distribution of qualitative variables is dispersed, indicating the existence of subpopulations with distinct tendencies in time. Dim1 is conditioned by the monitoring wells with the most irregular trends, from lower depths of groundwater levels (contribution close to -5, well 484/8) to higher depths of groundwater levels (contribution close to 9, well 453/18) (Fig. 6). Monitoring wells with the most constant trends are positioned in Dim 1 close to “0”, along Dim 2 (Fig. 6).

The Fig. 7 presents the FAMD results considering well “476/20” and other two wells included in a posterior stage of the analysis (518/30, and 528/16),it is to say that, although the outlier behaviour of variable “476/20”, the variance results for Dim1 and Dim2 don’t vary significantly. For this reason, and due to the importance of this monitoring well in the performed analysis, it was decided to consider FAMD results with the outlier “476/20”.

Fig. 7
figure 7

Projection of the contribution scores of qualitative variables in Dim1 and Dim2 with the consideration of monitoring well “476/20”

Full size image

In these conditions (Fig. 7), the monitoring wells with the highest scores in Dim2 present more accentuated non-constant tendential patterns on the depths of groundwater levels. The Dim2 in these conditions is, therefore, conditioned by well “476/20” which evolves from constant stationary trends (negative score contributions in Dim2 and closer to “0” in Dim1) to less constant trends (increasing or decreasing trends in positive score contributions in Dim2 and further apart to “0” in Dim1). Again, Dim1 is conditioned by the monitoring wells with the most irregular trends, from lower depths of groundwater levels (contribution of -5.4, well 484/8) to higher depths of groundwater levels (contribution of 9.1, well 458/18) (Fig. 7).

It is also observed an increasing tendency in the depth of groundwater levels in the monitoring wells with the highest score contributions for Dim1, like it is the case of wells 434/306, 442/94, 443/924, 445/7 and 453/18. The location of these monitoring wells can be observed in Fig. 8, which includes the interpretational kriging maps of the FAMD contribution scores (Table 3) for Dim 1 and Dim2 and the subsequent HCA classification of monitoring wells in 4 clusters. These results evidence the subsector in the Basin with deepest groundwater levels (scores with red and orange colours in Dim1), and the areas with groundwater levels closest to the ground surface (scores with blue and green colours in Dim1).

Fig. 8
figure 8

Interpretational kriging maps of FAMD contribution scores of Dim1 and Dim2, and locations of HCA cluster classification

Full size image
Table 3 The scores of contributions to Dim 1 and Dim2 of each well station
Full size table

From the score mapping of Dim2 in Fig. 7, it is also possible to observe a more constant stationary behaviour in GDL of the monitoring wells located at the North sector of Basin while towards the South sector, there is a growing trend to greater oscillations, mainly with an increasing in deep of groundwater levels as is the case of wells 476/21, 476/20, 484/8, 518/30 and 528/ 16, which present positive values in Dim2.

Monitoring well 476/20 has the heights increasing tendency the deep of groundwater levels (with more than 20 m in depth). The score map of FAMD results for Dim 1 and Dim 2 (Fig. 8) gives a good perspective of the distinct GDL trend groups in the aquifer systems between 2006 and 2021.

For a better understanding of the different characteristics of the distinct well trend groups, HCA was applied to the contribution score values of obtained from FAMD. The data was subjected to an iterative process to find the right number of clusters which represent the most adequate for the population. From that process, the number of clusters considered was 4 (Table 4). From the observation of Fig. 8 it is possible to understand the localization of the HCA clusters in the study area. It is possible to verify that HCA applied to FAMD scores enhances the results of FAMD making it possible do have a finer discretization of the results.

Table 4 Interpretation of HCA results considering the classification in 4 clusters
Full size table

ITA and MK

For ITA method, monthly information of GDL was used, from each well, to detect small variations in trends. In this way, all samples from Table 1, which refers information from 2006 until 2021, were used. It also included 4 wells with data from 2011 to 2021 and 3 others from outside the main aquifer system to understand the tendencies in some areas, which was not possible to conclude in the other analysis. The achieved results are presented in Table 5 and also in the Appendix A (from Figs.11, 12, 13, 14, 15, 16, 17, 18, 19).

Table 5 ITA results
Full size table
Fig. 9
figure 9

Map of ITA slope kriging results

Full size image

ITA slope kriging results are presented in Fig. 9, it is possible to observe that there is a more pronounced increase in GDL in the South sector of the Basin as it has been verified previously with FAMD. There are also situations where a decrease in GDL is observed (432/855, 442/36, 442/537, 442/94, 444/355, 453/18, 453/395, 454/151 and 476/19), and in cases even a constant tendency is verifiable (444/318 and 454/146).

Through the analysis of the graphs obtained from ITA, it is possible to verify two situations, which are also reflected in FAMD analysis:

  • There are monitoring wells with constant tendencies and monitoring wells with irregular tendencies. The monitoring wells with a more constant behaviour mostly show positive trends, defined in the confidence interval (α). The monitoring wells with irregular behaviours (10 wells) can present general negative trends of GDL (in 453/151, 432/855 442/36) or general positive trends, as is the case of 420/105, 432/68, 432/800, 476/20, 476/21, 484/8, and 528/16. Higher slopes (positive and negative) present a more pronounced anomalous trend, suggesting that anomalous behaviours register a very significant variation in short periods, which is the case of well 476/20 (Fig. 6).

  • The monitoring wells with constant tendency behaviour have smaller slope standard deviation values. All found correlation values are quite high, greater than 0.8 and in most of the cases close to 0.99, except for one monitoring well (420/105) that has a low correlation value, less than 0.5, which results from an episode in which the groundwater depth, at first, increased sharply.

Through Fig. 9 it is possible to verify that in the Southern sector and in a smaller area of the North study area, increasing tendencies of GDL (that is, increases in groundwater depth levels) occur, while the more coastal sectors and areas close to estuaries zones present a certain slight tendency to decreases in GDL. However, the well 466/21 shows a different tendency, with an increasing of GDL, which could result from exploitation in the area. Hence, from this result it possible to visualize an initial transition to the decreasing of GDL as shown in the Appendix A.

MKA method was applied to complement ITA results, and to reverify the tendencies observed with the previous methods. Like ITA, the graphical results of MKA are also presented in Appendix A.

It is possible to observe that most of the wells display a positive trend of the GDL, except in the cases of 432/855, 442/36, 442/537, 442/94, 444/355, 453/18, 453/395, 454/151 and 476/19, as it was stated in ITA.

Positive trends of GDL are predominant between 2006–2016 and 2018–2021, where some wells that display a minor transition period between 2008–2009 and 2017–2018. In 2018–2021, the slope of both lines is significant, which shows that in the last years the rate of GDL increase was escalating.

Negative trends in GDL began to manifest after the beginning of 2007 and in 2010 and 2011. The wells 432/855 and 454/151 display a GDL negative trend between 2015 and 2021. From the previous analyses, the well 476/20 represents a very significant positive trend since the beginning of 2019. It is also possible to verify that wells 434/280, 434/306, and 443/924, have three to five breaking points at different periods, which reinforces the already irregular profiles detected. In general, wells with anomalous tendencies have significant slopes in ITA after the breaking points in MKA.

Afte analysing the ITA and MK, was applied the IPTA methodology to complement the analyses of ITA as well. Ten wells, were analysed, 5 in the south sector and the other 5 in the North sector. The, results obtained, which are in Appendix B present some clarifications. It is possible to visualise that, in a general way, almost wells that show an increase in GDL manifest this trend for most months of the year, especially in the wells located in the southern sector of the study area. The wells with GDL decreasing behaviour show the opposite behaviour. It suggests that depletion and rising effects have been occurring consistently over the years.

By careful analysis, it becomes evident that some wells share a similar pattern in their monthly evolution. In wells 476/20 and 528/16 between the months Dec-Jan, there is an inflexion, whose slope is accentuated and coincides with the maximum trend line, indicating a tendency for the depth to increase in the month of Dec over the years in comparison to the month Jan. This suggests a decrease in the recharge rate in the southern sector in the winter months, with other factors of a structural nature in the basin. The wells 445/7 and 466/21 show a more constant trend of increasing depth over the months, except for the month of Aug for the well 445/7, where there is a decrease in GDL, indicating the possibility of recharge in the system by anthropogenic means (agricultural areas), to mitigate the effects of drought. The well 476/21, in comparison to the remaining wells, observes an inversion between the months Sep-Oct, corresponding to one of the maximum trend lines, followed by the months Apr-May. In addition, the month of Jan shows no trend relative to the other months. This could be due to changes in the recharge effect and rising sea levels during the dry season. In 442/241, there is an increase in GDL over the months, especially in the summer months, which is conditioned by the recharge rate.

In the wells 453/18 and 432/855 show irregular behaviour. The significant decrease observed in the well 432/855, could result from the combination of the rise of sea level and possibly from precipitation. In the well 453/18, the rise of sea level could also explain that effect in the summer combine with the precipitation but not so significate as the well 432/855. The well 476/19, on the other hand, shows a constant trend over the months, and in the months of Aug, Sep and Oct, this effect is significant due to the rise of sea level. The well 420/12 shows variations in the tendency, where the months Jan, Apr, May and Aug present a decrease in GDL, Feb, Mar, Jun, Jul, Nov and Dec, present a decrease in GDL, and last Sep and Oct don´t show tendency at all. This suggests a combination of factor like anthropic and the climate change.

Discussion and conclusions

The evaluation of annual and long-term changes in groundwater reserves, namely the variations in groundwater depth levels (GDL), assumes an enormous relevance in the context of hydrogeological resource management. Among others, the GDL trend analysis allows to estimate indirectly the groundwater recharge rate effectiveness, and allows to determine its gradients, to understand dynamic evolutions of aquifer systems and to design efficient and sustainable exploitation of groundwater wells.

In general, FAMD associated with HCA allows to obtain more reliable results in cases where the amounts of available data are small.

However, there were some difficulties and incongruencies in the clustering analysis process, probably due to the reduced number of observation wells when compared to the dimension of the study area, and the extreme outlier behaviour associated with the well “476/20” which affected the results.

When comparing the FAMD and ITA, there are correspondences in the detected trends observed with both methods, without a doubt,, ITA enables significantly a more efficient analysis of periods and can effectively leverage a larger pool of observation data in comparison to FAMD.

In this case-study, variations in GDL are likely relatable to deficiencies of the recharge rate of the aquifer system. From ITA it was possible to observe that the high slope values, that is, the most demarcated trends, occur central area of the Basin and the inverse situations in the bay areas.

With the IPTA analyses it's also possible to conclude that in most of the years, the increases and decreases of the GDL occur almost in all months. The evolution along the month reveals also that in some locations the combination of different factors, severely conditionate the transition between months, creating irregular polygons, showing the evolution of GDL is not constant.

When ITA results are complemented with MKA, it is possible to conclude with a certain level of accuracy that, in the period 2006–2010, there was an initial increase of GDL in the center of the Basin, and from 2010 to 2015, the opposite occurred in the bay areas. In the South sector, there are significant variations of GDL in the last five years, in which the well 476/20 represents the highest increase in GDL. This change is undoubtedly visible in both ITA and MKA.

The higher increase tendencies in GDL can be related to insufficient recharge effects, caused by anthropic action, which is reflected by the intensification of human activity in the NE and SE sectors of the study area. In the North sector, industrialization, urban areas, and population growth may be inducing some of the detected localized increases in GDL.

In the SE sector, besides the influence of agricultural activities, the generalized increase in GDL suggests the probable influence of other natural factors such as more pronounced drought effects, which has been evidenced by recent investigation studies in the area (Novo et al. 2020), and by the evolution of temperature and precipitation according to Fig. 4. Another reason the increase in GDL is associated with the probability of some localized hydrodynamic changes due to the influence of Variscan faulting and hydrothermal systems present in the Paleozoic basement massif that underlies the studied aquifer systems (Oliveira et al. 1998, 2001; Matos 2008, 2021; Matos et al. 2009). The southern sector of the Tagus-Sado Basin is affected by Paleozoic structures corresponding to the Iberian Pyrite Belt where VMS deposits are present (e.g., Lagoa Salgada) (Matos 2021). Distinct Alpine age faults intersect the area, compartmentalizing the Paleozoic basement in distinct horst and graben structures and it is likely that some of these faults are in an active tectonic regime (Oliveira et al. 1998, 2001; Matos 2008, 2021; Matos et al. 2009).

It is also important to mention that in the SE sector of the basin, some areas are classified as high rock temperatures until a depth 5 of km (Anderson et al. 2011). Under this geological context, hydrodynamic conditions of the aquifer systems may suffer in specific locations with slight or well demarked alterations in groundwater dynamics and hydrochemical composition This information is corroborated by the analysis of hydrochemical facies from data ranging from 2000 to 2010 shown in Fig. 10, in which there is a progression of the tendency from the ocean to the continent in the NW sector, with the appearance of transition facies, and to the south the increase of continental facies.

Fig.10
figure 10

Hydrochemical facies map distribution

Full size image

Due to some missing values in some data ranges, a certain level of uncertainty is presented in some of the results, which can mislead the observation of accurate tendencies in some few wells. It is to say that this is an exploratory study. Considering the detected tendencies, and the extension and complexity of the geological and hydrogeological conditions, it is advisable to increase the official ongoing monitoring plan, and future research works at regional scale.