Introduction

Increasing populations are resulting in a rise in hunger indexes and food insecurity. Over 23 million Pakistanis live in an agrarian economy (Abbas 2022). Despite an increase in demand for water in Pakistan, the supply side struggles to meet the requirements. Pakistan’s water availability per capita is 908 \({{\text{m}}}^{3}\), down from 5260 \({{\text{m}}}^{3}\) in 1951, and only 10% of its annual water flows are stored, which will be depleted within 30 days if Pakistan does not take action. Water is primarily used in agriculture. A major part of the labor force, roughly ~ 60%, depends on agriculture for their livelihoods, income, and employment, as well as value-added materials for industry. Climate change threatens the agriculture sector due to its devastating effects on productivity. As temperatures rise, rainfall patterns shift, floods occur, and water reservoirs disappear, major crops are affected by climatic changes (Chandio et al. 2021; Abbas 2020). Over the past several years, northern Pakistan has experienced changes in monsoon patterns and cyclones due to rising temperatures. In terms of climate change vulnerability, Pakistan ranks fifth worldwide. The quality of water is consistently declining due to anthropogenic activities, heavy metal accumulation, flooding due to urbanization, coliforms, and pollution. As Pakistan's population and urbanization grow, these impacts of climate change will be devastating (Anwar et al. 2020).

The increase in global warming/temperature is going to affect the hydrological cycle of the earth and disturb the average availability of water in hydrological systems by increasing the frequency and intensity of precipitation causing heavy rain (Mahmood et al. 2016). The spatial, temporal, and seasonal distribution of precipitation has been negatively affected by temperature change. The flowrate of the Catchment area of the Indus basin is almost 1.1  \({{\text{MKm}}}^{2}\) (Prasad 2016) and is shared among India, Afghanistan, China, and Pakistan. Globally, floods are one of the most devastating natural disasters. Floods damage homes, crops, roads, and infrastructure, causing people to relocate from flood-prone areas (Kuriqi and Hysa 2021; Kuriqi and Ardiçlioǧlu 2018). It is, however, difficult to develop a flood forecasting system based on a limited understanding of the variables that are effective at forecasting. Since flooding is nonlinearly related to several meteorological and topographic parameters, it is quite complex. For water resource management in a particular area, there will always be a need for developing regional models. A variety of data-driven stream flow forecasting models will be established and evaluated in Punjab, Pakistan's upper Indus basin (Ahmed et al. 2022). The purpose of this research is to critically examine key challenges in urban water resource management and sustainable solutions to those challenges. Additionally, the current situation of Pakistan’s water management is reviewed in depth. In addition, proper guidelines, practical implications, and institutional frameworks for improving water use efficiency and water resource volume should be considered (Mahfooz et al. 2022).

Growing populations are increasing the demand for freshwater, which necessitates optimal management of water resources (Tayyab et al. 2015; Fotovatikhah et al. 2018). (Penman 1961) describes hydrology as the science concerned with answering the question, “What happens to the rain after it rains?”. As a result of this query and its response, rainfall is converted into streamflow (Dariane and Karami 2014). Watersheds are spatially and temporally uneven in terms of rainfall, evaporation, runoff yield, and confluences as well as topography and human activities. In streamflow forecasting, upcoming streamflow is systematically evaluated using historical hydro-meteorological data (Boughton and Droop 2003; Taormina et al. 2015; Cheng and Chau 2004) to provide prearranged preparation and management of water resources, as well as an early warning of natural disasters, such as droughts and floods, streamflow forecasting is essential (Bürger et al. 2007; Chen et al. 2018; Zhou et al. 2018a). Understanding the leading issues of stream capacity, humidity, judgment, and energy input is critical to improving water management in the region. A vital part of Pakistan’s sustainable economic development, it is the country's largest source of freshwater (Akhtar et al. 2008). The Hindu Kush, Karakoram, and Himalaya (HKH) mountains are particularly vulnerable to floods and food shortages as agriculture plays a vital role in the Himalayan economy (Archer and Fowler 2008; Mir et al. 2015). The scarcity of runoff data has led many researchers to propose numerous forecasting methods over the past few decades (Tayyab 2017; Seo et al. 2018; Wu and Chau 2011). Methods driven by process and methods driven by data are generally classified into two categories (Barge and Sharif 2016; Carlson et al. 1970; Yu et al. 2017). A process-driven model, such as conceptual rainfall runoff, explains how watershed systems work (Sudheer et al. 2002). Using simple mathematical methods and intelligent algorithms, data-driven models forecast future streamflow without analyzing physical processes (Box and Jenkins 1976).

Time series models commonly used include autoregressive models (AR), AR moving averages (ARMAs), and AR integrated moving averages (ARIMAs) (Box et al. 2008). For streamflow forecasting, AR, ARMA, ARIMA, and other linear regression models are ineffective due to streamflow nonlinearity, and climate, and land use changes are particularly problematic (Chen and Rao 2003; Gilroy and Mccuen 2012; Zhang et al. 2015; Milly et al. 2008; Wang et al. 2009; Kisi 2015; Bai et al. 2016). Water management and climate change are both affected by Snow cover areas (SCA). In mountainous regions where streamflow is primarily caused by melting glaciers, this is extremely helpful for estimating streamflow (Adib et al. 2021). Snowmelt contributes to runoff based on the balance of these masses (Rastner et al. 2019). As a result of satellite remote sensing, we can determine SCA spatially and temporally with gridded datasets that observe many parameters simultaneously and provide a higher level of coverage from Ariel (Lutz et al. 2016a; Sakai et al. 2015). In complex terrains, such as UIB, grids are often larger than precipitation variability, causing interpolation schemes to provide uncertain results. In areas of above-average snowfall, satellite data show significant precipitation. Hydrological estimation cannot be conducted based solely on gridding datasets. In previous studies, satellite observations and on-ground observations of the UIB have been predictive. By combining these two types of data, UIB’s hydrological impact can be improved under changing climates (Ougahi et al. 2022) Snowmelt-runoff model (SRM) simulations have demonstrated the dependence of UIB flow on satellite-derived SCA. Snow-fed catchments are often complex and poorly gaged, which increases the importance of SCA derived from satellite images.

Artificial neural networks (ANNs) are performing well in modeling nonlinear hydrological interactions. However, if input and output data are not pre-processed, in the case of non-stationary data, the models may not be able to handle it (Cannas et al. 2006). A recent trend in data-driven streamflow forecasting is to combine artificial intelligence techniques with decomposition to further refine forecast accuracy through preprocessing (Yu et al. 2017; Wu et al. 2010; Kisi and Cimen 2011; Budu 2013). It has been shown in many hydrological studies that integrating different models into an ensemble is a highly accurate and effective approach. As different models possess unique characteristics of the data, the key idea is to combine the outputs of different models. This methodology allows the integration of forecasts from different models, either linearly or nonlinearly, resulting in better predictions than when using one or more models alone (Abrahart and See 2002; Ajami et al. 2006; Coulibaly et al. 2005; Hsu et al. 2009; Shoaib et al. 2014; Peng et al. 2017; Zhou, et al. 2018b; Sun et al. 2018). A hybrid wavelet data-driven model that uses multi-scale input data identifies valuable information for time series data (Wang et al. 2014; Sang 2013). Discrete Wavelet Transform (DWT) due to its resolution and information retention in frequency and time series data has been studied to assess temporal and spectral information in time series data of hydrological nature (Ünal et al. 2004). Despite its ability to correlate physical quantities, some limitations may arise due to false harmonic waves. EMD has several advantages over DWT approaches, including its self-adaptability, empirical nature, instinctiveness, straightness, and adaptation, which require no fixed basis function (Sang et al. 2014).

Considering the complexity of the Upper Indus basin's climate and its impact on its water resources, it was chosen as a case study. We are examining climate variables, such as temperature, streamflow, and precipitation, and their impact on related hydrological impacts in Pakistan's Upper Indus Basin as a result of climate change. In the Lower Indus Basin, Pakistan's economy is heavily dependent on the flow of this entire basin because it supplies water to millions of people. As the Indus emerges onto the Punjab plains, more than 80% of its flow is derived from seasonal and permanent snowfields and glaciers in the basin, which supports huge irrigated agriculture zones. Indus water resources management and flood forecasting could be improved through such relationships. Climate change and short-term fluctuations both affect Indus runoff. Since the climate characteristics of the Upper Indus Basin vary widely, a hydrological model is selected that is consistent and suitable. The stream flow of the Massan confluence is influenced by tributaries. A hybrid model is proposed in this study to capture the nonlinearities in the annual streamflow series, providing more satisfactory forecasting results. Hence, in this study, the time series decomposition technique is a combination of EMD and ANN. Streamflow forecasting using EMD is compared, and high-frequency components are analyzed for their influence on model performance. It is an ideal method for nonlinear and nonstationary time series because it has a very local capacity both in physical space and frequency space (Huang and Wu 2008; Lee and Ouarda 2010). We develop a hybrid MLP-EMD model. Besides the above-mentioned decomposition-based models, standalone ANN models are also developed for comparison. Based on their decompositions and neural network frames, models are unique. Analysis of peak values confirms all results. A one-month lead-time forecast of streamflow is conducted using three hydrological stations and seventeen meteorological stations in the UIB, Pakistan.

Study area

The Indus River Basin drains an area of about 1.08 × 106  km2, making it the largest transboundary river basin in the world. According to the statistics, Pakistan has 56% of total drainage, India has 26%, China has 10.7%, and Afghanistan has 6.7% (Ahmad 2018). This makes it a region with a complex geopolitical landscape. Mansarovar Lake in the Tibetan Plateau is the source of the Indus Basin, which flows through Pakistan before entering the Arabian Sea. Pakistan’s upper Indus Basin is primarily studied in the north of the country (Lutz et al. 2016b). Upper Indus River Basin (UIRB) lies between 32.48° and 37.07°N and 67.33° and 81.83°E. An area of 289,000 km2 lies in the UIB at an average elevation of 3750 m.a.s.l., varying from 200 to 8500 m.a.s.l (Archer et al. 2010). A total of 11,000 glaciers reside in these ranges, making it the world's most glaciated area, with nearly 22,000 km2 of glacial surface (Fowler et al. 2005). Due to the inaccessibility of data in China, India, and Afghanistan, the study area was confined to areas within the Pakistani border. Figure 1 shows the catchment area of the Indus Basin within Pakistani borders. UIB hydropower projects will be assessed for flood magnitudes during various seasons through this study (Diamer-Basha Hydropower, Bunji Hydropower, Pattan Hydropower, Dasu Hydropower, Thakot Hydropower).

Fig. 1
figure 1

UIB of Punjab, Pakistan

Full size image

Data collection

During this period, data were collected from the Water and Power Development Authority (WAPDA), the Pakistan Surface-water Hydrology Project (SWHP), and the Pakistan Meteorological Department (PMD). With original records, streamflow measurements in UIB are from the WAPDA-SWHP project that started in the 1960s. This research considers all hydrometric stations that are unregulated and relatively free of land-use changes. Multiple large tributaries are flowing into the Massan Basin from the glaciers of Karakoram, Himalaya, and Potohar plateau as a result of the wide variation in climate characteristics. The analysis included 17 Climatic stations (CS) and three hydraulic stations. Tables 1 and 2 provide information about the selected sites. These sites provided data from 1960 to 2012, 1969 to 2012, and 1972 to 2012.

Table 1 UIB Hydrometric stations
Full size table
Table 2 11 Climate observatories in the upper Indus Basin
Full size table

A standard practice with ANNs and decomposition models is to divide the data set into training and testing sets. A total of 40 years of data were used in this study zone Massan, 24 years (1972–1996, 60%) were used for training and 16 years (1997–2012, 40%) for testing the models. Using normalization between 0 and 1, all inputs were equalized in their relative significance.

$${\text{normalized x}} = \left( {\frac{{{\text{q}} - {\text{q}}_{{{\text{min}}}} }}{{{\text{q}}_{{{\text{max}}}} - {\text{q}}_{{{\text{min}}}} }}} \right)$$
(1)

To achieve this, the following relationship was used:

Methodology and ANN architecture

ANN-MLP

NN and BP

It has been demonstrated that artificial intelligence (AI) methods are effective and widely used in a variety of fields. As a feed-forward neural network (FFNN), a multilayer perceptron uses back propagation (BP) to train active models. High-accuracy results can be generated using a 3-layer NN using an appropriate/optimized set of biases and weight sets in a data-driven model. Theoretically, they can approximate any continuous nonlinear function without knowing detailed information about the real system. Furthermore, it is self-learning, self-adaptable, highly robust, fault-tolerant, and has many other superior features (Ye and Kim 2018). As a result, BP is a good and efficient method to model complex input–output interactions in hydrological time series forecasting (Kuriqi et al. 2020).

Figure 2 shows that BP is composed of three layers: a hidden layer an input layer, and an output layer, with hundreds of neurons attached in a non-linear, random, and compact configuration. The training of MLP is carried out till the error between the calculated output and the desired output is small enough. A brief description of the traditional BP in detail is elaborated in Haykin et al. (2009).

Fig. 2
figure 2

The general structure of BP

Full size image

The working mechanism of Forward propagation is done by following steps:

  1. (1)

    Utilize normalized input–output data pairs to calculate hidden layer outputs.

    $$y_{j} = f\left( {\sum\limits_{i = 1}^{{N_{I} }} {w_{ji} x_{i} + b_{j} } } \right)$$
    (2)

    The activation function f, which is typically sigmoid,\(w_{ji}\) specifies the weights of the connections between the input node i-th and the hidden unit j-th, \(b_{j}\) implying j-th connection bias for the output vector y.

  2. (2)

    BP neural network output values are calculated.

    $$\hat{O} = f_{k} \left( {\sum\limits_{j} {w_{kj} y_{j} + b_{k} } } \right)$$
    (3)

    where \(\hat{O}\) are networks combined output, \(w_{kj}\) specifies the weights of the connections between the input node j-th and the hidden unit k-th, \(b_{k}\) signifies the bias of the neuron, and activation function \(f_{k}\).

  3. (3)

    Calculate the output node's global error E.

    $$E = \frac{1}{2}\sum {\left( {\hat{O} - O} \right)^{2} }$$
    (4)

    where the actual output value is O.

BP: In back propagation, the weight adjustment is calculated as follows, where \(\Delta \omega\) represents the modification value of the weight in the range \(\alpha \epsilon (0-1)\) as given by Eq. (5)

$$\left\{ {\begin{array}{*{20}c} {\Delta w_{kj} = - \alpha \frac{\partial E}{{\partial w_{kj} }},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \hat{W}_{kj} = w_{kj} + \Delta w_{kj} } \\ {\Delta w_{ji} = - \alpha \frac{\partial E}{{\partial w_{ji} }},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \hat{W}_{ji} = w_{ji} + \Delta w_{ji} } \\ \end{array} } \right.$$
(5)

The gradient descent (GD) correction method has the potential to adjust BP weights and threshold parameters. However, GD exhibits a low learning rate, local maxima traps, and slow local convergence. Thus, Levenberg–Marquardt (LM), one of the most well-known improved learning algorithms, is used Training and convergence were accelerated in this study. The gradient descent algorithm combined with a Quasi-Newton approach ensures a locally fast convergence speed and maintains better performance combining the advantages of both methods.

LTU: linear threshold unit

In LTU, input x has n values, output y has one value and mathematical operations are performed between them for calculating a linear combination of inputs and their weights, and for applying an activation function (Figs. 3, 4, 5).

Fig. 3
figure 3

LTU

Full size image
Fig. 4
figure 4

Multilayer perceptron with three-layer LTU

Full size image
Fig. 5
figure 5

MLP with multiple LTUs

Full size image

Matrix product of w and x, the weighted sum is:

$${\text{z }} = { }w^{T} \cdot{ }x{ } = \mathop \sum \limits_{{{\mathfrak{i}} = 1}}^{n} w_{{\mathfrak{i}}} x_{{\mathfrak{i}}}$$
(6)

A Heaviside step activation function is used (Mirza et al. 2023):

$${\text{step }}\left( {\text{z}} \right){ } = { }\left\{ {\begin{array}{*{20}c} {0\,{\text{ if}} \,z < 0 } \\ {1 \,{\text{if}}\, z \ge 0} \\ \end{array} } \right.$$
(7)

Since the step function outputs only 0 and 1, the output value y is binary:

$$y=\mathrm{ step }(z) =\mathrm{ step }({ w}^{T}\cdot x)$$
(8)

Using a single LTU is like using Logistic Regression for binary classification.

Perceptron

Perceptrons are artificial neural networks (ANNs) using a single layer of LTUs, vector x and a bias vector b are associated with each of these inputs.

An input vector x is shown above, along with a bias vector as b = (1, 1, 1)T (consisting of only ones). This program produces three binary values of y as in Eq. (9). It is important to note that there is a weight vector for each LTU:

$$\begin{aligned} {\text{y}}_{1} = \, & {\text{step }}\left( {{\text{z}}_{1} } \right){ } = {\text{ step }}\left( {{\text{w}}_{1}^{{\text{T}}} { } \cdot {\text{x }} + {\text{ b}}_{1} } \right) \\ {\text{y}}_{2} = \, & {\text{step }}\left( {{\text{z}}_{2} } \right){ } = {\text{ step }}\left( {{\text{w}}_{2}^{{\text{T}}} { } \cdot {\text{ x }} + {\text{ b}}_{2} } \right) \\ {\text{y}}_{3} = & \,{\text{step }}\left( {{\text{z}}_{3} } \right){ } = {\text{step }}\left( {{\text{w}}_{3}^{{\text{T}}} \cdot {\text{x }} + {\text{ b}}_{3} } \right) \\ \end{aligned}$$
(9)

The equations can be combined to:

$$y={\text{step}}={\text{step}}\left(W.x+b\right)$$
(10)
$${\text{W }} = \left( {\begin{array}{*{20}c} {w_{1} } \\ \ldots \\ {w_{u} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {w_{{1,1 \ldots w_{1,n} }} } \\ {w_{{u,1 . \ldots w_{u,n} }} } \\ \end{array} } \right)$$

The matrix W is of the shape (u, n), with n = number of input values and u = number of LTUs. An input vector x has a shape of (n, 1), a bias vector b has the shape of (u, 1), and an output vector y has a shape of (u, 1). Multi-class classification is therefore possible with the Perceptron.

MLP: multi-layer perceptron

The MLP consists of three layers: a hidden layer, an input layer, and an output layer. DNNs are MLPs with two or more hidden layers.

Similar to a perceptron, but with more layers of LTUs to combine to reach the output y:

$$\begin{gathered} {\text{h}}^{1} = {\text{step}}\left( {{\text{z}}^{1} } \right) = {\text{step}}\left( {{\text{W}}^{1} \cdot {\text{x}} + {\text{b}}^{1} } \right) \hfill \\ {\text{y}} = {\text{step}}\left( {{\text{z}}^{2} } \right) = {\text{step}}\left( {{\text{W}}^{2} \cdot {\text{h}}^{1} + {\text{b}}^{2} } \right) \hfill \\ \end{gathered}$$
(11)

An ANN is usually trained in batches (each instance represents a single input vector x). From the m available instances, k instances are drawn:

$${\text{x}}_{1} = { }\left( {\begin{array}{*{20}c} {{\text{x}}_{1,1} } \\ \cdots \\ {{\text{x}}_{{1,{\text{ n}}}} } \\ \end{array} } \right){ },{ }...{ },{\text{ x}}_{{\text{k}}} = \left( {\begin{array}{*{20}c} {{\text{x}}_{{{\text{k}},1}} } \\ \cdots \\ {{\text{x}}_{{{\text{k}},{\text{n}}}} } \\ \end{array} } \right)$$
(12)

The k instances can be combined to:

$${\text{x}} = \left( {\begin{array}{*{20}c} {{\text{x}}_{1}^{{\text{T}}} } \\ \ldots \\ {{\text{x}}_{{\text{k}}}^{{\text{T}}} } \\ \end{array} } \right) = { }\begin{array}{*{20}c} {{\text{x}}_{{1,1{ }...{\text{ x}}_{{1,{\text{n}}}} }} } \\ {{\text{x}}_{{{\text{k}},1{ }...{\text{ x}}_{{{\text{k}},{\text{n}}}} }} } \\ \end{array}$$
(13)

In this case, X becomes a matrix with the shape (k, n), where k represents batches and n represents input values. The dimension of the W matrix has been altered to (n, u). Y is a matrix of shape (k, u) from a bias vector b of shape (u, 1) hence \({\text{y}}=\mathrm{step }({\text{z}})={\text{step}}\left({\text{X}}\cdot {\text{W}}+{\text{b}}\right)\).

EMD: empirical mode decomposition

A nonlinear and nonstationary time series can be analyzed using empirical mode decomposition (EMD). There are several intrinsic components to input signal modes functions (IMFs) and one residue. First, the time series must have the same number of extreme values as the number of zero crossings; second, the average value of the upper and lower extremes must be zero at all times. Following these conditions, x(t) can be decomposed by EMD as follows:

$$x\left( t \right) = \sum\limits_{i = 1}^{m} {h_{i} (t)} + r\left( t \right)$$
(14)

where \(h_{i} \left( t \right)\) specifies \(m\) number of IMFs with \(r\left( t \right)\) as a residual value in a series.

By applying cubic spline interpolation, using all local maximum and minimum values, upper and lower envelopes are constructed for the time series. In a study, extremes were selected to affect the envelope calculation if abnormal points were present in the original data. Thus, the envelopes derived from the real signal may consist of envelopes from abnormal points as well. As a result, the mode mixing phenomenon occurs.

Data decomposition for time series

Data decomposition techniques play a crucial role in time series data forecasting. Time series data often contains multiple underlying components, such as trends, seasonality, and irregular fluctuations, which can obscure the true patterns and make accurate predictions challenging. By employing data decomposition techniques, analysts can break down the time series into its constituent components, allowing a clearer understanding of individual patterns and trends. Methods like seasonal decomposition of time series (STL) or moving averages help isolate seasonal patterns, while trend decomposition methods like Holt–Winters or Singular Spectrum Analysis (SSA) extract trend information. With these decomposed components, forecasting models can be built more effectively, as they can be applied to each component separately, leading to more accurate predictions and better insights into the dynamics of the time series data. The importance of data decomposition techniques lies in their ability to enhance forecasting accuracy, reveal hidden patterns, and enable more informed decision-making in various domains, including finance, economics, weather forecasting, and many others. For this study, we have opted for EMD.

Application of EMD

Figure 6 shows the outcome of using the EMD method. Precipitation, streamflow, and temperature are decomposed into several independent IMFs and one residue series by EMD. The decomposition of the original time series into four independent IMF components and one residue component is done from high frequency to low frequency. Figure 6 display how the IMFs represent changing wavelengths, amplitudes, and frequencies. There is a minimum amplitude, a minimum frequency, and a maximum wavelength in IMF4. In addition, the other components of the IMF are increasing in frequency and amplitude, while the last residue is slowly evolving. Streamflow, precipitation, and temperature residue components indicate the overall trend. Therefore, EMD decompositions characterize physically meaningful decompositions: although they are independent of other instants in the spatial dimension, they are physically consistent with those of closely associated instants (Liu et al. 2009). EMD is used in transforming nonlinear, nonstationary time series into stationary ones, as well as improving prediction performance (Debert et al. 2011).

Fig. 6
figure 6

Input data IMFs with different decomposition levels (L)

Full size image

Hybrid ANN

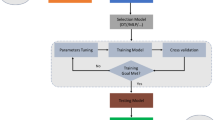
This study uses the decomposing method of EMD and MLP neural networks, resulting in four hybrid models: MLPQ, MLPQTP, MLPQ-EMD, and MLPQTP-EMD. Based on the autocorrelation function (ACF) (Farajpanah et al. 2020) and cross-correlation function, the methodology steps are as follows: first, the input vectors should be determined for hybrid models; Fig. 7 illustrates the oriented results for Massan based on autocorrelation and cross-correlation functions with decomposition level and mother wavelet. The input is decomposed using EMD and input into an ANN for stream flow predictions.

Fig. 7
figure 7

Massan hydrological station auto correlation discharge volume

Full size image

An ANN model using EMD is established instead of a DWT. The next step is to determine the white noise amplitude and ensemble number En for appropriate inputs. DWT-based ANN models follow a similar process. The flowchart in Fig. 8 illustrates how these hybrid neural networks work.

Fig. 8
figure 8

The hybrid EMD-NN model flowchart

Full size image

Result and discussion

This section provides an in-depth analysis of the results keeping in view the findings and improvements in light of not only forecasting but also the flood mitigation and management of water resources. Experimental results are presented concisely as per models developed and inputs summarized in Table 3. The interpretation and experimental conclusions are made using statistical indices given by Eqs. (15–18). Although the contribution of the present work mainly encapsulates forecasting accuracy of streamflow in UIB, it also helps in peak analysis that is synonymous with flood predictions. These anomalies usually are not rationalized by poor performing Neural Networks. Present work shows significant improvements in Peak Value forecasting given in Section “Peak value analysis”. During the recent epoch, severe natural disasters have increased in frequency and severity with catastrophic fatalities indicating mounting vulnerability. Human fatalities from natural calamities will be twice as high in 2050 (Wilkinson and Brenes 2014). The world's leading cause of death frequently occurs due to flooding, posing a public safety and economic risk. There has been a significant impact on human living due to climate dynamics, especially farming environmental ailments and developed physical infrastructure to cope with extreme weather such as heat or cold, and experienced successive disasters, such as floods and droughts. (Ahmad and Afzal 2019). Figure 9 shows a detailed month-by-month analysis of flood risk including the flood season (July–October) in UIB. Table 4 summarizes the statistical performance of the proposed model with existing ones and the graphical presentation of competing techniques for the discharge at Massan.

Table 3 Massan region streamflow forecasting models with transformed input
Full size table
Fig. 9
figure 9

Hydro station monthly discharge comparison a MLPQ, b MLPQTP, c MLPQ-EMD, and d MLPQTP-EMD

Full size image
Table 4 Statistical performance metrics
Full size table

Model development

A series of applied models like MLPQ, MLPQTP, MLPQ-EMD, and MLPQTP-EMD discussed in Section “Methodology and ANN architecture” are examined as a month-ahead streamflow forecasting for UIB. This research developed four models based on different combinations of inputs.

Model performance evaluation

All models are evaluated qualitatively based on five main criteria. There are several types of errors to consider, including Nash–Sutcliffe Efficiency (NSE) (Mansoor et al. 2023), mean absolute errors (MAE), correlation coefficient, root mean square errors (RMSE), and mean absolute percentage errors (MAPE) (Mirza et al. 2024). They are defined as follows:

$$R = \frac{{\sum\nolimits_{i = 1}^{N} {\left( {Q_{{{\text{com}},i}} - \overline{Q}_{{{\text{com}},i}} } \right)\,\left( {Q_{{{\text{obs}},i}} - \overline{Q}_{{{\text{obs}},i}} } \right)} }}{{\sqrt {\sum\nolimits_{i = 1}^{N} {\left( {Q_{{{\text{com}},i}} - \overline{Q}_{{{\text{com}},i}} } \right)^{2} } } \sqrt {\sum\nolimits_{i = 1}^{N} {\left( {Q_{{{\text{obs}},i}} - \overline{Q}_{{{\text{obs}},i}} } \right)^{2} } } }}$$
(15)
$${\text{RMSE}} = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^{n} {\left( {Q_{{{\text{obs}},i}} - Q_{{{\text{com}},i}} } \right)^{2} } }$$
(16)
$${\text{NSE}} = 1 - \left[ {\sum\limits_{i = 1}^{n} {\left( {Q_{{{\text{obs}},i}} - Q_{{{\text{com}},i}} } \right)^{2} } } \right]/\left[ {\sum\limits_{i = 1}^{n} {\left( {Q_{{{\text{obs}},i}} - \overline{Q}_{{{\text{obs}},i}} } \right)^{2} } } \right]$$
(17)
$${\text{MAE}} = \frac{1}{N}\sum\nolimits_{i = 1}^{N} {\left| {Q_{{{\text{obs}},i}} - Q_{{{\text{com}},i}} } \right|}$$
(18)
$${\text{MAPE }} = \,\frac{1}{N}\sum\nolimits_{i = 1}^{N} {\left| {\frac{{Q_{{{\text{obs}},i}} - Q_{{{\text{com}},i}} }}{{\overline{Q}_{{{\text{com}},i}} }}} \right|}$$
(19)

where \(Q_{{{\text{obs}},i}}\) \(Q_{{{\text{com}},i}}\) stream flows are represented as observed and computed magnitudes, streamflow is determined by \(\overline{Q}_{{{\text{obs}},i}}\), and sample number is determined by N.

Results analysis

In this study, we sought to develop an appropriate model for predicting discharge from UIB. As a result of this study, the flood magnitudes of hydropower plants, such as Dasu, Diamer-Basha, Pattan, Thakott, and Bunji Hydropower stations of UIB, for management and scheduling. The main discharge stream in this region in Bunji receives all the tributaries discharge of the Sindh River in UIB. For predicting discharge from Bunji, monthly rainfall and temperature data are collected from 5 to 11 meteorological stations, and monthly runoff data are analyzed for 50 years (1960 to 2012). Besham Meteorological Station aggregates monthly rainfall and temperature data from 3 sub-meteorological stations. The runoff data from 1969 to 2012 have been utilized (43 years). The monthly rainfall and temperature data for Massan were collected from nine meteorological stations, while the monthly runoff data were collected from hydrometric stations for the period 1972–2012. To simplify the computational load of the base model, the lowering of a number of inputs using only critical is adopted without compromising on the model performance. Different hybrid models are formed by FFNN MLP coupled with EMD: MLPQ, MLPQTP, MLPQ-EMD, and MLPQTP-EMD. Hybrid models utilize monthly average temperature (T), average precipitation (P), and average streamflow (Q) as inputs. Time series data of forecast stations and stream outflows were used to develop these models.

A significant result was obtained for applied neural networks MLP; performance evaluation criteria indicate that MLP outperforms FFNN with BP; in Table 4, all applied statistical indices, such as NSE, MAE, RMSE, MAPE, and correlation coefficient (R), indicate that MLPQTP-EMD outperforms the competing models. As shown in Fig. 9, the validation hydrograph of simulated (MLP-EMD) and observed time series shows that MLP performs best in picking all ranges of values.

It is necessary to perform a complete analysis based on Table 4 to reveal how different decomposing methods affect model precision. MLPQ, MLPQTP, MLPQ-EMD, and MLPQTP-EMD, are all optimal models. Hence, models coupled with decomposition techniques (DWT and EMD) provide better precision than single AI-based models. In validation periods, MLPQTP-EMD achieves a higher level of prediction accuracy than MLPQ, MLPQTP, and MLPQ-EMD. The use of decomposition techniques improves nonlinear time series forecasting as a result. Figure 6 of UIB, the EMD decomposing technique is better suited for modeling monthly streamflow in Massan.

Peak value analysis

A reaffirmation of previous findings, a peak value analysis is applied to studied hybrid models: MLPQ, MLPQTP, MLPQ-EMD, and MLPQTP-EMD. The peak stream flow is expected in UIB in May-Oct where peak temperatures cause rapid melting of Glaciers that contribute the main share of fresh water downstream. UIB's flooding season occurs in this period due to increased discharge. This study considers a relative error of 20% to be reasonable and acceptable, and the results of the MLPQ, MLPQTP, MLPQ-EMD, and MLPQTP-EMD during the validation period are given in Fig. 8 for Masan. The MLPQTP-EMD model forecasts the discharge with high precision as compared to BP-Q. Table 5 summarizes the eligible rate (ER) otherwise known as the percent of standard forecasts. The proposed MLPQTP-EMD achieves 91.3% for the Massan region achieving 5.6% higher than MLPQTP showing the impact of EMD for input data. The dominance of MLP over standard BP despite the number of input metrics is validated by achieving 39.3–32.3% higher ER scores. Thus, MLPQTP-EMD has the best capacity for predicting peak streamflow values.

Table 5 Peak values forecasted by Massan Region for the flood season (June–October)
Full size table

Table 5 further showcases the forecast accuracy for peak flood values in the Massan Region from June to October, comparing four models: BP-Q, BP-QTP, MLPQTP, and MLPQTP-EMD. The Error Rate (ER) percentages serve as the evaluation metric. The basic BP-Q model has an ER of 52%, indicating moderate accuracy. Incorporating more parameters, the BP-QTP model slightly improves this to 59%. A substantial accuracy increase is seen with the MLPQTP model at 86% ER, and the most accurate predictions are from the MLPQTP-EMD model, with a notable 91.3% ER. This progression suggests that advanced techniques and additional parameters significantly enhance flood forecasting precision in the region.

Conclusions

Developing countries like Pakistan have been extensively impacted by climate change due to a reduction in infrastructure and squat capacity. Climate change impacts on agriculture and livelihoods have made Pakistan the 12th most detrimentally impacted country due to its vulnerability to climate change. (Syed et al. 2022). Hydrological forecasting must be improved for UIB to provide future precautions against flooding. It is vital to make an accurate flood prediction with the right lead time. The ability to predict flood crests, flood magnitudes, and flood duration at the right time can save countless lives and huge amounts of money. The UIB forecast stations are Besham Qila, Bunji, and Massan. A performance evaluation criterion included Nash–Sutcliffe Efficiency, mean absolute errors, root mean square errors, mean absolute percentage errors, and we compared observed and simulated time series using correlation coefficients and flow hydrographs. Based on this study, we came to the following conclusions:

  1. (1)

    An improvement in accuracy is achieved by including QTP as input with transformed time series data. As per several studied sets of inputs, the best performing models are the MLPQTP and MLPQTP-EMD.

  2. (2)

    MLPQTP-EMD has shown better results than BP-Q and BP-QTP when applied. Therefore, MLPQTP-EMD is considered to be a better model on an individual basis.

  3. (3)

    EMD has performed well in all cases among the applied decomposition methods (DWT and EMD). Models based on individual ANN have been improved significantly by EMD.

  4. (4)

    The EMD method significantly improves the precision of monthly streamflow predictions. Based on performance indices and flow hydrographs, MLPQTP-EMD overtakes BP-QTP and dominates with a 91.3% eligible rate (ER) versus a 76% eligible rate (ER) from BP-QTP.

Limitations and future directions

ANN applications are successful when they have high-quality and abundant data, and this is not always easy to achieve. Long historical records are available, but circumstances may not have remained consistent. The lack of physical concepts and relationships is another major limitation of ANNs. As a result, the ANN structure is more complex. Moving forward, the focus of our research will be on merging Artificial Neural Networks (ANNs) with the fundamentals of physical science within hybrid models to improve tools for managing flood risks. We plan to apply these models in practical situations, including water management in construction sites across Punjab and in the context of the Indus River. Moreover, we intend to enhance our data processing methods to use partial or inconsistent historical data more effectively, aiming to boost the dependability of our flood forecasting in diverse environmental conditions.

Management implications

The rapid growth in population and the rise in urbanization have made managing water a major concern around the world in recent years. Agrarian crop production is constrained by the availability and accessibility of water. In this study, climate change overtakes land-use change as a factor affecting Indus flow regimes. Water availability will increase in the short term and decrease in the long term as a result of climate change. In response to global warming, the flow regime has changed dramatically. It is predicted that summer flow will increase in the early twenty-first century, followed by a decrease in the late decades. Excessive snowmelt in summer and late spring will increase discharge in the short term, but glacier disappearance will decrease discharge in the long term. To improve the condition of the waters in the basin, some current aspects need to be re-evaluated. There is a question as to whether the current water system in the basin is sustainable. It is recommended that water management practices be implemented to save water, which will alleviate the effects of extreme weather conditions, e.g., flooding and droughts. As the dry season approaches, the stored water will be used for agriculture, hydropower, industrial processes, and domestic consumption. As the sensitivity of streamflow in the study area is higher, plantations are suggested to mitigate the increasing trend of air temperature (Shah et al. 2021).