Introduction

The environmental degradations in different ecosystems have been highlighted in recent decades (Brears 2018). Rivers play a key role in water supply of urban area. Increasing population is a significant challenge for the governments who would like to rise water abstraction to develop urban areas. Reducing inflow is a serious threat for the river ecosystems that might need considerable available water to sustain the ecological status (Atazadeh et.al 2020). The present study aims to link the developing population of cities and ecological impacts on the river ecosystem through the optimization system. Thus, it is needed to review three aspects of the proposed method including 1) population carrying capacity of cities, 2) ecological impact models of river ecosystems and 3) optimization methods.

Estimating urban land carrying capacity (ULCC) is an interesting topic for a wide range of experts including biophysical scholars, economic scholars, social scientists and engineers. Hence, ULCC has been highlighted in the literature from several decades ago. Currently, there is not a straightforward method to estimate ULCC due to complex impacts of natural resources and environmental pollutions in the main factors of the ULCC such as inhabited population in urban areas. Moreover, a wide range of methods have been applied to determine the ULCC such as, time-series global factor analysis and hierarchical cluster analysis (Zhang et.al 2012; Liu, H. 2012), analytic hierarchy process (Lu et al. 2017), ecological footprint analysis (Budihardjo et al. 2013; Guzman et al. 2013; Gupta et.al 2022), system dynamics (Li et.al 2018). Improving ULCC methods consistent with the current environmental challenges is a requirement for sustainability of the cities and urban areas development.

Traditionally, environmental flows have been highlighted as a key parameter to sustain the ecological status of rivers (Kuriqi et.al 2019). Many methods have been proposed to assess environmental flow regime (More details by Sedighkia et.al 2022). Some desktop methods assess the minimum environmental flow requirement in which a base flow might be recommended as the inflow (Arthington 2018; Suwal et.al 2020). In contrast, habitat-based methods and holistic methods might be able to assess the environmental flow regime considering the ecological values in river basins (Choi et.al 2019; Ćosić-Flajsig et.al 2020). Ecological requirements of each river basin are different which means minor changes in ecological assessment might be needed case by case. Some studies indicated that the ecological impacts might be beyond the simple assessment of the environmental flows (e.g., Sedighkia et.al 2022). Hence, linking the ecological impact models of water resources and development models of river basins might be helpful for sustainable planning of river basins. Development in river basins include agricultural, industrial and urban areas. Utilizing an optimization framework can balance the development scenarios and the ecological suitability of the river basins. Due to escalating challenges regarding water supply and food supply in the current condition and future, using optimization frameworks for balancing environment and humans’ needs could be useful. Some previous studies highlighted these challenges (Islam et.al 2022; Fahim et.al 2021).

Different optimization methods have been proposed in the literature. Using the linear programming (LP) methods is an appropriate solution for the linear objective functions (Taslimi et.al 2021; Zhou et.al 2018). However, complex engineering problems are non-linear which means the linear programming is not able to provide the optimal solution for complex functions. Thus, non-linear programming (NLP) and dynamic programming have been recommended to solve the non-linear objective functions. Using LP and NLP methods have been corroborated in the literature for the water resource management (Bahlawan et.al 2019; Li et.al 2020). Not only an optimization method should be able to find an appropriate solution, it also has to be efficient in terms of computational costs. Hence, improving the optimization solutions is a serious need. The evolutionary optimization is an improved method for finding the optimal solution, which has been extensively addressed in the literature (Reddy and Kumar 2020). Many classic and new generation algorithms have been recommended in the water resources management and other engineering branches (e.g. Ehteram et.al 2018; Ahmadianfar et.al 2021).

We need combined models to determine ULLC in which different aspects of natural resources and environmental challenges should be highlighted. In other words, outputs of these models could be combined to determine the final ULLC of different regions. One of the vital natural resources for developing urban areas is water, which should be highlighted for determining ULLC. Surface water resources such as rivers are the main source for satisfying the urban water demand. However, enough water availability in rivers is vital for aquatic species those living in river ecosystems. Thus, developing the new framework, which is able to balance the needs of the freshwater ecosystems and the carrying capacity of the cities, is a requirement for sustainable development of urban areas. Due to this research need, the present study proposes a novel form of the optimization to determine population carrying capacity of cities in which the ecological impact model of the river ecosystem and water supply of urban areas are linked. The present study might open the new windows for improving ULLC models due to current environmental challenges in the environment, which might be exacerbated in future years.

Application and methodology

Overview on the method and case study

Three main parts were considered in the proposed model as follows (Fig. 1).

  1. 1-

    Ecological impacts model of the river ecosystem: several data driven models have been used in the ecological impact model, which are able to assess the habitats suitability of the target species

  2. 2-

    Initial population scenario of the city: initial planned population was defined based on available urban development plan in the case study

  3. 3-

    Optimization model: a multi-objective optimization was used to assess the sustainable population of the city in which the outputs of the ecological impact and the population scenario were applied

Fig. 1
figure 1

Workflow of the present study

Full size image

First a wide range of required data are collected including recorded stream flow and water quality parameters at downstream of water diversion project. Moreover, field studies of fish habitats were carried out in which electrofishing was used in fish observation and physical and water quality parameters were measured by the portable devices. Based on collected data and field studies, three models were developed to simulate water quality parameters, physical parameters of flow and potential fish population at downstream river habitats of water diversion project. Then, all developed models were applied in the optimization model to balance environmental requirements and water supply of urban areas for having a sustainable urban development in the study area.

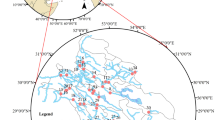
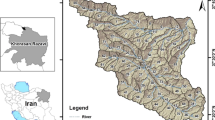
The Haraz River is one of the known basin in Iran located in the Tehran and Mazandaran province. Due to increasing population in these provinces, this river is vital to satisfy the urban water demand. The population of these provinces is continuously increased in recent years. Hence, supply of water demand is a challenge for the regional water authority in the available urban areas as well as developing urban areas. A plan is available to construct a diversion dam to supply the urban water demand of the new regions of Pardis city in Tehran province. It is critical for regional water authority to supply water demand based on the development plan of this city. However, department of environment is concerned regarding the significant water abstraction from the river due to ecological values of the river habitats. The downstream river is a valuable habitat for the Brown trout, which is a protected aquatic species in the Tehran province. Hence, one of the important factors to determine the population carrying capacity of the developing urban areas is sustainable ecological status of the river habitats. Figure 2 displays the location of the planned diversion dam at the midstream of the Haraz River.

Fig. 2
figure 2

The location of planned diversion dam in the Haraz River

Full size image

Initial population scenario

The regional water authority has a long-term plan to abstract water from the river. However, environmental advocators point out that defined environmental flow is not able to mitigate the downstream environmental degradation. Based on the current development plan, Fig. 3 displays the initial target of population of the water diversion project for supplying the urban water demand.

Fig. 3
figure 3

Population carrying capacity in the initial plan of the case study- changes of natural flow, environmental flow and water supply for average year based on long-term hydrological analysis in initial planning study of urban areas in the case study (Time in daily scale and flow in m3/s)

Full size image

Ecological impact model of river

As presented, the target species of the case study is the Brown trout highlighted in this research work. According to the literature, abiotic factors are effective on the suitability of the Brown trout habitats. However, many abiotic factors are important which might not be possible to simulate them in terms of computational and field studies costs. Hence, it is needed to select the most important parameters in the environmental modeling of the habitats. According to our initial survey of the habitats, five physical and water quality factors are effective on the suitability of the Brown trout habitats including 1) depth of flow 2) velocity of the flow 3) water temperature 4) concentration of dissolved oxygen (DO) and 5) concentration of total dissolved solids (TDS).

Our research team carried out the field studies at downstream of the planned diversion dam to sample the fish population and simultaneous measurement of the selected effective factors. As a brief description on the field studies, fish sampling was carried out by the electrofishing methods, which is a known method for studying river habitats. More details regarding this method and its advantages and disadvantages have been addressed by Goutte et.al 2020. It should be noted that the Haraz river at downstream of planned project is walkable which means measuring the depth and velocity is possible by the metal ruler and propeller, respectively. Moreover, water quality factors including water temperature, air temperature, DO and TDS were measured using the available portable water quality devices. Two hundred samples in different rates of river flow were collected in the study area, which were used to develop a data driven model for assessing the habitats suitability. 197 samples were collected in different types of meso-habitats, which were applied to develop fish population model and other used models. Moreover, some recorded data were used as well in the water quality models and regression models of depth and velocity.

Different models might be useable to develop the data driven models. Recent studies demonstrated that using artificial intelligence methods (AI) is beneficial for developing data driven models due to their abilities for generating a computational map between the inputs and outputs. Neural networks are one of the known AI methods, which have broadly been addressed in the literature (Li et.al 2021). Adaptive neuro fuzzy inference systems is an improved neural network in which a fuzzy inference system is used in the structure of the neural network to improve the capabilities of the model and interpretability. Figure 4 displays the simple structure of the ANFIS based model with two inputs. However, we have five inputs in the present study including depth, velocity, dissolved oxygen (DO), total dissolved solids (TDS) and water temperature. Furthermore, the output of the model is normalized population of the fish based on the sampling of the river habitats. We applied 10 membership functions for the inputs in the form of Gaussian function. The number of membership functions (linear function) for the output is 10 as well. The subtractive clustering was applied to reduce the complexity of the model. Furthermore, hybrid method was used in the training process of the model.

Fig. 4
figure 4

Simple structure of ANFIS based data driven model with two inputs (X and Y are the inputs of data driven model and f is output of the model, W1 and W2 are coefficient for connecting neurons in different layers for simulating output in unseen scenarios)

Full size image

Due to changing flow in the optimization model, it is needed to estimate the depth and velocity of the flow. We applied the outputs of the field studies to develop two regression models for estimating depth and velocity as displayed in the Eq. 1.

$$Downstream reach\left\{\begin{array}{c}Velocity=-0.0045\left({Q}^{2}\right)+\left(0.201Q\right)+0.0.41\\ Depth=-0.0008\left({Q}^{2}\right)+\left(0.0874Q\right)+0.0247\end{array}\right.$$
(1)

Moreover, assessing the water quality factors needs different data driven models in which environmental factors are the inputs and each selected water quality parameters would be the outputs of the model. Data driven models are applicable for water quality assessment in two aspects. First, models are generated and used to elicit further insights from the data on their distributions and variations. Moreover, the data driven models can be applied for predicting or simulating water quality factors in the unseen scenarios. In the present study, the data driven models were used for simulating water quality parameters in unseen scenarios such as impact of changing stream flow on the water quality in the aquatic habitats. We utilized a modeling process to simulate water quality factors in which three ANFIS based models were developed including water temperature (Model A), DO (Model B) and TDS (Model C). The number and form of the membership functions for inputs in all models are 10 and Gaussian respectively. Furthermore, 10 linear membership functions were used for the outputs. Inputs of Model A are flow rate, Wetted perimeter, Elevation level from the Sea, Air temperature. Inputs of model B and C are the same including flow rate, Water temperature, Total load. Clustering and training method are the same with the fish population model.

It was required to measure the goodness of fit of the data driven models in the ecological impacts modeling. Hence, two known indices including the Nash–Sutcliffe efficiency index (NSE) and root means square error (RMSE) were selected in this regard (Chai and Draxler 2014). Equations 2 and 3 show these indices where O is observed data and M is modelled data. m means average and i is sample number and I is total number of samples.

$$NSE=1-\frac{\sum_{t=1}^{T}{({M}_{i}-{O}_{i})}^{2}}{\sum_{t=1}^{T}{({O}_{i}-{O}_{m})}^{2}}$$
(3)
$$RMSE=\sqrt{\frac{\sum_{i=1}^{I}{({M}_{t}-{O}_{t})}^{2}}{I}}$$
(4)

Optimization model

In the present study, a new of multi-objective optimization model was developed in which two objective functions as displayed in the Eqs. 5 and 6. NFI is the potential fish population in the natural flow, OFI is the potential fish population in the optimal ecological flow, IP is carrying capacity of population in the initial plan and SP is carrying capacity of population in the sustainable plan. T is time horizon of the flow time series.

$$Minimize(OF1)=\sum_{t=1}^{T}{(\frac{{NFI}_{t}-{OFI}_{t}}{{NFI}_{t}})}^{2}$$
(5)
$$Minimize(OF2)={(\frac{IP-SP}{IP})}^{2}$$
(6)

We developed two objectives function to balance the environmental requirements and population planning. OF1 is able to minimize ecological impact in which reduction of fish population due to water diversion project will be minimized. In other words, environmental degradations in the aquatic habitats will be mitigated. OF2 is able to minimize water supply loss in the study area. In fact, water diversion project has initially been planned to supply water demand for a certain population without considering ecological impacts at downstream river habitats. The second objective function (OF2) minimizes difference between population in sustainable operation of water diversion project and population in initial plan for water supply.

Each optimization would have some specific constraints which are effective on the proposed optima solution. In the present study the following constraints were considered.

  1. 1.

    1-The environmental flow in each time step should not be more than natural flow in the same time step.

  2. 2.

    2-The sustainable carrying capacity of population should not be more than initial planned carrying capacity of population.

Different multi-objective algorithms are available in the literature to solve the two or more objective functions simultaneously. We utilized the multi-objective particle swarm optimization (MOPSO) in the present study. One of the challenges in the application of MOPSO is how to select the best solution among the proposed non-dominated solutions by the algorithms. In the developed framework of the present study, the purpose of the model is to balance the population development scenarios and environmental degradations of the ecosystem for enhancing the sustainability of developing urban areas. Thus, minimum squared difference might be a good computational index to select the best solution, which was applied to finalize the results. Figure 5 displays the flowchart of MOPSO for finding the best solution. More details have been addressed in the literature (Coello et al. 2004).

Fig. 5
figure 5

Multi-objective particle swarm optimization (MOPSO) flowchart

Full size image

Two indices were used to evaluate the performance of the model in terms of balancing the ecological degradations and sustainability of the population development in the study area including root mean deviation index (RDM) and sustainability reduction index (SDI). The first index was used to evaluate the optimization model in terms of reducing ecological degradations in the simulated habitats. Moreover, SDI was applied to evaluate the optimization model in terms of changing population carrying capacity. The following equations displayed these indices.

$$RMD=\sqrt{\frac{\sum_{t=1}^{T}{({OFI}_{t}-{NFI}_{t})}^{2}}{T}}$$
(7)
$$SDI\%=100-(100*\frac{SP}{IP})$$
(8)

As a summary of simulation–optimization model developed in this study, Fig. 6 displays the flowchart of simulation–optimization model for clarifying the computational method.

Fig. 6
figure 6

Computational method of simulation–optimization system by MOPSO (T is time horizon or 365 days for the average year based on hydrological analysis of river flow)

Full size image

Results

In the first step, the outputs of the simulation in the study area should be shown. Figure 7 displays the training and testing process of the model for estimating the population of the fish consistent with changing the abiotic factors in the river. NSE and RMSE are shown in the figure, which demonstrate the acceptability of the model to simulate fish population in the river. According to the literature, if NSE is more than 0.5, the outputs of the model is reliable. It should be noted that maximum of the NSE is 1 that indicates the model and observations are the same. Moreover, RMSE is low which means the model is able to estimate the fish population at downstream of the water diversion project with acceptable error. These indices were applied to measure the goodness of fit of the water quality parameters as well. Table 1 displays the NSE and RMSE of the water quality models, which indicate the acceptability of the water quality data driven models in the present study.

Fig. 7
figure 7

Training and testing process of the fish population model

Full size image
Table 1 Measured indices of the water quality
Full size table

In the next step, the outputs of the optimization model should be shown. Figure 8 displays the non-dominated solutions proposed by the MOPSO in the case study. As a description of this figure, MOPSO as a multi-objective optimization algorithm is able to propose a group of optimal solution. However, the performance of these solutions is slightly different which means the most optimal solution should be selected among the proposed solutions by MOPSO. Figure 8 shows the trades-off between two defined objectives in the present study which is helpful for electing the most optimal solution for the problem. As presented, minimum difference between the objectives was considered as the criterion for making decision regarding the best solution. Based on the computations, [0.5308,0.5360] was selected as the best solution in the case study which indicates the optimization algorithm is able to balance the losses of the system in terms of population and ecological impacts. Based on the selected best solution, Fig. 9 displays the downstream ecological flow of the diversion dam. Figure 9A shows natural flow and environmental flow by the initial plan and the proposed model to highlight increase in environmental flow or inflow using the new method. In contrast, Fig. 9B shows portion of environmental flow and water supply by the new model compared with the natural flow. It is observable that the sustainable plan increased the ecological flow at downstream of the dam considerably. However, many fluctuations could be seen in the results, which is due to balancing the water demands, and the ecological requirements. Moreover, this figure shows water supply in different time steps (daily time steps). It seems that reduction of water supply compared with the initial plan is inevitable which means diminishing the potential population of this city might be inevitable as well. The water supply in some time steps is zero, which means the secondary storage of water, might be essential to supply the demands.

Fig. 8
figure 8

Trades-off between objectives by MOPSO

Full size image
Fig. 9
figure 9

Water supply of the urban areas B and proposed inflow by the novel method A

Full size image

It is required to investigate how the optimization model is able to restore the fish population in the habitats. In other words, potential fish population in three statuses including natural flow, sustainable plan and initial plan for water supply should be assessed. As displayed in Fig. 10, the initial plan for water supply is disastrous in terms of ecological impacts on the aquatic habitats because the potential fish population is too low compared with the natural flow. Hence, using the initial water supply plan is not recommendable especially for a long-term period which might damage the health of the rive habitats completely. This output indicates the weaknesses of determining environmental flow by unreliable methods. We recommend stopping the use of these methods in all the river basins. Conversely, the sustainable plan of water supply is able to increase the potential fish population in many time steps. However, the performance of the optimization model is not similar in all the time steps because the model tries to balance the demands and ecological impacts, which might reduce the available flow in the river in some time steps remarkably. Using RMD might be helpful to evaluate the performance of the model in terms of increasing potential fish population in the case study. It is 25 and 16.5 in the sustainable and initial plan respectively, which means the role for the sustainable plan for restoration of the fish habitat in the river would be brilliant. However, low difference between the potential population in the natural flow and the optimal flow might not be possible due to needs for inhabiting considerable population in the city. Finally, it should be investigated how the carrying capacity of the land population should be changed consistent with the sustainable plan of water supply. SDI is 45%, which means reducing 45% of the initial carrying capacity of the population is required to increase the sustainability of the river ecosystem as the source of water supply in the developing urban areas. It should be noted that habitat loss is less than 35% which means the optimization model is able to find an optimal solution for balancing environmental requirements and humans’ needs. In other words, the optimization model balances the needs by reducing 45% of population and increasing habitat loss to 35%.

Fig. 10
figure 10

SDI and RMD of the optimal solution in the case study, A RMD for potential fish population in river habitats, B SDI for city population)

Full size image

Discussion

A discussion on technical and computational aspects of the developed method is required. In fact, the advantages, shortcoming and limitations of the further application of the developed framework is needed to clarify the applicability of the method. Moreover, why we need this framework or similar framework in the current condition and why the proposed mechanism could be applied in the case study successfully.

Significance of the proposed framework

Environmental degradations of the freshwater ecosystem are undeniable which means assessing the ecological impacts of these ecosystems is a need. Many previous studies corroborated the impact of urban development on the freshwater ecosystems. Increasing population would exacerbate these impacts. The negotiations between the environmental advocators and stakeholders are escalated in recent years due to increasing degradations in the freshwater ecosystems. It seems that integrating the possible ecological impacts and development scenarios in different scales is an unquestionable research need. It should be noted that the impact of unsustainable development on the river ecosystem might be long-term. Furthermore, it might be very difficult to change the directions of incorrect development scenarios especially in the developing countries. The present study is an effort to link the ecological impacts of the river and the carrying capacity of the population in the urban areas where need water supply by the river. A disadvantage of the environmental flow models is inability of these methods for integrating the ecological and socio-economic aspects of the river basin. In other words, the environmental flow methods might proposes a minimum environmental flow or environmental flow regime, which might not be implementable in many case studies. In fact, the ecological flow model are not able to optimize the impacts, which might weaken the feasibility of the proposed flow. On the one hand, if an ecological flow model assesses the flow regime based on the maximizing the quality of the river habitats, it might not be welcome by the stakeholders because it would restrict the developing of urban areas in the river basins. On the other hand, if the ecological flow model assesses the flow regime based on minimum suitability of the habitats, degrading the habitats is a concern for environmental advocators. Thus, the best solution is to balance the benefits of water supply for the ecosystem and the human. In other words, aquatic species should be considered as the lawful user of the water in the development. This strategy is helpful to be ensured regarding the sustainable development of the urban areas. The carrying capacity of the population in terms of water consumption is a vital socio-economic aspect, which might have long-term effects on the communities and the environment. It should be noted that determining carrying capacity of the population in the urban areas should not only be highlighted in terms of water use. In other words, it is recommendable to combine different models of the carry capacity to determine the final recommendations in the developing areas. Furthermore, it should be highlighted that it is worthy to use the proposed method before development of the new areas. It could be applicable for determining the carrying capacity in the current cities. However, changing directions of the population development might not be practical in many cases.

Advantages/disadvantages and possible improvements

Each environmental model might have some advantages and drawback that may be noticed in the future applications. The propose method should be investigated in terms of technical as well as computational issues. Developing a robust environmental model in which different abiotic factors are considered is the technical advantages of the method. However, due to environmental challenges of the case study, we focused on a target species that might be a shortcoming of the model. In some case studies, different species should be highlighted simultaneously, which means adding several target species might be essential. Moreover, biotic factors were not effective in our case study. However, biotic factors such as competition and predation might be effective on the habitats election by the species. Hence, adding biotic interaction among different species might be very important. It should be noted that adding other environmental factors in the optimization model might need significant changes in the structure of the simulation–optimization model. The present study demonstrated that defining carrying capacity of the population in the cities should be based on different natural resources. Thus, adding other types of environmental models such as impact of population on the water quality or impacts on the terrestrial ecosystems might be necessary for finalizing the carrying capacity of the land population in cities.

In the present study, the average flow time series in low flows were used to simulate the carrying capacity. However, analysis of carrying capacity of the land population in the long-term period will be useful for assessing the impact of changing flow on the sustainable water supply. Availability of the recorded flow in a long-term period might be a challenge in this regard. Thus, utilizing the rainfall-runoff models to simulate the river flow would be beneficial in these cases. We focused on a water diversion project, which was responsible for satisfying the water demand. However, this research work could be carried out in the large scales such as a river basin. It might be useful in terms of investigating interactions of different cities in a river basin. It should be noted that the water demand of the case study is only supplied using the surface water resources while simultaneous use of surface and ground water might be the source of water supply in other cases. Thus, integrating surface water and ground water is recommendable in other case studies.

The computational aspects matter for applying the proposed method as well. The computational complexities are very important to apply the simulation–optimization methods. In other words, more computational complexities mean more time and memory would be needed for simulation of the parameters and convergence of the optimization model. The main disadvantage of the proposed method is considerable computational complexities. In other words, the computational costs of the proposed method are very high which means remarkable time and memory are needed for convergence of the optimization model. Two culprits are involved regarding increasing computational complexities including 1- using ANFIS model to simulate ecological impacts and 2- utilizing a multi-objective optimization algorithm. In the case study, the number of iterations was considered 10,000 for finding the optimal solution. Moreover, we ran several tests. Due to high computational complexities, each test took more than a day, which might be a hindrance for applying the proposed method in the projects. It should be noted that the water resources engineers and urban planners might not be interested in using complex methods, which might need considerable time and memory for several tests. Thus, high computational complexities would be the main limitation of this method. A significant advantage of using multi-objective optimization is ability to visualize the trades-off between the objectives. However, its complexities might limit the popularity of this type of the optimization. A single objective optimization is simpler compared with multi-objective algorithms which means its application might be reasonable. However, the nature of the problem in the present study is multi-objective, which means using single objective algorithms is not possible for developed objective functions. One of the future research fields is to change the nature of the problem from a multi-objective to a single objective. Combining the objective of the problem might be a logical solution in this regard. However, a single objective method is not able to visualize the trades-off between the objectives, which might increase the ambiguity of finding the optimal solution. It should be noted that visualization of the trades-off between the objectives would be helpful for further negotiations to finalize the sustainable plan for development of cities. Another computational aspect is the capabilities of the algorithms for the global optimization. The evolutionary optimization is not able to guarantee the global optimization inherently, which might increase the uncertainties of the optimization process. In other words, using more than one optimization algorithms might be recommendable in many cases for having the best solution. Hence, it is recommendable to apply different algorithms in the optimization process. Then, a robust decision-making system could be applied to finalize the best solution.

We do not recommend utilizing the outputs of the present framework directly. It is needed to assess the carrying capacity of the land population in terms of different economic and environmental aspects. Then the results could be finalized in an expert panel who is able to integrate technical considerations consistent with the needs of the development in the river basin. Developing similar frameworks to determine the carrying capacity of the cities considering other natural resources is recommendable in the future studies.

Conclusions

The present study developed a novel optimization model to determine the sustainable population in which the ecological impact of water supply is mitigated. Several data driven models were used to assess the ecological impact in the structure of optimization model. Based on the results in the case study, the sustainable carrying capacity of the population in the new city is 45% less than initial plan of the population development. Hence, it is required to change the plan of population development in the case study considerably. In fact, the optimization model balances the needs of environment and water supply by reducing 45% of population and increasing habitat loss to 35%.