Introduction

Arsenic concentration above 0.01 mg/L in groundwater exceeds the limit set by the World Health Organization (WHO) as suitable for human consumption as drinking water (WHO 2011). The conditions under which arsenic can be released to the groundwater may expose the Indo-Gangetic plains to particular risks. The fluvial sediments from the Himalayas, which are composed of clay sand and silt, have been identified as the source of arsenic in the aquifers of the Indo-Gangetic plains (McArthur et al. 2004). The arsenic is released from the sediments into the groundwater through a microbiologically mediated reductive dissolution process (McArthur et al. 2001, 2004; Akai et al. 2004; Charlet and Polya 2006). This process is accelerated by high rates of vertical percolation of water from the surface to the aquifers through arsenic rich sediments, and facilitated by the presence of organic matter that influences the solubility and mobility of arsenic (Islam et al. 2004; Rowland et al. 2006).

Some knowledge is at hand about high exposure in Bangladesh, where nearly 50 % of the country’s population is exposed to the risk of drinking arsenic contaminated water. In India, the most severe arsenic contamination has been reported from West Bengal (Khan 1997; Smith et al. 2000; Kinniburgh and Smedley 2001; Ravenscroft et al. 2005; Nickson et al. 2007; Shamsudduha et al. 2008). Other high arsenic concentrations in groundwater have been reported from Chandigarh (Datta and Kaul 1976), Jharkhand (Bhattacharjee et al. 2005), Uttar Pradesh (Ahamed et al. 2006), Manipur (Chakraborti et al. 2008), Assam (Hazarika and Bhuyan 2013), from highland upstream areas like Uttarakhand (Gaur et al. 2013) and Himachal Pradesh (Chakraborti et al. 2003; Shah 2010). Arsenic contamination in Bihar was first reported in 2002 in Ojha Patti village, Shahpur block of Bhojpur district (Chakraborti et al. 2003). Nickson et al. (2007) have reported on arsenic concentration in 11 districts of Bihar; Singh and Ghosh (2012) have monitored arsenic contamination in Maner block in Patna district and found arsenic concentration within the range of 0.14–0.49 mg/L. The highest levels of arsenic concentration in the groundwater (2.18 mg/L) were reported from Buxar district of Bihar (Singh et al. 2014a, b). High arsenic concentrations have also been detected in Patna (0.498 mg/L) (Singh and Ghosh 2012), Samastipur (0.060 mg/L) (Gupta et al. 2014) and Bhagalpur districts (0.1 mg/L) (Kumar et al. 2014), Saran (0.15 mg/L), Begusari (0.0943 mg/L) (Agrawal et al. 2011), Khagaria, Munger and Katihar districts of Bihar (range of 0.05–0.1 mg/L) (Singh et al. 2014a, b; Singh 2015; Singh and Vedwan 2015). These publications suggest that in 16 out of 38 districts of Bihar, groundwater contains high arsenic concentrations (Ghosh et al. 2007; Saha et al. 2009; Singh and Ghosh 2012). The government of India has been testing arsenic contamination all over Bihar between 2005 and 2014, in some 114,737 deep tube-wells installed by the government under the national rural drinking water program (NRDWP) in 107,640 habitations. The results show that the concentration of arsenic significantly varies from one block to another even within a single district (Ghosh et al. 2007), and overall, in about 10 % of the habitations tested, arsenic levels were higher than the Indian permissible limit for drinking water of 0.05 mg/L (BIS 2012). This led to an estimate that more than 10 million people in Bihar state are exposed to arsenic concentrations of 0.01 mg/L or above (Singh et al. 2014a, b), and to acute arsenicosis. The screening of the wells is still ongoing, and new arsenic contaminated areas are being identified.

However, the testing under NRDWP is probably giving an underestimate of the risk exposure, considering that it covers only NRDWP installed deep hand tube-wells, whereas most rural households depend on privately installed hand tube-wells that are commonly installed at depths where the arsenic concentration in the aquifer would be much higher (Srikanth 2013). Moreover, the dependence on groundwater as a source of fresh water increased due to the combined effect of high population growth, overutilization of agricultural land and contamination of surface water (Central Ground Water Board 2007).

This situation raises the imperative need to conduct a systematic assessment of the vulnerable areas in this region, characterized by a dense river network and fluvial Holocene sediments (naturally rich in arsenic) that are ideal settings for arsenic dissolution and accumulation in groundwater in Bihar where arsenic concentrations in the aquifers are already known to be very high (Chakraborti et al. 2009; Singh et al. 2014a, b).

Estimation of the spatial manifestation and magnitude of the exposure to arsenic contamination throughout the state based on testing would take several years to complete. Consequently, this systematic assessment cannot rely on testing alone. In the past, researchers have proposed different models for the prediction of arsenic concentration in unsampled areas based on the geostatistical interpolation methods (Goovaerts et al. 2005; Hossain et al. 2007; Lee et al. 2007; Winkel et al. 2008). Applying similar methods, we present in this study a statistical regression model to predict the arsenic concentration of untested locations in the groundwater in all the 16 blocks of Vaishali district, Bihar. The model utilizes digitally available geomorphological and hydrogeological parameters, which are considered to impact physical processes governing the solubility of arsenic in the groundwater, as well as laboratory test results on arsenic concentration of water from sampled hand tube-wells across the district, carried out for calibration. The purpose of this analysis is to validate the model so that it could then be applied to obtain estimates in other untested locations in the Indo-Gangetic plain, where some one billion people live and where much of the food of South Asia is produced (Agrawal et al. 2011).

The article is structured as follows: the study area is described, followed by a section on methods. This is followed by results and a discussion of these results. The conclusions are then presented.

Methods

Study area

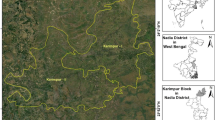
The study was conducted in Vaishali district in northern Bihar, India, (Fig. 1). Vaishali district covers an area of 2016 km2 and consist of 16 blocks and 1531 villages inhabited by a total population of around 3.5 million (Census of India 2011). The study area is an interfluvial alluvial plain bounded by the Ganga River in the south and Gandak River on the western side with point of confluence at Hajipur. Hydrologically, the study area can be divided into two sub-basins; Gandak sub-basin and Burhi Gandak sub-basin. The majority of the area lies in the Burhi Gandak sub-basin. The study area is mostly flat with a maximum elevation of 78 m near the banks of the Gandak River in the north-west and an average gradient of −3.5 m/km towards the south-east. Vaishali’s fertile plains are formed by regular deposition of arsenic rich alluvium brought by the Gandak and Ganga rivers over time from the Himalayas. The region encompasses three types of morphostratigraphic units, namely Hajipur (Late Pleistocene–Early Holocene), Vaishali (Middle–Late Holocene) and Diara (Late Holocene) formation and comprises a confined and prolific unconfined aquifer system formed by an alternate deposition of the sand, clay, silt and gravel of quaternary alluvial deposit (Central Ground Water Board 2007).

Fig. 1
figure 1

Study area

Full size image

Data

Table 1 lists the data used along with the data sources comprising primary data on arsenic concentration from sampled hand tube-wells and secondary data used for the calibration of the prediction model.

Table 1 Primary and secondary data used
Full size table

Methods

Sampling and testing of arsenic content in water from hand tube-wells

For this study, 34 water samples from hand tube-wells were collected from all 16 blocks of Vaishali district in Bihar, 2–3 samples from each block (Fig. 2). The villages and hand tube-wells within a village were randomly selected. The hand tube-wells served as a source of fresh water for humans, domestic and livestock needs. Each hand tube-well was flushed for 10 min prior to collection of the water samples to remove the stagnant water. After the water samples had been stored in sterilized opaque polyethylene bottles, concentrated nitric acid (HNO3) had been added, and the samples were kept refrigerated (2–4 °C) adhering to standard procedures, e.g., followed by UNICEF (2008). A private testing laboratory in India (Delhi Test House Pvt. Ltd, New Delhi) was mandated to test the arsenic concentrations of the collected water samples. The laboratory employed the inductively coupled plasma mass spectrometry (ICP-MS) technique to measure the arsenic content with minimum arsenic detection limit of 0.001 mg/L and uncertainty error of ±2 ppb at 10 ppb. The latitude and longitude coordinates and the depths of the sampled hand tube-wells were captured while the water samples were collected.

Fig. 2
figure 2

Sampled locations and test results of arsenic in freshwater of 34 hand tube-wells across Vaishali district, Bihar. Black and grey circles indicate arsenic concentrations above 0.07 mg/L and between 0.05 and 0.07 mg/L, respectively

Full size image

Digital spatial data processing

All digital spatial data sets were transformed into the geographic information system (GIS) framework in the Universal Transverse Mercator (UTM) coordinate system with a spatial resolution of 90 m, and modeled arsenic concentration maps were prepared using GIS software ArcGIS version 9.1 (ESRI 2005).

Digital elevation model (DEM)

Topographic information was extracted from the ‘ASTER GDEM’ digital elevation model (DEM), available at 30 m resolution. The DEM was projected into the UTM coordinate system to develop the raster products of elevation (m), slope (degrees) flow accumulation cell values and ‘distance to river’. Flow accumulation cell values represent accumulated water flowing into each corresponding downslope cell in a raster image. Pixels with high flow accumulation values denote areas with higher water flow along the gradient, whereas pixels with null values represent local peaks or ridges with no water inflow (Jenson and Domingue 1988). Flow accumulation has already been identified as a good predictor of arsenic concentration pathways (Weerasiri et al. 2013). Gao et al. (2007) studied the relationship of flow accumulation and arsenic speciation. They showed that cells with concentrated flow paths have high reducing conditions promoting reductive dissolution of arsenic. Furthermore, cells with high flow accumulation values also act as sinks for arsenic rich Holocene sediments.

‘Distance to river’ is another important factor believed to govern spatial variability of arsenic concentration (Winkel et al. 2008). The distance from each point in the study areas to the river system was calculated with the ArcHydro tool in ArcGIS 9.1 using the DEM data. It has been observed that in Asian river basins in close proximity to main rivers and their tributaries, arsenic concentration in groundwater is higher (Erban et al. 2013). According to Central Ground Water Board (2007), the area comprising flood plains and riparian stripes in the Ganga basin are composed of deep Holocene sediments, which explain the higher concentration of arsenic in the groundwater.

NDVI (Normalized Difference vegetation Index) and spectral ratio

Twelve mid-month images of the ‘normalized difference vegetation index’ (NDVI) (Rouse et al. 1974) of the year 2011 were used to calculate a 12-months average NDVI value. The NDVI value was then algebraically converted into the spectral ratio. The spectral ratio is the quotient of near infrared and visible red spectral reflectance measurements. Vegetation indices are indicators for biomass, and hence availability of water. These indices can thus also serve as a proxy for organic matter in the soil, which is considered to enhance the release of arsenic from soils and sediments (Wang and Mulligan 2006; Rodríguez-Lado et al. 2013).

Land use land cover (LULC)

Different land use/cover classes were mapped to 1 and 0 depending on the vegetation. Agricultural land, forests and other vegetated areas were assigned a value of 1; and barren, waste land, and urban clusters were assigned a value of 0.

Agricultural land and other vegetated areas are regions with increased transport of organic material into the aquifer which instigates the reductive dissolution of arsenic to the groundwater (Wang and Mulligan 2006).

Soil map (estimation of hydraulic conductivity based on soil type)

The hydraulic conductivity for each soil type has been calculated based on the soil texture (combinations of sand, silt and clay) using a methodology developed by (Saxton et al. 1986).

Net groundwater recharge

The net groundwater recharge was calculated applying Eq. (1) following (Chaturvedi 1973) for the estimation of net recharge in the Ganga-Yamuna river basin:

$$R\;{ = }\; 2. 5 \sqrt {\left( {P - 0.6} \right)} ,$$
(1)

where R is the net annual recharge in cm and P the total annual rainfall in cm. This simplified formula only takes account of rainfall, but not of local topography. The impacts of local topography on groundwater recharge are indirectly considered by incorporating the factors ‘flow accumulation cell values’ and LULC.

The total annual rainfall for Vaishali district was calculated by interpolating the past 5 years’ average annual rainfall (2009–2013) from Vaishali and four neighboring districts (Patna, Saran, Muzzafarpur, Samastipur) using the inverse distance weightage (IDW) method (Shepard 1968). Recent studies have reported that net recharge can play an important role in the mobilization of arsenic in the groundwater (Harvey et al. 2002; Ashfaque 2007; Meliker et al. 2009). Biodegradable organic carbon present on the surface and in subsurface layers of the soil strata instigate the reductive dissolution processes of arsenic release in the groundwater and higher recharge would increase the transport of dissolved arsenic to the groundwater.

Depth of hand tube-wells

When we collected water samples, we also measured the depth of each hand tube-well sampled. The reason for measuring the depth is to include this parameter in modeling arsenic concentration, considering recent studies which indicate that higher concentrations have been observed for deep tube-wells in Bangladesh (Burgess et al. 2010), India (Chakraborti et al. 2009) and in North Vietnam (Winkel et al. 2008; Erban et al. 2013) In the studied area, (Saha et al. 2009, 2011) claimed that arsenic contaminated zone in the Ganga river basin is mostly located within the shallow aquifer range (<50 m) and deeper aquifers located below 190 m can be used to extract water for drinking purpose (Saha and Shukla 2013). However, our working assumption is that the depth of the arsenic rich Holocene sediments varies substantially in any aquifer.

Regression model with arsenic concentration as dependent variable

We ran a multiple linear regression model to predict the arsenic concentration (dependent variable) using statistical software “R” version 3.2.2. The following parameters were considered as potential independent variables: elevation, slope and flow accumulation value, NDVI, spectral ratio, LULC, hydraulic conductivity, distance to river, groundwater recharge and hand tube-well depth. The regression model was calibrated at the 34 sample sites where the arsenic concentration has been determined, by using the point information of all the selected parameters (independent variables) at the same locations for all hand tube-wells at different installation depths. These point values were extracted from the geospatial layers using the “spatial analyst tool” of the software ArcGIS version 9.1 (ESRI 2005).

The statistical significance between the arsenic concentration and each potential independent variable was initially evaluated through a simple linear regression analysis. Only parameters which showed significance above 95 % (p value <0.05) were included in the subsequent multiple linear regression. Then, the multiple linear regression were performed only with those significant parameters as independent variables.

Results

Arsenic concentration in the groundwater of entire Vaishali District based on in situ testing of hand tube-wells

In total, 34 groundwater samples were collected from hand tube-wells in all 16 blocks of the study area, whose depths ranged from 10 to 50 m. All tested samples displayed arsenic concentrations ranging from 0.050 to 0.088 mg/L, i.e., above the permissible limit of 0.05 mg/L set by government of India (BIS 2012) (Fig. 2). In passing we note that during the data collection, we observed that villagers in most of the locations displayed visible skin lesions, which are assumed to be arsenicosis as a result of chronic exposure to arsenic.

The highest arsenic concentration values (0.07 mg/L or higher) were measured in the low lying flood plain surfaces of the Gandak and Ganga river: (1) on the eastern flood plain of Gandak River in Vaishali block (0.079, 0.072 mg/L) and Lalganj block (0.076, 0.071 mg/L), (2) at the confluence of Ganga and Gandak at Hajipur block (0.070 mg/L), (3) on the northern bank of Ganga river in Bidupur block (0.088, 0.072 mg/L) and Desri block (0.072, 0.071 mg/L), and (4) on the island between two rivulets of the Ganga river in Raghopur block (0.071 mg/L).

Prediction of arsenic concentration across entire Vaishali District, Bihar

The p values of the simple linear regressions of measured arsenic concentration against each of the potential independent variables for the multiple linear regression are given in Table 2. We included only the spectral ratio, which can be derived through an algebraic transformation from the NDVI, which shows better results than the NDVI (higher R 2 value).

Table 2 p values of simple linear regression with measured arsenic concentration as dependent variable
Full size table

The characteristics of the multiple linear regression are presented in Table 3. The R 2 value is with 0.7157 quite high indicating that the identified parameters describe the arsenic concentration well.

Table 3 Results of the multiple linear regression with arsenic concentration as the dependent variable
Full size table

The arsenic concentration in groundwater is positively correlated with flow accumulation value, spectral ratio, LULC, hydraulic conductivity, recharge, hand tube-well depth, slope, elevation, and negatively correlated with distance to river. Flow accumulation values, spectral ratio, LULC, distance to river, groundwater recharge and depth of hand tube-wells were significantly correlated with the arsenic concentration (p value <0.05), and were thus, included in the multiple linear regression.

Observed and predicted arsenic concentration values are shown for all 34 sample sites in Fig. 3. The R 2 value of 0.7157 for the entire data set of 34 points corresponds to a correlation of 0.8460 between observed and predicted arsenic concentration values. To conduct a comparison between in-sample and out-of-sample accuracy, the set of 34 observations has been divided into sets of 27 and 7 data points. This division is based on the rule of thumb consideration that the sample size should be at least around 5 times the number of independent variables (Stoelting 2002). In this study we used a sample size of 27 for the in-sample training set to have a least 7 data points for the out-of-sample testing. For 100,000 random divisions, the correlations between observed and predicted arsenic values for in-sample and out-of-sample have been calculated and the averages determined. In-sample average correlation was 0.8536 and out-of-sample average correlation was 0.7239. The average out-of-sample root-mean-square error (RMSE), the standard deviation of the differences between predicted values and observed values for the 7 data points, was 0.006489. The analysis reveals that the predicted and actual arsenic concentrations even in untested areas can be expected to differ less than 0.01 mg/L in most of the cases.

Fig. 3
figure 3

Comparative analysis of measured and predicted arsenic concentration at the 34 sample sites

Full size image

Three arsenic maps were prepared illustrating the model predictions for arsenic concentrations at three different depths, namely 10, 30, and 50 m, see Fig. 4. The arsenic concentrations were grouped into five classes; 0.05–0.06, 0.06–0.07, 0.07–0.08, 0.08–0.09 and 0.09–0.1 mg/L. The arsenic concentration has a distinguished gradient with decreasing values from the rivers in the west and south to the north-east. The same gradient was observed in the 34 sample sites, and is introduced in the prediction model through the independent variable “distance to river”.

Fig. 4
figure 4

Predicted arsenic concentrations in Vaishali district, Bihar, at 10 (left), 30 (middle) and 50 m (right) hand tube-well depth

Full size image

These results show that when a hand tube-well is 10 m deep, the majority of the district area (53 %) would be exposed to an arsenic concentration in the range of 0.061–0.07 mg/L (Fig. 5). At 30 to 50 ms depth, the majority of the area would be exposed to a higher concentration of 0.071–0.08 mg/L. And when hand tube-well depth exceeds 50 ms, virtually the entire area would be threatened by higher arsenic levels.

Fig. 5
figure 5

Distribution of area predicted to fall under 0.05–0.06, 0.06–0.07, 0.07–0.08, 0.09–0.10 mg/L arsenic concentration for 10 (left), 30 (middle) and 50 m (right) hand tube-well depth in Vaishali district, Bihar

Full size image

Discussion and conclusion

This study predicts the arsenic concentration in Vaishali district, Bihar, India based on a multiple linear regression model that has been calibrated with regional hydro-geomorphological characteristics. Water samples were collected from the sampled hand tube-wells at different depths, and tested for arsenic concentration levels. Results of the groundwater sample tests revealed that all blocks of the district are exposed to arsenic concentrations exceeding 0.05 mg/L (the permissible limit of arsenic in drinking water set by the government of India; the limit for acceptable safe drinking water is 0.01 mg/L). Arsenic concentrations of 0.07 mg/L and higher were observed in sample sites located in low lying flood plain areas of Ganga and Gandak rivers. Moreover, arsenic concentrations higher than the safe limit have been found in previously considered “safe” blocks of North-Eastern Vaishali district, including Patepur, Sahdei Buzurg, Chehra Kala, Jandaha, Rajapakar, Mahnar, Mahua and Garauls. Generally speaking, arsenic concentrations gradually decrease as the distance from the rivers increases (and previous studies (Chakraborti et al. 2009; Shah 2010) claimed that the lower arsenic concentration in those locations is due to older alluvium from the Pleistocene era, covering the Holocene sediments).

The model predicted unsafe arsenic concentrations of above 0.05 mg/L across the entire study area and correctly identifies the blocks of Bidupur, Raghopur and Hajipur as most exposed—the same blocks where arsenic contamination has already been detected (Central Ground Water Board 2007; Chakraborti et al. 2009). High arsenic concentrations have been predicted in the aquifers located in the vicinity of the rivers in the entire study area.

The spatial variability of the predicted arsenic concentration was relatively high, ranging from 0.05 to around 0.10 mg/L with proximity to river being an important predictor. Although distance to river is the major factor determining the arsenic concentrations (for a uniform tube-well depth), points of equal distance to the river system still exhibit differences in the arsenic levels mainly because of variations in flow accumulation values and land use and land cover, which are the conditions favorable for inducing reductive dissolution of arsenic.

One limitation of the present study is that the proposed model can only be applied for tube-well depths up to around 50 m. This is satisfactory for the majority of installation depths, and the depths of the hand tube-wells we sampled ranged from 10 to 50 m. However, some tube-wells are much deeper, for example, the government installed ones. The multiple linear regression models indicates that with increasing depth the arsenic concentration increases linearly, which would hold true only within the range of the sampled tube-well depths. Deeper tube-wells would have to be sampled to analyze the impact of larger ranges of depths, which cannot be assumed to be linear, considering various reports that beyond 50 m the arsenic concentration in the groundwater decreases due to the presence of old Holocene sediments (Yadav et al. 2012).

Another limitation is the relatively small sample size. To control the risk of overfitting, we conducted out-of-sample tests. Even in the out-of-sample sets the correlation between observed and predicted arsenic values was good and the average out-of-sample root-mean-square error (RMSE) low. This underlines that the prediction model is not over-fitted and that extending the training set used for model calibration would not lead to material changes in the prediction model. However, for other regions additional/different input parameters might have to be considered.

Those limitations notwithstanding, the model and results described in this article demonstrate a relatively easy and cheap way to identify the areas of high risk with high spatial resolution. This diagnosis is the essential prerequisite for targeted preventive and corrective interventions to protect the local population from excessive exposure to arsenic. As this model is based on easily and freely available input parameters, which can be obtained for the entire Bihar state, and even the entire Indian Indo-Gangetic Plain, we submit that the model could be applied to model and accurately predict the arsenic exposure in groundwater for larger regions, with only a relatively small sample size required to calibrate the model to other regions. Thus, the model adds to the existing tools, at considerably reduced cost and time to obtain estimates, with comparable accuracy.