Abstract
Formal enforcement punishing defectors can sustain cooperation by changing incentives. In this paper, we introduce a second effect of enforcement: it can also affect the capacity to learn about the group’s cooperativeness. Indeed, in contexts with strong enforcement, it is difficult to tell apart those who cooperate because of the threat of fines from those who are intrinsically cooperative types. Whenever a group is intrinsically cooperative, enforcement will thus have a negative dynamic effect on cooperation because it slows down learning about prevalent values in the group that would occur under a weaker enforcement. We provide theoretical and experimental evidence in support of this mechanism. Using a lab experiment with independent interactions and random rematching, we observe that, in early interactions, having faced an environment with fines in the past decreases current cooperation. We further show that this results from the interaction between enforcement and learning: the effect of having met cooperative partners has a stronger effect on current cooperation when this happened in an environment with no enforcement. Replacing one signal of deviation without fine by a signal of cooperation without fine in a player’s history increases current cooperation by 10%; while replacing it by a signal of cooperation with fine increases current cooperation by only 5%.



Similar content being viewed by others
Notes
Learning about the honesty of others matters not only if tax compliance relies on social interactions (Fortin et al., 2007) but more generally in all daily decisions that are not legally enforceable.
Another strand of recent literature highlights the existence of possible unexpected effects of naive policy interventions in the presence of social norms by focusing on how the incentives introduced by policies interact with the endogenous emergence of these norms (see for instance Dutta et al. 2021).
This paper relies on the same data as Galbiati et al. (2018), who focus on games occurring late in the experiment, when learning about norms prevalent in the group has converged. Herein, we rather analyze the entire dataset, including early games.
In a related work, Dal Bó and Dal Bó (2014) show that explicit information about moral values affect cooperation in a standard voluntary contribution game. In their setting however the information is provided by the experimenter and does not allow for dynamic learning about the distribution of prevalent types in the lab.
More precisely Dal Bó and Fréchette (2011) document that the behavior of the partner in the previous match affects the subjects’ behavior.
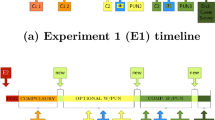
We distinguish early and late games by splitting the matches in three groups, in such a way that one third of the observed decisions are classified as “early”, and one third as “late”. Observed matches are accordingly defined as “early” up to the 7th, as late after the 13th, in line with the definitions used in the “Alternative identification strategy” in Appendix 2. Note that the matches we exclude from the working sample all appear in late games. As a result, Fig. 2a is not affected by the choice of the working sample.
This is a specific functional form of the more general function in, e.g., Kartal amb Müller (2018).
We drop this dependency of \(p_{it}\) on \({F}_{it}\) in the notation.
In the generalized model presented in the “The dynamics of learning with behavioral spillovers” in Appendix 2, we introduce spillovers by assuming that the values \(\beta _{it}\) depend on t and in particular can be affected by past experiences.
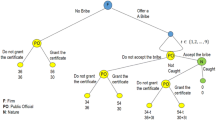
We explicitly use the fact that players are restricted to choosing between Grim Trigger, Tit For Tat and Always Defect.
In the case of the experiment, \(\varPi _{1} =23\), \(\varPi _{2}= -3 \) and \(\varPi _{3} =5\).
Stability guarantees that when the current match is played with a fine, the probability of cooperation increases.
\(q_{it} (0,C)\) corresponds to the third bar in Fig. 2b, \(q_{it} (0,C)\) to the fourth, \(q_{it} (0,D)\) to the first and \( q_{it} (1,D)\) to the second.
The specification of the empirical model is the same as the one used in the “Alternative identification strategy” in Appendix 2. All results are robust to alternative definitions of the number of previous matches included in the past history. The results are available from the authors upon request.. The “Replication of the main results with bootstrapped standard errors” in Appendix 4, provides the results from a robustness exercise with bootstrapped standard errors.
The model can easily be extended to allow for longer histories to impact values. For instance, the effect on past institutions on values could be extended to:
$$\begin{aligned} \beta _{it} { } = { } \beta _{i} { } + { } \sum _{\tau =1} ^{T} \phi _{F\tau } { } \mathbbm {1}_{\{F_{it-\tau }=1\}} { } + { } \sum _{j =1} ^{T} \phi _{C\tau } { } \mathbbm {1}_{\{a_{j_{t-\tau },t-\tau }=C\}}, \end{aligned}$$with \( \phi _{F\tau }\) and \( \phi _{C\tau }\) increase in \(\tau \), in other words the more recent history having more impact. This could be introduced at the cost of added complexity.
As stated above, we work under the assumption that players are myopic and choose between C and D to maximize their payoff in the current match. Without this assumption, when spillover are introduced, a player would need to take into account that her current action would influence her partner’s future actions and thus influence the partner’s future partners. An alternative would be to assume that players are negligible enough so that current actions cannot influence future beliefs.
All results are robust to alternative definitions of these thresholds. The results are available from authors upon request.
Note that we do not separately estimate these parameters according to the current enforcement environment, but rather estimate weighted averages \(\varLambda _{k,l} = \mathbbm {1}_{\{F_{it} = 0\}} \varLambda ^0_{k,l} + \mathbbm {1}_{\{F_{it} = 1\}} \varLambda ^1_{k,l}\).
References
Acemoglu, D., & Jackson, M. O. (2015). History, expectations, and leadership in the evolution of social norms. Review of Economic Studies, 82(2), 423–456.
Acemoglu, D., & Jackson, M. O. (2017). Social norms and the enforcement of laws. Journal of the European Economic Association, 15(2), 245–295.
Ali, S. N., & Bénabou, R. (2020). Image versus information: Changing societal norms and optimal privacy. American Economic Journal: Microeconomics, 12(3), 116–164.
Azrieli, Y., Chambers, C. P., & Healy, P. J. (2018). Incentives in experiments: A theoretical analysis. Journal of Political Economy, 126(4), 1472–1503.
Bell, R. M., & McCaffrey, D. F. (2002). Bias reduction in standard errors for linear regression with multi-stage samples. Survey Methodology, 28(2), 169–179.
Benabou, R., & Tirole, J. (2011). Laws and norms. NBER WP 17579.
Bérgolo, M., Ceni, R., Cruces, G., Giaccobasso, M., & Pérez-Truglia, R. (2021). Tax audits as scarecrows. Evidence from a large-scale field experiment. American Economic Journal: Economic Policy, 2021, 1.
Bowles, S. (2008). Policies designed for self-interested citizens may undermine the moral sentiments: Evidence from economic experiments. Science, 320(5883), 1605–1609.
Cameron, A. C., Gelbach, J. B., & Miller, D. L. (2008). Bootstrap-based improvements for inference with clustered errors. Review of Economics and Statistics, 90(3), 414–427.
Dal Bó, E., & Dal Bó, P. (2014). ‘Do the right thing’: The effects of moral suasion on cooperation. Journal of Public Economics, 117, 28–38.
Dal Bó, P., & Fréchette, G. R. (2011). The evolution of cooperation in infinitely repeated games: Experimental evidence. American Economic Review, 101(1), 411–429.
Deffains, B., & Fluet, C. (2020). Social norms and legal design. Journal of Law, Economics, and Organization, 36(1), 139–169.
Dohmen, T., Falk, A., Huffman, D., Sunde, U., Schupp, J., & Wagner, G. G. (2011). Individual risk attitudes: Measurement, determinants, and behavioral consequences. Journal of the European Economic Association, 9(3), 522–550.
Duffy, J., & Fehr, D. (2018). Equilibrium selection in similar repeated games: Experimental evidence on the role of precedents. Experimental Economics, 21(3), 573–600.
Dutta, R., Levine, D. K., & Modica, S. (2021). Interventions with sticky social norms: A critique. Journal of the European Economic Association., 2021, 1.
Engl, F., Riedl, A., & Weber, R. (2021). Spillover effects of institutions on cooperative behavior. Preferences, and Beliefs, American Economic Journal: Microeconomics, 13(4), 261–299.
Falk, A., & Kosfeld, M. (2006). The hidden costs of control. American Economic Review, 96(5), 1611–1630.
Fortin, B., Lacroix, G., & Villeval, M.-C. (2007). Tax evasion and social interactions. Journal of Public Economics, 91(11–12), 2089–2112.
Friebel, G., & Schnedler, W. (2011). Team governance: Empowerment or hierarchical control. Journal of Economic Behavior and Organization, 78(1–2), 1–13.
Galbiati, R., Henry, E., & Jacquemet, N. (2018). Dynamic effects of enforcement on cooperation. Proceedings of the National Academy of Sciences, 115(49), 12425–12428.
Galbiati, R., Schlag, K. H., & Van Der Weele, J. J. (2013). Sanctions that signal: An experiment. Journal of Economic Behavior and Organization, 94, 34–51.
Galizzi, M. M., & Whitmarsh, L. E. (2019). How to measure behavioural spillovers? A methodological review and checklist. Frontiers in Psychology, 10, 342.
Gill, D., & Rosokha, Y. (2020). Beliefs, learning, and personality in the indefinitely repeated Prisoner’s dilemma. CAGE online working paper series 489.
Kartal, M., & Müller, W. (2018). A new approach to the analysis of cooperation under the shadow of the future: Theory and experimental evidence. Working paper.
Nowak, M. A., & Roch, S. (2007). Upstream reciprocity and the evolution of gratitude. Proceedings of the Royal Society B-Biological Sciences, 274(1610), 605–609.
Peysakhovich, A., & Rand, D. G. (2016). Habits of virtue: Creating norms of cooperation and defection in the laboratory. Management Science, 62(3), 631–647.
Sliwka, D. (2007). Trust as a signal of a social norm and the hidden costs of incentive schemes. American Economic Review, 97(3), 999–1012.
Van Der Weele, J. J. (2009). The signaling power of sanctions in social dilemmas. Journal of Law, Economics, and Organization, 28(1), 103–126.
Zasu, Y. (2007). Sanctions by social norms and the law: Substitutes or complements? The Journal of Legal Studies, 36(2), 379–396.
Acknowledgements
This paper supersedes “Learning, Spillovers and Persistence: Institutions and the Dynamics of Cooperation”, CEPR DP n\(^{\text {o}}\) 12128. We thank Bethany Kirkpatrick for her help in running the experiment, and Gani Aldashev, Maria Bigoni, Frédéric Koessler, Bentley McLeod, Nathan Nunn, Jan Sonntag, Sri Srikandan and Francisco Ruiz Aliseda as well as participants to seminars at ENS-Cachan, ECARES, Middlesex, Montpellier, PSE and Zurich, and participants to the 2018 Behavioral Public Economic Theory workshop in Lille, the 2019 Behavioral economics workshop in Birmingham, the 2018 Psychological Game Theory workshop in Soleto, the 2016 ASFEE conference in Cergy-Pontoise, the 2016 SIOE conference in Paris, the 2017 JMA (Le Mans) and the ESA European Meeting (Dijon) for their useful remarks on earlier versions of this paper. Jacquemet gratefully acknowledges funding from ANR-17-EURE-001.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix 1: Data description
Our data delivers 934 game observations, 48% of which are played with no fine. Figure 4a displays the empirical distribution of game lengths in the sample split according to the draw of a fine. With the exception of two-rounds matches, the distributions are very similar between the two environments. This difference in the share of two-rounds matches mainly induces a slightly higher share of matches longer than 10 rounds played with a fine. In both environments, one third of the matches we observe lasts one round, and one half of the repeated matches last between 2 and 5 rounds. A very small fraction of matches (less than 5% with a fine, less than 2% with no fine) feature lengths of 10 rounds or more.
Sample characteristics: distribution of game lengths and repeated-game strategies. Note: Left-hand side: empirical distribution of game lengths in the experiment, split according to the draw of the fine. Right-hand side: distribution of repeated-games strategies observed in the experiment. One-round matches are excluded. AD: Always Defect; AC: Always Cooperate; TFT: Tit-For-Tat; GT: Grimm Trigger
As explained in the text, Sect. 2.2, for matches that last more than one round (2/3 of the sample), we thus reduce the observed outcomes to the first round decision in each match, consistently with the theory. The first round decision is a sufficient statistic for the future sequence of play if subjects choose among the following repeated-game strategies: Always Defect (AD), Tit-For-tat (TFT) or Grim Trigger (GT). While AD dictates defection at the first round, both TFT and GT induce cooperation and are observationally equivalent if the partner chooses within the set restricted to these three strategies and give rise to the same expected payoff. Figure 4b displays the distribution of strategies we observe in the experiment (excluding games that last one round only). Decisions are classified in each repeated game and for each player based on the observed sequence of play. For instance, a player who starts with C and switches forever to D when the partner starts playing D will be classified as playing GT. In many instances, TFT and GT cannot be distinguished (so that the classes displayed in Fig. 4b overlap): it happens for instance for subjects who always cooperate against a partner who does the same (in which case, TFT and GT also include Always Cooperate, AC), or if defection is played forever by both players once it occurs. Last, the Figure also reports the share of Always Cooperate that can be distinguished from other match strategies—when AC is played against partners who do defect at least once.
All sequences of decisions that do not fall in any of these strategies cannot be classified—this accounts for 14% of the games played without a fine, and 24% of those played with fine. The three strategies on which we focus are thus enough to summarize a vast majority of match decisions: AD accounts for 70% of the repeated-game observations with no fine, and 41% with a fine, while TFT and GT account for 14% and 34% of them.
Appendix 2: Alternative identification strategy
The empirical evidence presented in the paper relies on the insights from the model to provide a reduced-form statistical analysis of the interaction between learning and enforcement institutions. As a complement to this evidence, this section provides a structural analysis which takes into account both learning and behavioral spillovers. To that end, we first generalize the model presented in Sect. 3.2 to the case in which individual values evolve over time as a result of past experience. We then estimate the parameters of the model. This provides an alternative strategy to separately estimate learning and spillovers.
1.1 The dynamics of learning with behavioral spillovers
Consistent with Galbiati et al. (2018), we allow both for past fines and past behaviors of the partners to affect values:
According to this simple specification, personal values evolve through two channels. First, direct spillovers increase the value attached to cooperation in the current match if the previous one was played with a fine, as measured by parameter \(\phi _{F}\). Second, indirect spillovers, measured by \(\phi _{C}\), increase the value attached to cooperation if in the previous match the partner cooperated.Footnote 16
1.1.1 Introducing behavioral spillovers in the benchmark
We start by introducing spillovers in the benchmark model. Under the assumption that values follow the process in (3) and \(\phi _{F}>0, \phi _{C}>0\), the indifference condition (1) remains unchanged,Footnote 17 but now \(\beta _{it}\) is no longer constant and equal to \(\beta _{i}\) since past shocks affect values. In this context, individual i cooperates at t if and only if:
The cutoff value is defined in the same way as before:
The main difference with the benchmark model is in the value of \(p^{*}_{t}(F_{it})\). There is now a linkage between the values of the cutoffs at match t, \(\beta _{t}^{*}\), and the values of the cutoffs \(\beta _{t'}^{*}\) in all the preceding matches \(t'<t\) through \(p^{*}_{t}(F_{it})\). Indeed, when an individual evaluates the probability that her current partner in t, player \(j_{t}\), will cooperate, she needs to determine how likely it is that she received a direct and/or an indirect spillover from the previous period. The probability of having a direct spillover is given by \(P[F_{jt-1}=1]=1/2\) and is independent of any equilibrium decision. By contrast, the probability of having an indirect spillover is linked to whether the partner of \(j_{t}\) in her previous match cooperated or not. This probability in turn depends on the cutoffs in \(t-1\), \(\beta _{t-1}^{*}\), which also depends on whether that individual himself received indirect spillovers, i.e on the cutoff in \(t-2\). Overall, these cutoffs in t depend on the entire sequence of cutoffs.
In the remaining, we focus on stationary equilibria, such that \(\beta ^{*}\) is independent of t. We show in Proposition C that such equilibria do exist.
Proposition C
(Spillovers) In an environment with spillovers (\(\phi _{F}>0\) and \(\phi _{C}>0\)) and no uncertainty on values, there exists a stationary equilibrium. Furthermore all equilibria are of the cutoff form, i.e individuals cooperate if and only if \(\beta _{it} \ge \beta ^{*} (F_{it})\).
Proof
See “Appendix 5: Proofs”. \(\square \)
Proposition C proves the existence of an equilibrium and presents the shape of the cutoffs. The Proposition also allows to express the probability that a random individual cooperates as:
where
1.1.2 The dynamics of cooperation with learning and spillovers
We now solve the full model with uncertainty about the group’s values and with spillovers. As in the main text, we denote \(q_{it}\) the belief held by player i at match t that the state is H.
In this expanded model, the beliefs on how likely it is that the partner cooperates in match t, \(p^{*}_{t}(F_{it},q_{it})\), depends on the probability that the partner experienced spillovers. In addition, the probability that the partner j had an indirect spillover itself depends on whether his own partner k in the previous match did cooperate, and thus depends on the beliefs \(q_{kt-1}\) of that partner in the previous match. The general problem requires to keep track of the higher order beliefs. The proof of the following Proposition shows the existence of such a stationary equilibrium, under a natural restriction on higher order beliefs, i.e if we assume that a player who had belief \(q_{it}\) in match t believes that players in the preceding match had the same beliefs \(q_{j',t-1} = q_{it}\).
Proposition D
In an environment with spillovers and learning, if an equilibrium exists, all equilibria are of the cutoff form, i.e individuals cooperate if and only if \(\beta _{i} \ge \beta ^{*} (F_{it},q_{it})\). Furthermore, if in equilibrium \(\beta ^{*} (0,q) > \beta ^{*} (1,q) \) for all beliefs q, then the beliefs are updated in the following way given the history in the previous interaction:
Proof
See “Appendix 5: Proofs”. \(\square \)
Proposition D derives a general property of equilibria. The Proposition also allows to express the probability of cooperation for given belief \(q_{it-1}\) as:
where
Note that the parameters \( \varLambda _{3}\), \( \varLambda _{4}\) and \(\varLambda ^{j}_{k,l}\) in Eq. (6) depend on \(q_{it-1}\). Compared to the case without learning, there are 6 additional parameters, reflecting the updating of beliefs. According to the result in Proposition D, these parameters, both in the case where the current match is played with a fine and when it is not, are such that:
Overall, having fines in the previous match can potentially decrease average cooperation in the current match. There are two countervailing effects. On the one hand, a fine in the previous match increases the direct and indirect spillovers and thus increases cooperation. On the other hand, if the state is low, a fine can accelerate learning if, on average, sufficiently many people deviate in the presence of a fine. This then decreases cooperation in the current match.
1.1.3 Statistical implementation of the model
The main behavioral insights from the model are summarized by Eq. (6), which involves both learning and spillover parameters. As the equation clearly shows, exogenous variations in legal enforcement are not enough to achieve separate identification of learning and spillover parameters—an exogenous change in any of the enforcement variables, or past behavior of the partner, involves both learning and a change in the values \(\beta _{it}\). In the main text, identification relies on the assumption that spillovers are short-living in the sense that their effect on behavior is smaller the earlier they happen in one’s own history—while learning should not depend on the order in which a given sequence of actions happens. In this section, we report the results from an alternative identification strategy that relies on the assumption that learning has converged once a large enough number of matches has been played. Under this assumption, in late games, behavior is described by Eq. (5), which involves only spillover parameters. Exogenous variations in enforcement thus provide identification of spillover parameters in late games, which in turn allows to identify learning parameters in early ones.
To that end, as explained in the text, we split the matches in three groups, in such a way that one third of the observed decisions are classified as “early”, and one third as “late”. We use matches, rather than periods, as a measure of time since we focus on games for which the first stage decision summarizes all future actions within the current repeated game—hence ruling out learning within a match. Observed matches are accordingly defined as “early” up to the 7th, as late after the 13th—we disregard data coming from intermediary stages.Footnote 18 Denote \(\mathbbm {1}_{\{\text {Early}\}}\) the dummy variable equal to 1 in early games and to 0 in late games. Under the identifying assumption that learning has converged in late games, the model predicts that behavior in the experiment is described by:
which is the structural form of a Probit model on the individual decision to cooperate. This probability results from equilibria of the cutoff form involving the primitives of the model. Denoting \(\varepsilon _{it}\) observation specific unobserved heterogeneity, \({\varvec{\theta }}\) the vector of unknown parameters embedded in the above equation, \({\varvec{x}}_{it}\) the associated set of observables describing participant i experience up to t and \(C^*_{it}\) the latent function generating player i willingness to cooperate at match t, observed decisions inform about the model parameters according to:
The structural parameters govern the latent equation of the model. Our empirical test of the model is thus based on estimated coefficients, \({\varvec{\theta }}=\frac{\partial C^*}{\partial {\varvec{x}}_{it}}\), rather than marginal effects, \(\frac{\partial C}{\partial {\varvec{x}}_{it}}={\varvec{\theta }} \frac{\partial \varPhi ({\varvec{x}}_{it}{\varvec{\theta }})}{\partial {\varvec{x}}_{it}}\).
In the set of covariates, both current (\(\mathbbm {1}_{\{F_{it}=1\}}\)) and past enforcement (\(\mathbbm {1}_{\{F_{it-1}=1\}}\)) are exogenous by design. The partner’s past decision to cooperate, \(C_{jt-1}\), is exogenous to \(C_{it}\) as long as player i and j have no other player in common in their history. Moreover, due to the rematching of players from one match to the other, between subjects correlation arises over time within an experimental session. We address these concerns in three ways. We include the decision to cooperate at the first stage of the first match in the set of control variables, as a measure of individual unobserved ex ante willingness to cooperate. To further account for the correlation structure in the error of the model, we specify a panel data model with random effects at the individual level, control for the effect of time thanks to the inclusion of the match number, and cluster the errors at the session level to account in a flexible way for within sessions correlation.
Table 3 reports the estimation results from several specifications, in which each piece of the model is introduced sequentially. The parameters of interest are the learning parameters \( \varLambda _{k,l}, k \in \{0,1 \}, l \in \{C,D \}\).Footnote 19 Columns (1) and (2) focus on the effect of past and current enforcement. While we do not find any significant change due to moving from early to late games per se (the Early variable is not significant), the effect of current enforcement on the current willingness to cooperate is much weaker in early games. This is consistent with participants becoming less confident that the group is cooperative, thus less likely to cooperate, as time passes—i.e., prior belief over-estimate the average cooperativeness of the group. The disciplining effect of current fines is thus stronger in late games.
Column (3) introduces learning parameters. As stressed above, the learning parameters play a role before beliefs have converged. They are thus estimated in interaction with the Early dummy variable. Once learning is taken into account, enforcement spillovers turn-out significant. More importantly, the model predicts that learning is stronger when observed decisions are more informative about societal values, which in turn depends on the enforcement regime under which behavior has been observe: cooperation is more informative about cooperativeness under weak enforcement, while defection is stronger signal of non-cooperative values under strong enforcement. This results in a clear ranking between learning parameters—see Eq. (7). We use defection under weak enforcement as a reference for the estimated learning parameters. The results show that cooperation under weak enforcement (\(\text {Early}\times {C_0}\)) leads to the strongest increase in the current willingness to cooperate. Observing this same decision but under strong enforcement institutions rather than weak ones (\(\text {Early}\times {C_1}\)) has almost the same impact as observing defection under strong institutions (the reference): in both cases, behavior is aligned with the incentives implemented by the rules and barely provides any additional insights about the distribution of values in the group. Last, defection under strong institutions (\(\text {Early}\times D_0\)) is informative about a low willingness to cooperate in the group, and results in a strongly significant drop in current cooperation.
Column (4) adds indirect spillovers, induced by the cooperation of the partner in the previous game. The identification of learning parameters in this specification is quite demanding since both past enforcement and past cooperation are included as dummy variables. We nevertheless observe a statistically significant effect of learning in early games, with the expected ordering according to how informative the signal delivered by a cooperative decision is, with the exception of \(C_1\)—i.e., when cooperation has been observed under fines. Finally, column (5) provides a robustness check for the reliability of the assumption that learning has converged in late games. To that end, we further add the interaction between observed behavior from partner in the previous game and the enforcement regime. Once learning has converged, past behavior is assumed to affect the current willingness to cooperate through indirect spillovers only. Absent learning, this effect should not interact with the enforcement rule that elicited this behavior. As expected, this interaction term is not significant: in late games, it is cooperation per se, rather than the enforcement regime giving rise to this decision, that matters for current cooperation.
Appendix 3: Replication of the statistical analysis on the full sample
In this section, we replicate the results on the full sample of observations: instead of restricting the analysis to the working sample made of decisions consistent with the subset of repeated-game strategies described in Sect. 2.2, we include all available observations. As already mentioned in the text, the matches we exclude from the working sample all appear in late games so that Fig. 2a is not affected by the choice of the working sample. Figure 5 below replicates Fig. 3 in the paper; and Table 4 replicates Table 2. In both instances, the data is more noisy but the qualitative conclusions all remain the same.
Appendix 4: Replication of the main results with bootstrapped standard errors
As explained in the main text, the statistical analysis presented in Table 2 clusters the standard errors at the session level, so as to take into account in a flexible way the possible correlations between subjects due to random rematching of subjects within pairs. While this approach is conservative (since it does not impose any structure on the correlation between subjects over time), the number of clusters is small and there is a risk of small sample downward bias in the estimated standard errors. Table 5 provides the results from a robustness exercise replicating Table 2 in the text with bootstrapped standard error based a delete-one jackknife procedure (see Bell & McCaffrey, 2002; Cameron et al. 2008).
Appendix 5: Proofs
1.1 Proof of Proposition 1
As derived in the main text, if an equilibrium exists, it is necessarily such that players use cutoff strategies. Reexpressing characteristic Eq. (2), we can show that the cutoffs are determined by the equation \(g(\beta ^{*} [F_{it}])=0\), where g is given by
The function g has the following properties: \(g(x)>0\) when x converges to \(-\infty \) and \(g(x)<0\) when x converges to \(+\infty \). Thus, since g is continuous, there is at least one solution to the equation \(g(\beta ^{*} [F_{it})]=0\). At least one equilibrium exists.
If g is non monotonic, there could exist multiple equilibria. However, in all stable equilibria, \(\beta ^{*}\) is such that g is decreasing at \(\beta ^{*}\), i.e.,
Using the implicit theorem we have:
where \(\phi _{H}\) is the density corresponding to distribution \(\varPhi _{H}\). For stable equilibria, the denominator is negative as shown in (8), so that overall
Similarly,
Again, in stable equilibria the denominator is negative by (8). Furthermore we have \( \frac{\partial \varPhi _{H} \left[ \beta ^{*} \right] }{\partial \mu _{H}}<0\) since an increase in the mean of the normal distribution decreases \(\varPhi _{H} \left[ x \right] \) for any x. Overall we get
1.2 Proof of Lemma 1
We first show the result: \(q_{i2} (1,D)< q_{i2} (0,D) < q_{0}\). According to Baye’s rule, the belief that the state is H following a deviation by the partner in the first match (which has been played with a fine) is:
Furthermore, since \(\varPhi _{L} \left[ \beta ^{*}(1) \right] > \varPhi _{{H}} \left[ \beta ^{*}(1) \right] \), we have \(q_{i2} (1,D) {<} q_{0}\). Similarly we have:
Thus,
Using the fact that \( \frac{\varPhi _{L} \left[ x \right] }{\varPhi _{H} \left[ x \right] }\) is decreasing in x as shown in Property 1 below, and the fact that in stable equilibria, we have \( \beta ^{*}(1) \le \beta ^{*}(0)\), as shown in Proposition 1, implies directly that \(q_{i2} (1,D) < q_{i2} (0,D)\). The proof that \(q_{i2} (0,C)> q_{i2} (1,C) > q_{0}\) follows similar lines.
Property 1
\( \frac{\varPhi _{H} \left[ x \right] }{\varPhi _{L} \left[ x \right] }\) is increasing in x.
Proof
Denote \(\phi _{H}\) (resp. \(\phi _{L}\)) the density of \(\varPhi _{H}\) (resp. \(\varPhi _{L}\)). Given that \(\phi _{H}\) (resp. \(\phi _{L}\)) is the density of a normal distribution with standard deviation \(\sigma \) and mean \(\mu _{H}\) (resp. \(\mu _{L}\)), it is the case that:
Thus \(\frac{\phi _{H} }{\phi _{L}}\) is increasing in x. In particular for \(y<x\), we have: \(\phi _{H} \left[ y \right] \phi _{L} \left[ x \right] < \phi _{L} \left[ y \right] \phi _{H} \left[ x \right] \). By definition, \(\varPhi _{s} (x) = \int _{-\infty }^{x} \phi _{s} (y) dy\). Integrating with respect to y between \(-\infty \) and x thus yields:
Consider now the function \(\frac{\varPhi _{H} }{\varPhi _{L}}\). The derivative of this function is given by \(\frac{\phi _{H}\varPhi _{L} - \phi _{L}\varPhi _{H} }{\varPhi _{L}^{2}}\), which is positive by Eq. (11). This establishes Property 1 that \( \frac{\varPhi _{H} \left[ x \right] }{\varPhi _{L} \left[ x \right] }\) is increasing in x. \(\square \)
1.3 Proof of Proposition D (that generalizes Proposition 2)
In the first part of the proof we assume a stationary equilibrium exists and is such that the equilibrium cutoffs are always higher without a fine in the current match \(\beta ^{*} (0,q) > \beta ^{*} (1,q) \) for any given belief q. We then derive the property on updating of beliefs. In the second part of the proof we show existence under a natural restriction on beliefs.
Part 1: We first derive the properties on updating. We have
We can express the probability that the partner \(j_{t-1}\) in match \(t-1\) cooperated, by considering all the possible environments this individual might have faced in the past, in particular what his partner in match \(t-2\), individual \(k_{t-1}\) chose:
Denote
and
Using expression (12), we have:
We then use all possible values of the vector \((F_{j_{t-1},t-2}, a_{k_{t-1},t-2}, q_{j_{t-1},t-1})\) in turn. Take such a value v for this vector and denote
We clearly have \(a<b\). Furthermore, we can write
We have \(\beta ^{*} (0,q) > \beta ^{*} (1,q) \) imply that \(\gamma ^{*} \left( 0, a_{k't-2}, q_{j't-1} \right) > \gamma ^{*} \left( 1, a_{k't-2}, q_{j't-1} \right) \). Thus, using Property 2 below, it implies that \(R(1) \ge R(0) \) and thus \(q_{it} (1, D,q_{it-1}) < q_{it} (0, D,q_{it-1})\).
Property 2
\( \frac{a + p\varPhi _{H} \left[ x \right] }{ b + p\varPhi _{L} \left[ x \right] }\) where \(b>a\) is increasing in x.
Proof
The derivative of the ratio is given by
We showed in the proof of Property 1 that: \(\phi _{H} \varPhi _{L} - \phi _{L}\varPhi _{H} >0\). Furthermore, we also showed that \(\frac{\phi _{H}}{\phi _{L}}\) is increasing and since \(a<b\) this implies: \(\phi _{H} b - \phi _{L} a >0\). Combining these two results in condition (13) establishes Property 2.\(\square \)
Part 2: We show that an equilibrium exists if we assume that a player who has belief \(q_{it}\) in match t believes that other players in match t and \(t-1\) shared the same belief \(q_{j_{t},t} = q_{k_{t},t} = q_{it}\).
If a stationary equilibrium exists, it is necessarily such that players use cutoff strategies where the cutoff is defined by:
We have:
Furthermore, we have
we assumed that a player who had belief \(q_{it-1}\) in match \(t-1\) believes that all other players in that match share the same belief \(q_{it-1}\). Under this restriction, we have \(f_{t}(q_{j't-1} | s=.) = \mathbbm {1}_{(q_{j't-1} = q_{it-1})} \)
We get a similar expression as in the proof of Proposition 2:
This implies that for each belief q, there is a system of equation equivalent to system A in the proof if Proposition 2. We thus have a solution of this system for each value q.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Galbiati, R., Henry, E. & Jacquemet, N. Learning to cooperate in the shadow of the law. J Econ Sci Assoc (2024). https://doi.org/10.1007/s40881-023-00159-x
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s40881-023-00159-x