Monetary lotteries have been playing a lead role in studies of how people should and do make decisions under risk (e.g., Arrow 1951; Allais 1953; Bernoulli 1738/1954; Edwards 1954; Ellsberg 1961; Kahneman and Tversky 1979; Savage 1954; von Neumann and Morgenstern 1947). Typically, people are asked to choose among two or more options with explicitly stated risks and rewards (e.g., “Do you prefer \(\$30\) for sure or \(\$40\) with a probability of .8?”). A decision under risk is thought to be rational if the decision-maker weighs each option’s outcomes, that is, their subjective values (utilities) by their probabilities, and chooses the option with the higher expected utility. Although expected utility theory does not specify how rational decision-makers are to achieve this goal, it is typically understood to imply that decision-makers need to process all the available information.

Complete search, however, may be unrealistic for actual decision-makers facing constraints on time and cognitive resources (Gigerenzer 2001; Hertwig et al. 2019; Simon 1955). A boundedly rational decision-maker still seeking to make the best possible decision must look for shortcuts and often—as when people use size, shape, or other visual cues to infer the distance of an object (e.g., Kleffner and Ramachandran 1992)—these shortcuts make use of environmental regularities. In risky choice, one potential regularity on display is the inverse relationship between probabilities and payoffs, or risks and rewards, which are often present in natural environments. Whether the gamble is a lottery ticket, a bet at the horse track, or a high-impact publication, the high rewards people desire are typically unlikely (Pleskac and Hertwig 2014). Note that when referring to the risk–reward relationship, we use the term ’risk’ in terms of the reward probability (more precisely, its inverse probability) and not in terms of variance among the outcomes within an option.

In the aforementioned domains, the probability of winning is usually such that the gamble is sufficiently attractive to both buyers and sellers—that is, such that the cost of buying the gamble should be offset by the expected gain. To illustrate, for a cost of \(\$2\), a casino may offer gambles of the sort \(\$5\) with \(p = .4\), \(\$10\) with \(p = .2\), or \(\$20\) with \(p = .1\) (typically with a slightly lower probability, creating a “house advantage”). Such a set of gambles in which the probabilities decrease as payoffs increase constitutes a negative risk–reward structure. Conversely, a high reward tied to a relatively high probability (e.g., \(\$20\) with \(p = .4\)) and vice versa (e.g., \(\$5\) with \(p = .1\)) would be consistent with a (probably rare) positive risk–reward structure. In an uncorrelated environment, any payoff can be teamed up with any probability.

Past research has demonstrated that in decisions under uncertainty people exploit their knowledge about such risk–reward structures. Specifically, they enlist the risk–reward heuristic to infer unknown probabilities from the magnitude of the payoffs (Leuker et al. 2018; Pleskac and Hertwig 2014), and, vice versa, also to infer payoffs from probabilities (Skylark and Prabhu-Naik 2018). Moreover, in decisions from experience people have been shown to sample less information about possible outcome distributions in decisions from experience (Hertwig 2015) when a choice environment displays the typically negative relationship between risks and rewards compared to when risks and rewards are positively related, or uncorrelated (Hoffart et al. 2018).

In decision-making under risk—that is, when both the payoffs (or outcomes) of an action and their probabilities are known (Luce and Raiffa 1957)—the risk–reward relationship may serve different functions. When evaluating options one-by-one, it allows people to detect highly desirable opportunities, that is, high-reward/high-probability options in an environment where high rewards are typically unlikely and, therefore, unexpected (Leuker et al. 2019). Our focus here is to examine how risk–reward structures may affect the processing of decisions under risk especially under circumstances that prompt a person to curtail search of available information. If a decision-maker’s time is limited, they may need to simplify their processing. Recurrent statistical regularities in the environment such as the risk–reward relationship may empower the reliance on less information: if risks and rewards are inversely related, then payoff and probability information can operate as probabilistic cues that can inform or substitute each other. Brunswik (1952) referred to this as the mutual substitutability or vicarious functioning of cues and applied it to contexts where cues are missing. Here, we extend this notion to a context in which time pressure leaves a person little choice but to process fewer pieces of information and substitutability permits an informed guess about information that can remain unattended.

1 Overview of the experiment and key hypotheses

During the study, people learned about negatively correlated, positively correlated and uncorrelated risk–reward environments in a between-participants design. Subsequently, they completed a risky choice task in which they were instructed to make either the ‘best possible’ or a ‘fast’ choice within 1.5 s (manipulated within participants) while their eye movements were tracked. The choice task consisted of two classes of gambles. Test gambles (60% of all stimuli), on which we based our analyses and computational model, were the same across the three risk–reward conditions. They included problems with EV differences of various sizes and different types of payoff–probability combinations. The structure of these gambles necessarily deviated from the risk–reward conditions people experienced in the learning phase. Environment gambles (40% of the stimuli) were constructed to be consistent (in terms of their risk–reward structure) with the gambles from the learning phase. They were intermixed with the test gambles to reinforce the condition-dependent risk–reward structure. Using this experimental design, we examined whether and how people adjust their information processing in different risk–reward environments.Footnote 1

1.1 Simplification hypothesis (H1): participants in correlated risk–reward environments simplify their information processing relative to participants in an uncorrelated environment

In environments in which probabilities and payoff are independent, both attributes are important for gauging the attractiveness of an option. Therefore, one may expect that people attend to all attributes in such environments (which has been supported in empirical studies; Fiedler and Gloeckner 2012; Manohar and Husain 2013; Pachur et al. 2013, 2018; Stewart et al. 2006). In environments in which probability and payoff information are correlated, however, people may exploit this relationship to simplify processing and ease computational demands. In the extreme, this could mean that one of the attributes (e.g., probabilities) will be completely ignored; after all, it can be inferred from the other (e.g., payoffs).

In environments in which risks and rewards are correlated, it is impossible to know, based on the observed choice alone, whether an attribute is inferred versus attended. Eye-tracking data, however, can help to discern between these two mechanisms. In a choice between two gambles of the form “p chance of winning x, otherwise nothing”, participants can inspect up to four areas of interest (AOIs)—two payoffs and two probabilities—to make their choice. Simplified processing—a possible result of vicarious functioning according to which one attribute is inferred from the other—would be indicated by a lower number of AOIs inspected per trial. Furthermore, eye-tracking data can be used to compute the average number of within-gamble transitions (between payoffs and probabilities) per condition. This type of transitions should be less frequent if people simplified their processing in correlated conditions. Last, eye-tracking data can be used to investigate the extent to which gaze is biased to either payoffs or probabilities.

1.2 Processing constraint hypothesis (H2): environment-dependent simplification is more pronounced under strong processing constraints

We hypothesized that simplified processing in correlated risk–reward environments may only, or at least more strongly, emerge when participants need to make a fast choice. Here, participants in a negative or positive risk–reward environment may ignore probability information altogether; participants in an uncorrelated risk–reward environment may handle the need to respond quickly differently—for example, by attempting to process information faster (Payne et al. 1993; Zur and Breznitz 1981). We used the same dependent variables as for the Simplification Hypothesis (H1). More expansive information processing—as expected in the uncorrelated condition—should lead to higher rates of EV maximization. Consistent with the bulk of past psychological research investigating how the structure of the environment affects processing and subsequent choice under different processing constraints, we rely on choice of the option with the higher EV as an indicator of success or accuracy in the long run (Payne et al. 1993; Pachur et al. 2017).

1.3 Exploring environment-dependent responses to processing constraints with a drift-diffusion model

Attention not only enables the decision-maker to integrate information to thus prepare a decision (Orquin and Mueller Loose 2013), it has also been found to be linked with preference for an option, with the option that is eventually chosen receiving more attention (Busemeyer and Townsend 1993; Cavanagh et al. 2014; Stewart et al. 2016; Wulff et al. 2018). Recent models assume that attention plays an active role in preference construction, such that decision-makers accumulate evidence for an option when fixating it (Krajbich et al. 2010, 2012; Krajbich and Rangel 2011). In addition to permitting to take such attentional processes into account, the drift-diffusion model (DDM) is particularly useful in our experimental setup. The imposition of time pressure typically results in lower decision thresholds as measured with the DDM (Ratcliff and McKoon 2008). We preregistered the use of a DDM in our analyses but did not specify how parameters might differ between risk–reward environments (see section “follow-up analyses” in preregistration). Consistent with the behavioral analyses, we focused on a DDM that rests on EV maximization as an indicator for long-term success. However, we also report a DDM analysis using EU maximization, thus accounting for individual risk preferences, in Supplementary Material S4.4.

In addition to these hypotheses, we preregistered a number of other hypotheses that go beyond the scope of this article. Some of them represent manipulation checks (e.g., lower proportion of EV choices under time pressure); others pertain to a comparison of the results to those in a different learning task (explicit learning).Footnote 2 A systematic test of all preregistered hypotheses is posted on the Open Science Framework.

2 Methods

2.1 Participants

A total of 92 participants (54 female, mean age = 24.73, SD = 4.25) completed the experiment (\(N_\mathrm{negative}\) = 31; \(N_\mathrm{positive}\) = 30; \(N_\mathrm{uncorrelated}\) = 31). Being unsure of effect sizes (but expecting them to be small), we set our sample size to be larger than those of previous and comparable eye-tracking studies (Glöckner and Herbold 2011; Stewart et al. 2016). We excluded one participant due to poor eye tracking. Participants were paid a fixed rate of €12 plus a bonus based on their performance in the learning phase and the choice task (€1.13–€10.04). The experiment was approved by the ethics board of the Max Planck Institute for Human Development.

2.2 Procedure

Fig. 1
figure 1

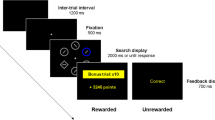
Experimental setup. a Learning phase gambles were drawn from one of three risk–reward environments. Each dot represents one learning phase gamble. b Participants learned about one of these risk–reward environments incidentally, from pricing gambles. c Participants completed a choice phase where they chose among two nondominated gambles while their eye movements were tracked. The choice phase consisted of test gambles (60%) that were identical across risk–reward conditions and were used to model the data and environment gambles (40%) that were used to reinforce the previously learned risk–reward structure. Eye-tracking analyses are based on the first screen in the choice phase, before participants indicated their choice. ‘Best’ (no time pressure) and ‘fast’ choices were made in interleaved blocks with 16 choices each

Full size image

2.2.1 Learning phase

Participants were presented with 100 gambles. For each gamble, they were asked to indicate the minimum price at which they would sell the right to play it (willingness to sell; Fig. 1b). The gambles were constructed such that across gambles, payoffs and probabilities were either correlated (negatively or positively) or uncorrelated (between participants; Fig. 1a). To motivate participants to report their true valuations of the gambles, we implemented a Becker–DeGroot–Marschak procedure (Becker et al. 1964). Specifically, ten gambles were selected at the end of the experiment and participants either played out the gamble or received their stated selling price. Participants were never explicitly asked to pay attention to the underlying risk–reward structure and learning the structure was not the central task; we, therefore, refer to this mode of learning as incidental learning (Leuker et al. 2018). Across all gambles, we used the same range for payoffs and probabilities (1–100), and defined an experimental currency, the \(E\)$(conversion rate \(100\,E\)$ = €1, disclosed in the instructions). The instructions are reported in Supplementary Material S1.

2.2.2 Choice task

In each trial of the choice task, participants chose between two nondominated monetary gambles of the form “p chance of winning x, otherwise nothing.” There were two different types of rounds: Rounds in which participants had to decide within 1.5 s (‘fast’) and rounds in which they were asked to make the best possible decision (‘best’), presented in interleaved blocks (16 choices per block). Participants received information about the upcoming block before it started (“time limit: make a fast decision” or “no time limit: make a good decision”). Participants who took longer than 1.5 s in a fast trial would loose the chance to win a bonus if that particular trial was to be played out at the end. Participants completed five practice trials both for the best and the fast trials. Across participants, we randomized the positions of the gambles on the screen and counterbalanced the location of payoffs and probabilities (top/bottom) and the order of blocks (best/fast first).

The choice task consisted of pairs of test gambles (which made up \(60\%\) of the stimuli) on the basis of which we examined our hypotheses and research questions. To ensure comparability, these gambles were identical across risk–reward conditions. In these gambles, payoffs and probabilities were uncorrelated. That is, for the two correlated conditions, the structure of the test gambles deviated from the previously learned risk–reward structures (e.g., the gamble pairs \(E\$90\) with \(p = .91\) vs. \(E\$99\) with \(p = .82\); or \(E\$2\) with \(p = .90\) vs. \(E\$12\) with \(p = .88\) appeared in each condition). The EV differences for the test gambles were approximately \(7E\) (absolute difference: Md = 7.02, IQR = 0.85–8.7, ratio larger EV gamble/smaller EV gamble: Md = 2.01, IQR = 1.26–2.69). The other gambles were environment gambles (which made up 40% of the stimuli), constructed in accordance with the risk–reward environments in Fig. 1a). These gambles served to strengthen the previously learned risk–reward structure. The same set of gambles appeared twice for each participant, once in the ‘best trials’ and once in the ‘fast trials’.

2.2.3 Estimating probabilities from payoffs

To assess how well people had grasped the risk–reward structures, we asked them to infer probabilities from payoffs following the pricing and choice tasks (see Supplementary Material S1.2 for details).

2.2.4 Eye tracking

During the choice task, we collected binocular eye position data with an EyeTribe tracker, sampled at 60 Hz. The experiment was implemented in PsychoPy 1.83.01 and the eye-tracking interface PyTribe (Dalmaijer et al. 2013). Each participant’s eye movements were calibrated using the Eyetribe UI with a nine-point grid before each task (\(<0.7\)° of visual angle). Participants were seated approximately 60cm from the screen using a chin rest affixed to the table, in a room with negligible ambient light. We preprocessed raw samples by parsing eye-tracking data into fixations and saccades (von der Malsburg 2015). Four areas of interest (AOIs) were defined as non-overlapping rectangles from the center of the screen (700 \(\times\) 500 px each). For each individual, we plotted all fixations over time to ensure that they fell into these four AOIs (corresponding to the two payoffs and two probabilities in Fig. 1b). Analyses are based on fixation data.

3 Results

We applied Bayesian generalized linear mixed models using Stan in R for regression analyses (Stan Development Team 2016). We entered “participant” as a random effect to account for individual variation beyond condition-dependent effects. We report the mean of the posterior distribution of the parameter or statistic of interest and two-sided, symmetric \(95\%\) credible intervals (CI) around each value.

3.1 Learning phase

The prices participants set for the gambles followed the EVs relatively closely and no reliable differences between risk–reward environments emerged. On average, prices exceeded the corresponding EV of the gamble by around \(7\,E\)$ (\(M_\mathrm{deviation} = 7.12\,E\)$, \(b_\mathrm{neg.} = 9.6\,E\)$, CI = \([6.7; 12.5\,E\$]\); \(b_{\mathrm{pos.}} > {\mathrm{neg.}} = -4.0\,E\)$, CI = \([-8.1,1.0\,E\$]\); \(b_{\mathrm{unc.}} > {\mathrm{neg.}} = -3.5\,E\)$, CI = \([-7.6,4.8\,E\$]\)).Footnote 3 In the payoff–probability estimation task at the end of the experiment, the estimates differed credibly across risk–reward environments, suggesting that participants learned the risk–reward structures. In general, however, all estimates were biased toward a negative risk–reward relationship (Supplementary Material S3.3).

3.2 Choice task

Across both the best and fast conditions, choices varied by the risk–reward environment that participants had been exposed to in the learning phase: participants in the negative environment were less likely to pick the higher EV option than participants in the uncorrelated environment (\(b_\mathrm{best,negative} = -\,0.35\), CI = \([-0.60, -0.11]\), \(b_\mathrm{fast,negative} = -0.23\), CI = \([-0.42, -0.03]\)). A similar pattern emerged for the positive and uncorrelated environments (regression 1 in Table 1; Fig. 2a). Figure 2b depicts the average response times in the three risk–reward environments. In best trials (left panel), participants in the negative environment responded credibly faster (\(M_\mathrm{neg.} = 2.78s\)) than participants in the uncorrelated environment (\(b_\mathrm{best,negative} = -1.10\), CI = \([-1.86, -0.34]\), regression 2 in Table 1). Although we did not formalize predictions for response-time differences, they are consistent with the observation that the higher EV option was also chosen less often in these conditions.

Fig. 2
figure 2

Behavioral (a, b) and eyetracking (c, d, e) results of the choice task. Colors indicate means and \(95\%\) highest density intervals of the posterior predictive distributions. Black triangles/circles indicate means. Posterior predictive distributions are based on a model accounting for individual variation and EV differences. Posterior predictive distributions in a are based on the median EV difference in the experiment (\(7\,E\)$), and across EV differences in the other panels. Dashed lines in c indicate the average number of areas of interest (AOIs) that can be inspected (2.5). Dashed line in e indicates an equal distribution of gaze to both payoffs and probabilities

Full size image

According to the simplification hypothesis (H1), participants in correlated environments simplify their processing relative to participants in an uncorrelated risk–reward environment. To test this hypothesis, we first examined the number of unique AOIs participants inspected in each trial (minimum 1, maximum 4). Although participants in the negative environment indeed inspected fewer attributes than participants in the uncorrelated environment, these differences were not credible (\(b_{best,negative} = -0.20\), CI = \([-0.53, 0.13]\), \(b_{fast,negative} = -0.03\), CI = \([-0.42, 0.36]\), regression 3 in Table 1).

Table 1 Overview of regression models for processing and choice. Reference group set for environment: “uncorrelated”. Models included a random effect for “participant.” Coefficients are the mean and the 95% credible intervals of the posterior distributions. Credible differences in bold
Full size table

As a second indicator for simplified processing, we determined the number of within-gamble transitions: if participants in the correlated environment inspected fewer attributes because they inferred one attribute from the other and thus ignore one of them, there should be fewer within-gamble transitions in these relative to the uncorrelated environment. This was indeed the case for the negative condition, but again the differences were not credible (\(b_\mathrm{best,negative} = -\,0.30\), CI = \([-0.79, 0.26]\), \(b_\mathrm{fast,negative} = -0.05\), CI = \([-0.21, 0.10]\), regression 4 in Table 1).Footnote 4 We did find a reliable difference in how participants in the three risk–reward conditions distributed their gaze across the options: whereas in the uncorrelated environment, participants distributed their gaze quite evenly across payoffs and probabilities (i.e., proportion of gaze on payoffs = .5), gaze was reliably biased towards payoffs in both correlated environments. This was the case in both best and fast trials (regression 5 in Table 1).

In sum, the most extreme manifestation of the simplification hypothesis (H1)—namely that participants in correlated environments ignore one attribute (either payoff or probability information) because it can be inferred from the other attribute—can clearly be rejected. We obtained some indications for processing differences, but they were rather small and not all of them were credible.

The processing constraints hypothesis (H2) predicted that indications for simplification in processing in the correlated conditions would be more pronounced in the fast relative to the best condition. As panels C–D in Fig. 2 indicate, this hypothesis can be rejected: processing constraints had a similar effect on processing in all three risk–reward conditions. Last, linking process data to choice data, consistent with prior research (Payne et al. 1988), the higher EV option was chosen more frequently the more attributes were inspected, but only in best trials (\(b_\mathrm{AOI,best} = 0.13\), CI = [0.06, 0.21], regression 6 in Table 1).

4 A computational model of attention, response times, and choice

Although the eye-tracking data showed hardly any support for the simplification hypothesis and processing constraint hypothesis, there were some indications for environment-dependent process simplification. Specifically, in the negatively correlated environment participants made faster choices and decreased EV maximization compared to the other conditions. Using a drift-diffusion model (DDM) analysis, we explored the mechanisms that might give rise to this pattern. As preregistered in our follow-up analyses, we tested how choice mechanisms may differ across different risk–reward conditions and processing constraints by fitting an extended DDM to the data (Fig. 3). According to DDMs (Busemeyer and Townsend 1993; Krajbich et al. 2010; Pleskac et al. 2015, 2019b), preference accumulates over time: as people consider which gamble to choose, they accumulate evidence for or against each option. Once preference for an option reaches a threshold, people choose accordingly. How far apart people set these thresholds determines how quickly they reach a decision: the closer they set the thresholds, the less time they will take to reach a decision, but the more error prone their choices will be (e.g., fail to choose the gamble with the higher value).

Fig. 3
figure 3

Depiction of the DDM and conditions for which parameters were estimated. We set the bias parameter z to .5 because participants cannot be biased to either the higher or lower EV option before inspecting it. In the best-fitting DDM (see Table 2), the drift rate was a function of individual differences in ability/effort to detect the higher EV option (intercept), an EV coefficient \(\beta _\mathrm{EV}\) measuring how much the use of EV differences contributed to the drift rate, and a gaze coefficient \(\beta _\mathrm{gaze}\) measuring how much gaze differences or biases contribute to choice. In this model, the interaction between value and gaze, \(\beta _{\mathrm{EV}} \times {\mathrm{gaze}}\), was 0

Full size image

4.1 DDM parameters

Our extended DDM has several free parameters. The nondecision time parameter \(\tau\) models the part of the response time that is unrelated to the processing of the option itself, such as motor time. The threshold separation parameter \(\alpha\) denotes response caution. The parameter \(\alpha\) should be relatively high when the goal was to make the best choice and relatively low when the goal was to make a fast choice. Finally, the drift rate \(\delta\) is a measure of the change in accumulated evidence at each unit in time, with \(-\infty< \delta < \infty\). The sign of the drift rate indicates the average direction of the incoming incremental change in preference, with positive values indicating preference in favor of the higher EV option. Prior research has identified two critical factors that determine how people accumulate information when making preferential choices: the value of the options and gaze or differences in gaze to the alternatives (Cavanagh et al. 2014; Krajbich et al. 2012; Stewart et al. 2016). To accommodate these findings, we parameterized the drift rate to be a function of these two variables, summarized in the parameters \(\beta _\mathrm{EV}\) and \(\beta _\mathrm{gaze}\). Positive values indicate that EV differences or gaze differences, respectively, reliably impact the drift rate. In one model, we allowed for an interaction effect between gaze and EV differences as a part of the drift rate (\(\beta _{\mathrm{gaze}} \times {\mathrm{EV}}\)). Positive values indicate a reliable interaction between gaze and value. For each \(\beta\) coefficient, higher values indicate stronger impact. We used a model comparison, described next, to identify the best formulation of these two variables to account for the data.

4.2 Model comparison and model estimation

To identify how these factors determine the drift rate, we conducted a model comparison among four models. The drift rate in all four models was parameterized using the following equation:

$$\begin{aligned} \delta = \,&\beta _{0} \, + \beta _\mathrm{EV} \, (\mathrm{EV}_\mathrm{higher}-\mathrm{EV}_\mathrm{lower}) \\&+ \beta _\mathrm{gaze}\,(\mathrm{gaze}_\mathrm{higher}-\mathrm{gaze}_\mathrm{lower}) \\&+ \beta _{\mathrm{EV} \times \mathrm{gaze} }\,((\mathrm{gaze}_\mathrm{higher}\times \mathrm{EV}_\mathrm{higher})-(\mathrm{gaze}_\mathrm{lower} \times \mathrm{EV}_\mathrm{lower})). \end{aligned}$$

In DDM 1, the drift rate was solely a function of the EV differences and thus ignored gaze differences (\(\beta _\mathrm{gaze} = \beta _{\mathrm{EV}} \times {\mathrm{gaze}} = 0)\). DDM 2 only accounted for gaze differences on the drift rate and thus ignored EV differences (\(\beta _\mathrm{EV} = \beta _{\mathrm{EV}} \times {\mathrm{gaze}} = 0)\). DDM 3 accounted for both gaze and EV differences in an additive manner (\(\beta _{\mathrm{EV}} \times {\mathrm{gaze}} = 0)\). DDM 4, the full model accounted for both gaze and EV differences in an additive manner and, in addition, permitted for an interaction between gaze and value.Footnote 5

We estimated all four models using the observed distributions of choices and response times using a Bayesian hierarchical implementation (Vandekerckhove et al. 2011; Wabersich and Vandekerckhove 2014). Table 2 compares the deviance information criteria (DIC; Spiegelhalter et al. 2002) for these four models, indicating that DDM 3 (Fig. 3) provided the best fit.

Table 2 Deviance information criteria (DIC) for four different formalizations of the drift-diffusion model using the gamble with the higher expected value at the threshold. Lower DIC indicates better fit. Best-fitting model (DDM 3) in bold
Full size table

Further details including posterior predictive checks can be found in Supplementary Material 4.3. The models reported here focus on EV maximization as a common indicator for the success—or accuracy—of the decisions in the long run (also see Payne et al. 1988, 1993). However, we also investigated the extent to which our conclusions are robust after accounting for individual differences in risk preferences. We did so by first fitting a utility model—with a risk aversion parameter per person and separately for conditions with and without time pressure (see Saqib and Chan 2015; Pahlke et al. 2011)—to the data to determine which gamble offered the higher subjective utility for a person on a given trial (e.g., a risk averse person may prefer a gamble offering \(30\,E\) with \(p = 1.0\) to a gamble offering \(40\,E\) with \(p = .8\) even though the latter gamble offers a higher expected value). Consistent with the EV-based analysis reported here, DDM 3, in which the drift rate was an additive function of the value differences and the gaze differences, provided the best fit to the data (see Supplementary Material 4.5).

4.3 Parameter estimates

Figure 4 displays the group-level estimates for the nondecision time \(\tau\), threshold separation \(\alpha\), and the two coefficients that determined the drift rate—the EV coefficient \(\beta _\mathrm{EV}\) and the gaze coefficient \(\beta _\mathrm{gaze}\) for DDM 3 (Fig. 3).

4.3.1 Nondecision time (\(\tau\))

As Fig. 4b shows, nondecision times were higher in best than in fast trials (\(M_\mathrm{best.>fast.} = 0.19\) [0.07, 0.31]), and there were no reliable differences between risk–reward environments.

4.3.2 Threshold (\(\alpha\))

Consistent with response times, the threshold separation was credibly higher in the best (\(M_\mathrm{best} = 1.44\) [1.27, 1.60]) compared to the fast trials (\(M_\mathrm{fast} = 1.80\) [1.20, 2.30]). In fast choices, boundaries are often hit by mistake and this leads to lower proportions of EV-maximizing choices. Moreover, when best choices were emphasized, consistent with the behavioral data, participants in the negative environment set a lower threshold than participants in the uncorrelated environment (\(M_\mathrm{neg.>unc.} = -0.56\)\([-.86,-.24]\)). This was not the case in the fast condition, nor was it the case in both positive and uncorrelated environments (Fig. 4a).

Fig. 4
figure 4

Parameter estimates for the winning model (additive value and gaze). Group means and 95% highest density intervals of the posterior distributions

Full size image

4.3.3 EV coefficient (\(\beta _\mathrm{EV}\))

Figure 4c shows that the EV coefficient exceeded 0 in all conditions, indicating that EV differences between the gambles in a choice problem impacted the drift rate. Moreover, the figure shows that this impact was similar in best and fast trials. If anything, the influence of EV differences was slightly more important in the fast compared to the best trials—but also note the larger highest density interval, suggesting that the EV coefficient was more variable between individuals in the fast conditions. There were no differences in the EV coefficient across risk–reward environments.

4.3.4 Gaze coefficient (\(\beta _\mathrm{gaze}\))

As shown in Fig. 4d, the gaze coefficient was somewhat higher in the fast than in best trials, indicating a stronger impact of differences in gaze between the options in a choice problem on the drift rate. This difference, however, was not credible. Gaze contributed weakly, and not credibly, to the drift rate in the uncorrelated environment (\(M_\mathrm{unc.} = 0.05\)\([-0.02,0.14]\)). In both the negative and the positive environments, by contrast, the gaze coefficient exceeded 0, as well as the gaze coefficient estimated for the uncorrelated environment (best: \(M_\mathrm{neg.>unc.} = 0.20\) [0.05, 0.37], fast: \(M_\mathrm{neg.>unc.} = 0.27\) [0.10, 0.45]; best: \(M_\mathrm{pos.>unc.} = 0.24\) [0.04, 0.45], fast: \(M_\mathrm{pos.>unc.} = 0.28\) [0.02, 0.51], Fig. 4d). This suggests that gaze played a role in preference formation in the correlated, but not in the uncorrelated environment; this echoes the differences between the correlated and uncorrelated environments in participants’ distribution of attention across the options (also see Fig. 2e).

5 Discussion and conclusion

We investigated how risk–reward structures impact attentional processes in decisions under risk under different processing constraints. We found no evidence for the simplification hypothesis, according to which people may, in the most extreme case, completely ignore one of the attributes (e.g., probabilities) because it can be inferred from the other (e.g., payoffs). If anything, participants who learned the risk–reward relationship to be negative simplified their processing gradually: when participants were instructed to make the best possible choice, the experience of a negative relationship appeared to trigger faster responses. Moreover, participants in correlated risk–reward environments shifted their attention to payoffs rather than probabilities. Participants in the uncorrelated environment took more time and distributed their attention relatively evenly across attributes. In contrast to the processing constraint hypothesis, there was no evidence that people exploited risk–reward structures to simplify their processing when processing constraints were high. We also explored possible environment-dependent responses to processing constraints using an extended drift-diffusion model. Results showed that all participants set similarly low decision thresholds in the fast conditions. In the best conditions, participants in the negative risk–reward environment set lower decision thresholds than participants in an uncorrelated or positive risk–reward environment, at the cost of choosing the higher EV option less often. The gaze coefficient derived from the diffusion model also suggests a higher impact of differences in gaze between the options on evidence accumulation in the correlated compared to the uncorrelated environments.

Since choices were between two nondominated options, participants who used simpler processing strategies still paid a “simplification premium”—that is, they chose the higher value option less frequently. This cost occurs because people can only maximize EV choices and simultaneously rely on noncompensatory processing strategies in environments with dominated options (Payne et al. 1988). People in the negative risk–reward environment may have been well aware that searching less may compromise the chances to find and select the objectively better option; but when attention and time are scarce resources, people may still simplify their processing when they believe that environments allow them to do so and the marginal benefits of searching more are subjectively low.

To control for EV differences, the majority of gambles in the choice phase was identical across risk–reward environments, and necessarily mismatched the previously learned risk–reward environment (e.g., the common gambles included gamble pairs with high payoffs/high probabilities—these are unexpected in an environment in which risks and rewards are otherwise inversely related). Thus, the differences we found between the conditions in people’s choices are due to their priors about a risk–reward environment—the risk–reward environment they assume or have been exposed to previously.

More generally, consistent with earlier research (Krajbich et al. 2010, 2012; Krajbich and Rangel 2011; Zeigenfuse et al. 2014), we found evidence that gaze plays a role in preference formation. Specifically, using a drift-diffusion model in which the drift rate was determined by both value differences and gaze differences outperformed both a model that only relied on value differences and a model that only relied on gaze differences. As mentioned before, parameter estimates of the best-performing model also revealed that gaze played a greater role in preference formation in the correlated environments compared to the uncorrelated environment.

In sum, many insights about decision-making under risk have been derived from laboratory studies with uncorrelated risks and rewards—while the world is full of negatively correlated risks and rewards (Pleskac et al. (2019a), in press). Our work shows that different environmental structures can impact processes in decision-making under uncertainty (Leuker et al. 2018), but also to some extent in decision-making under risk. In this case, if risks and rewards in a choice environment are assumed to be uncorrelated, people may exert more effort and make more EV-maximizing choices than when they are assumed to be unrelated. Thus, the decision processes commonly triggered in the laboratory may be different from those people use in real-world domains, where negative risk–reward relationships dominate.